Pipelined Dynamic Scheduling of Big Data Streams
Abstract
1. Introduction
- It does not offer optimality in terms of throughput;
- It does not take into account the resource (memory, CPU, bandwidth) requirements/availability when scheduling;
- It is unable to handle cases in which system changes incur.
2. Related Work
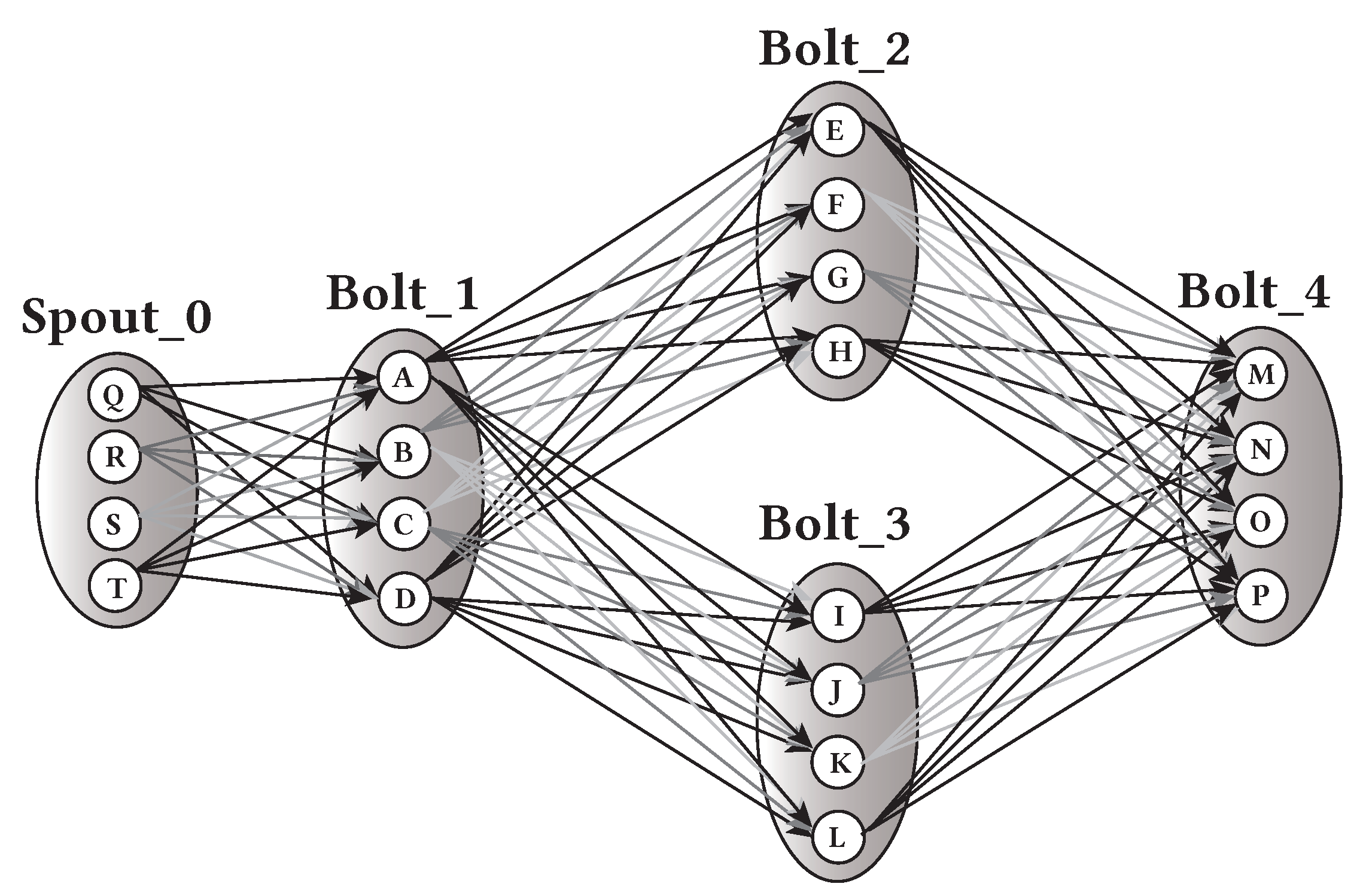
3. A Motivating Example
- It reduces the buffering space required by each task, and the system’s throughput therefore increases (most of the tuples are processed as soon as they arrive at the processing node);
- Load balancing is achieved (each node receives from only one node at each communication step, and thus lower communication latencies are achieved (no links are overloaded—instead, all links are equally loaded); and
- The scheduling procedure has a log complexity.
4. Mathematical Background
- The maximum number of classes that exist in a redistribution problem is g;
- There may be two or more classes with the same value of c. This means that our communication schedule, which requires each node to send or receive tuples only from one node at a time, can freely mix elements from two or more such classes, which can also be considered homogeneous between them.
5. The PMOD Scheduler
- 1.
- Each node receives tuples from only one other node. In other words, each node’s tasks receive tuples previously processed by the tasks of only one other node. The communicating tasks are defined by the application’s topology.
- 2.
- Load balancing is achieved.
- 3.
- The overall communication schedule is simple and fast, as it has to be implemented during runtime.
5.1. Transforming the Class Table into a Scheduling Matrix
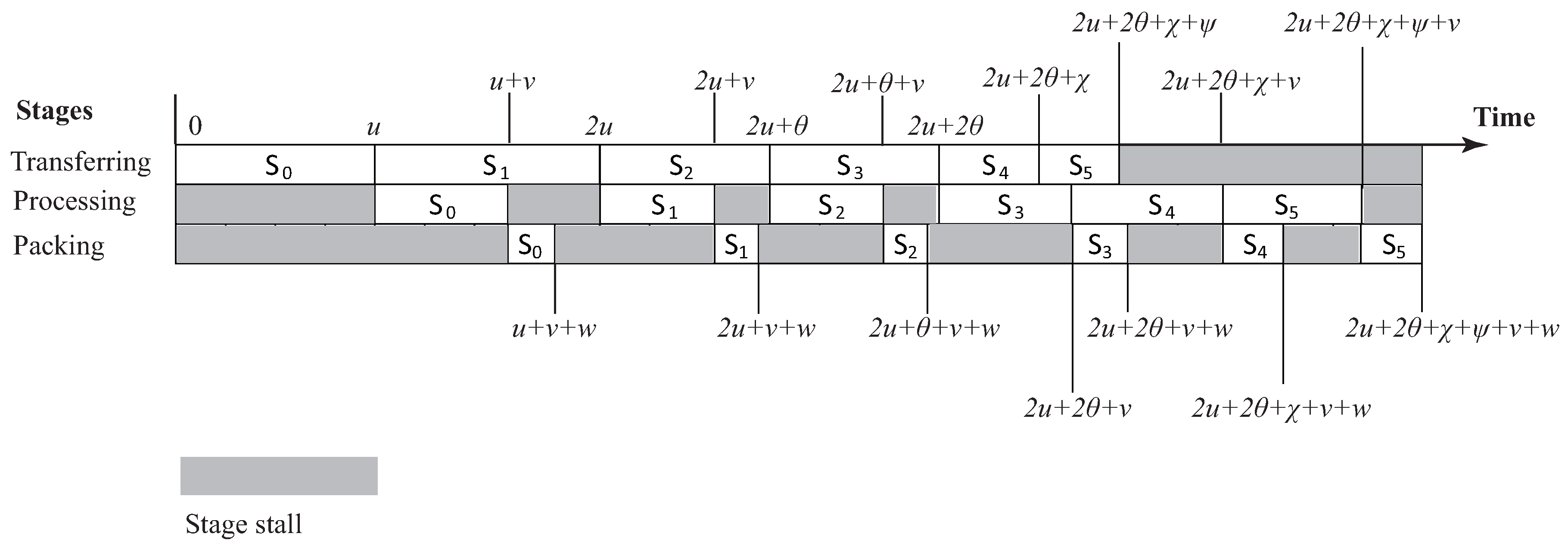
5.2. Pipelined Scheduling
5.3. Putting the Ideas Together
| Algorithm 1: MOD Scheduler |
| input: An application graph organized in spouts/bolts of t tasks |
| A cluster of N nodes |
| Changes in t or N or both, during runtime |
| output: A dynamic pipelined scheduler, , with reduced overall cost |
| 1 begin |
| 2 Read parameter changes, that is, new values of t and N |
| 3 Define the distributions and |
| 4 Solve Equation (9) to Find all the classes k and produce the Class Table (CT) |
| 5 //Step 1: Transform CT into a Single Index Matrix (SIM) |
| 6 For each node pair in row k, |
| 7 place the q value to columnn n |
| 8 end For; |
| 9 // Step 2: Mix Class Elements to Produce the Scheduling Matrix () |
| 10 Interchange elements of homogeneous classes, that reside in corresponding columns. |
| 11 The rows of the correspond to communicating steps between the system’s nodes |
| 12 |
| 13 Read the application DAG and define all the communications between components. |
| 14 Define the three pipeline stages (transferring, processing, and packing) |
| 15 |
| 16 // Organize the three operations in a pipeline fashion: |
| 17 Repeat |
| 18 // Stages S1-S2 are simultaneous and correspond to transferring, processing, packing: |
| 19 S1. Let the transferring stage hardware implement communication step k |
| 20 S2. If , let the processing stage hardware process the data from step |
| 21 S3. If , let the packing stage hardware pack data from step |
| 22 Increment k by one and repeat the simultaneous stages S1-S3. |
| 23 Until all the communications from k communication steps are implemented. |
| 24 If more streams are left unprocessed, go to line 15 and re-execute the pipeline stages. |
| 25 end; |
6. Simulation Results and Discussion
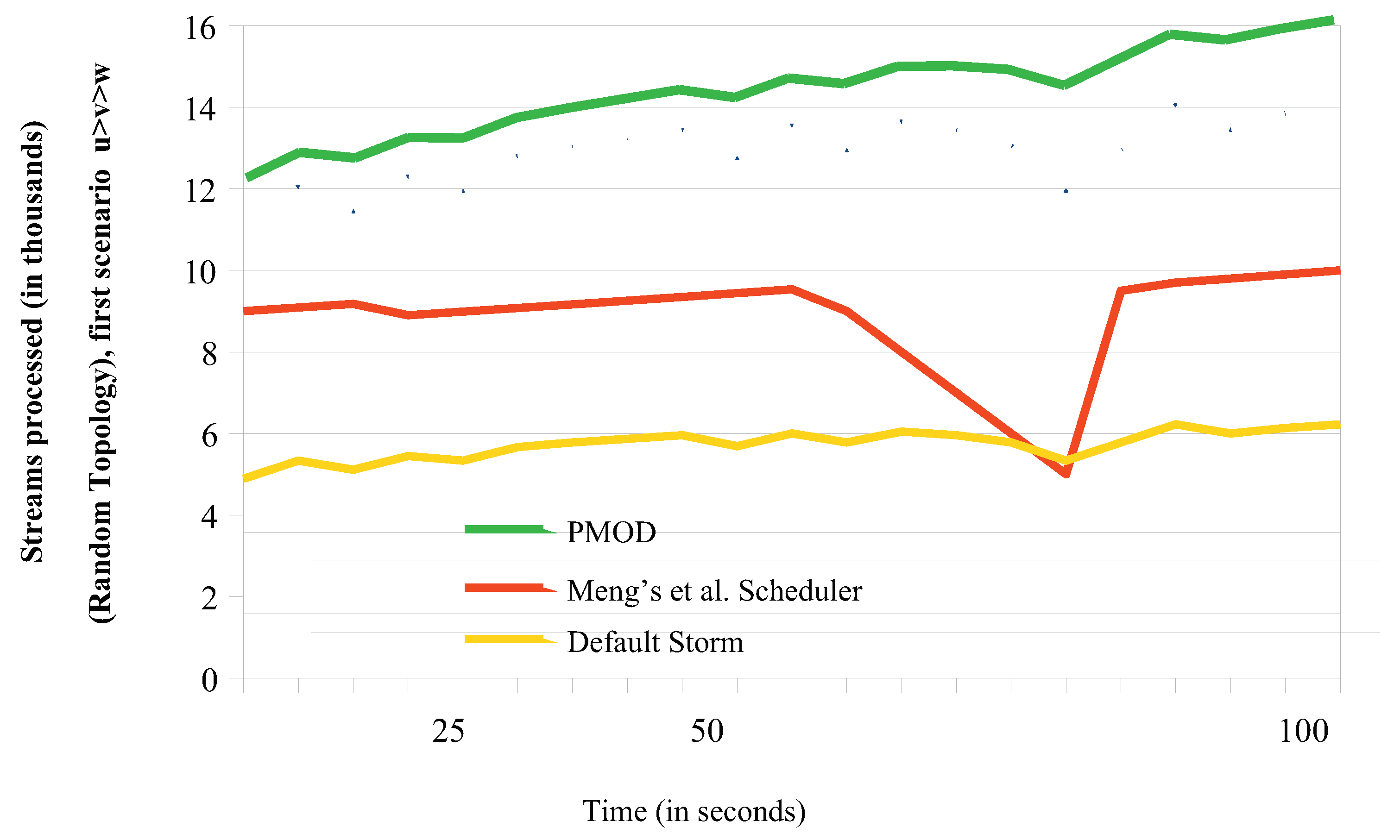
6.1. Throughput Comparisons
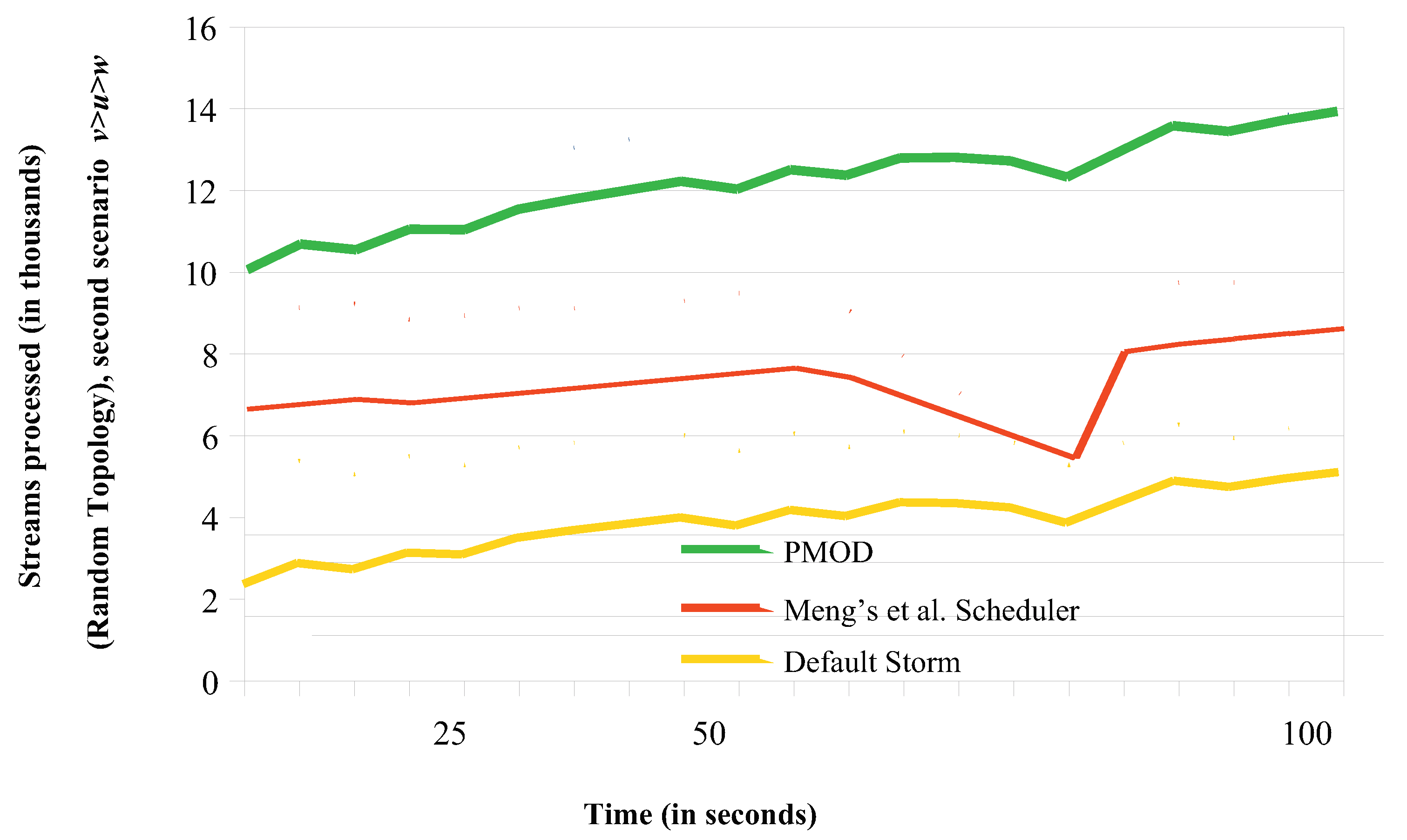
6.1.1. Throughput Comparisons for the Random Topology
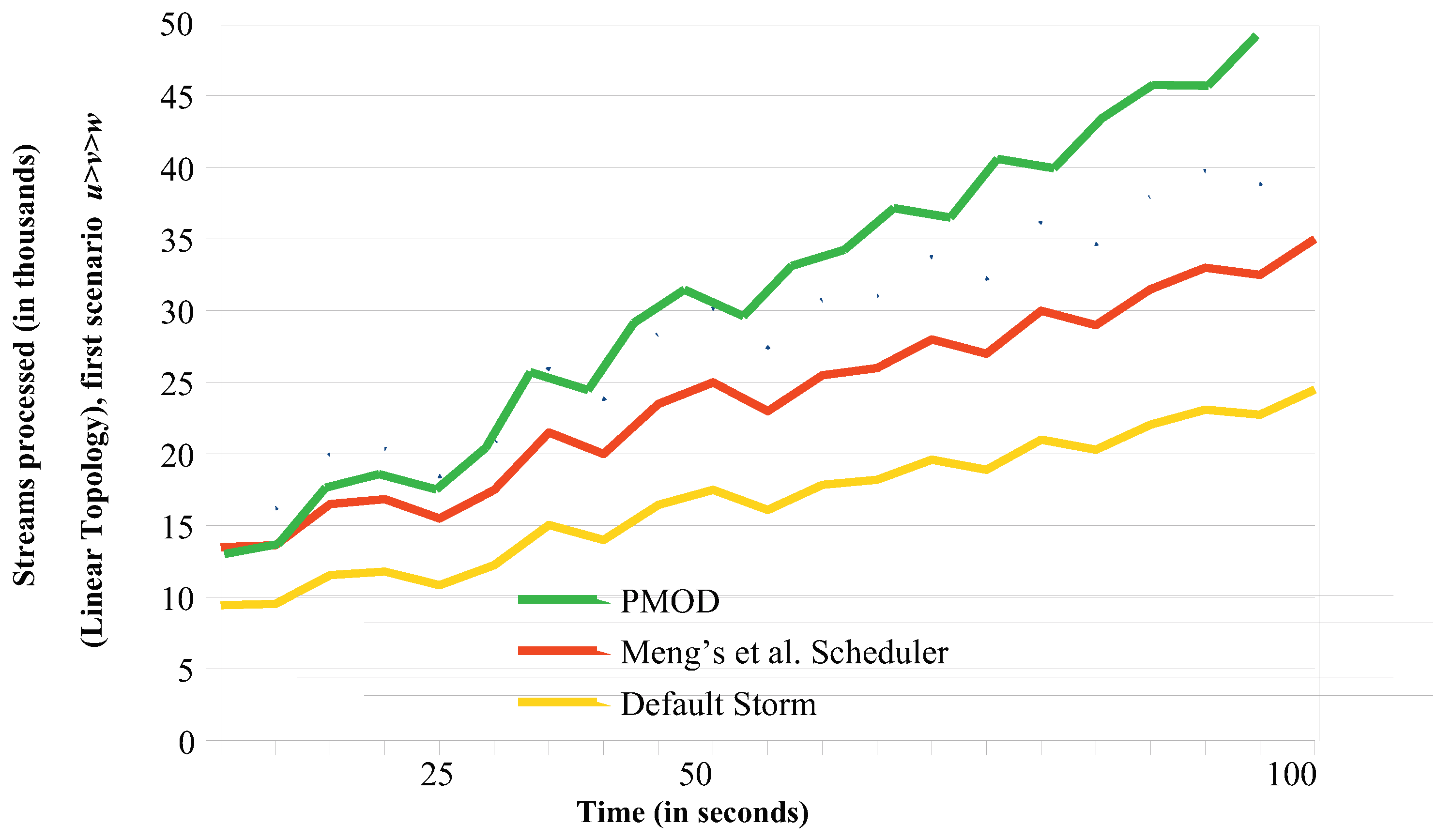
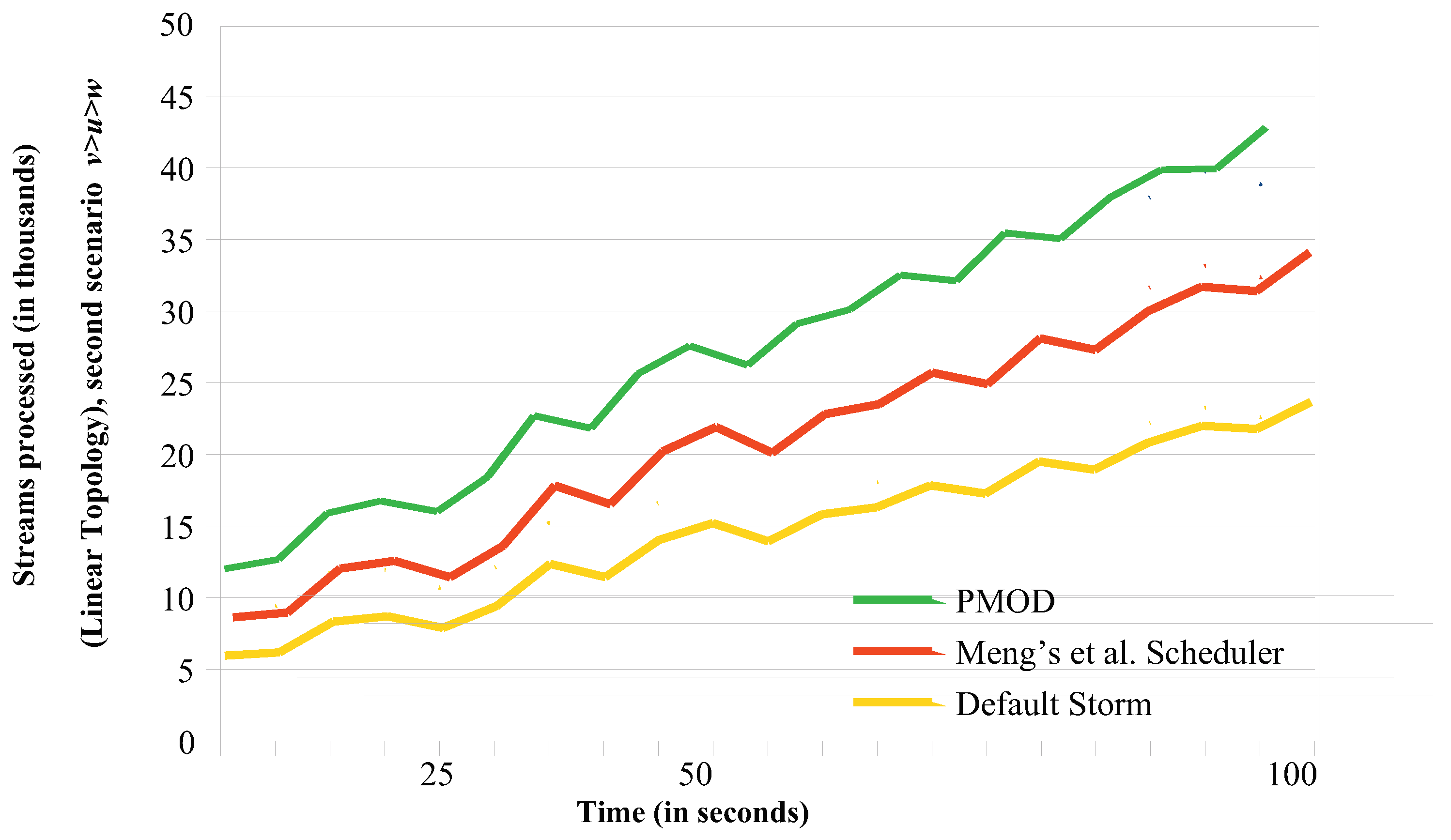
6.1.2. Throughput Comparisons for the Linear Topology
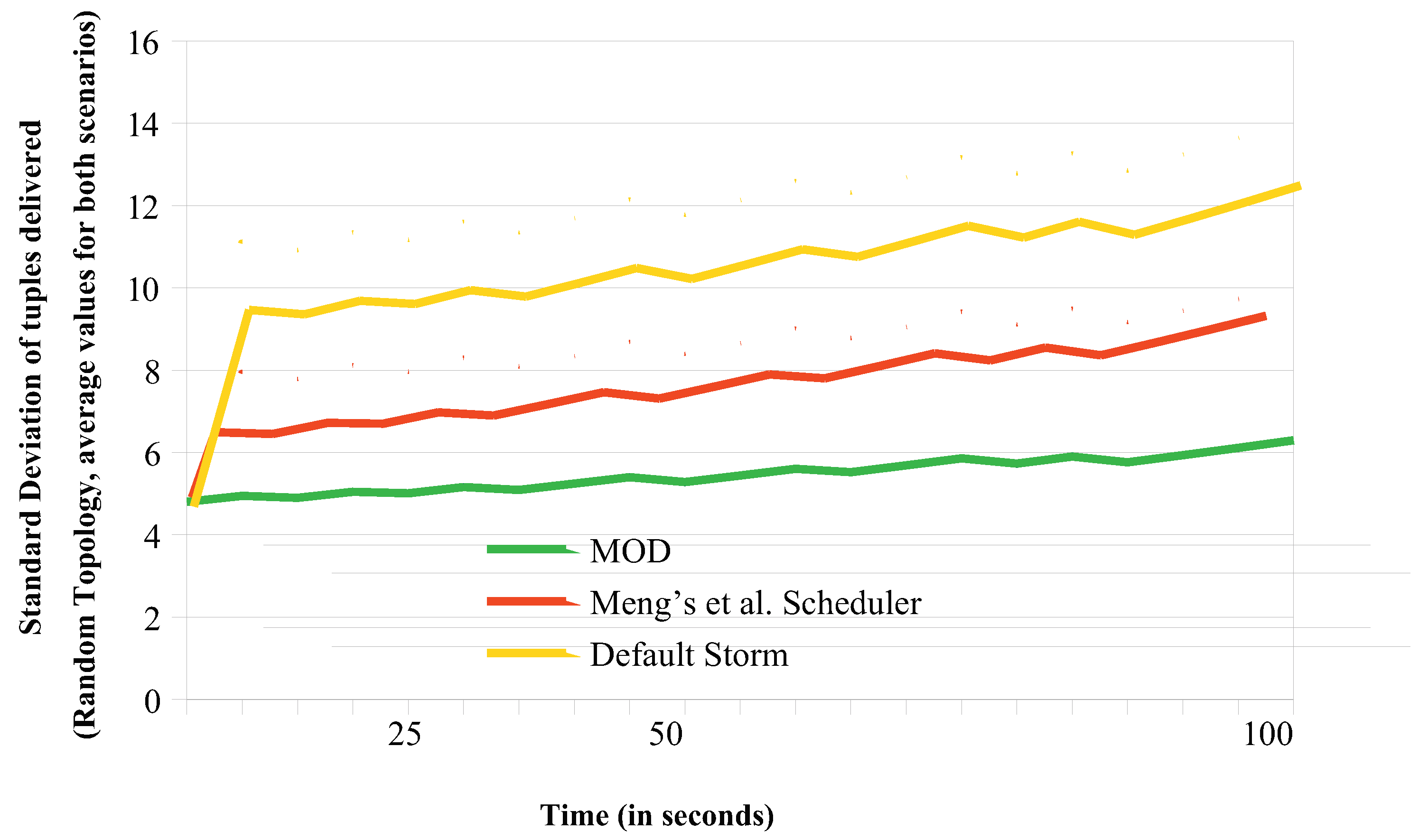
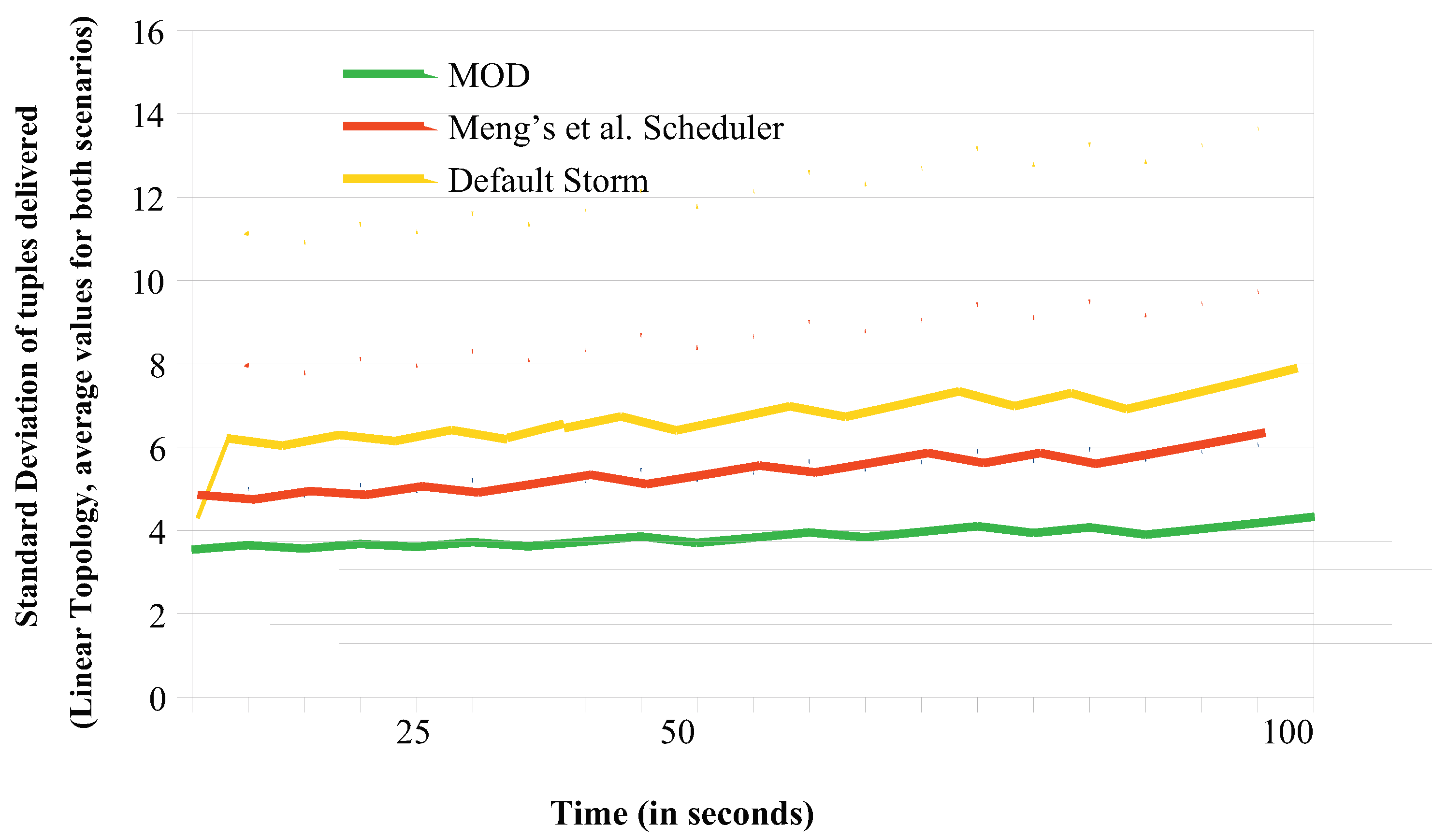
6.2. Load Balancing Comparisons
7. Conclusions—Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Tantalaki, N.; Souravlas, S.; Roumeliotis, M. A review on Big Data real-time stream processing and its scheduling techniques. Int. J. Parallel Emerg. Distrib. Syst. 2019. [Google Scholar] [CrossRef]
- Tantalaki, N.; Souravlas, S.; Roumeliotis, M.; Katsavounis, S. Linear scheduling of big data streams on multiprocessor sets in the cloud. In Ser. WI’19, Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence, Thessaloniki, Greece, 14–17 October 2019; ACM: New York, NY, USA, 2019; pp. 107–115. [Google Scholar]
- Apache Software Foundation. Apache Storm. Available online: http://storm.apache.org/ (accessed on 5 June 2019).
- Apache Software Foundation. Spark Streaming-Apache Spark. Available online: http://spark.apache.org/streaming/ (accessed on 5 June 2019).
- Apache Software Foundation. Apache Samza—A Distributed Stream Processing Framework. Available online: https://samza.apache.org (accessed on 5 June 2019).
- Apache Software Foundation. Apache Flink-Stateful Computations over Data Streams. Available online: https://flink.apache.org/ (accessed on 5 June 2019).
- Souravlas, S. ProMo: A Probabilistic Model for Dynamic Load-Balanced Scheduling of Data Flows in Cloud Systems. Electronics 2019, 8, 990. [Google Scholar] [CrossRef]
- Aniello, L.; Baldoni, R.; Querzoni, L. Adaptive Online Scheduling in Storm. In Proceedings of the 7th ACM International Conference on Distributed Event-based Systems (DEBS ’13), Arlington, TX, USA, 29 June–3 July 2013; pp. 207–218. [Google Scholar] [CrossRef]
- Eskandari, L.; Huang, Z.; Eyers, D. P-Scheduler: AdaptiveHierarchical Scheduling in Apache Storm. In Proceedings of the Australasian Computer Science Week Multiconference (ACSW ’16), Canberra, Australia, 2–5 February 2016; Article 26. p. 10. [Google Scholar] [CrossRef]
- Eskandari, L.; Mair, J.; Huang, Z.; Eyers, D. Iterative scheduling for distributed stream processing systems. In Ser.DEBS ’18, Proceedings of the 12th ACM International Conference on Distributed and Event-Based Systems, Hamilton, New Zealand, 25–29 June 2018; ACM: New York, NY, USA, 2018; pp. 234–237. [Google Scholar]
- Shukla, A.; Simmhan, Y. Model-driven scheduling for dis-tributed stream processing systems. J. Parallel Distrib. Comput. 2018, 117, 98–114. [Google Scholar] [CrossRef]
- Eidenbenz, R.; Locher, T. Task allocation for distributed stream pro-cessing. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE InternationalConference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Xiang, D.; Wu, Y.; Shang, P.; Jiang, J.; Wu, J.; Yu, K. Rb-storm: Resourcebalance scheduling in Apache storm. In Proceedings of the 2017 6th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Hamamatsu, Japan, 9–13 July 2017; pp. 419–423. [Google Scholar]
- Al-Sinayyid, A.; Zhu, M. Job scheduler for streaming applications inheterogeneous distributed processing systems. J. Supercomput. 2020. [Google Scholar] [CrossRef]
- Janssen, G.; Verbitskiy, I.; Renner, T.; Thamsen, L. Scheduling streamprocessing tasks on geo-distributed heterogeneous resources. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 5159–5164. [Google Scholar]
- Peng, B.; Hosseini, M.; Hong, Z.; Farivar, R.; Campbell, R. R-storm: Resource-aware scheduling in storm. In Proceedings of the 16th Annual Middleware Conference, Ser. Middleware ’15, Vancouver, BC, Canada, 7–11 December 2015; pp. 149–161. [Google Scholar]
- Smirnov, P.; Melnik, M.; Nasonov, D. Performance-aware schedulingof streaming applications using genetic algorithm. Procedia Comput. Sci. 2017, 108, 2240–2249. [Google Scholar] [CrossRef]
- Fu, T.Z.J.; Ding, J.; Ma, R.T.B.; Winslett, M.; Yang, Y.; Zhang, Z. DRS: Dynamic Resource Scheduling for Real-Time Analyticsover Fast Streams. In Proceedings of the IEEE 35th International Conference on Distributed Computing Systems, Columbus, OH, USA, 29 June–2 July 2015; pp. 411–420. [Google Scholar] [CrossRef]
- Cardellini, V.; Grassi, V.; Presti, F.L.; Nardelli, M. Optimal Operator Replication and Placement for Distributed Stream Processing Systems. ACM Sigmetrics Perform. Eval. 2017, 44, 11–22. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Z.; Tang, J.; Su, S. T-Storm: Traffic-AwareOnline Scheduling in Storm. In Proceedings of the 2014 IEEE 34th International Conference on Distributed Computing Systems (ICDCS ’14), Madrid, Spain, 30 June–3 July 2014; pp. 535–544. [Google Scholar] [CrossRef]
- Chen, M.-M.; Zhuang, C.; Li, Z.; Xu, K.-F. A Task Scheduling Approach for Real-Time Stream Processing. In Proceedings of the International Conference on Cloud Computing and Big Data, Wuhan, China, 12–14 November 2014; pp. 160–167. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Yu, Y.; Qi, J.; Sun, Y. A dynamic assignment scheduling algorithm for big data stream processing in mobile Internet services. Pers. Ubiquitous Comput. 2016, 20, 373–383. [Google Scholar] [CrossRef]
- Floratou, A.; Agrawal, A.; Graham, B.; Rao, S.; Ra-masamy, K. Dhalion: Self-regulating Stream Processing. Proc. VLDB Endow. 2017, 10, 1825–1836. [Google Scholar] [CrossRef]
- Souravlas, S.; Roumeliotis, M. A pipeline technique for dynamic data transfer on a multiprocessor grid. Int. J. Parallel Program. 2004, 32, 361–388. [Google Scholar] [CrossRef]
- Souravlas, S.; Roumeliotis, M. On further reducing the cost of parallel pipelined message broadcasts. Int. J. Comput. Math. 2006, 83, 273–286. [Google Scholar] [CrossRef]
- Souravlas, S.; Roumeliotis, M. Scheduling array redistribution with virtual channel support. J. Supercomput. 2015, 71, 4215–4234. [Google Scholar] [CrossRef]
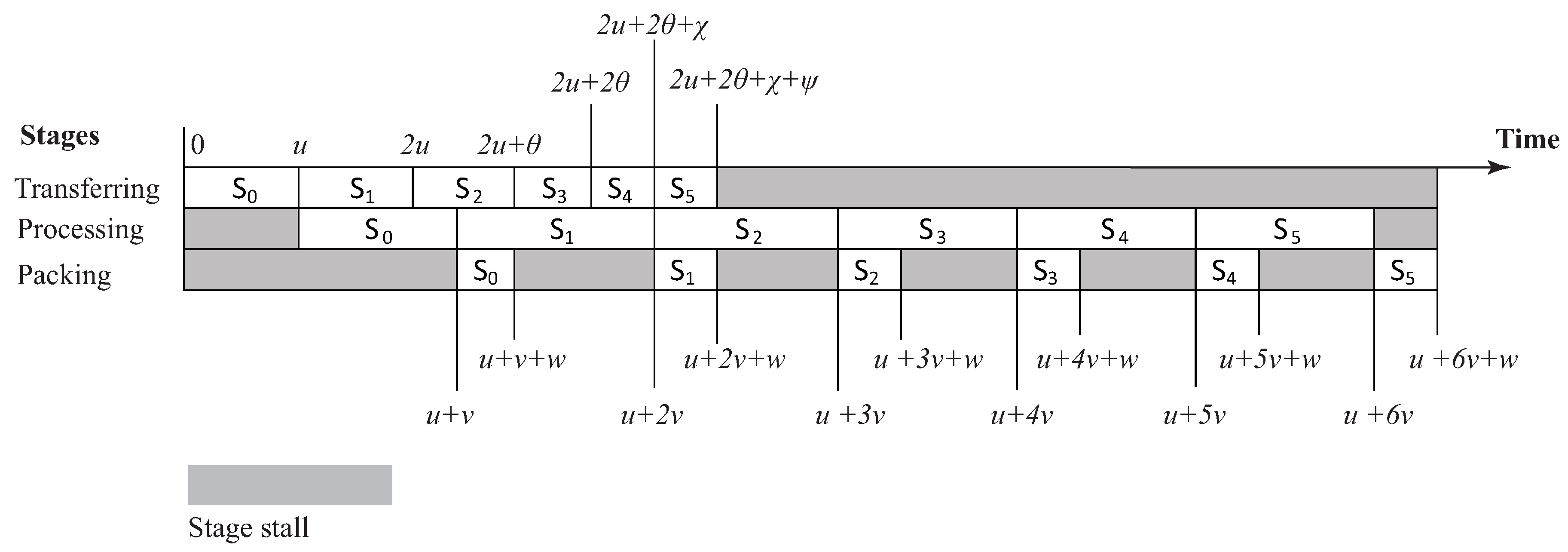
| Class | Communicating Nodes | c |
|---|---|---|
| 0 | (0,0), (3,0), (1,2), (4,2), (2,4), (5,4) | 4 |
| 1 | (0,1), (3,1), (1,3), (4,3), (2,5), (5,5) | 4 |
| 2 | (2,0), (5,0), (0,2), (3,2), (1,4), (4,4) | 3 |
| 3 | (2,1), (5,1), (0,3), (3,3), (1,5), (4,5) | 3 |
| 4 | (1,0), (4,0), (2,2), (5,2), (0,4), (3,4) | 3 |
| 5 | (1,1), (4,1), (2,3), (5,3), (0,5), (3,5) | 3 |
| Latency | Number of Communicating Nodes Exhibiting This Latency |
|---|---|
| Q | |
| ⋮ | ⋮ |
| 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souravlas, S.; Anastasiadou, S. Pipelined Dynamic Scheduling of Big Data Streams. Appl. Sci. 2020, 10, 4796. https://doi.org/10.3390/app10144796
Souravlas S, Anastasiadou S. Pipelined Dynamic Scheduling of Big Data Streams. Applied Sciences. 2020; 10(14):4796. https://doi.org/10.3390/app10144796
Chicago/Turabian StyleSouravlas, Stavros, and Sofia Anastasiadou. 2020. "Pipelined Dynamic Scheduling of Big Data Streams" Applied Sciences 10, no. 14: 4796. https://doi.org/10.3390/app10144796
APA StyleSouravlas, S., & Anastasiadou, S. (2020). Pipelined Dynamic Scheduling of Big Data Streams. Applied Sciences, 10(14), 4796. https://doi.org/10.3390/app10144796






