Analysis of Narrow-Line Laser Cooling and Trapping of Sr Atoms in Microgravity Environments

Abstract

Obtaining ultracold alkaline earth(-like) atoms in space encounters the problem of performing narrow-line laser cooling in microgravity environments ($\mathsf{\mu }$-gEs). This paper reports an analysis of the magneto-optical trap (MOT) based on the narrow-line transition in ${}^{88}$Sr, while paying special attention to the role of the gravity. This analysis suggests the MOTs based on narrow-line transitions cannot be cold and dense enough in a $\mathsf{\mu }$-gE. We thus propose a strategy: that one can use a dual-frequency MOT to realize a low-temperature, high density, and high transfer efficiency, narrow-line red MOT in $\mathsf{\mu }$-gEs.

1. Introduction

Great efforts have been made in recent decades to push cold atoms into microgravity environments [1]. Atomic clocks based on cold atoms in space are of particular interest to scientific experiments in space [2], such as measuring the gravitational wave [3], redshift of the earth [4], and testing of Einstein’s theory of general relativity [5]. Several projects of microwave cold atom clocks in space have been proposed, such as ACES (Atomic Clock Ensemble in Space), PARCS (Primary Atomic Reference Clock in Space), RACE (Rubidium Atomic Clock Experiment), and CACES (The Chinese Atomic Clock Ensemble in Space) [6,7,8]. Since optical clocks have been demonstrated to be about two orders of magnitude higher than microwave atomic clocks in terms of stability and uncertainty [9], optical clocks in space have been proposed [10], such as, the Space Optical Clocks (SOCs) [11] by the European Space Agency (ESA) program. Besides the cold atom clocks, Bose–Einstein Condensation (BEC) in $\mathsf{\mu }$-gEs (microgravity environments) is another example that is highly interested in application of fundamental physics and inertial sensing [1,12,13,14,15].

Currently, all the demonstrated space-borne cold atom clocks and BEC are based on alkali atoms [1,7,12]. However, neutral atom optical clocks are based on alkaline earth(-like) atoms, such as Mg [16], Ca [17], Sr [18,19], Yb [20], and Hg [21], some of which are also interested in BEC [22,23,24]. A distinctive advantage of these alkaline earth(-like) atoms over alkali atoms is the existence of spin-forbidden transition of ${}^1{S}_0{-}^3{P}_1$ by which one can perform a narrow-line laser cooling [25,26]. The strontium optical lattice clock is one of the payloads in SOC [11] and the ground-based ones have reached the level of ${10}^{-18}$ in fractional frequency stability and uncertainty [18,27,28], promising it to be chosen as an optical clock in space. The more recently proposed project—SAGE (Space Atomic Gravity Explorer) is also based on a strontium optical lattice clock in space [29]. Furthermore, strontium atoms can be a good candidate for developing atom interferometry in space [29,30].

Thanks to the existence of the transition line of ${\left(5s^2\right)}^1{S}_0-{\left(5s5p\right)}^3{P}_1$, experiments of narrow-line laser cooling of strontium atoms in magneto-optical traps (MOTs) show that the temperature can be down to the recoil limit for both bosons and fermions [31,32,33,34]. Another interesting property of the narrow-line laser cooling of strontium atoms is that the ratio of the maximum radiative force to the gravitational force $R=\hslash k\Gamma /2mg$ is about 16, where ℏ, k, $\Gamma$, m, and g are the reduced Plank’s constant, the light field wave vector, the transition natural width, the atomic mass, and the gravitational acceleration, respectively. This ratio is much different from the laser cooling based on the broadlines, where R is typically on the order of ${10}^5$. One can observe that the atoms tend to sag to the bottom of the MOT where the Zeeman shift balances the laser frequency detuning. This phenomenon demonstrates that the gravity of earth can play a strong influence on the behavior of the strontium atoms in the MOT held by this narrow-line transition. One question then arises: how would the narrow-line laser cooling be if the experiment runs in a $\mathsf{\mu }$-gE. To the best of our knowledge, this problem has not been studied in detail. Meanwhile, it is costly to establish a $\mathsf{\mu }$-gE on the ground for such an experiment. Simulation is thus important and necessary for understanding and designing a narrow-line MOT in a $\mathsf{\mu }$-gE. We herein show the numerical modeling of the atoms’ behaviors to understand the role gravity plays in narrow-line MOTs of strontium atoms and propose a possible solution to realize efficient, narrow-line laser cooling with microgravity.

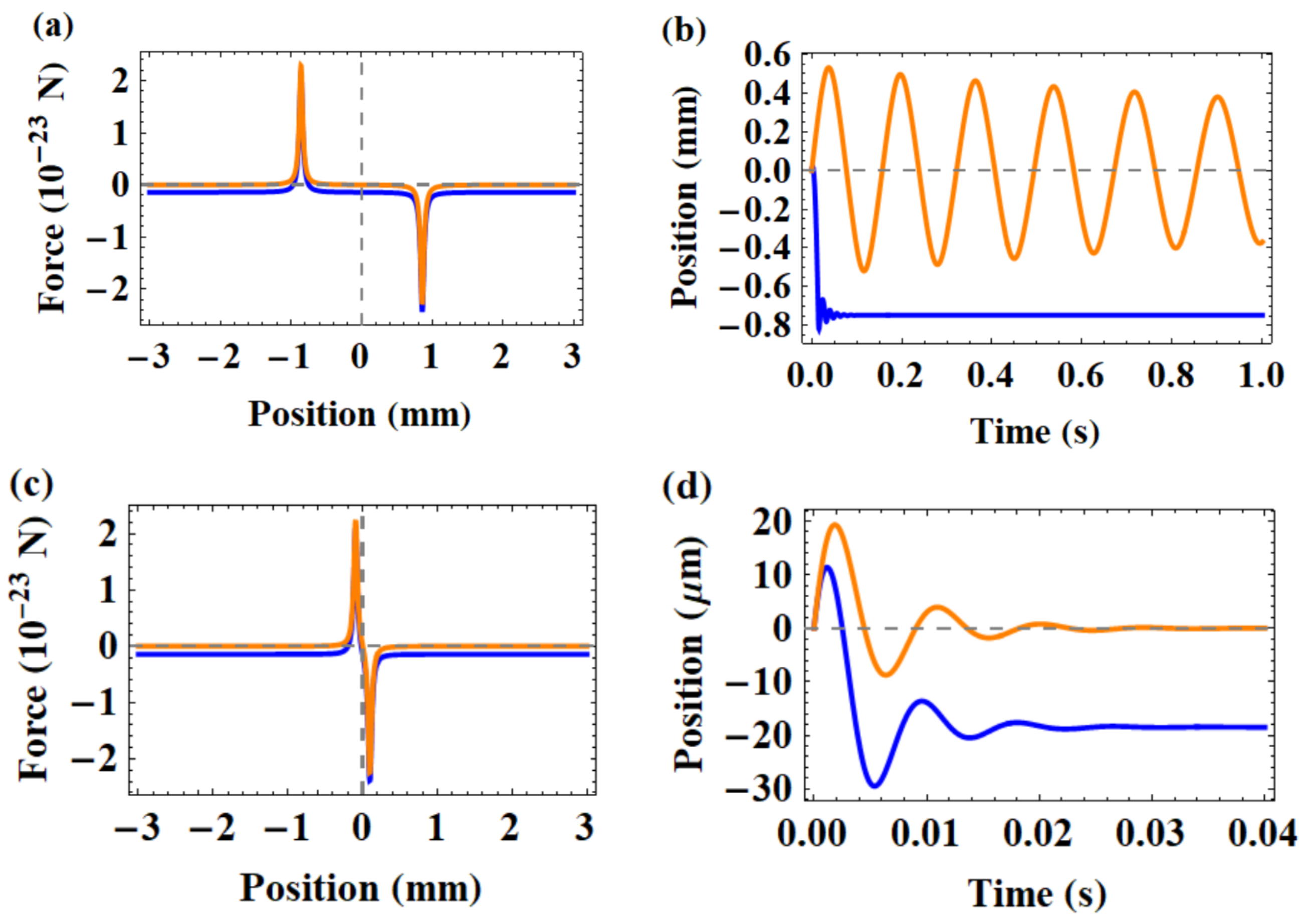
2. Simulation of Behaviors of a Single Atom Driven by Mean Force

Before being loaded into the narrow-line MOT, atoms need to undergo some pre-cooling stages which force the velocity distribution into the capture range of the narrow-line MOT. A typical MOT configuration is shown in Figure 1a and the corresponding time sequence is shown in Figure 1b for strontium bosons on the ground. Atoms are firstly loaded into a blue MOT where the radiation forces are given by the transition of ${\left(5s^2\right)}^1{S}_0-{\left(5s5p\right)}^1{P}_1$ which is characterized by a 32-MHz natural linewidth and a 461-nm transition wavelength. The R value of this broadline is about $1.0\times {10}^5$, so the gravity can be neglected at this stage. The second stage laser cooling is carried out in a red MOT based on transition of ${\left(5s^2\right)}^1{S}_0-{\left(5s5p\right)}^3{P}_1$ at 689 nm. To make an efficient transfer from blue MOT to red MOT, the 689 nm laser is modulated to be broadband, about 2 MHz, and then changed to be at a single frequency. As mentioned above, the transition ${\left(5s^2\right)}^1{S}_0-{\left(5s5p\right)}^3{P}_1$ has a natural linewidth of $7.6$ kHz, giving a R value of about 16.

To illustrate the role of the gravity in the single-frequency, red MOT, we model the trajectory of a single ${}^{88}$Sr atom in one dimension. The isotope of ${}^{88}$Sr has a simpler energy level configuration than ${}^{87}$Sr [35,36], allowing us to abstract the physics essence in a most direct way.

The dynamics of the atoms in this narrow-line-based MOT are mainly governed by the scattering force and gravitational force, which are given as below according to the semiclassical theory.

$$\begin{array}{ccc}{\mathit{F}}_{\alpha }(\mathit{v},\mathit{x})\hfill & =& {\mathit{F}}_{-}(\mathit{v},\mathit{x})-{\mathit{F}}_{+}(\mathit{v},\mathit{x})-m{\mathit{g}}_{\alpha },\hfill \end{array}$$

(1)

$$\begin{array}{ccc}{\mathit{F}}_{\mp }(\mathit{v},\mathit{x})\hfill & =& \frac{\hslash \mathit{k}\Gamma }{2}\frac{s}{1+s^{\prime }+\frac{4{\left[\Delta \mp \mathit{k}·\mathit{v}\mp \mu \frac{d{B}_x}{dx}x\right]}^2}{{\Gamma }^2}},\hfill \end{array}$$

(2)

where subscripted $\alpha =G$ or M denotes the case on ground or in $\mathsf{\mu }$-gEs, respectively. $\mathit{v}$ is the velocity of atom, and $\mathit{x}=\{x,y,z\}$. $s=I/I_s$ is the saturation parameter where I is the single beam peak intensity and $I_s$ is the transition saturation intensity. $s^{\prime }\ge s$ accounts for saturation induced by other four trapping beams. $\Delta ={\omega }_L-{\omega }_A$ where ${\omega }_L$ is the laser angular frequency and ${\omega }_A$ is the angular frequency of atomic resonance. $\mu =g_J{\mu }_B/\hslash$ where $g_J$ is the Lande g-factor of ${}^3{P}_1$ state and ${\mu }_B$ is the Bohr magneton. m is the mass of atom. ${\mathit{g}}_G$ and ${\mathit{g}}_M$ are the gravitational accelerations on ground and in $\mathsf{\mu }$-gEs, respectively. Here, we suppose a value ${\mathit{g}}_M=5\times {10}^{-4}\times 9.8$ m/s${}^2$.

To simulate the trajectory of a single atom in z direction (vertical direction), we numerically solve the differential equations as:

$$\begin{array}{ccc}{F}_{\alpha ,z}[z\left(t\right),v_z\left(t\right)]\hfill & =& m\frac{d{v}_z\left(t\right)}{dt},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill v_z\left(t\right)& =& \frac{dz\left(t\right)}{dt},\hfill \end{array}$$

(4)

with initial condition $v_z\left(0\right)=v_0$, and $z\left(0\right)=z_0$, where $v_z\left(t\right)$ is the velocity in z direction and $z\left(t\right)$ denotes the atom position in z direction. Here, $t=0$ is the starting point of single-frequency MOT, as shown in Figure 1b.

Figure 2a,b show the simulation results with typical values of laser detuning ($\Delta =-2\pi \times 1.8$ MHz) and laser intensity ($s=s^{\prime }=250$). The parameters used in this simulation are $m=88\times 1.66\times {10}^{-27}$ kg, $\Gamma =2\pi \times 7.6$ kHz, $k=2\pi /(689\times {10}^{-9})$m${}^{-1}$, $g_J=1.5$, $\left(d{B}_z\right)/dz=0.1$ T/m, $g_G=9.8$ m/s${}^{-2}$, $g_M=5\times {10}^{-4}\times 9.8$ m/s${}^{-2}$, $v_z\left(0\right)=2$ cm/s, and $z\left(0\right)=0$. Figure 2a compares the mean force between the cases on ground and in a $\mathsf{\mu }$-gE of a rest atom in different position. Although the difference between these two forces is small, the resultant behaviors are quite different. As an example, we suppose the initial conditions as $z\left(0\right)=0$ and $v_z\left(0\right)=2$ cm/s. Given the experiment runs on ground, the atom can quickly sag to the position where the scattering force balances the gravity, as shown by the blue curve in Figure 2b. However, the orange curve in Figure 2b shows that the atom would oscillate with a slight damping, indicating a poor effect of cooling without the favor of gravity. One, thus, can see that gravity plays a pivotal role in the red MOT of strontium atoms.

The simulation shown in Figure 2a,b illustrates the dynamics when the detuning and intensity of the cooling laser satisfy the conditions of $|\Delta |>>\Gamma \sqrt{1+s}$ and $s>>1$. With such conditions, atoms are not driven by linear restoring force which is preferred for a typical MOT based on the broad transition line. To this end, the dynamics under the circumstance of $|\Delta |\sim \Gamma \sqrt{1+s}$ and $s>>1$ are also simulated as shown in Figure 2c,d. A linear restoring force is formed around the center, though the linearity is not so high. This form of force can make the atoms be strongly damped and cooled down in about only 20 ms no matter the MOT on the ground or in a $\mathsf{\mu }$-gE. Unfortunately, the diameter of the MOT with such a near detuning would become only about 40 microns which is extremely small compared to the broadband red MOT, which is typically about 2 mm in diameter. It is thus hard to achieve a reasonable atom loading efficiency with such a tiny MOT.

3. Monte Carlo Simulation of Behaviors of Ensemble Atoms Associated with Spontaneous Emission

We only consider a single atom only driven by the mean force in the modeling above. More rigorous modeling should calculate the collective behaviors of an ensemble consisting of a large number of atoms which is characterized by an initial velocity distribution and an initial position distribution. On the other hand, the random force must be considered to predict its temperature which is mainly determined by the momentum diffusion induced by spontaneous emission. The following modeling thereby takes the spontaneous emission into account. We consider the random process driven by spontaneous emissions as a Weiner process, meaning the momentums of the atoms in red MOT evolve as Brownian motions. With these considerations, the behaviors of the atom ensemble are simulated with a set of stochastic differential equations as:

$$\begin{array}{ccc}md{v}_{z,i}\left(t\right)\hfill & =& F_{\alpha ,z,i}[z_i\left(t\right),v_{z,i}\left(t\right)]dt+\sigma [z_i\left(t\right),v_{z,i}\left(t\right)]d{w}_i\left(t\right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}{v}_{z,i}\left(t\right)dt\hfill & =& d{z}_i\left(t\right),\hfill \end{array}$$

(6)

where the subscript i denotes the ith numbered atom, ${\sigma }^2[z_i\left(t\right),v_{z,i}\left(t\right)]=D[z_i\left(t\right),v_{z,i}\left(t\right)]$ represents the momentum diffusion coefficient, and $w_i\left(t\right)$ is associated with the Weiner process. The momentum diffusion originates from the fluctuations during the many elementary absorption–spontaneous-emission cycles, leading to a diffusion coefficient given by:

$$D[z_i\left(t\right),v_{z,i}\left(t\right)]=\frac{1}{2}{\hslash }^2{k}^2\gamma [z_i\left(t\right),v_{z,i}\left(t\right)],$$

(7)

where

$$\gamma [z_i\left(t\right),v_{z,i}\left(t\right)]=\frac{F_{z,-}[z_i\left(t\right),v_{z,i}\left(t\right)]+F_{z,+}[z_i\left(t\right),v_{z,i}\left(t\right)]}{\hslash k/2}$$

(8)

is equal to the number of fluorescence cycles per second.

To simulate the ensemble of the atom, the initial position $z_i\left(0\right)$ and initial velocity $v_{z,i}\left(0\right)$ are randomized. Since the narrow-line red MOT is the small part centered at the broadband red MOT, we thus approximate the distribution of the $z_i\left(0\right)$ as an even distribution. The initial velocity $v_{z,i}\left(0\right)$ is supposed to be a normal distribution with a mean velocity of zero and a variance of $k_B{T}_0/m$ where $T_0$ is the temperature at the end of broadband red MOT. The interaction between the atoms has been neglected, so one run of an experiment with $N_0$ atoms is equivalent to $N_0$ runs of an experiment with a single atom. By doing $N_0$ runs of independent trials of solving the above stochastic differential equations, we can obtain the collective behaviors of $N_0$ atoms.

Figure 3 shows a simulation of ensemble atoms. Parameters used in this simulation are $N_0=1000$, $T_0=12$ $\mathsf{\mu }$K, while other parameters are the same as the simulation shown in Figure 2. In this simulation, the number of atoms left inside the MOT till the time of 100 ms is 771 on the ground and 1000 in $\mathsf{\mu }$-gEs, indicating some of atoms escaped out of the MOT. Since we are interested more in the atoms’ behavior inside the MOT, the results shown in Figure 3 only display the data of atoms left inside the MOT. Comparing the traces of the moving atoms, as shown in Figure 3(a1,b1), one can find that the atoms inside MOT in a $\mathsf{\mu }$-gE are flying in sinusoid-like trajectories, while the atoms inside the MOT in the ground segment fly rapidly to the bottom. This behavior leads to a striking difference in the atom distribution, as can be visualized in Figure 3(a2,b2), which show the atom distribution at the time of 60 ms. The atom density indicated by the relative value of the bins in the histograms is much higher for the case of on the ground than in a $\mathsf{\mu }$-gE. More importantly, the difference on the cooling effect can be found by comparing the Figure 3(a3,b3). Figure 3(a3) shows that the temperature goes up and falls down rapidly during the 20 ms from the beginning of the MOT on the ground, and then keeps stable to be about 2.5 $\mathsf{\mu }$K, which is consistent with the experimental results [31] and the theory predication that the equilibrium temperature is $T_{eq}=\hslash \Gamma \sqrt{1+s}/\left(2k_B\right)$ according to the Doppler theory. The rapid rising of the temperature in the beginning can be attributed to the acceleration due to the gravity. However, Figure 3(b3) shows that the temperature of the MOT in a $\mathsf{\mu }$-gE slowly falls down and tends to be an equilibrium temperature about 7.5 $\mathsf{\mu }$K, which is much higher than the temperature of the counterpart on ground. This simulation suggests about 70% to 80% of the atoms can be held inside the MOT till the time of 100 ms for the MOT on ground, and almost 100 percent atoms can be held for the case of in a $\mathsf{\mu }$-gE, meaning the ratio of the captured atoms to the overall is much lower on the ground than in space. We again attribute this phenomenon to the fact that the acceleration of atoms due to the gravity can speed up those atoms possessing relative higher gravity potential and escape out of the capture range of the MOT.

To make the dynamics more intuitive to understand, we can interpret it with a moving ping-pong ball in a stiff-wall box. If it happens on the ground, this ball can be damped until it rests on the bottom wall after a short time. However, the ball would be hard to stop if this experiment happened in the space station due to the microgravity. The MOT based on such a narrow-line transition functions like a stiff-wall box. The resultant force of gravity and the scattering force drives the atoms into damped oscillation around the balance point, while the atoms in a $\mathsf{\mu }$-gE cannot find a balance point in the box-like MOT, leading to be flying back and forth in the MOT. This explains why the atoms can be cold and dense at the bottom of the MOT with gravity, but be much hotter and dispersed without gravity.

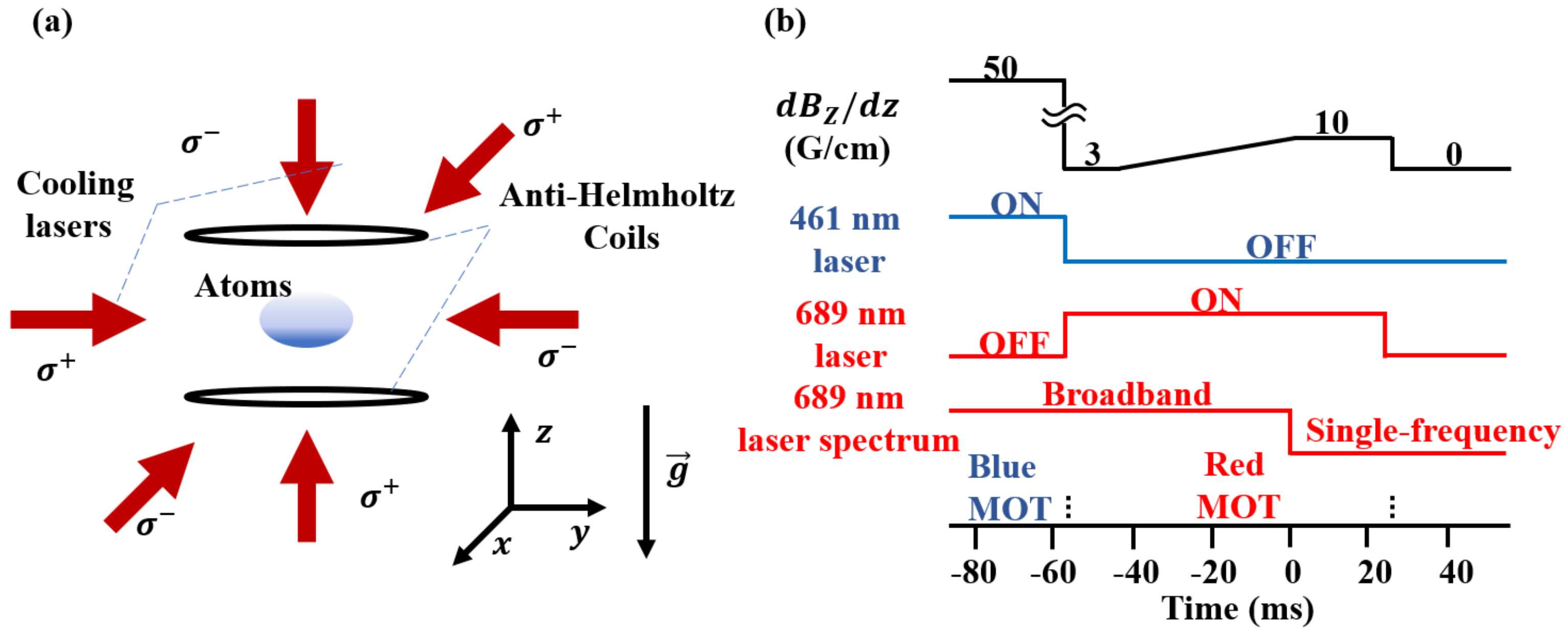
4. A Proposal of Designing the MOTs Based on Narrow-Line Transitions in Microgravity Environments

Until now, one could see that the narrow-line MOT in $\mathsf{\mu }$-gEs cannot be as cold and dense as the on ground due to the absence of favor from gravity if the MOT has $\Delta >>\Gamma \sqrt{1+s}$ and $s>>1$. Although a high cooling efficiency is possible if the cooling lasers are detuned to be similar to the power broadened transition linewidth, i.e., $\Delta \sim \Gamma \sqrt{1+s}$, the loading efficiency would be another problem. One then wonders how to realize a cold and dense enough MOT in a $\mathsf{\mu }$-gE, which is based on narrow-line transitions. This question leads to our proposal of a possible strategy: that one can utilize a dual-frequency laser for the red MOT instead of single frequency. More specifically, one frequency is nearly detuned to form a damping trapping around the center of the MOT, while the other frequency is greatly detuned to form a box-like outer shell which enables high efficiency of the transfer from the previous cooling stage. Figure 4 shows an example of dual-frequency, red MOT in a $\mathsf{\mu }$-gE. Figure 4a shows the mean radiation force of a dual-frequency red MOT depending on the location of one atom with velocity of zero. By performing a similar Monte Carlo simulation as before, we obtain the evolution of the positions shown in Figure 4b, the position distribution in Figure 4c, and the evolution of temperature in Figure 4d. With $N_0=1000$ in the beginning, about 60% of the atoms are left inside the MOT at the time of 100 ms. These results show that the atoms can be gathered and be cooled at the center of the MOT with high density within about 60 ms. The temperature can reach as low as 3.2 $\mathsf{\mu }$K which is a little higher than the Doppler limit of 2.9 $\mathsf{\mu }$K as predicted by $\hslash \Gamma \sqrt{1+s}/2k_B$. This difference can be attributed to the deviation of the laser detuning of ${\Delta }_1=-2\pi \times 200$ kHz from $-\Gamma \sqrt{1+s}/2=-2\pi \times 60$ kHz, at which point the Doppler limit is achieved. Furthermore, lower temperature and higher density can be obtained by optimizing the parameters of intensity and detuning.

5. Conclusions

In conclusion, we have performed an analysis of narrow-line MOT of Sr atoms both for earth gravity and microgravity environments by Monte Carlo simulation. This analysis suggests that the single-frequency, red MOT based on the narrow-line transition ${\left(5s^2\right)}^1{S}_0-{\left(5s5p\right)}^3{P}_1$ in Sr atoms can be substantially influenced by gravity. With the favor of gravity, the atoms in MOT on the ground can be cooled down in a manner of damped oscillation near the bottom of the box-like MOT. However, if the same MOT is in a $\mathsf{\mu }$-gE, atoms will fly back and forth due to the bouncing at the edge of the MOT. We herein propose a possible solution to realize a dense and cold enough red MOT in a $\mathsf{\mu }$-gE, i.e., utilizing a dual-frequency laser for the MOT instead of single-frequency laser, where one frequency is detuned a small amount to form a strong damping trapping at the center of the MOT, and the other frequency is greatly detuned to form an outer shell with enough volume to allow obtaining a high transfer efficiency from the previous stage. This study paves a way for the space-borne scientific experiments, such as optical lattice clocks, BEC, and atom interferometry, based on the alkaline earth ultracold atoms.