Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics

Abstract

Ethnomathematics makes school mathematics more relevant and meaningful for students. The current research aims to study the effect of using ethnomathematics in the context of Islamic ornamentation on learning the topic of congruent triangles. To achieve this aim, 30 10th-grade students engaged in ethnomathematics by learning about congruent triangles using Islamic ornamentation. Data was gathered via (a) videotaping and transcribing students’ learning and (b) students answering two parallel questionnaires that included proof questions on the three congruence theorems. The students were required to answer one questionnaire before the learning process and one after it. The main results indicated that the students succeeded in constructing the concepts of congruence and congruent triangles via the ethnomathematics learning process. In addition, the students succeeded in arriving at and formulating the three congruence theorems. Moreover, findings obtained from the questionnaires indicated that the students improved their proving processes as a result of ethnomathematics-based learning. Furthermore, paired sample t-tests indicated significant differences between the students’ mean scores before and after the learning process.

1. Introduction

D’Ambrosio [1] described ethnomathematics as “the mathematics which is practised among identifiable cultural groups, such as national-tribal societies, labor groups, children of a certain age bracket, professional classes, and so on” (p. 45). The adoption of an ethnomathematical perspective in developing informal mathematical curricula ensures that both contextualized problems and students’ cultural links and are considered [2]. This function of ethnomathematics is satisfied by implementing a culturally relevant pedagogy in the school curriculum, which helps to increase students’ cognitive and emotional aptitude [3]. In addition, it helps students understand the role that mathematics plays in a societal context [4]. The ethnomathematics perspective was applied in different countries with different groups of students, from different ages, where these students made connections between ethno-contexts and school mathematics. For example, Irwin [5] reported that using contextualized problems to teach primary students, from Pacific Island nations that live in New Zealand, enhanced their understanding of decimal numbers. The ethnomathematics context was utilized to emphasize the multi-culturist feature of knowledge, especially mathematical knowledge [6]. Massarwe, Verner, and Bshouty [7] reported that high school students found the construction of geometrical ornaments, from different cultures in Israel, and the discovery of their mathematical properties to be both meaningful and enjoyable. In addition, the construction of geometrical ornaments can foster creativity and lead to deep inquiry from both mathematical and cultural perspectives [7]. Furthermore, Widada, Herawaty, and Lubis [8] found that ethnomathematics-oriented materials improved the mathematical understanding of participating students in Indonesia. Adam [9] reported that the implementation of ethnomathematical unit on measurement (area, perimeter, volume) facilitated the understanding of mathematical concepts among fifth-grade students in the Maldives, which was done through practical examples using cultural objects, investigations, and by relating school mathematics to real world activities. This relatedness motivated and interested the students to learn mathematical concepts. Ogunkunle and George [10] reported that integrating ethnomathematics instructional approach affected positively the acquisition of creative skills among Nigerian students.

Geometry is considered the core of culture and ethnomathematics [11,12], whereas art connects the two. Art is considered an important code for cultural groups, and it can serve as a powerful tool for teachers in the classroom [13]. This is particularly true for Islamic art, the most dominant aspect of which is its ornamentation [14]. In the current study, we used Islamic geometrical ornamentation to design ethnomathematics learning regarding triangle congruence. The triangle congruence theorems are one of the essential topics in classical geometry [15], but students often struggle to understand it [16]. Little research has been done on the teaching of congruence; at least, little research that is written in English [17] or is related to learning the concept of congruence, especially with regard to reasoning and proof [18]. The lack of research already carried out on triangle congruence, in addition to its importance and its complexity, led us to choose this topic for the current study. The main aim of the study is to examine the effect of ethnomathematics on the learning of triangle congruence by middle school students who carry out activities based on Islamic geometrical ornamentation.

2. Theoretical Background

2.1. Ethnomathematics

Researchers stressed that in order for the learning system to be able to personalize its learning processes, it must characterize the learners [19]. This is one of the foundations of ethnomathematics; i.e., to characterize the learner and fit the context according to the learner’s features. D’Ambrosio [20] defined ethnomathematics by describing the three elements which comprise the term: ethno, mathema, and tics. Ethno refers to the sociocultural context, which includes codes and symbols; mathema means to explain, to know, to activate, to infer, and to model; and tics is derived from techne and has the same root as technique.

Ethnomathematics forms a bridge between culture and education and therefore can be perceived as a lens for viewing and understanding mathematics as a cultural product [21,22]. A good example of this is the geometry of transformation as reflected in Batak society, in which craftspeople use the principles of rotation, translation, dilation, and reflection when making Gorga motifs [23].

Ethnomathematics can make school mathematics more relevant and meaningful to students, motivating them and helping them develop self-confidence [24]. It also increases students’ intellectual, social, emotional, and political learning by using their unique cultural reference points to convey their knowledge, skills and attitudes [25]. Moreover, ethnomathematics can enhance pupils’ achievement more than the conventional method [26] and promote students’ understanding of abstract mathematical concepts [27]. For that, researchers and educators have adapted ethnomathematics for learning and teaching mathematical concepts, such as linear equations [28]. Nursyahidah et al. [28] reported the enhancement of students’ knowledge of the linear equation system with two variables through utilizing the selling and buying traditions in the Peterongan traditional market in Central Java.

2.2. Islamic Geometric Ornamentation

The term ornament comes from the Latin verb ornare, which means to adorn [23]. Ornaments are defined as “geometric patterns of cultural value composed of basic units repeated under different transformations” [7]. An ornament is a decorative art form [29] rich in patterns and structures [30]. The main purpose of ornament is to improve the products or items decorated. The functions of ornaments could be categorized as (1) purely aesthetic functions, (2) symbolic functions, and (3) constructive engineering functions [23].

The ornament is considered to be at the heart of Islamic architectural heritage, and it can be categorized into three types of patterns—geometric, arabesque, and calligraphic [31]. Islamic ornaments involve many regular shapes placed inside circular forms, where the shapes inside the circular forms emerge as star-shaped polygons. The rhythmical repetition of circles produces different arrangements formed at the connection points, creating motifs with more circles and polygons [32]. Every ornament is based on a motif derived from the contemplation of divine unity, where the ornaments are placed as if they extend in four directions from the center: upward, downward, to the right, and to the left [32].

Islamic geometric ornamental designs are based on the principles of symmetry and repetition [32]. Repetition is the most effective and important theme for geometric patterns, where ornamental designs generally generated by repeating square and triangle shapes [33]. Most geometric motifs are based on the hypothesis that each pattern can be repeated and expanded infinitely [34]. Symmetry is the key factor in deriving both geometric and floral patterns, where the use of bilateral symmetry means that a figure is mirrored through the vertical axis [33]. Another property of Islamic ornaments is their two-dimensionality; most Islamic designs are two dimensional, even though they are not applied to flat surfaces only. In addition, the patterns themselves rarely have shading in the background [35]. Moraová and Novotná [36] described the potential of utilizing ornaments of different cultures in the mathematics classroom, emphasizing that it could affect the minority or migrant students’ learning and integration. They suggested different activities based on ornaments for teaching and learning various mathematical topics such as symmetry, rotation, translation, plane geometry, tessellation, proportionality, linear functions, ratio, and the Pythagoras theorem. The use of ornaments has a positive effect on students learning geometry; Massarwe, Verner, and Bshouty [7] reported that students became aware of ornaments not only as a form of decoration but also as interesting geometrical objects in their own right.

2.3. Congruent Triangles

Clapham and Nicholson [37] identified congruent figures in geometry, as follows: “Two geometrical figures are congruent if they are identical in shape and size, or if one shape mirrors the other in shape and size”. Triangles are congruent if six conditions are met: the three sides are equal, and the three angles are equal [38]. Anyone of the following four conditions is sufficient for congruence—S.S.S., A.S.A., S.A.S., or R.H.S. All four conditions are taught in secondary grades and are called congruence theorems [15]. The minimal number of conditions sufficient for congruence is key to understanding the concept, but many students find it difficult to justify congruence [39,40]. Triangle congruence is taught in the secondary school [41] and is considered a core topic in school geometry because the sufficient conditions for congruent triangles are useful for proving geometrical theorems. In addition, a triangle’s congruence connects it with similar triangles [17]. Reasoning and proof related to congruent triangles are considered the beginning of formal mathematical reasoning, since students start to use formal language in order to prove claims related to congruent triangles [18]. Little research has studied the impact of ethnomathematical contexts rich in ornaments on the development of students’ conceptions of triangles congruence, where more research has paid attention to the impact of technology on these conceptions [42].

2.4. Research Aim and Questions

Little research has been done on students’ learning of the congruence concept [17], which is especially true for students who have difficulties in mathematics. The topic of congruent triangles is considered difficult for students [16]. Since ethnomathematics makes school mathematics more relevant and meaningful for students [21], it is a possible candidate for overcoming students’ difficulties in mathematics. The current research aims to study the effect of using Islamic ornamentation to teach congruent triangles to students who find mathematics difficult by answering the following questions:

• What characterizes students’ definitions of congruence and congruent triangles?
• What characterizes students’ learning processes when they are taught about congruent triangles based on Islamic ornamentation?
• To what extent does ethnomathematical learning of congruent triangles based on Islamic ornamentation affect students’ knowledge of congruent triangles?

3. Method

To meet the aim and objectives of the study, we used a mixed-method design with both qualitative and quantitative components. In our qualitative analysis, we followed students’ ethnomathematics learning processes concerning congruent triangles based on Islamic ornamentation; we also followed students’ identification of congruent triangles and their strategies for proving claims about congruent triangles. Our quantitative analysis had a quasi-experimental (pre-post) design, which was used to examine the effects on students participating in the learning process when solving congruent triangle problems.

3.1. Participants

The research was conducted among 30 students in 10th grade (aged 15–16 years), all of whom have difficulties in mathematics. The students had already learned the congruent triangles topic formally, in the eighth and ninth grades, including the three congruence theorems and proving claims about congruent triangles according to these theorems. However, according to both their mathematics teacher’s diagnosis and the pre-test results, the students did not succeed in solving congruent triangle problems. Throughout the study, the participants worked in groups of 4–5 students, and we videoed three groups—Group A: Marah, Taqwa, Reem, Saja, and Nagam; Group B: Abed, Aya, Doa’a, Noor, and Zahran; and Group C: Nader, Rula, Majed, and Rawan. In the Findings Section (Section 4), we focus on the first group, mention the second group when necessary, and do not refer to the third group’s work in order to avoid repletion. The sampling process was based on convenience sampling, as the participants were selected based on their availability and willingness to take part in the learning process.

3.2. Data Sources and Procedure

Data collected from two sources—video recording and questionnaires.

3.2.1. Video Recording

Video recording was used to observe the three groups during their ethnomathematics learning of congruent triangles based on Islamic ornamentation. All of the video recordings were transcribed.

3.2.2. Questionnaires

Two parallel questionnaires, A and B, were used in the present research, and each questionnaire consisted of five questions. The first question consisted of two parts about definitions of congruence and congruent triangles; the second, third, and fourth questions were proof questions based on the first, second, and third theorems of congruent triangles; and the fifth question was also a proof question, this time combining the three theorems. Two of these questions (Task 1 and 2) are presented in the Findings Section (Section 4).

The students were requested to answer questionnaire A; they were then engaged in ethnomathematics-based learning of the congruent triangles over the course of six meetings. Each meeting lasted for 60 min. Afterward, the students were requested to answer questionnaire B.

3.3. Data Analyses

3.3.1. Video Recordings

We analyzed students’ learning via conceptual analysis, as it enabled us to study students’ learning according to instructional goals [43]. For greater detail, we organized the transcribed data from the video recording according to instructional goals. The first goal was related to congruence and congruent triangles, while the second was related to insufficient conditions for congruent triangles. The third to fifth goals were related to the three congruent triangles theorems. To assess the students’ learning in relation to each goal, we set ways to understand ideas targeted by the particular instruction. In this setting, we defined students’ learning processes as imagining, connecting, inferring, and understanding situations in particular ways [44]. To validate the analysis process, each researcher analyzed individually 25% of the statements for identifying the central themes. The agreement between the coders (Cohen’s Kappa coefficient) was 0.849, which is an accepted percentage in educational research.

3.3.2. Questionnaires

We analyzed the data obtained from the questionnaires using two methods. In the first method, we examined students’ solution strategies based on the constant comparison method [45]. In the second method, we used a statistical test—namely, the paired sample t-test. Each question in the questionnaires was assigned 20 points, where these points were divided among the claims needed to be stated in order to prove the triangles congruence in addition to the conclusion of this congruence. If the claim was wrong, the student was given zero points for the specific claim. If it included correct as well as incorrect statements related to the claim, it was given half the points for that claim. If all the statements for the claim were correct, the claim was given full points. For each student, we assigned a score for the questioner A and a score in questioner B. Using these scores, we examined the changes in students’ performances in the questionnaires before and after the ethnomathematics learning. Specifically, we measured the scores differences by conducted paired sample t-test which is a statistical test used across the sciences [46,47].

3.4. Ethnomathematics Activities

Researchers prepared activities for six meetings based on ethnomathematics using Islamic ornamentation for 10th-grade students learning congruence and congruent triangles. The learning included both concrete and abstract processes, and students were engaged in the processes of copying, cutting, and transforming shapes, as well as abstract solving. The following is a summary of each meeting with the students.

3.4.1. The First Meeting

The first meeting had the following three main objectives: First, to be familiar with Islamic ornamentation and its patterns. Second, to reveal the concept of congruence, in general, and then connect it with Islamic ornamentation; and third to use geometric transformations (rotation, reflection, and translation). This meeting consisted of several activities:

• Exhibition and discussion of the different types of Islamic ornamentation, such as animal, plant, and geometric ornamentation.
• Finding geometric shapes in the ornamentation.
• Cutting out different shapes and discussing their congruence.
• Discussing the meaning of congruence.
• Using different transformations as a mathematical process to enable movement from one shape to another in the ornamentation.
• Analyzing the geometrical properties of ornaments, as well as constructing them.

3.4.2. The Second Meeting

The second meeting involved three main objectives: First, to recognize congruent triangles. Second, to recognize symmetry between the sides and angles in congruent triangles. Third, to record the precise properties of congruent triangles. The meeting involved activities such as:

• Cutting out triangles and discussing which of them are congruent.
• Examining the congruence between a concrete triangle and the triangles used in ornamentation.
• Cutting out triangles and discussing which of them are congruent.
• Examining the congruence between a concrete triangle and the triangles used in ornamentation.
• Discussing the reasons why triangles are congruent.
• Drawing congruent triangles.
• Presenting the congruent notion and trying to record the properties of congruent triangles.

3.4.3. The Third Meeting

The third meeting consisted five main objectives: First, to find out the sufficient conditions for two triangles to be congruent. Second, to find out the sufficient conditions related to the first theorem (S, A, S). Third, to formulate the first theorem (S, A, S). Forth, to write a claim, and its explanation, as a mathematical proof. Fifth, to solve different exercises based on the first congruence theorem. The meeting included several activities such as:

• Inquiry about incongruent triangles in the ornamentation, e.g., Which triangles are equal in one side; equal in one side and one angle; or equal in three angles.
• Inquiry through drawing the ornamentation, measuring its angles, then cutting out its triangles and making comparisons between them.
• Distinguishing congruent triangles in ornamentation based on (S, A, S).
• Writing the proof processes for congruent triangles based on (S, A, S).

3.4.4. The Fourth Meeting

This meeting included five main objectives: First, to find out the sufficient conditions for two triangles to be congruent. Second, to find out the sufficient conditions related to the first theorem (A, S, A). Third, to formulate the first theorem (A, S, A). Forth, to write a claim, and its explanation, as a frame of mathematical proof. Fifth, to solve different exercises based on the first congruence theorem. The meeting included the following activities:

• Inquiry about congruent triangles according to (A, S, A), through drawing triangles in the ornamentation.
• Inquiry about congruent triangles according to (A, S, A), through cutting out and pasting triangles.
• Distinguishing congruent triangles based on (A, S, A) in ornamentation.
• Writing the proof phases of congruent triangles based on (A, S, A).

3.4.5. The Fifth Meeting

The meeting consisted five main objectives: To find out the sufficient conditions for two triangles to be congruent. Second, to find out the sufficient conditions related to the first theorem (S, S, S). Third, to formulate the first theorem (S, S, S). Forth, to write a claim and its explanation, as a frame of mathematical proof. Fifth, to solve different exercises based on the first congruence theorem. The meeting consisted the following activities:

• Drawing ornaments that include equal-side triangles.
• Drawing ornaments that include triangles with unequal sides.
• Inquiry about congruent triangles according to (S, S, S) through cutting out and pasting triangles.
• Distinguishing congruent triangles based on (S, S, S) in the ornamentation.
• Writing the proof processes for congruent triangles based on (S, S, S).

3.4.6. The Sixth Meeting

The meeting included three main objectives: First, to solve various questions based on congruent triangles. Second, to choose an appropriate theorem for proving that triangles are congruent. Third, to write sufficient conditions to prove that triangles are congruent. The meeting included the following activities:

• Completing different processes in a given proof.
• Distinguishing data about triangles from the figure and expressing them as conditions for congruence/incongruence.
• Solving questions based on the three congruence theorems.

4. Findings

In this section, we will present our findings according to the instructional goals (i.e., congruence and congruent triangles, and insufficient conditions for congruent triangles and each of the three congruent triangle theorems). The findings are based on conceptual analyses [27] of students’ discourses and activities throughout their ethnomathematics learning. In addition, the findings target students’ solutions in questionnaires A and B.

The students’ discourse throughout their Islamic-ornamentation-based learning indicated that they succeeded—through imagining, connecting, inferring, and understanding—in defining the concepts of congruence and congruent triangles. In doing so, they found and formulated the sufficient conditions for two triangles to be congruent, i.e. the three theorems of congruent triangles, (S, A, S), (A, S, A), and (S, S, S). The students also succeeded in carrying out justification activities that depended on the theorems. In the following section, we detail the features of each phase in the students’ learning. To avoid repetition, we focus on one group, describing what happened in the other two groups only when different processes occurred.

4.1. Defining Congruence in General and the Congruence of Triangles in Particular

4.1.1. Defining Congruence in General

Our analyses of the students’ discourse in the three groups indicated that, at the beginning of the learning process, students defined the concept of congruence in terms of the equality of areas or shapes covering each other, and any description of covering was without detail, as presented in Episodes 1 and 2, below.

Episode 1: Group A’s definition of congruence as the equality and covering of shapes

(2)	Marah:	Congruence is that one shape covers another.
(3)	Taqwa:	That means that the two shapes are equal.

Episode 1 shows that Marah (2) and Taqwa (3) each provided an incomplete definition of congruence, for they did not detail that the covering must be precise.

Episode 2: Group B’s definition of congruence as the equality of shapes’ areas

(8)	Abed	These rhombuses [pointing to the rhombuses in the ornamentation] are congruent.
(9)	Doa’a	Yes, because they have the same area.

In Episode 2, Doa’a incorrectly connected congruence to the equality of the shapes’ area. The students then identified the congruence concept via concrete work with ornamentation, including the repetition and symmetry of different shapes in the ornamentation, which helped them to arrive at a precise definition. To do this, the students cut shapes from the ornamentation and tried to move them to cover other shapes. Throughout this process, the students needed to use different forms of transformation (rotation, reflection, and translation), as presented in Episode 3, below.

Episode 3: Group A’s inquiry of congruent shapes using ornamentation

(16)	Reem:	Look at the squares [cutting out some squares in the ornamentation].
(19)	Taqwa:	Put the squares here.
(21)	Saja:	They are the same, they are congruent [pointing at two squares with a minor difference].
(22)	Nagam:	Why? These squares are not congruent.
(23)	Saja:	Because they do not cover each other exactly.
(24)	Taqwa:	Congruence is when the two shapes cover each other exactly.
(26)	Saja:	The two shapes have the same length of sides.
(29)	Reem:	When we compare between the two rhombuses, do we have to do direct coverage? (Pointing at two opposite rhombuses.)
(36)	Nagam:	You can translate…
(37)	Saja:	Ahh, we can rotate this rhombus to get this rhombus.

Episode 3 shows that students arrived, by working with ornamentation, at the exact definition of congruence, which is presented in Taqwa’s inference (24). They also arrived at the features of two congruent shapes, which is demonstrated by Saja’s conclusion (26). Also, by using their imagination, Nagam (36) and Saja (37) indicate that utilizing transformation supports the examination of congruent shapes.

4.1.2. Defining the Congruence of Triangles

Through concrete and visual work with ornamentation, students in all the groups were able to define congruent triangles. The students cut out and covered triangles in the ornamentation, and drew new ornamentation using triangles and their reflections. They concluded, as presented in Episode 4, that there are many different congruent triangles.

Episode 4: The definition of congruent triangles in Group A

(54)	Nagam:	Triangles 1 and 2 (see Figure 1) are congruent, because they cover each other completely.
	(After cutting out the numbered triangles in the ornamentation.)
(68)	Saja:	There are other congruent triangles in the ornamentation.
(74)	Marah:	The vertex of the triangle must be D. (Drawing a triangle that is congruent to triangle ABC; see Figure 2)
(82)	Nagam:	I drew a triangle in the opposite position to the ABC triangle.
(83)	Teacher:	You can check if they are congruent.
(84)	Nagam:	I can do reflection.
(91)	Saja:	All these triangles are congruent.
(94)	Saja:	All these triangles are equal in their sides and angles.

Episode 4 shows that Nagam (54) understood the meaning of congruent triangles through her concrete experience, enabling her to define congruent triangles correctly. Saja (68) showed her understanding, too, by indicating that there are congruent triangles different to the ABC triangle. Marah (74) inferred what the position of the vertex should be, in order for two triangles to be congruent. Nagam (82) showed her understanding, by indicating that she succeeded in drawing congruent triangles that were in different positions. This indicates that she knows the conditions for congruent triangles. Nagam (84), using her imagination, argued that reflection could help her in checking the congruence of triangles. Saja (91,94) formulated the properties of congruent triangles.

Our analysis of all the students’ answers in questionnaires 1 and 2 indicated changes in how they defined congruent triangles. Before the learning process, students’ definitions were organized into the following six categories: equal sides, equal angles, similarities, complete covering, covering of the sides, and covering of the angles. However, after the learning process, we identified only four categories of definition.

Table 1. Students’ definitions of the congruent triangles, before and after the learning process.

Category	Before Learning	After Learning
Equal sides: When the sides of the triangles are equal, they are congruent.	6.6%	0
Equal angles: When the angles of the triangles are equal, they are congruent.	13.3%	6.6%
Similarities: When there is a similarity between the triangles, they are congruent.	20%	10%
Coverage of sides and angles: When the sides and angles of two triangles cover each other, the two triangles are congruent.	10%	33.3%
Complete cover: Triangles are congruent when one covers the other precisely.	6.6%	50%
No answer.	43.3%	0

presents the distribution of students’ definition categories before and after the learning process.

Table 1 shows that, before the learning process, students either did not provide definitions of congruent triangles, or their definitions related to similarity only; whereas, after the learning process, students’ definitions related more to the coverage of triangles.

4.2. Investigating the Sufficient Conditions for Congruent Triangles by Using Islamic Ornamentation

The investigation of ornamentation led students in all the groups to discover the sufficient conditions for congruent triangles. Through cutting out and covering, students realized which conditions do not lead to triangle congruence: equality in one side; equality in one side and one angle; and, equality in three angles. Episode 5 presents how students investigated insufficient conditions for triangle congruence.

Episode 5: Insufficient conditions for triangle congruence

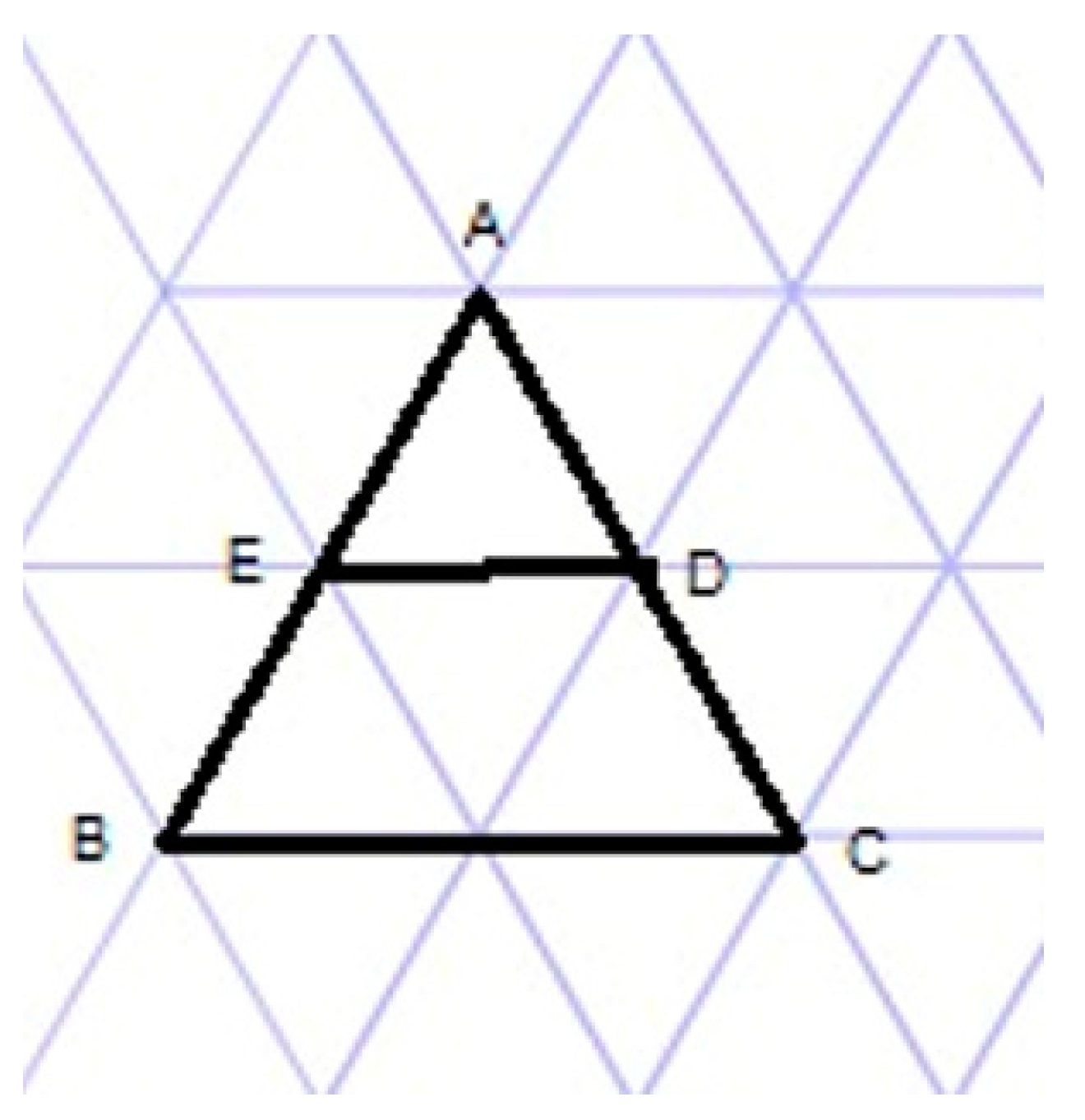
(102)	Reem:	There are corresponding sides that are equal in triangles BDE and BDA (see Figure 3).
(105)	Nagam:	ED.
(107)	Saja:	No, it is BD.
(111)	Reem:	In this ornamentation the triangles are not congruent; one is a big ornament, and one is a small ornament.
(116)	Reem:	Two equal corresponding sides in two triangles is not a sufficient condition for congruence.
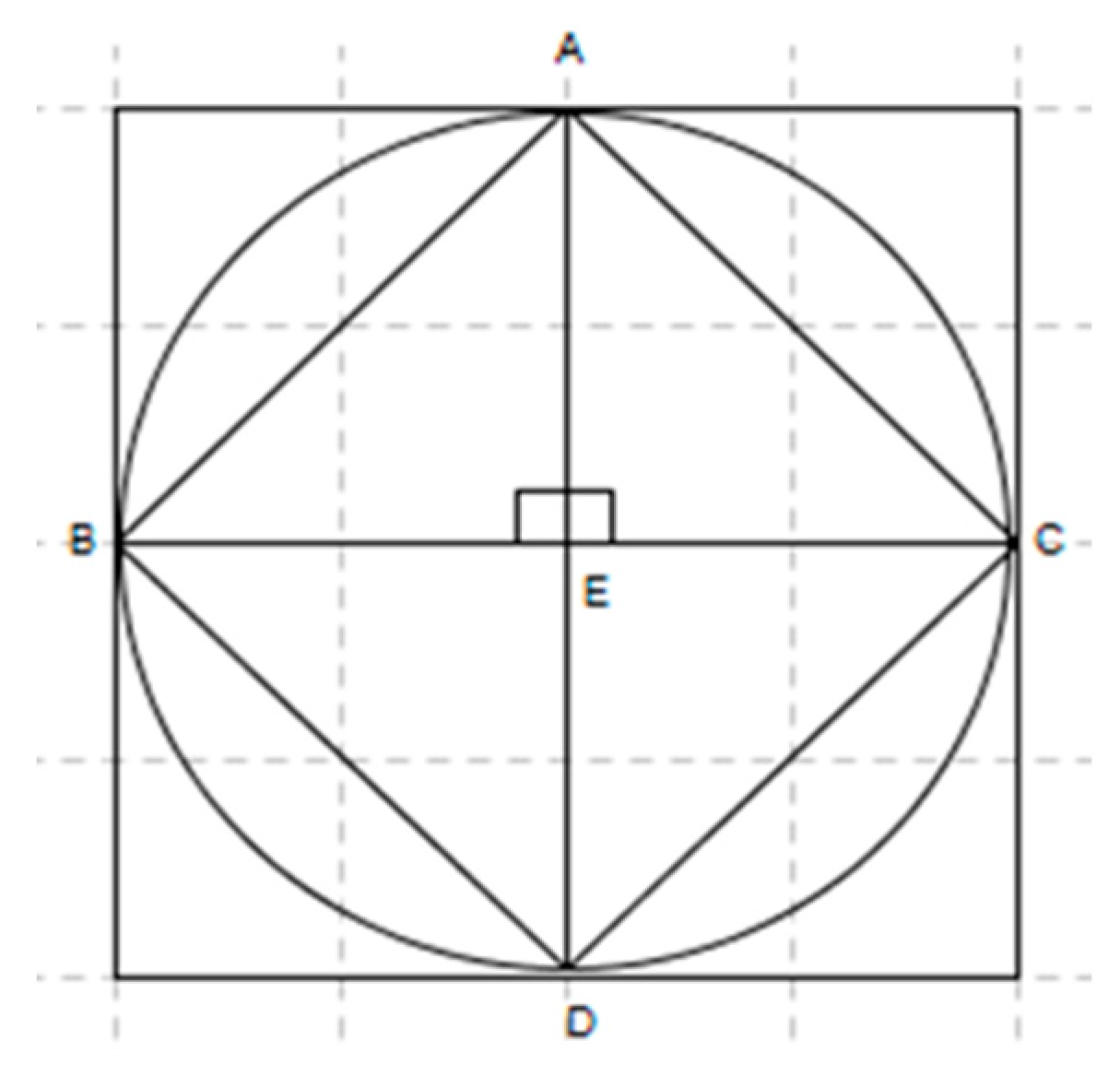
(117)	Marah:	Look at this ornamentation (see Figure 4), we need to find out if all the corresponding angles and sides are equal in triangles ABC and BDC.
(119)	Saja:	The side BC.
(123)	Nagam:	The angles B and D.
(126)	Saja:	One side and one angle are sufficient for congruence.
(127)	Marah:	No, not enough—one is big, and one is small.
(130)	Saja:	Now, the third ornamentation (see Figure 5). We need to check if the angles in triangles ABC and AED are equal.
(132)	Saja:	We have two parallel lines here, so the corresponding angles are equal.
(133)	Marah:	All the corresponding angles are equal.
(135)	Nagam:	But the triangles are not congruent; one is big, and the other is small.
(137)	Saja:	That means, three equal angles are not sufficient for congruent triangles.

Episode 5 demonstrates an insufficient condition for congruence in triangles. Looking at one big and one small ornament, Saja (107) found that BD is a mutual side in the two triangles BDE and BDA; Reem (111) showed understanding of the concept of congruence, claiming that the triangles are not congruent, and emphasizing in (116) that one side is an insufficient condition for congruent triangles. Similarly, Saja (126) and Marah (127) inferred that one side and one angle were insufficient conditions for congruent triangles. Nagam (135) explained why three equal angles are insufficient for congruence, while Saja (137) inferred an appropriate conclusion.

4.2.1. The First Theorem of Triangle Congruence: (S, A, S)

Students in all the groups performed a construction task which involved drawing the ornamentation, then cutting out and covering the triangles to verify their congruence. The students concluded that two sides and their included angle are sufficient conditions for triangle congruence. Afterwards, the students succeeded in formulating the first theorem (S, A, S), as presented in Episode 6.

Episode 6: Investigation of the first congruence theorem (S, A, S)

(139)	Reem:	There are equal corresponding angles and sides in triangles AEB and AEC in the ornamentation (see Figure 6).
(140)	Saja:	EC and BE.
(142)	Reem	According to the ornamentation, the length of each one of their lengths is half the big square’s side.
(143)	Nagam:	AE and AE; AE is mutual.
(145)	Saja:	The angle, E, is equal to 90.
(147)	Taqwa:	So that means we have two sides and their included angle, which are equal.
(148)	Teacher	What about the congruence?
(149)	Saja:	Yes.
(150)	Taqwa:	They are congruent. What can we say about the conditions?
(151)	Saja:	Two equal sides.
(153)	Taqwa:	And angle?
(154)	Saja:	The angle must be in the middle.
(157)	Nagam:	Three elements, two sides, and one angle between the sides.

Episode 6 shows that Saja (140, 145) and Nagam (143) were able to infer the equal sides and equal angles between the triangles in the ornamentation, by making connections between the ornamentation characteristics and geometric shapes. Saja (151 and 154) and Taqwa (153) inferred the conditions for the congruence of the triangles, while Nagam (157) formulated the conclusion of the first congruence theorem.

4.2.2. The Second Theorem of Triangle Congruence: (A, S, A)

When they drew triangle ornamentation using a protractor and ruler, the students found it difficult to draw triangles according to two angles and one side. The teacher’s guidance helped them to overcome this difficulty. After drawing the ornamentation, the students cut out and covered it with triangles; in doing so, they arrived at the second theorem of congruent triangles (A, S, A). Finally, the students formalized their knowledge by writing the proof of the second theorem (A, S, A). Episode 7 presents the students’ discussion while performing the above task.

Episode 7: Inquiry about the second congruent triangle theorem: (A, S, A)

(160)	Saja:	We need to draw triangles with angles 50° and 60°, and sides with a 5 cm length between them.
(161)	Taqwa:	How can we do it?
(162)	Teacher:	You must use the protractor to draw the angles.
(163)	Nagam:	Does it measure the sides?
(164)	Taqwa:	No, it is only for angles.
(165)	Teacher:	This point is the zero point, and the rays assign any angle we want…
(167)	Nagam:	First, we draw a segment 5 cm long.
(177)	Saja:	So, we need to put the protractor on the end point of the segment [she draws while talking] and here, 50° [using the protractor]. We assign a mark, and we assign an angle of 60° on the other side of the segment [again, using the protractor]. Now we draw the lines that connect these two points.
(178)	Marah:	We want to cut out one triangle.
Students draw several triangles using the same method.
(181)	Reem:	They are congruent.
(186)	Teacher:	What is the condition for congruence?
(187)	Nagam:	That they [the triangles] have the same angles.
(189)	Saja:	Two angles.
(191)	Marah:	And one side between the angles.
(195)	Taqwa:	We can conclude that, with the three conditions present—two angles, and one side between them—we have triangle congruence.

Episode 7 presents the difficulties students had when drawing angles; for example, Taqwa struggled (161). However, with the teacher’s guidance they overcame these difficulties, as seen when Saja (177) and Nagam (163) tried to make a connection between the geometric tool and the task itself. Marah (178) and Reem (181) used cutting and covering to prove congruence. Nagam (187), Saga (189), and Marah (191) infer the conditions for the second theorem, while Taqwa (195) formulated the theorem.

4.2.3. The Third Theorem of Triangle Congruence: (S, S, S)

Students in all the groups arrived at the third congruence theorem through their engagement in drawing ornamentation. Here too, they used the cutting and covering of ornaments, and afterwards recorded the corresponding sides of the congruent triangles. The students also discussed different options for the congruent triangle side lengths; i.e. either an isosceles triangle, an equilateral triangle or a different-sided triangle. In doing this, the students concluded the third congruence theorem. Episodes 8 and 9 represent the group’s discussions regarding isosceles and equilateral triangles (Episode 8), and different-sided triangles (Episode 9).

Episode 8: Discussing the third congruence theory, regarding isosceles and equilateral triangles

(306)	Doa’a:	Draw a triangle, each side is 3 cm.
(The students draw and cut out different equilateral triangles)
(309)	Abed:	All these triangles [he puts the triangles on top of one another] are congruent.
(314)	Aya:	We need to write down the corresponding sides.
(318)	Noor:	DE=AB; DF=AC; EF=BC.
(321)	Aya:	Now we need to draw triangles with sides 4,3,4
		[The students draw and cut out different isosceles triangles]
(329)	Doa’a:	The triangles are congruent.
(339)	Doa’a:	It is sufficient that three sides in two triangles are equal, to have congruence.

Episode 8 shows that students arrived at the sufficient condition (S, S, S). To start with, Doa’a (306) showed her understanding of the task by describing an equilateral triangle, while Abed (309) showed understanding of the congruence concept. Aya (321) and Doa’a (329), discussed the congruence of isosceles triangles. As a result of this discussion, they inferred and formulated the sufficient conditions. as presented in Doa’a’s (339) declaration.

Episode 9: Discussing the third congruence theory, regarding isosceles and equilateral triangles

(200)	Marah:	This triangle (she draws a triangle in the ornamentation; see Figure 7).
(201)	Nagam:	See these triangles [she cuts out and covers one triangle with another].
(207)	Teacher:	Try to name the triangles in the ornamentation and write down the corresponding sides.
(208)	Nagam:	[Pointing at two triangles in the ornamentation] This is DEF, and this is ABC.
(211)	Marah:	AB=DE
(212)	Taqwa:	DF=AC
(213)	Saja:	EF=BC
(215)	Marah:	These triangles, DEF and ABC, have different lengths.
(218)	Reem:	They are congruent.
(223)	Marah:	When three corresponding sides are equal in two triangles, the triangles are congruent.

Episode 9 presents how the students inferred the third congruence theorem, with regard to isosceles and equilateral triangles. They managed it through drawing, like Marah (200), and through cutting and covering, like Nagam (201). Afterwards, the students were able to write down the corresponding sides in the congruent triangles (211–213). At the end of the activity, Marah (223) formalized the third congruence theory (S, S, S).

4.3. The Impact of Working with Ornamentation on Students’ Proving Processes

The results obtained from analyzing students’ proving processes indicated the positive influence of working with ornamentation. Before working with ornamentation, the students wrote claims which were without any justification; they also added data which were neither provided for the task nor concluded as a result of doing the task. Moreover, they wrote the congruence theorem without all the sufficient conditions, or wrote the sufficient conditions without indicating the specific congruence theorem. In addition, some students used incorrect justification before working with ornamentation. These processes are exemplified in Tasks 1 and 2, below.

Task 1: AC is an angle bisector of ∢BAD and ∢BCD (see Figure 8)

Prove that:

ΔABC ≅ ΔADC

BC = DC

Task 2: In Figure 9, given:

∢C = ∢A

E is the middle of AC

Prove that E is the midpoint of BD

• Writing the claim without an explanation: Student’s text indicates that the proof did not include explanations regarding the properties of the triangle. An example on students’ writing a claim without an explanation is shown in Figure 10.
• Writing the congruent theory only—writing the congruent theory only, without writing the phases of the proof. As an example, students wrote (A, S, A) only in their explanation of Task 1.
• Additional data: Students added data through their proofing, such as the equalities between the sides (BC=DC; AB=AD) in Task 1, where these equalities were not given in the question.
• The congruent theory is not mentioned—students write the qualities in the two triangles but did not wrote the appropriate congruent theory. An example is shown in Figure 11.
• One of the conditions is missing—students wrote only two conditions. An example is shown in Figure 12.
• Writing the wrong explanation—an explanation is shown in Figure 13.

The processes mentioned previously are examples of the students’ justification processes with regard to the three congruence theorems. Our analysis of students’ answers to questionnaires A and B indicated the positive effect of the Islamic-ornamentation-based learning process. This was reflected in how the students’ geometric proving processes regarding congruent triangles improved. The paired simple t-test indicated a significant difference (t (29) = −17.14, p < 001) between students’ mean scores in questionnaire B (M = 88.6, SD = 11.57) and questionnaire A (M = 15.9, SD = 10.137), in favor of the questionnaire B answers.

5. Discussion

The current research aimed to study the effect of using Islamic ornamentation on 10th-grade Muslim students learning the topic of congruent triangles. As observed in the pre-test results, the students had various difficulties in defining the concepts of congruence and congruent triangles, and in their proving processes related to this topic. Most of the difficulties observed in the pre-test related to students writing claims without justification, adding data not included in the task, concluding the congruence theorem without writing the sufficient conditions, or writing the sufficient conditions but not indicating the specific congruence theorem. The students’ difficulties were anticipated, as they have been highlighted previously by various researchers [16]. Most of these difficulties were also reported, in Wang et al. [18], as being specific to eighth grade students. The rationale for the current study emerged from the results of previous researchers’ studies, and the study itself is designed to contribute to the existing body of research on ethnomathematics.

The Islamic ornamentation at the core of the ethnomathematics learning in the current study includes different forms of geometry transformation—reflection, translation, and rotation. Students engaged in these transformations through their drawing, by making connections between the ornaments and geometric shapes, imagining transformations of these shapes, and inferring the conditions for the theorems. Thus, ornamentation enabled the students to advance from concrete to abstract thinking. This is in line with Gravemeijer [48], who argues that realistic mathematics allows for the consideration of different aspects of society through mathematics, including cultural aspects. This is because concrete things can be observed, or understood, by learners through the process of mathematization, as mathematics becomes a reflection of the real world via an empirical abstraction process. In the present research, ornamentation was a realistic ethnomathematics tool that enabled the empirical abstraction process.

The main findings indicated that sequences of activities that are based on Islamic ornamentation had a positive effect on Muslim students learning the topic of congruent triangles. The students succeeded in defining the congruent triangles, inferring the conditions for congruent triangles, formulating the corresponding theorems, and engaging in proving based on the congruence theorems. The students’ success in proving claims can be attributed to their imagining, connecting, and inferring processes, which enabled them to understand the minimal number of conditions sufficient for congruence, which is considered a key concept for understanding congruence [40]. The study results emphasize the positive effect of integrating ethnomathematics activities into students’ learning of geometric concepts and relationships; here, the congruence theorems. As such, it supports other studies emphasizing the effect of ethnomathematics on learning various mathematical concepts and subjects. Specifically, ethnomathematics previously had a positive effect on students’ understanding of the linear equation system in two variables [28] and on the learning of fractions via pattern that is familiar to many students after the second grade [49]. It also had a positive effect on senior high school students’ learning of problem solving [50]. The previous literature and the present study both confirm that ethnomathematics could be utilized in learning different mathematical topics.

The findings, relating to students’ processes when learning the congruence theorems by working with ornamentation, indicated that the students succeeded in formulating the congruent triangle theorems and proofing claims based on the congruent triangles. These findings can be explained by two main factors.

First, the ornamentation related to the shared culture of the students, and thus it positively influenced their motivation for learning and inquiring; this factor is already supported by different studies [24,51]. The increase in students’ motivation positively affected their learning strategies, cognitive resources, and learning achievements [52].

The second factor relates to the concrete and abstract ornamentation activities and the different features of the ornamentation, such as repetitive and symmetrical shapes. Thus, the concrete and abstract activities designed for the current study, and considered as a supportive learning environment for students, enabled students to interact physically with objects via feeling, seeing, and touching [53]. The students’ successful answers to proofing questions in questionnaire B can be connected to their use of geometric transformations. Our findings support those of Fan, Qi, Liu, Wang, and Lin [54], who reported that geometric transformations can help improve students’ ability to solve geometric proofing problems.

In the present research, we studied students’ conceptual understanding of triangles’ congruence using a conceptual framework, where it is recommended to use other conceptual frameworks and other methodologies that are suggested to assess different aspects of students’ learning. Examples are the commognition framework [55,56], which is suggested to assess sharing knowledge; facial expression recognition, which is suggested to assess engagement [57]; or multi-block deep learning, which is suggested to assess emotions [58].

6. Conclusions

Ethnomathematics is involved in fitting the learning context to learners’ features. Fitting the context of the learner’s features included in our case providing a learning context that is related to the learner’s culture. This fitting is expected to result in enriching the various aspects of students’ learning, where here we focused on the cognitive aspect of this learning.

The findings of the present study indicated that the ethnomathematics context supports students; even those with difficulties in mathematics leaning, in understanding the triangles’ congruence, in overcoming their different mistakes, and difficulties through proving activities and tasks that are based on Islamic ornamentation and art to target the triangle congruence theorems. Based on these findings, the following conclusions are in place. The first conclusion is that the Islamic ornamentation is a rich tool for teaching and learning the triangles’ congruence, where the features of the ornaments provide the opportunity to understand the sufficient and insufficient conditions for triangles’ congruence. The second conclusion is related to the efficiency of students’ learning in a cultural context. The ethnomathematics activities were fruitful for students’ concrete and abstract learning processes regarding geometric concepts and relationships; even for students with difficulties as described in the present research. The previous argument emphasizes the importance of designing ethnomathematics activities for various mathematical topics and students of various mathematics levels.

We join the call to design mathematics curricula that relate to students’ ethnic backgrounds and which help build a bridge between the students’ background knowledge and their knowledge of formal mathematics. The ethno-aspect could be extended to be utilized not only in mathematics but in the sciences in general, in addition to blending of disciplines as STEM (science, technology, engineering, and mathematics) and STEAM (science, technology, engineering, art, and mathematics).

Future research is requested to study the various aspects of students’ learning in ethnomathematics contexts, including the cognitive, metacognitive, affective, meta-affective, social, and behavioral aspects. In addition, we suggest that ethnomathematics be utilized not only in real classroom environments but also in virtual ones, where this utilization has been reported in teacher’s education. Little attempts have been reported for students’ learning in K12, where these attempts and relevant research are needed.