Development of Energy-Based Impact Formula—Part I: Penetration Depth
Abstract
:1. Introduction
2. Literature Review
3. Development of New Energy-Based Penetration Formula
3.1. Concept of New Formula
3.1.1. Impact Mechanism and Energy Conservation
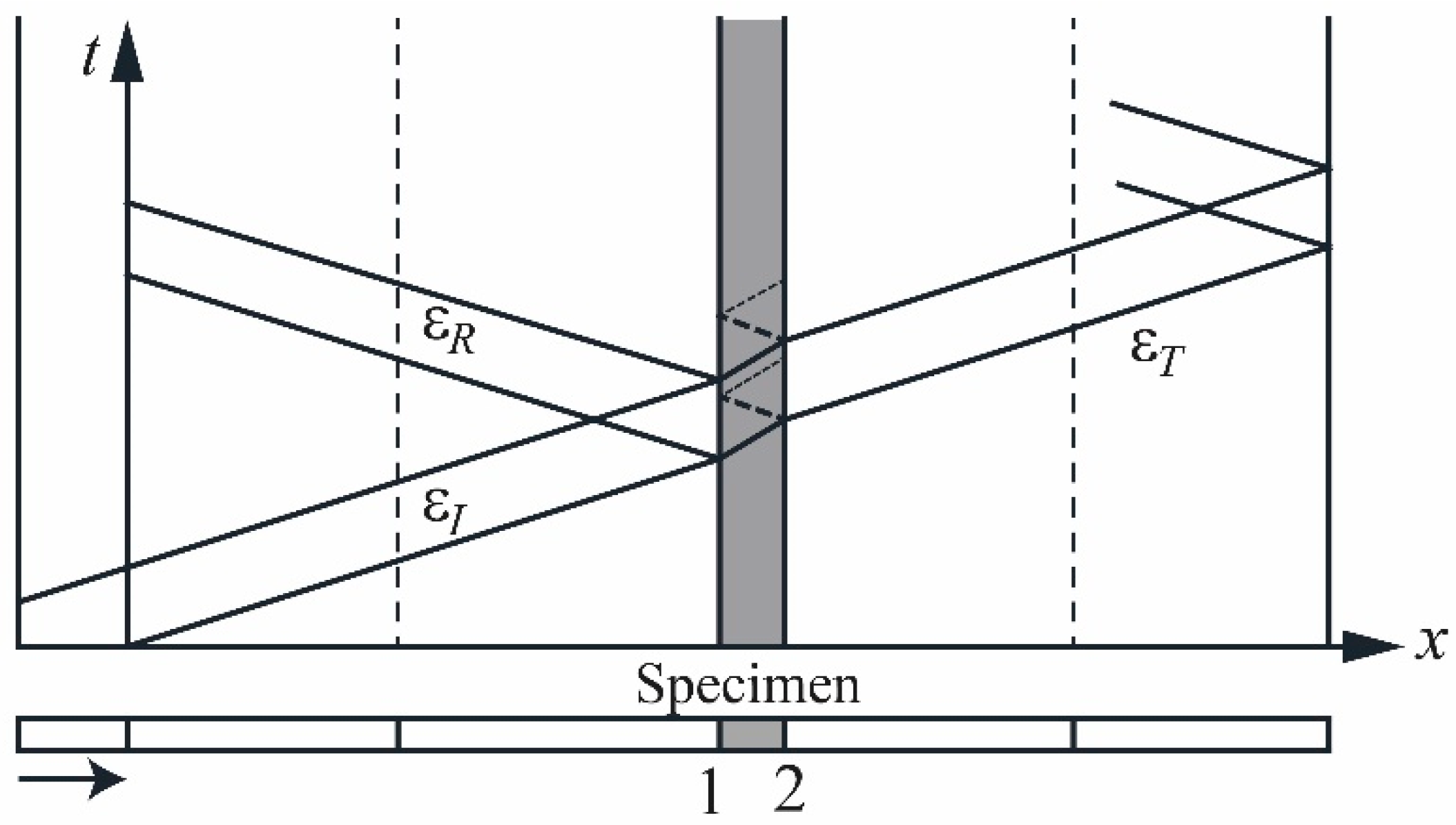
3.1.2. Forces Acting in Impact Mechanism
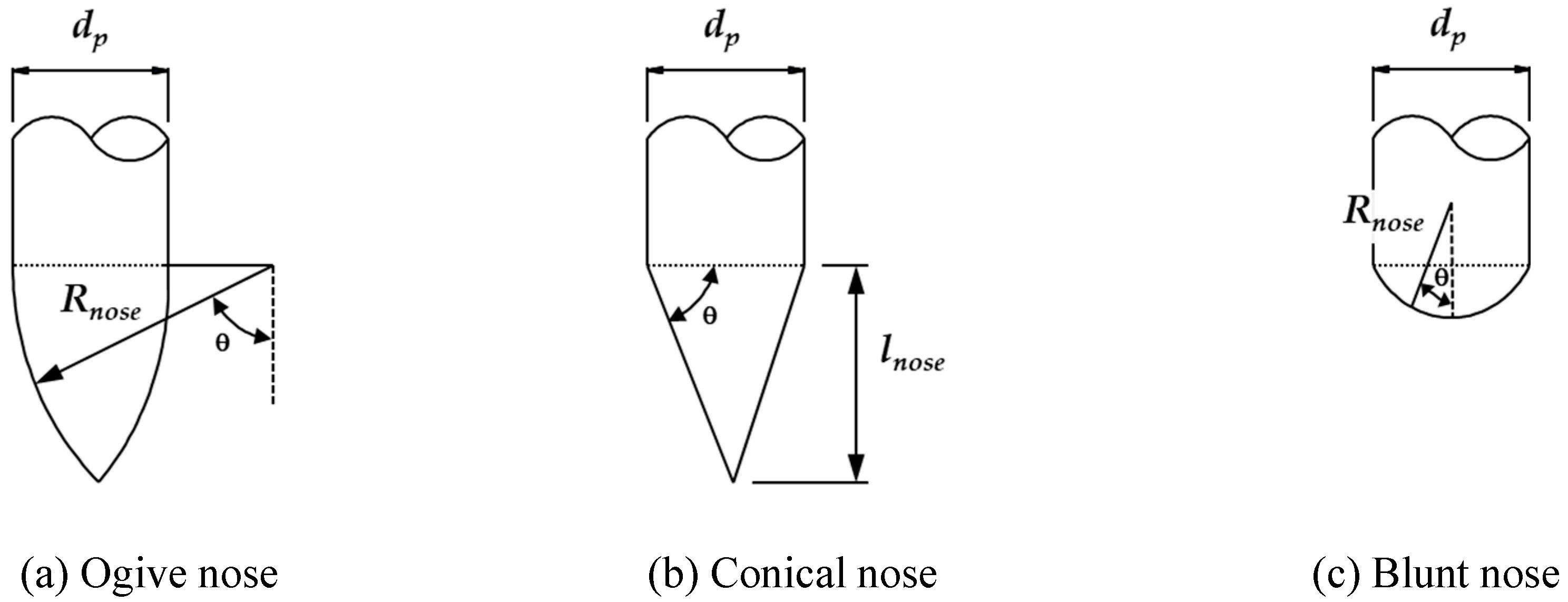
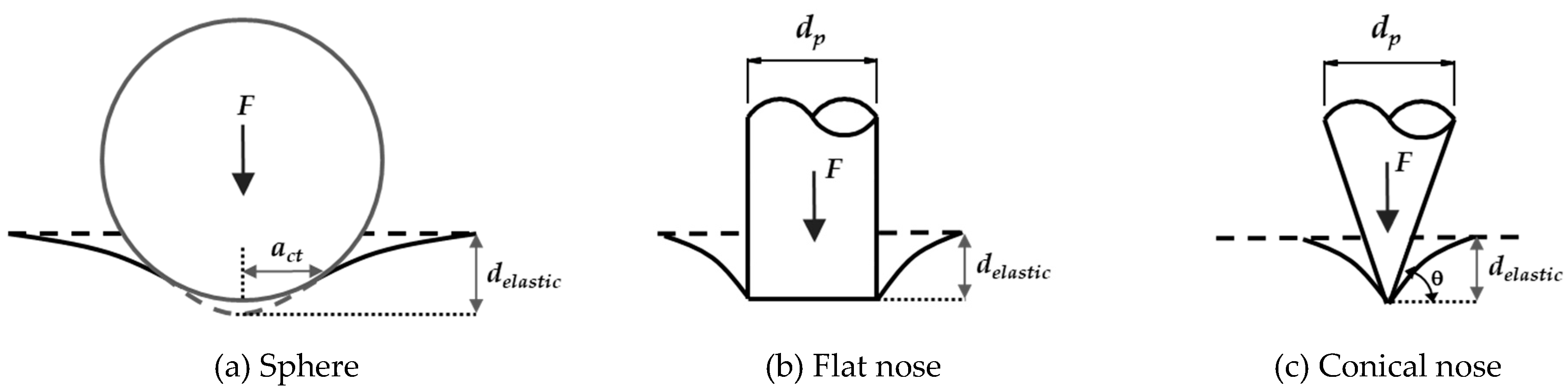
3.1.3. Force on the Nose of a Projectile
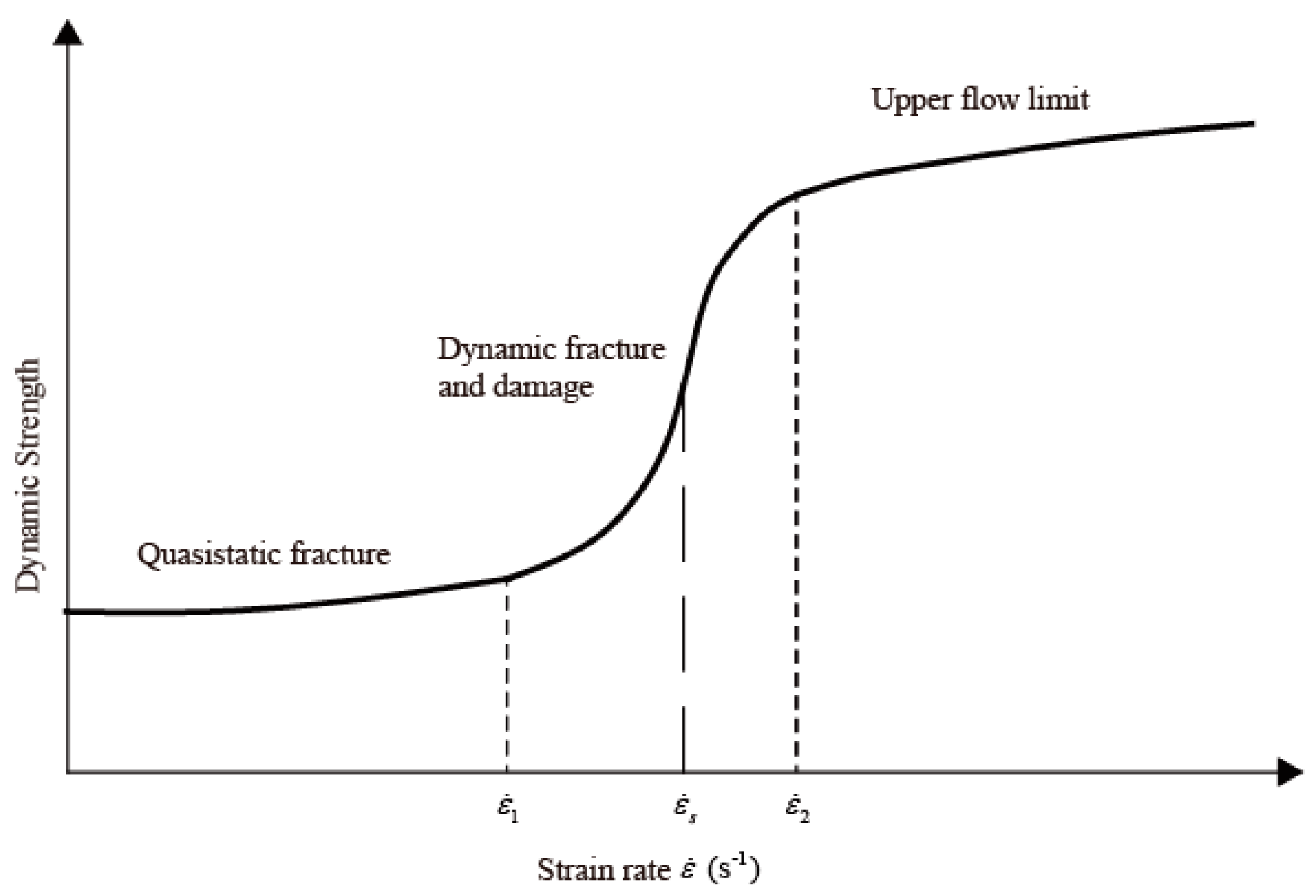
3.1.4. Properties of Materials Affected by Strain Rate
- a
- Properties of concrete affected by strain rate
- b
- Properties of steel affected by strain rate
3.2. Involved Energies in Impact Mechanism
3.2.1. Kinetic Energy (EK)
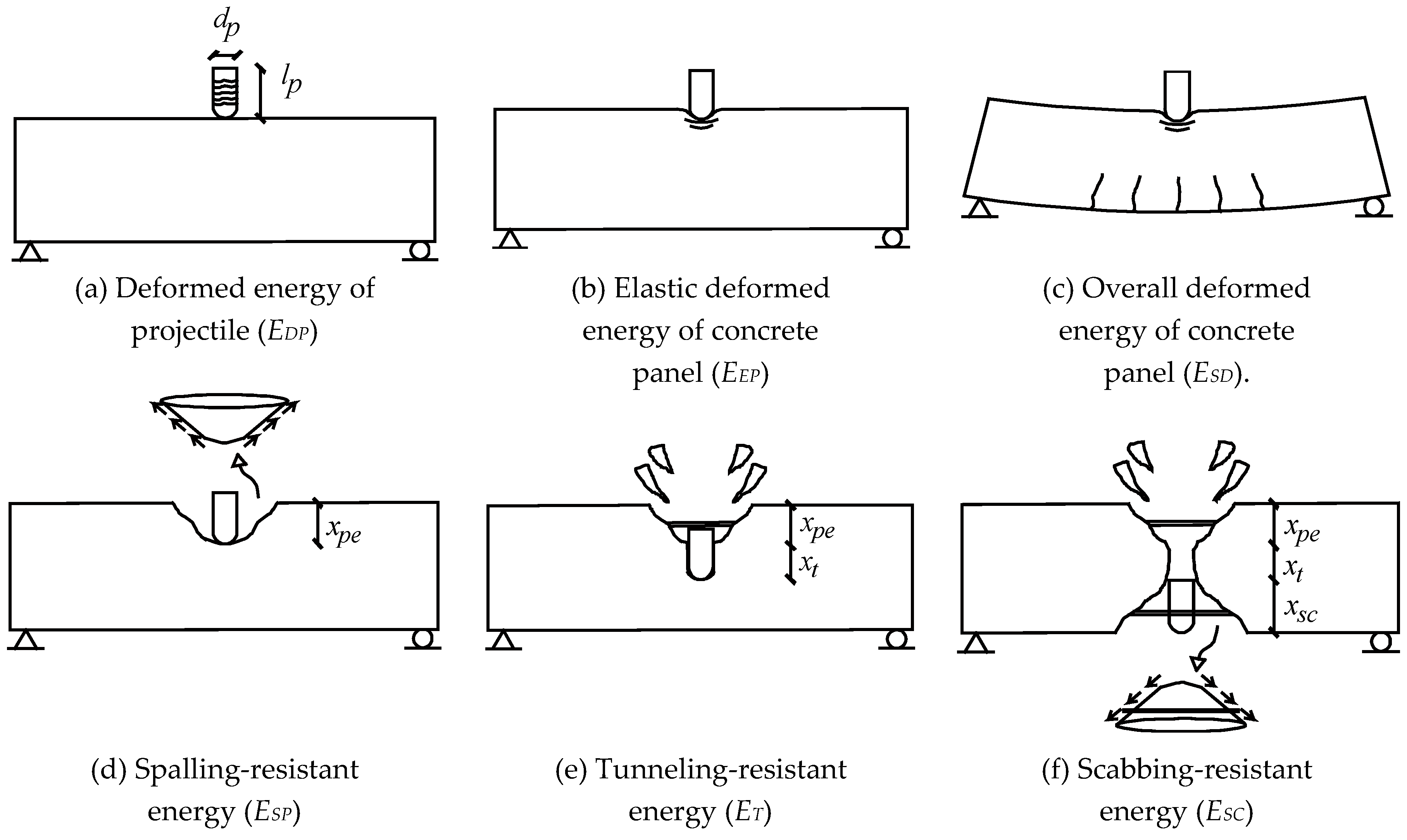
3.2.2. Deformed Energy of Projectile (EDP)
3.2.3. Elastic Penetrated Energy of Concrete Panel (EEP)
3.2.4. Overall Deformed Energy of Concrete Panel (ESD)
3.2.5. Spalling-Resistant Energy (ESP)
3.2.6. Tunneling-Resistant Energy (ET)
3.3. Penetration Depth Formula
4. Verification of Developed Impact Formula
4.1. Comparison between Test Results and Predictions
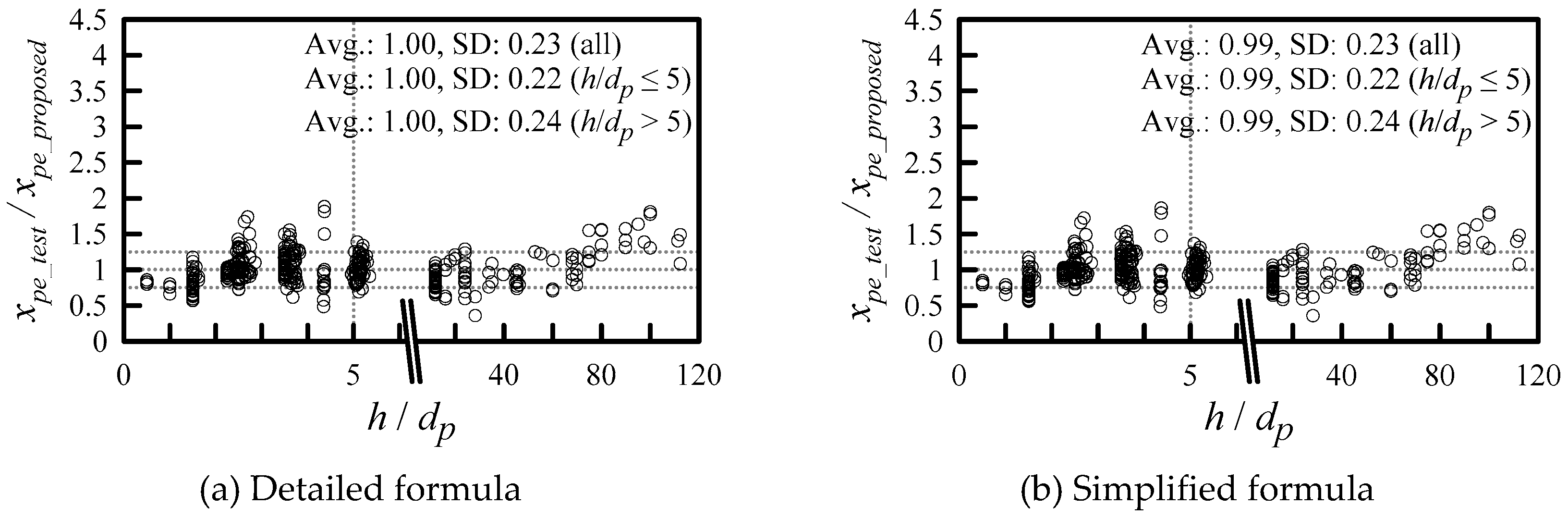
4.2. Penetration Depth Assessment
4.3. Critical Impact Mechanism
5. Conclusions
- There are six types of energies involved in the penetration failure of a concrete panel colliding with a high-velocity projectile. These are the kinetic energy of a projectile (EK), deformed energy of a projectile (EDP), elastic penetrated energy of the target concrete panel (EEP), overall deformed energy (ESD), spalling-resistant energy of a concrete panel (ESP), and tunneling-resistant energy (ET), which occurs when the kinetic energy is concentrated by a long projectile and/or high velocity. Using these energies and energy conservation law, a new energy-based penetration depth formula is derived.
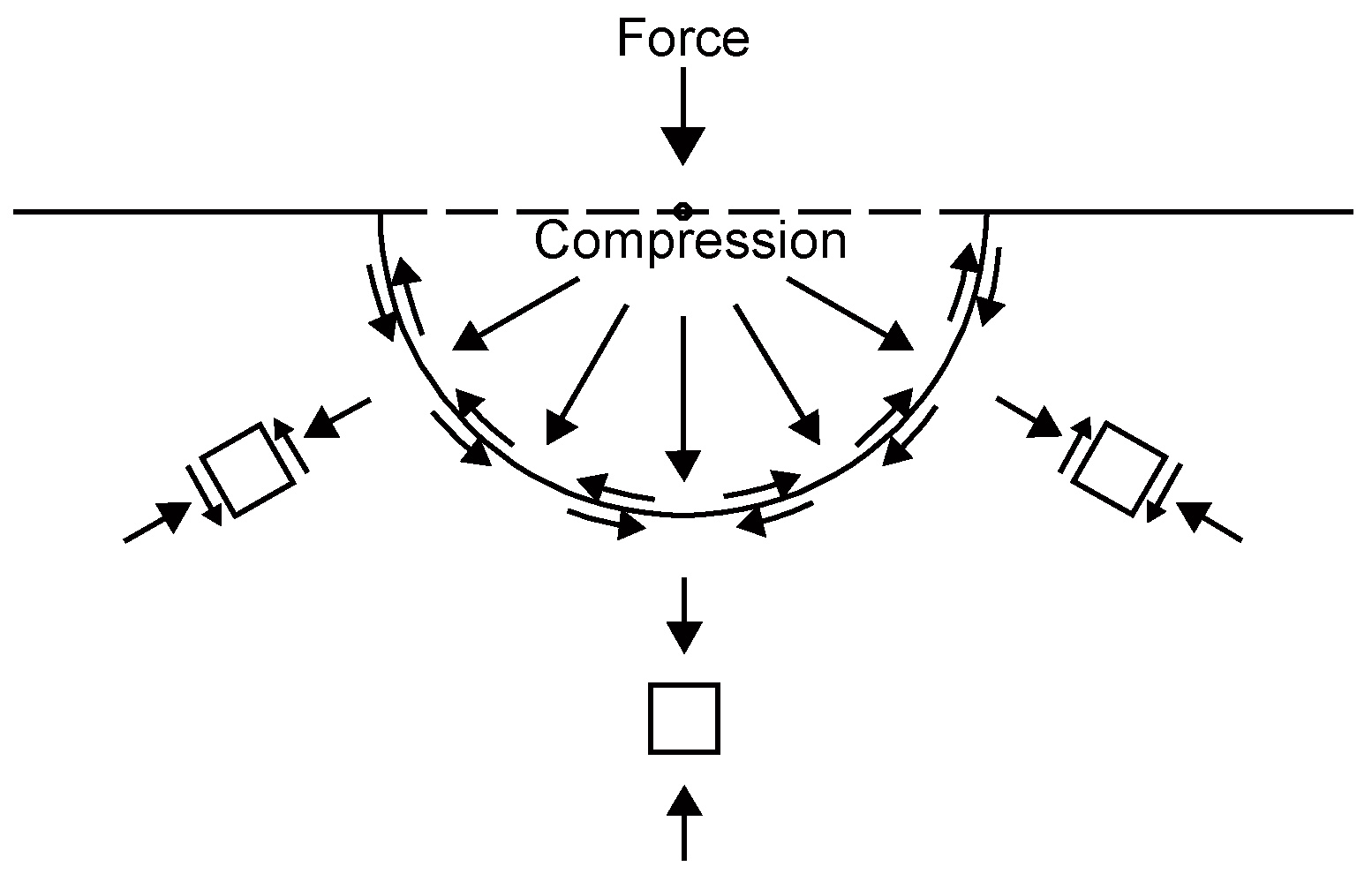
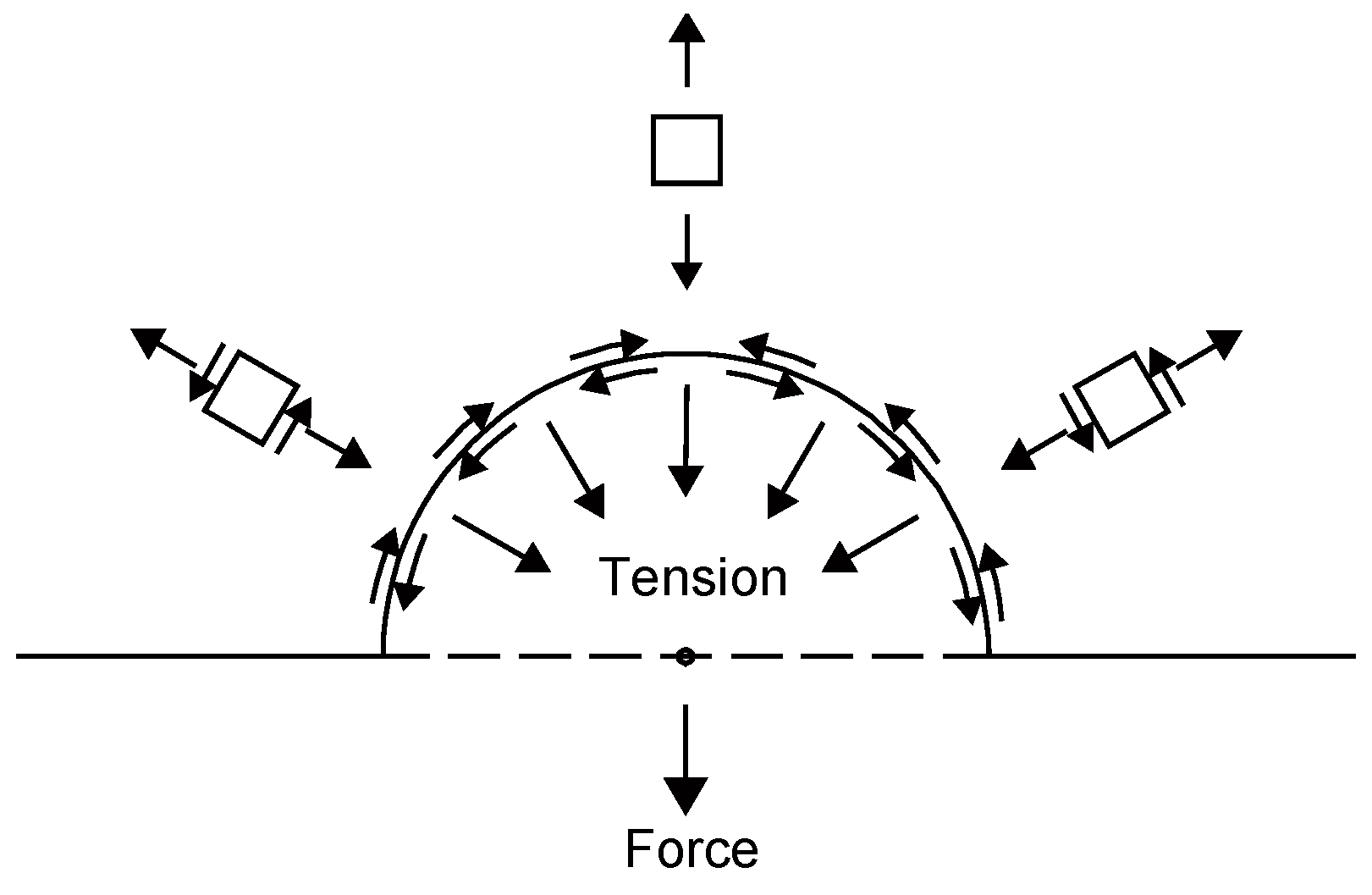
- The spalled cone is related to the shear stress controlled by compression, while the scabbed cone is related to that controlled by tension. These shear stresses must account for the strain rate effect, where the fib Model Code 2010 (fib, 2010) is used in this study. The strain rate is defined as the force applied on the projectile’s nose, as suggested by Forrestal et al. (1994), and is newly derived in this paper by using the theoretical background.
- The penetration depth formula is derived using the drag force, volume, and area of the spalled cone, which leads to an energy density. The spalling energy can be concentrated by a high velocity and/or a long projectile, and these effects can be applied to the penetration depth formula. The concentrated energy can produce the tunneling depth, which is also derived from the energy density.
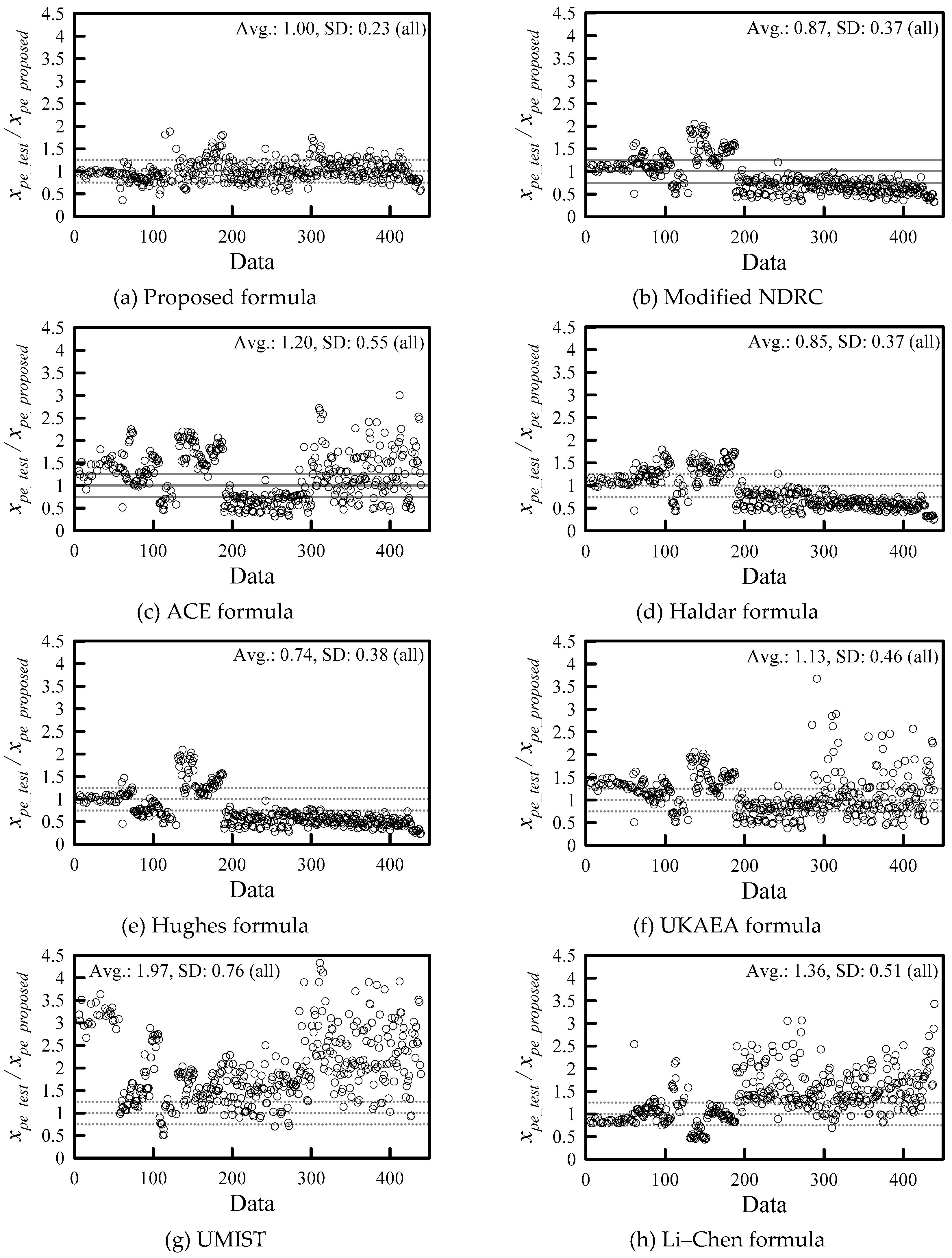
- The accuracy of the new penetration depth formula is examined and compared to the existing impact formulae, such as the modified NDRC, ACE, Haldar, UKAEA, UMIST, and Li–Chen formulae. The mean value of the tested penetration depth compared to the predicted penetration depth of the new impact formula is 1, meaning that it is the best of these impact formulae. The standard deviation of the new impact formula for predicting the penetration depth is 0.23, which is also the best.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Probst, A.D.; Kang, T.H.-K.; Ramseyer, C.; Kim, U. Composite Flexural Behavior of Full-Scale Concrete Filled Tubes without Axial Loads. ASCE J. Struct. Eng. 2010, 136, 1401–1412. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Kim, W.; Massone, L.M.; Galleguillos, T.A. Shear-Flexure Coupling Behavior of Steel Fiber-Reinforced Concrete Beams. ACI Struct. J. 2012, 109, 435–444. [Google Scholar]
- Kang, T.H.-K.; Wallace, J.W. Punching of Reinforced and Post-Tensioned Concrete Slab-Column Connections. ACI Struct. J. 2006, 103, 531–540. [Google Scholar]
- Lee, C.H. Structural Behavior and Progressive Collapse Prevention under Abnormal Extreme Loading. Mag. Archit. Inst. Korea 2007, 51, 15. (In Korean) [Google Scholar]
- Li, Q.M.; Reid, S.R.; Wen, H.M.; Telford, A.R. Local Impact Effects of Hard Missiles on Concrete Targets. Int. J. Impact Eng. 2005, 32, 224–284. [Google Scholar] [CrossRef]
- Kim, T.W.; Hahm, H.G. The Strength Properties Activated Granulated Ground Blast Furnace Slag with Aluminum Potassium Sulfate and Sodium Hydroxide. J. Korea Concr. Inst. 2015, 27, 95–102. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.J.; Kim, S.; Kang, T.H.K. Energy-Based Penetration Model for Local Impact Damaged Concrete Members. ACI Struct. J. 2017, 114, 1189–1200. [Google Scholar] [CrossRef]
- ACE. Fundamentals of Protective Structures; Technical Report No. AT120 AT1207821; Army Corps of Engineering: Washington, DC, USA, 1946. [Google Scholar]
- NDRC. Effect of impact and explosion. In Summary Technical Report of Division 2; National Defense Research Committee: Washington, DC, USA, 1946; Volume 1. [Google Scholar]
- Kennedy, R.P. A Review of Procedures for the Analysis and Design of Concrete Structures to Resist Missile Impact Effects. Nucl. Eng. Des. 1976, 37, 183–203. [Google Scholar] [CrossRef]
- Haladar, A.; Miller, F.J. Penetration Depth in Concrete for Nondeformable Missiles. Nucl. Eng. Des. 1982, 71, 79–88. [Google Scholar] [CrossRef]
- Haldar, A.; Hamieh, H. Local Effect of Solid Missiles on Concrete Structures. ASCE J. Struct. Eng. 1984, 110, 948–960. [Google Scholar] [CrossRef]
- Hughes, G. Hard Missile Impact on Reinforced Concrete. Nucl. Eng. Des. 1984, 77, 23–25. [Google Scholar] [CrossRef]
- Barr, P. Guidelines for the Design and Assessment of Concrete Structures Subjected to Impact; Technical Report No. SRD-R-439; UK Atomic Energy Authority, Safety and Reliability Directorate: Abingdon, UK, 1990. [Google Scholar]
- Reid, S.R.; Wen, H.M. Predicting Penetration, Cone Cracking, Scabbing and Perforation of Reinforced Concrete Targets Struck by Flat-Faced Projectiles; Technical Report No. ME/AM/02.01/TE/G/018507/Z; University of Manchester Institute of Science and Technology (UMIST): Manchester, UK, 2001. [Google Scholar]
- BNFL. Appendix H reinforced concrete slab local damage assessment. In R3 Impact Assessment Procedure; Magnox Electric plc & Nuclear Electric Limited: Berkeley, Gloucestershire, UK, 2003; Volume 3. [Google Scholar]
- Kong, X.Z.; Wu, H.; Fang, Q.; Peng, Y. Rigid and Eroding Projectile Penetration into Concrete Targets Based on an Extended Dynamic Cavity Expansion Model. Int. J. Impact Eng. 2017, 100, 13–22. [Google Scholar] [CrossRef]
- Bishop, R.F.; Hill, R.; Mott, N.F. The Theory of Indentation and Hardness Test. Proc. Phys. Soc. 1945, 57, 147–159. [Google Scholar] [CrossRef]
- Li, Q.M.; Tong, D.J. Perforation Thickness and Ballistic Limit of Concrete Target Subjected to Rigid Projectile Impact. J. Eng. Mech. 2003, 129, 1083–1091. [Google Scholar] [CrossRef]
- Hopkins, H.G. Dynamic expansion of spherical cavities in metal. In Progress in Solid Mechanics; Sneddon, I.N., Hill, R., Eds.; North-Holland Publishing Company: Amsterdam, North Holland, The Netherlands, 1960; Volume 1. [Google Scholar]
- Forrestal, M.J.; Luk, V.K. Dynamic Spherical Cavity-Expansion in a Compressible Elastic-Plastic Solid. J. Appl. Mech. 1988, 55, 275–297. [Google Scholar] [CrossRef]
- Luk, V.K.; Forrestal, M.J. Penetration into Semi-Infinite Reinforced-Concrete Targets with Spherical and Ogival Nose Projectiles. Int. J. Impact Eng. 1987, 6, 291–301. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Luk, V.K. Penetration into Soil Targets. Int. J. Impact Eng. 1992, 12, 427–444. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Altman, B.S.; Cargile, J.D.; Hanchak, S.J. An Empirical Equation for Penetration Depth of Ogive-Nose Projectiles into Concrete Targets. Int. J. Impact Eng. 1994, 15, 395–405. [Google Scholar] [CrossRef]
- Li, Q.M.; Chen, X.W. Dimensionless Formulae for Penetration Depth of Concrete Target impacted by a non-deformable Projectile. Int. J. Impact Eng. 2003, 28, 93–116. [Google Scholar] [CrossRef]
- Chen, X.W.; Li, Q.M. Deep Penetration of a Non-Deformable Projectile with Different Geometrical Characteristics. Int. J. Impact Eng. 2002, 27, 619–637. [Google Scholar] [CrossRef]
- Choi, K.K.; Park, H.G. Shear Strength Model for Interior Flat Plate-Column Connections. J. Korea Concr. Inst. 2010, 22, 345–356. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Choi, K.K.; Kim, S.H.; Kim, D.H.; Park, H.G. Direct Punching Shear Strength Model for Interior Slab-Column Connections and Column Footings with Shear Reinforcement. J. Korea Concr. Inst. 2011, 23, 159–168. (In Korean) [Google Scholar] [CrossRef]
- Choi, K.K.; Park, H.G.; Kim, H.M. Shear Strength Model for Slab-Column Connections. J. Korea Concr. Inst. 2010, 22, 585–593. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Choi, K.K.; Shin, D.W.; Park, H.G. Shear-Strength Model for Slab-Column Connections Subjected to Unbalanced Moment. ACI Struct. J. 2014, 111, 491–502. [Google Scholar] [CrossRef]
- Park, H.G.; Choi, K.K.; Chung, L. Strain-Based Strength Model for Direct Punching Shear of Interior Slab-Column Connections. Eng. Struct. 2011, 33, 1062–1073. [Google Scholar] [CrossRef]
- fib. Model Code for Concrete Structures 2010 (fib Model Code 2010); Ernst & Sohn: Berlin, Germany, 2010. [Google Scholar]
- ACI Committee 224. Control of Cracking in Concrete Structures (ACI 224R-01); American Concrete Institute: Farmington Hills, MI, USA, 2001. [Google Scholar]
- ACI Committee 318. Building Code Requirement for Structural Concrete and Commentary (ACI 318-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Musmar, M. Tensile Strength of Steel Fiber Reinforced Concrete. Contemp. Eng. Sci. 2013, 6, 225–237. [Google Scholar] [CrossRef]
- Williams, M.S. Modeling of Local Impact Effects on Plain and Reinforced Concrete. ACI Struct. J. 1994, 91, C178–C187. [Google Scholar]
- Thoma, K. Predictive Modeling of Dynamic Processes; Springer: New York, NY, USA, 2009. [Google Scholar]
- Qi, C.Z.; Wang, M.Y.; Qian, Q.H. Strain-Rate Effects on The Strength and Fragmentation Size of Rocks. Int. J. Impact Eng. 2009, 36, 1355–1364. [Google Scholar] [CrossRef]
- Hong, S.; Kang, T.H.K. Dynamic Strength Properties of Concrete and Reinforcing Steel Subject to Extreme Loads. ACI Struct. J. 2016, 113, 983–995. [Google Scholar] [CrossRef]
- Ramesh, K.T. High rates and impact experiments. In Springer Handbook of Experimental Solid Mechanics; Sharpe, W.N., Jr., Ed.; Springer: New York, NY, USA, 2008; pp. 929–960. [Google Scholar]
- Ramesh, K.T.; Narasimhan, S. Finite Deformations and the Dynamic Measurement of Radial Strains in Compression Kolsky Bar Experiments. Int. J. Solids Struct. 1996, 33, 3723–3738. [Google Scholar] [CrossRef]
- Comité Euro-International du Béton (CEB). Concrete Structures Under Impact and Impulsive Loading—Synthesis Report; Technical Report CEB Bulletin No. 187; fib International: Lausanne, Switzerland, 1988. [Google Scholar]
- Hertz, H. Über die berührung fester elastischer Körper (On the contact of rigid elastic solids). J. Reine Und Angew. 1881, 92, 156–171. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Hanaor, D.A.H.; Gan, Y.; Einav, I. Contact Mechanics of Fractal Surfaces by Spline Assisted Discretisation. Int. J. Solids Struct. 2015, 59, 121–131. [Google Scholar] [CrossRef]
- Sneddon, I.N. The Relation Between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Hypersonic and High. Temperature Gas. Dynamics, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Eligenhausen, R.; Popov, E.P.; Bertero, V.V. Local Bond. Stress-Slip Relationships of Deformed Bars under Generalized Excitations; Earthquake Engineering Research Council Technical Report No. 83/23; University of California: Berkeley, CA, USA, 1983; p. 162. [Google Scholar]
- Lowes, L.N.; Altoontash, A. Modeling Reinforced-Concrete Beam-Column Joints Subjected to Cyclic Loading. ASCE J. Struct. Eng. 2003, 129, 1686–1697. [Google Scholar] [CrossRef]
- Hwang, H.-J.; Eom, T.-S.; Park, H.-G. Bond-Slip Relationship of Beam Flexural Bars in Interior Beam-Column Joints. ACI Struct. J. 2015, 112, 827–837. [Google Scholar] [CrossRef]
- Kim, S.; Kang, T.H.K.; Yun, H.D. Evaluation of Impact Resistance of Steel Fiber-Reinforced Concrete Panel Using Design Equations. ACI Struct. J. 2017, 114, 911–921. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Frew, D.J.; Hanchak, S.J.; Brar, N.S. Penetration of Grout and Concrete Targets with Ogive-Nose Steel Projectiles. Int. J. Impact Eng. 1996, 18, 465–476. [Google Scholar] [CrossRef] [Green Version]
- Forrestal, M.J.; Frew, D.J.; Hickerson, J.P.; Rohwer, T.A. Penetration of Concrete Targets with Deceleration-Time Measurements. Int. J. Impact Eng. 2003, 28, 479–497. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Cargile, J.D. The Effect of Concrete Target Diameter on Projectile Deceleration and Penetration Depth. Int. J. Impact Eng. 2006, 32, 1584–1594. [Google Scholar] [CrossRef]
- Frew, D.J.; Hanchak, S.J.; Green, M.L.; Forrestal, M.J. Penetration of Concrete Targets with Ogive-Nose Steel Rods. Int. J. Impact Eng. 1998, 21, 489–497. [Google Scholar] [CrossRef]
- Zhang, M.H.; Shim, V.P.W.; Lu, G.; Chew, C.W. Resistance of High-Strength Concrete to Projectile Impact. Int. J. Impact Eng. 2005, 31, 825–841. [Google Scholar] [CrossRef]
- Almusallam, T.H.; Siddiqui, N.A.; Iqbal, R.A.; Abbas, H. Response of Hybrid-Fiber Reinforced Concrete Slabs to Hard Projectile Impact. Int. J. Impact Eng. 2013, 58, 17–30. [Google Scholar] [CrossRef]
- Soe, K.T.; Zhang, Y.X.; Zhang, L.C. Impact Resistance of Hybrid-Fiber Engineered Cementitious Composite Panels. Compos. Struct. 2013, 104, 320–330. [Google Scholar] [CrossRef]
- Abdel-Kader, M.; Fouda, A. Effect of Reinforcement on the Concrete Panels to Impact of Hard Projectiles. Int. J. Impact Eng. 2014, 63, 1–17. [Google Scholar] [CrossRef]
- Kim, S. Impact Resistance of High Performance Concrete Panels under High Velocity Projectile Collision. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2018. [Google Scholar]
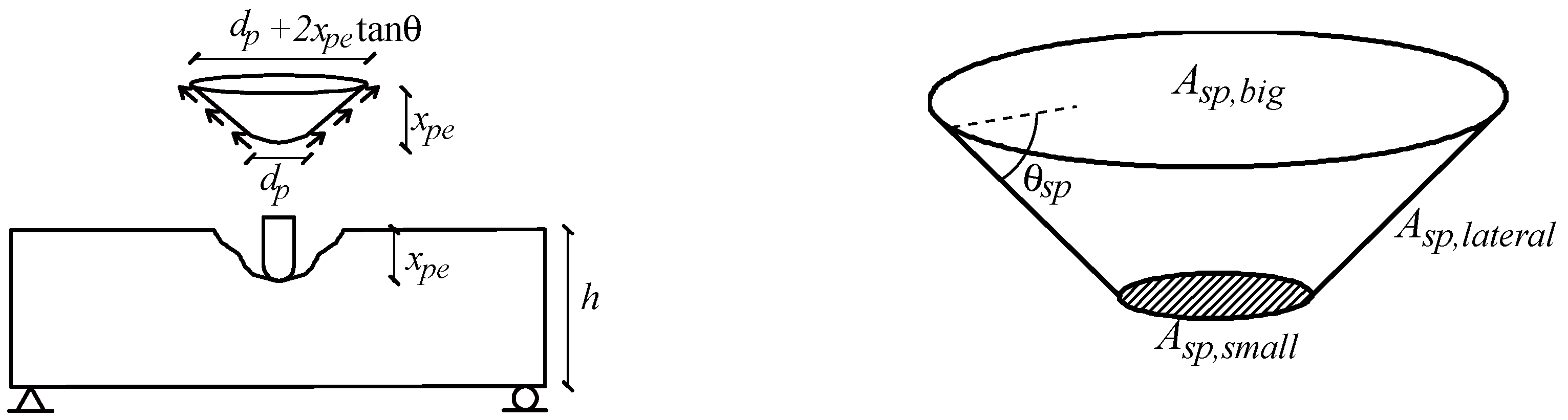
| Tests | Projectile | Concrete panel | |||||||
|---|---|---|---|---|---|---|---|---|---|
| dp | lp | Mp | Vimp | Np | f’c | h | Vf | ρsteel (%) | |
| Abdel-Kader and Fouda [59] | 23 | 64 | 175 | 201–354 | Blunt | 26 | 100 | - | 0.4 |
| Almusallam et al. [57] | 40 | 115 | 800 | 91–135 | Sharp | 29–71 | 90 | 0–0.9 | 0.75 |
| Soe et al. [58] | 13 | 24 | 15 | 306–658 | Ogive | 45–90 | 55 | 0–2.33 | |
| Frew et al. [54] | 76 | 531 | about 13,000 | 164–335 | Ogive | 23 | 910–1830 | ||
| Zhang et al. 56] | 12.6 | 24 | 15 | 620–704 | Ogive | 45–237 | 150 | 0–1.5 | |
| Forrestal et al. [53] | 76 | 531 | about 13,000 | 200–448 | Ogive | 23–39 | 1220–1830 | - | |
| Frew et al. [55] | 20–31 | 203,305 | 478,1600 | 442–1225 | Ogive | 58 | 940–3050 | ||
| Forretal et al. [52] | 20–31 | 203,305 | 478,1600 | 405–1358 | Ogive | 51–63 | 910–2740 | ||
| Forrestal et al. [24] | 27 | 242 | 906 | 277–800 | Ogive | 32–108 | 760–1830 | - | |
| Kim [60] (first test) | 20 | 20 | 33 | 270,350 | Hemisphere | 29–42 | 30–70 | 0.5–2.0 | |
| Kim [60] (second test) | 20 | 20–40 | 33–90 | 95–200 | Hemisphere, Sharp | 41–103 | 50–100 | ||
| Kim [60] (third test) | 20 | 20 | 33 | 200 | Hemisphere | 168 | 10–30 | 1.5 | |
| Total | 20–76 | 20–531 | 15–13,000 | 91–1358 | Ogive, Blunt, Sharp, Hemisphere | 26–237 | 10–2740 | 0–2.33 | |
| Tests | Data (ea) | Proposed Formula | Modified NDRC | ACE | Halar | Hughes | UKAEA | UMIST | Li–Chen |
|---|---|---|---|---|---|---|---|---|---|
| Abdel-Kader and Fouda [59] | 7 | 0.76 | 0.62 | 0.56 | 0.57 | 0.6 | 0.64 | 0.69 | 1.78 |
| Almusallam et al. [57] | 24 | 0.97 | 1.09 | 1.09 | 1.4 | 1.01 | 1.36 | 3.17 | 0.84 |
| Soe et al. [58] | 16 | 1.23 | 0.77 | 0.91 | 0.8 | 0.58 | 0.8 | 1.12 | 1.27 |
| Frew et al. [54] | 7 | 1.03 | 1.85 | 1.5 | 2.01 | 1.87 | 1.88 | 1.87 | 0.48 |
| Zhang et al. [56] | 33 | 0.86 | 1.13 | 1.35 | 1.31 | 0.78 | 1.16 | 1.88 | 1.04 |
| Forrestal et al. [53] | 15 | 0.88 | 1.62 | 1.34 | 1.89 | 1.63 | 1.64 | 1.67 | 0.58 |
| Frew et al. [55] | 18 | 1.35 | 1.59 | 1.55 | 1.81 | 1.41 | 1.53 | 1.65 | 0.91 |
| Forretal et al. [52] | 18 | 1.06 | 1.29 | 1.27 | 1.54 | 1.19 | 1.3 | 1.33 | 1.06 |
| Forrestal et al. [24] | 17 | 0.88 | 1.27 | 1.18 | 1.57 | 1.13 | 1.28 | 1.27 | 1.08 |
| Kim [60] (first test) | 86 | 0.95 | 0.68 | 0.71 | 0.63 | 0.55 | 0.76 | 1.5 | 1.69 |
| Kim [60] (second test) | 149 | 1.06 | 0.65 | 0.59 | 1.22 | 0.53 | 1.12 | 2.32 | 1.47 |
| Kim [60] (third test) | 12 | 0.76 | 0.42 | 0.31 | 1.7 | 0.29 | 1.59 | 2.69 | 2.31 |
| Total | 402 | 1 | 0.87 | 0.85 | 1.2 | 0.74 | 1.13 | 1.97 | 1.36 |
| Test | EDP/EK (%) | EEP/EK (%) | ESD/EK (%) | (ESP+ET)/EK (%) |
|---|---|---|---|---|
| Abdel-Kader and Fouda [59] | 0.07 (0.06–0.08) | 0.24 (0.2–0.28) | 0.04 (0.02–0.06) | 99.7 (99.6–99.7) |
| Almusallam et al. [57] | 0.3 (0.1–0.5) | 0.7(0.5–1.2) | 0.1 | 98.9 (98.1–99.4) |
| Soe et al. [58] | 1.86 (1–4.2) | 0.2 (0.1–0.5) | 0.1 (0.1–0.3) | 97.8 (95.1–98.8) |
| Frew et al. [54] | 0.9 (0.7–1.7) | 0.2 (0.1–0.4) | 0.1 (0–0.1) | 98.8 (97.9–99.2) |
| Zhang et al. [56] | 3.3 (0.1–7.4) | 0.5 (0.3–0.9) | 0.2 (0.1–0.3) | 95.9 (91.4–98.7) |
| Forrestal et al. [53] | 1.6 (0.6–4.8) | 0.2 (0.1–0.5) | 0.2 (0.1–0.5) | 98 (94.8–99.2) |
| Frew et al. [55] | 1 (0.9–1.3) | 0.1 (0–0.1) | 0.1 (0–0.1) | 98.8 (98.5–99.0) |
| Forretal et al. [52] | 1 (0.8–1.4) | 0.1 | 0.1 (0–0.2) | 98.8 (98.4–99.0) |
| Forrestal et al. [24] | 0.8 (0.4–1.3) | 0.2 (0.1–0.3) | 0.3 (0.1–0.6) | 98.7 (98.0–99.2) |
| Kim [60] (first test) | 0.2 | 0.4 (0.2–0.8) | 0 | 99.3 (98.9–99.6) |
| Kim [60] (second test) | 1.2 (0.2–4.6) | 1.9 (0.4–3.8) | 0.1 (0–0.3) | 96.8 (92.2–99.2) |
| Kim [60] (third test) | 2.4 (1.9–3.1) | 1.1 (0.5–2.1) | 0.4 (0.2–2.7) | 96 (94–97.1) |
| Total | 1.1 (0.1–7.4) | 0.9 (0–3.8) | 0.1 (0–2.7) | 97.9 (91.4–99.6) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Kang, T.H.-K. Development of Energy-Based Impact Formula—Part I: Penetration Depth. Appl. Sci. 2020, 10, 4964. https://doi.org/10.3390/app10144964
Kim S, Kang TH-K. Development of Energy-Based Impact Formula—Part I: Penetration Depth. Applied Sciences. 2020; 10(14):4964. https://doi.org/10.3390/app10144964
Chicago/Turabian StyleKim, Sanghee, and Thomas H.-K. Kang. 2020. "Development of Energy-Based Impact Formula—Part I: Penetration Depth" Applied Sciences 10, no. 14: 4964. https://doi.org/10.3390/app10144964





