A Gap Waveguide-Based Compact Rectangular Waveguide to a Packaged Microstrip Inline Transition
Abstract
:1. Introduction
2. Transition Concepts
2.1. Dielectric-Filled Ridge and Groove Gap Waveguide Based Transition
2.2. Ridge and Groove Gap Waveguide-Based Transition
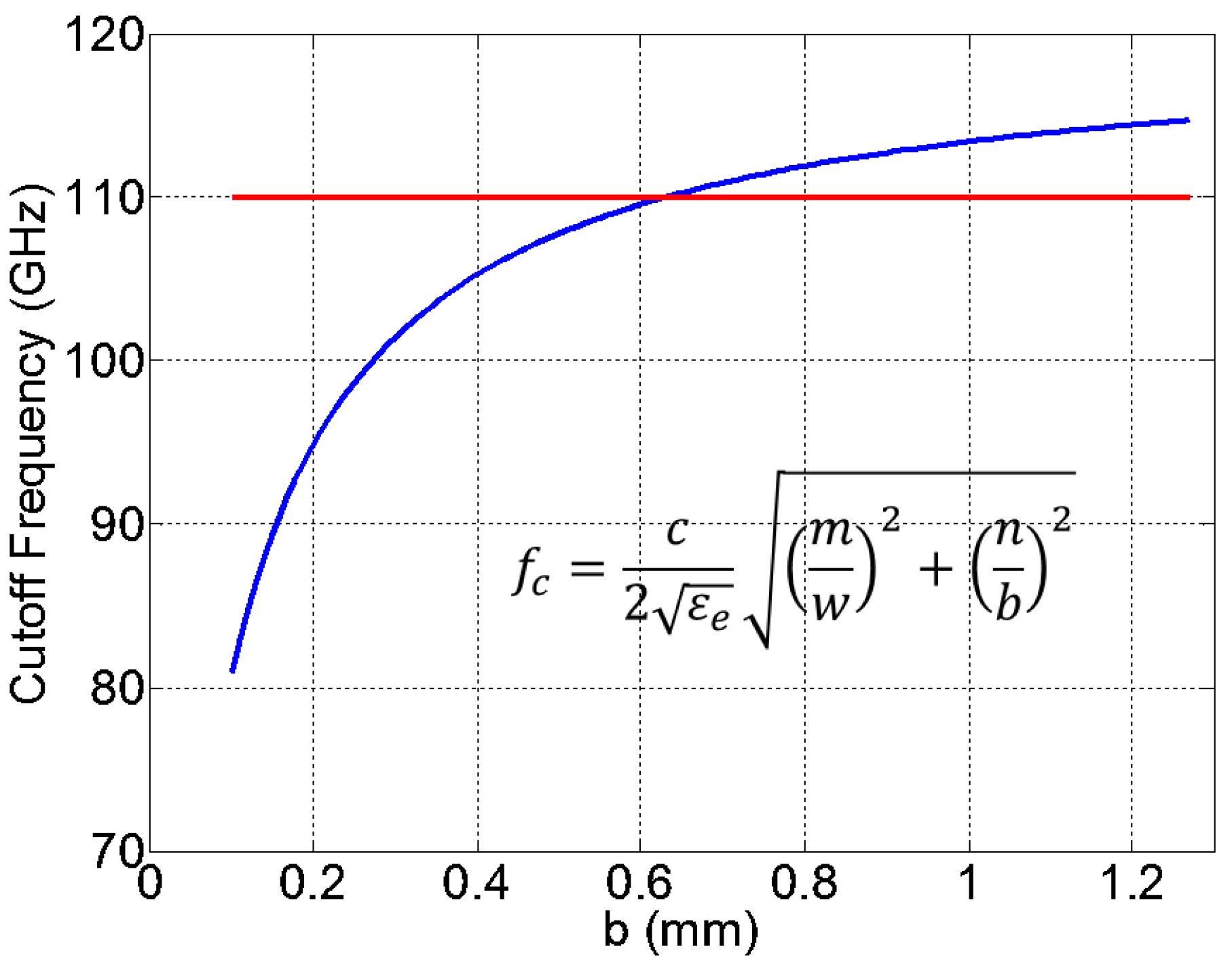
3. Groove Gap Waveguide Characteristics
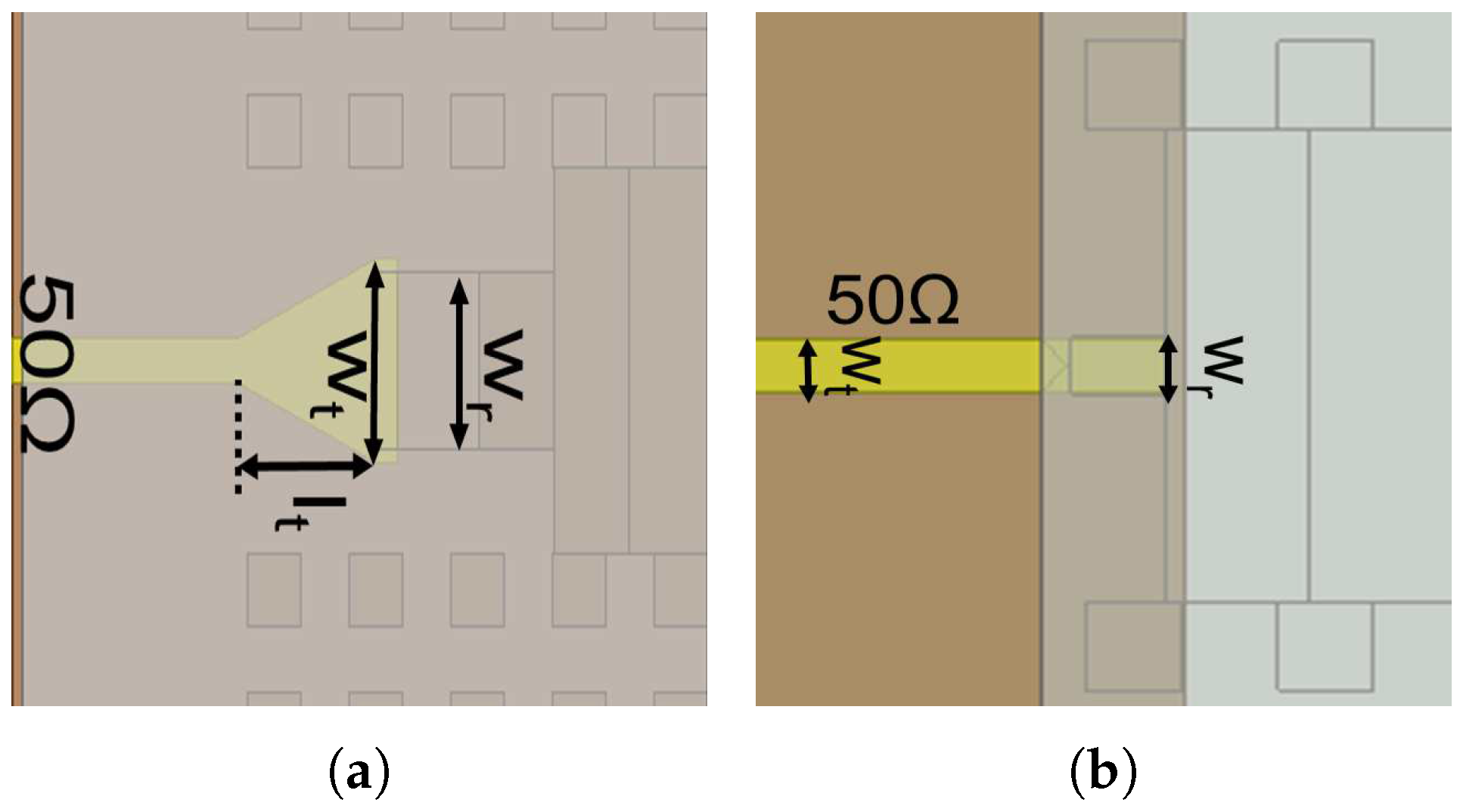
4. Transition Design
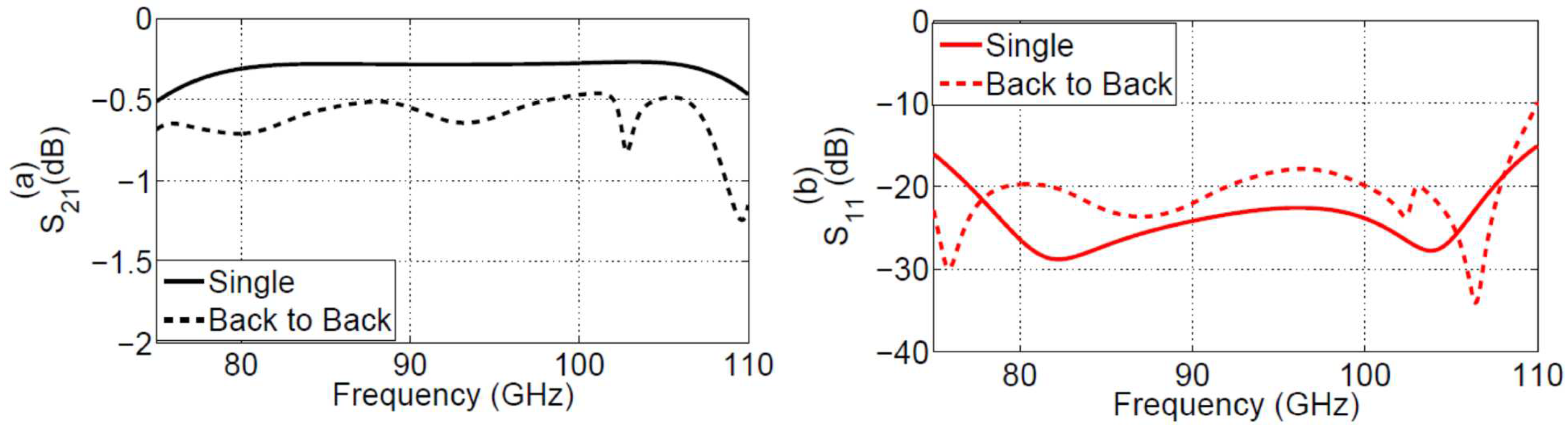
5. Simulation Results
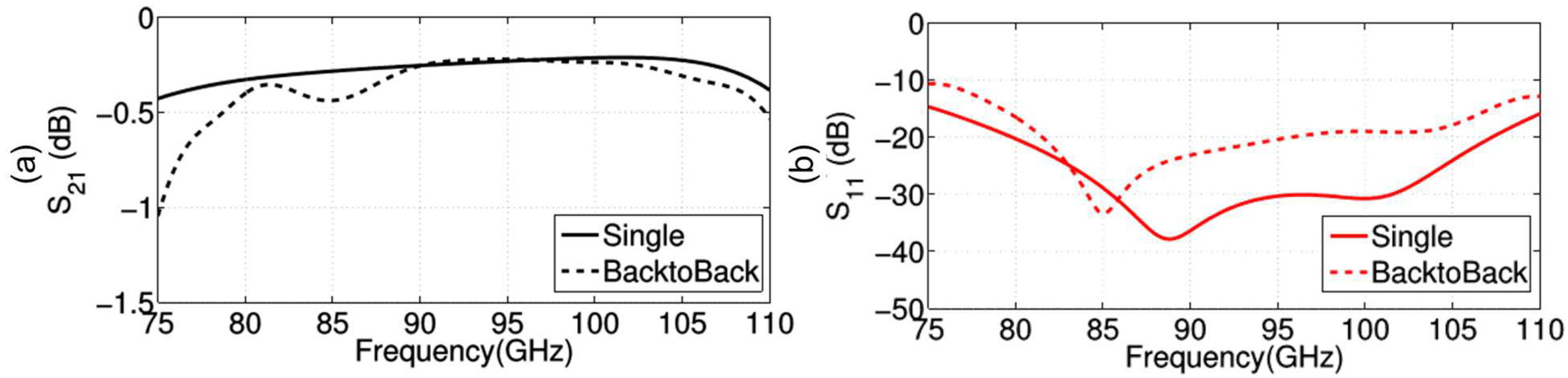
6. Experimental Validation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AMC | Artificial Magnetic Conductor |
| DFRGW | Dielectric-Filled Ridge Gap Waveguide |
| GGW | Groove Gap Waveguide |
| HFSS | High Frequency Structure Simulator |
| HIS | High Impedance Surface |
| MMIC | Monolithic microwave and integrated circuits |
| RGW | Ridge Gap Waveguide |
| RW | Rectangular Waveguide |
References
- Zaman, A.U.; Kildal, P.S. Gap Waveguides. In Handbook of Antenna Technologies; Chen, Z., Ed.; Springer: Singapore, 2015. [Google Scholar]
- Rajo-Iglesias, E.; Ferrando-Rocher, M.; Zaman, A.U. Gap Waveguide Technology for Millimeter-Wave Antenna Systems. IEEE Commun. Mag. 2018, 56, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Rajo-Iglesias, E.; Kildal, P.S. Numerical studies of bandwidth of parallel-plate cut-off realised by a bed of nails, corrugations and mushroom-type electromagnetic bandgap for use in gap waveguides. IET Microw. Antennas Propag. 2011, 5, 282–289. [Google Scholar] [CrossRef] [Green Version]
- Rajo-Iglesias, E.; Zaman, A.U.; Kildal, P.S. Parallel plate cavity mode suppression in microstrip circuit packages using a lid of nails. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 31–33. [Google Scholar] [CrossRef]
- Rajo-Iglesias, E.; Pucci, E.; Kishk, A.A.; Kildal, P.S. Suppression of parallel plate modes in low frequency microstrip circuit packages using lid of printed zigzag wires. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 359–361. [Google Scholar] [CrossRef] [Green Version]
- Zaman, A.U.; Alexanderson, M.; Vukusic, T.; Kildal, P.S. Gap waveguide PMC packaging for improved isolation of circuit components in high-frequency microwave modules. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 16–25. [Google Scholar] [CrossRef] [Green Version]
- Rebollo, A.; Gonzalo, R.; Ederra, I. Optimization of a Pin Surface as a Solution to Suppress Cavity Modes in a Packaged W-band Microstrip Receiver. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 975–982. [Google Scholar] [CrossRef]
- Kildal, P.S.; Alfonso, E.; Valero-Nogueira, A.; Rajo-Iglesias, E. Local metamaterial-based waveguides in gaps between parallel metal plates. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 84–87. [Google Scholar] [CrossRef]
- Kildal, P.S.; Zaman, A.U.; Rajo-Iglesias, E.; Alfonso, E.; Valero-Nogueira, A. Design and experimental verification of ridge gap waveguide in bed of nails for parallel-plate mode suppression. IET Microw. Antennas Propag. 2011, 5, 262–270. [Google Scholar] [CrossRef]
- Vosoogh, A.; Zaman, A.U.; Vassilev, V.; Yang, J. Zero-Gap Waveguide: A Parallel Plate Waveguide with Flexible Mechanical Assembly for mm-Wave Antenna Applications. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 2052. [Google Scholar] [CrossRef]
- Farahbakhsh, A.; Zarifi, D.; Zaman, A.U. 60-GHz Groove Gap Waveguide Based Wideband H-Plane Power Dividers and Transitions: For Use in High-Gain Slot Array Antenna. IEEE Trans. Microw. Theory Technol. 2017, 65, 4111–4121. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.M.M.; Sebak, A. Compact Printed Ridge Gap Waveguide Crossover for Future 5G Wireless Communication System. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 549–551. [Google Scholar] [CrossRef]
- Chieh, J.C.S. A Substrate-Less Microwave Power-Combining Module Utilizing Ridge Gap Waveguide. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 972–974. [Google Scholar] [CrossRef]
- Horestani, A.K.; Shahabadi, M. Balanced Filter With Wideband Common-Mode Suppression in Groove Gap Waveguide Technology. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 132–134. [Google Scholar] [CrossRef]
- Vosoogh, A.; Sorkherizi, M.S.; Zaman, A.U.; Yang, J.; Kishk, A.A. An Integrated Ka-Band Diplexer-Antenna Array Module Based on Gap Waveguide Technology With Simple Mechanical Assembly and No Electrical Contact Requirements. IEEE Trans. Microw. Theory Tech. 2018, 66, 962–972. [Google Scholar] [CrossRef]
- Aljarosha, A.; Smolders, A.B.; Ivashina, M.; Maaskant, R. Toward wide-band low-loss gap-waveguide- integrated grid amplifiers. In Proceedings of the 2017 International Symposium on Antennas and Propagation (ISAP), Phuket, Thailand, 30 October–2 November 2017; pp. 1–2. [Google Scholar]
- Shi, Y.; Feng, W.; Wang, H.; Che, W.; Xue, Q.; Wang, J.; Cao, B. Novel W-band LTCC Transition from Microstrip Line to Ridge Gap Waveguide and Its Application in 77/79 GHz Antenna Array. IEEE Trans. Antennas Propag. 2019, 67, 915–924. [Google Scholar] [CrossRef]
- Cao, J.; Wang, H.; Mou, S.; Quan, S.; Ye, Z. W-Band High-Gain Circularly Polarized Aperture-Coupled Magneto-Electric Dipole Antenna Array With Gap Waveguide Feed Network. IEEE Antennas Wirel. Propag. Lett. 2017, 6, 2155–2158. [Google Scholar] [CrossRef]
- Zaman, A.U.; Vukusic, T.; Alexanderson, M.; Kildal, P.S. Design of a Simple Transition From Microstrip to Ridge Gap Waveguide Suited for MMIC and Antenna Integration. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1558–1561. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, J.; Zeng, S.; Zhou, M. Novel W-band Millimeter Wave Transition From Microstrip Line to Groove Gap Waveguide for MMIC Integration and Antenna Application. IEEE Trans. Antennas Propag. 2018, 66, 3172–3176. [Google Scholar] [CrossRef]
- Nandi, U.; Zaman, A.U.; Vosoogh, A.; Yang, J. Millimeter wave contactless microstrip-gap waveguide transition suitable for integration of RF MMIC with gap waveguide array antenna. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 1682–1684. [Google Scholar]
- Hassan, E.; Berggren, M.; Scheiner, B.; Michler, F.; Weigel, R.; Lurz, F. Design of Planar Microstrip-to- Waveguide Transitions Using Topology Optimization. In Proceedings of the IEEE Radio and Wireless Symposium (RWS), Orlando, FL, USA, 20–23 January 2019; pp. 1–3. [Google Scholar]
- Li, J.; Li, L.; Qiao, Y.; Chen, J.; Chen, J.; Zhang, A. Full Ka band waveguide-to-microstrip inline transition design. J. Infrared Millim. Terahertz Waves 2018, 39, 714–722. [Google Scholar] [CrossRef]
- Algaba-Brazález, A.; Flygare, J.; Yang, J.; Vassilev, V.; Baquero-Escudero, M.; Kildal, P.S. Design of F-Band Transition From Microstrip to Ridge Gap Waveguide Including Monte Carlo Assembly Tolerance Analysis. IEEE Trans. Microw. Theory Tech. 2016, 64, 1245–1254. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ruiz-Cruz, J.A.; Zaki, K.A.; Piloto, A.J. A Waveguide to Microstrip Inline Transition With Very Simple Modular Assembly. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 480–482. [Google Scholar] [CrossRef]
- Rebollo, A.; Gonzalo, R.; Ederra, I. An Inline Microstrip-to-Waveguide Transition Operating in the Full W-Band. J. Infrared Millim. Terahertz Waves 2015, 36, 734–744. [Google Scholar] [CrossRef]
- Pérez-Escudero, J.M.; Torres-García, A.E.; Gonzalo, R.; Ederra, I. A Simplified Design Inline Microstrip-to- Waveguide Transition. Electronics 2018, 7, 215. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Escudero, J.M.; Torres-García, A.E.; Gonzalo, R.; Ederra, I. A Chebyshev Transformer Based Microstrip to Groove Gap Waveguide Inline Transition for MMIC Packaging. IEEE Trans Compon. Packag. Manuf. Technol. 2019, 9, 1595–1602. [Google Scholar] [CrossRef] [Green Version]
- Rajo-Iglesias, E.; Kildal, P.S. Groove gap waveguide: A rectangular waveguide between contactless metal plates enabled by parallel-plate cut-off. In Proceedings of the Fourth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–4. [Google Scholar]
- Berenguer, A.; Fusco, V.; Zelenchuk, D.E.; Sánchez-Escuderos, D.; Baquero-Escudero, M.; Boria-Esbert, V.E. Propagation characteristics of groove gap waveguide below and above cutoff. IEEE Trans. Microw. Theory Technol. 2016, 4, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Orfanidis, S.; Electromagnetic Waves and Antennas. ECE Department Rutgers University. Available online: https://www.ece.rutgers.edu/~orfanidi/ewa/ (accessed on 4 August 2017).
- Eshrah, I.A.; Kishk, A.A.; Yakovlev, A.B.; Glisson, A.W. Rectangular waveguide with dielectric-filled corrugations supporting backward waves. IEEE Trans. Microw. Theory Technol. 2005, 53, 3298–3304. [Google Scholar] [CrossRef]
- Harrington, R.F. Time Harmonic Electromagnetic Field; Wiley-IEEE Press: Hoboken, NJ, USA, 2001. [Google Scholar]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 256–261. [Google Scholar]
- Maestrojuan, I.; Palacios, I.; Ederra, I.; Gonzalo, R. Use of COC substrates for millimeter-wave devices. Microw. Opt. Technol. Lett. 2015, 57, 371–377. [Google Scholar] [CrossRef]
- Peytavit, J.; Donche, C.; Lepilliet, S.; Ducournau, G.; Lampin, J.-F. Thin film transmission lines using cyclic olefin copolymer for millimeter-wave and terahertz integrated circuits. Electron. Lett. 2011, 47, 453–454. [Google Scholar] [CrossRef]

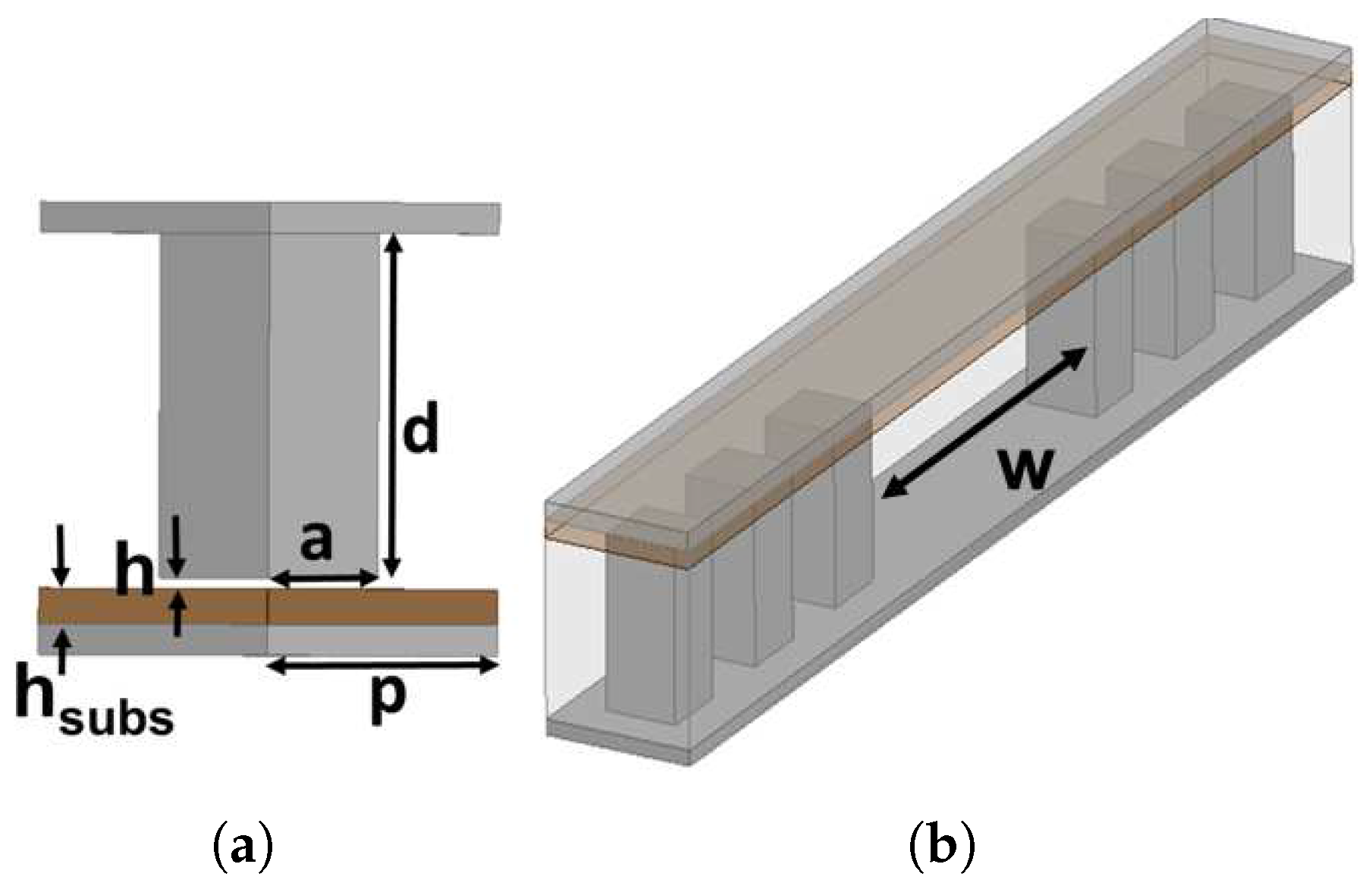







| Parameter | Description | Value (μm) Transition (a) | Value (μm) Transition (b) |
|---|---|---|---|
| a | pin size | 500 | 600 |
| d | pin height | 1120 | 1190 |
| h | air gap | 34 | 80 |
| p | period | 1050 | 1240 |
| substrate thickness | 100 | 100 |
| Parameter | Design Value | Fabricated Value |
|---|---|---|
| w | 2650 | 2590 |
| 1200 | 1130 | |
| 115 | 116 | |
| 130 | 116 | |
| 377 | 361 | |
| 852 | 909 | |
| 1200 | 1212 | |
| 400 | 470 | |
| 550 | 470 | |
| 673 | 685 | |
| 705 | 683 | |
| 726 | 697 | |
| 1500 | 1467 | |
| 1300 | 1256 |
| Parameter | Design | Fabricated |
|---|---|---|
| 300 | 317 | |
| 325 | 256 | |
| 115 | 158 | |
| 325 | 378 | |
| 700 | 758 | |
| 975 | 957 | |
| 1195 | 1053 | |
| 1270 | 1253 | |
| 500 | 430 | |
| 820 | 826 | |
| 820 | 830 | |
| 820 | 870 | |
| 840 | 807 | |
| 840 | 907 | |
| w | 2650 | 2590 |
| b | 1270 | 1280 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Escudero, J.M.; Torres-García, A.E.; Gonzalo, R.; Ederra, I. A Gap Waveguide-Based Compact Rectangular Waveguide to a Packaged Microstrip Inline Transition. Appl. Sci. 2020, 10, 4979. https://doi.org/10.3390/app10144979
Pérez-Escudero JM, Torres-García AE, Gonzalo R, Ederra I. A Gap Waveguide-Based Compact Rectangular Waveguide to a Packaged Microstrip Inline Transition. Applied Sciences. 2020; 10(14):4979. https://doi.org/10.3390/app10144979
Chicago/Turabian StylePérez-Escudero, José M., Alicia E. Torres-García, Ramón Gonzalo, and Iñigo Ederra. 2020. "A Gap Waveguide-Based Compact Rectangular Waveguide to a Packaged Microstrip Inline Transition" Applied Sciences 10, no. 14: 4979. https://doi.org/10.3390/app10144979
APA StylePérez-Escudero, J. M., Torres-García, A. E., Gonzalo, R., & Ederra, I. (2020). A Gap Waveguide-Based Compact Rectangular Waveguide to a Packaged Microstrip Inline Transition. Applied Sciences, 10(14), 4979. https://doi.org/10.3390/app10144979







