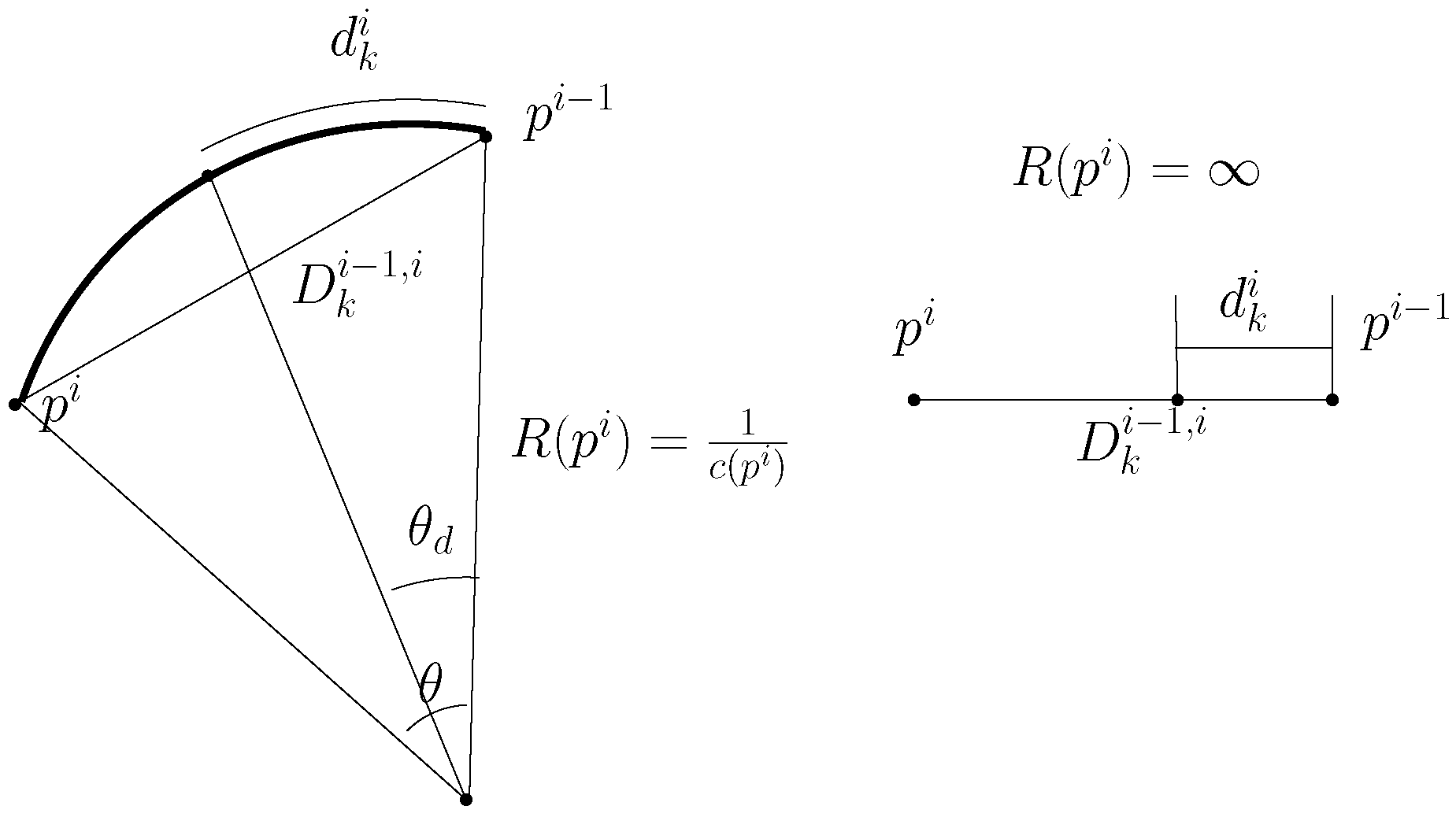1. Introduction
This paper is on developing technology that enables autonomous heterogeneous trucks to drive in platoons. A platoon is defined as a collection of trucks where a manually driven truck (leader truck) is followed by several automatically controlled following trucks. In this case, only one trained truck driver is required to lead the entire platoon. Moreover, it is well known that a truck platooning can reduce fuel consumption of a following truck considerably [
1].
In the literature on autonomous cars, many works have been done on tracking a curve (lane for autonomous cars) while avoiding collision assisted by vision sensors [
2], range sensors [
3], or sonar sensors [
4]. Specifically, [
5] proposed a lane detection algorithm based on Support Vector Machines (SVM) classifier, and a splines-based lane model combined with Kalman filters was used for the tracking algorithm. Reference [
6] presented a method of detecting and tracking the boundaries of drivable regions in a road without road-markings. Using vision sensors, an autonomous truck can follow a lane. However, vision sensors may not work in the case where a lane is not clearly visible. Moreover, there may be a case where a vision sensor on an autonomous car is disabled.
This paper considers the scenario where the leader truck is driven by a trained truck driver. A trained driver has the ability to perform reliable driving in unstructured environments. For instance, a human driver can control a truck even in environments where there is no lane. Thus, this paper considers the scenario where the leader truck is driven by a trained truck driver. Then, all autonomous trucks follow the leader’s trajectory.
In summary, driving in truck platoons has the following benefits: 1. Fuel consumption decreases compared to the case where the trucks do not form a platoon. 2. Only one trained truck driver is required to lead the entire platoon even in unstructured environments.
The truck platoon control is composed of the lateral control and the longitudinal control. The
lateral control is to keep a following truck behind its predecessor truck [
7]. In addition, an autonomous truck must change its speed to maintain a designated distance with its predecessor truck. Controlling the speed of a truck is called the
longitudinal control of the truck.
As far as the author knows, only a few papers handled the lateral control of the truck platoon. Reference [
8] introduced a lateral control which depends on lane markings, which are captured by a monocular camera. However, lane markings may not exist in unstructured environments. The lateral control can be performed by letting every truck set its predecessor truck as its reference point. Suppose that one truck is broken and it gets out of its lane. In this case, all trucks behind the broken truck also get out of the lane, since each truck sets its predecessor truck as its reference point. This implies that this following strategy is not robust to truck failures.
This paper presents a lateral control which does not depend on lane markings. For lateral maneuver, this paper proposes making every autonomous truck keep following the leader’s waypoints while maintaining a designated distance from its predecessor truck.
By following the leader’s waypoints, one can avoid the case where all trucks after a broken truck get out of the lane. This implies that this following strategy is robust to truck failures. Moreover, [
9] mentioned that information on the leader position can stabilize the string of the truck platoon.
Many papers developed longitudinal control of the truck platoon as follows. Reference [
10] developed a longitudinal control based on a distributed controller known as Cooperative Adaptive Cruise Control (CACC). Reference [
11] used consensus control strategy for longitudinal control of truck platoons. The consensus control was used to make the speed of every vehicle converge to the speed of the leader. Reference [
12] proposed a reference model-based control approach for automotive longitudinal control. Reference [
13] developed an autonomous intelligent cruise control (AICC) system for automatic vehicle following, examined its effect on traffic flow, and compared its performance with that of the human driver models. Reference [
14] presented a two-layered hierarchical framework for truck platoon speed control: a speed planning layer for en route speed profile calculation and a control layer for vehicle speed tracking.
Considering longitudinal control, many papers discussed the string stability of platoons as follows. The authors of [
15] analyzed the string stability of platoons of Adaptive Cruise Control (ACC) trucks. Reference [
16] provided a means to evaluate the ACC systems applying the sliding-mode controller, and designed the ACC controller from the perspective of the practical string stability. Reference [
17] proposed a spacing policy to maximize the traffic throughput, and reduced the inter-vehicle distances while ensuring the string stability.
Many papers handled longitudinal control under external disturbance, network-induced disturbance, delay, or packet losses as follows. In [
18], the problem of longitudinal control of networked intelligent vehicles with external disturbance and network-induced disturbance was studied. Reference [
19] considered both communication and parasitic delays in the design of longitudinal control of truck platoon. Reference [
20] synthesized performance-aware safe cruise control policies for longitudinal motion of platoons of autonomous vehicles. Using set-invariance theories, reference [
20] guaranteed infinite-time collision avoidance in the presence of bounded additive disturbances, while ensuring that the length and the cruise speed of the platoon are bounded within specified ranges. Reference [
21] investigated the effect of packet losses on string stability while varying the control gains, and determined the minimum achievable time gap below which stability cannot be achieved.
This paper handles a truck platoon with heterogeneous vehicles. Heterogeneous trucks imply that the hardware information (e.g., truck length, break, accelerator, or engine) of a truck may be distinct from that of another truck. This is a feasible scenario, since the functionality of a truck’s hardware system (e.g., break, accelerator, or engine) gets worse as time goes on. Thus, we argue that no two trucks are identical in practice. In addition, there may be a practical scenario where we need to use various trucks with distinct size.
Many papers on a truck platoon considered heterogeneous vehicles. Reference [
22] handled the adaptive longitudinal control of 1-D platoon of non-identical (heterogeneous) vehicles. Reference [
23] studied a heterogeneous vehicle platoon equipped with CACC systems. The influence of controller parameters and headway time on string stability was studied in [
23]. Reference [
24] proposed nonlinear consensus-based control strategies for a truck platoon under different communication topologies. In [
25], a switched control strategy of heterogeneous vehicle platoon for multiple objectives with state constraints was proposed. Reference [
26] considered analysis and synthesis problems of the cooperative control of a platoon of heterogeneous connected vehicles with directed acyclic interactions.
As far as the author knows, all papers on the longitudinal control of truck platoon considered the case where the trucks move along a straight lane. In practice, the trucks may need to maintain a designated distance with its predecessor truck while they move along a curved lane. Platoon dissolution in winding roads is a critical problem to solve in a platoon of vehicles [
27]. This paper is novel in presenting the longitudinal control of truck platoon, as the trucks move along a curved lane as well as a straight lane.
This paper handles both lateral maneuver and speed control considering heterogeneous trucks. Extensive simulations, which consider noise in the system, are used to present the stability of the control system.
This paper is organized as follows.
Section 2 presents definitions and assumptions used in the paper.
Section 3 presents the multi-vehicle control proposed in this paper.
Section 4 presents MATLAB simulations to verify the effectiveness of the proposed control laws.
Section 5 provides conclusions.
2. Definitions and Assumptions
Suppose that there are N heterogeneous trucks. denotes the i-th truck (). The predecessor of is . is the leader truck driven by a trained truck driver.
One considers discrete-time systems. Let T denote the sampling interval. The subscript k denotes the time step k. denotes the position of the i-th truck at time step k.
The global coordinate of a truck is given by , while its orientation in the global frame is represented by . In the body frame of , is the steering angle of the truck at time step k.
The truck’s speed at time step
k is
in the truck’s x-direction (body frame), and zero in the y-direction (body frame), since this paper assumes that the wheels cannot slip sideways [
28].
If the front wheel is located at distance
from the rear wheel along the orientation of the truck
, then the Ackermann Steering model [
29] is
In Ackermann steering model, each wheel has its own pivot point and the system is constrained in such a way that all wheels of the car drive on circles with a common center point, avoiding skid [
29]. It is acknowledged that in the case where slip sideways are allowed, more complicated truck models in [
30,
31,
32] are required. However, as we consider slip sideways, we need to set various parameters, such as the truck mass or inertia.
Considering heterogeneous trucks, each truck has a distinct motion model from other trucks. Setting complicated models for each individual truck is time-consuming, and a truck’s model may not represent the true dynamics of the truck as the truck runs a longer distance. For instance, the functionality of a truck’s hardware (such as engine, accelerator, or braking system) gets worse as time goes on. In addition, various road (or tire) situations may make effects on slip sideways. Accurate motion modeling in various environments may be impossible in practice.
Equation (
1) can handle heterogeneous trucks by allowing
for
.
implies that the length of the
i-th truck is distinct from that of the
j-th truck. Thus, this paper uses (
1) as the motion model of each heterogeneous truck.
A car cannot arbitrarily change its speed within one time step. Thus, let
denote the maximum acceleration of a truck
. Additionally, let
denote the maximum deceleration of
. Here,
and
are determined by hardware information of
, such as engine, accelerator, or braking system of
. This implies that
Equation (
2) presents the feasible range of
considering the maximum acceleration and deceleration of
. The maximum speed of
is
, i.e.,
for all
k.
Considering heterogeneous trucks, () is feasible. In addition, () is feasible. This is due to the fact that the hardware information (such as engine or braking system) of may be distinct from that of .
A car cannot change its heading abruptly between adjacent time steps, due to the car’s geometry such as the maximum steering angle of the car. Let
present the maximum yaw rate of
. One has
Let
denote the maximum steering angle of a truck
. Then,
is derived as
This implies that as the length of a truck increases, the maximum yaw rate of decreases. In addition, as the maximum steering angle of increases, the maximum yaw rate of increases. Since we consider heterogeneous trucks, () is feasible. Thus, () is also feasible.
We further present important notations in this paper. Whenever the leader travels meters, the leader’s position is stored as a waypoint for the following trucks. Let denote the m-th waypoint. This implies that waypoints are generated as in this order. The distance between and is by its definition.
The distance between and at time step k is . The reference platooning distance at time step k for a truck is denoted as . This implies that the desired distance between and at time step k is .
The main source of time delay between trucks is from the parasitic time delay induced by the mechanical systems and the communication delay generated by the communication and computing devices. It is assumed that the time delay in communication between the leader and a truck is bounded by a certain constant, say .
The travel distance of
within
seconds can be estimated as
. In order to avoid collision due to delayed communication, the reference distance
is set as a bigger value than
. Additionally, we set the lower bound for
for the safety of trucks. Let
present the lower bound for
. This paper uses
Here, is a positive constant. In simulations, this paper uses in meters.
As the speed of a truck converges to
,
converges to
, which is a positive constant. This separation change approach in (
5) was inspired by the constant time headway spacing policy, which was also used in [
16].
It is assumed that each truck can estimate the curvature of the lane using vision sensors [
33]. A truck
moves along an arc lane with radius
as the truck estimates the lane curvature as
. As
goes to zero,
goes to
∞ using (
6).
It is assumed that a truck
accesses both
and
. To enable this, each truck needs to access the position and speed of its predecessor truck. These data are accessible using local sensors, such as radar, lidar, or local communication with its predecessor truck. Moreover, in practice, sensor noise exists in the measurements of
and
. In simulations (
Section 4), one added independent and identically distributed (i.i.d.) Gaussian noise in the measurements of
and
.
3. Multi-Vehicle Control
This paper considers the scenario where the leader truck is driven by a trained truck driver. The proposed approach is to make all trucks follow the leader’s trajectory.
An autonomous truck keeps tracking the leader by following the waypoints of the leader. Whenever a following truck’s distance from a waypoint is less than , the truck heads towards the next waypoint .
To enable this, each truck localizes itself in the global coordinate system using various sensors, such as Lidar, Distance Measurement Instruments (DMI), Global Positioning Systems (GPS) or, Inertial Measurement Units (IMU). (Localization based on multiple sensors is not within the scope of this paper and is presented in various papers, such as [
34,
35,
36]. In the case where there are sensing or communication infrastructure along a road, we can use the infrastructure to localize a truck. In order to localize a truck, many estimation methods were utilized, such as time of arrival (TOA), time difference of arrival (TDOA), angle of arrival (AOA), and received signal strength [
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48].)
Using V2V communication [
49], the leader’s information (
) is transmitted to every following truck. At each time step
k, the leader’s information (
) is transmitted to every other truck in real time.
3.1. Longitudinal Control
This subsection describes how to control the speed of each truck for longitudinal control of the truck. The leader is controlled using ACC so that it maintains a constant speed. In addition, the speed of a following autonomous truck is controlled to maintain a desired distance (reference platooning distance) from its predecessor truck.
Consider the case where
moves along a curved lane. In the left sub-figure of
Figure 1. The arc lane connecting
and
is depicted with a bold arc.
As illustrated in
Figure 1, the arc angle associated to
is
Recall that the desired distance between
and
at time step
k is
. The arc angle associated to
is
At time step
k,
moves along the arc lane with speed
within one sampling interval. The arc angle associated to the travel distance
is
Note that
is the predecessor of
, thus it moves away from
. See
Figure 1.
At each time step
k, the
i-th truck sets its reference speed, say
, as follows.
In the case where both
and
move along a straight path,
in (
6) is
∞. In the case where
becomes
∞, the left sub-figure of
Figure 1 becomes the right sub-figure of
Figure 1. This implies that a curved lane is transitioned into a straight lane. Considering a straight lane as in the right sub-figure of
Figure 1, the following equation is used to set the reference speed
.
Recall that the leader is controlled using ACC so that it maintains a constant speed. While the leader moves using ACC, we set the bound for
as
This implies that if
using (
10) or (
11) is above
, then we set
(
13) implies that the reference speed of
cannot be much faster than the speed of
. The effect of changing
is analyzed in
Section 4.
The reference speed
is used to change the speed of the truck at each time step. In the case where
, the reference speed
cannot be reached within one time step. Thus, we use
In the case where
,
cannot be reached within one time step. Thus, we use
Otherwise, the reference speed
can be reached within one time step. Thus, we can set
3.2. Lateral Control
This subsection describes how to control the lateral maneuver of each truck. Consider the case where
at time step
k heads towards a waypoint whose coordinate is
. The reference
yaw angle
is calculated as
At each time step k, we control the yaw of so that it converges to the reference yaw angle . Recall is set to make the truck head towards the next waypoint. Let for convenience.
One changes
so that it exists between
and
.
Recall that
denotes the maximum yaw rate of a truck
. If
, then we set the steering angle as
The third equation of (
1) is
(
19) and (
20) lead to
Here, denotes the sign of . This implies that we change the yaw of the truck with maximum yaw rate .
If
, then we set the steering angle as
(
22) and (
20) lead to
This implies that the yaw angle of the truck converges to the reference yaw angle.
3.3. Collision Avoidance
This subsection handles the case where a truck is too close to its predecessor truck. In other words, we handle the case where . Recall that the distance between and at time step k is . In addition, is the minimum distance between neighboring trucks for safety. In simulations, one uses in meters.
If happens, then needs to stop abruptly to avoid collision. Thus, we set the reference speed as zero in the case where is satisfied.
Even in the case where we set the reference speed
as zero, it takes some time to decrease the truck’s speed from
to zero. The required time to stop is
. Then, the travel distance of the truck while decreasing its speed to zero is
. To avoid collision, it is desirable to set
so that
is satisfied. However, as
increases, the separation between neighboring trucks increases. Thus, the effect of fuel reduction under truck platoon decreases. Thus, there is a trade-off between fuel reduction and vehicle safety.
4. MATLAB Simulations
MATLAB simulations are presented to verify the proposed control laws. The initial speed of every heterogeneous truck is zero. (
1) is used to model the motion of every truck.
The simulation settings are as follows. As a method to simulate localization error in the waypoints, we added i.i.d. Gaussian noise with mean 0 and standard deviation 0.01 (m) to each element in every waypoint. This error is associated to GPS error which exists in practice.
Recall that a truck
needs to access
and
in order to derive
in (
10). A truck accesses these values using local sensors, such as radar or lidar, or local communication with
. Considering noise in local distance measurements, we added i.i.d. Gaussian noise with mean 0 and standard deviation 0.01 (m) to
. Additionally, we added i.i.d. Gaussian noise with mean 0 and standard deviation 0.001 (m/s) to speed measurements in
.
In simulations, the following variables are used. The time delay bound is , and the sampling interval is (s). The maximum steering angle is degrees. For all , the maximum speed is 80 km/h.
Initially, five trucks are located at , , , , in km. The speed of every truck is 0 initially.
Heterogeneous trucks are simulated as follows. In the case where
is 0,
(m). In addition,
m/s
and
m/s
. In the case where
is 1,
(m). Additionally,
m/s
and
m/s
. In the case where
is 2,
(m). In addition,
m/s
and
m/s
. Using (
4), each truck with distinct length has distinct maximum yaw rate. In this way, we consider heterogeneous trucks composed of various kinds of trucks.
In practice, the leader is controlled by a trained truck driver. In simulations, the leader truck follows one lane initially. Simulations also handle the case where the leader changes its lane to avoid obstacles.
The leader increases its speed with the maximum acceleration until the speed reaches 80 km/h. Then, the leader maintains its speed as 80 km/h using ACC. After the leader moves for 16 min, the scenario ends.
Figure 2a shows the lanes that the trucks follow. In addition,
Figure 2b shows the trajectory of every truck.
Figure 3 shows the enlarged figure of
Figure 2a. Waypoints of the leader are shown with red circles. Simulations handle the case where the leader changes its lane to avoid obstacles. See that waypoints jump from one lane to another. The jump is marked with an arrow in this figure.
Figure 4 shows the speed of each heterogeneous truck with respect to time(sec).
is used. The speed of every truck converges to the speed of the leader (truck 1) as time goes on. Due to the noise in the system, the truck speed is also noisy.
Figure 5 shows the separation between every neighboring truck. Initially, the separation between neighboring trucks increases. However, the separation converges to the desired separation as time goes on. An overshoot (marked with arrow in
Figure 5) happens at the moment when the truck changes its lane. See
Figure 3 for the moment when the truck changes its lane.
4.1. The Effect of Changing
Next, we analyze the effect of changing
.
Figure 6 shows the speed of each heterogeneous truck with respect to time(sec). The only difference from
Figure 4 is that we use
instead of
. See that the deviation of every truck’s speed decreased, compared to the case where
in
Figure 4. Compared to the case where
, the speed noise decreases.
Figure 7 shows the separation between every neighboring truck. Initially, the separation between neighboring trucks increases. See that it takes more time in making the separation converge to the desired separation, compared to the case where
in
Figure 5. Compared to the case where
, the separation noise decreases.
4.2. The Effect of Gaussian Noise
Next, we analyze the effect of Gaussian noise. is used. No Gaussian noise is added to . In addition, no Gaussian noise is added to speed measurements in .
Figure 8 shows the speed of each heterogeneous truck with respect to time(sec). The only difference from
Figure 4 is that no Gaussian noise is used. See that the deviation of every truck’s speed decreased, compared to the case where Gaussian noise is used. A truck speed overshoot (marked with an arrow in
Figure 8) happens at the moment when the truck changes its lane. See
Figure 3 for the moment when the truck changes its lane.
Figure 9 shows the separation between every neighboring truck. The only difference from
Figure 5 is that no Gaussian noise is used. Initially, the separation between neighboring trucks increases. See that the deviation of every truck’s separation decreased, compared to the case where Gaussian noise is used (
Figure 5).