Validation of a Bar Linkage Model for Joint Angle Estimation during Cycling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Design
2.3. Instrumentation
2.3.1. Bicycle Instrumentation
2.3.2. Vicon Motion Capture System
2.3.3. Data Acquisition and Synchronization
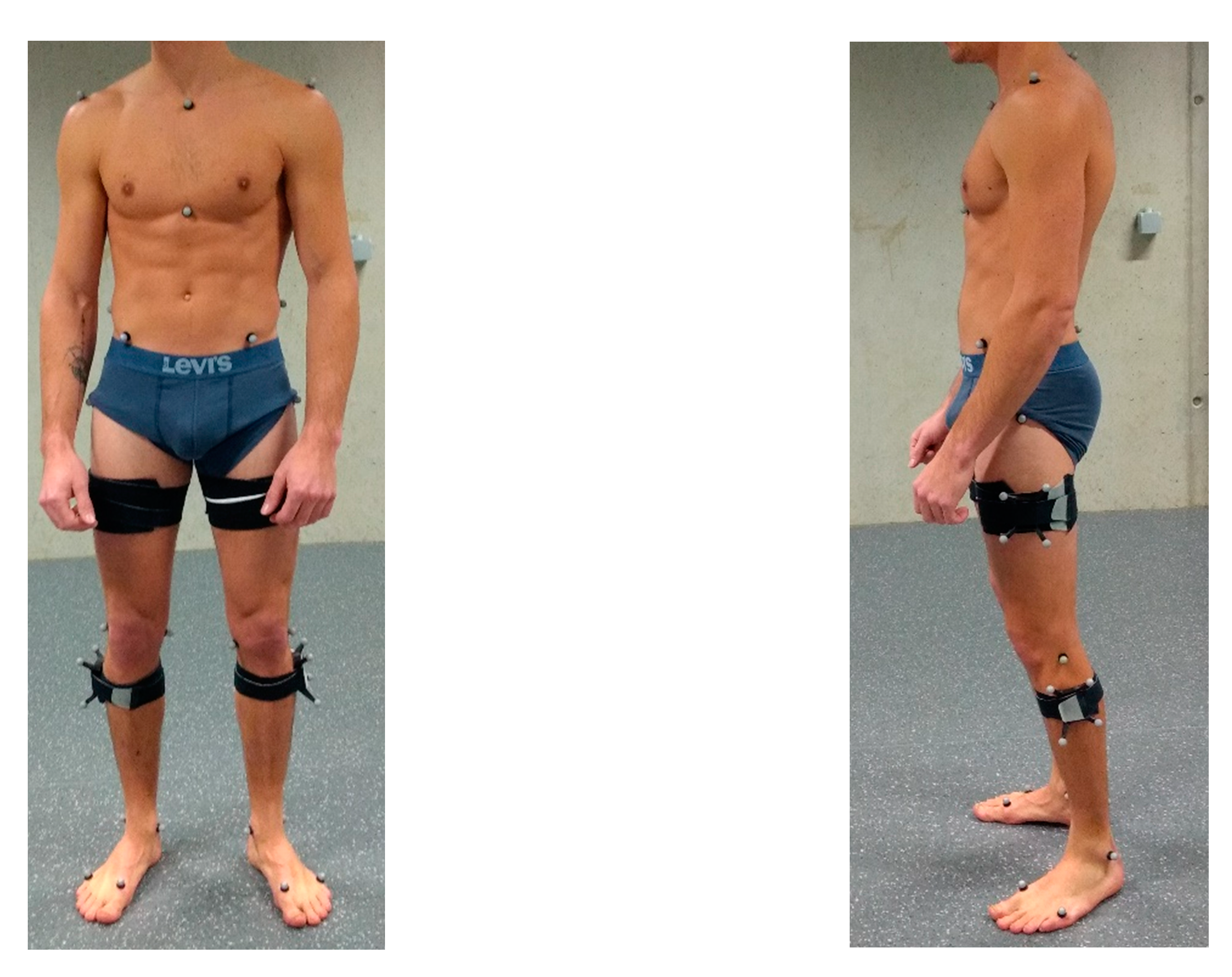
2.4. Setup
2.5. Protocol
2.6. Angle Calculation
2.7. Statistical Analysis
3. Results
3.1. Method Specific AVCs
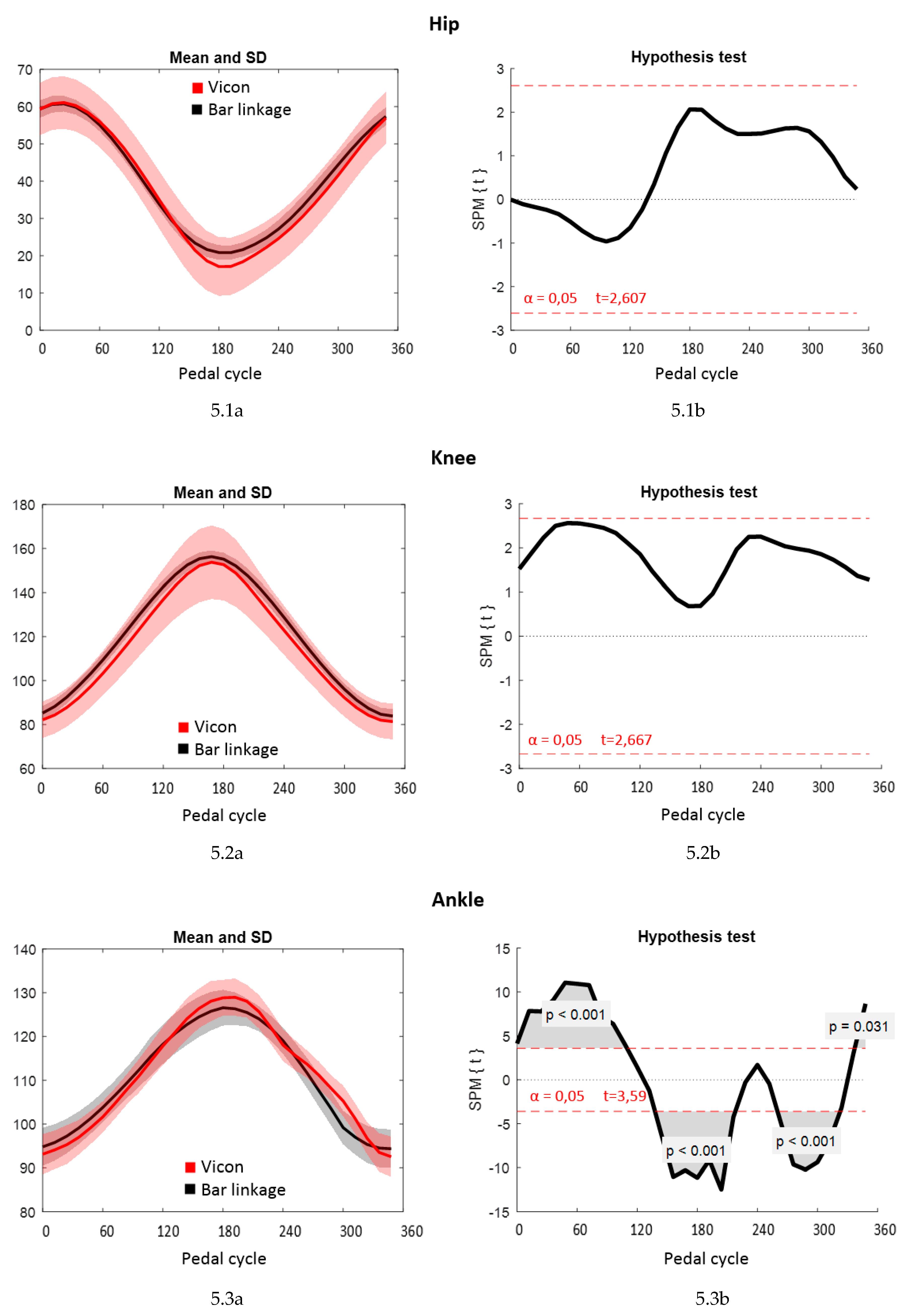
3.1.1. Paired t-Test
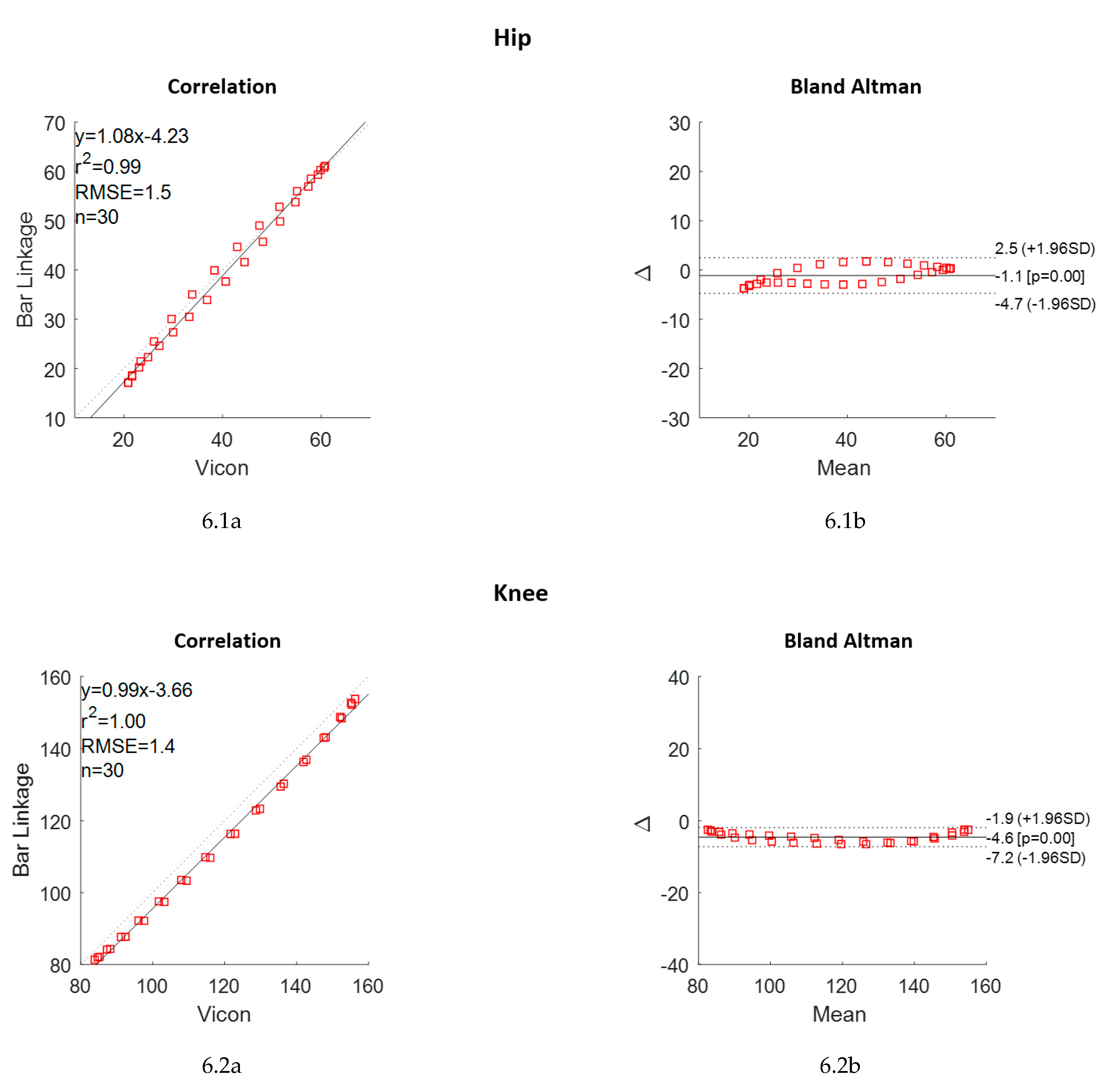
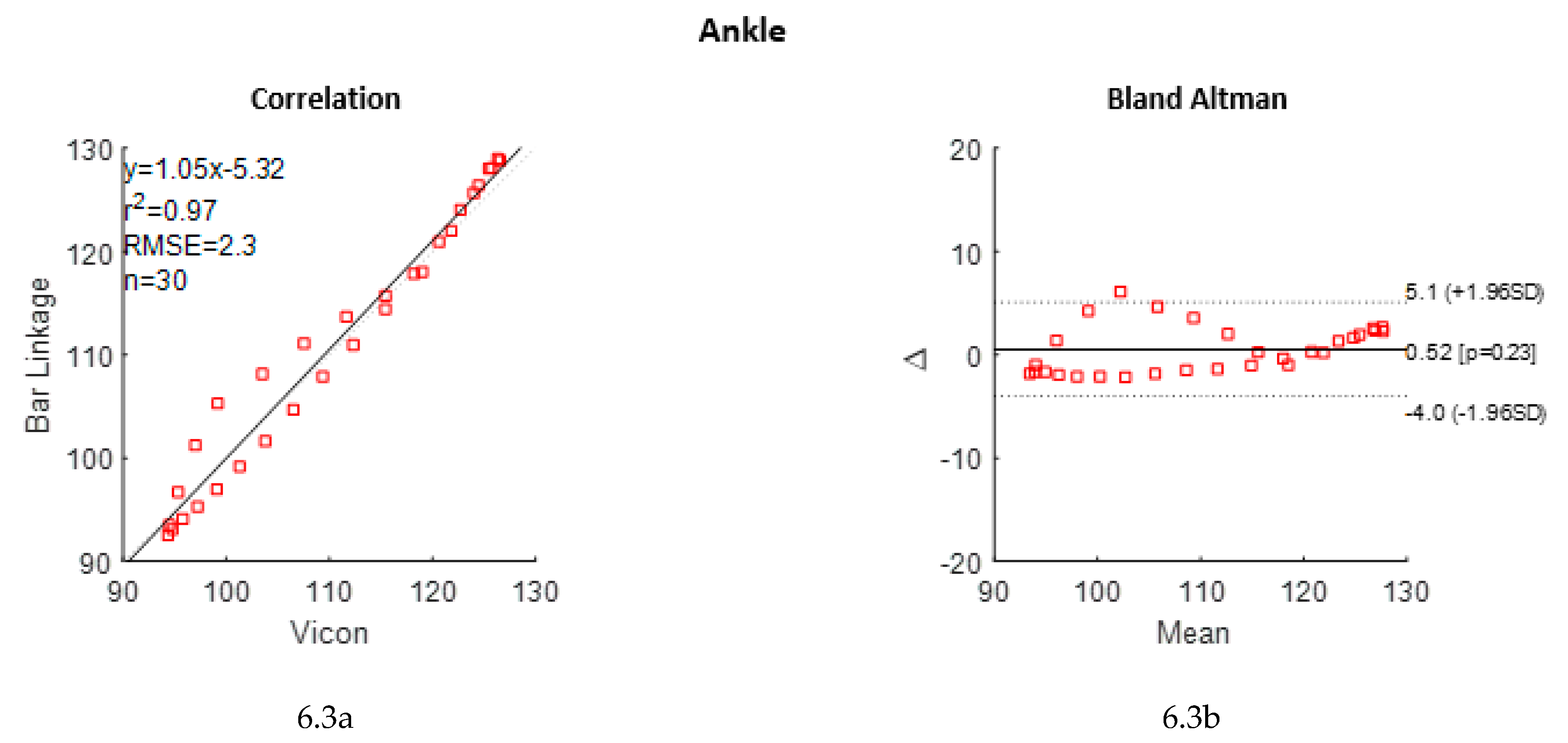
3.1.2. Correlation and Bland Altman
3.2. Subject-Specific AVCs
3.2.1. Correlation Analysis
3.2.2. Bland Altman
4. Discussion
4.1. Method Specific AVCs
4.1.1. Paired t-Test
4.1.2. Correlation and B&A Analysis
4.2. Subject-Specific AVCs
4.3. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schepers, P.; Fishman, E.; Hertog, P.D.; Wolt, K.K.; Schwab, A.L. The safety of electrically assisted bicycles compared to classic bicycles. Accid. Anal. Prev. 2014, 73, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Twisk, D.; Platteel, S.; Lovegrove, G. An experiment on rider stability while mounting: Comparing middle-aged and elderly cyclists on pedelecs and conventional bicycles. Accid. Anal. Prev. 2017, 105, 109–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Visentini, P. A systematic review of parameters related to cycling overuse injuries or pain. J. Sci. Med. Sport 2017, 20, e69–e70. [Google Scholar] [CrossRef]
- Callaghan, M.J. Lower body problems and injury in cycling. J. Bodyw. Mov. Ther. 2005, 9, 226–236. [Google Scholar] [CrossRef]
- Bernardo, N.; Barrios, C.; Vera, P.; Laiz, C.; Hadala, M. Incidence and risk for traumatic and overuse injuries in top-level road cyclists. J. Sports Sci. 2012, 30, 1047–1053. [Google Scholar] [CrossRef] [PubMed]
- Heijink, A.; Gomoll, A.H.; Madry, H.; Drobnič, M.; Filardo, G.; Mendes, J.E.; Van Dijk, C.N. Biomechanical considerations in the pathogenesis of osteoarthritis of the knee. Knee Surg. Sports Traumatol. Arthrosc. 2011, 20, 423–435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyazaki, T.; Wada, M.; Kawahara, H.; Sato, M.; Baba, H.; Shimada, S. Dynamic load at baseline can predict radiographic disease progression in medial compartment knee osteoarthritis. Ann. Rheum. Dis. 2002, 61, 617–622. [Google Scholar] [CrossRef] [PubMed]
- Redfield, R.; Hull, M. On the relation between joint moments and pedalling rates at constant power in bicycling. J. Biomech. 1986, 19, 317–329. [Google Scholar] [CrossRef]
- Sien, D.; D’Hondt, J.; Juwet, M.; Versteyhe, M. development of a low-cost measurement system to determine 3-Dimensional pedal loads during in-situ cycling. Transp. Probl. 2019, 14, 151–160. [Google Scholar] [CrossRef] [Green Version]
- Sien, D.; Jordi, D.; Juwet, M.; Shariatmadar, K.; Versteyhe, M. Design and calibration of an instrumented seat post to measure sitting loads while cycling. Sensors 2020, 20, 1384. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bini, R.R.; Dagnese, F.; Da Rocha, E.S.; Silveira, M.C.; Carpes, F.P.; Mota, C.B. Three-dimensional kinematics of competitive and recreational cyclists across different workloads during cycling. Eur. J. Sport Sci. 2016, 16, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Mesquita, I.; Fonseca, P.; Pinheiro, A.R.V.; Correia, M.; Silva, C. Methodological considerations for kinematic analysis of upper limbs in healthy and poststroke adults Part II: A systematic review of motion capture systems and kinematic metrics. Top. Stroke Rehabil. 2019, 26, 464–472. [Google Scholar] [CrossRef] [PubMed]
- Cordillet, S.; Bideau, N.; Bideau, B.; Nicolas, G. Estimation of 3D knee joint angles during cycling using inertial sensors: Accuracy of a novel sensor-to-segment calibration procedure based on pedaling motion. Sensors 2019, 19, 2474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, Y.; Li, X.; Zhang, X. An adaptive compensation algorithm for temperature drift of micro-electro-mechanical systems gyroscopes using a strong tracking kalman filter. Sensors 2015, 15, 11222–11238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hull, M.; Jorge, M. A method for biomechanical analysis of bicycle pedalling. J. Biomech. 1985, 18, 631–644. [Google Scholar] [CrossRef]
- Vanrenterghem, J.; Gormley, D.; Robinson, M.; Lees, A. Solutions for representing the whole-body centre of mass in side cutting manoeuvres based on data that is typically available for lower limb kinematics. Gait Posture 2010, 31, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Robinson, M.A.; Vanrenterghem, J. An evaluation of anatomical and functional knee axis definition in the context of side-cutting. J. Biomech. 2012, 45, 1941–1946. [Google Scholar] [CrossRef] [PubMed]
- Timmer, C.A.W. Cycling biomechanics: A literature review. J. Orthop. Sports Phys. Ther. 1991, 14, 106–113. [Google Scholar] [CrossRef] [PubMed]
- Pataky, T.; Vanrenterghem, J.; Robinson, M.A. Zero- vs. one-dimensional, parametric vs. non-parametric, and confidence interval vs. hypothesis testing procedures in one-dimensional biomechanical trajectory analysis. J. Biomech. 2015, 48, 1277–1285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]



| Mean | Standard Deviation | |
|---|---|---|
| Age (years) | 26 | 2 |
| Weight (kg) | 65.83 | 15.63 |
| Length (m) | 1.73 | 0.19 |
| BMI | 22.00 | 0.35 |
| Segment | Link | Proximal Reference | Distal Reference |
|---|---|---|---|
| 1 | Thigh | Greater Trochanter | Lateral Femoral Epicondyle |
| 2 | Shank | Lateral Femoral Epicondyle | Lateral Malleolus |
| 3 | Mid-Foot | Medial Malleolus | Os Naviculare |
| Left Hip | Right Hip | Left Knee | Right Knee | Left Ankle | Right Ankle | |
|---|---|---|---|---|---|---|
| r2 minimal | 0.963 | 0.972 | 0.983 | 0.984 | 0.922 | 0.919 |
| r2 maximal | 0.996 | 0.996 | 0.999 | 0.999 | 0.979 | 0.981 |
| RMSE minimal | 0.907 | 1.041 | 0.725 | 0.530 | 0.979 | 1.746 |
| RMSE maximal | 2.879 | 2.467 | 3.500 | 3.396 | 3.409 | 3.318 |
| Left Hip | Right Hip | Left Knee | Right Knee | Left Ankle | Right Ankle | |
|---|---|---|---|---|---|---|
| Subject-specific AVCs without outliers | 10 | 10 | 6 | 7 | 5 | 4 |
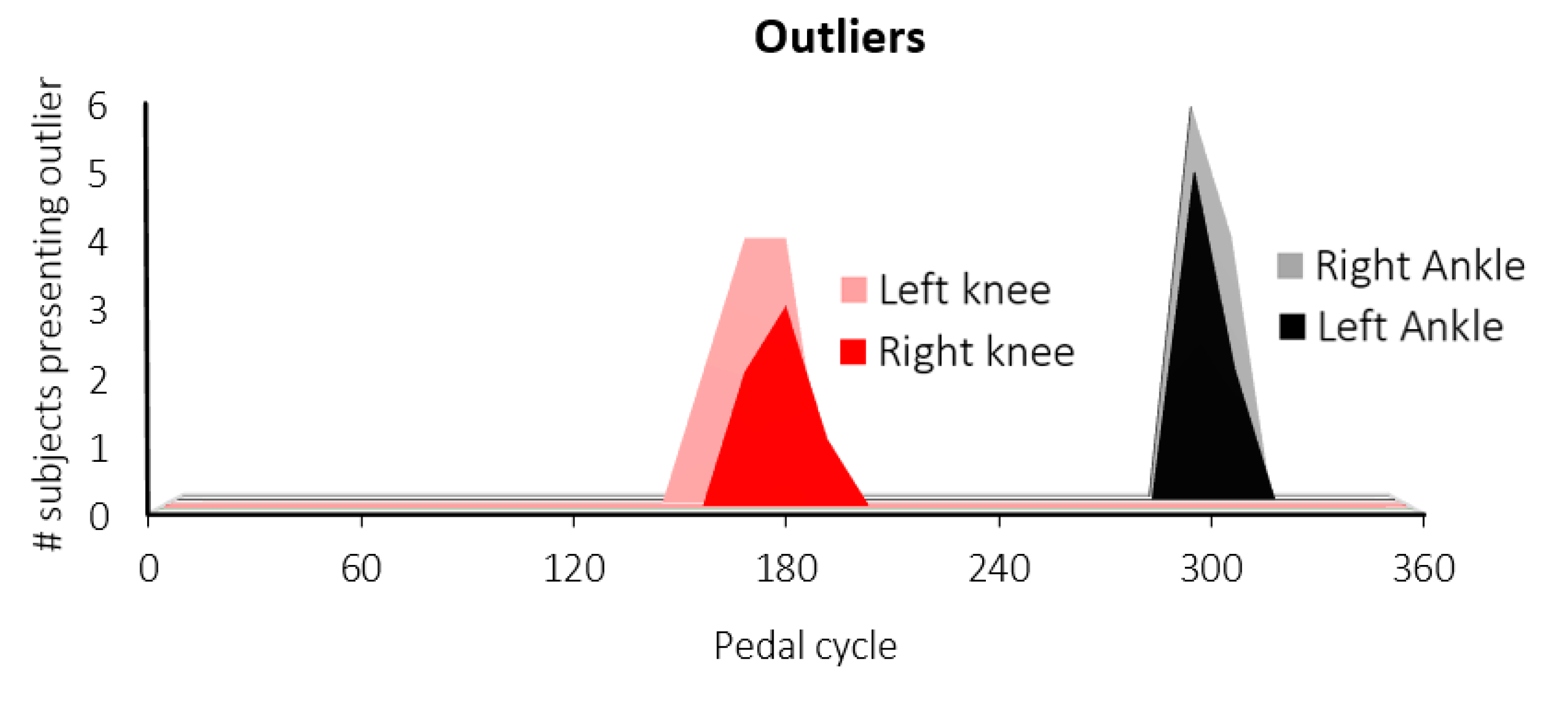
| Subject-specific AVCs with outliers x (y) = x subjects present an outlier at location y | 0 | 0 | 2 (156°) 4 (168°) 4 (180°) | 2 (168°) 3 (180°) (1 (192°) | 5 (300°) 2 (312°) | 6 (300°) 4 (312°) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dieltiens, S.; Claeys, K.; D’hondt, J.; Devroey, H.; Juwet, M.; Demeester, E. Validation of a Bar Linkage Model for Joint Angle Estimation during Cycling. Appl. Sci. 2020, 10, 5104. https://doi.org/10.3390/app10155104
Dieltiens S, Claeys K, D’hondt J, Devroey H, Juwet M, Demeester E. Validation of a Bar Linkage Model for Joint Angle Estimation during Cycling. Applied Sciences. 2020; 10(15):5104. https://doi.org/10.3390/app10155104
Chicago/Turabian StyleDieltiens, Sien, Kurt Claeys, Jordi D’hondt, Henri Devroey, Marc Juwet, and Eric Demeester. 2020. "Validation of a Bar Linkage Model for Joint Angle Estimation during Cycling" Applied Sciences 10, no. 15: 5104. https://doi.org/10.3390/app10155104
APA StyleDieltiens, S., Claeys, K., D’hondt, J., Devroey, H., Juwet, M., & Demeester, E. (2020). Validation of a Bar Linkage Model for Joint Angle Estimation during Cycling. Applied Sciences, 10(15), 5104. https://doi.org/10.3390/app10155104





