A Hybrid Deep Learning Framework for Unsupervised Anomaly Detection in Multivariate Spatio-Temporal Data
Abstract
1. Introduction
- In multivariate time series data, strong temporal dependency exists between time steps. Due to this reason, distance-/clustering-based methods, may not perform well since they cannot capture temporal dependencies properly across different time steps.
- On the other hand, for the case of high-dimensional data, even the data locality may be ill-defined because of data sparsity [3].
- Despite the effectiveness of IsolationForest technique, it isolates data points based on one random feature at a time which may not represent spatial and temporal dependencies between data points properly in the spatio-temporal dataset.
- The definition of distance between data points in multivariate spatio-temporal data with mixed attributes is often challenging. This difficulty may have an adverse effect on outlier detection performance of distance-based clustering algorithms.
- In the aforementioned neighborhood methods, the biggest challenge is to combine the contextual attributes in a meaningful way. In the proposed approach, spatial and temporal contexts are handled by different deep learning components as these contextual variables refer to different types of dependencies.
- All distance-/clustering-based algorithms are proximity-based algorithms and dependent on some notion of distance. Many distance functions used for proximity quantification (such as Euclidean and Manhattan) are not meaningful for all datatypes.
- The proposed hybrid framework is designed to be trained in a truly unsupervised fashion without any labels indicating normal or abnormal data. The architecture is robust enough to learn the underlying dynamics even if the training dataset contains noise and anomalies.
- In the proposed hybrid architecture, CNN and LSTM layers are combined into one unified framework that is jointly trained. Unlike proximity-based methods, the framework can be easily implemented on data with mixed-type attributes and scales well to multivariate datasets with high number of features.
2. Related Work
3. Background
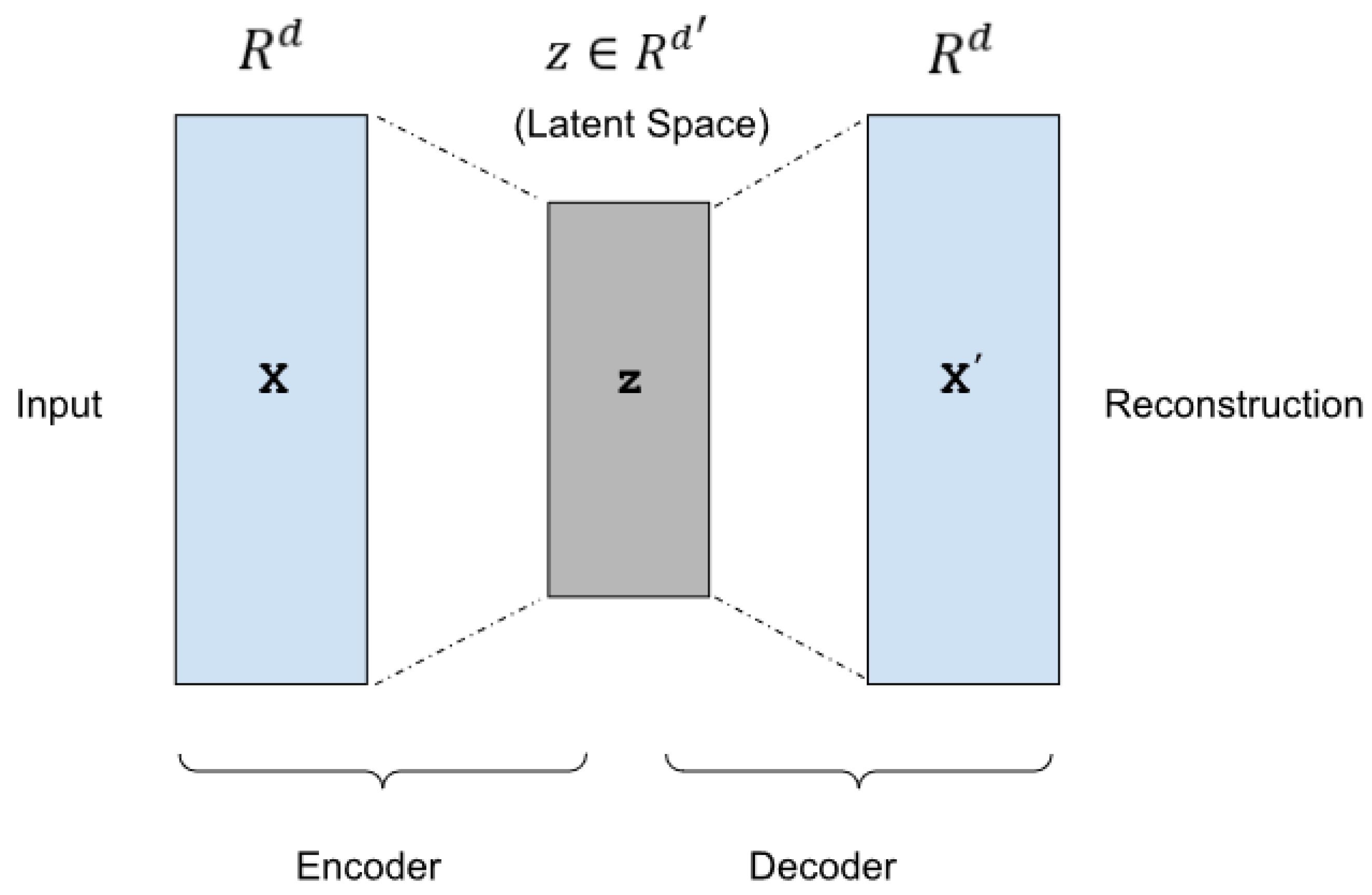
3.1. Autoencoders
3.2. Anomaly Detection with Autoencoders
3.3. Convolutional Neural Networks (CNNs)
3.4. Long Short-Term Memory (LSTM) Networks
4. Methodology
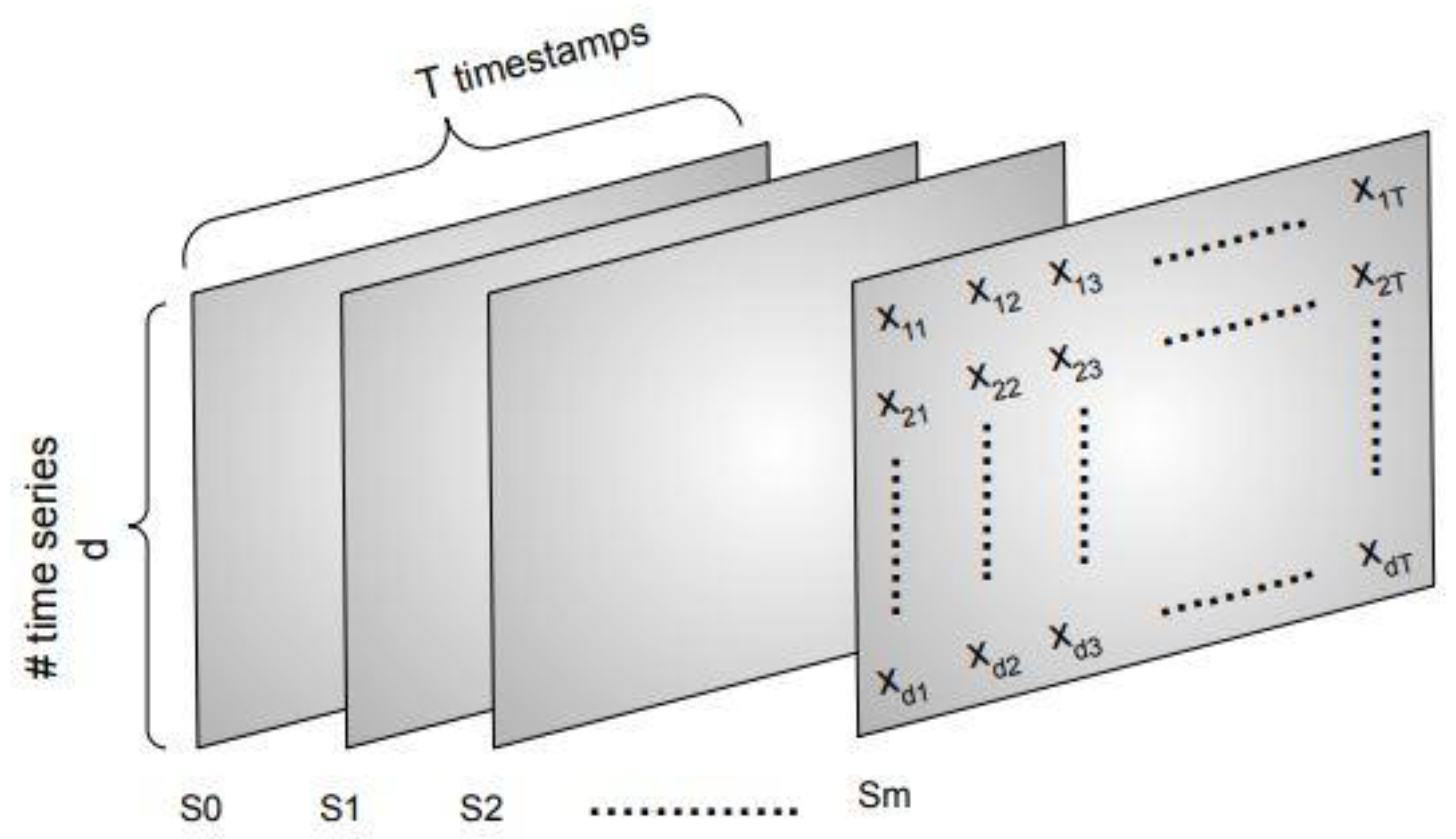
4.1. Spatio-Temporal Data Pre-Processing
4.2. Anomaly Detection Procedure
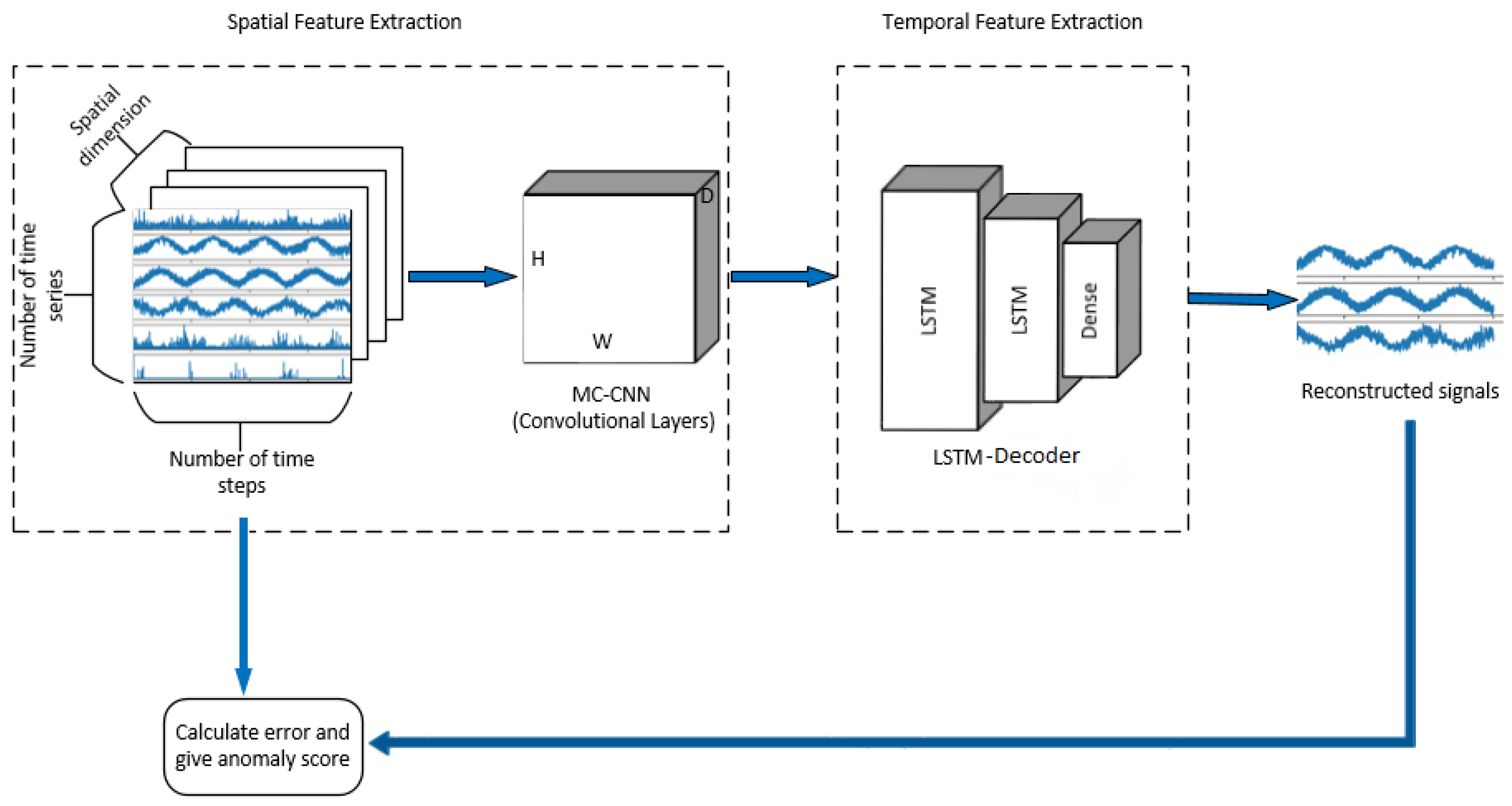
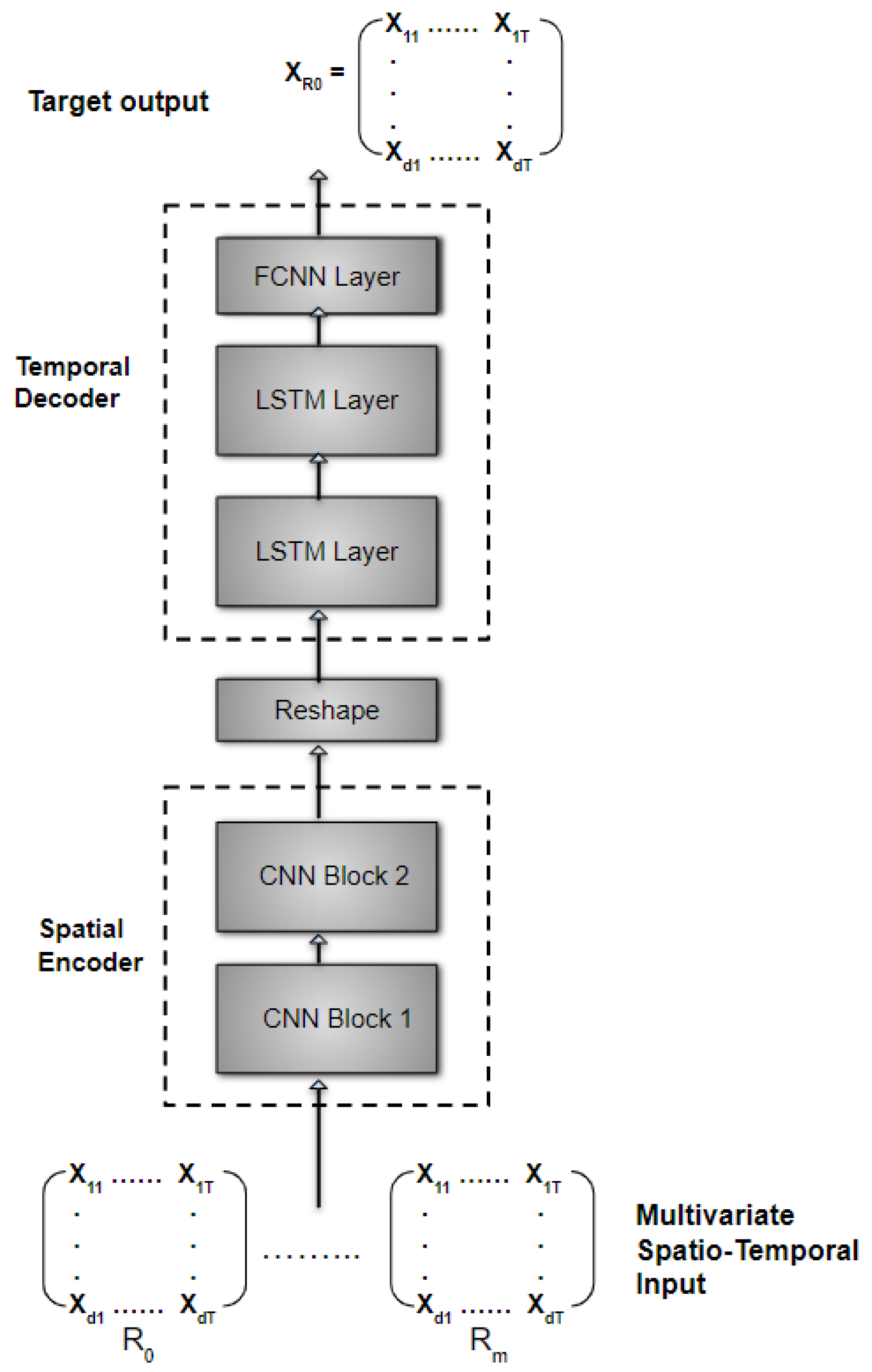
4.3. Proposed Hybrid Framework
4.3.1. MC-CNN-Encoder
4.3.2. LSTM-Decoder
5. Experiments
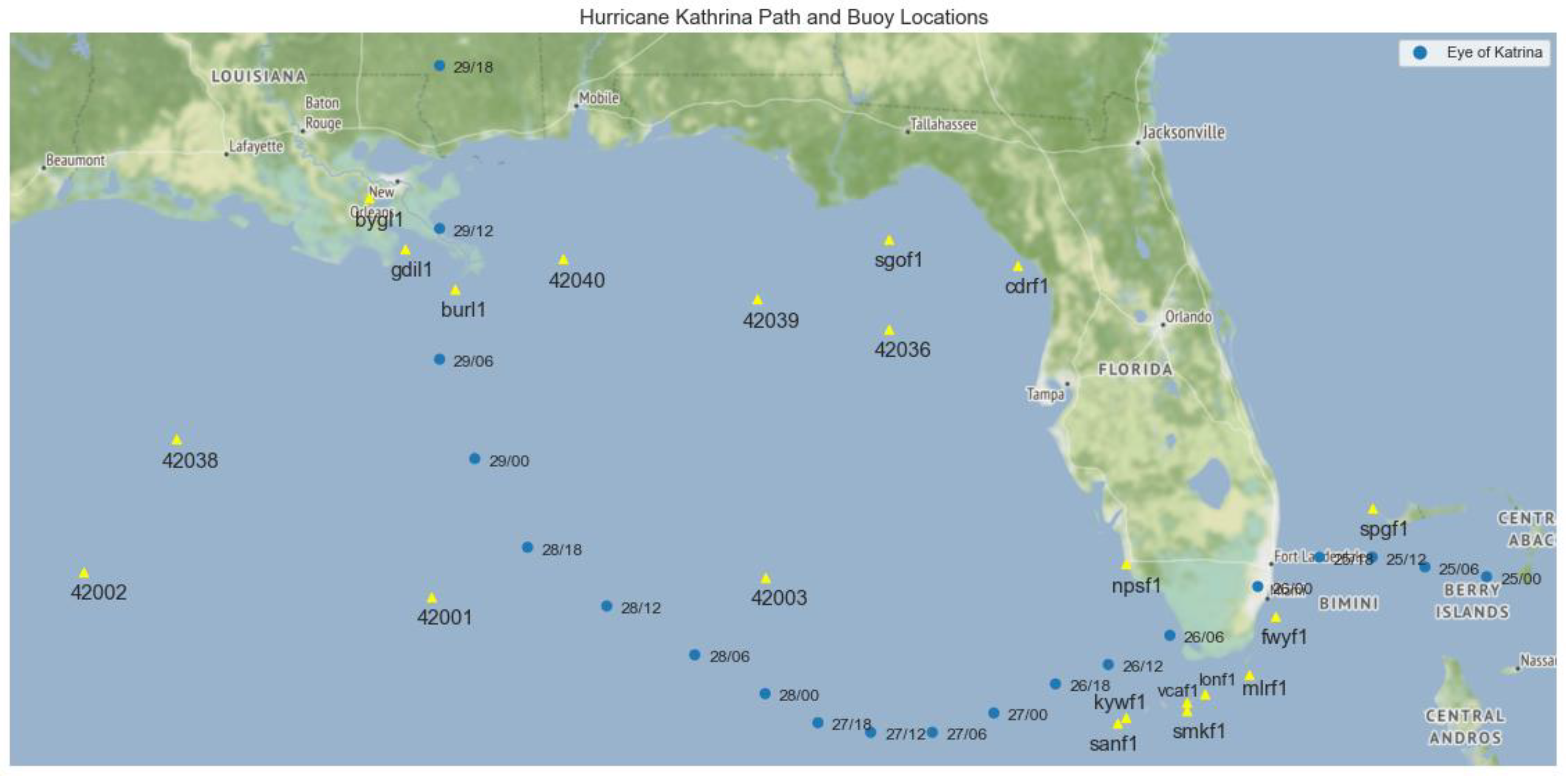
- Due to the difficulty of finding a labelled spatio-temporal multivariate real-world dataset for anomaly detection, we decided to use the buoy dataset full with well-known natural phenomena (anomalies) such as hurricanes.
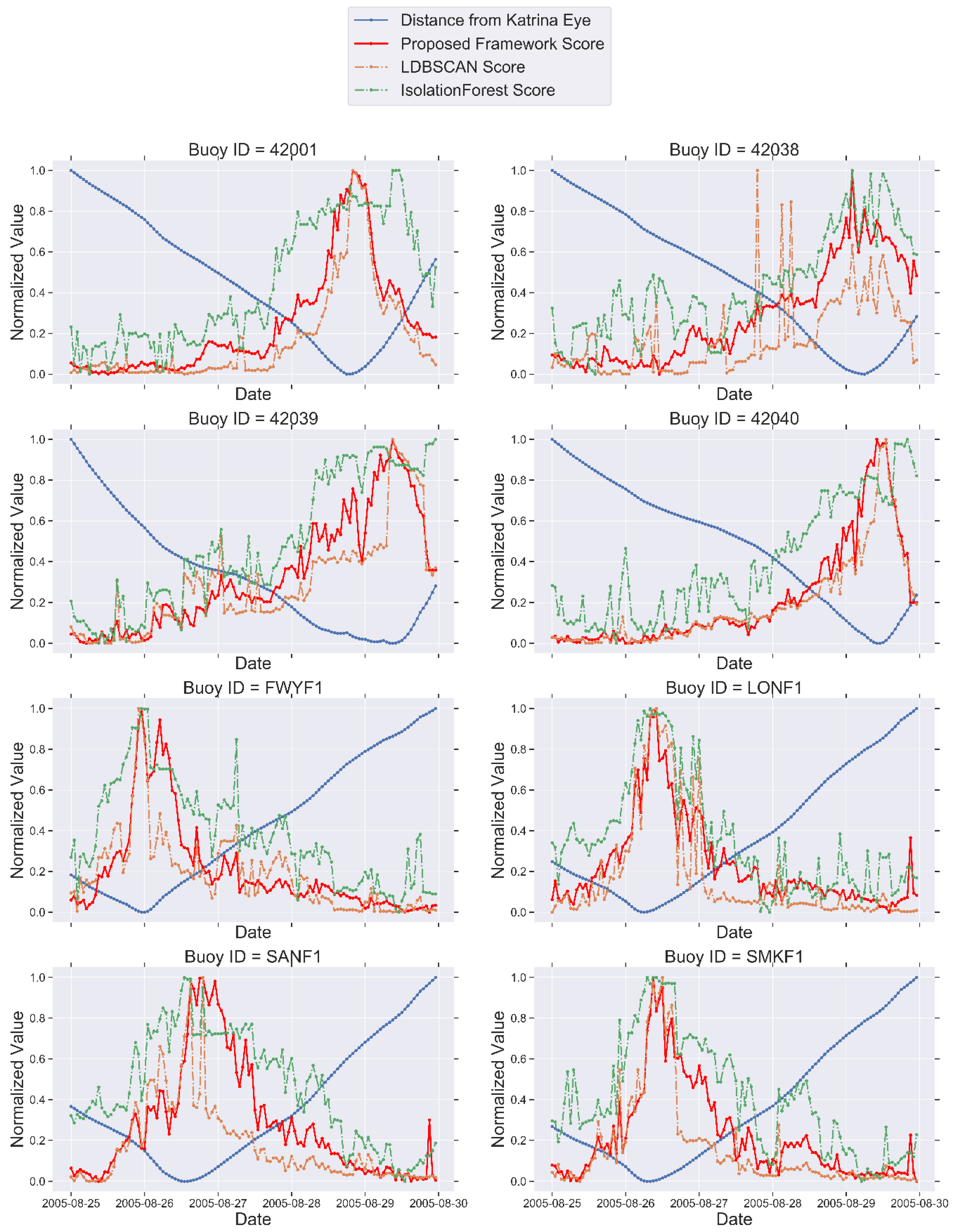
- Associating the spatio-temporal outliers detected between August 25th and August 30th with the path of Hurricane Katrina helps us to compare our approach with other algorithms.
- To get a better understanding about the performance of algorithms, we used OAHII (Outliers Association with Hurricane Intensity Index) measures developed by Duggimpudi et al. [6] using the same buoy dataset. Using these measures, we were able to quantitatively compare the anomaly scores generated by algorithms.
5.1. Dataset Description
5.2. Data Preparation
5.3. Algorithms Used for Comparison
5.4. Framework Tuning
| Algorithm 1 Sliding window algorithm used in subsequence generation |
|
5.5. Results
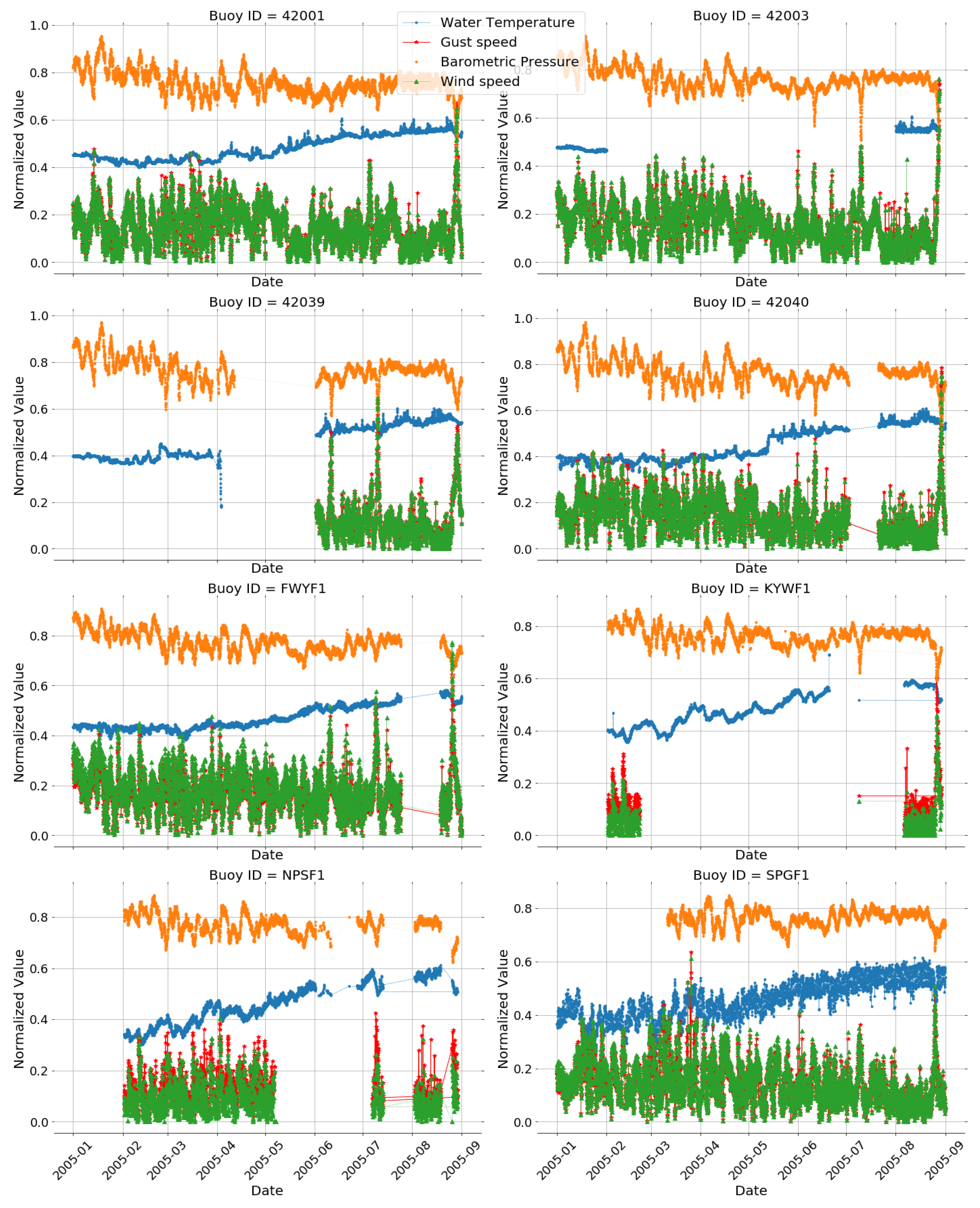
5.5.1. Anomaly Detection Results
5.5.2. Quantitative Evaluation of Models
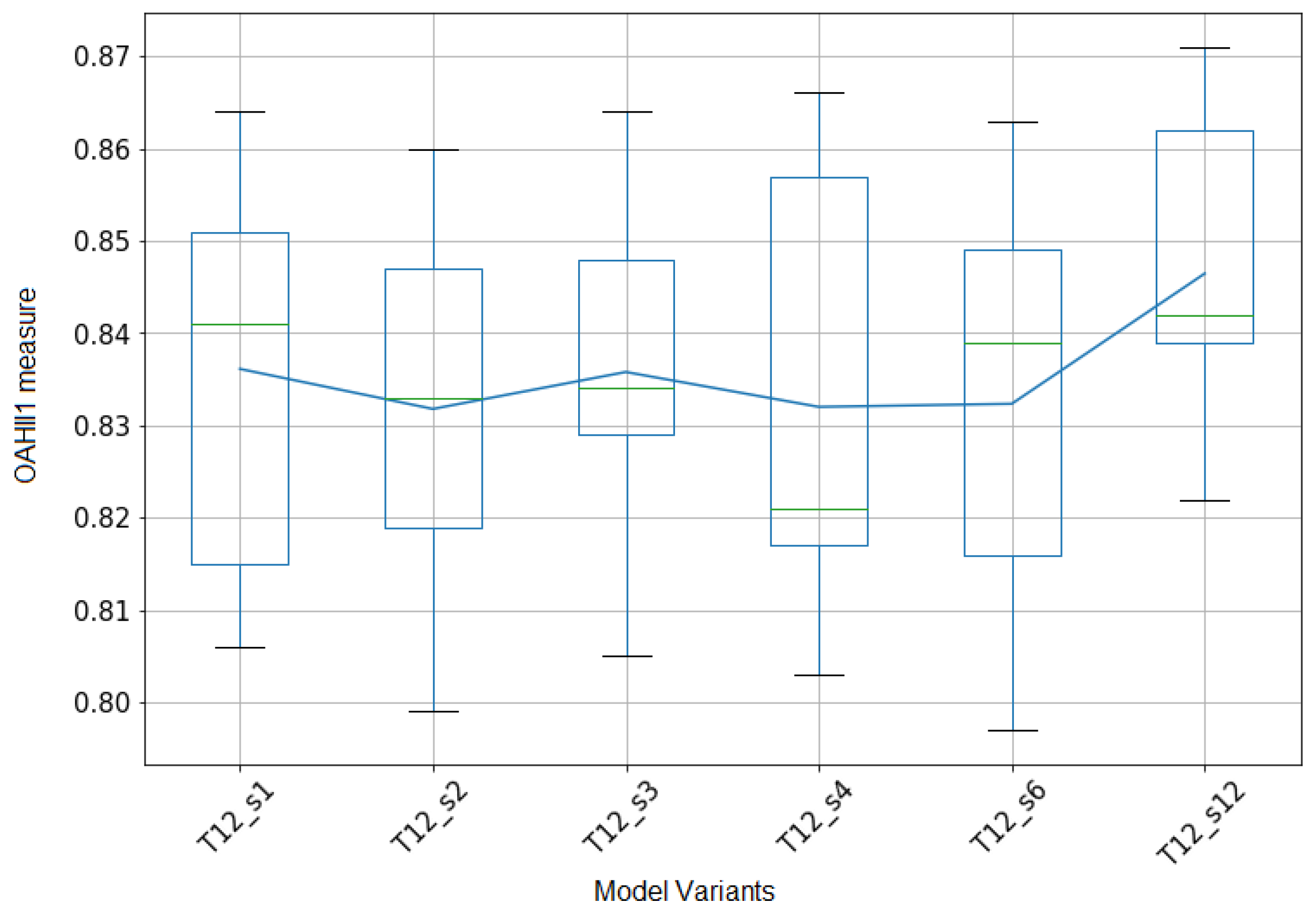
5.5.3. Quantitative Evaluation of Framework Variants
6. Discussions
- In the proposed hybrid model, we handle spatial and temporal contexts by different deep learning components as these contextual variables refer to different types of dependencies.
- Unlike proximity-based methods, the proposed model can be easily implemented on datasets with mixed-type behavioral attributes and it scales well to multivariate datasets with high number of features.
- The crafting of multivariate spatio-temporal dataset for unsupervised anomaly detection is also novel. The multi-channel CNN encoder network provides better representative spatial features for the anomaly detection process by using spatial neighborhood data.
Author Contributions
Funding
Conflicts of Interest
References
- Gupta, M.; Gao, J.; Aggarwal, C.C.; Han, J. Outlier Detection for Temporal Data: A Survey. IEEE Trans. Knowl. Data Eng. 2014, 26, 2250–2267. [Google Scholar] [CrossRef]
- Cheng, T.; Li, Z. A Multiscale Approach for Spatio-temporal Outlier Detection. Trans. GIS. 2006, 10, 253–263. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Spatial Outlier Detection. In Outlier Analysis, 2nd ed.; Springer Nature: New York, NY, USA, 2017; pp. 345–367. [Google Scholar]
- Hodge, V.J.; Austin, J. A Survey of Outlier Detection Methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar]
- Birant, D.; Kut, A. Spatio-temporal outlier detection in large databases. J. Comput. Inform. Technol. 2006, 14, 291–297. [Google Scholar] [CrossRef]
- Duggimpudi, M.B.; Abbady, S.; Chen, J.; Raghavan, V.V. Spatio-temporal outlier detection algorithms based on computing behavioral outlierness factor. Data Knowl. Eng. 2019, 122, 1–24. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Duan, L.; Xu, L.; Guo, F.; Lee, J.; Yan, B. A local-density based spatial clustering algorithm with noise. Inform. Syst. 2007, 32, 978–986. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. In Proceedings of the ACM SIGMOD 2000 International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 93–104. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. 2012, 6, 31–39. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Linear Models for Outlier Detection. In Outlier Analysis, 2nd ed.; Springer Nature: New York, NY, USA, 2017; pp. 65–110. [Google Scholar]
- Knabb, R.D.; Rhome, J.R.; Brown, D.P. Tropical Cyclone Report: Hurricane Katrina, 23–30 August 2005. National Hurricane Center. Available online: https://www.nhc.noaa.gov/data/tcr/AL122005_Katrina.pdf (accessed on 16 October 2019).
- Yaminshi, K.; Takeuchi, J. A unifying framework for detecting outliers and change points from non-stationary time series data. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 676–681. [Google Scholar]
- Cheng, H.; Tan, P.N.; Potter, C.; Klooster, S. Detection and Characterization of Anomalies in Multivariate Time Series. In Proceedings of the 2009 SIAM International Conference on Data Mining, Sparks, NV, USA, 30 April–2 May 2009. [Google Scholar]
- Shekhar, S.; Lu, C.-T.; Zhang, P. A Unified Approach to Detecting Spatial Outliers. GeoInformatica 2003, 7, 139–166. [Google Scholar] [CrossRef]
- Lu, C.-T.; Chen, D.; Kou, Y. Algorithms for spatial outlier detection. In Proceedings of the Third IEEE International Conference on Data Mining, Melbourne, FL, USA, 19–22 November 2003; pp. 597–600. [Google Scholar]
- Shekhar, S.; Lu, C.-T.; Zhang, P. Detecting Graph-based Spatial Outliers: Algorithms and Applications. In Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–19 August 2001; pp. 371–376. [Google Scholar]
- Sun, P.; Chawla, S. On local spatial outliers. In Proceedings of the Fourth IEEE International Conference on Data Mining, Brighton, UK, 1–4 November 2004; pp. 209–216. [Google Scholar]
- Gupta, M.; Sharma, A.B.; Chen, H.; Jiang, G. Context-Aware Time Series Anomaly Detection for Complex Systems. In Proceedings of the SDM Workshop of SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002; pp. 1–76. [Google Scholar]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 88–106. [Google Scholar]
- Alonso, F.; Ros, M.C.V.; Castillo, F.G. Isolation Forests to Evaluate Class Separability and the Representativeness of Training and Validation Areas in Land Cover Classification. Remote Sens. 2019, 11, 3000. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, D.; Castro, P.S.; Li, N.; Sun, L.; Li, S.; Wang, Z. iBOAT: Isolation-Based Online Anomalous Trajectory Detection. IEEE Trans. Intell. Transp. Syst. 2013, 14, 806–818. [Google Scholar] [CrossRef]
- Stripling, E.; Baesens, B.; Chizi, B.; Broucke, S. Isolation-based conditional anomaly detection on mixed-attribute data to uncover workers’ compensation fraud. Decis. Support. Syst. 2018, 111, 13–26. [Google Scholar] [CrossRef]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection. ICML 2016, Anomaly Detection Workshop. arXiv 2016, arXiv:1607.00148v2. [Google Scholar]
- Kim, T.-Y.; Cho, S.-B. Web traffic anomaly detection using C-LSTM neural networks. Expert Syst. Appl. 2018, 106, 66–76. [Google Scholar] [CrossRef]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumezanu, C.; Cheng, W.; Ni, J.; Zong, B.; Chen, H.; Chawla, N.V. A Deep Neural Network for Unsupervised Anomaly Detection and Diagnosis in Multivariate Time Series Data. arXiv 2018, arXiv:1811.08055. [Google Scholar] [CrossRef]
- Christiansen, P.; Nielsen, L.N.; Steen, K.A.; Jørgensen, R.N.; Karstoft, H. DeepAnomaly: Combining Background Subtraction and Deep Learning for Detecting Obstacles and Anomalies in an Agricultural Field. Sensors 2016, 16, 1904. [Google Scholar] [CrossRef]
- Oh, D.Y.; Yun, I.D. Residual Error Based Anomaly Detection Using Auto-Encoder in SMD Machine Sound. Sensors 2018, 18, 1308. [Google Scholar] [CrossRef]
- Munir, M.; Siddiqui, S.A.; Chattha, M.A.; Dengel, A.; Ahmed, S. FuseAD: Unsupervised Anomaly Detection in Streaming Sensors Data by Fusing Statistical and Deep Learning Models. Sensors 2019, 19, 2451. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Bengio, Y. Learning Deep Architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Replicator Neural Networks for Universal Optimal Source Coding. Science 1995, 269, 1860–1863. [Google Scholar] [CrossRef]
- Japkowicz, N.; Hanson, S.; Gluck, M. Nonlinear autoassociation is not equivalent to PCA. Neural Comput. 2000, 12, 531–545. [Google Scholar] [CrossRef] [PubMed]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Rifai, S.; Vincent, P.; Muller, X.; Glorot, X.; Bengio, Y. Contractive auto-encoders: Explicit invariance during feature extraction. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 833–840. [Google Scholar]
- Sakurada, M.; Yairi, T. Anomaly detection using autoencoders with nonlinear dimensionality reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, Gold Coast, Australia, 2 December 2014. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 2016; pp. 493–549. [Google Scholar]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cumberland, RI, USA, 1995; Volume 3361. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems Conference, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Aggarwal, C.C. Convolutional Neural Networks. In Neural Networks and Deep Learning, 1st ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 315–373. [Google Scholar]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition. In Proceedings of the 20th International Conference on Artificial Neural Networks, Part III, Thessaloniki, Greece, 15–18 September 2010; Springer: Berlin/Heidelberg, Germany; pp. 92–101. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. Adv. Neural Inform. Proc. Syst. 2014, 27, 3104–3112. [Google Scholar]
- Graves, A.; Jaitly, N. Towards end-to-end speech recognition with recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1764–1772. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhutdinov, R. Unsupervised Learning of Video Representations using LSTMs 2015. arXiv 2015, arXiv:1502.04681v3. [Google Scholar]
- Wu, Z.; Wang, X.; Jiang, Y.G.; Ye, H.; Xue, X. Modeling Spatial-Temporal Clues in a Hybrid Deep Learning Framework for Video Classification. In Proceedings of the 23rd ACM International Conference, Seattle, WA, USA, 3–6 November 2015. [Google Scholar]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, Long Short-Term Memory, fully connected Deep Neural Networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time Series Classification Using Multi-Channels Deep Convolutional Neural Networks. In Proceedings of the International Conference on Web-Age Information Management, Macau, China, 16–18 June 2014; pp. 298–310. [Google Scholar]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Exploiting multi-channels deep convolutional neural networks for multivariate time series classification. Front. Comput. Sci. 2016, 10, 96–112. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556v6. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
| Buoy ID | # Observations | # Training Subsequences | # Validation Subsequences | # Testing Subsequences |
|---|---|---|---|---|
| 42,001 | 5822 | 4325 | 731 | 730 |
| 42,002 | 5807 | 4295 | 732 | 725 |
| 42,003 | 1421 | 755 | 0 | 642 |
| 42,036 | 5452 | 4304 | 372 | 729 |
| 42,038 | 5811 | 4316 | 732 | 715 |
| 42,039 | 2178 | 682 | 730 | 723 |
| 42,040 | 5348 | 4297 | 274 | 723 |
| BURL1 | 5760 | 4327 | 732 | 665 |
| BYGL1 | 3953 | 2195 | 697 | 574 |
| CDRF1 | 5625 | 4105 | 732 | 730 |
| FWYF1 | 5231 | 4325 | 565 | 305 |
| GDIL1 | 5782 | 4321 | 732 | 693 |
| KYWF1 | 880 | 399 | 0 | 444 |
| LONF1 | 5825 | 4326 | 732 | 731 |
| MLRF1 | 5827 | 4328 | 732 | 731 |
| NPSF1 | 2638 | 2044 | 100 | 397 |
| SANF1 | 5818 | 4323 | 731 | 728 |
| SGOF1 | 5573 | 4268 | 539 | 730 |
| SMKF1 | 3622 | 2124 | 732 | 730 |
| SPGF1 | 4172 | 2674 | 732 | 730 |
| VCAF1 | 1437 | 108 | 706 | 573 |
| Buoy ID | IsolationForest | LOF | LDBSCAN | ST-Outlier Detection | MC-CNN-LSTM (T = 12) |
|---|---|---|---|---|---|
| 42,001 | 2005-08-29 09:00 | 2005-08-28 20:00 | 2005-08-28 20:00 | 2005-08-27 08:00 | 2005-08-28 20:00 |
| 2005-08-29 10:00 | 2005-08-28 21:00 | 2005-08-28 21:00 | 2005-08-28 19:00 | 2005-08-28 21:00 | |
| 2005-08-29 11:00 | 2005-08-28 19:00 | 2005-08-28 22:00 | 2005-08-28 20:00 | 2005-08-29 00:00 | |
| 2005-08-29 12:00 | 2005-08-29 09:00 | 2005-08-29 00:00 | 2005-08-28 21:00 | 2005-08-28 22:00 | |
| 2005-08-29 19:00 | 2005-08-29 11:00 | 2005-08-28 23:00 | 2005-08-31 23:00 | 2005-08-28 19:00 | |
| 42,003 | 2005-08-27 05:00 | 2005-08-07 20:00 | 2005-08-27 17:00 | 2005-08-24 20:00 | 2005-08-28 01:00 |
| 2005-08-27 03:00 | 2005-08-27 00:00 | 2005-08-28 01:00 | 2005-08-24 21:00 | 2005-08-28 04:00 | |
| 2005-08-27 04:00 | 2005-08-27 06:00 | 2005-08-27 18:00 | 2005-08-24 22:00 | 2005-08-28 02:00 | |
| 2005-08-28 05:00 | 2005-08-27 08:00 | 2005-08-27 16:00 | 2005-08-28 04:00 | 2005-08-28 03:00 | |
| 2005-08-28 04:00 | 2005-08-27 09:00 | 2005-08-27 20:00 | 2005-08-28 05:00 | 2005-08-28 00:00 | |
| 42,040 | 2005-08-29 20:00 | 2005-08-29 16:00 | 2005-08-29 13:00 | 2005-08-29 12:00 | 2005-08-29 13:00 |
| 2005-08-29 16:00 | 2005-08-29 10:00 | 2005-08-29 12:00 | 2005-08-29 13:00 | 2005-08-29 12:00 | |
| 2005-08-29 17:00 | 2005-08-29 09:00 | 2005-08-29 11:00 | 2005-08-29 14:00 | 2005-08-29 10:00 | |
| 2005-08-29 18:00 | 2005-08-29 08:00 | 2005-08-29 14:00 | 2005-08-29 15:00 | 2005-08-29 11:00 | |
| 2005-08-29 19:00 | 2005-08-29 23:00 | 2005-08-29 10:00 | 2005-08-31 19:00 | 2005-08-29 09:00 |
| Models | IF | LOF | LDBSCAN | ST-BDBCAN | HDLF (T = 3) | HDLF (T = 6) | HDLF (T = 12) | |
|---|---|---|---|---|---|---|---|---|
| Measures | ||||||||
| OAHII1 | 0.722 | 0.386 | 0.681 | 0.595 | 0.810 | 0.823 | 0.866 | |
| OAHII2 | 0.741 | 0.327 | 0.662 | 0.664 | 0.791 | 0.822 | 0.856 | |
| OAHII3 | 0.660 | 0.210 | 0.484 | 0.632 | 0.741 | 0.770 | 0.843 | |
| Model Variants | T = 12, s = 1 | T = 12, s = 2 | T = 12, s = 3 | T = 12, s = 4 | T = 12, s = 6 | T = 12, s = 12 |
|---|---|---|---|---|---|---|
| CNN(1)-LSTM(1) | 0.815 | 0.833 | 0.864 | 0.857 | 0.863 | 0.862 |
| CNN(1)-LSTM(2) | 0.864 | 0.841 | 0.834 | 0.866 | 0.853 | 0.841 |
| CNN(1)-LSTM(3) | 0.841 | 0.847 | 0.851 | 0.857 | 0.797 | 0.826 |
| CNN(2)-LSTM(1) | 0.815 | 0.828 | 0.818 | 0.817 | 0.849 | 0.871 |
| CNN(2)-LSTM(2) | 0.862 | 0.811 | 0.829 | 0.842 | 0.817 | 0.842 |
| CNN(2)-LSTM(3) | 0.851 | 0.860 | 0.832 | 0.803 | 0.841 | 0.839 |
| CNN(3)-LSTM(1) | 0.806 | 0.799 | 0.805 | 0.807 | 0.816 | 0.869 |
| CNN(3)-LSTM(2) | 0.830 | 0.819 | 0.841 | 0.821 | 0.839 | 0.846 |
| CNN(3)-LSTM(3) | 0.841 | 0.848 | 0.848 | 0.818 | 0.816 | 0.822 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karadayı, Y.; Aydin, M.N.; Öğrenci, A.S. A Hybrid Deep Learning Framework for Unsupervised Anomaly Detection in Multivariate Spatio-Temporal Data. Appl. Sci. 2020, 10, 5191. https://doi.org/10.3390/app10155191
Karadayı Y, Aydin MN, Öğrenci AS. A Hybrid Deep Learning Framework for Unsupervised Anomaly Detection in Multivariate Spatio-Temporal Data. Applied Sciences. 2020; 10(15):5191. https://doi.org/10.3390/app10155191
Chicago/Turabian StyleKaradayı, Yıldız, Mehmet N. Aydin, and A. Selçuk Öğrenci. 2020. "A Hybrid Deep Learning Framework for Unsupervised Anomaly Detection in Multivariate Spatio-Temporal Data" Applied Sciences 10, no. 15: 5191. https://doi.org/10.3390/app10155191
APA StyleKaradayı, Y., Aydin, M. N., & Öğrenci, A. S. (2020). A Hybrid Deep Learning Framework for Unsupervised Anomaly Detection in Multivariate Spatio-Temporal Data. Applied Sciences, 10(15), 5191. https://doi.org/10.3390/app10155191





