A Novel Variable Step Size Incremental Conductance Method with an Adaptive Scaling Factor
Abstract
:1. Introduction
2. Determination of the Optimal Scaling Factor Values
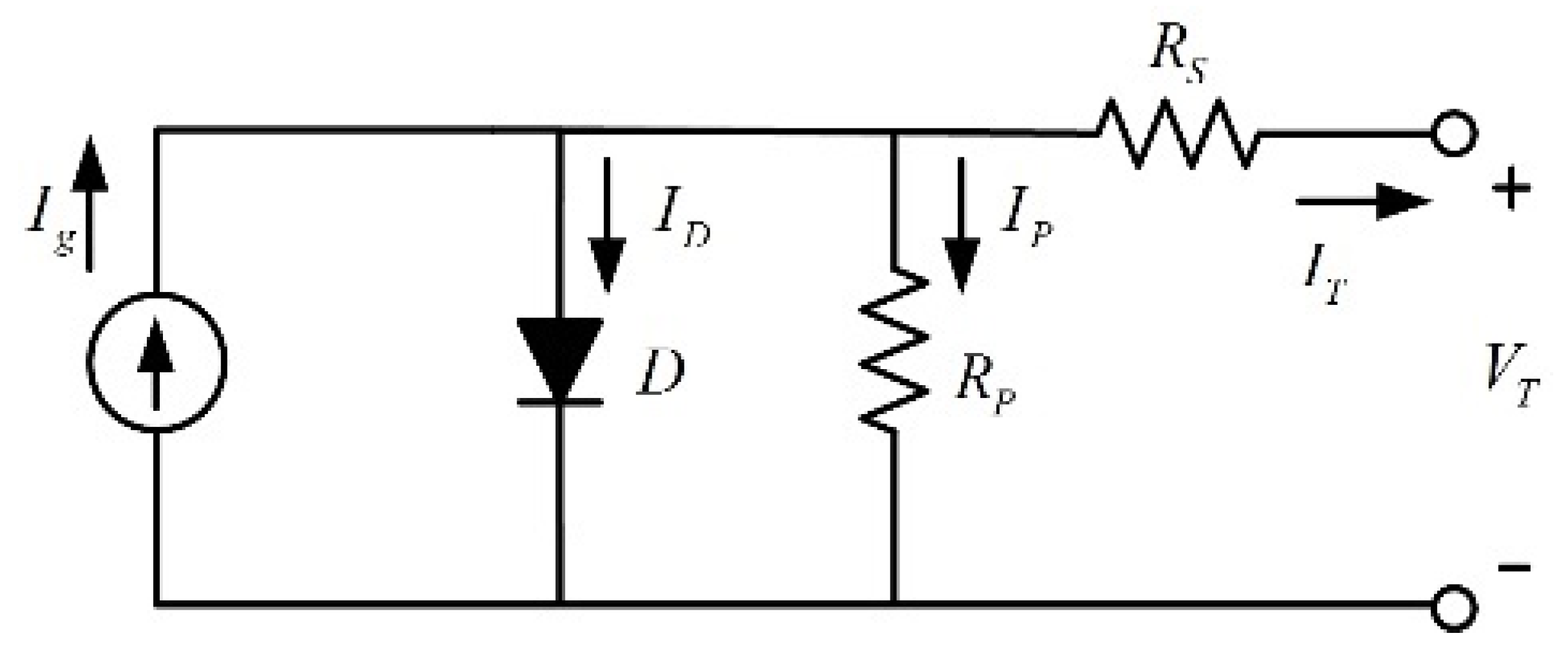
2.1. Solar Cell Characteristics
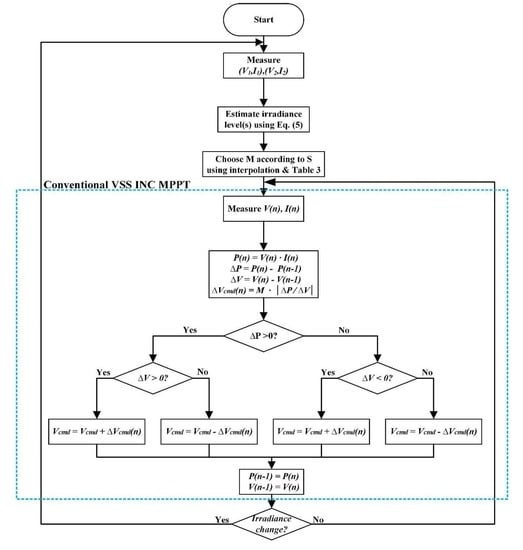
2.2. Conventional VSS INC MPPT Algorithm
2.3. Optimal Scaling Factor for Different Irradiance Levels
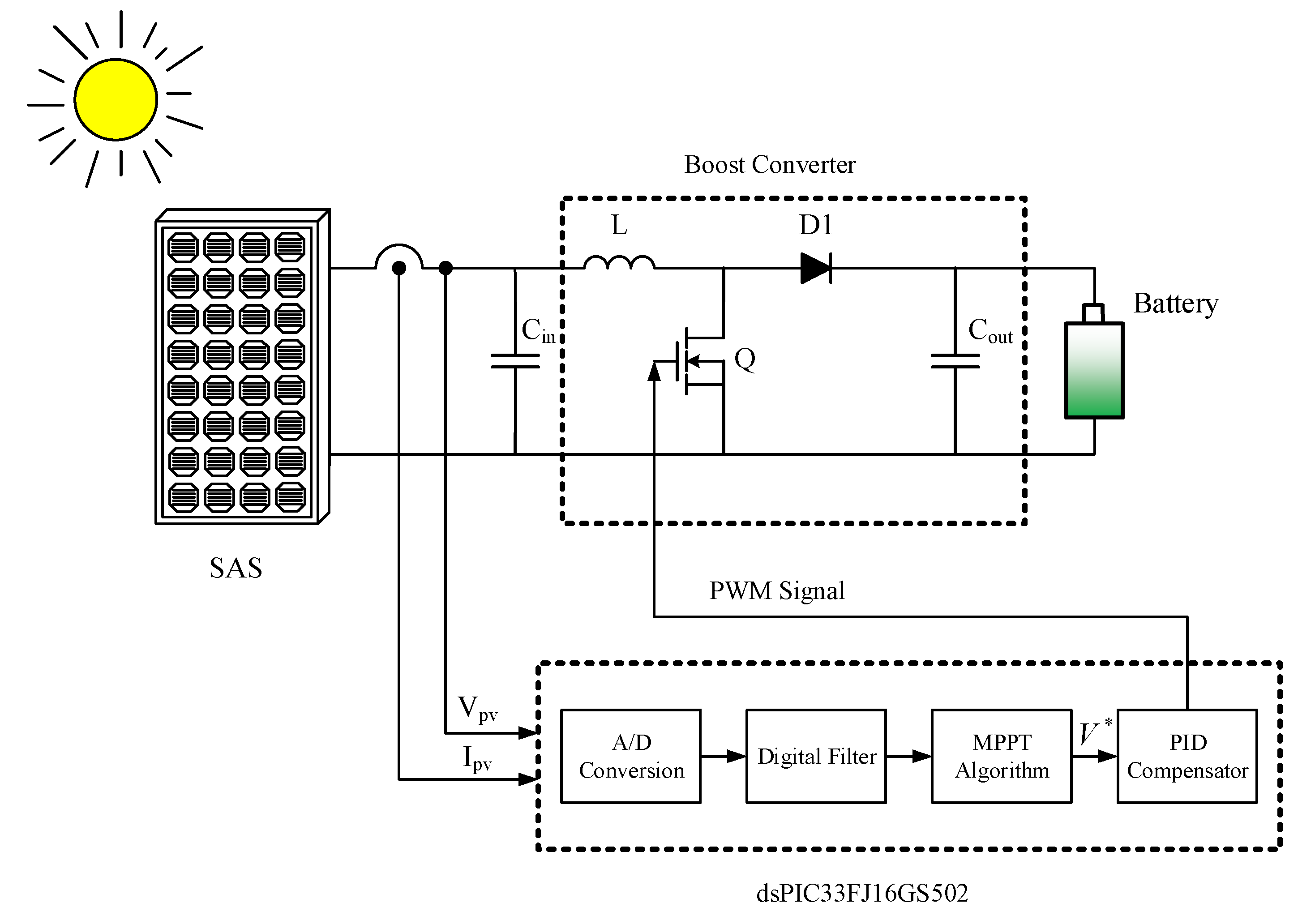
3. Description of the Proposed Method
3.1. Irradiance Level Estimation Method
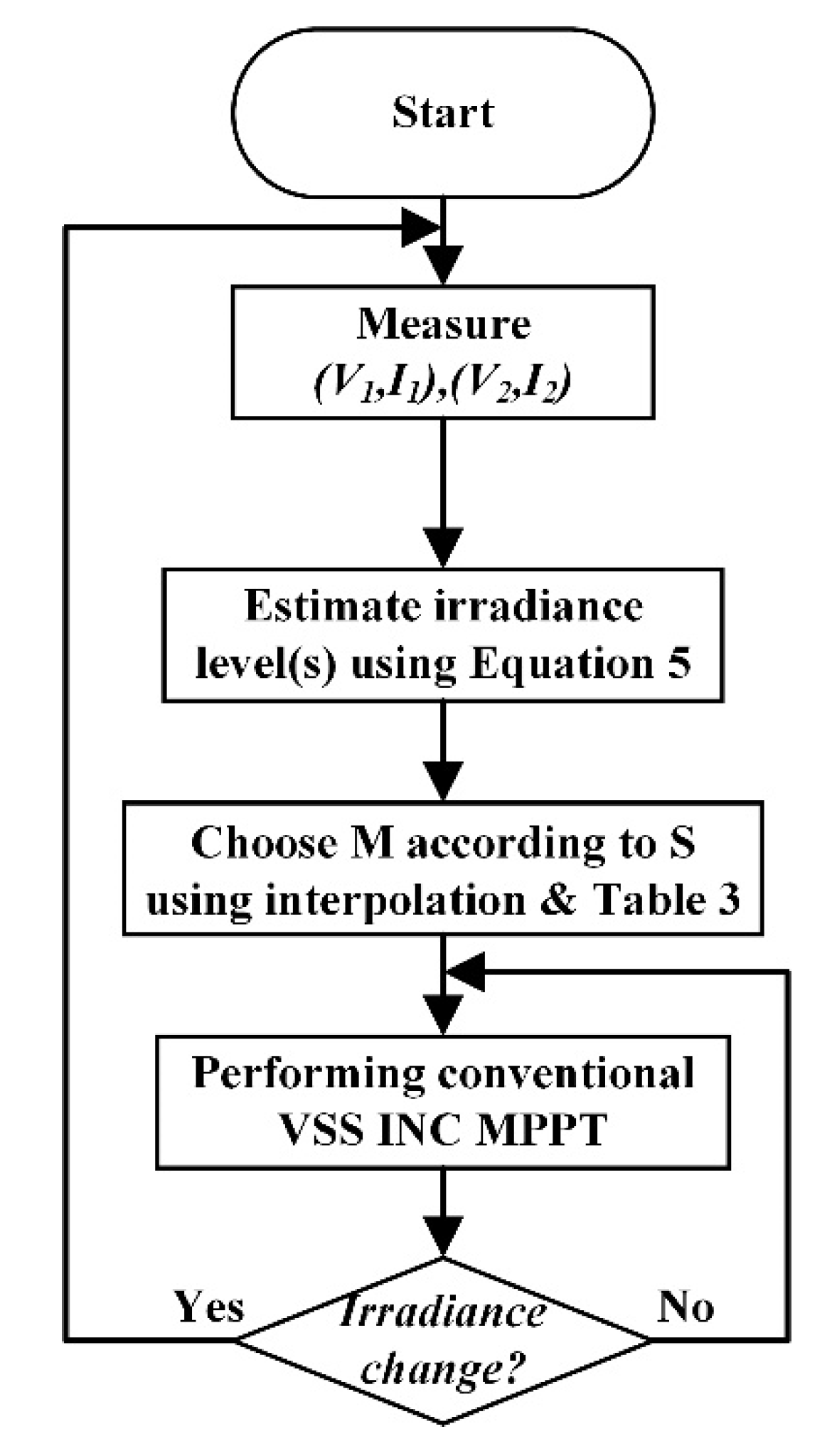
3.2. Flowchart of the Proposed Method
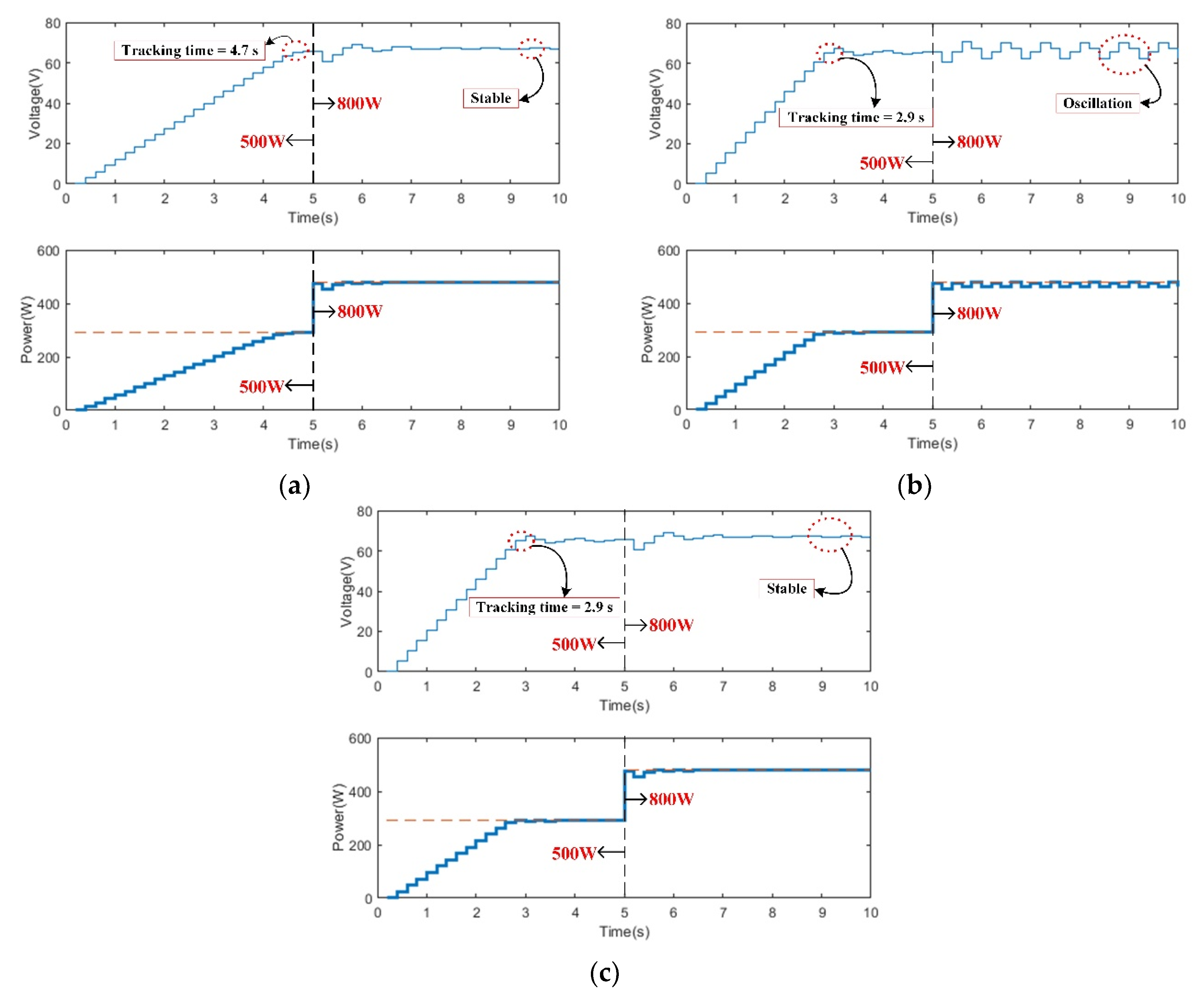
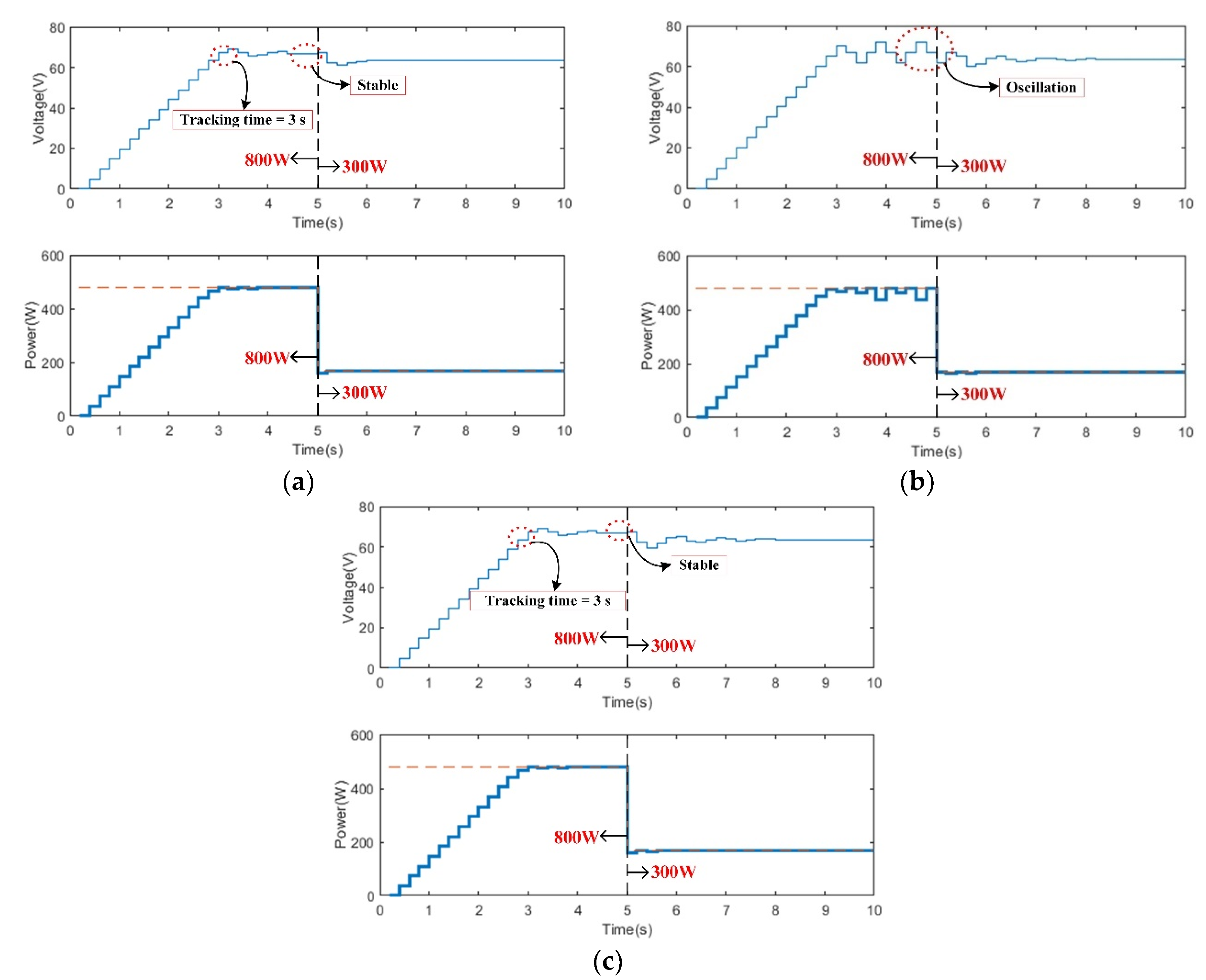
4. Simulation and Experimental Results
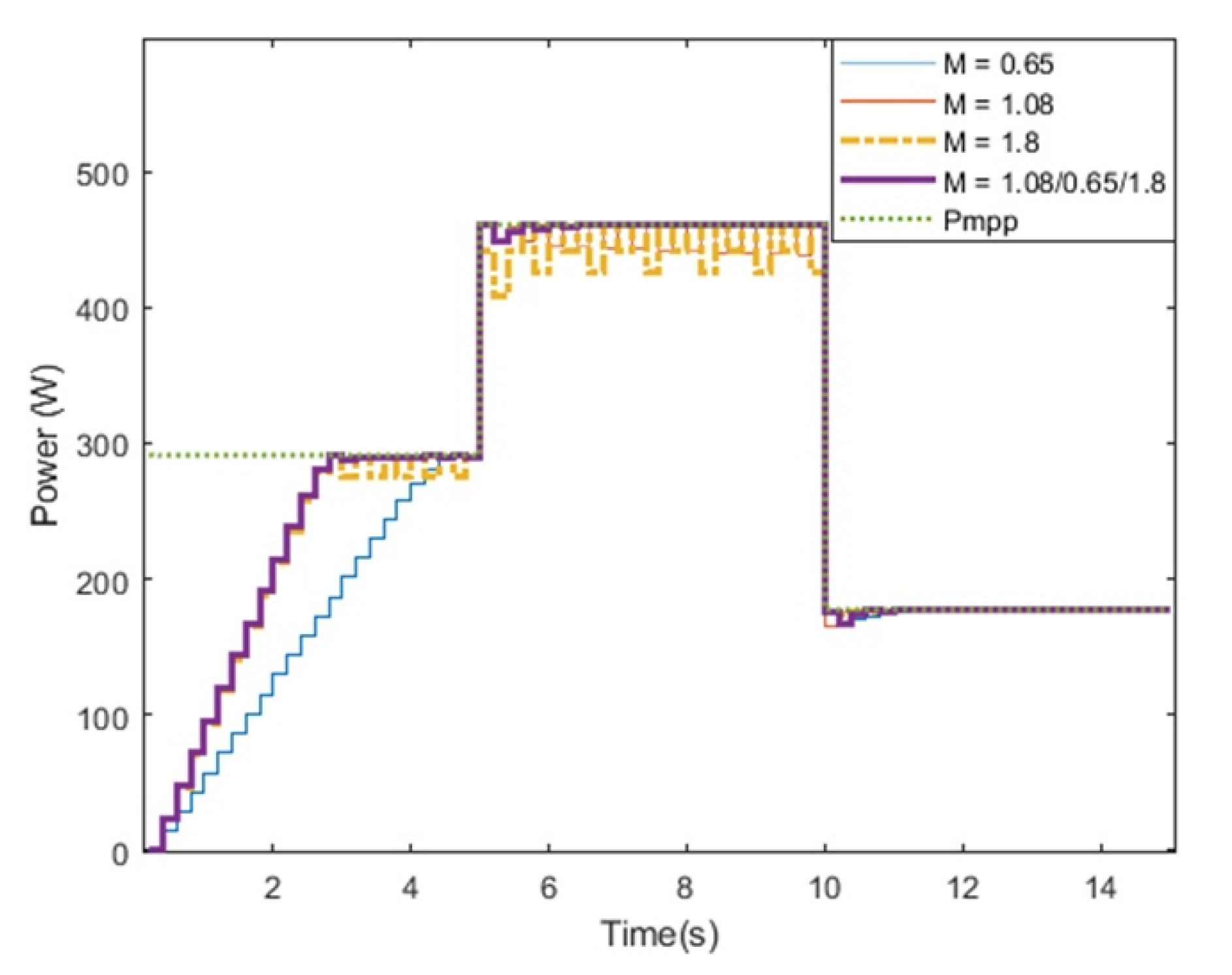
4.1. Simulation Result
4.2. Experimental Results
5. Discussions and Limitations
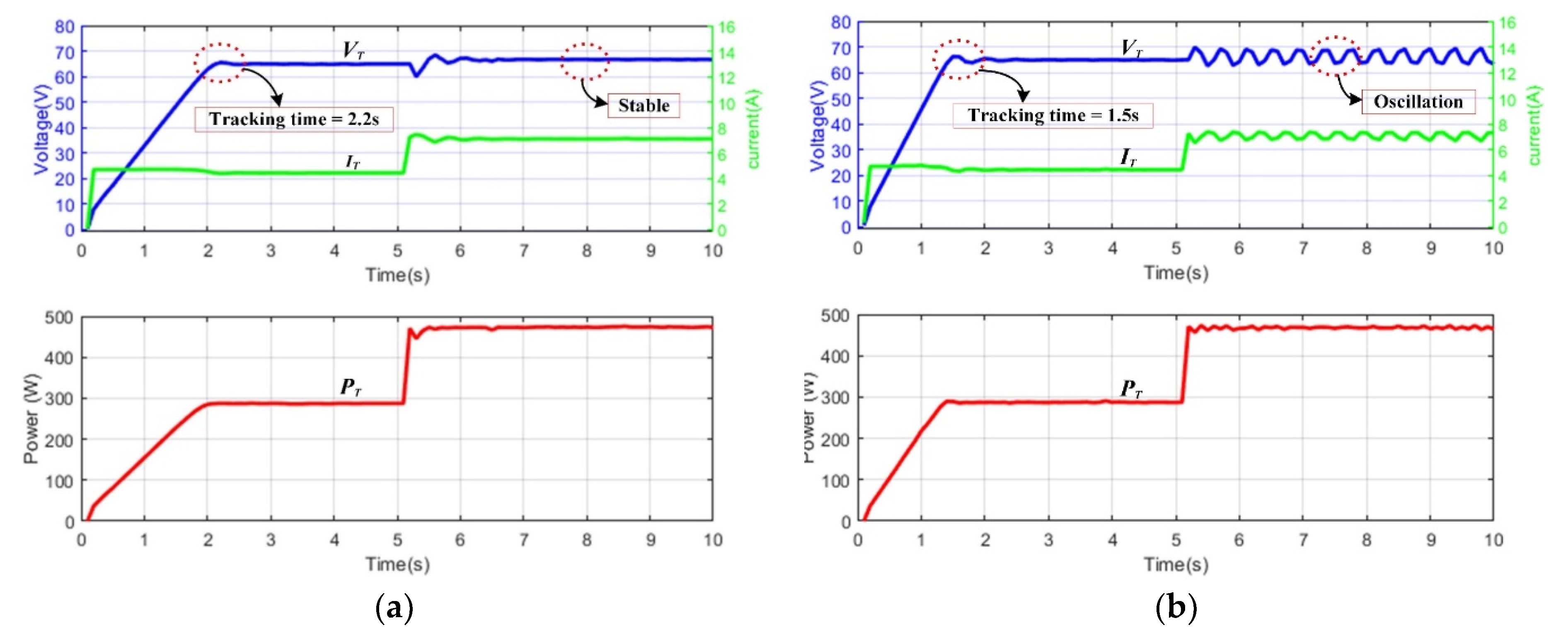
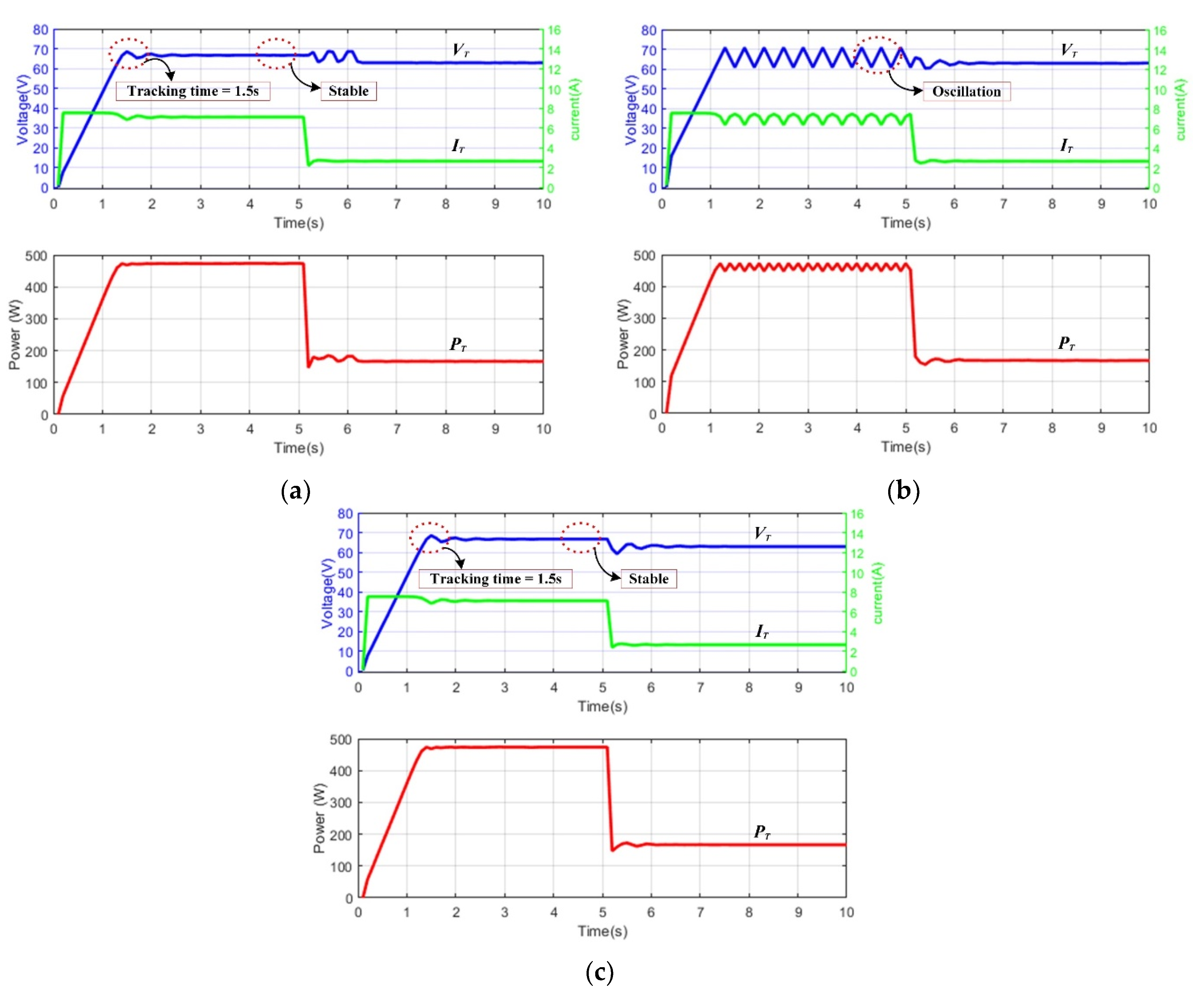
5.1. Tracking Time
5.2. Tracking Accuracy
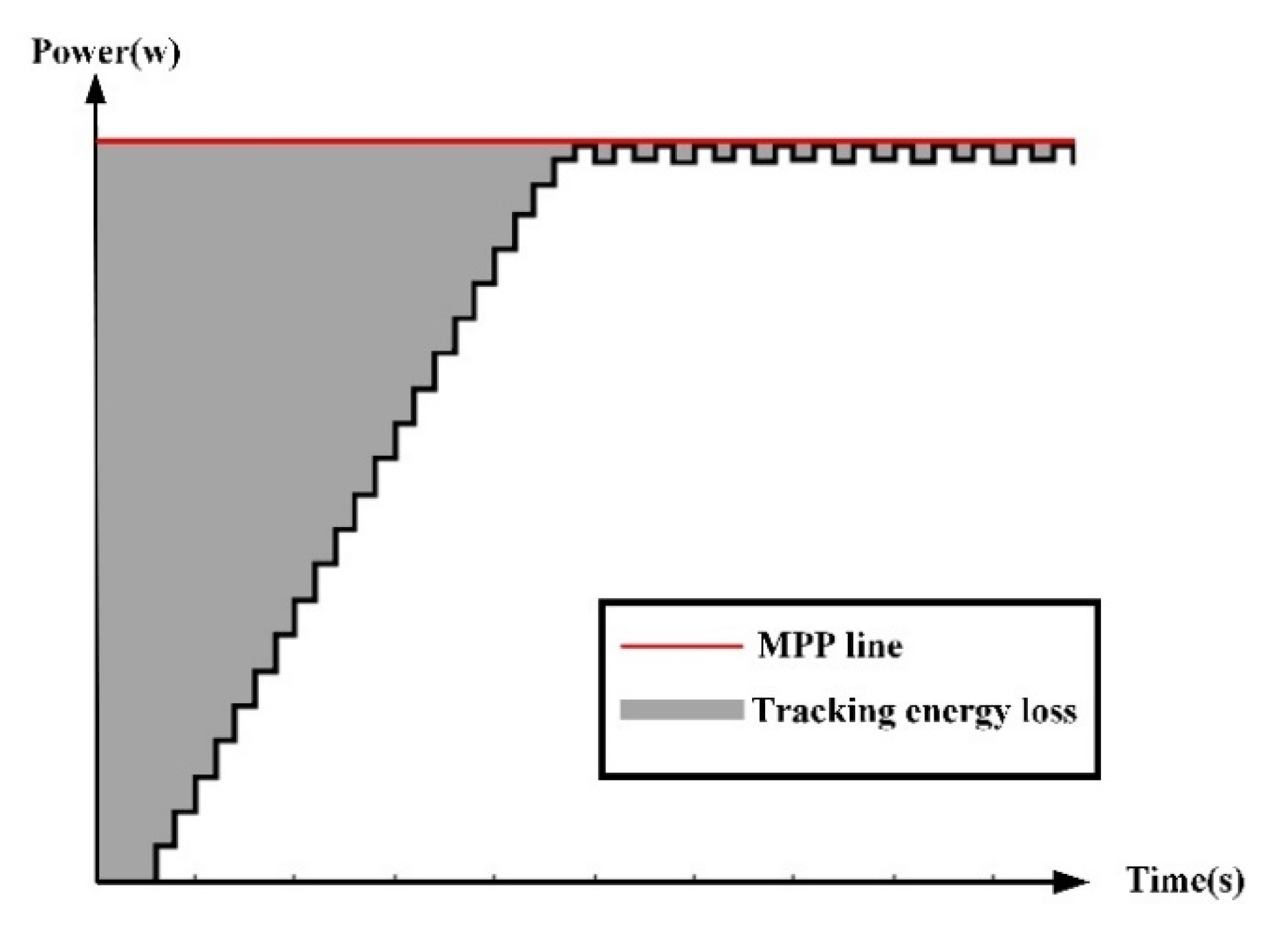
5.3. Tracking Energy Loss
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kalaiarasi, N.; Dash, S.S.; Padmanaban, S.; Paramasivam, S.; Morati, P.K. Maximum power point tracking implementation by dspace controller integrated through z-source inverter using particle swarm optimization technique for photovoltaic applications. Appl. Sci. 2018, 8, 145. [Google Scholar]
- Chen, P.C.; Chen, P.Y.; Liu, Y.H.; Chen, J.H.; Lu, Y.F. A comparative study on maximum power point tracking techniques for photovoltaic generation systems operating under fast changing environments. Sol. Energy 2015, 119, 261–276. [Google Scholar] [CrossRef]
- Antonio, A.; Rujula, B.; Antonio, J.; Abia, C. A novel MPPT method for PV systems with irradiance measurement. Sol. Energy 2014, 109, 95–104. [Google Scholar]
- Fathabad, H. Novel fast dynamic MPPT (maximum power point tracking) technique with the capability of very high accurate power tracking. Energy 2016, 94, 466–475. [Google Scholar] [CrossRef]
- Pandey, A.; Dasgupta, N.; Mukerjee, A.K. High-performance algorithms for drift avoidance and fast tracking in solar MPPT system. IEEE Trans. Enegry Cover. 2008, 23, 681–689. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kan, Y. A VSS INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Lalili, D.; Mellit, A.; Lourci, N.; Medjahed, B.; Berkouk, E.M. Input output feedback linearization control and VSS MPPT algorithm of a grid-connected photovoltaic inverter. Renew. Energy 2011, 36, 3282–3291. [Google Scholar] [CrossRef]
- Mei, Q.; Shan, M.; Liu, L.; Guerrero, J.M. A novel improved variable step-size incremental-resistance MPPT method for PV systems. IEEE Trans. Ind. Electron. 2011, 58, 2427–2434. [Google Scholar] [CrossRef]
- Jiang, Y.; Qahouq, J.A.A.; Haskew, T.A. Adaptive step size with adaptive-perturbation-frequency digital MPPT controller for a single-sensor photovoltaic solar system. IEEE Trans. Power Electron. 2013, 28, 3195–3205. [Google Scholar] [CrossRef]
- Lalili, D.; Mellit, A.; Lourci, N.; Medjahed, B.; Boubakir, C. State feedback control and VSS MPPT algorithm of three-level grid-connected photovoltaic inverter. Sol. Energy 2013, 98, 561–571. [Google Scholar] [CrossRef]
- Killi, M.; Samant, S. An adaptive voltage-sensor-based MPPT for photovoltaic systems with SEPIC converter including steady-state and drift analysis. IEEE Trans. Ind. Electron. 2015, 62, 7609–7618. [Google Scholar] [CrossRef]
- Shi, Y.; Li, R.; Xue, Y.; Li, H. High-frequency-link-based grid-tied PV system with small DC-link capacitor and low-frequency ripple-free maximum power point tracking. IEEE Trans. Power Electron. 2016, 31, 328–339. [Google Scholar] [CrossRef]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced VSS incremental conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Amir, A.; Amir, A.; Selvaraj, J.; Rahima, N.A.; Abusorrah, A.M. Conventional and modified MPPT techniques with direct control and dual scaled adaptive step-size. Sol. Energy 2017, 157, 1017–1031. [Google Scholar] [CrossRef]
- Thangavelu, A.; Vairakannu, S.; Parvathyshankar, D. Linear open circuit voltage-variable step-sizeincremental conductance strategy-based hybrid MPPT controller for remote power applications. IET Power Electron. 2017, 10, 1363–1376. [Google Scholar] [CrossRef]
- Teng, J.H.; Huang, W.H.; Hsu, T.A.; Wang, C.Y. Novel and fast maximum power point tracking for photovoltaic generation. IEEE Trans. Ind. Electron. 2016, 63, 4955–4966. [Google Scholar] [CrossRef]
- Na, W.; Chen, P.; Kim, J. An improvement of a fuzzy logic-controlled maximum power point tracking algorithm for photovoltic applications. Appl. Sci. 2017, 7, 326. [Google Scholar] [CrossRef]
- Hamed, H.D.; Keypour, R.; Khalghani, M.R.; Khooban, M.H. A new approach in MPPT for photovoltaic array based on extremum seeking control under uniform and non-uniform irradiances. Sol. Energy 2013, 94, 28–36. [Google Scholar]
- Kchaou, A.; Naamane, A.; Koubaa, Y.; M’sirdi, N. Second order sliding mode-based MPPT control for photovoltaic applications. Sol. Energy 2017, 155, 758–769. [Google Scholar] [CrossRef]
- Renaudineau, H.; Donatantonio, F.; Fontchastagner, J.; Petrone, G.; Spagnuolo, G.; Martin, J.P.; Pierfederici, S. A PSO-based global MPPT technique for distributed PV power generation. IEEE Trans. Ind. Electron. 2015, 62, 1047–1058. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Ding, M.; Lv, D.; Yang, C.; Li, S.; Fang, Q.; Yang, B.; Zhang, X. Global maximum power point tracking of PV systems under partial shading condition: A transfer reinforcement learning approach. Appl. Sci. 2019, 9, 2769. [Google Scholar] [CrossRef] [Green Version]
- Kalogerakis, C.; Koutroulis, E.; Lagoudakis, M.G. Global MPPT based on machine-learning for PV arrays operating under partial shading conditions. Appl. Sci. 2020, 10, 700. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.H.; Chen, J.H.; Huang, J.W. Global maximum power point tracking algorithm for PV systems operating under partially shaded conditions using the segmentation search method. Sol. Energy 2014, 103, 350–363. [Google Scholar] [CrossRef]
- Patel, H.; Agarwal, V. Maximum power point tracking scheme for PV systems operating under partially shaded conditions. IEEE Trans. Ind. Electron. 2008, 55, 1689–1698. [Google Scholar] [CrossRef]
- Boztepe, M.; Guinjoan, F.; Velasco-Quesada, G.; Silvestre, S.; Chouder, A.; Karatepe, E. Global MPPT scheme for photovoltaic string inverters based on restricted voltage window search algorithm. IEEE Trans. Ind. Electron. 2014, 61, 3302–3312. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Ruan, X. High-accuracy and fast-speed MPPT methods for PV string under partially shaded conditions. IEEE Trans. Ind. Electron. 2016, 63, 235–245. [Google Scholar] [CrossRef]


| Specification | Designed Parameter | ||
|---|---|---|---|
| Input Voltage | Vin = 20–100 V | L1 | 1.08 mH |
| Rated Output Voltage | Vo = 200 V | C1 | 100 μF |
| Rated Output Current | Io = 3 A | Q1 | IPP65R110CFDA |
| Rated Output Power | Po = 600 W | D1 | C3D10060 |
| Switching Frequency | fs = 50 kHz | ||
| Output Voltage Ripple | ∆Vo/Vo ≤ 1% | ||
| Parameters | Value |
|---|---|
| Maximum PV Power | 599.8 W |
| Voltage at MPP | 67.52 V |
| Current at MPP | 8.885 A |
| Open circuit voltage, Voc | 79.08 V |
| Short circuit current, Isc | 9.41 A |
| W/m2 | Optimal M | W/m2 | Optimal M |
| 100 | 5.40 | 600 | 0.90 |
| 200 | 2.70 | 700 | 0.78 |
| 300 | 1.80 | 800 | 0.65 |
| 400 | 1.35 | 900 | 0.60 |
| 500 | 1.08 | 1000 | 0.54 |
| tt of 500 W/m2 | tt of 800 W/m2 | tt of 300 W/m2 | ta of 500 W/m2 | ta of 800 W/m2 | ta of 300 W/m2 | Total Energy Loss | |
| VSS INC (M = 0.65) | 4.7 s | 0.4 s | 0.6 s | 99.8% | 99.9% | 99.9% | 3145.6 W |
| VSS INC (M = 1.08) | 2.9 s | 0.4 s | 0.4 s | 99.8% | 98.2% | 99.9% | 2175.7 W |
| VSS INC (M = 1.8) | 2.9 s | 0.4 s | 0.4 s | 97.5% | 97.8% | 99.9% | 2446.3 W |
| Proposed method | 2.9 s | 0.4 s | 0.4 s | 99.8% | 99.9% | 99.9% | 1970.2 W |
| tt of ii Case | tt of di Case | ta of ii Case | ta of di Case | Total Energy Loss of ii Case | Total Energy Loss of di Case | |
| VSS INC (M = 0.65) | 2.2 s | 1.5 s | 99.8% | 99.1% | 401.5 W | 402.5 W |
| VSS INC (M = 1.08) | 1.5 s | X | 97.7% | X | 275.6 W | X |
| VSS INC (M = 1.8) | X | N.A. | X | 96.3% | X | 358.6 W |
| Proposed method | 1.5 s | 1.5 s | 99.8% | 99.8% | 225.5 W | 282.3 W |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuang, M.-T.; Liu, Y.-H.; Ye, S.-P. A Novel Variable Step Size Incremental Conductance Method with an Adaptive Scaling Factor. Appl. Sci. 2020, 10, 5214. https://doi.org/10.3390/app10155214
Chuang M-T, Liu Y-H, Ye S-P. A Novel Variable Step Size Incremental Conductance Method with an Adaptive Scaling Factor. Applied Sciences. 2020; 10(15):5214. https://doi.org/10.3390/app10155214
Chicago/Turabian StyleChuang, Man-Tsai, Yi-Hua Liu, and Song-Pei Ye. 2020. "A Novel Variable Step Size Incremental Conductance Method with an Adaptive Scaling Factor" Applied Sciences 10, no. 15: 5214. https://doi.org/10.3390/app10155214