Energy-Based Prediction of the Displacement of DCFP Bearings
Abstract
:1. Introduction
2. State-of-the-Art Isolator Displacement Prediction
- (I)
- (1)
- Equivalent Lateral Force Procedure (ASCE [6])
- (2)
- Simplified Linear Analysis (Euro Code [7])
- (3)
- Simplified Response Prediction Method for the Maximum Response Using an Equivalent Single-Degree-of-Freedom System (AIJ [8]
- (4)
- Response Prediction of the Seismic Isolation Level Based on Energy Balance (AIJ [8])
- (II)
- (1)
- Approximate Inelastic Input Energy Spectra
- (2)
- Another Method Proposed by Uang [11]
3. Performed Experiments
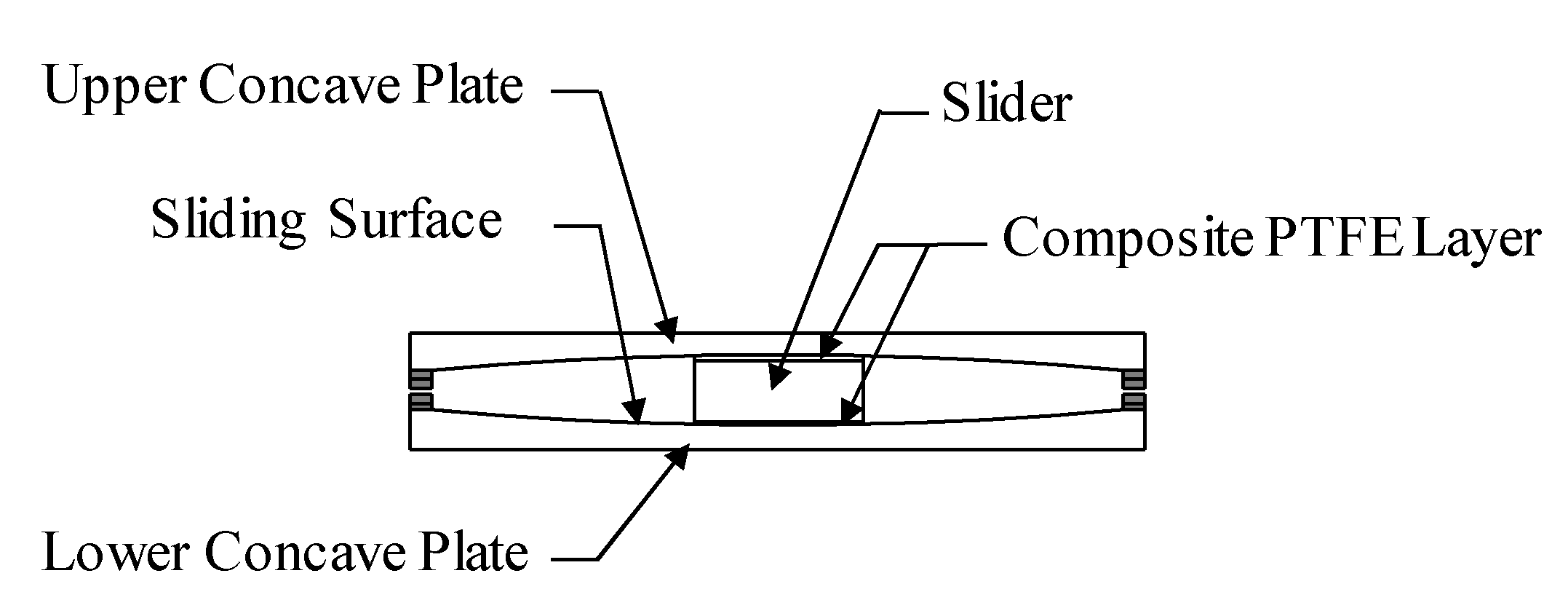
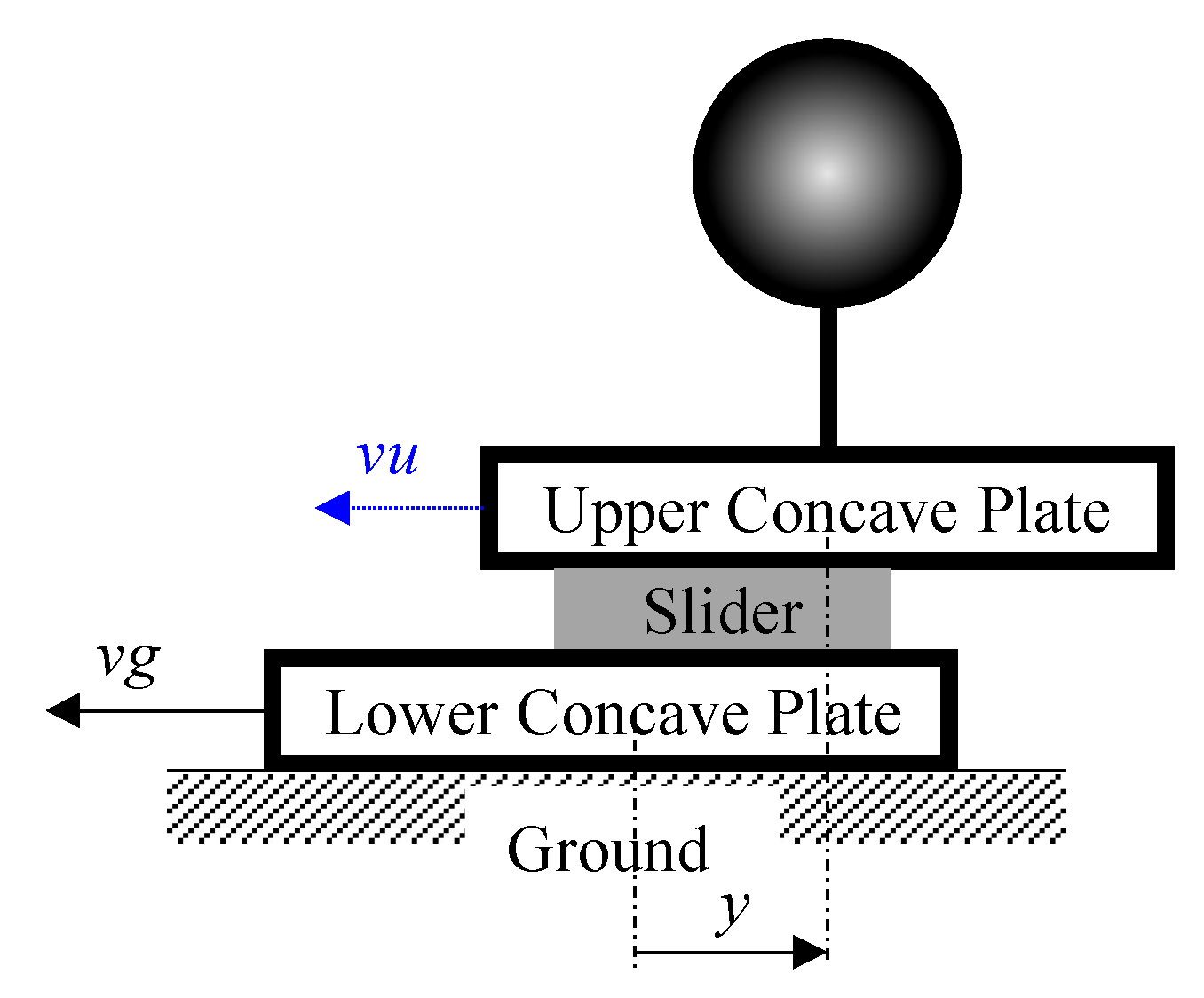
3.1. Testing Setup
3.2. Dependency Tests
3.3. ASCE Tests
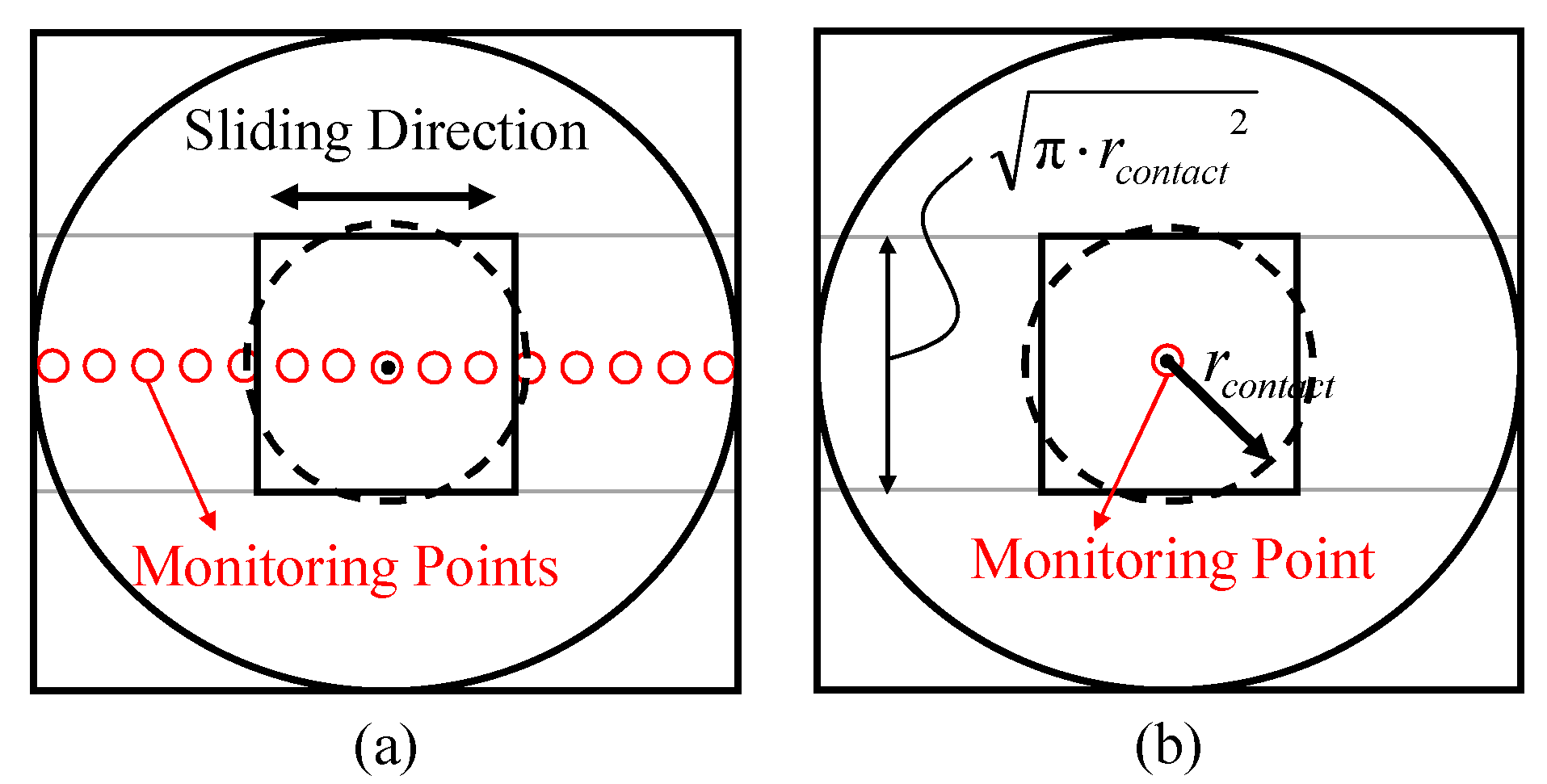
4. Numerical Simulation of the Experiments
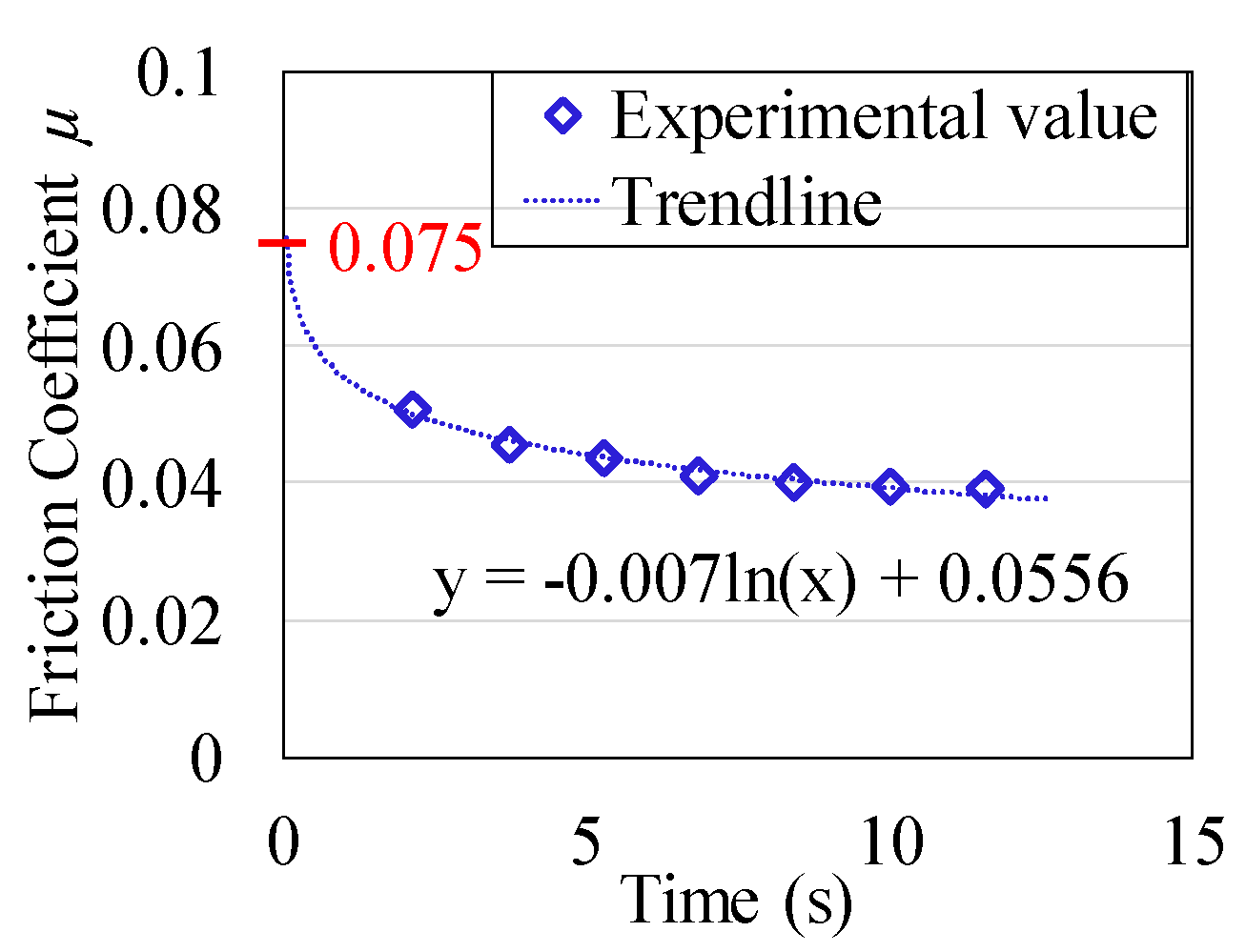
4.1. Friction Dependency
4.2. Friction Models
4.3. Numerical Results Using Friction Models
4.4. Numerical Results Using a Constant Friction Coefficient
5. Numerical Analyses of the Dynamic Response of Isolated Structures
5.1. Mechanical Model
5.2. Input Ground Motions
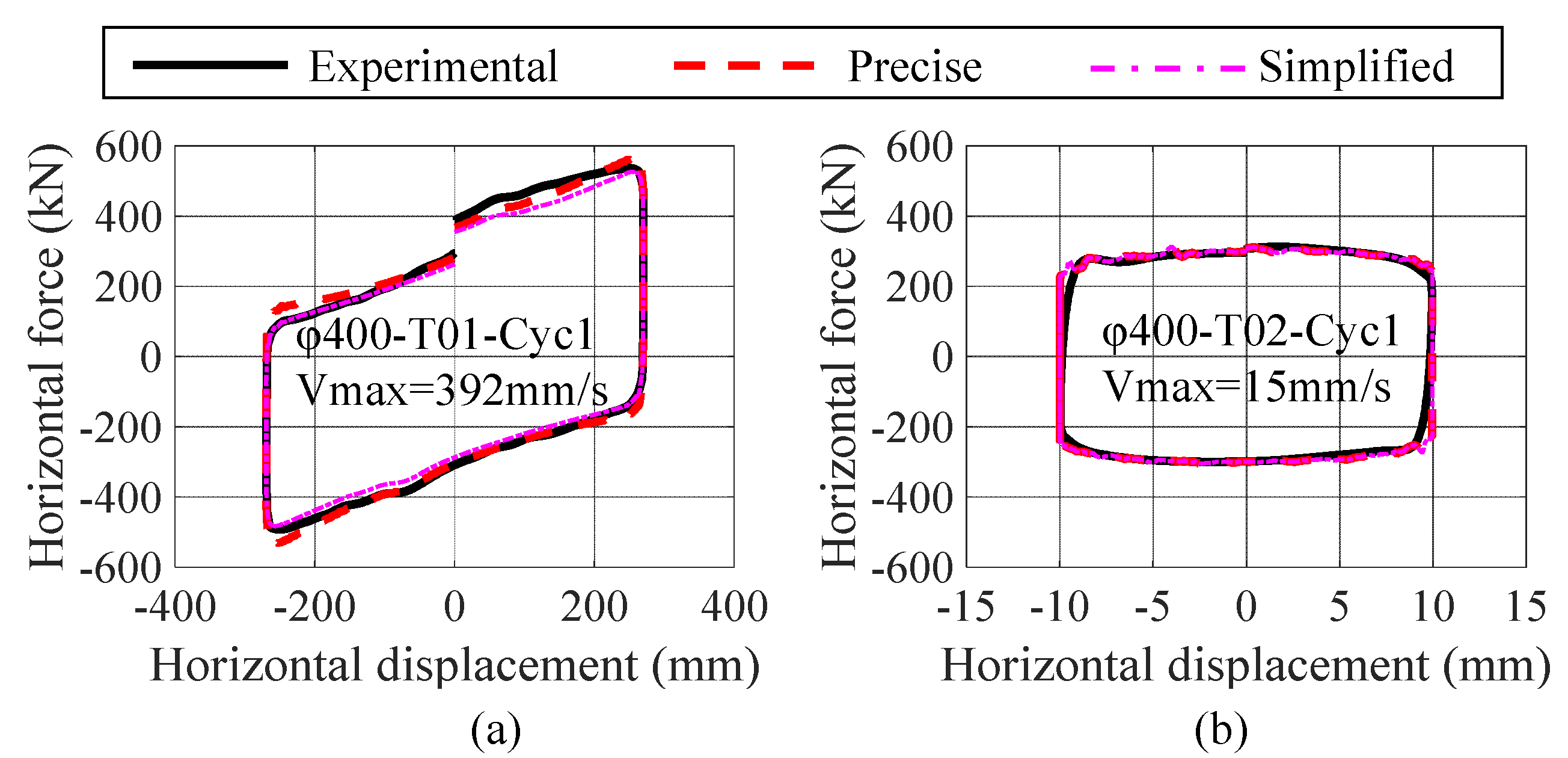
5.3. Accuracy of the Simplified Model
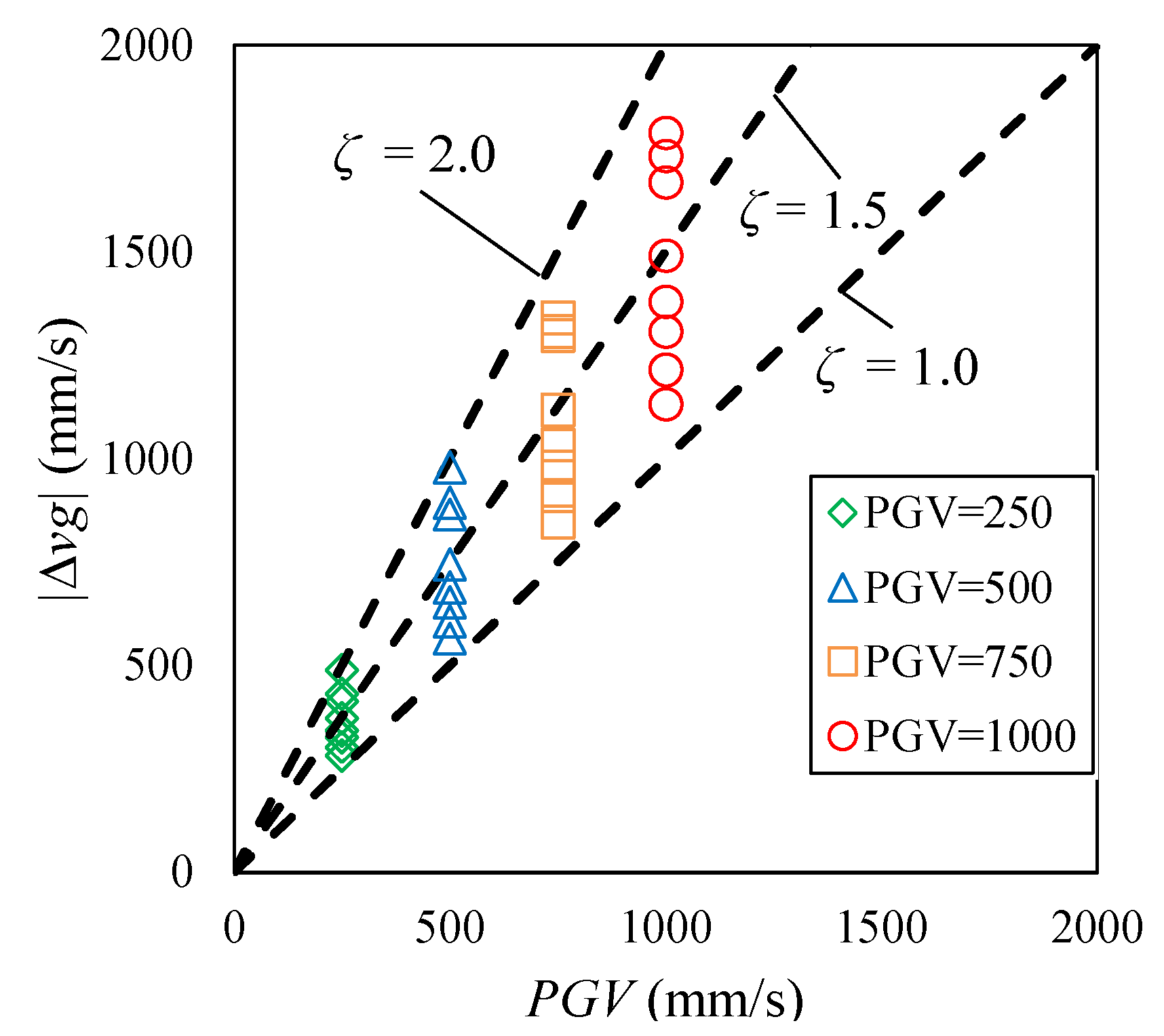
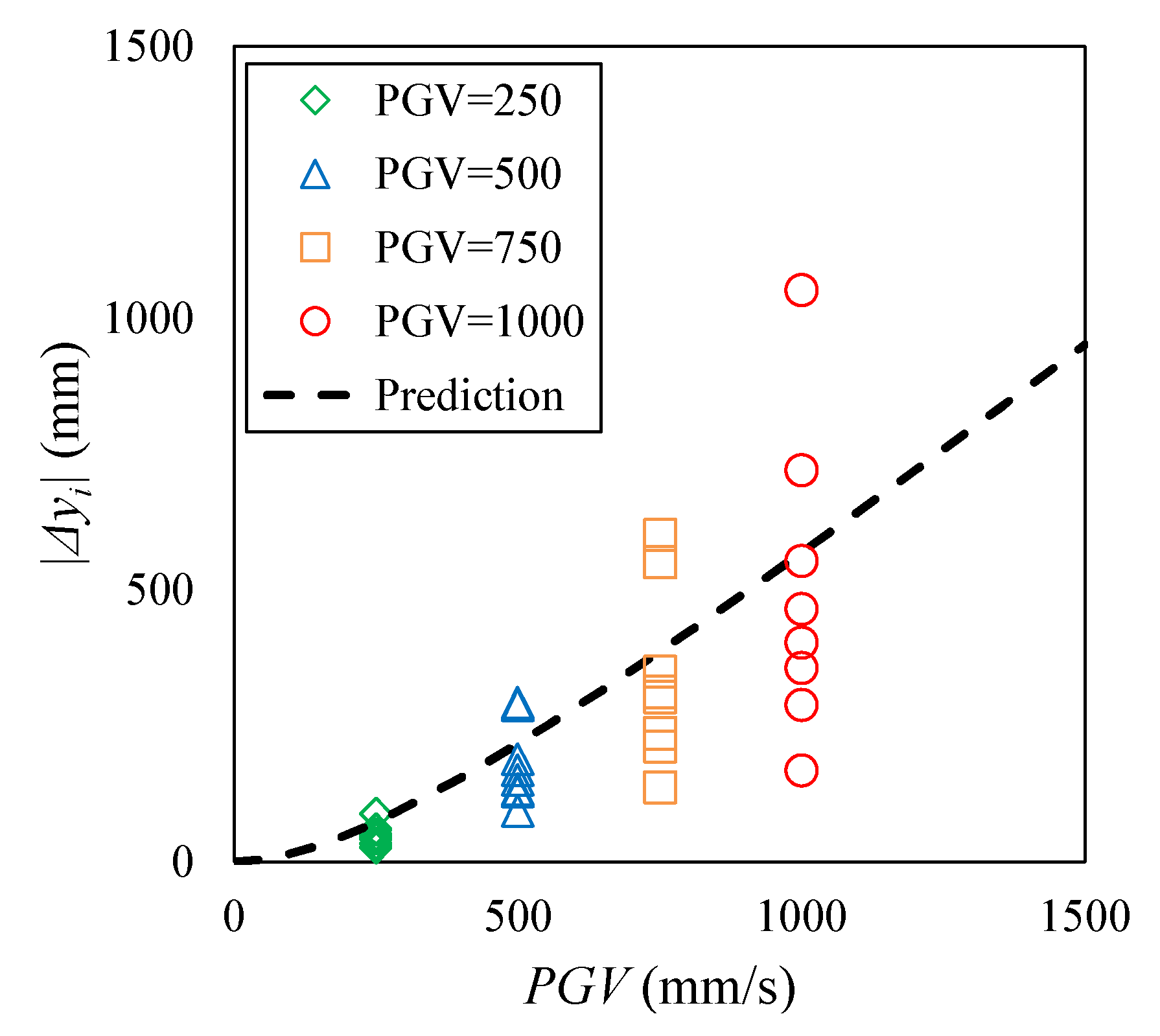
5.4. Relation between Maximum Response Displacement and PGV
6. Proposed Prediction Method
6.1. Mechanical Model
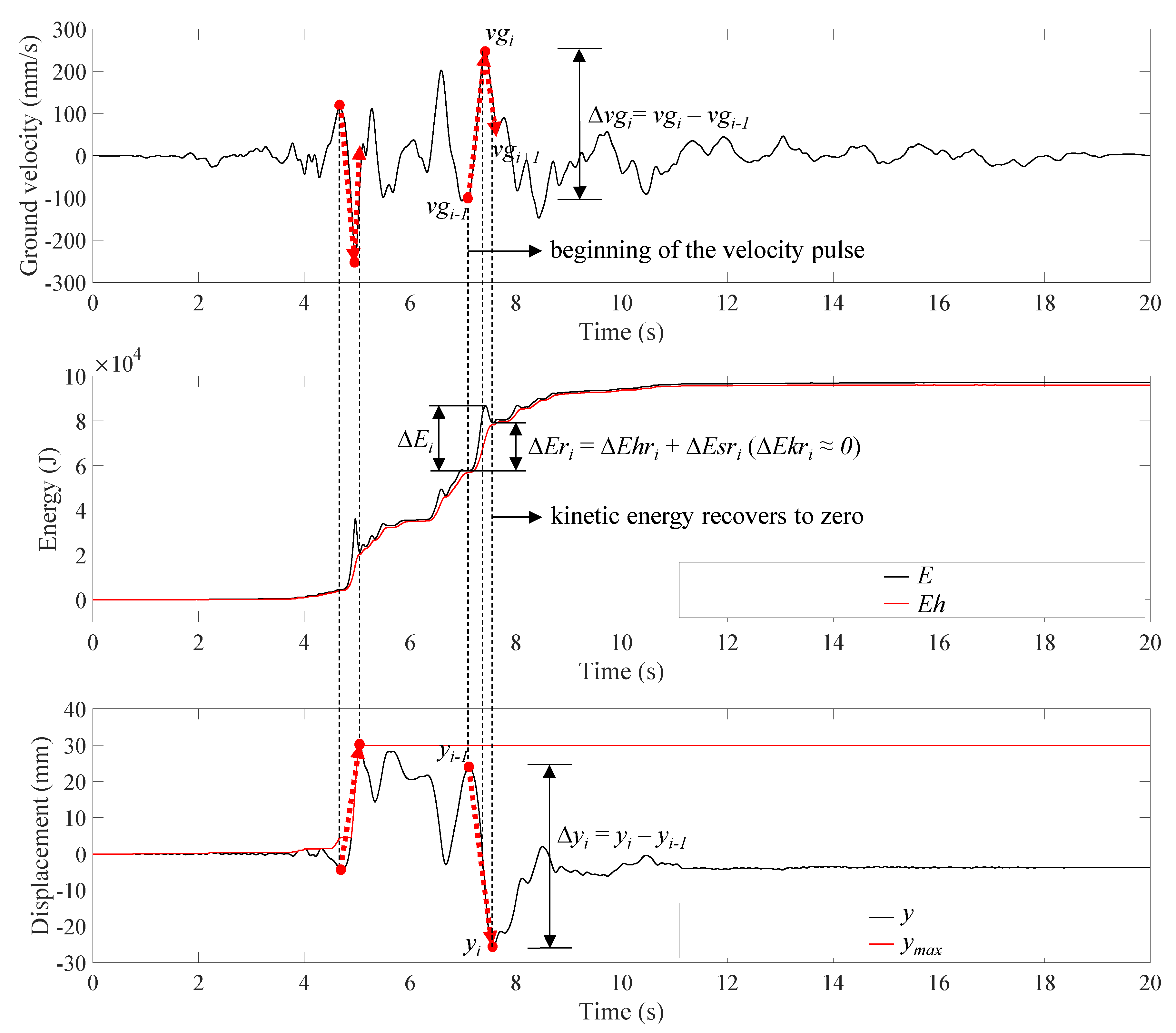
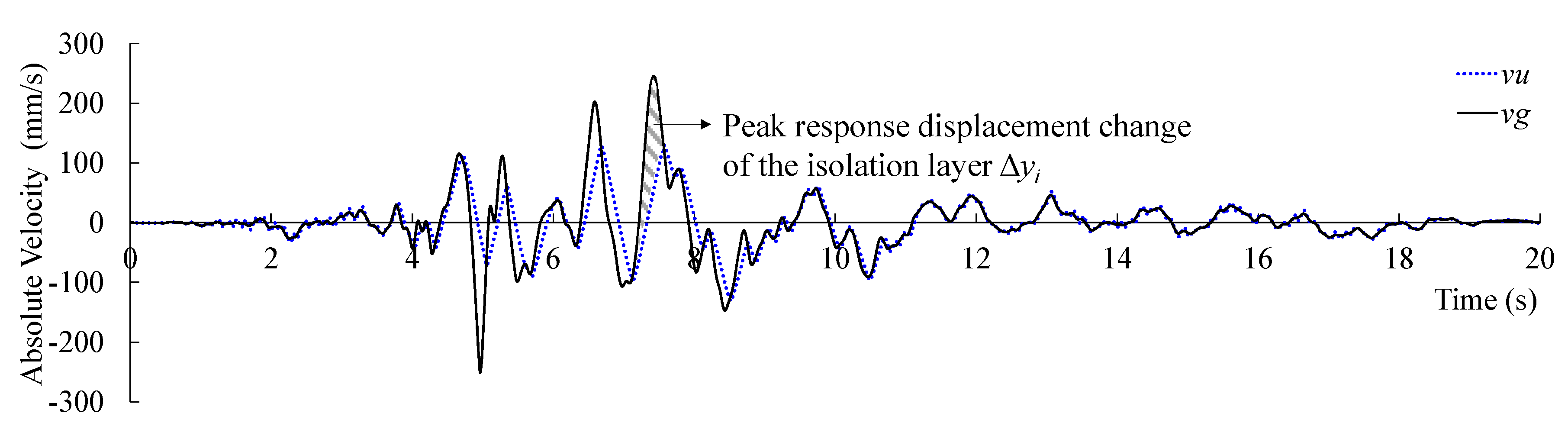
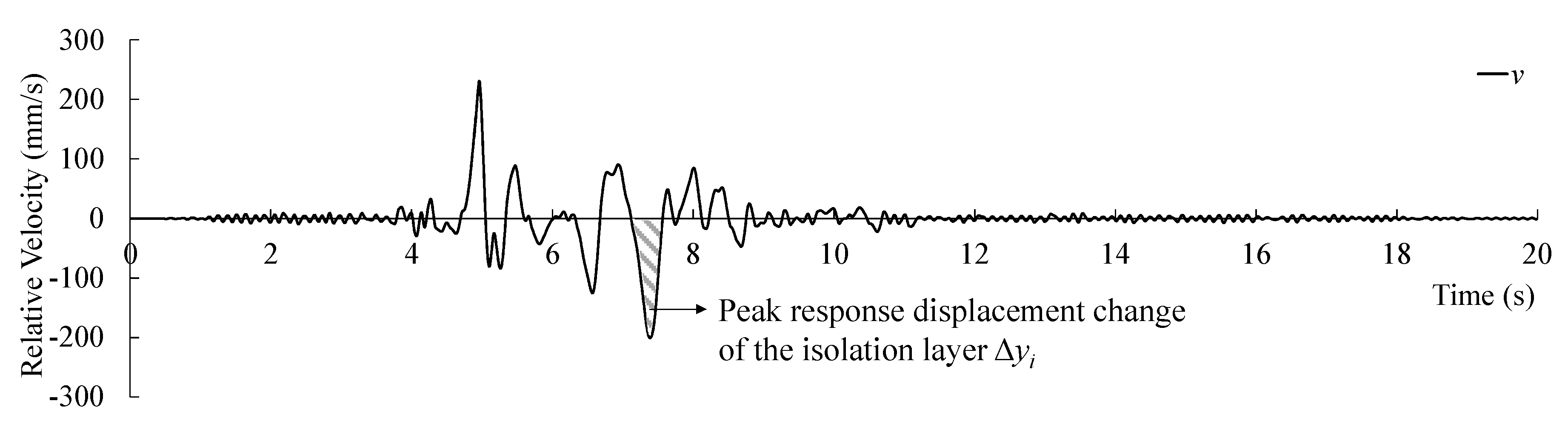
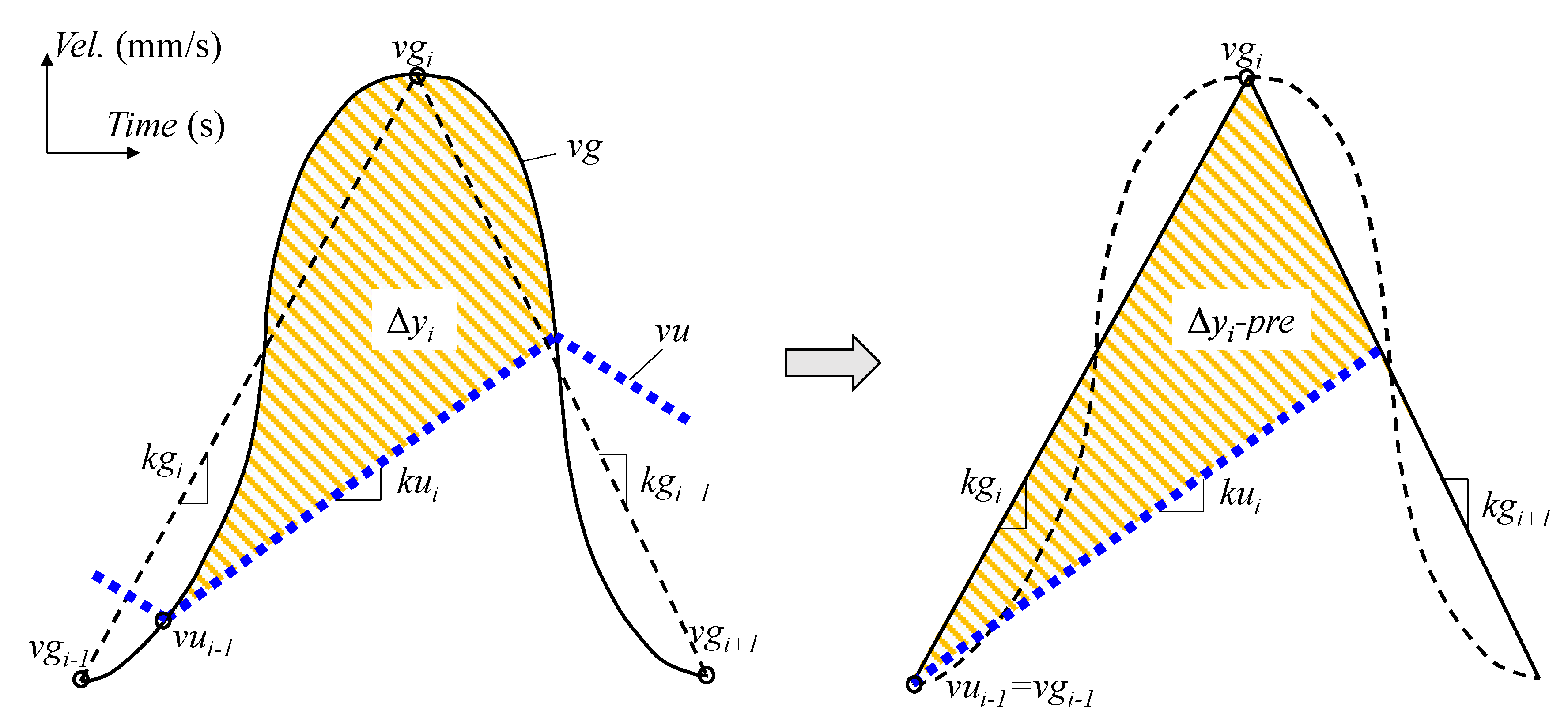
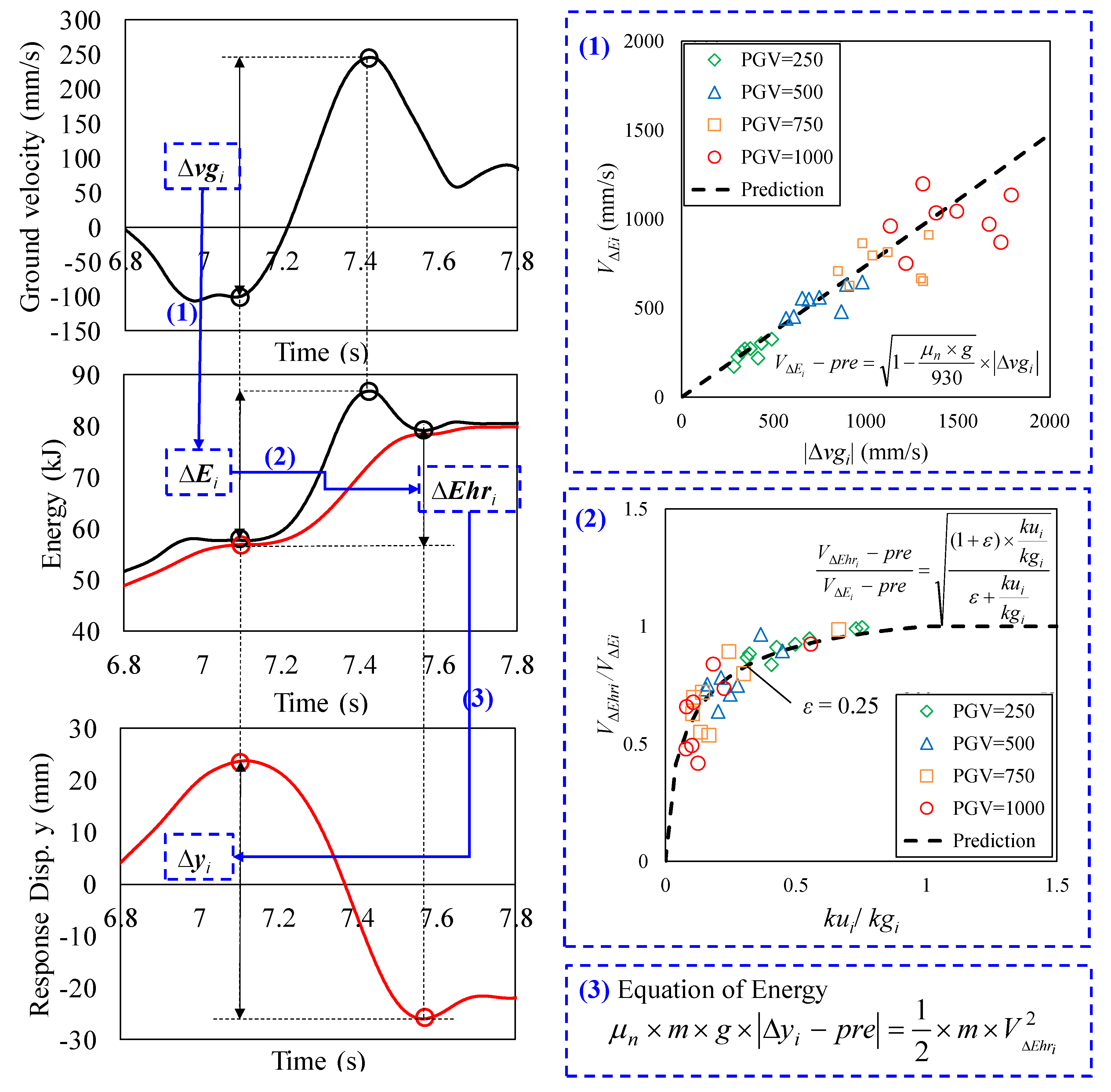
6.1.1. Relationship between Ground Velocity, the Response Displacement and the Input Energy of the Isolation Layer.
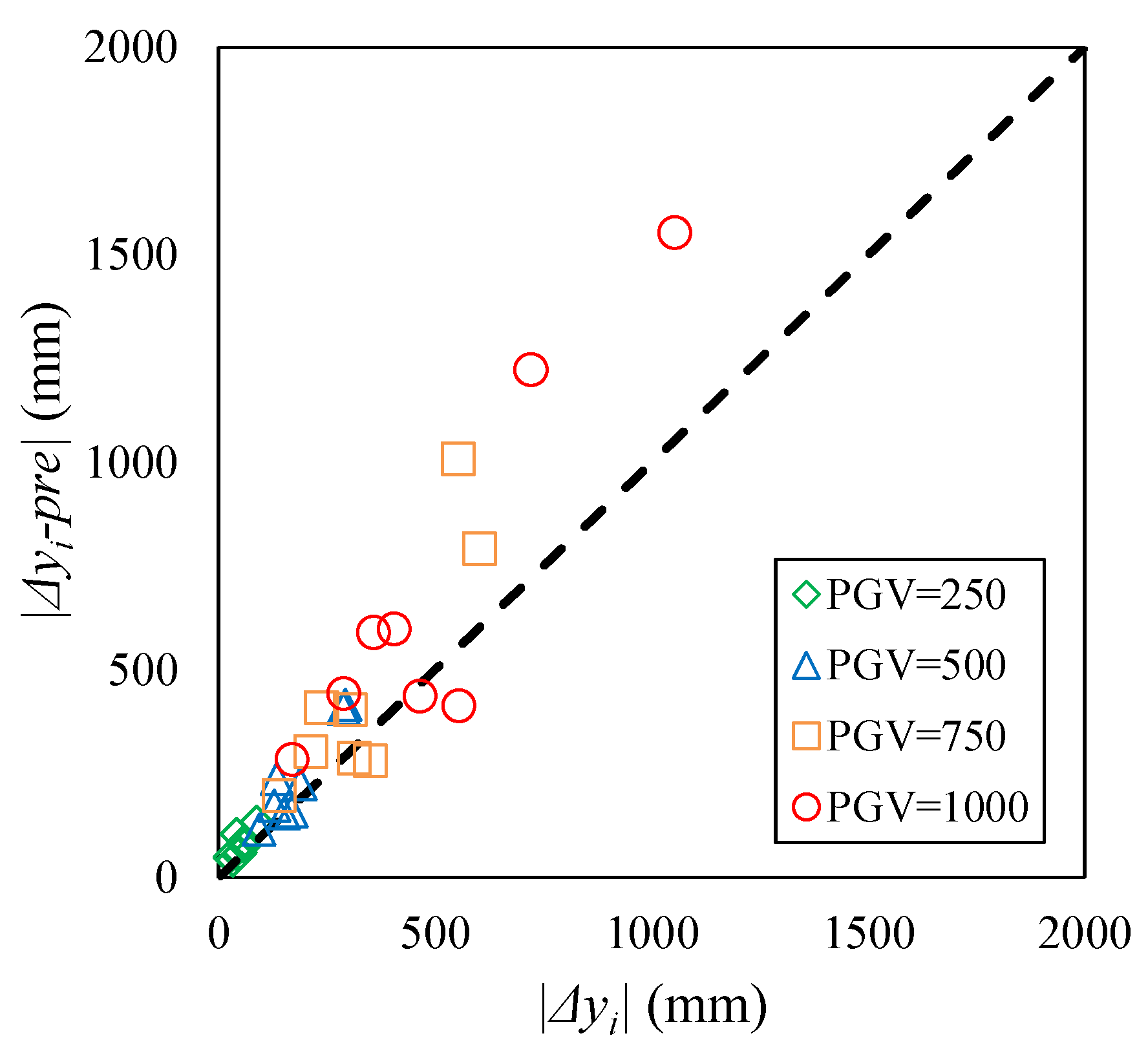
6.1.2. Prediction of the Response Displacement of the Isolation Layer
6.1.3. Prediction of Energy Transfer
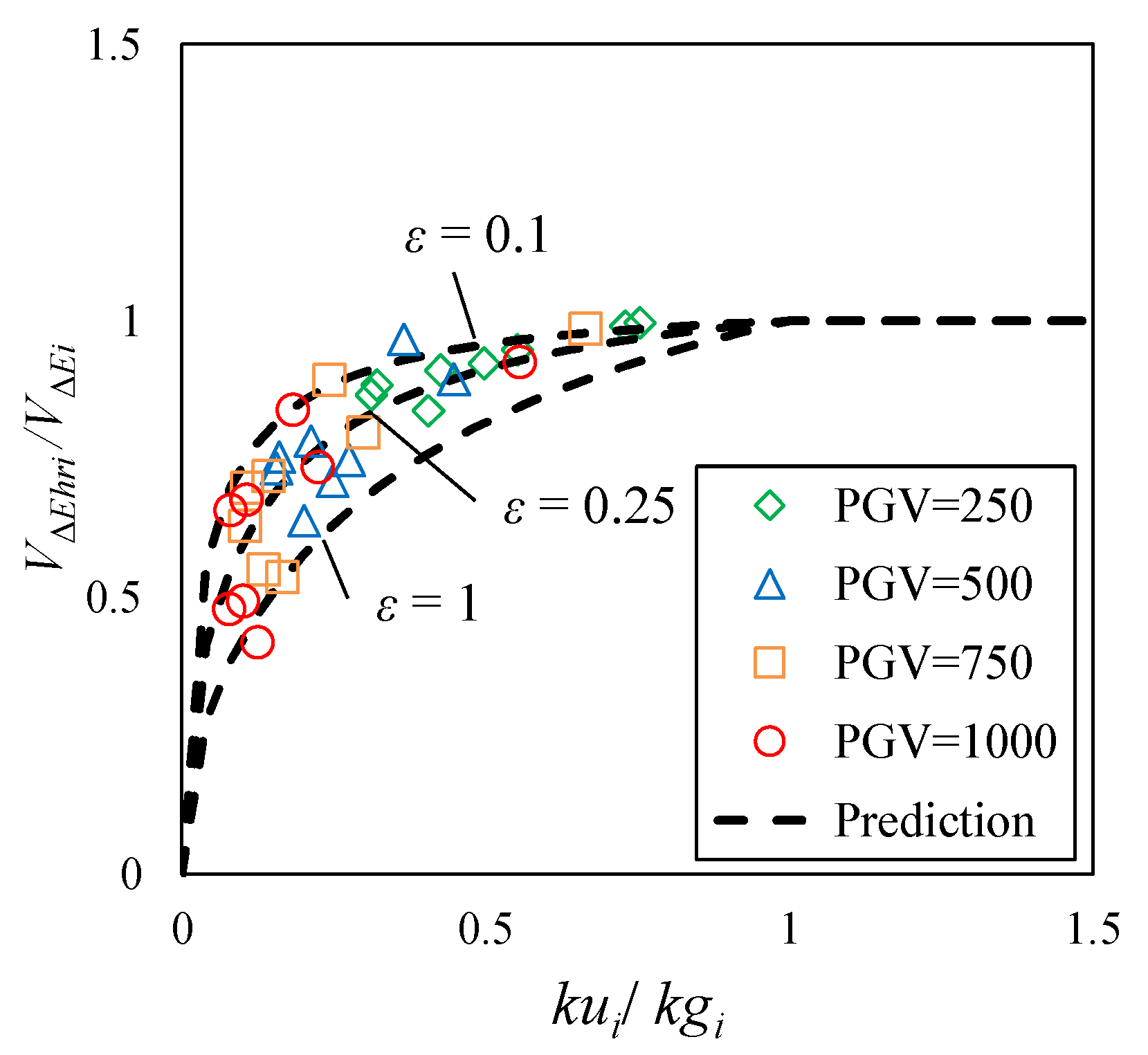
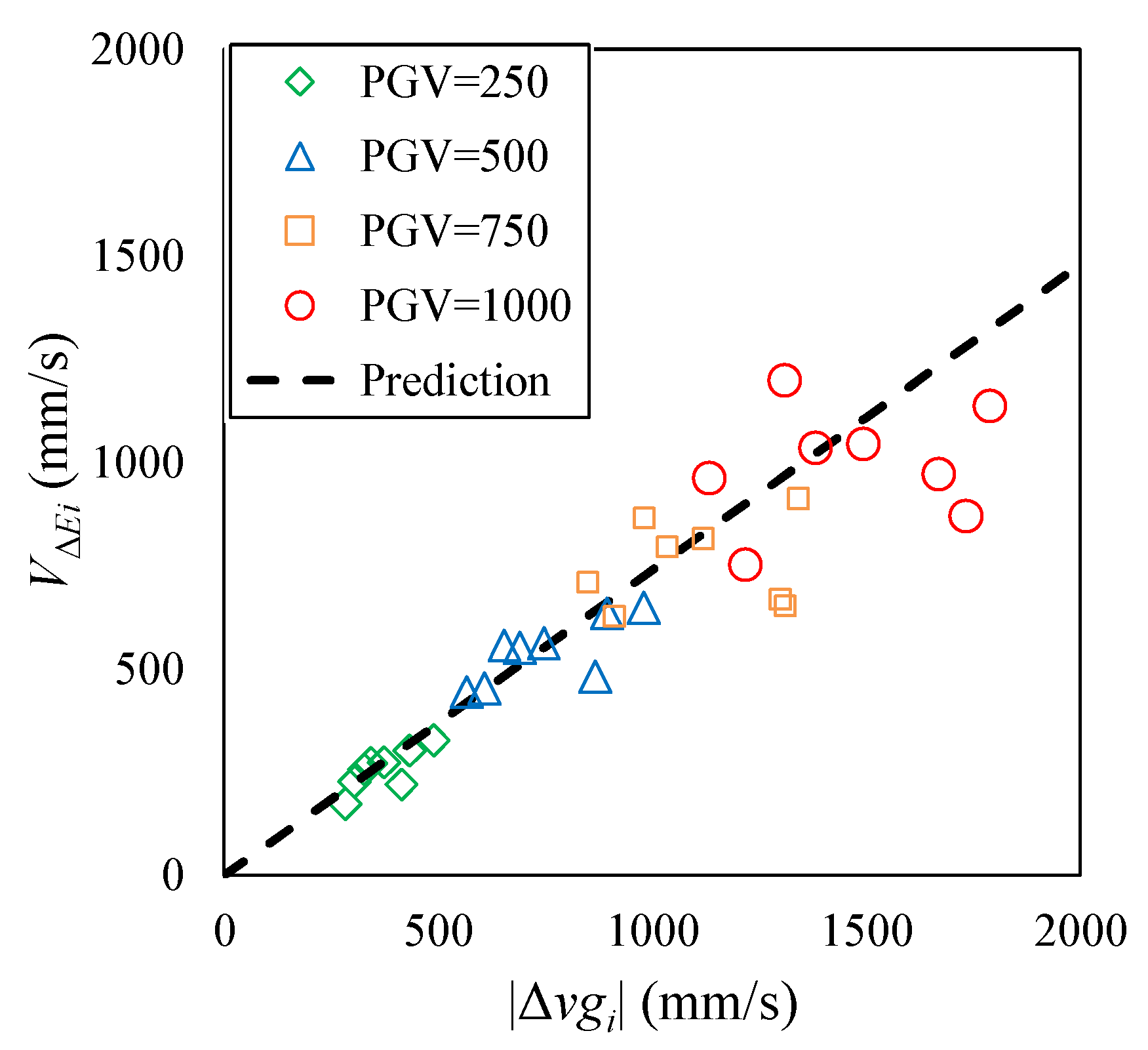
6.2. Simplification and Optimization of the Prediction Method Based on the Analysis Results
6.2.1. Simplification of kgi+1
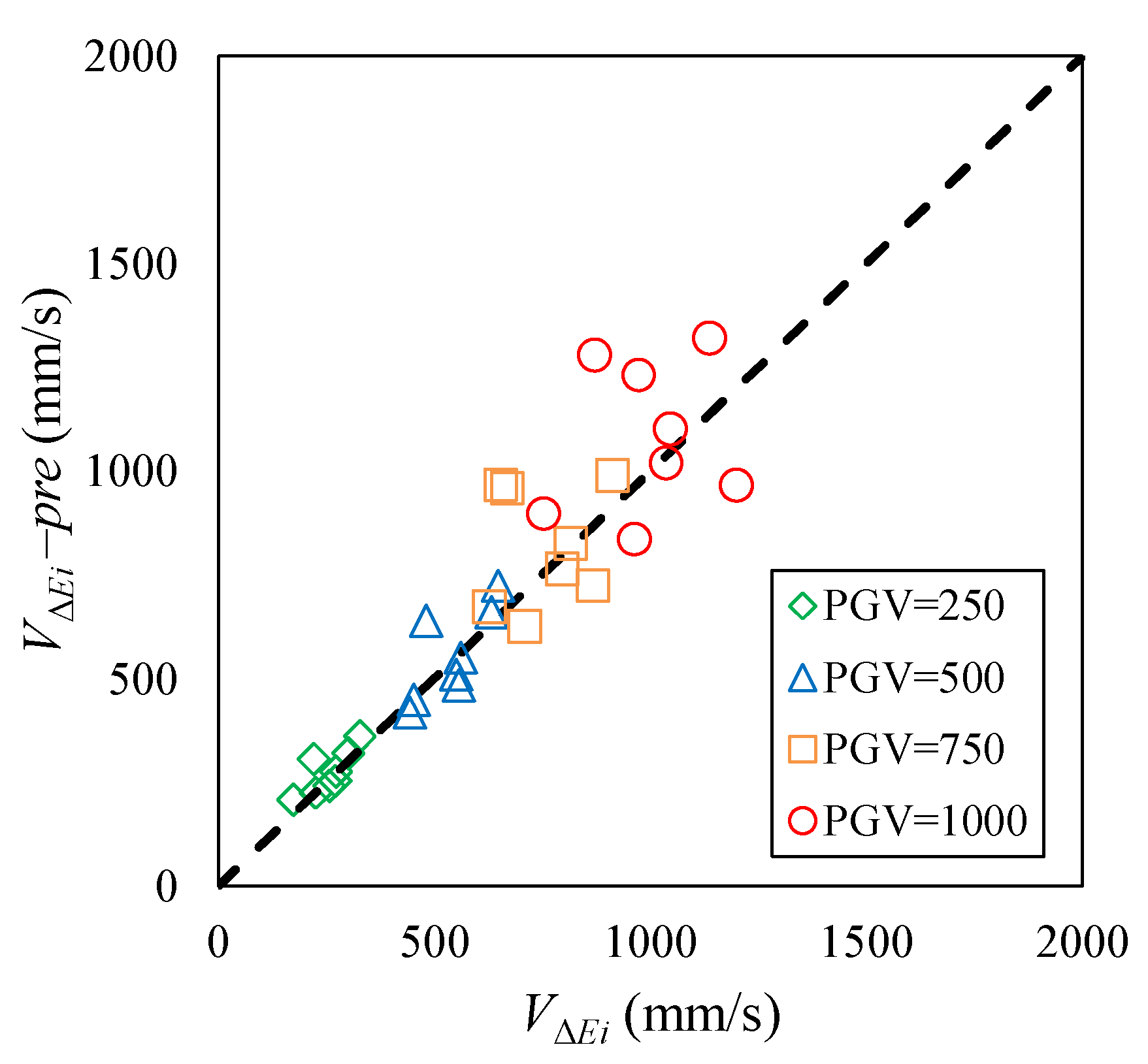
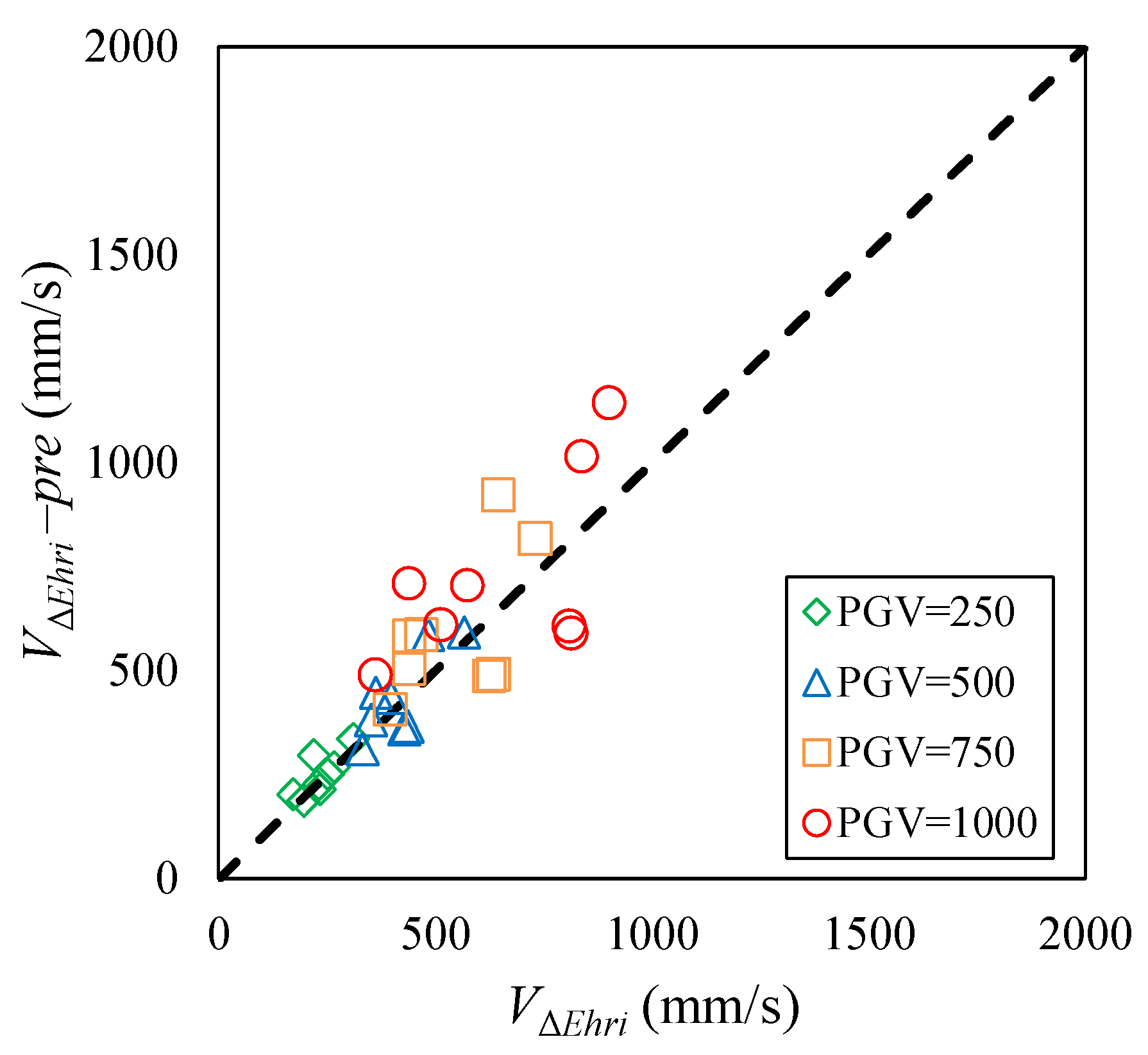
6.2.2. Simplification of the Prediction Equation of VΔEi-pre
6.2.3. Simplified and Optimized Prediction Method
6.3. Application of the Prediction Method in Design
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quaglini, V.; Dubini, P.; Poggi, C. Experimental assessment of sliding materials for seismic isolation systems. Bull. Earthq. Eng. 2012, 10, 717–740. [Google Scholar] [CrossRef]
- Lomiento, G.; Bonessio, N.; Benzoni, G. Friction Model for Sliding Bearings under Seismic Excitation. J. Earthq. Eng. 2013, 17, 1162–1191. [Google Scholar] [CrossRef]
- Quaglini, V.; Bocciarelli, M.; Gandelli, E.; Dubini, P. Numerical Assessment of Frictional Heating in Sliding Bearings for Seismic Isolation. J. Earthq. Eng. 2014, 18, 1198–1216. [Google Scholar] [CrossRef]
- Kumar, M.; Whittaker, A.S.; Constantinou, M.C. Characterizing friction in sliding isolation bearings. Earthquake Engng Struct. Dyn. 2015, 44, 1409–1425. [Google Scholar] [CrossRef]
- Bianco, V.; Bernarddini, D.; Mollaioli, F.; Monti, G. Modeling of the temperature rises in multiple friction pendulum bearings by means of thermomechanical rheological elements. Arch. Civ. Mech. Eng. 2018, 19, 171–185. [Google Scholar] [CrossRef]
- Minimum Design Loads and Associated Criteria for Buildings and Other Structures; ASCE/SEI 7-16; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2016.
- General rules, Eurocode 8. Design Provisions for Earthquake Resistance of Structures; Part 1: Seismic actions and rules for buildings. BS EN 1998-1; European Committee for Standardization: Brussels, Belgium, 2004.
- Design Recommendations for Seismically Isolated Buildings; Architectural Institute of Japan: Tokyo, Japan, 2016; ISBN 978-4-8189-5000-9.
- Akiyama, H. Earthquake-Resistant Limit-State Design for Buildings; University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- Iwan, W.D. Estimating Inelastic Response Spectra from Elastic Spectra. Earthq. Eng. Struct. Dyn. 1980, 8, 375–388. [Google Scholar] [CrossRef]
- Uang, C.M.; Bertero, V.V. Use of Energy as a Design Criterion in Earthquake Resistant Design; Technical report, UCB/EERC88/18; University of California: Berkeley, CA, USA, 1988. [Google Scholar]
- Hadjian, A.H. A Re-evaluation of Equivalent Linear Models for Simple Yielding Systems. Earthq. Eng. Struct. Dyn. 1982, 10, 759–767. [Google Scholar] [CrossRef]
- Benzoni, G.; Seible, F. Design of the Caltrans Seismic Response Modification Device (SRMD) test facility (IWGFR–96). International Atomic Energy Agency (IAEA); International Working Group on Fast Reactors: Vienna, Austria, 1998; 325p, pp. 101–115. [Google Scholar]
- Nishimoto, K.; Nakamura, H.; Hasegawa, H.; Wakita, N. Bearing Stress and Velocity Dependency of Spherical Sliding Bearing through Full-scale tests, Paper No. 21223. In Proceedings of the Summaries of Technical Papers of Annual Meeting, Fukuoka, Japan, 24–26 August 2016. (In Japanese). [Google Scholar]
- Nakamura, H.; Nishimoto, K.; Hasegawa, H.; Nakamura, H. Predictive Method of a Temperature Rise and the Friction Coefficient of Spherical Sliding Bearing (Part 3), Paper No. 21232. In Proceedings of the Summaries of Technical Papers of Annual Meeting, Kanto, Japan, 4–6 September 2015. (In Japanese). [Google Scholar]
- Yamazaki, S.; Nishimoto, K.; Watanabe, A. Experimental and Analytical Study of Spherical Sliding Bearing for Long Period Ground Motion, Paper No. 21059. In Proceedings of the Summaries of Technical Papers of Annual Meeting, Hokuriku, Japan, 3–6 September 2019. (In Japanese). [Google Scholar]
- Constantinou, M.C.; Whittaker, A.S.; Kalpakidis, Y.; Fenz, D.M.; Warn, G.P. Performance of Seismic Isolation Hardware under Service and Seismic Loading; Report No. MCEER-07-0012; Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 2007. [Google Scholar]
- Japan Society of Mechanical Engineers (JSME). Heat Transfer, 5th ed.; JSME Data Books: Tokyo, Japan, 2009; pp. 284–285. [Google Scholar]
- Li, J.; Kishiki, S.; Yamada, S.; Yamazaki, S.; Watanabe, A.; Nishimoto, K.; Nishimoto, K. Comparative Study of Numerical Models for Double Concave Friction Pendulum Bearing, Paper No. 21058. In Proceedings of the Summaries of Technical Papers of Annual Meeting, Hokuriku, Japan, 3–6 September 2019. [Google Scholar]
- Takanori, I.; Masashi, N.; Shoichi, K.; Satoshi, Y.; Koji, N.; Atsushi, W. Experimental and Analytical Study on Spherical Sliding Bearing Subjected to Bidirectional Excitation (Part 1 Bidirectional loading tests and verification of mechanical model), Paper No. 21491. In Proceedings of the Summaries of Technical Papers of Annual Meeting, Tohoku, Japan, 4–6 September 2018; Volume 24, pp. 981–982. [Google Scholar]
- Kikuchi, M.; Ishii, K.; Yamamoto, M.; Higashino, M.; Kamoshita, N.; Nakamura, T.; Kouchiyama, O. Experimental study on horizontal Bi-axial mechanical properties of sliding supports with rubber-pad (Part 3: Simulation Analysis), Paper No. 21160. In Proceedings of the Summaries of Technical Papers of Annual Meeting, Nagoya, Japan, 12–14 September 2012. (In Japanese). [Google Scholar]
- Kamoshita, N.; Yamamoto, M.; Minewaki, S.; Kikuchi, M.; Ishii, K.; Kouchiyama, O.; Nakamura, T. Horizontal bidirectional characteristics of elastic sliding bearings under various fluctuant vertical condition. AIJ J. Struct. Constr. Eng. 2014, 79, 453–461. (In Japanese) [Google Scholar] [CrossRef] [Green Version]


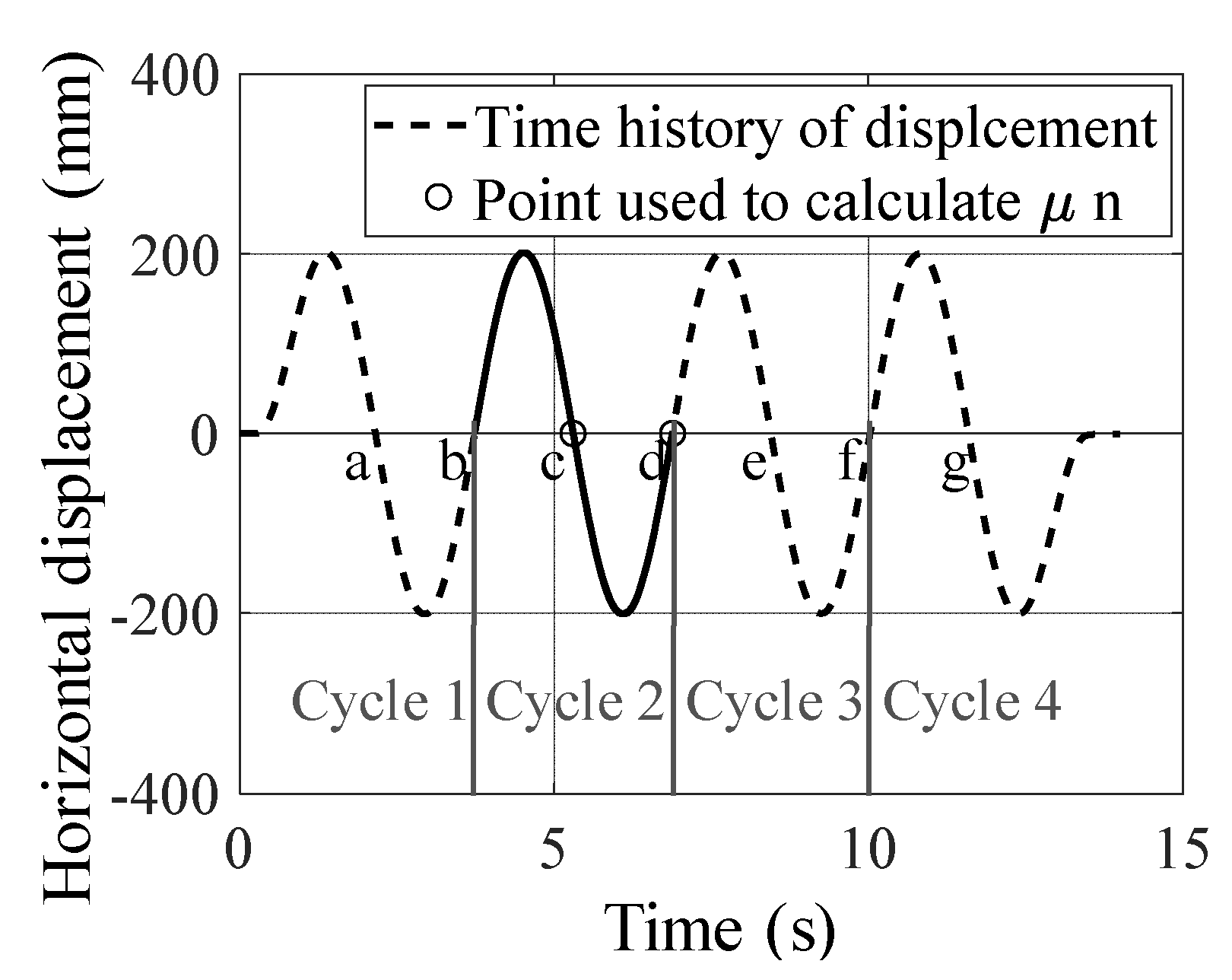
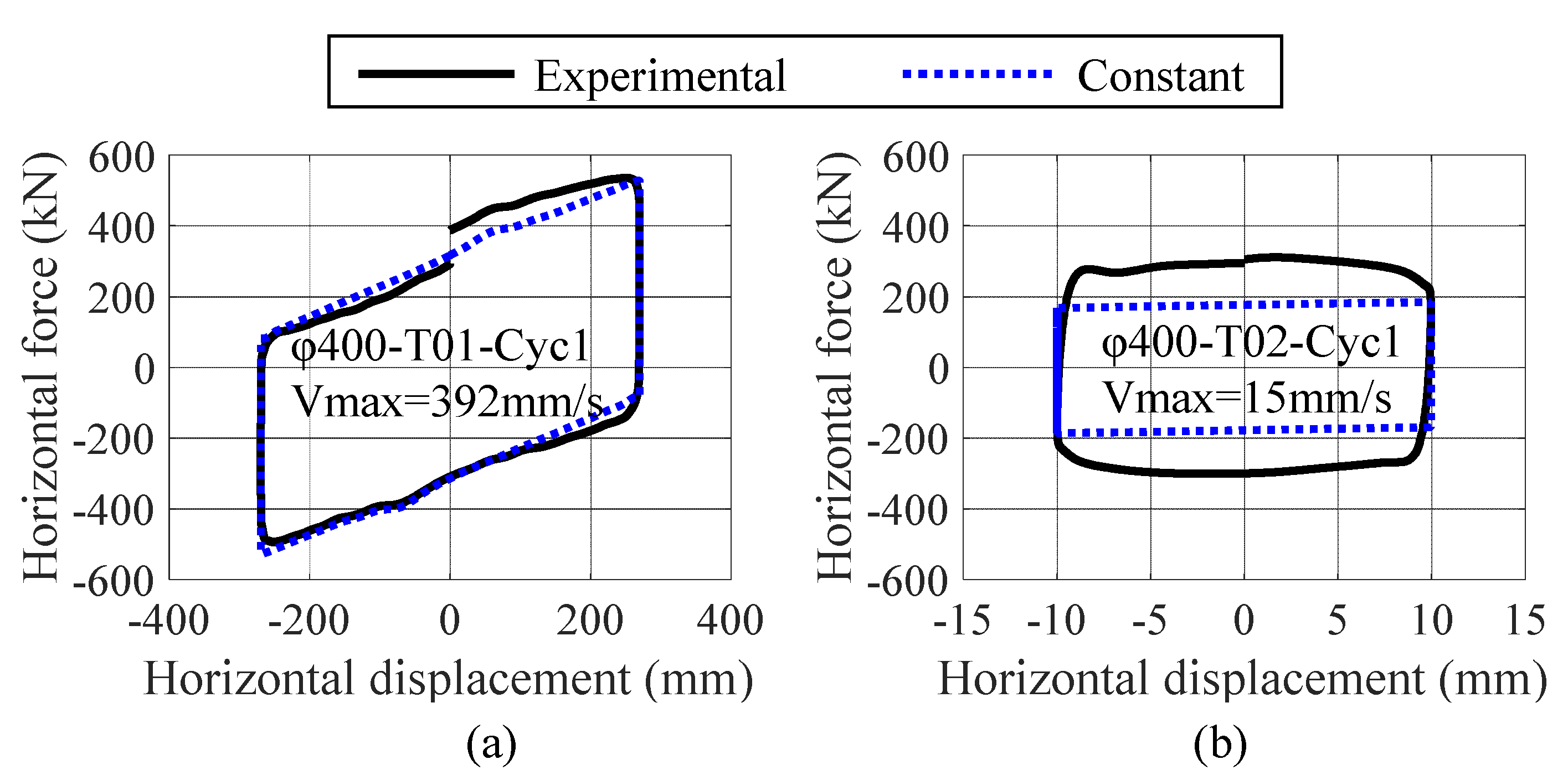
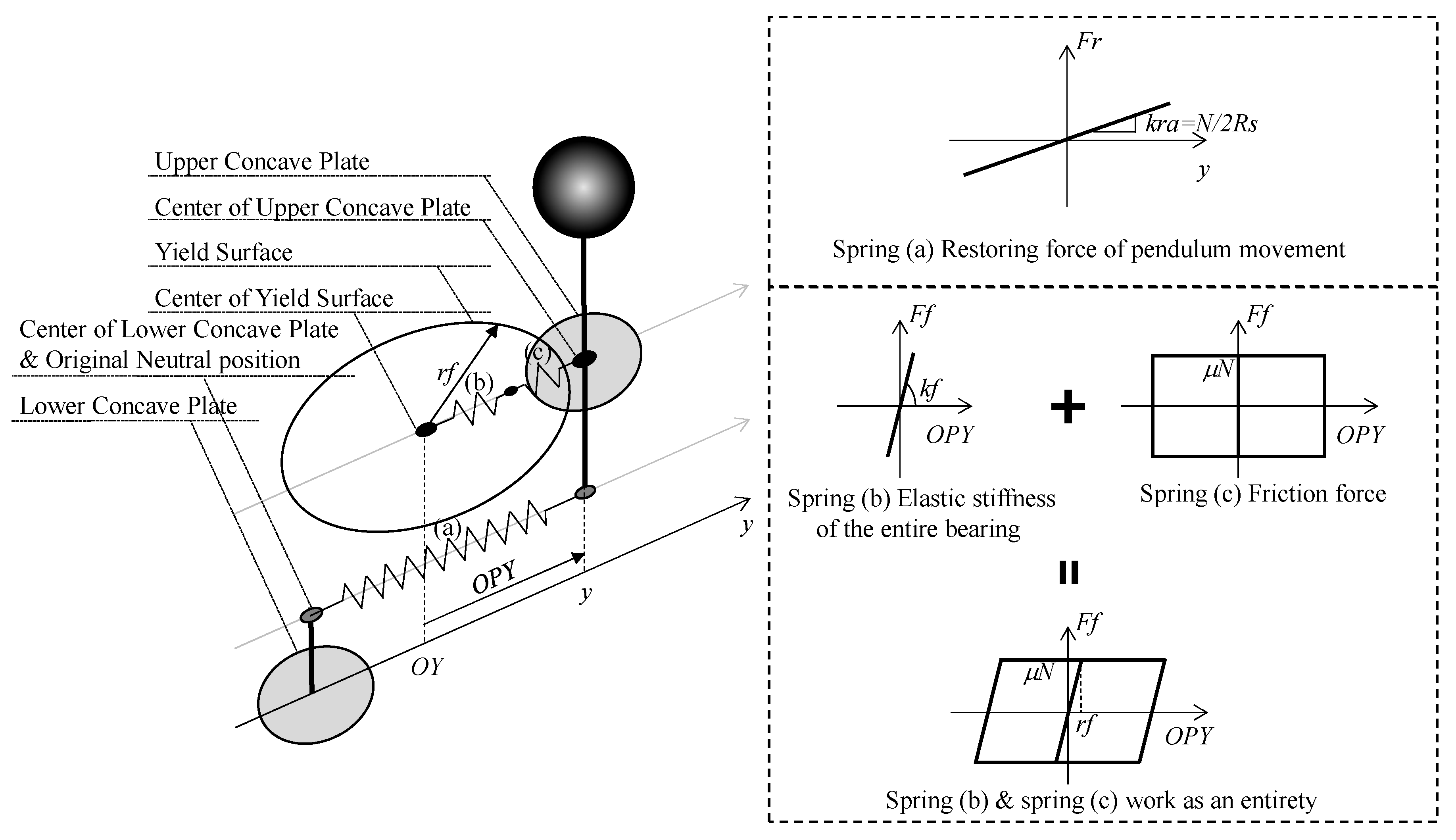

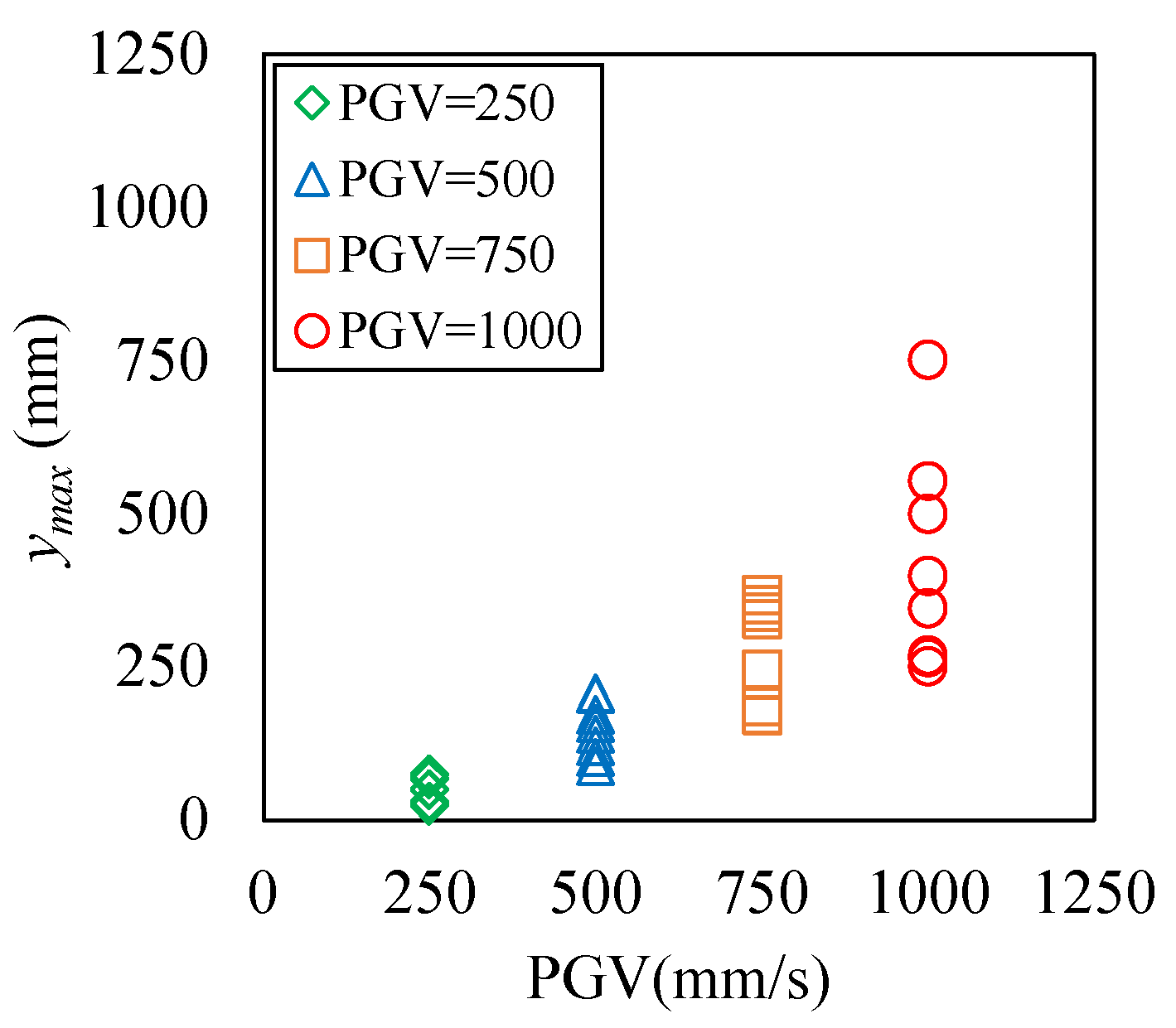



| Spec. | Test | Pressure | Amplitude | Vmax | Period | Cycle |
|---|---|---|---|---|---|---|
| num. | num. | N/mm2 | ±mm | mm/s | s | num. |
| φ300 φ400 | (1) Velocity dependency test | |||||
| T01 | 60 | 200 | 400 | 3.14 | 4 | |
| (2) Pressure dependency test | ||||||
| T02 | 40 | 200 | 20 | 62.83 | 4 | |
| T03 | 60 | 20 | 62.83 | 4 | ||
| T04 | 80 | 20 | 62.83 | 4 | ||
| Spec. | Test | Pressure | Amplitude | Vmax | Period | Cycle |
|---|---|---|---|---|---|---|
| num. | num. | N\mm2 | ±mm | mm/s | s | num. |
| φ300 φ400 | T01 | 60 | 268 | 392 | 4.26 | 3 |
| T02 | 10 | 14.646 | 4.26 | 20 | ||
| T03 | 100 | 146.369 | 4.26 | 3 | ||
| T04 | 200 | 292.738 | 4.26 | 3 | ||
| T05 | 268 | 392.269 | 4.26 | 3 | ||
| T06 | 400 | 585.476 | 4.26 | 3 | ||
| T07 | 400 | 585.476 | 4.26 | 3 | ||
| T08 | 40 | 400 | 585.476 | 4.26 | 3 | |
| T09 | 80 | 400 | 585.476 | 4.26 | 3 | |
| T10 | 30 | 440 | 644.024 | 4.26 | 1 | |
| T11 | 90 | 440 | 644.024 | 4.26 | 1 | |
| T12a | 60 | 300 | 439.107 | 4.26 | 7 | |
| T12b | 7 | |||||
| T12c | 6 | |||||
| T13 | 268 | 392.269 | 4.26 | 3 |
| Abv. | Earthquake | Station | PGV (m/s) | Duration (s) | Field |
|---|---|---|---|---|---|
| JKB | Kobe | JMA Kobe | 0.893 | 30 | Far |
| KNA | Kobe | Nishi-Akashi | 0.373 | 41 | Near |
| TC1 | Chi-Chi | TCU129 | 0.554 | 90 | Near |
| NCC | Northridge | Canyon Country-WLC | 0.449 | 20 | Far |
| LPG | Loma Prieta | Gilroy Array | 0.447 | 40 | Near |
| IVD | Imperial Valley | Delta | 0.330 | 100 | Near |
| TSD | Tohoku | JMA Sendai | 0.545 | 180 | Near |
| TIM | Tohoku | JMA Ishinomaki | 0.376 | 300 | Near |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Kishiki, S.; Yamada, S.; Yamazaki, S.; Watanabe, A.; Terashima, M. Energy-Based Prediction of the Displacement of DCFP Bearings. Appl. Sci. 2020, 10, 5259. https://doi.org/10.3390/app10155259
Li J, Kishiki S, Yamada S, Yamazaki S, Watanabe A, Terashima M. Energy-Based Prediction of the Displacement of DCFP Bearings. Applied Sciences. 2020; 10(15):5259. https://doi.org/10.3390/app10155259
Chicago/Turabian StyleLi, Jiaxi, Shoichi Kishiki, Satoshi Yamada, Shinsuke Yamazaki, Atsushi Watanabe, and Masao Terashima. 2020. "Energy-Based Prediction of the Displacement of DCFP Bearings" Applied Sciences 10, no. 15: 5259. https://doi.org/10.3390/app10155259





