A Novel Artificial Pancreas: Energy Efficient Valveless Piezoelectric Actuated Closed-Loop Insulin Pump for T1DM
Abstract
:1. Introduction
1.1. Diabetes Mellitus
1.2. Closed-Loop Insulin Pumps
1.3. Piezoelectric Actuated Pumps
1.4. Insulin/Glucose Models
2. Mathematical Modeling
2.1. The Piezoelectric Pump Analytical Modeling
2.2. Insulin/Glucose Plant Modeling
3. Numerical Implementation
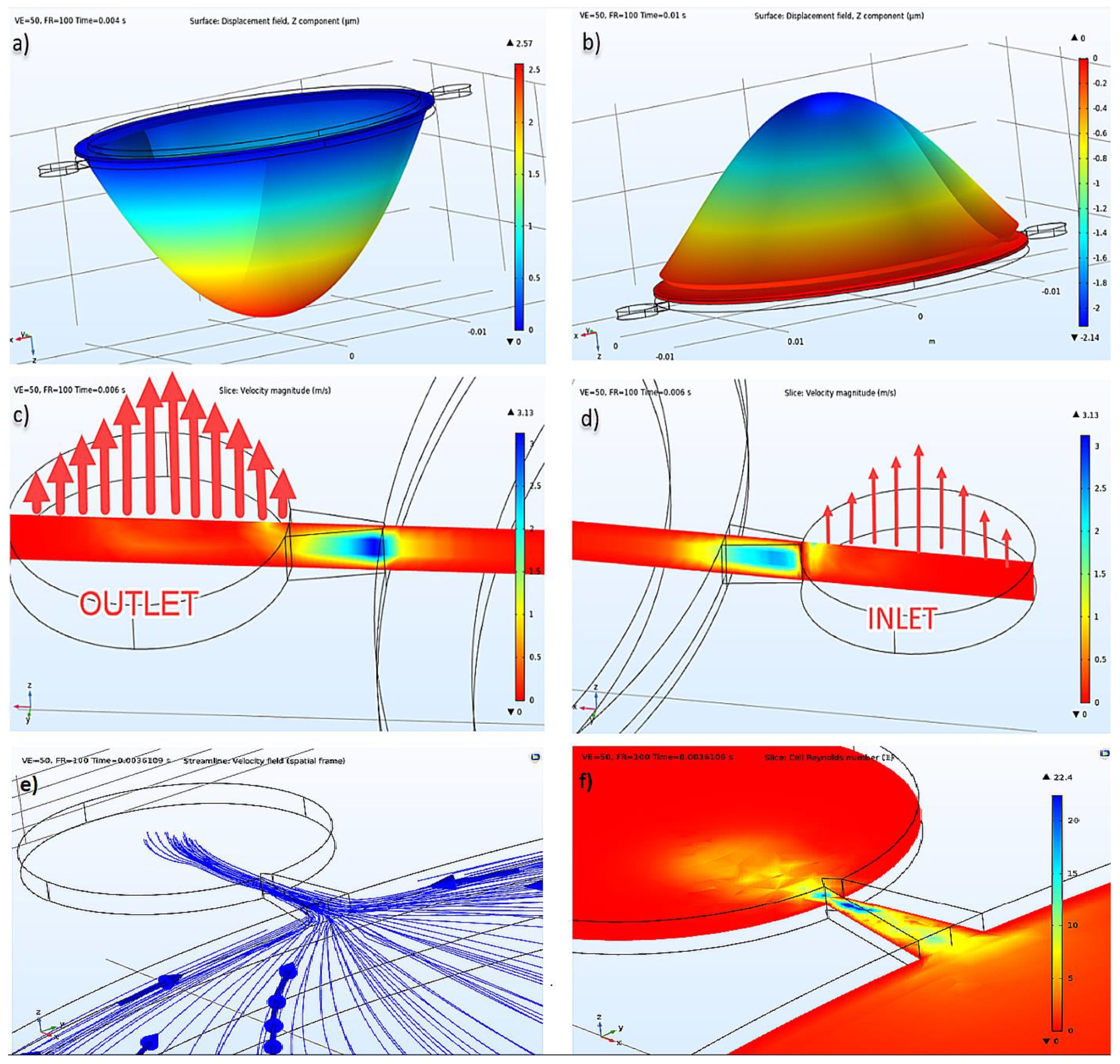
3.1. Piezoelectric Pump Finite Element Implementation
3.2. Piezoelectric Pump Optimization
4. Controller Design
5. Model-Based Simulation and Results
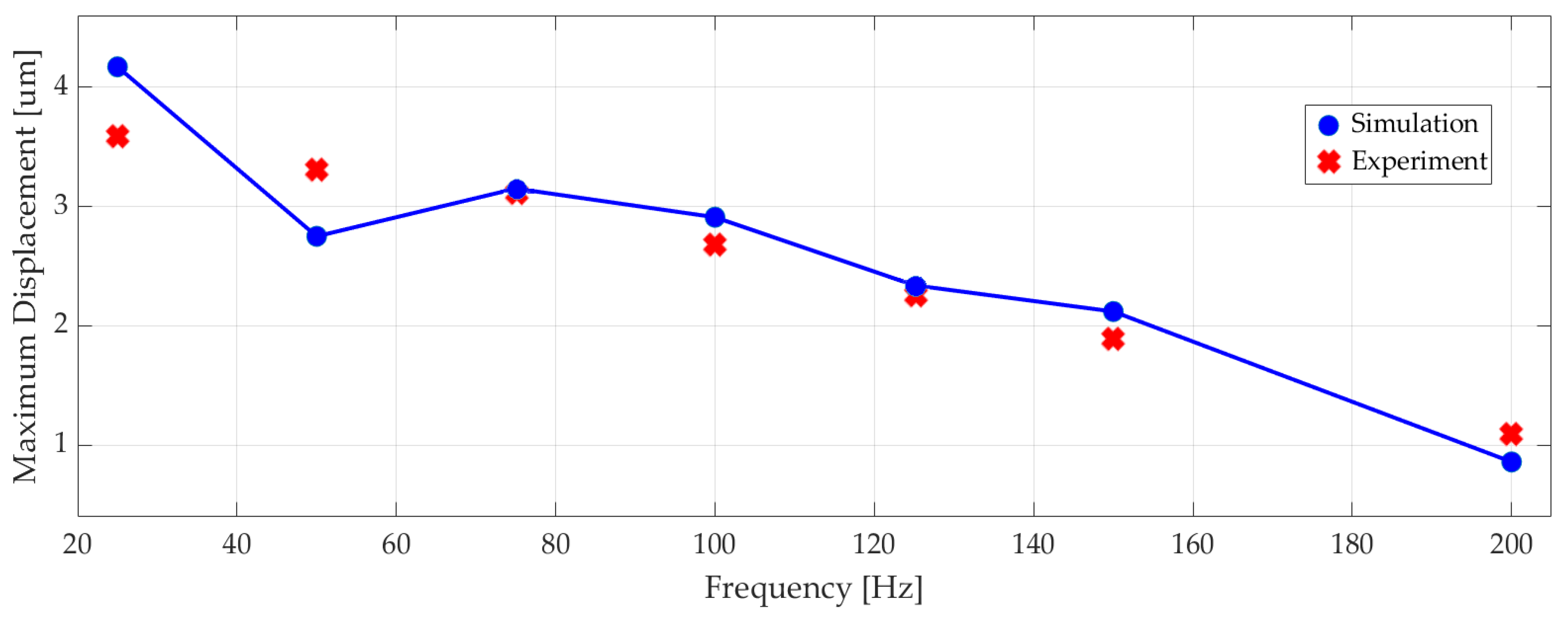
6. Experimental Verification and Results
7. Discussion and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Ntaganda, J.M.; Minani, F.; Banzi, W.; Mpinganzima, L.; Niyobuhungiro, J.; Gahutu, J.B.; Rutaganda, E.; Kambutse, I.; Dusabejambo, V. Simplified mathematical model of glucose-insulin system. Am. J. Comput. Math. 2018, 8, 233–244. [Google Scholar] [CrossRef] [Green Version]
- Saleem, M.U.; Farman, M.; Meraj, M.A. Stability analysis of sorensen’s model for controllability and observability. Proc. Pak. Acad. Sci. Part B 2017, 54, 133–145. [Google Scholar]
- IDF. IDF Diabetes Atlas, 9th ed.; IDF: Brussels, Belgium, 2019. [Google Scholar]
- Kovacs, L.; Kulcsar, B.; Bokor, J.; Benyo, Z. Model-based nonlinear optimal blood glucose control of Type I diabetes patients. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 1607–1610. [Google Scholar] [CrossRef]
- Lunze, -I.K.; Singh, T.; Walter, M.; Brendel, M.D.; Leonhardt, S. Blood glucose control algorithms for type 1 diabetic patients: A methodological review. Biomed. Signal Process. Control 2013, 8, 107–119. [Google Scholar] [CrossRef]
- Nath, A.; Biradar, S.; Balan, A.; Dey, R.; Padhi, R. Physiological models and control for type 1 diabetes mellitus: A brief review. IFAC PapersOnLine 2018, 51, 289–294. [Google Scholar] [CrossRef]
- MiniMedTM 670G Insulin Pump System. Available online: https://www.medtronicdiabetes.com/products/minimed-670g-insulin-pump-system (accessed on 1 June 2020).
- Beta Bionics: Introducing the iLet. Available online: http://www.betabionics.com/ (accessed on 1 June 2020).
- T:slim X2 Insulin Pump w/ Dexcom G6 CGM. Available online: https://www.tandemdiabetes.com/products/t-slim-x2-insulin-pump (accessed on 1 June 2020).
- Jung, B.; Seo, K.-S.; Kwon, S.J.; Lee, K.; Hong, S.; Seo, H.; Kim, G.-Y.; Park, G.-M.; Jeong, J.; Seo, S.W. Efficacy evaluation of syringe pump developed for continuous drug infusion. J. Dent. Anesthesia Pain Med. 2016, 16, 303–307. [Google Scholar] [CrossRef]
- Yang, J. An Introduction to the Theory of Piezoelectricity; Kluwer Academic Publishers: Boston, MA, USA, 2005; Volume 9. [Google Scholar]
- Lumentut, M.; Friswell, M.I. A smart pipe energy harvester excited by fluid flow and base excitation. Acta Mech. 2018, 229, 4431–4458. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Kumar, N.; George, D.; Sen, A.K. Analytical modeling, simulations and experimental studies of a PZT actuated planar valveless PDMS micropump. Sens. Actuators A Phys. 2015, 225, 81–94. [Google Scholar] [CrossRef]
- Khalilian, S. Development of a Low Cost Micro-Pump. Master’s Thesis, University of Calgary, Calgary, AB, Canada, 2012; pp. 1–185. [Google Scholar] [CrossRef]
- Atul, S.T.; Lenin Babu, M.C. Characterization of valveless micropump for drug delivery by using piezoelectric effect. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 2138–2144. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35–R64. [Google Scholar] [CrossRef]
- Nisar, A.; Afzulpurkar, N.; Tuantranont, A.; Mahaisavariya, B. Three dimensional transient multifield analysis of a piezoelectric micropump for drug delivery system for treatment of hemodynamic dysfunctions. Cardiovasc. Eng. 2008, 8, 203–218. [Google Scholar] [CrossRef]
- Yipintsoi, T.; Gatewood, L.C.; Ackerman, E.; Spivak, P.L.; Molnar, G.D.; Rosevear, J.W.; Service, F.J. Mathematical analysis of blood glucose and plasma insulin responses to insulin infusion in healthy and diabetic subjects. Comput. Boil. Med. 1973, 3, 71–78. [Google Scholar] [CrossRef]
- Chee, F.; Fernando, T. Closed-Loop Control of Blood Glucose; Springer: Berlin/Heidelberg, Germany, 2007; Volume 368. [Google Scholar]
- Ceresa, F.; Ghemi, F.; Martini, P.F.; Martino, P.; Segre, G.; Vitelli, A. Control of blood glucose in normal and in diabetic subjects: Studies by compartmental analysis and digital computer technics. Diabetes 1968, 17, 570–578. [Google Scholar] [CrossRef]
- Bergman, R.N.; Phillips, L.S.; Cobelli, C. Physiologic evaluation of factors controlling glucose tolerance in man: Measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to Intravenous glucose. J. Clin. Investig. 1981, 68, 1456–1467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, A.; Parker, R.S. Dynamic modeling of exercise effects on plasma glucose and insulin levels. J. Diabetes Sci. Technol. 2007, 1, 338–347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Furler, S.M.; Kraegen, E.W.; Smallwood, R.H.; Chisholm, D. Blood glucose control by intermittent loop closure in the basal mode: Computer simulation studies with a diabetic model. Diabetes Care 1985, 8, 553–561. [Google Scholar] [CrossRef] [PubMed]
- Sorensen, J.T. A Physiologic Model of Glucose Metabolism in Man and Its Use to Design and Assess Improved Insulin Therapies for Diabetes. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1985; p. 557. [Google Scholar]
- Cobelli, C.; Mari, A. Control of diabetes with artificial systems for insulin delivery algorithm independent limitations revealed by a modeling study. IEEE Trans. Biomed. Eng. 1985, 32, 840–845. [Google Scholar] [CrossRef]
- Hovorka, R.; Shojaee-Moradie, F.; Carroll, P.V.; Chassin, L.J.; Gowrie, I.J.; Jackson, N.C.; Tudor, R.S.; Umpleby, A.M.; Jones, R.H. Partitioning glucose distribution/transport, disposal, and endogenous production during IVGTT. Am. J. Physiol. Metab. 2002, 282, E992–E1007. [Google Scholar] [CrossRef] [Green Version]
- Kaçar, A.; Özer, M.B.; Taşcıoğlu, Y. Piezoelectric actuated insulin pump simulation model and controller design. In Proceedings of the 8th International Conference, ICAT’19, Sarajevo, Bosnia and Herzegovina, 26–30 August 2019; pp. 351–356. [Google Scholar]
- Chandrasekaran, A.; Packirisamy, M. Improved efficiency of microdiffuser through geometry tuning for valveless micropumps. J. Fluids Eng. 2015, 138, 031101. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Huang, X. Miniature valveless pumps based on printed circuit board technique. Sens. Actuators A Phys. 2001, 88, 104–111. [Google Scholar] [CrossRef]
- Gidde, R.R.; Pawar, P.M.; Dhamgaye, V.P. Fully coupled modeling and design of a piezoelectric actuation based valveless micropump for drug delivery application. Microsyst. Technol. 2019, 26, 633–645. [Google Scholar] [CrossRef]
- Hariri, A.; Wang, L.Y. Observer-based state feedback for enhanced insulin control of type ‘I’ diabetic patients. Open Biomed. Eng. J. 2011, 5, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Swan, G.W. An optimal control model of diabetes mellitus. Bull. Math. Biol. 1982, 44, 793–808. [Google Scholar] [CrossRef]
- Acikgoz, S.U.; Diwekar, U.M. Blood glucose regulation with stochastic optimal control for insulin-dependent diabetic patients. Chem. Eng. Sci. 2010, 65, 1227–1236. [Google Scholar] [CrossRef]
- COMSOL: Multiphysics Software for Optimizing Designs. Available online: https://www.comsol.com/ (accessed on 1 June 2020).
- Piezo Round Bimorph Actuator for Pumps 27 × 0.5mm. Available online: https://www.steminc.com/PZT/en/piezo-round-bimorph-actuator-for-pumps-27x05mm (accessed on 1 June 2020).
- Schmandt, B.; Herwig, H. Diffuser and nozzle design optimization by entropy generation minimization. Entropy 2011, 13, 1380–1402. [Google Scholar] [CrossRef]
- Ben Mansour, R.; Sahin, A.Z. Optimization of conical micro-diffusers and micro-nozzles considering entropy generation. Arab. J. Sci. Eng. 2012, 38, 3161–3170. [Google Scholar] [CrossRef] [Green Version]
- Laxminarayan, S.; Reifman, J.; Steil, G.M. Use of a food and drug administration-approved type 1 Diabetes mellitus simulator to evaluate and optimize a proportional-integral-derivative controller. J. Diabetes Sci. Technol. 2012, 6, 1401–1412. [Google Scholar] [CrossRef]
- Maeder, M.D.; Damjanovic, D.; Setter, N. Lead free piezoelectric materials. J. Electroceram. 2004, 13, 385–392. [Google Scholar] [CrossRef]
- SPETEC—Syringe Pump Symax. Available online: https://www.spetec.de/en/products/laboratory-equipment/syringe-pumps/syringe-pump-symax (accessed on 1 June 2020).

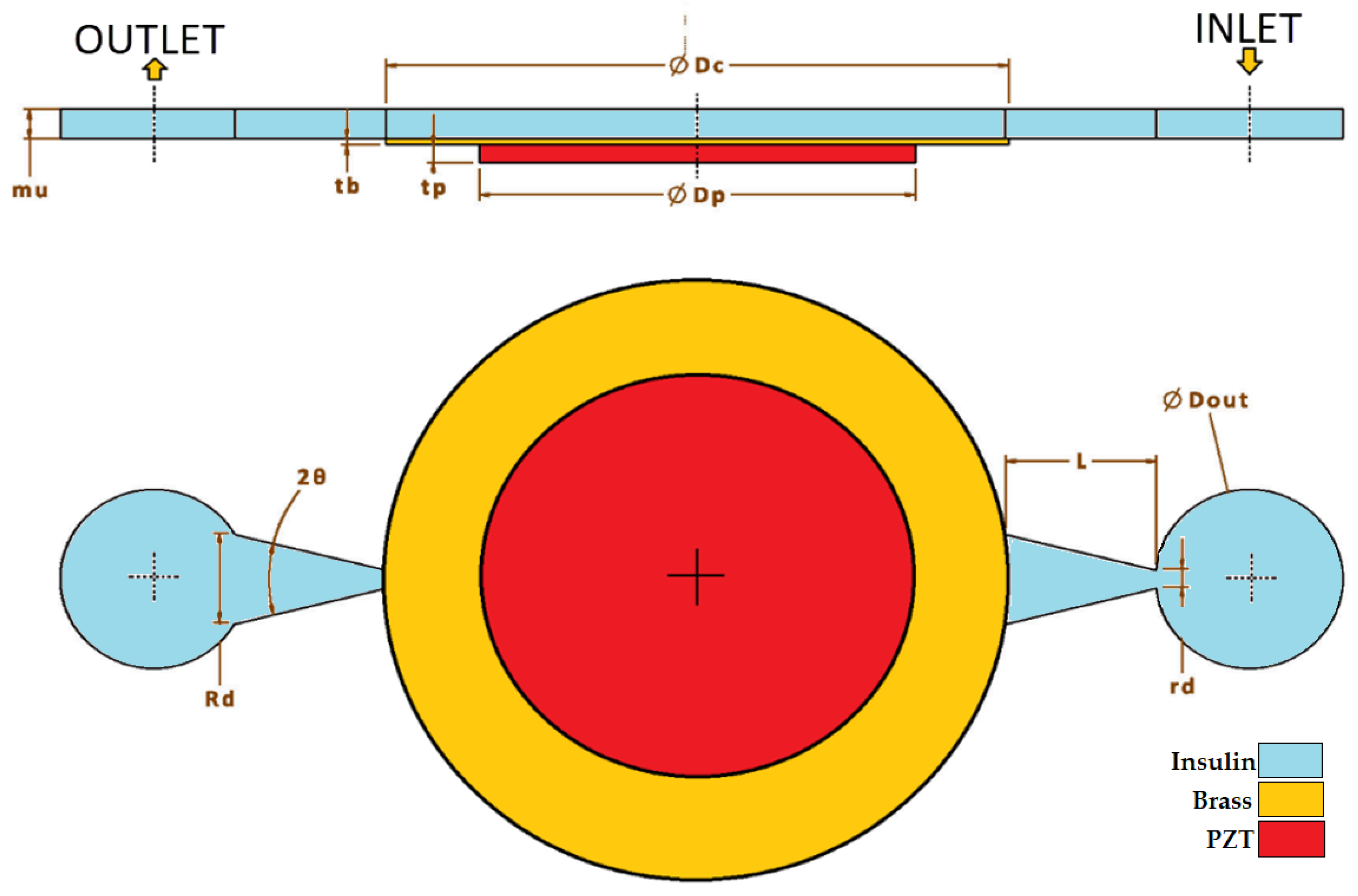










| Material/Dimensions | Parameter | Value | Unit |
|---|---|---|---|
| PZT-5J | Density | 7800 | kg/m3 |
| Diameter (Dp): 25 mm Thickness (tp): 0.4 mm | Elasticity matrix | N/m2 | |
| Chamber Dimensions: Inlet/Outlet Diameter (Dout): 3 mm Nozzle Small Radius (rd): 50 µm | Piezoelectric Coupling Matrix | C/m2 | |
| Nozzle Big Radius (Rd): 0.25 mm (Initial) Chamber Height (mu): 0.5 mm (Initial) | Permittivity , where | 1 | |
| Nozzle Length (L): 0.5 mm (Initial) | Damping (Isotropic Loss Factor) ηs | 0.02 | 1 |
| Divergence Angle (θ): 11° (Initial) | Dielectric Loss (Isotropic Loss Factor) for Electrical Permittivity | 0.02 | 1 |
| Brass | Density | 8500 | kg/m3 |
| Diameter (Dc): 27 mm | Young modulus | 90,000 | MPa |
| Thickness(tb): 0.2 mm | Poisson’s ratio | 0.32 | 1 |
| Insulin | Density | 997 | kg/m3 |
| Kinematic viscosity | 0.0014 | kg/m.s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaçar, A.; Özer, M.B.; Taşcıoğlu, Y. A Novel Artificial Pancreas: Energy Efficient Valveless Piezoelectric Actuated Closed-Loop Insulin Pump for T1DM. Appl. Sci. 2020, 10, 5294. https://doi.org/10.3390/app10155294
Kaçar A, Özer MB, Taşcıoğlu Y. A Novel Artificial Pancreas: Energy Efficient Valveless Piezoelectric Actuated Closed-Loop Insulin Pump for T1DM. Applied Sciences. 2020; 10(15):5294. https://doi.org/10.3390/app10155294
Chicago/Turabian StyleKaçar, Alp, Mehmet Bülent Özer, and Yiğit Taşcıoğlu. 2020. "A Novel Artificial Pancreas: Energy Efficient Valveless Piezoelectric Actuated Closed-Loop Insulin Pump for T1DM" Applied Sciences 10, no. 15: 5294. https://doi.org/10.3390/app10155294
APA StyleKaçar, A., Özer, M. B., & Taşcıoğlu, Y. (2020). A Novel Artificial Pancreas: Energy Efficient Valveless Piezoelectric Actuated Closed-Loop Insulin Pump for T1DM. Applied Sciences, 10(15), 5294. https://doi.org/10.3390/app10155294





