Secondary Breakup Characteristics and Mechanism of Single Electrified Al/N-Decane Nanofluid Fuel Droplet in Electrostatic Field
Abstract
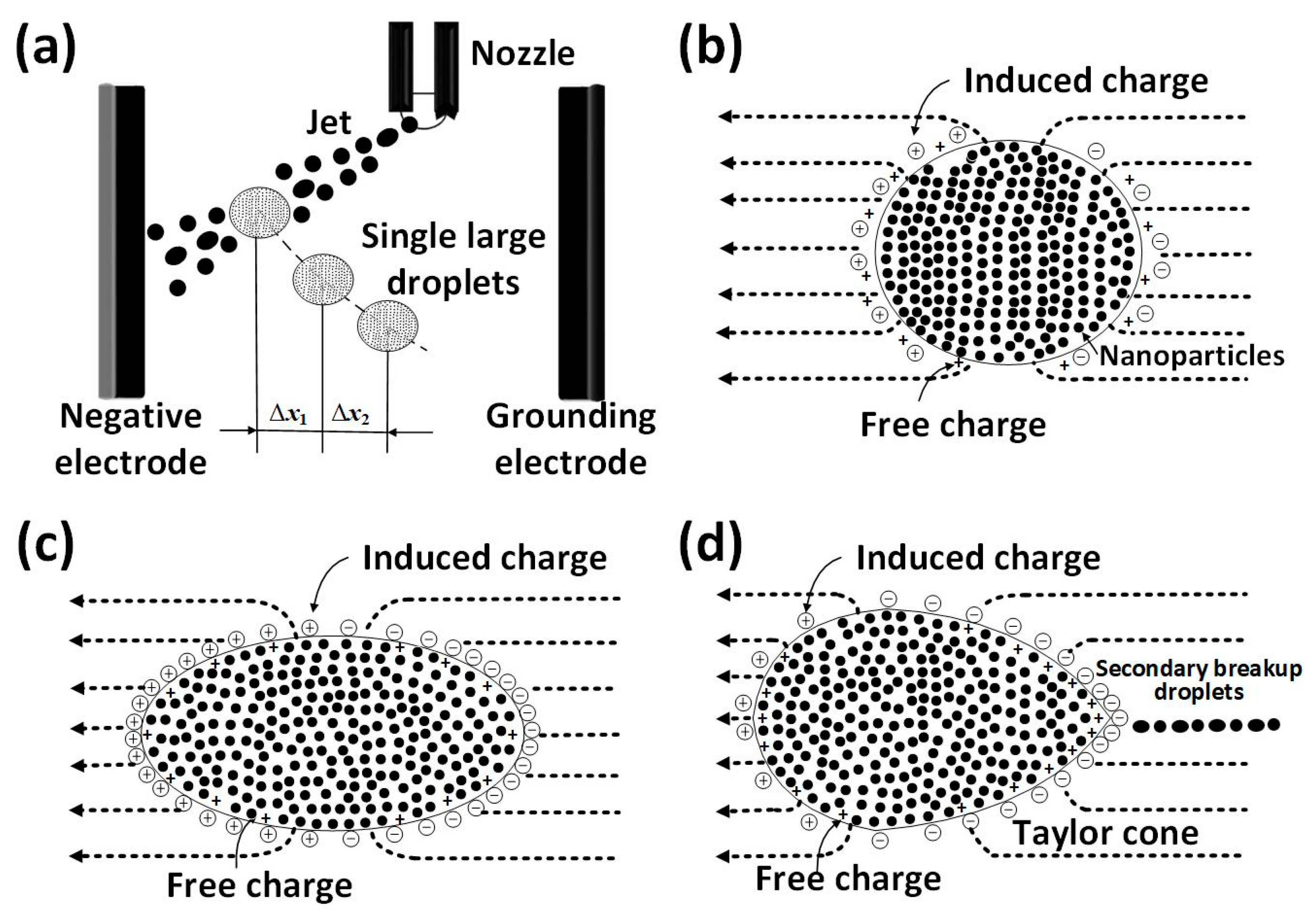
:1. Introduction
2. Materials and Methods
2.1. Preparation of Al/n-Decane Nanofluid Fuel
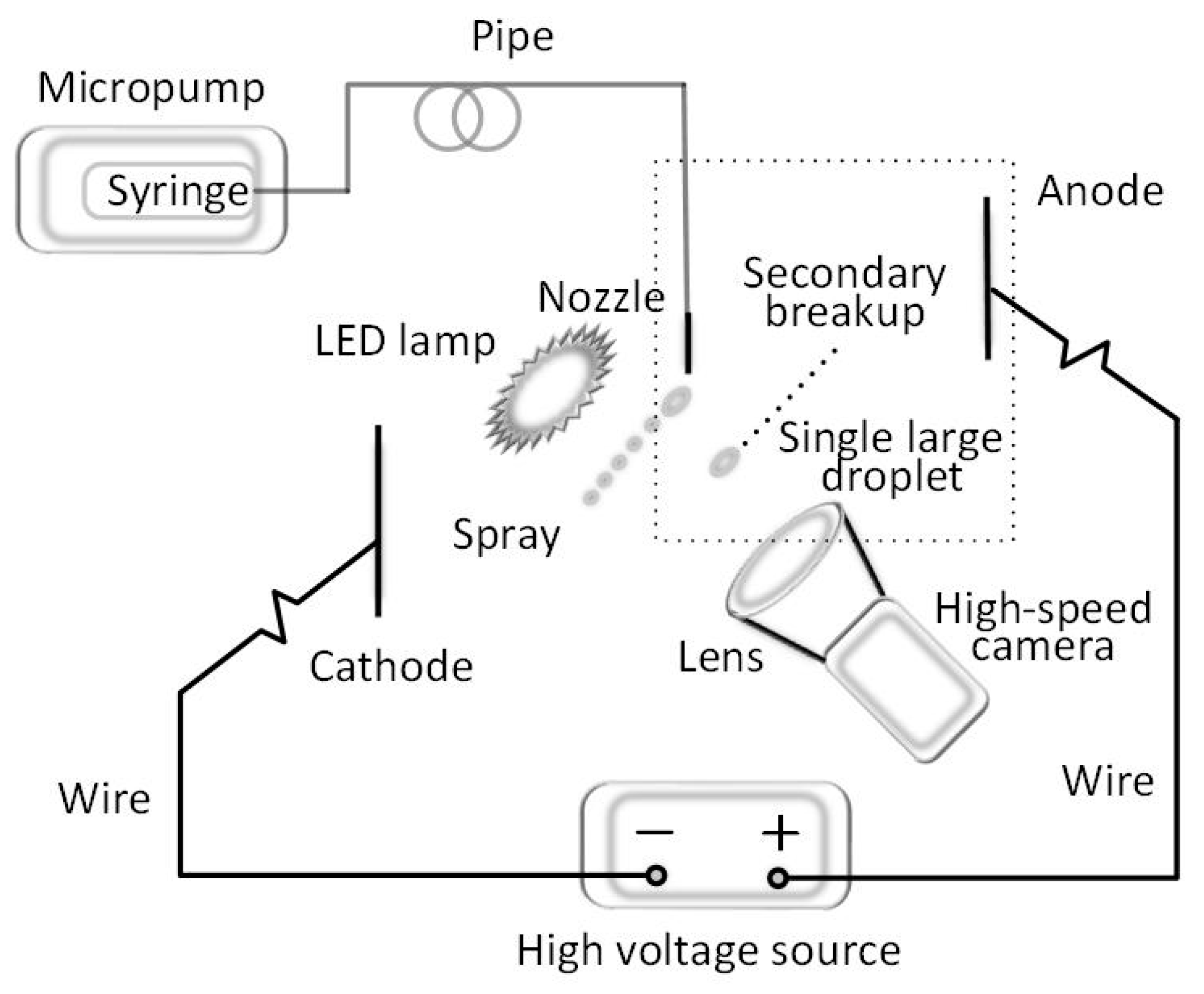
2.2. Experimental Setup
3. Results and Discussion
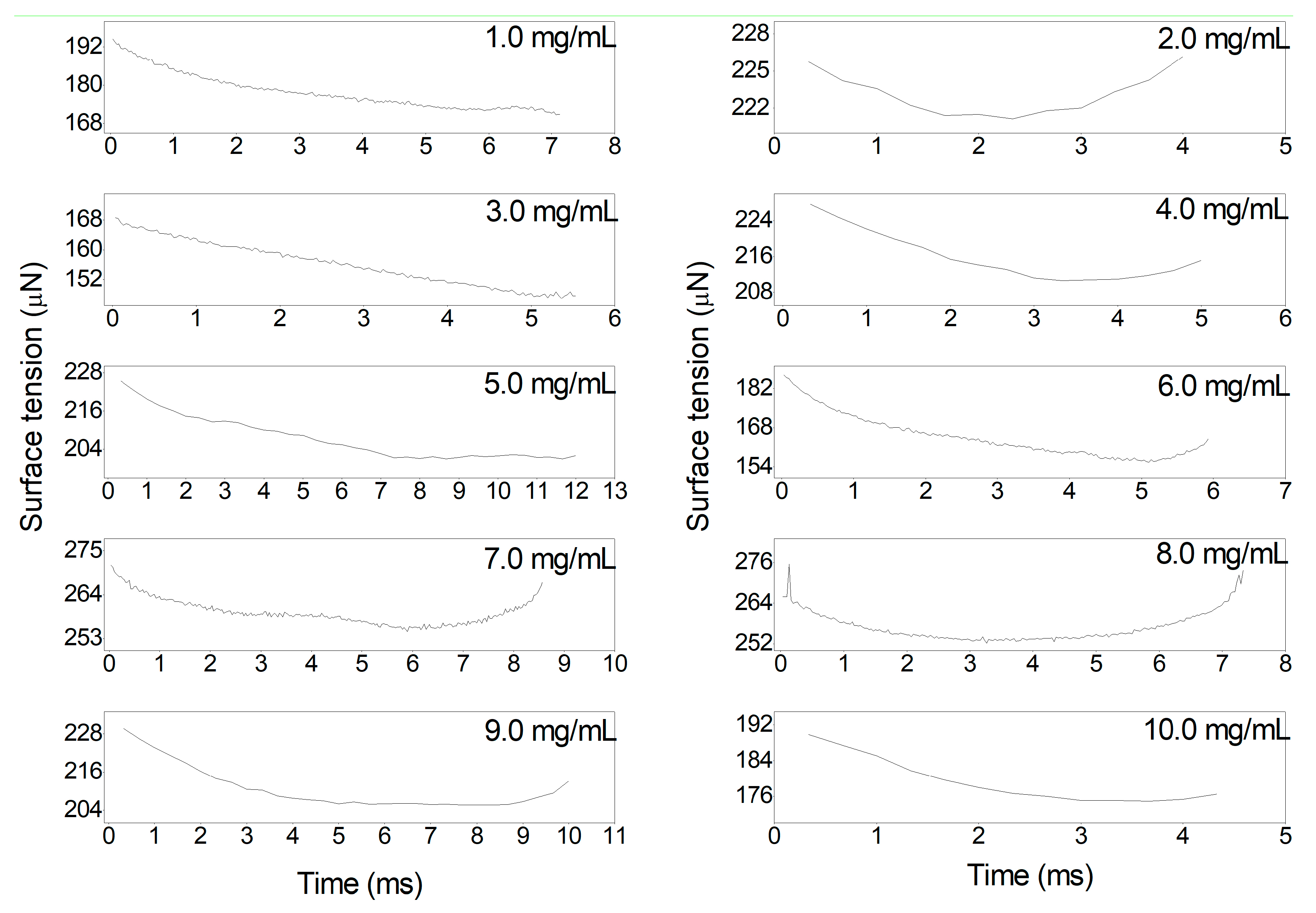
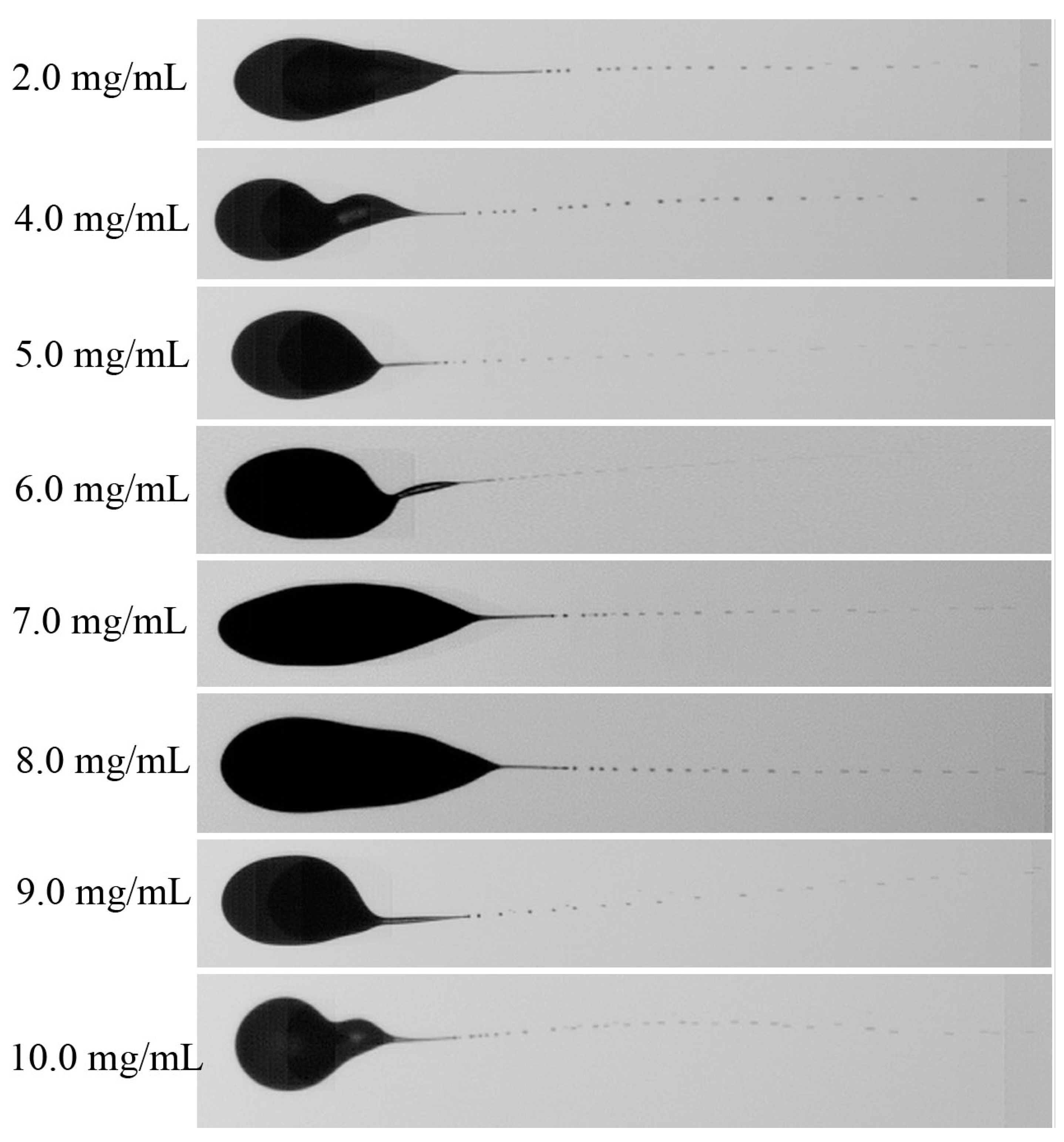
3.1. Taylor Cone Formation of Single Electrified Al/N-Decane Nanofluid Fuel Droplets
3.2. Charge-to-Mass Ratio of Single Electrified Al/N-Decane Nanofluid Fuel Droplets
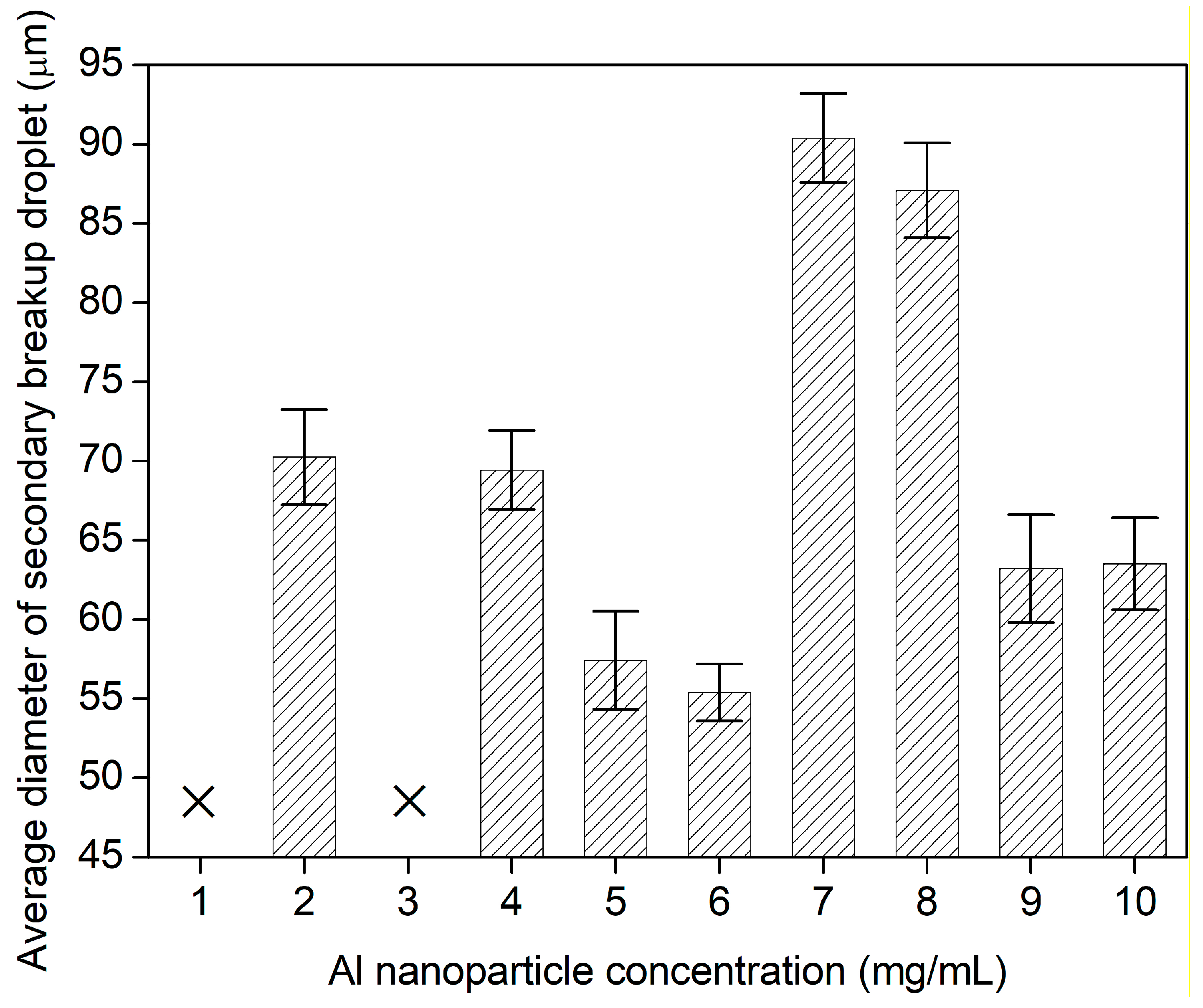
3.3. Secondary Breakup of Single Electrified Al/N-Decane Nanofluid Fuel Droplets
3.4. Mechanism of the Secondary Breakup of Single Electrified Al/N-Decane Nanofluid Fuel Droplets
4. Conclusions
- 1
- The charge distribution is non-uniform at the droplet surface, resulting in a gradient of the electric field within the droplet and locally deforming the droplet to produce the Taylor cone. The Charge-to-Mass ratio ranges from 10−7~10−5 C/kg. Overall, one cone was formed, occasionally two cones at Al nanoparticle concentration of 8.0 mg/mL.
- 2
- The C’/E values keep constant of~0.20 at most of Al nanoparticle concentrations, testifying that the reasonability of equilibrium dominated by the electrical force and the surface tension. On breakup, the surface charges are saturated but much less than the Rayleigh limit. At 6.0 mg/mL, the surface charge density reaches a maximum of 24.0%. The average diameters of secondary breakup sub droplets almost reached a minimum, suggesting that the large surface charge density achieves better breakup performance of single droplets.
- 3
- Nanoparticle concentration has a significant effect on the charging of droplets, and the secondary breakup performance. At dilute concentrations below 3.0 mg/mL, the jet possibly does not produce, while at dense concentrations of 4.0~10.0 mg/mL, the jet filaments are formed and break up into uniform fine sub droplets. The minimum average diameter of secondary breakup droplets is 55.4 µm at 6.0 mg/mL.
Author Contributions
Funding
Conflicts of Interest
References
- Basu, S.; Miglani, A. Combustion and heat transfer characteristics of nanofluid fuel droplets: A short review. Int. J. Heat. Mass Trans. 2016, 96, 482–503. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sust. Energ. Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Wen, D. Nanofuel as a potential secondary energy carrier. Energ. Environ. Sci. 2010, 3, 591–600. [Google Scholar] [CrossRef]
- Tyagi, H.; Phelan, P.E.; Prasher, R.; Peck, R.; Lee, T.; Pacheco, J.R.; Arentzen, P. Increased hot-plate ignition probability for nanoparticle-laden diesel fuel. Nano Lett. 2008, 8, 1410–1416. [Google Scholar] [CrossRef] [PubMed]
- Sabourin, J.L.; Dabbs, D.M.; Yetter, R.A.; Dryer, F.L.; Aksay, I.A. Functionalized Graphene Sheet Colloids for Enhanced Fuel/Propellant Combustion. ACS Nano 2009, 3, 3945–3954. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.N.; Liu, D. Treatment of efficiency for temperature and concentration profiles reconstruction of soot and metal-oxide nanoparticles in nanofluid fuel flames. Int. J. Heat. Mass Trans. 2019, 133, 494–499. [Google Scholar] [CrossRef]
- Mandal, S.; Kanagaraj, S. Reduction of emission in a diesel engine using nanofuel–ceria nanoparticle dispersed diesel. J. ASTM Int. 2012, 9, 1–9. [Google Scholar] [CrossRef]
- Mehta, R.N.; Chakraborty, M.; Parikh, P.A. Nanofuels: Combustion, engine performance and emissions. Fuel 2014, 120, 91–97. [Google Scholar] [CrossRef]
- Salata, O.V. Tools of nanotechnology: Electrospray. Curr. Nanosci. 2005, 1, 25–33. [Google Scholar] [CrossRef]
- Jaworek, A.; Sobczyk, A.T. Electrospraying route to nanotechnology: An overview. J. Electrostat. 2008, 66, 197–219. [Google Scholar] [CrossRef]
- Takáts, Z.; Wiseman, J.M.; Gologan, B.; Cooks, R.G. Mass spectrometry sampling under ambient conditions with desorption electrospray ionization. Science 2004, 306, 471–473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agathou, M.S.; Kyritsis, D.C. Electrostatic atomization of hydrocarbon fuels and bio-alcohols for engine applications. Energ. Convers. Manag. 2012, 60, 10–17. [Google Scholar] [CrossRef]
- Ganan-Calvo, A.M. On the general scaling theory for electrospraying. J. Fluid Mech. 2004, 507, 203–212a. [Google Scholar] [CrossRef]
- Collins, R.T.; Sambath, K.; Harris, M.T.; Basaran, O.A. Universal scaling laws for the disintegration of electrified drops. Proc. Natl. Acad. Sci. USA 2003, 110, 4905–4910. [Google Scholar] [CrossRef] [Green Version]
- Ejim, C.E.; Fleck, B.A.; Amirfazli, A. Analytical study for atomization of biodiesels and their blends in a typical injector: Surface tension and viscosity effects. Fuel 2007, 86, 1534–1544. [Google Scholar] [CrossRef]
- Chinnam, J.; Das, D.K.; Vajjha, R.S.; Satti, J.R. Measurements of the surface tension of nanofluids and development of a new correlation. Int. J. Therm. Sci. 2015, 98, 68–80. [Google Scholar] [CrossRef]
- Sharma, T.; Sangwai, J.S. Silica nanofluids in polyacrylamide with and without surfactant: Viscosity, surface tension, and interfacial tension with liquid paraffin. J. Petrol. Sci. Eng. 2017, 152, 575–585. [Google Scholar] [CrossRef]
- Maheshwary, P.B.; Handa, C.C.; Nemade, K.R. A comprehensive study of effect of concentration, particle size and particle shape on thermal conductivity of titania/water based nanofluid. Appl. Therm. Eng. 2017, 119, 79–88. [Google Scholar] [CrossRef]
- Żyła, G.; Fal, J. Viscosity, thermal and electrical conductivity of silicon dioxide–ethylene glycol transparent nanofluids: An experimental studies. Thermochim. Acta 2017, 650, 106–113. [Google Scholar] [CrossRef]
- Zhuo, Z.; Li, S.; Lu, Y.; Huang, X. Synergetic effects of nanoparticle concentration and electrification on the breakup performance of nanofluid fuel. Int. J. Heat. Mass Trans. 2019, 137, 940–950. [Google Scholar] [CrossRef]
- Cloupeau, M.; Prunet-Foch, B. Electrostatic spraying of liquids in cone-jet mode. J. Electrostat. 1989, 22, 135–159. [Google Scholar] [CrossRef]
- Ivancsy, T.; Suda, J.M. Behavior of polydisperse dust in electrostatic predipitators. J. Electrostat. 2005, 63, 923–927. [Google Scholar] [CrossRef]
- Li, S.; Zhuo, Z.; He, L.; Huang, X. Atomization characteristics of nano-Al/ethanol nanofluid fuel in electrostatic field. Fuel 2019, 236, 811–819. [Google Scholar] [CrossRef]
- Taylor, G.I. Disintegration of water drops in an electric field. Proc. Royal Soc. A 1964, 280, 383–397. [Google Scholar]
- Rigit, A.R.H.; Shrimpton, J.S. Electrical Performance of charge injection electrostatic atomizers. At. Spray. 2006, 16, 401–419. [Google Scholar] [CrossRef]
- Ganan-Calvo, A.M.; Davila, J.; Barrero, A. Current and droplet size in the electrospraying of liquids. Scaling laws. J. Aerosol Sci. 1997, 28, 249–275. [Google Scholar] [CrossRef]
- Raut, J.S.; Akella, S.; Singh, A.K.; Naik, V.M. Catastrophic Drop Breakup in Electric Field. Langmuir 2009, 25, 4829–4834. [Google Scholar] [CrossRef]
- Kourmatzis, A.; Ergene, E.L.; Shrimpton, J.S.; Kyritsis, D.C.; Mashayek, F.; Huo, M. Combined aerodynamic and electrostatic atomization of dielectric liquid jets. Exp. Fluids 2012, 53, 221–235. [Google Scholar] [CrossRef]
- Watson, P.K.; Chadband, W.G.; Sadeghzadeh-Araghi, M. The Role of Electrostatic and Hydrodynamic Forces in the Negative-Point Breakdown of Liquid Dielectrics. IEEE Trans. Dielect. Electr. Insul. 1991, 26, 543–559. [Google Scholar] [CrossRef]
- Fernandes De La Mora, J. On the Outcome of the Coulombic Fission of a Charged Isolated Drop. J. Colloid Interface Sci. 1996, 178, 109–218. [Google Scholar] [CrossRef]
- Bailey, A.G. Theory and practice of electrostatic spraying. At. Spray. 1986, 2, 95–134. [Google Scholar]
- Atten, P. Electrohydrodynamic instability and motion induced by injected space charge in insulating liquids. IEEE Trans. Dielect. Electr. Insul. 1996, 3, 1–17. [Google Scholar] [CrossRef]
- Shrimpton, J.S. Dielectric Charged Drop Break up at Sub-Rayleigh Limit Conditions. IEEE Trans. Dielect. Electr. Insul. 2005, 12, 573–578. [Google Scholar] [CrossRef]
- Shrimpton, J.S. Charge Injection Systems: Phycical Principles, Experimental and Theoretical Work; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Okuda, H.; Kelly, A.J. Electrostatic atomization-Experiment, theory and industrial applications. Phys. Plasmas 1996, 3, 2191–2196. [Google Scholar] [CrossRef]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Cerkanowicz, A.E. Rayleigh limit for nonstationary drops. In Proceedings of the IEEE-IAS Conference Record, New York, NY, USA, 28 September–3 October 1980; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1980; pp. 1161–1165. [Google Scholar]
- Inculet, I.I.; Kromann, R. Break up of Large Water Droplets by Electric Fields. IEEE Trans. Ind. Appl. 1989, 25, 945–948. [Google Scholar] [CrossRef]



| Concentration (mg/mL) | Time (ms) | Average Time and Error (ms) | Taylor Cone Angle (°) | Average Taylor Cone Angle and Error (°) |
|---|---|---|---|---|
| 1.0 | 7.10 | 7.05 ± 0.07 | 75.8 | 77.0 ± 1.6 |
| 2.0 | 4.00 | 4.17 ± 0.23 | 60.8 | 63.5 ± 0.6 |
| 3.0 | 5.50 | 5.60 ± 0.14 | 86.8 | 88.4 ± 1.6 |
| 4.0 | 5.00 | 5.15 ± 0.21 | 53.6 | 58.9 ± 7.5 |
| 5.0 | 11.33 | 11.83 ± 0.71 | 54.5 | 52.4 ± 2.1 |
| 6.0 | 5.90 | 5.95 ± 0.07 | 36.0 | 35.1 ± 1.3 |
| 7.0 | 8.53 | 8.60 ± 0.10 | 50.8 | 53.3 ± 3.5 |
| 8.0 | 7.30 | 7.30 ± 0.21 | 46.5 | 48.3 ± 2.5 |
| 9.0 | 10.00 | 13.00 ± 4.2 | 40.8 | 39.0 ± 2.5 |
| 10.0 | 4.33 | 4.50 ± 0.23 | 61.8 | 58.3 ± 5.0 |
| Concentration (mg/mL) | q/m in These Cases (×10−6 C/kg) | Average q/m (×10−6 C/kg) | Error (×10−6 C/kg) | ||||
|---|---|---|---|---|---|---|---|
| A | B | C | R2 | ||||
| 1.0 | −2.97 | −84.90 | 10.51 | 0.999 | −9.55 | 8.05 | 1.13 |
| 2.0 | 1.90 | −76.62 | 7.37 | 0.999 | 6.15 | 4.46 | 0.64 |
| 3.0 | −1.70 | −174.14 | 4.15 | 1.000 | −5.47 | 5.49 | 2.93 |
| 4.0 | 4.57 | −46.31 | −1.12 | 0.995 | 14.7 | 6.406 | 2.05 |
| 5.0 | 1.22 | −99.67 | 16.80 | 1.000 | 3.92 | 2.17 | 0.80 |
| 6.0 | 2.90 | −39.86 | 46.89 | 0.982 | 9.32 | 11.4 | 0.05 |
| 7.0 | 4.82 | −182.33 | 13.55 | 1.000 | 15.5 | 7.48 | 2.04 |
| 8.0 | 0.23 | −77.75 | 9.54 | 1.000 | 0.74 | 2.44 | 1.70 |
| 9.0 | 0.19 | −63.91 | 4.61 | 0998 | 0.61 | 3.92 | 2.42 |
| 10.0 | 3.56 | −13.63 | 0.78 | 0.942 | 11.4 | 11.4 | 1.67 |
| Concentration (mg/mL) | C’/E (m/N1/2) | Concentration (mg/mL) | C’/E (m/N1/2) |
|---|---|---|---|
| 2.0 | 0.206 ± 0.006 | 7.0 | 0.203 ± 0.006 |
| 4.0 | 0.193 ± 0.005 | 8.0 | 0.208 ± 0.006 |
| 5.0 | 0.203 ± 0.006 | 9.0 | 0.203 ± 0.006 |
| 6.0 | 0.180 ± 0.005 | 10.0 | 0.189 ± 0.005 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Li, S.; Du, H.; Lu, Y.; Huang, X. Secondary Breakup Characteristics and Mechanism of Single Electrified Al/N-Decane Nanofluid Fuel Droplet in Electrostatic Field. Appl. Sci. 2020, 10, 5332. https://doi.org/10.3390/app10155332
Lu H, Li S, Du H, Lu Y, Huang X. Secondary Breakup Characteristics and Mechanism of Single Electrified Al/N-Decane Nanofluid Fuel Droplet in Electrostatic Field. Applied Sciences. 2020; 10(15):5332. https://doi.org/10.3390/app10155332
Chicago/Turabian StyleLu, Heng, Shengji Li, Hongzhe Du, Yibin Lu, and Xuefeng Huang. 2020. "Secondary Breakup Characteristics and Mechanism of Single Electrified Al/N-Decane Nanofluid Fuel Droplet in Electrostatic Field" Applied Sciences 10, no. 15: 5332. https://doi.org/10.3390/app10155332
APA StyleLu, H., Li, S., Du, H., Lu, Y., & Huang, X. (2020). Secondary Breakup Characteristics and Mechanism of Single Electrified Al/N-Decane Nanofluid Fuel Droplet in Electrostatic Field. Applied Sciences, 10(15), 5332. https://doi.org/10.3390/app10155332





