Hybrid Data Hiding Based on AMBTC Using Enhanced Hamming Code
Abstract
1. Introduction
- (i)
- We introduce a general framework for DH based on AMBTC with the minimal squared error by the optimal Hamming code using a Lookup Table (LUT).
- (ii)
- Our method calculates the codeword corresponding to the minimum distance from the standard array of the (7,4) Hamming code table and then extracts the corresponding code. The method has little effect on program performance and can be easily conducted.
- (iii)
- We provide a comparative analysis and evaluate the efficiency based on the specified criteria.
- (iv)
- Sufficient experimental results are used to show the effectiveness and advantages of the proposed method.
2. Preliminaries
2.1. AMBTC
2.2. Hamming Code
2.3. Bai and Chang’s Method
- Step 1:
- For each , obtain seven bits from the two pixels at two quantization levels, and rearrange the seven bits to form a seven bit unit. Let and be the two original pixels. The rearranged seven bit unit is obtained by , where the symbol denotes that the four bits from a are concatenated with the three bits from b. Three secret message bits are read from the secret bit set M.
- Step 2:
- Compute the syndrome of the codeword y, and then, the value is changed into a decimal value and is assigned to the variable i. To obtain the stego codeword , flip the ith bit of the codeword y.
- Step 3:
- To reconstruct two quantization levels with the codeword y, is replaced with four LSBs of the low-mean value a, and is replaced with three LSBs of the high-mean value b.
- Step 4:
- It is possible to hide an additional bit by using the order of two quantization levels and the difference between them. In this case, it may be acceptable to embed an additional bit when the criterion is satisfied. Otherwise, it is not accepted to embed an additional bit. If the bit to be embedded is “1”, swap the order of the two quantization levels as (), otherwise no change is conducted.
3. The Proposed Scheme
3.1. Embedding Procedure
- Input:
- Original grayscale image with a size of , threshold T, and secret data .
- Output:
- Stego AMBTC .
- Step 1:
- The original image G is divided into non-overlapping blocks.
- Step 2:
- Step 3:
- The quantization levels are a and b , where is the Most Significant Bit (MSB) of a and is the LSB of a. Similarly, is the MSB of b, and is the LSB of b. The rearranged seven bit codeword is obtained by:where the symbol denotes concatenation. Note that and are the MSB and LSB of the rearranged pixel y, respectively.
- Step 4:
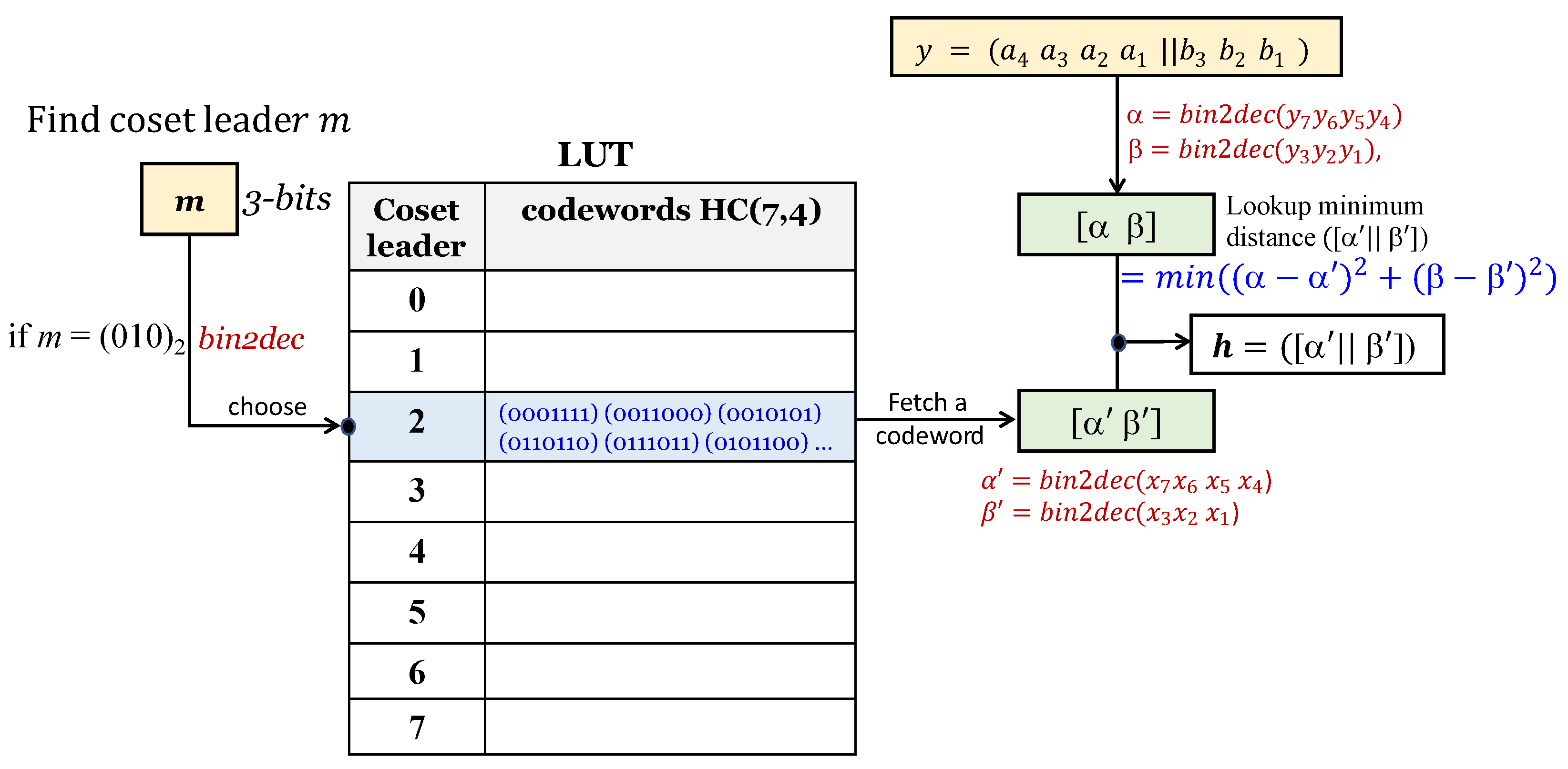
- In Figure 3b, the location of the coset leader that matches the decimal number d for bits is retrieved from the Lookup Table (LUT) using the procedure in Figure 4. Assuming that , the codewords corresponding to the retrieved coset reader are converted to . That is, and . Meanwhile, for codeword y generated in Step 3, and are converted; that is, . The distances for x and are calculated using Equation (9). After calculating for all codewords, the value with the minimum distance among them is obtained. The obtained minimum distance codeword is .For the codeword h, two quantization levels, a and b, are constructed as follows:Before next step, three is added to the index variable i.
- Step 5:
- If , it may be a smooth block. For the smooth block, we use DBS. The bits replace the pixels of the BM. Fifteen is added to the index variable i before the next step. If and , OTQL is launched. If , transpose the order of two quantization levels, a and b, of the , otherwise put the as the original state.
- Step 6:
- Repeat Steps 2∼5 until all image blocks are processed. Then, the stego AMBTC compressed codes’ is constructed.
3.2. Extraction Procedure
- Input:
- Stego AMBTC compressed codes , matrix , and threshold T.
- Output:
- Secret data .
- Step 1:
- Read one block of from a set of as a defined order, where the consists of two quantization levels and one bitmap.
- Step 2:
- The quantization levels are and , where is the MSB of a and is the LSB of a. Similarly, is the MSB of b and is the LSB of b. The rearranged seven bit codeword is by Equation (8).
- Step 3:
- Obtain the syndrome . Then, assign S to , and add three to i.
- Step 4:
- If , it is a smooth block . In this case, this means that the hidden bits were embedded in the BM in the form of pixels. Therefore, by assigning the pixels of the BM to m in order, all the values concealed in the BM can be obtained. That is, and . If and , one bit is hidden in the by using the order of two quantization levels. If the order of two quantization levels is , this means that , otherwise .
- Step 5:
- Repeat Steps until all the are completely processed, and the extracted bit sequence constitutes the secret data m.
3.3. Examples
- (1)
- The two quantization levels of a given are assigned to variables a and b and then converted to binary, i.e., and .
- (2)
- For the two converted binary numbers, the four LSB ( of a and the three LSB () of b are extracted.
- (3)
- To form a codeword, the extracted binary numbers are combined; that is, .
- (4)
- Calculate .
- (5)
- After converting the bit to decimal, the value is retrieved from the coset leaders of the standard array of HC (7,4).
- (6)
- Using Equation (9), the codeword having the minimum distance from the given codeword is retrieved from the table. Here, corresponds to the minimum distance.
- (7)
- The new codeword is .
- (8)
- Two quantization levels embedding three secret bits are recovered by using the codeword h. A new quantization level is obtained by replacing the upper four bits and the lower three bits of h obtained in the process of (7), respectively, with four LSB and three LSB of two quantization levels. That is, the recovered codewords are and .
- (1)
- First, it is necessary to check whether a given block belongs to a smooth block. That is, if the difference between the absolute values of two given quantization levels is less than the threshold T, it is a smooth block, otherwise it belongs to a complex block. In Figure 6b, the difference between two given quantization levels is less than the defined threshold T, so it belongs to a smooth block.
- (2)
- Since the block in the given example is a smooth block, sixteen bits are concealed in the bitmap by replacing the 16 bit secret bits (m = (1010 1111 0000 1100)) directly with the bitmap.
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, C.C.; Li, C.T.; Shi, Y.Q. Privacy-aware reversible watermarking in cloud computing environments. IEEE Access 2018, 6, 70720–70733. [Google Scholar] [CrossRef]
- Byun, S.W.; Son, H.S.; Lee, S.P. Fast and robust watermarking method based on DCT specific location. IEEE Access 2019, 7, 100706–100718. [Google Scholar] [CrossRef]
- Kim, C.; Yang, C.N. Watermark with DSA signature using predictive coding. Multimed. Tools Appl. 2015, 74, 5189–5203. [Google Scholar] [CrossRef][Green Version]
- Kim, H.J.; Kim, C.; Choi, Y.; Wang, S.; Zhang, X. Improved modification direction methods. Comput. Math. Appl. 2010, 60, 319–325. [Google Scholar] [CrossRef]
- Kim, C. Data hiding by an improved exploiting modification direction, Multimed. Tools Appl. 2010, 69, 569–584. [Google Scholar] [CrossRef]
- Petitcolas, F.A.P.; Anderson, R.J.; Kuhn, M.G. Information hiding—A survey. Proc. IEEE 1999, 87, 1062–1078. [Google Scholar] [CrossRef]
- Kim, C.; Shin, D.; Yang, C.N.; Chen, Y.C.; Wu, S.Y. Data hiding using sequential hamming + k with m overlapped pixels. KSII Trans. Internet Inf. 2019, 13, 6159–6174. [Google Scholar]
- Mielikainen, J. LSB matching revisited. IEEE Signal Proc. Lett. 2006, 13, 285–287. [Google Scholar] [CrossRef]
- Chan, C.K.; Cheng, L.M. Hiding data in images by simple LSB substitution. Pattern Recognit. 2004, 37, 469–474. [Google Scholar] [CrossRef]
- Kim, C.; Shin, D.; Kim, B.G.; Yang, C.N. Secure medical images based on data hiding using a hybrid scheme with the Hamming code. J. Real-Time Image Process. 2018, 14, 115–126. [Google Scholar] [CrossRef]
- Tian, J. Reversible data embedding using a difference expansion. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 890–896. [Google Scholar] [CrossRef]
- Hu, Y.; Lee, H.-K.; Li, J. DE-based reversible data hiding with improved overflow location map. IEEE Trans. Circuits Syst. Video Technol. 2008, 19, 250–260. [Google Scholar]
- Celik, M.U.; Sharma, G.; Tekalp, A.M.; Saber, E. Lossless generalized-LSB data embedding. IEEE Trans. Image Process. 2005, 14, 253–266. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.; Shi, Y.-Q.; Ansari, N.; Su, W. Reversible data hiding. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 354–362. [Google Scholar]
- Kim, C.; Baek, J.; Fisher, P.S. Lossless Data Hiding for Binary Document Images Using n-Pairs Pattern. In Proceedings of the Information Security and Cryptology—ICISC 2014, Lecture Notes in Computer Science (LNCS), Seoul, Korea, 3–5 December 2014; Volume 8949, pp. 317–327. [Google Scholar]
- Hong, W.; Chen, T.-S.; Chang, Y.-P.; Shiu, C.W. A high capacity reversible data hiding scheme using orthogonal projection and prediction error modification. Signal Process. 2010, 90, 2911–2922. [Google Scholar] [CrossRef]
- Carpentieri, B.; Castiglione, A.; Santis, A.D.; Palmieri, F.; Pizzolante, R. One-pass lossless data hiding and compression of remote sensing data. Future Gener. Comput. Syst. 2019, 90, 222–239. [Google Scholar] [CrossRef]
- Zhang, X. Reversible data hiding in encrypted image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Puteaux, P.; Puech, W. An efficient MSB prediction-based method for high-ca- pacity reversible data hiding in encrypted images. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1670–1681. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, W.; Liu, H.; Yeung, Y.; Xue, Y. Reversible data hiding in binary images based on image magnification. Multimed. Tools Appl. 2019, 78, 21891–21915. [Google Scholar] [CrossRef]
- Leng, L.; Li, M.; Kim, C.; Bi, X. Dual-source discrimination power analysis for multi-instance contactless palmprint recognition. Multimed. Tools Appl. 2017, 76, 333–354. [Google Scholar] [CrossRef]
- Leng, L.; Zhang, J.S.; Khan, M.K.; Chen, X.; Alghathbar, K. Dynamic weighted discrimination power analysis: A novel approach for face and palmprint recognition in DCT domain. Int. J. Phys. Sci. 2010, 5, 2543–2554. [Google Scholar]
- Deeba, F.; Kun, S.; Dharejo, F.A.; Zhou, Y. Wavelet-Based Enhanced Medical Image Super Resolution. IEEE Access 2020, 8, 37035–37044. [Google Scholar] [CrossRef]
- Delp, E.; Mitchell, O. Image compression using block truncation coding. IEEE Trans. Commun. 1979, 27, 1335–1342. [Google Scholar] [CrossRef]
- Lema, M.D.; Mitchell, O.R. Absolute moment block truncation coding and its application to color images. IEEE Trans. Commun. 1984, COM-32, 1148–1157. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Jung, K.H. Human visual system based enhanced AMBTC for color image compression using interpolation. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; Volume 385, pp. 903–907. [Google Scholar]
- Hong, W.; Chen, T.S.; Shiu, C.W. Lossless steganography for AMBTC compressed images. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, China, 27–30 May 2008; pp. 13–17. [Google Scholar]
- Chuang, J.C.; Chang, C.C. Using a simple and fast image compression algorithm to hide secret information. Int. J. Comput. Appl. 2006, 28, 329–333. [Google Scholar]
- Ou, D.; Sun, W. High payload image steganography with minimum distortion based on absolute moment block truncation coding. Multimed. Tools Appl. 2015, 74, 9117–9139. [Google Scholar] [CrossRef]
- Bai, J.; Chang, C.C. High payload steganographic scheme for compressed images with Hamming code. Int. J. Netw. Secur. 2016, 18, 1122–1129. [Google Scholar]
- Kumar, R.; Kim, D.S.; Jung, K.H. Enhanced AMBTC based data hiding method using hamming distance and pixel value differencing. J. Inf. Secur. Appl. 2019, 47, 94–103. [Google Scholar] [CrossRef]
- Chen, J.; Hong, W.; Chen, T.S.; Shiu, C.W. Steganography for BTC compressed images using no distortion technique. Imaging Sci. J. 2013, 58, 177–185. [Google Scholar] [CrossRef]
- Hong, W. Efficient data hiding based on block truncation coding using pixel pair matching technique. Symmetry 2018, 10, 36. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S. A novel data embedding method using adaptive pixel pair matching. IEEE Trans. Inf. Forensics Secur. 2012, 7, 176–184. [Google Scholar] [CrossRef]
- Huang, Y.H.; Chang, C.C.; Chen, Y.H. Hybrid secret hiding schemes based on absolute moment block truncation coding. Multimed. Tools Appl. 2017, 76, 6159–6174. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Chi, K.Y. Cloud image watermarking: High quality data hiding, and blind decoding scheme based on block truncation coding. Multimed. Syst. 2019, 25, 551–563. [Google Scholar] [CrossRef]
- Malik, A.; Sikka, G.; Verma, H.K. An AMBTC compression-based data hiding scheme using pixel value adjusting strategy. Multidimens. Syst. Signal Process. 2018, 29, 1801–1818. [Google Scholar] [CrossRef]
- Lin, J.; Weng, S.; Zhang, T.; Ou, B.; Chang, C.C. Two-Layer Reversible Data Hiding Based on AMBTC Image With (7, 4) Hamming Code. IEEE Access 2019, 8, 21534–21548. [Google Scholar] [CrossRef]
- Sampat, M.P.; Wang, Z.; Gupta, S.; Bovik, A.C.; Markey, M.K. Complex wavelet structural similarity: A new image similarity index. IEEE Trans. Image Process. 2009, 18, 2385–2401. [Google Scholar] [CrossRef]








| Images | T | Ou and Sun [29] | Bai and Chang’s [30] | W Hong [33] | The Proposed | ||||
| EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | ||
| Boats | 5 | 129,249 | 31.3506 | 64,011 | 31.2928 | 149,368 | 31.3203 | 166,176 | 31.2846 |
| Goldhill | 53,873 | 32.7028 | 21,291 | 32.7076 | 73,408 | 32.6373 | 100,853 | 31.4917 | |
| Airplane | 154,545 | 31.7405 | 78,477 | 31.6604 | 175,203 | 31.7181 | 187,268 | 31.2018 | |
| Lena | 135,089 | 33.1929 | 67,400 | 33.1760 | 155,889 | 33.1454 | 168,498 | 33.1059 | |
| Peppers | 100,977 | 33.6253 | 48,164 | 33.6888 | 121,072 | 33.5682 | 138,714 | 33.4999 | |
| Zelda | 109,585 | 35.7438 | 53,096 | 35.8680 | 128,346 | 35.6618 | 145,526 | 35.5624 | |
| Average | 113,886 | 33.0593 | 55,407 | 33.0656 | 133,881 | 33.0085 | 151,173 | 32.6911 | |
| Images | T | Ou and Sun [29] | Bai and Chang’s [30] | W Hong [33] | The Proposed | ||||
| EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | ||
| Boats | 10 | 160,913 | 31.0204 | 82,644 | 31.1508 | 186,330 | 30.9774 | 201,272 | 30.9316 |
| Goldhill | 127,409 | 31.6842 | 64,721 | 32.2382 | 150,349 | 31.6372 | 169,667 | 30.7147 | |
| Airplane | 194,897 | 31.3173 | 102,018 | 31.4875 | 221,824 | 31.2796 | 232,682 | 30.8072 | |
| Lena | 193,249 | 32.3724 | 101,530 | 32.7961 | 220,205 | 32.3277 | 231,077 | 32.2792 | |
| Peppers | 200,369 | 32.2246 | 106,357 | 32.9962 | 227,287 | 32.1842 | 236,657 | 32.1617 | |
| Zelda | 212,753 | 33.6013 | 113,380 | 34.7771 | 240,483 | 33.5452 | 247,727 | 33.5333 | |
| Average | 164,799 | 31.8075 | 85,108 | 32.5743 | 190,170 | 31.7623 | 219,847 | 31.7379 | |
| Images | T | Ou and Sun [29] | Bai and Chang’s [30] | W Hong [33] | The Proposed | ||||
| EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | EC (bits) | PSNR (dB) | ||
| Boats | 20 | 205,809 | 29.5664 | 110,433 | 30.7138 | 233,709 | 29.5557 | 243,122 | 29.5228 |
| Goldhill | 212,193 | 29.1224 | 117,286 | 31.2597 | 240,231 | 29.1121 | 249,392 | 28.5724 | |
| Airplane | 226,977 | 30.1906 | 122,037 | 31.1269 | 256,110 | 30.1792 | 262,802 | 29.8300 | |
| Lena | 233,697 | 30.7508 | 126,667 | 32.2383 | 264,366 | 30.7356 | 269,432 | 30.7074 | |
| Peppers | 240,977 | 30.691 | 131,514 | 32.4373 | 271,132 | 30.6750 | 276,077 | 30.6495 | |
| Zelda | 253,841 | 31.5579 | 138,904 | 33.9124 | 284,866 | 31.5299 | 288,527 | 31.4777 | |
| Average | 221,128 | 29.9278 | 124,474 | 31.9481 | 250,207 | 29.9158 | 264,892 | 30.1266 | |
| Images | Ou and Sun [29] | Bai and Chang [30] | W Hong [33] | The Proposed | ||||
|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Boats | 31.3506 | 0.6433 | 30.3823 | 0.6675 | 31.3846 | 0.6828 | 31.4158 | 0.7298 |
| Goldhill | 31.7499 | 0.6942 | 31.1779 | 0.7345 | 32.2203 | 0.7279 | 31.4158 | 0.7642 |
| Airplane | 31.7282 | 0.6614 | 31.1754 | 0.6526 | 31.9034 | 0.7042 | 31.3737 | 0.7305 |
| Lena | 33.2362 | 0.6614 | 32.4231 | 0.6870 | 33.3540 | 0.7094 | 33.4090 | 0.7566 |
| Peppers | 33.3636 | 0.6556 | 32.7389 | 0.6966 | 33.3905 | 0.7081 | 33.5822 | 0.7316 |
| Zelda | 35.4041 | 0.6936 | 34.5442 | 0.7177 | 35.7839 | 0.7335 | 35.9442 | 0.7778 |
| Average | 32.8054 | 0.6683 | 32.0736 | 0.6943 | 33.0061 | 0.7110 | 32.8568 | 0.7484 |
| Images | Ou and Sun [29] | Bai and Chang [30] | W Hong [33] | The Proposed | ||||
|---|---|---|---|---|---|---|---|---|
| MSE | NC | MSE | NC | MSE | NC | MSE | NC | |
| Boats | 49.9795 | 0.9946 | 97.2898 | 0.9932 | 51.0112 | 0.9945 | 47.6810 | 0.9950 |
| Goldhill | 50.2434 | 0.9939 | 70.2292 | 0.9934 | 53.1714 | 0.9938 | 52.0115 | 0.9940 |
| Airplane | 43.4923 | 0.9960 | 88.157 | 0.9952 | 44.2237 | 0.9960 | 48.1400 | 0.9961 |
| Lena | 32.3098 | 0.9954 | 57.5453 | 0.9948 | 33.3644 | 0.9953 | 31.3258 | 0.9957 |
| Peppers | 32.3199 | 0.9955 | 55.0679 | 0.9948 | 34.0308 | 0.9943 | 30.4184 | 0.9958 |
| Zelda | 21.1771 | 0.9943 | 32.3215 | 0.9938 | 21.4966 | 0.9943 | 18.0991 | 0.9948 |
| Average | 38.2537 | 0.9943 | 66.7685 | 0.9942 | 39.5497 | 0.9949 | 37.9460 | 0.9952 |
| Methods | Hidden Bits | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20,000 | 50,000 | 70,000 | 90,000 | 100,000 | 120,000 | 150,000 | 170,000 | 190,000 | 200,000 | |
| Ou and Sun | 1.4531 | 1.5313 | 1.6094 | 1.6563 | 1.7188 | 1.7969 | 1.8281 | 1.9063 | 1.9219 | 1.9531 |
| W Hong | 1.4688 | 1.5938 | 1.6406 | 1.7813 | 1.8281 | 1.8594 | 1.875 | 1.9063 | 1.9531 | 2.0313 |
| Bai and Chang | 2.4688 | 3.7344 | 5.25 | 5.9688 | 6.5625 | 7.3594 | 8.4219 | - | - | - |
| The proposed | 1.6875 | 1.8281 | 2.125 | 2.2656 | 2.5625 | 2.8594 | 3.1563 | 3.5313 | 3.5938 | 3.6094 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Shin, D.-K.; Yang, C.-N.; Leng, L. Hybrid Data Hiding Based on AMBTC Using Enhanced Hamming Code. Appl. Sci. 2020, 10, 5336. https://doi.org/10.3390/app10155336
Kim C, Shin D-K, Yang C-N, Leng L. Hybrid Data Hiding Based on AMBTC Using Enhanced Hamming Code. Applied Sciences. 2020; 10(15):5336. https://doi.org/10.3390/app10155336
Chicago/Turabian StyleKim, Cheonshik, Dong-Kyoo Shin, Ching-Nung Yang, and Lu Leng. 2020. "Hybrid Data Hiding Based on AMBTC Using Enhanced Hamming Code" Applied Sciences 10, no. 15: 5336. https://doi.org/10.3390/app10155336
APA StyleKim, C., Shin, D.-K., Yang, C.-N., & Leng, L. (2020). Hybrid Data Hiding Based on AMBTC Using Enhanced Hamming Code. Applied Sciences, 10(15), 5336. https://doi.org/10.3390/app10155336








