Induction Motor Fault Classification Based on FCBF-PSO Feature Selection Method
Abstract
1. Introduction
2. Signal Analysis and Neural Network
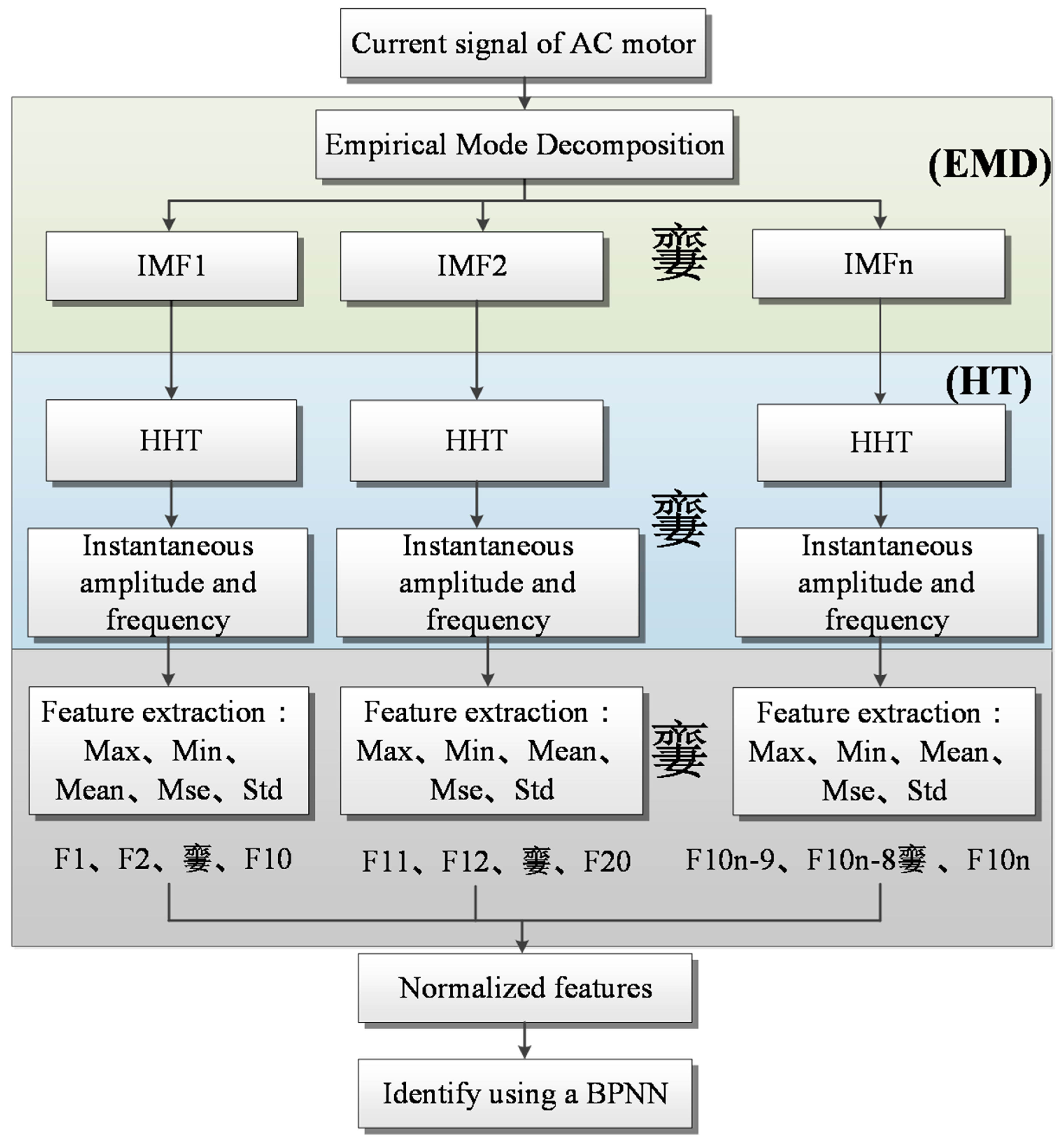
2.1. Hilbert–Huang Transform (HHT)
2.1.1. Intrinsic Mode Functions
- The sum of the number of local maximum and local minima must be the same as or different from the number of zero-crossings, which means that an extreme value must have a zero-crossing point behind it.
- At any time, the upper envelope defined by the local maximum and the lower envelope defined by the local minimum must be averaged to approach zero.
2.1.2. Empirical Mode Decomposition
- Step 1.
- Input the original signal to find the local maximum and local minima. Connect their values to upper envelope and lower envelope respectively;
- Step 2.
- Calculate the average of the upper envelope and the lower envelope to get the mean envelope ;
- Step 3.
- Subtract the original signal from the mean line to get ;
- Step 4.
- Check whether meets the conditions of the IMF. If not, go back to Step 1 and replace with . Rescreen until meets the conditions and termination of IMF, and store as the component of IMF;
- Step 5.
- Subtract the from original signal to get ;
- Step 6.
- Check whether is monotonic function or not. If yes, stop decomposition. If not, repeat Step 1 to Step 5.
2.2. Hilbert Transform (HT)
2.3. Neural Network (NN)
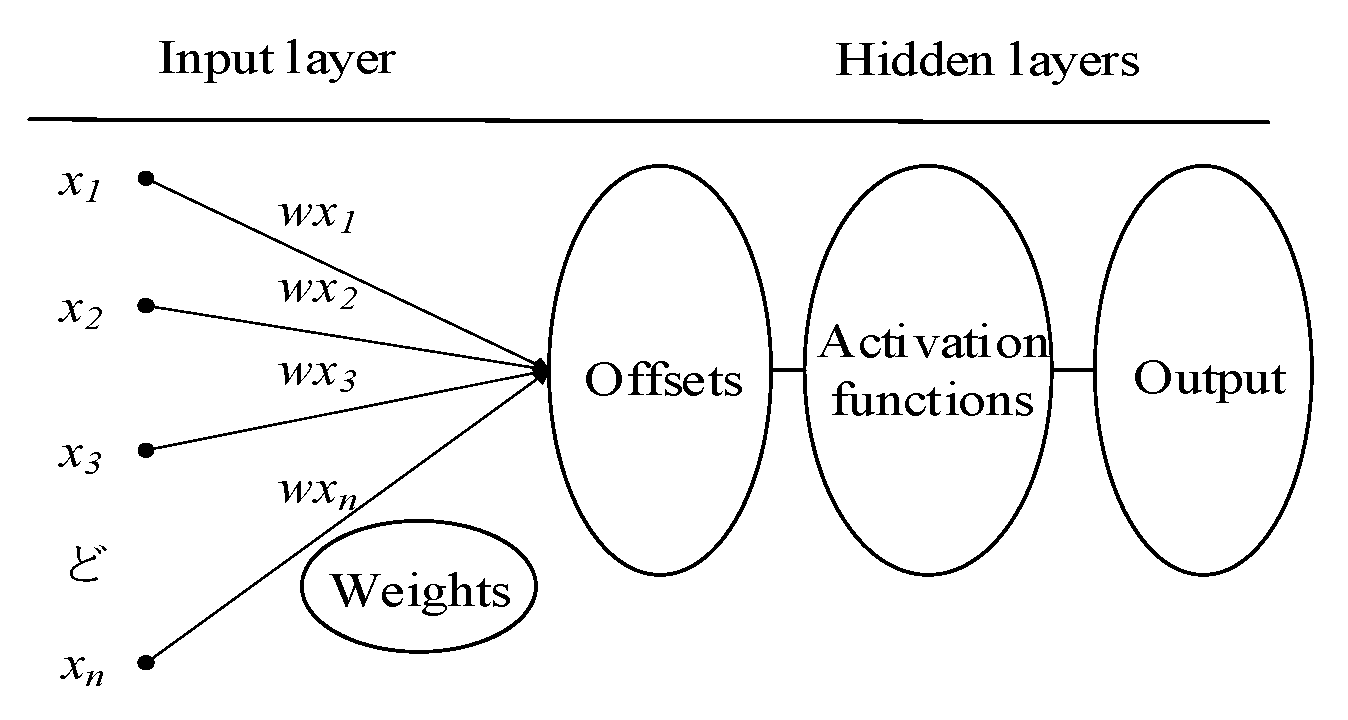
2.3.1. Architecture of NN
2.3.2. Back Propagation Neural Network (BPNN)
3. Feature-Selection Method and Application
3.1. ReliefF
- Step 1.
- Set feature set }, sample category, , sampling times Z, the number of neighbor samples K, the threshold r of feature weights and the initial weight of each feature are zero;
- Step 2.
- Randomly select any sample from all the sample types of Y;
- Step 3.
- Extract K adjacent samples of the same category as the sample ;
- Step 4.
- K Near-misses are also found from the sample set sums different from the category;
- Step 5.
- Calculate the weight of each feature in (4);
- Step 6.
- Repeat sampling to determine whether the number of sampling times Z was reached. If not, return to Step 2 and repeat until the maximum number of sampling times is reached;
- Step 7.
- Sorting features according to feature weights from large to small is mean the importance of the selected features;
- Step 8.
- Calculate the sum of the feature weights of the first n items (expressed as W_all)
- Step 9.
- If W_all < r then n + 1 and repeat Step 8 until W_all > r stops, where r is 90% of the sum of all feature weights;
- Step 10.
- Output the feature.
3.2. Symmetrical Uncertainty (SU)
3.2.1. Information Entropy
3.2.2. Symmetrical Uncertainty Method
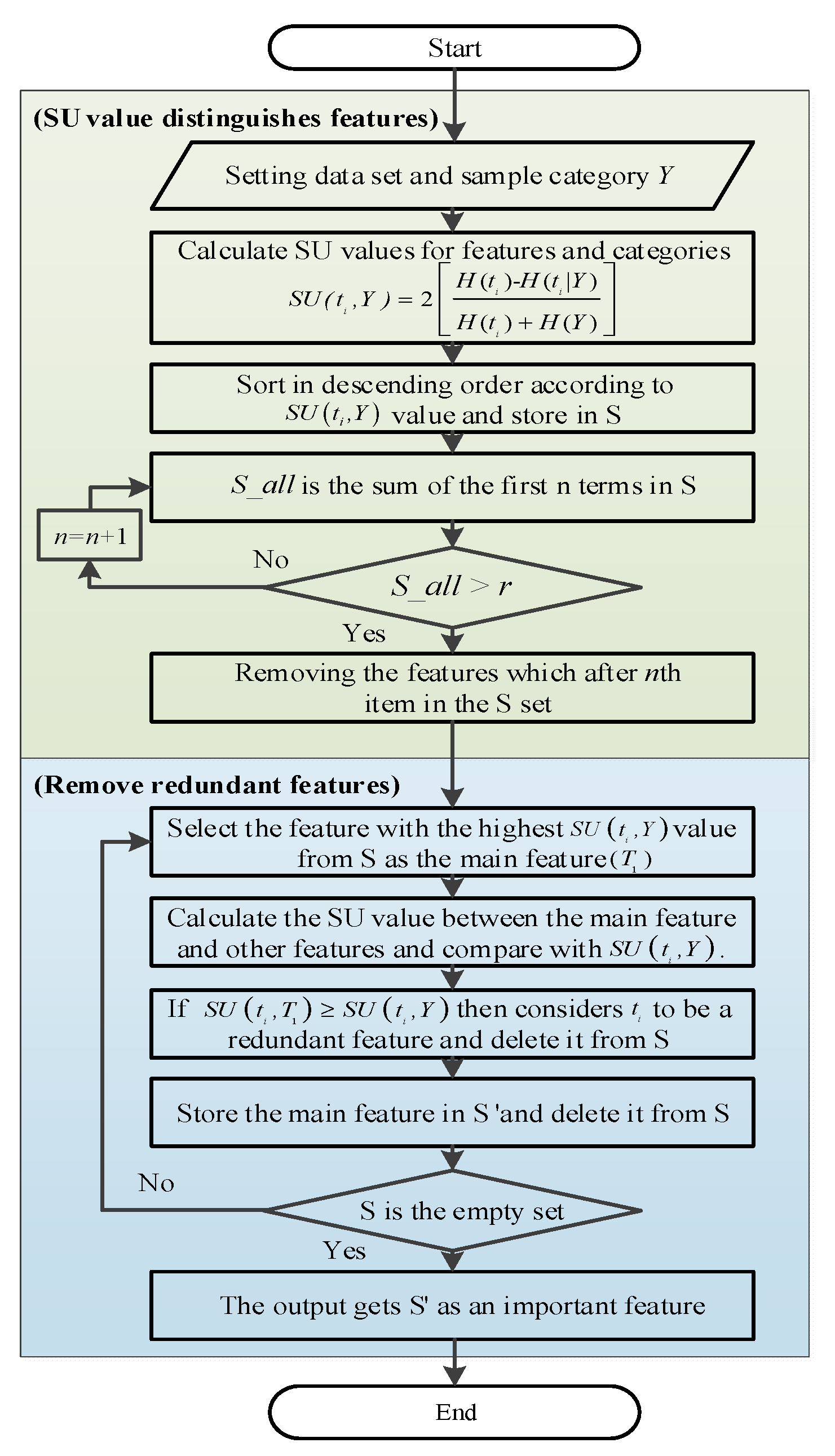
3.3. Fast Correlation-Based Filter (FCBF)
- Step 1.
- Set the data set ,,. Sample category is ;
- Step 2.
- Calculate the SU value between each feature and category Y;
- Step 3.
- Store the values of each feature and category in descending order into the S set;
- Step 4.
- Calculate the sum of SU in the first n items in the S set (expressed as );
- Step 5.
- If , then n+1 repeat to Step 4 until > r stops, where r is 90% the sum of the S set;
- Step 6.
- Remove features after nth from S (Remove features with less influence);
- Step 7.
- Select the feature with the largest value from S as the main feature for selecting;
- Step 8.
- Calculate the of other features and main features in order and the values between this feature and category Y;
- Step 9.
- If , it is regarded as a redundant feature and deleted from S;
- Step 10.
- The main feature is stored in S’ and deleted from S;
- Step 11.
- Repeat Step 7 to Step 10 until S is the empty set and stop;
- Step 12.
- The output S’ is expressed as an important feature.
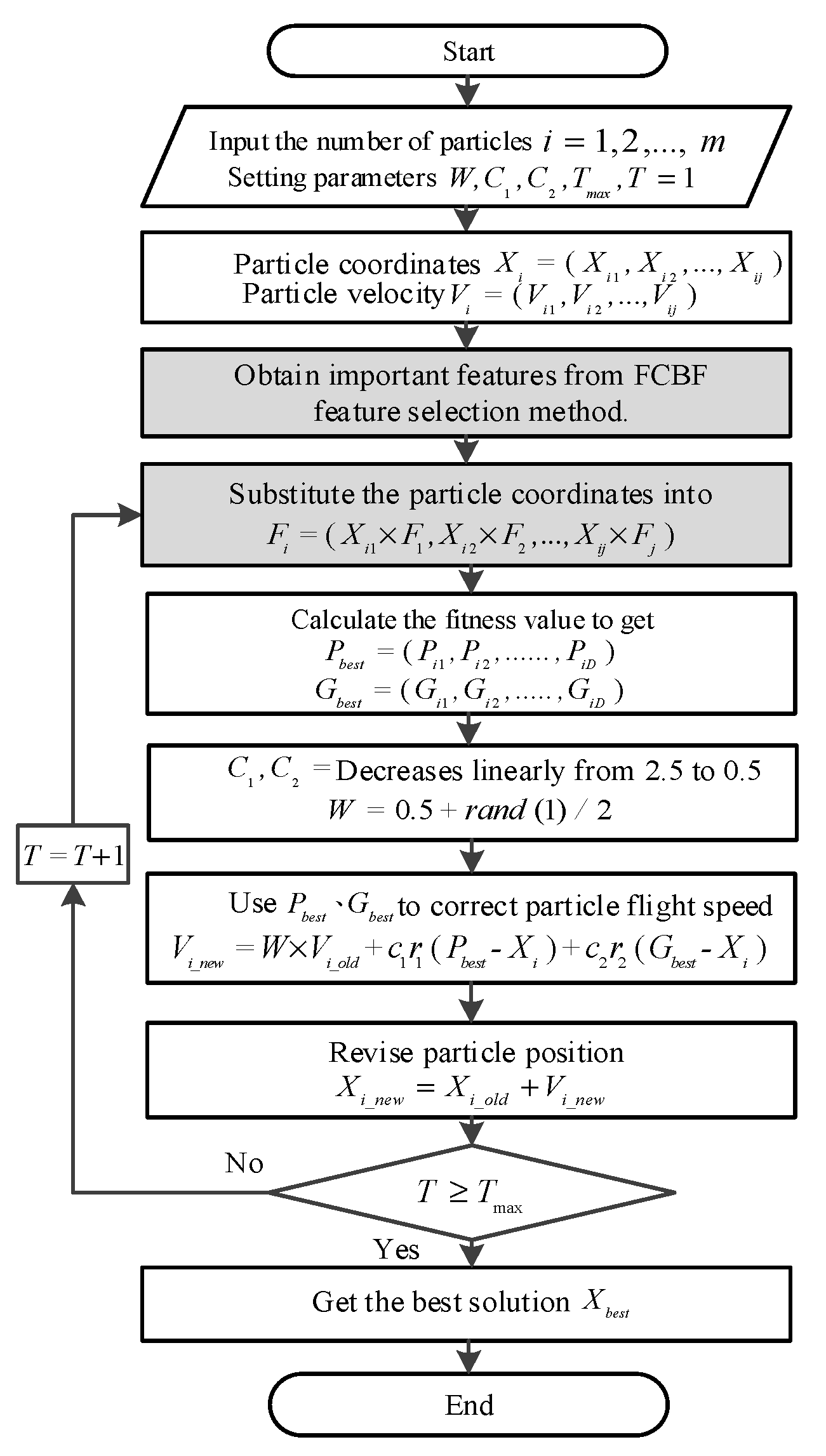
3.4. Application of FCBF–PSO
- Step 1.
- Initially, in the d-dimensional space, parameters including particle number, number of iteration T, acceleration factors , and its own weight are set to form a particle population;
- Step 2.
- In space, assume that each feature is the coordinate of each particle and the flying speed of each particle is ;
- Step 3.
- Use FCBF feature-selection method to output important features ;
- Step 4.
- Bring the coordinates of the particles into the features to obtain the individual best solution and the group best solution ;
- Step 5.
- Use and to modify the particle’s flight speed as shown in (10);
- Step 6.
- Correct the position of the particle with the updated flight speed to find a new position and speed;
- Step 7.
- If it meets the set number of iterations , it will stop, otherwise repeat Step 3 to Step 5, usually the termination condition is to reach the best solution or to reach the number of iterations set by yourself;
- Step 8.
- All particles converge to obtain the best solution;
- Step 9.
- Finally, after the optimization process, a set of solutions with the optimal particle coordinates can be obtained, which is the optimized feature weight.
4. Experiment of Motor Failure and Measurement Signal Method
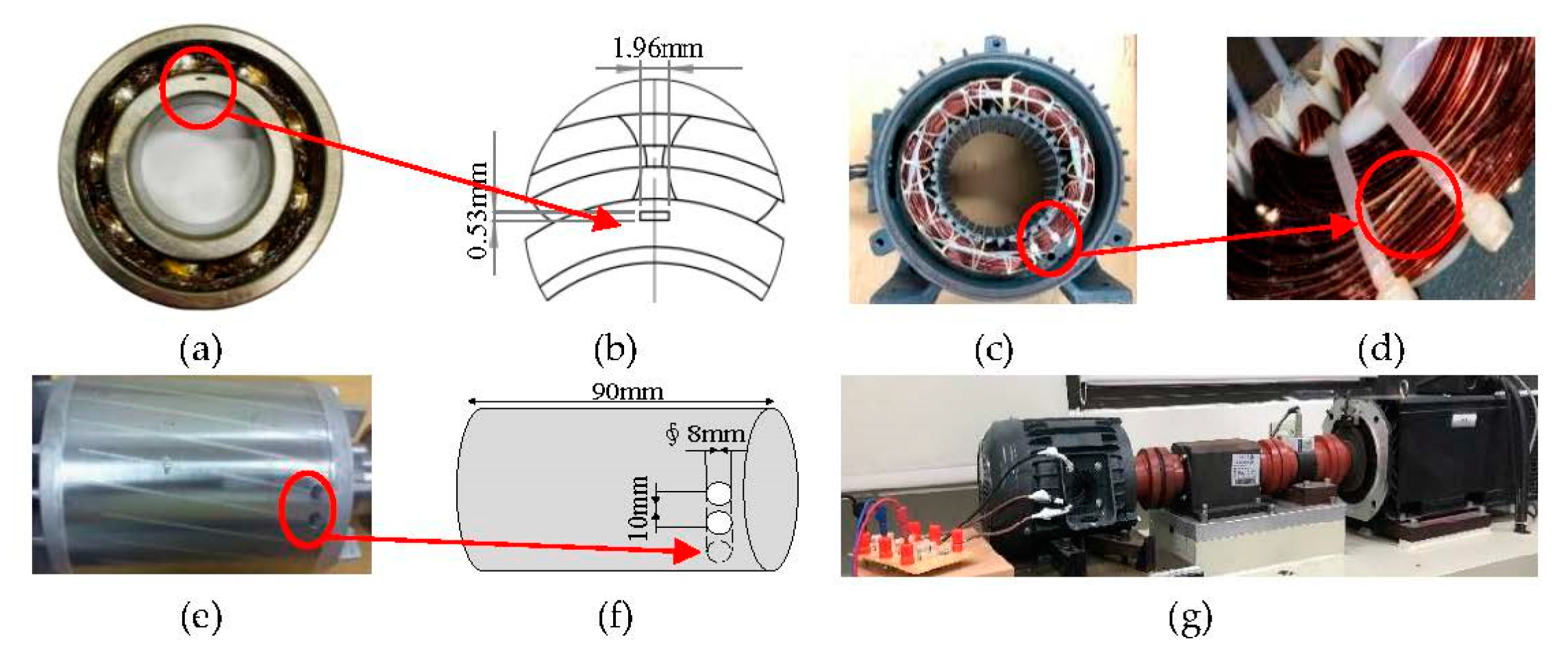
4.1. Experiment Apparatus
4.2. Experiment Process
5. Identification Result of Motor Fault Type
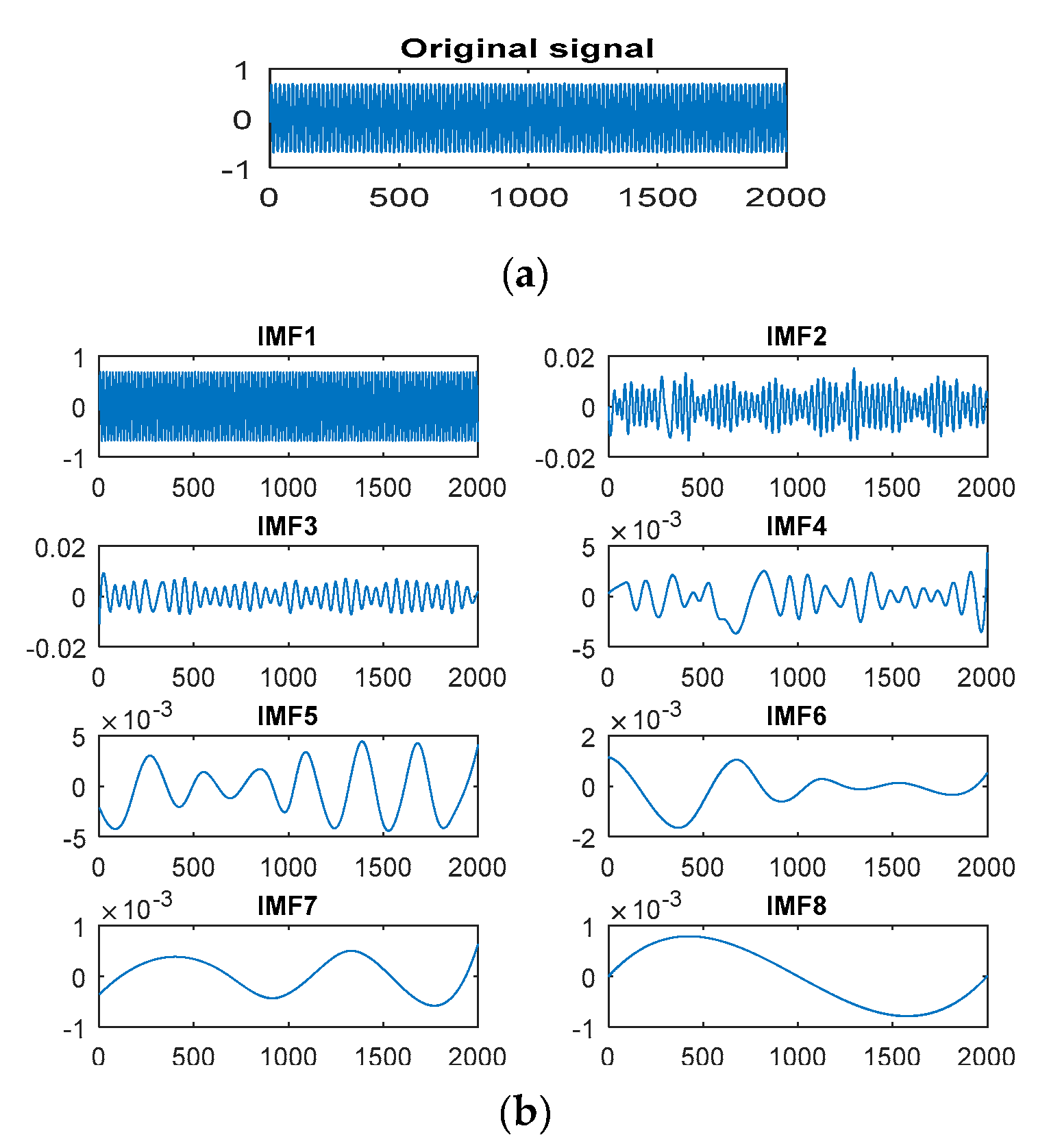
5.1. Original Signal
5.2. HHT Feature Extraction
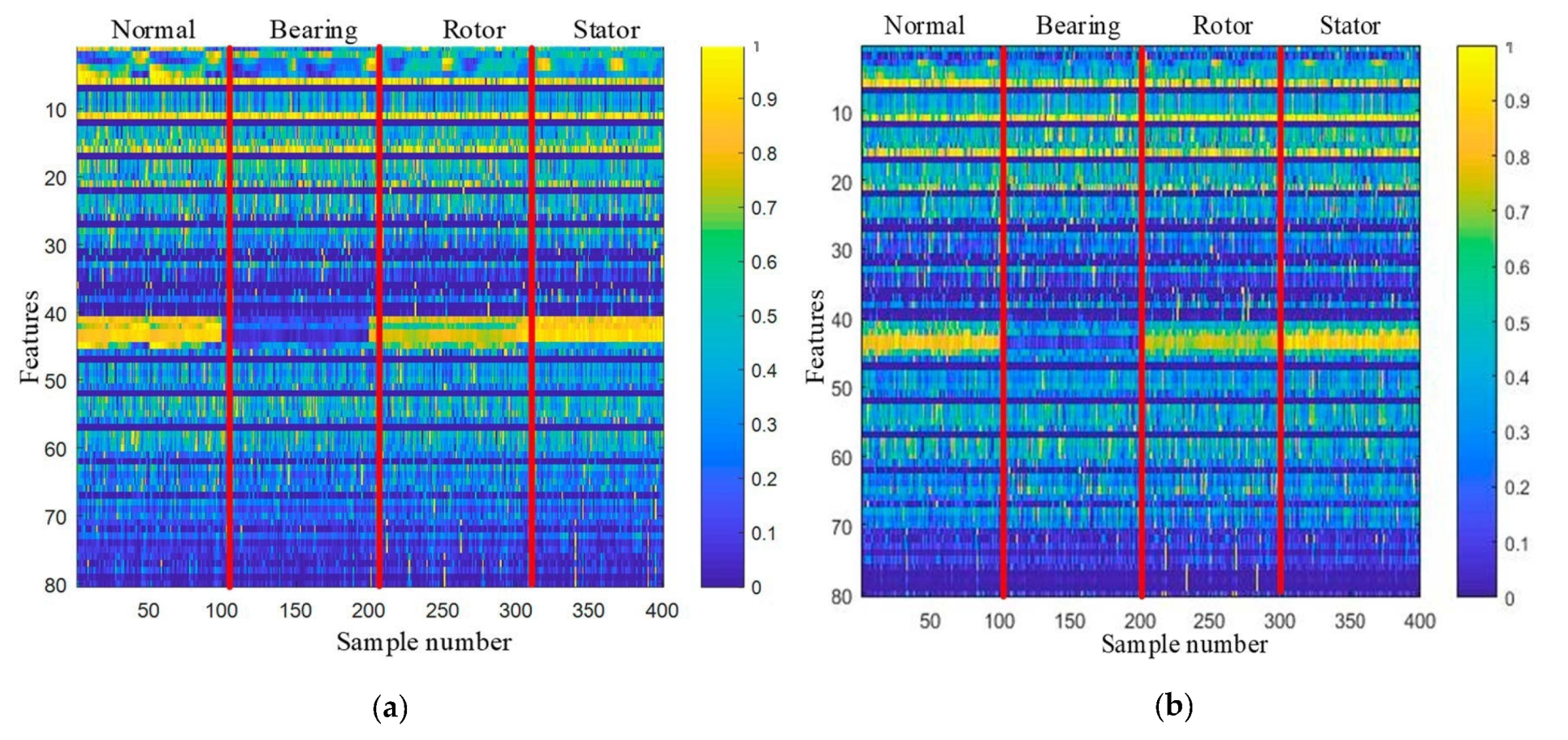
5.3. Results of Induction Motor Fault Classification
5.4. Feature Selection and Results
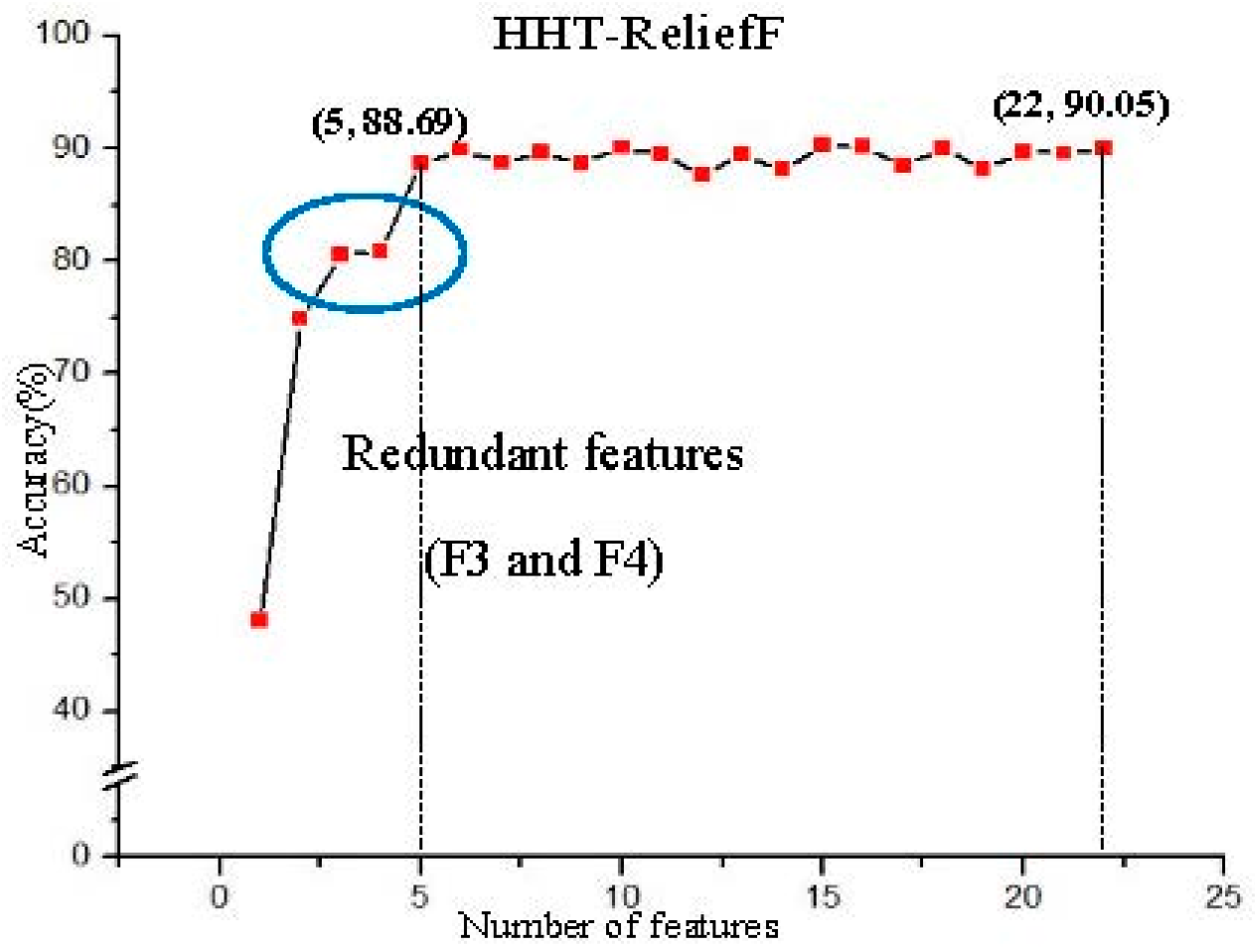
5.4.1. ReliefF Screening and Accuracy
5.4.2. SU Value Screening and Accuracy
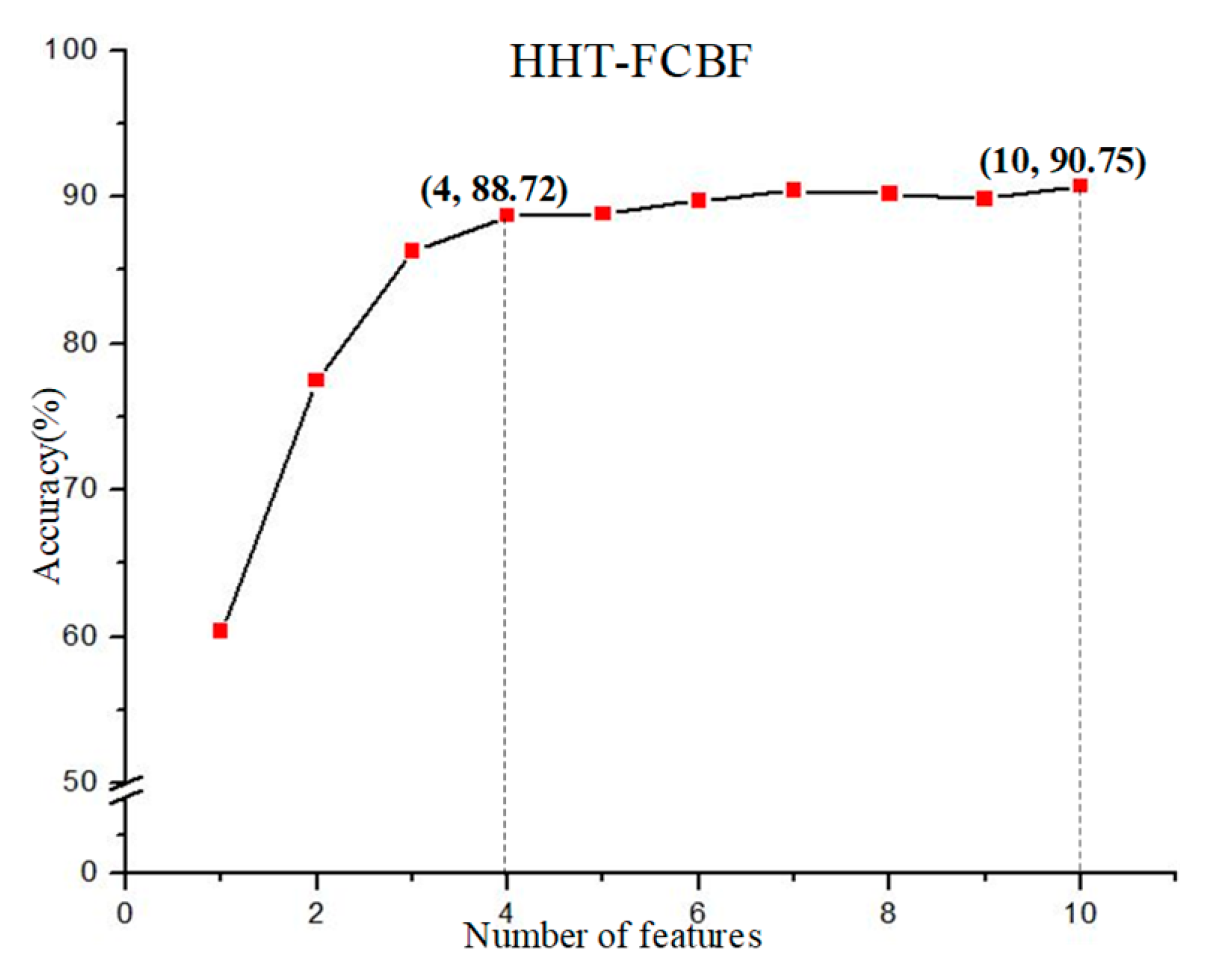
5.4.3. FCBF Screening and Accuracy
5.4.4. Influence of Various Characteristics on Accuracy
6. Conclusions
- In this study, through the comparison of feature-selection methods, ReliefF, SU value and FCBF were used to improve the invalid or poor features on the classifier. Under normal circumstances, the number of features decreased by 72.5%, 76.25% and 87.5%, respectively. In terms of accuracy of classification, only the SU method values decreased slightly by 1.16%. The other two feature screening methods were optimized. When adding severe noise (SNR = 20 dB), the number of features of the three screening feature methods improved. As far as accuracy was concerned, in addition to the obvious improvement of FCBF, the other two methods still could achieve more than 70% classification ability.
- This study also used a PSO optimization model to optimize the feature weights of the three-phase induction motor signals obtained by the FCBF feature-selection method. This method also preserved all the features of FCBF. Under normal circumstances, its classification accuracy through BPNN could reach 92.85%, which was superior to other feature-selection methods. It also improved the accuracy of 4.59% higher than that of HHT. Then doping it with different noise SNR = 40 dB, SNR = 30 dB and SNR = 20 dB white noise, its accuracy also increased by 4.51%, 3.12% and 3.02%. Therefore, it was shown that this method could obtain a higher classification accuracy.
Author Contributions
Funding
Conflicts of Interest
References
- Bazurto, A.J.; Quispe, E.C.; Mendoza, R.C. Causes and failures classification of industrial electric motor. In Proceedings of the 2016 IEEE ANDESCON, Arequipa, Peru, 19–21 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Susaki, H. A fast algorithm for high-accuracy frequency measurement: Application to ultrasonic Doppler sonar. IEEE J. Ocean. Eng. 2002, 27, 5–12. [Google Scholar] [CrossRef]
- Borras, D.; Castilla, M.; Moreno, N.; Montano, J.C. Wavelet and neural structure: A new tool for diagnostic of power system disturbances. IEEE Trans. Ind. Appl. 2001, 37, 184–190. [Google Scholar] [CrossRef]
- Jin, N.; Liu, D.-R. Wavelet Basis Function Neural Networks for Sequential Learning. IEEE Trans. Neural Netw. 2008, 19, 523–528. [Google Scholar] [CrossRef] [PubMed]
- Perera, N.; Rajapakse, A.D. Recognition of fault transients using a probabilistic neural-network classifier. IEEE Trans. Power Deliv. 2010, 26, 410–419. [Google Scholar] [CrossRef]
- Tripathy, M.; Maheshwari, R.; Verma, H. Power Transformer Differential Protection Based On Optimal Probabilistic Neural Network. IEEE Trans. Power Deliv. 2009, 25, 102–112. [Google Scholar] [CrossRef]
- Ying, S.; Jianguo, Q. A Method of Arc Priority Determination Based on Back-Propagation Neural Network. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 38–41. [Google Scholar]
- Wu, W.; Feng, G.; Li, Z.; Xu, Y. Deterministic Convergence of an Online Gradient Method for BP Neural Networks. IEEE Trans. Neural Netw. 2005, 16, 533–540. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Senliol, B.; Gulgezen, G.; Yu, L.; Çataltepe, Z. Fast Correlation Based Filter (FCBF) with a different search strategy. In Proceedings of the 2008 23rd International Symposium on Computer and Information Sciences, Istanbul, Turkey, 27–29 October 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A Deterministic Particle Swarm Optimization Maximum Power Point Tracker for Photovoltaic System under Partial Shading Condition. IEEE Trans. Ind. Electron. 2012, 60, 3195–3206. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Jia, D.; Liu, T.; Zhang, Y. Automatic Interference Term Retrieval from Spectral Domain Low-Coherence Interferometry Using the EEMD-EMD-Based Method. IEEE Photonics-J. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Kijewski-Correa, T.; Kareem, A. Efficacy of Hilbert and Wavelet Transforms for Time-Frequency Analysis. J. Eng. Mech. 2006, 132, 1037–1049. [Google Scholar] [CrossRef]
- Sharma, V.; Rai, S.; Dev, A. A Comprehensive Study of Artificial Neural Networks. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2012, 2, 278–284. [Google Scholar]
- Kumar, A.; Tyagi, N. Comparative analysis of backpropagation and RBF neural network on monthly rainfall prediction. In Proceedings of the 2016 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; Volume 1, pp. 1–6. [Google Scholar]
- Upadhyay, P.K.; Pandita, A.; Joshi, N. Scaled Conjugate Gradient Backpropagation based SLA Violation Prediction in Cloud Computing. In Proceedings of the 2019 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), Dubai, UAE, 11–12 December 2019; pp. 203–208. [Google Scholar]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A Survey on Evolutionary Computation Approaches to Feature Selection. IEEE Trans. Evol. Comput. 2015, 20, 606–626. [Google Scholar] [CrossRef]
- Ang, J.C.; Mirzal, A.; Haron, H.; Hamed, H.N.A. Supervised, Unsupervised, and Semi-Supervised Feature Selection: A Review on Gene Selection. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 13, 971–989. [Google Scholar] [CrossRef] [PubMed]
- Gopika, N.; Kowshalaya, A.M.M.E. Correlation Based Feature Selection Algorithm for Machine Learning. In Proceedings of the 2018 3rd International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 15–16 October 2018; pp. 692–695. [Google Scholar]
- Sawhney, H.; Jeyasurya, B. A feed-forward artificial neural network with enhanced feature selection for power system transient stability assessment. Electr. Power Syst. Res. 2006, 76, 1047–1054. [Google Scholar] [CrossRef]
- Song, Q.; Ni, J.; Wang, G. A Fast Clustering-Based Feature Subset Selection Algorithm for High-Dimensional Data. IEEE Trans. Knowl. Data Eng. 2011, 25, 1–14. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution. In Proceedings of the Twentieth International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Armay, E.F.; Wahid, I. Entropy simulation of digital information sources and the effect on information source rates. In Proceedings of the 2011 2nd International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering, Bandung, Indonesia, 8–9 November 2011; pp. 74–78. [Google Scholar]
- Hall, M.A. Correlation Based Feature Selection for Machine Learning. Ph.D. Thesis, University of Waikato, Hamilton, NewZealand, 1999. [Google Scholar]
- Djellali, H.; Guessoum, S.; Ghoualmi-Zine, N.; Layachi, S. Fast correlation based filter combined with genetic algorithm and particle swarm on feature selection. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017; pp. 1–6. [Google Scholar]
- Lee, C.-Y.; Tuegeh, M. Optimal optimisation-based microgrid scheduling considering impacts of unexpected forecast errors due to the uncertainty of renewable generation and loads fluctuation. IET Renew. Power Gener. 2020, 14, 321–331. [Google Scholar] [CrossRef]

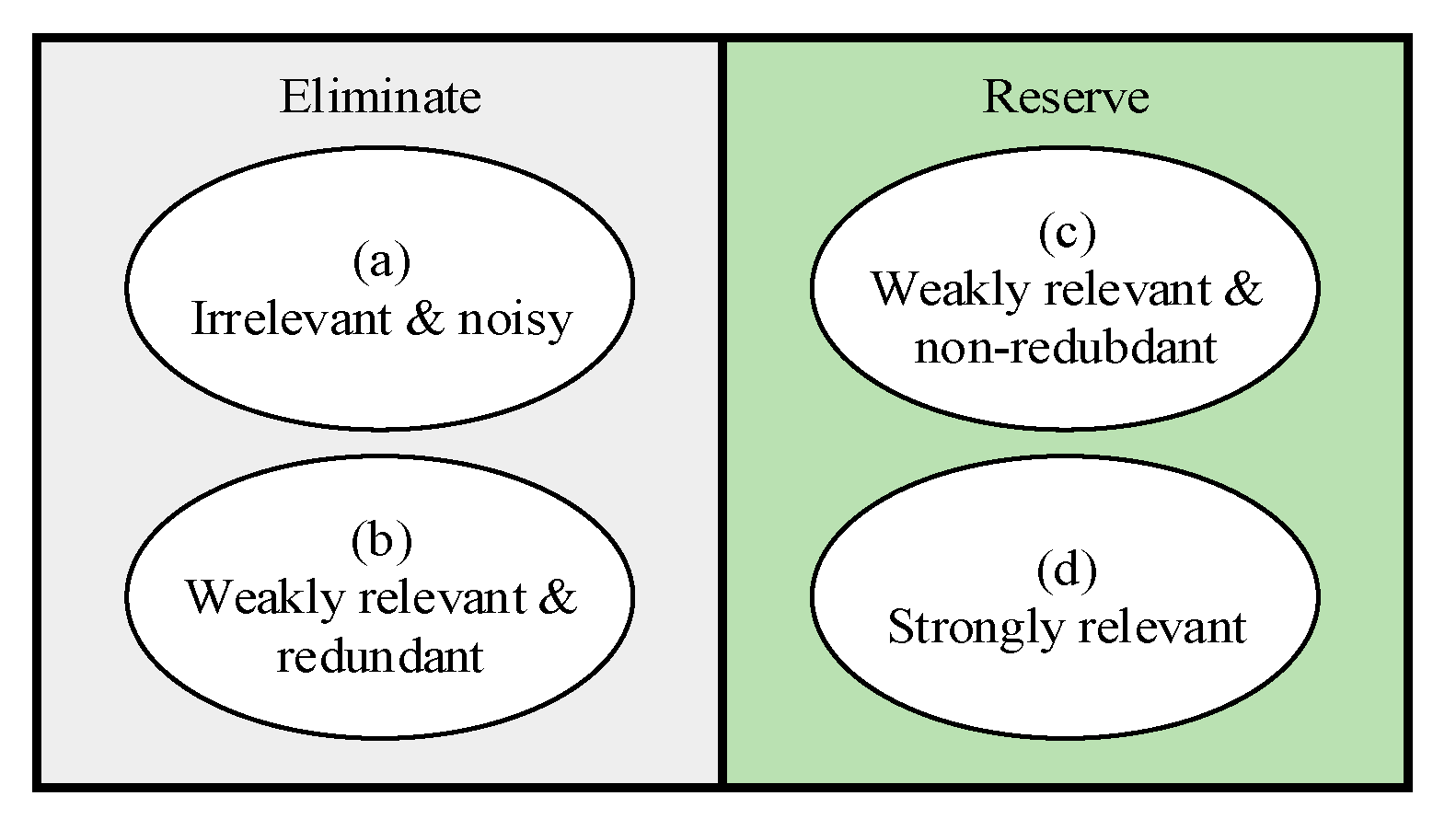



| Failure Type | Occurrence Percentage |
|---|---|
| Bearing damage | 45% |
| Stator damage | 35% |
| Rotor damage | 10% |
| Others damage | 10% |
| Three-Phase Squirrel-Cage Induction Motor Specifications | |||
|---|---|---|---|
| Voltage | 220 V/380 V | Output | 2 HP 1.5 kW |
| Speed | 1715 rpm | Current | 5.58 A/3.23 A |
| Insulation | E | Poles | 4 |
| Effectiveness | 83.5(100%) | Frequency | 60 Hz |
| Method | Number of Features |
|---|---|
| HHT | 80 |
| HHT-ReliefF | 22 |
| HHT-SU | 19 |
| HHT-FCBF | 10 |
| HHT | ReliefF | SU | FCBF | |
|---|---|---|---|---|
| ∞ dB | 0.413 | 0.336 | 0.334 | 0.311 |
| 40 dB | 0.418 | 0.345 | 0.335 | 0.320 |
| 30 dB | 0.407 | 0.358 | 0.339 | 0.326 |
| 20 dB | 0.413 | 0.373 | 0.345 | 0.330 |
| Normal | Accuracy (BPNN%) | ||||
|---|---|---|---|---|---|
| Method | Normal | Bearing | Rotor | Stator | Average |
| HHT | 72.44 | 95.71 | 94.01 | 90.9 | 88.26 |
| ReliefF | 75.64 | 93.9 | 96.76 | 94.03 | 90.05 |
| SU | 75.67 | 96.34 | 95.12 | 92.97 | 90.02 |
| FCBF | 75.21 | 98.63 | 96.51 | 92.68 | 90.75 |
| FCBF–PSO | 78.41 | 98.73 | 98.98 | 95.28 | 92.85 |
| 40 dB | Accuracy (BPNN%) | ||||
|---|---|---|---|---|---|
| Method | Normal | Bearing | Rotor | Stator | Average |
| HHT | 70.61 | 94.52 | 93.49 | 90.39 | 87.25 |
| ReliefF | 70.03 | 95.5 | 94.75 | 93.15 | 88.35 |
| SU | 70.56 | 92.25 | 91.02 | 89.66 | 85.87 |
| FCBF | 71.19 | 96.96 | 93.4 | 93.89 | 88.86 |
| FCBF–PSO | 75.56 | 98.6 | 96.72 | 95.16 | 91.76 |
| 30 dB | Accuracy (BPNN%) | ||||
|---|---|---|---|---|---|
| Method | Normal | Bearing | Rotor | Stator | Average |
| HHT | 63.89 | 91.24 | 84.56 | 82.91 | 80.64 |
| ReliefF | 62.17 | 91.66 | 87.75 | 86.69 | 82.06 |
| SU | 63.24 | 92.56 | 85.66 | 82.88 | 81.08 |
| FCBF | 62.67 | 92.49 | 87.15 | 84.19 | 81.62 |
| FCBF–PSO | 65.87 | 93.57 | 89.04 | 86.56 | 83.76 |
| 20 dB | Accuracy (BPNN%) | ||||
|---|---|---|---|---|---|
| Method | Normal | Bearing | Rotor | Stator | Average |
| HHT | 60.77 | 83.56 | 67.55 | 67.28 | 69.66 |
| ReliefF | 61.06 | 89.47 | 66.99 | 68.18 | 71.42 |
| SU | 58.35 | 85.1 | 69.85 | 68.11 | 70.35 |
| FCBF | 61.54 | 87.25 | 64.72 | 65.88 | 69.84 |
| FCBF–PSO | 65.42 | 88.78 | 68.9 | 67.62 | 72.68 |
| Analytical Method | Noise | Methods | Number of Features | Sort by Important Features after Screening (The Redundant Features are Bold) |
|---|---|---|---|---|
| HHT | dB | ReliefF | 22 | F5, F45, F3, F1, F42, F2, F4, F16, F44, F43, F41, F61, F30, F6, F15, F33, F29, F77, F65, F26, F66, F55 |
| SU | 19 | F41, F43, F44, F42, F45, F5, F1, F2, F4, F31, F49, F11, F3, F38, F67, F56, F48, F30, F15 | ||
| FCBF | 10 | F41, F45, F5, F4, F31, F49, F11, F38, F67, F30 | ||
| 40 dB | ReliefF | 28 | F3, F5, F45, F1, F42, F5, F44, F43, F2, F31, F56, F26, F23, F6, F28, F37, F66, F53, F13, F14, F16, F35, F63, F54, F51, F41, F60, F33 | |
| SU | 19 | F41, F43, F44, F42, F45, F5, F1, F4, F2, F69, F33, F25, F80, F3, F54, F35, F67, F22, F40 | ||
| FCBF | 11 | F41, F45, F5, F4, F2, F69, F33, F25, F80, F67, F22 | ||
| 30 dB | ReliefF | 34 | F3, F5, F45, F1, F38, F42, F28, F44, F4, F43, F26, F29, F30, F63, F46, F16, F37, F51, F8, F6, F75, F9, F20, F61, F10, F11, F48, F41, F15, F64, F50, F40, F68, F49 | |
| SU | 24 | F43, F44, F41, F42, F45, F5, F4, F3, F16, F72, F58, F1, F59, F27, F71, F76, F6, F32, F37, F78, F62, F68, F70, F56 | ||
| FCBF | 13 | F43, F42, F45, F4, F16, F72, F58, F27, F71, F76, F6, F37, F62 | ||
| 20 dB | ReliefF | 49 | F3, F45, F5, F11, F42, F44, F6, F43, F15, F55, F67, F19, F18, F21, F60, F51, F8, F40, F56, F1, F4, F70, F37, F10, F23, F26, F72, F62, F9, F66, F16, F61, F2, F25, F22, F24, F30, F20, F54, F53, F39, F48, F50, F29, F36, F73, F69, F46, F76 | |
| SU | 29 | F43, F44, F45, F42, F41, F4, F74, F10, F76, F65, F11, F9, F3, F78, F8, F73, F22, F80, F63, F29, F64, F72, F5, F79, F46, F19, F30, F14, F69 | ||
| FCBF | 15 | F43, F45, F42, F41, F4, F74, F10, F65, F11, F22, F80, F29, F46, F14, F69 |
| SNR(dB) | Without Feature Selection | Feature-Selection Methods | Compare FCBF–PSO with HHT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Typical Feature-Selection Methods | New Method | ||||||||||
| ReliefF | SU | FCBF | FCBF–PSO | ||||||||
| Number of Features | Acc (%) | Number of Features | Acc (%) | Number of Features | Acc (%) | Number of Features | Acc (%) | Number of Features | Acc (%) | Acc (%) | |
| 80 | 88.26 | 22 | 90.05 | 19 | 90.02 | 10 | 90.75 | 10 | 92.85 | +4.59 | |
| 40 | 80 | 87.25 | 28 | 88.35 | 19 | 85.87 | 11 | 88.86 | 11 | 91.76 | +4.51 |
| 30 | 80 | 80.64 | 34 | 82.06 | 24 | 81.08 | 13 | 81.62 | 13 | 83.76 | +3.12 |
| 20 | 80 | 69.66 | 49 | 71.42 | 29 | 70.35 | 15 | 69.84 | 15 | 72.68 | +3.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Lin, W.-C. Induction Motor Fault Classification Based on FCBF-PSO Feature Selection Method. Appl. Sci. 2020, 10, 5383. https://doi.org/10.3390/app10155383
Lee C-Y, Lin W-C. Induction Motor Fault Classification Based on FCBF-PSO Feature Selection Method. Applied Sciences. 2020; 10(15):5383. https://doi.org/10.3390/app10155383
Chicago/Turabian StyleLee, Chun-Yao, and Wen-Cheng Lin. 2020. "Induction Motor Fault Classification Based on FCBF-PSO Feature Selection Method" Applied Sciences 10, no. 15: 5383. https://doi.org/10.3390/app10155383
APA StyleLee, C.-Y., & Lin, W.-C. (2020). Induction Motor Fault Classification Based on FCBF-PSO Feature Selection Method. Applied Sciences, 10(15), 5383. https://doi.org/10.3390/app10155383




