Local Phase-Amplitude Joint Correction for Free Surface Velocity of Hopkinson Pressure Bar
Abstract
:Featured Application
Abstract
1. Introduction
2. Principle
2.1. Propagation Characteristics of Elastic Stress Wave in Cylindrical Bar
2.1.1. Phase Velocity Curve in Bar
2.1.2. Group Velocity Curve
2.1.3. Relationship Between Normalized Frequency and Propagation Time
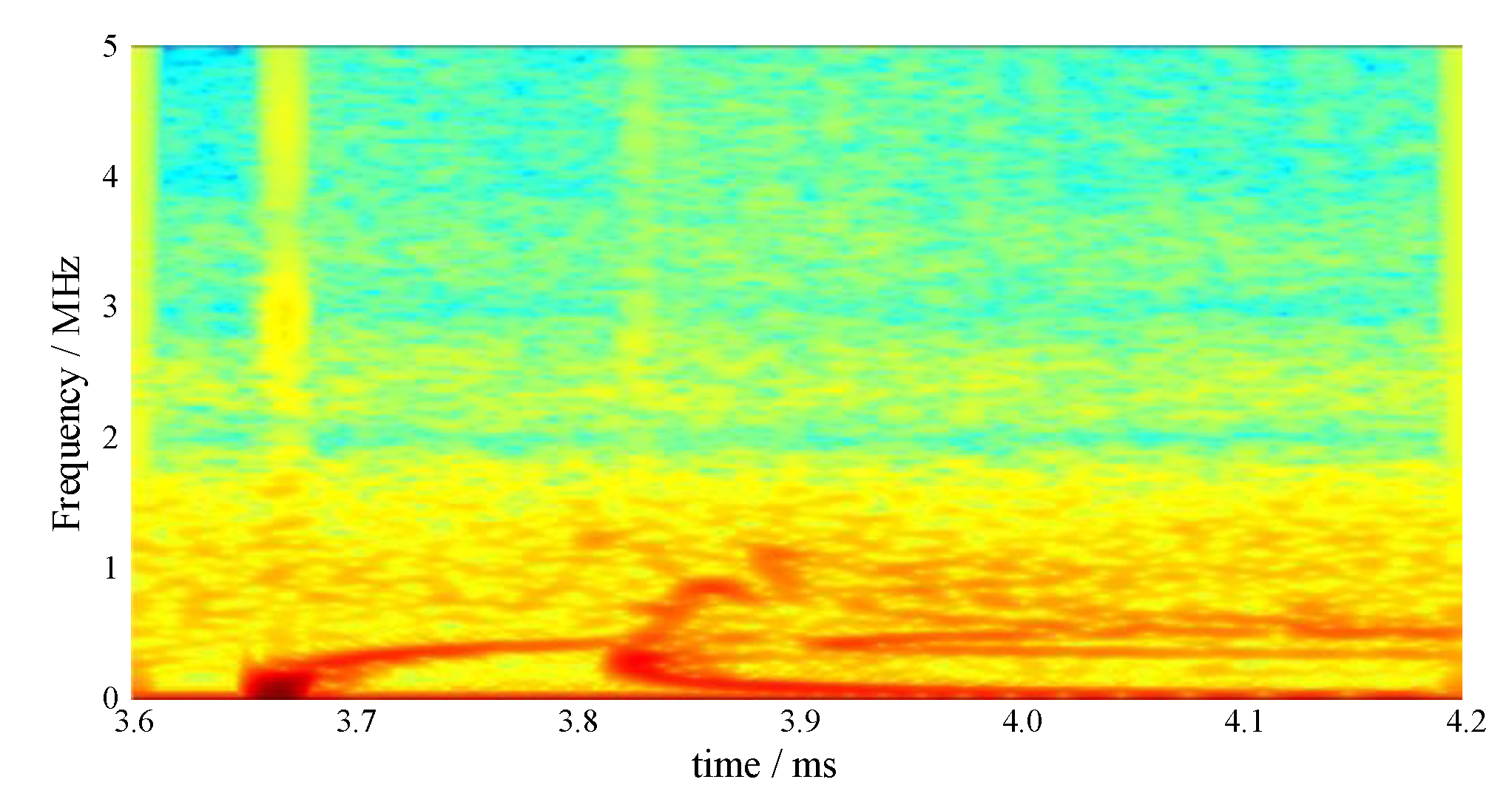
2.2. Propagation Mode Analysis Based on the Short-Time Fourier Transform
2.3. Proposed Local Phase-Amplitude Joint Correction Method
3. Results and Discussion
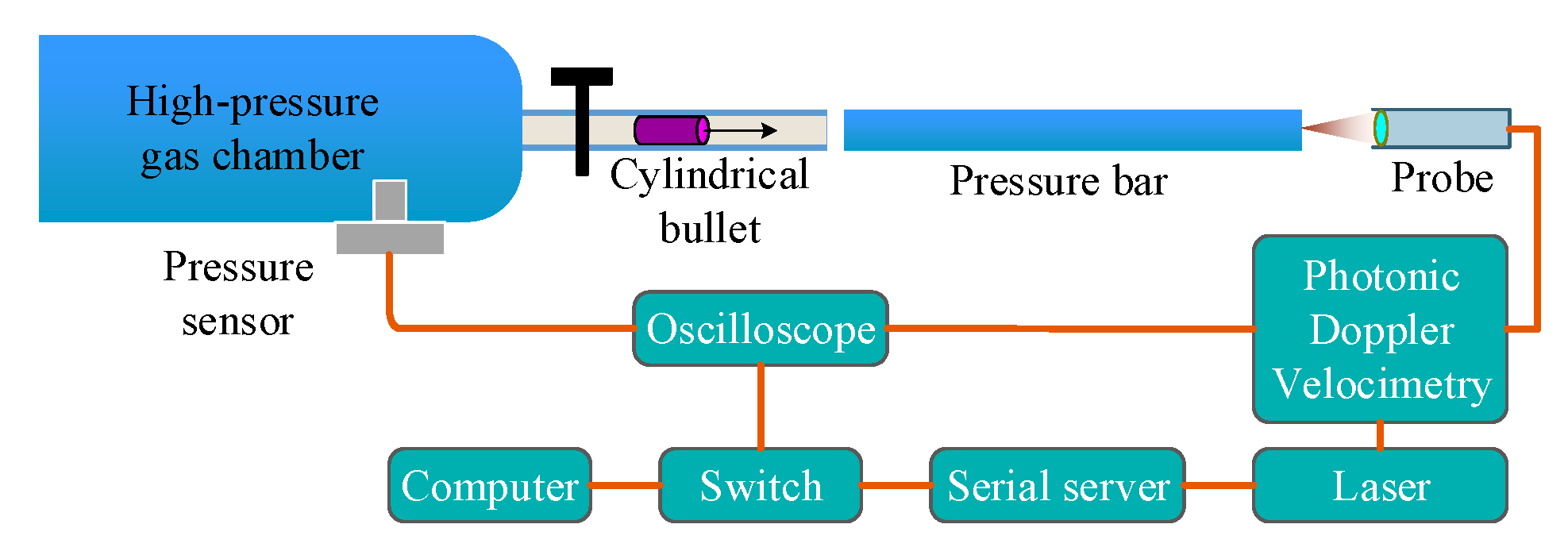
3.1. Setup of the Testing System
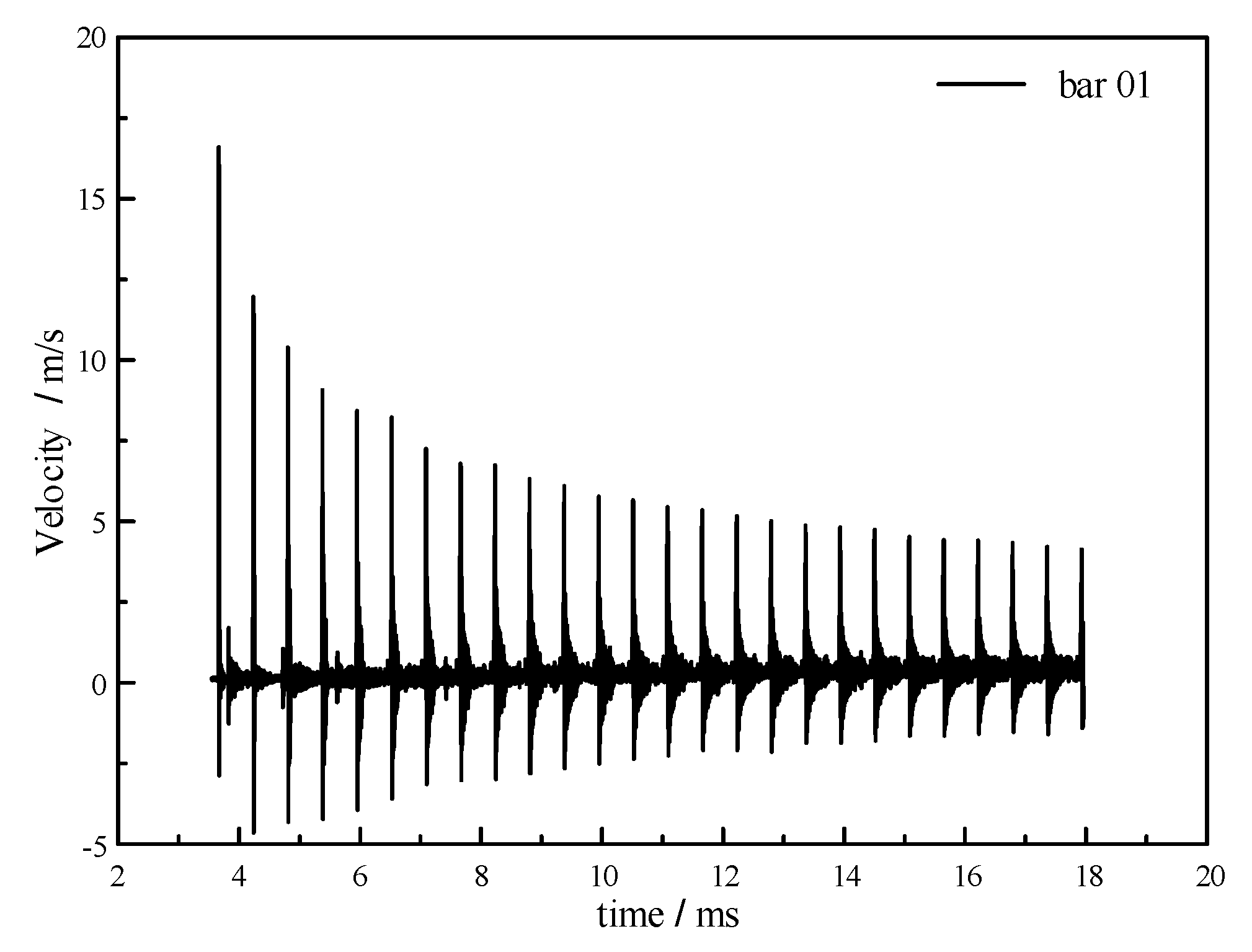
3.2. Preliminary Analysis of Experimental Signals
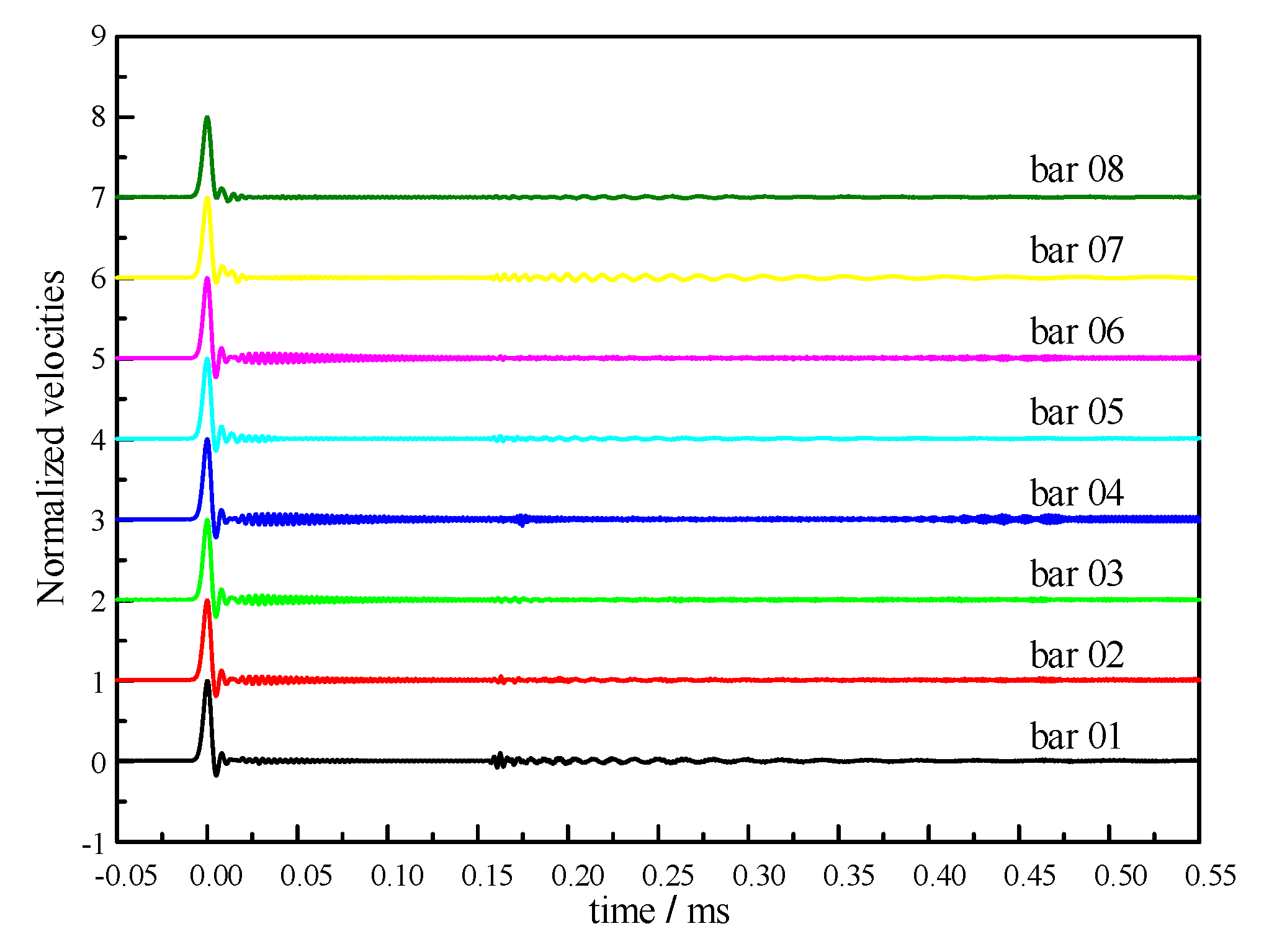
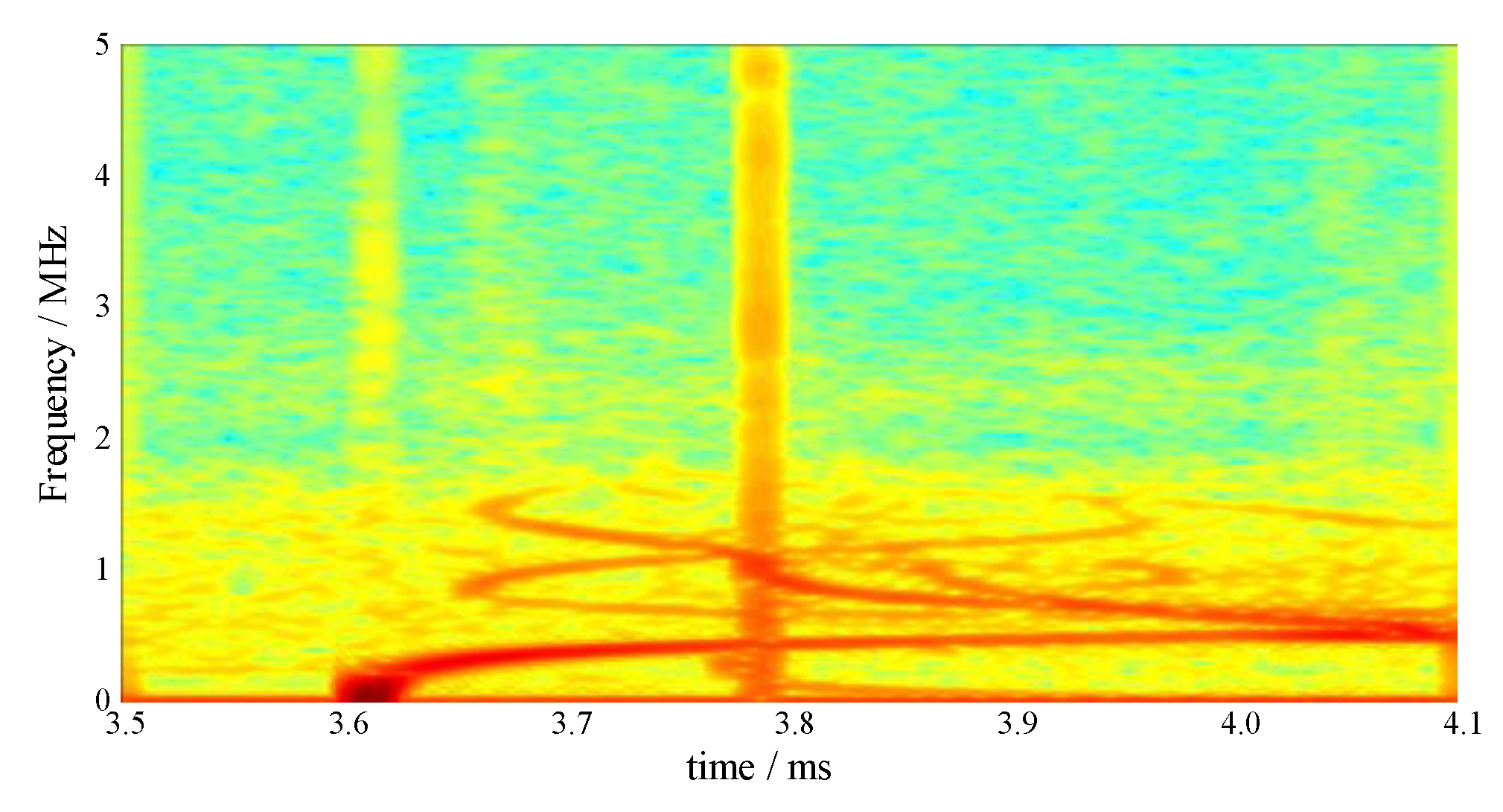
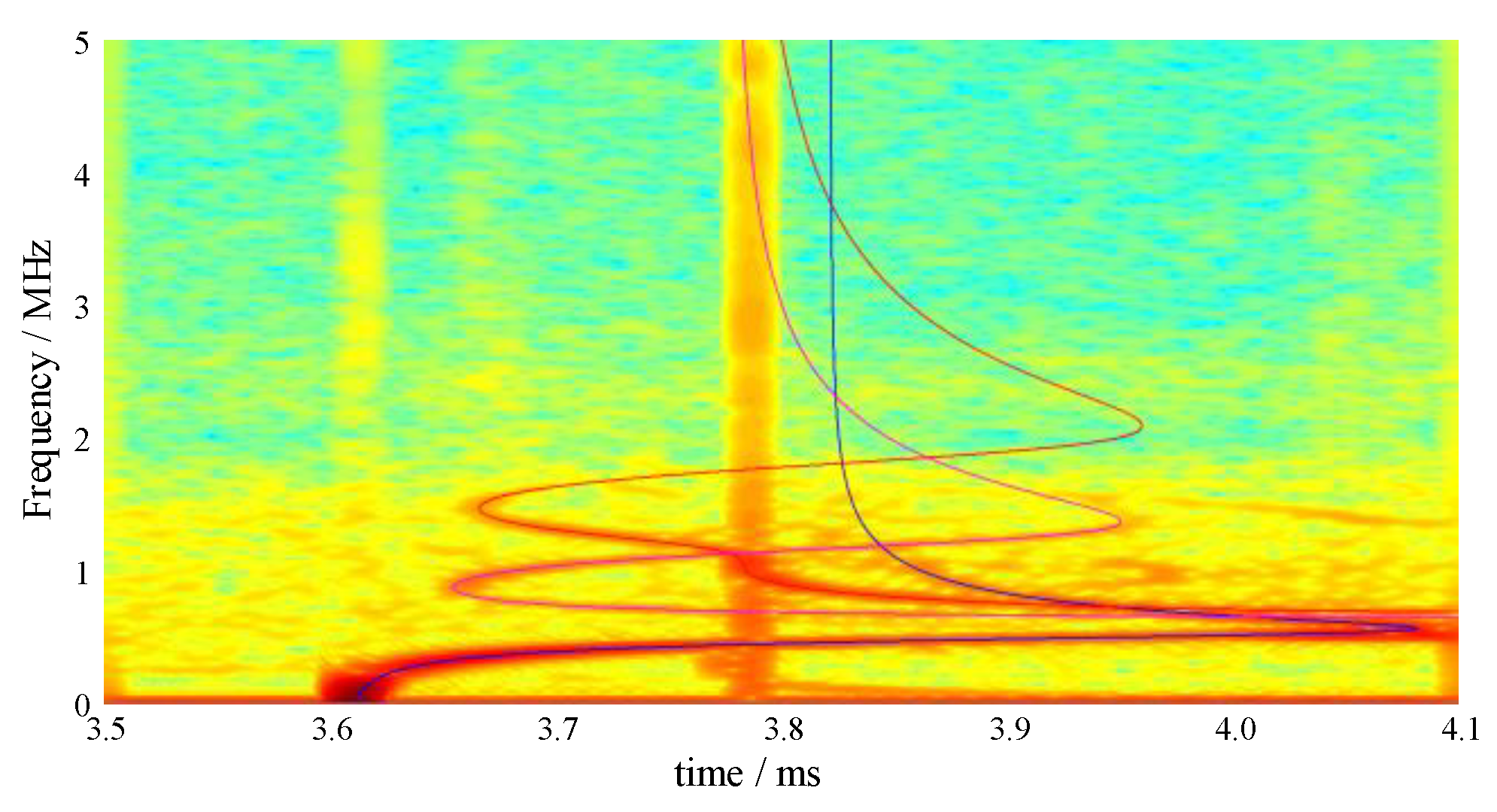
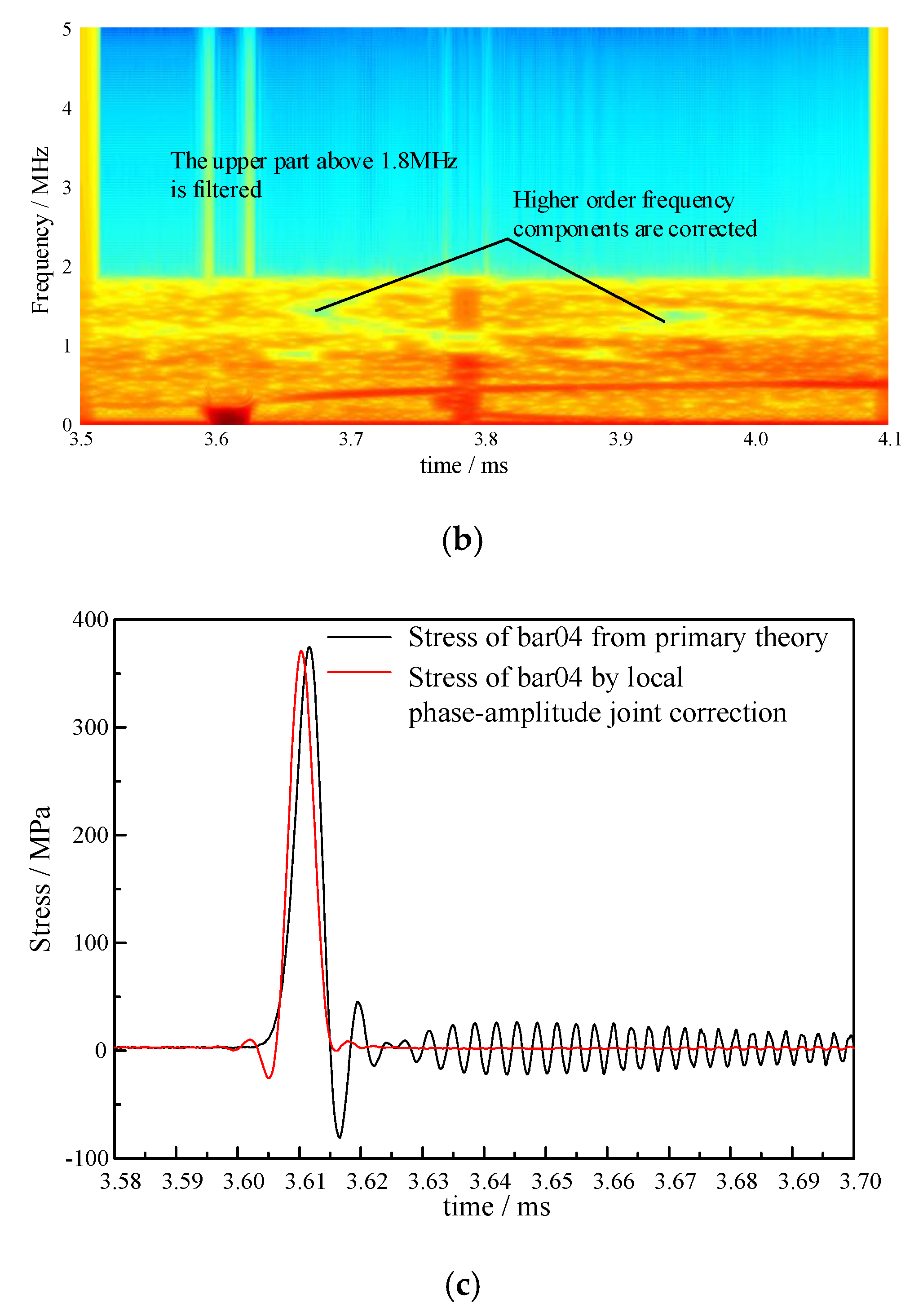
3.3. Propagation Modes Analysis
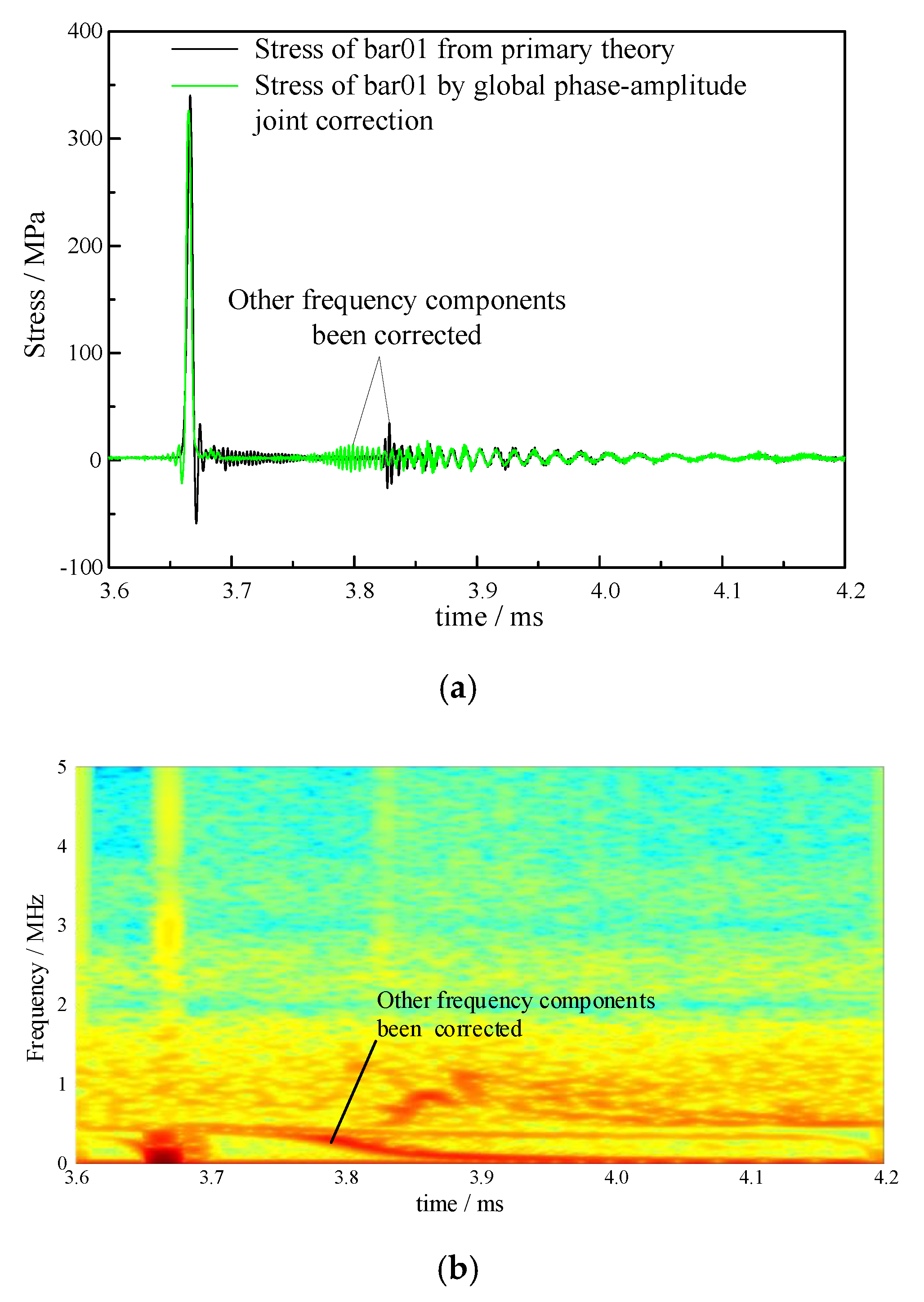
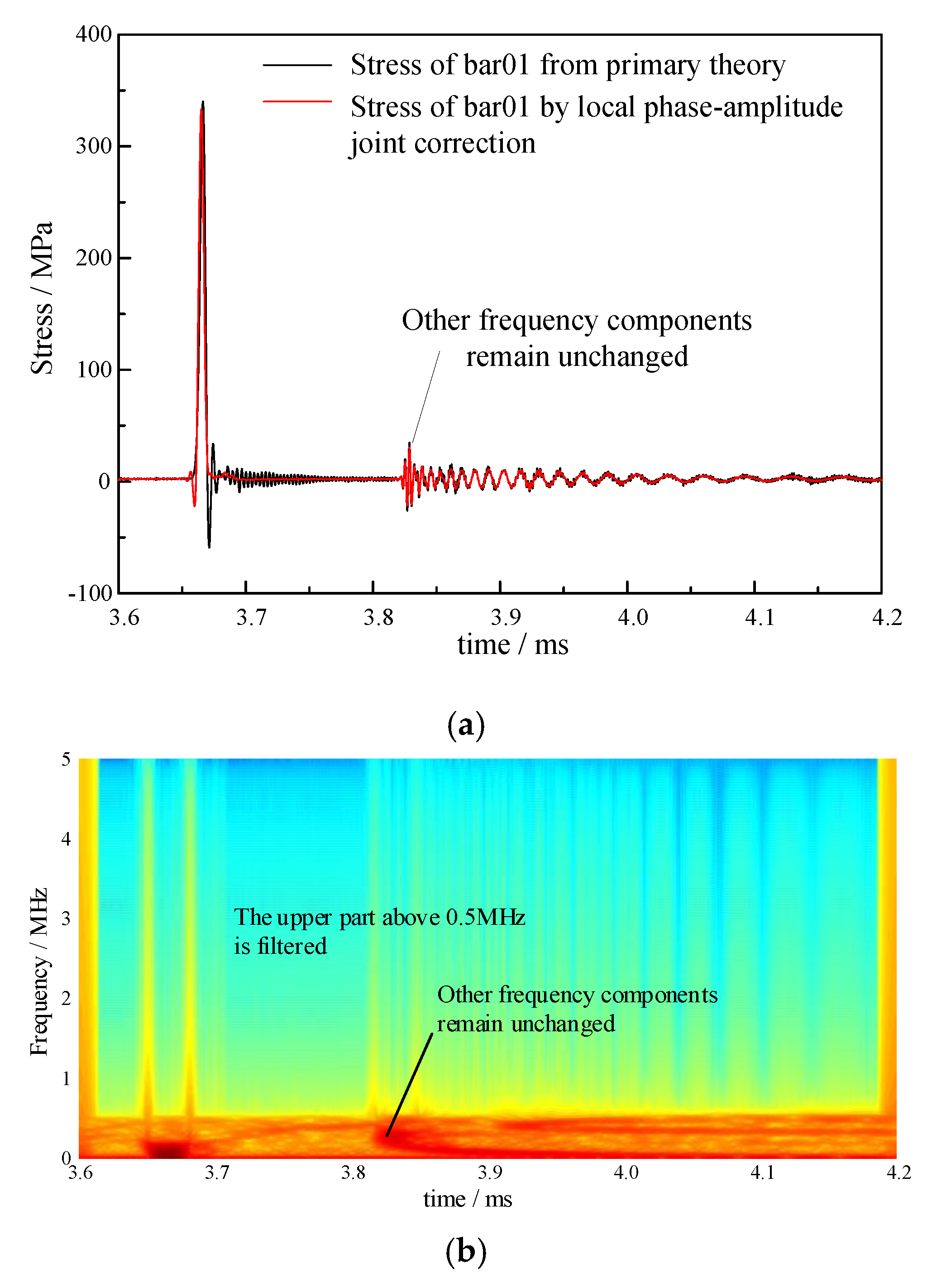
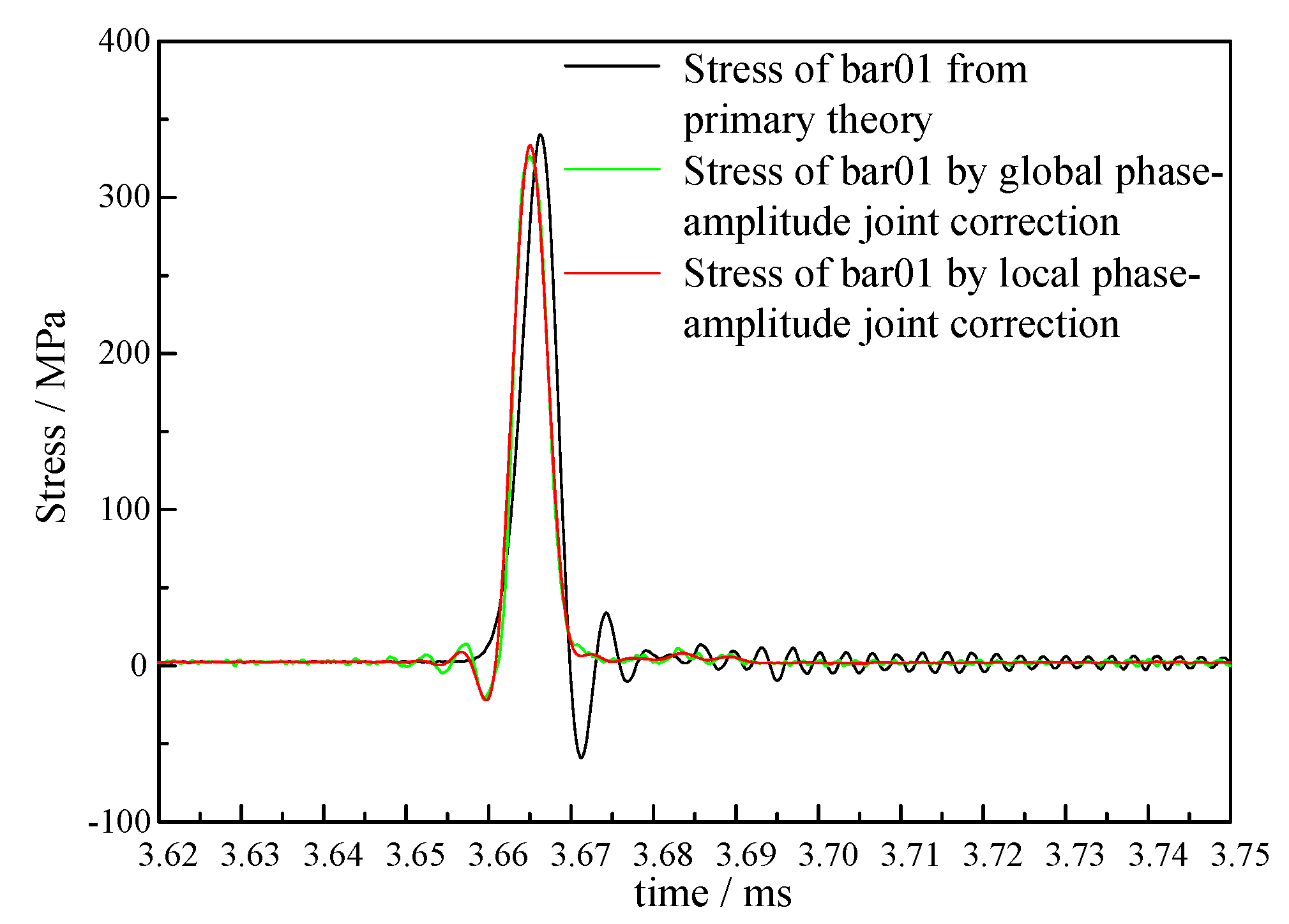
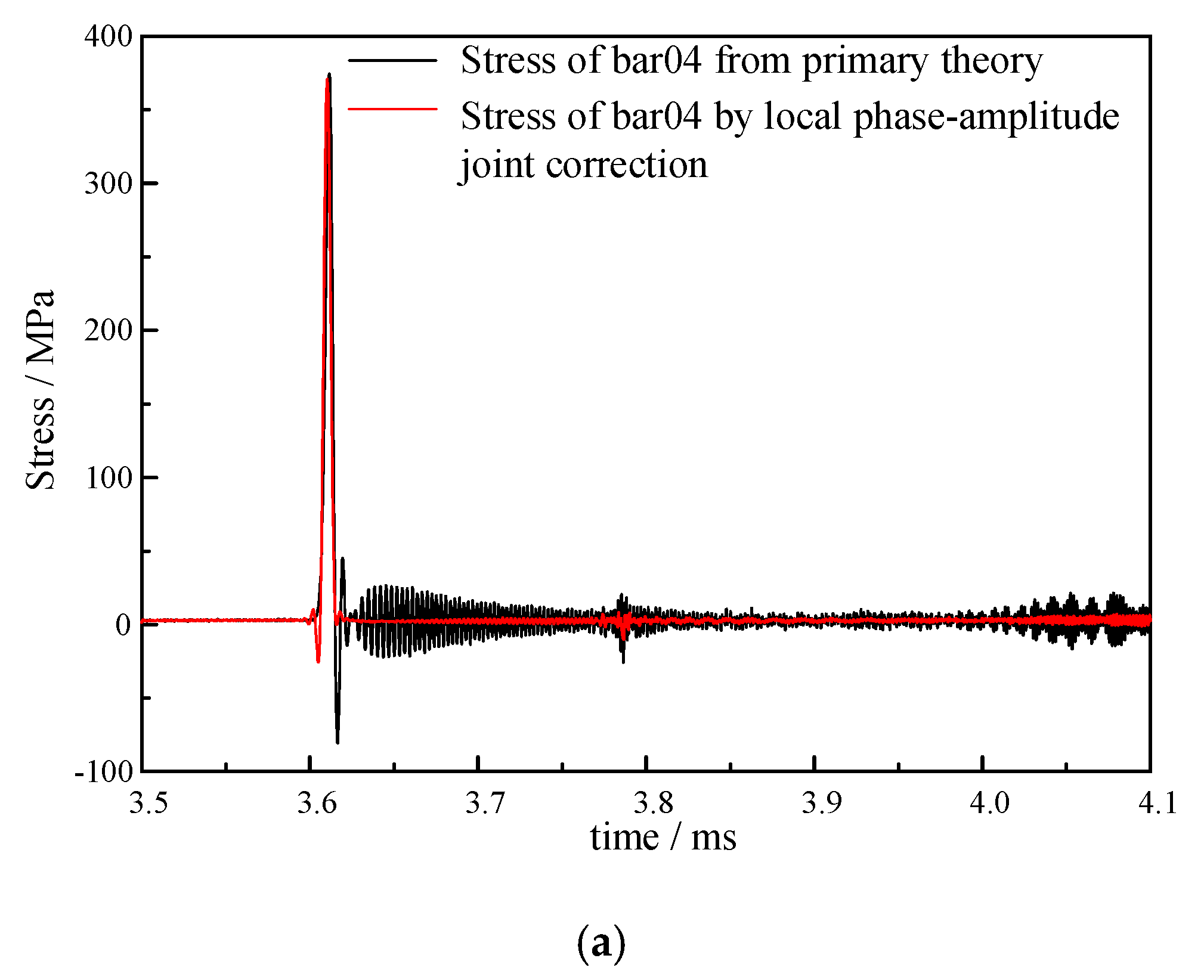
3.4. Local Phase-Amplitude Joint Correction
4. Conclusions
- (1)
- The propagation mode analysis method based on short-time Fourier transform is intuitive and clear and gives all the propagation modes of the axial elastic stress wave.
- (2)
- In the eight sets of pressure bars, the pressure bar 04 excited the first three orders of the propagation mode, while the stress waves in the remaining pressure bars propagated in the first-order mode.
- (3)
- The local phase-amplitude joint correction method only corrected the frequency component corresponding to the propagation mode excited in the pressure bars.
- (4)
- Testing experiments verify the feasibility of the correction method. The rising edges of the pressure bars 01 and 04 are corrected from 4.13 μs and 4.09 μs to 2.70 μs, respectively.
Author Contributions
Funding
Conflicts of Interest
References
- Hopkinson, B. A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1914, 213, 437–456. [Google Scholar]
- Cloete, T.J.; Nurick, G.N. Blast characterization using a ballistic pendulum with a centrally mounted hopkinson bar. Int. J. Prot. Struct. 2016, 7, 367–388. [Google Scholar] [CrossRef]
- Rigby, S.E.; Knighton, R.; Clarke, S.D.; Tyas, A. Reflected near-field blast pressure measurements using high speed video. Exp. Mech. 2020, 1–14. [Google Scholar] [CrossRef]
- Clarke, S.D.; Fay, S.D.; Warren, J.A.; Tyas, A.; Rigby, S.E.; Elgy, I. A large scale experimental approach to the measurement of spatially and temporally localised loading from the detonation of shallow-buried explosives. Meas. Sci. Technol. 2014, 26, 15001. [Google Scholar] [CrossRef]
- Davies, R.M. A critical study of the hopkinson pressure bar. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 240, 375–457. [Google Scholar]
- Hauser, F.E. Techniques for measuring stress-strain relations at high strain rates. Exp. Mech. 1966, 6, 395–402. [Google Scholar] [CrossRef]
- Yang, J.; Li, Y.; Zhang, D. Measuring technique of reflected blast wave pressure based on pressure bar and photonic doppler velocimeter. Acta Armamentarii 2017, 38, 1368–1374. [Google Scholar]
- Pochhammer, L. On the propagation velocities of small oscillations in an unlimited isotropic circular cylinder. J. Reine Angew. Math. 1876, 81, 324–326. [Google Scholar]
- Chree, C. The equations of an isotropic elastic solid in polar and cylindrical coordinates, their solution and application. Trans. Camb. Philos. Soc. 1889, 14, 250–369. [Google Scholar]
- Bancroft, D.; Jacobs, R.B. An electrostatic method of measuring elastic constants. Rev. Sci. Instrum. 1938, 9, 279–281. [Google Scholar] [CrossRef]
- Yew, E.H.; Chen, C.S. Experimental study of dispersive waves in beam and rod using fft. J. Appl. Mech. 1978, 45, 940–942. [Google Scholar] [CrossRef]
- Gorham, D.A. A numerical method for the correction of dispersion in pressure bar signals. J. Phys. E Sci. Instrum. 1983, 16, 477–479. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Frantz, C. Wave propagation in the split hopkinson pressure bar. J. Eng. Mater. Technol. 1983, 105, 61–66. [Google Scholar] [CrossRef]
- Gong, J.C.; Malvern, L.E.; Jenkins, D.A. Dispersion investigation in the split hopkinson pressure bar. J. Eng. Mater. Technol. 1990, 112, 309–314. [Google Scholar] [CrossRef]
- Lifshitz, J.M.; Leber, H. Data processing in the split hopkinson pressure bar tests. Int. J. Impact Eng. 1994, 15, 723–733. [Google Scholar] [CrossRef]
- Zhao, H.; Gary, G.; Klepaczko, J.R. On the use of a viscoelastic split hopkinson pressure bar. Int. J. Impact Eng. 1997, 19, 319–330. [Google Scholar] [CrossRef]
- Lee, C.K.B.; Crawford, R.C.; Mann, K.A.; Coleman, P.; Petersen, C. Evidence of higher pochhammer chree modes in an unsplit hopkinson bar. Meas. Sci. Technol. 1995, 6, 853–859. [Google Scholar] [CrossRef]
- Tyas, A.; Watson, A.J. A study of the effect of spatial variation of load in the pressure bar. Meas. Sci. Technol. 2000, 11, 1539–1551. [Google Scholar] [CrossRef]
- Tyas, A.; Pope, D.J. Full correction of first-mode pochammer-chree dispersion effects in experimental pressure bar signals. Meas. Sci. Technol. 2005, 16, 642–652. [Google Scholar] [CrossRef]
- Tyas, A.; Watson, A.J. An investigation of frequency domain dispersion correction of pressure bar signals. Int. J. Impact Eng. 2001, 25, 87–101. [Google Scholar] [CrossRef]
- Rigby, S.E.; Barr, A.D.; Clayton, M. A review of pochhammer-chree dispersion in the hopkinson bar. Proc. Inst. Civ. Eng. Eng. Comput. Mech. 2018, 171, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Yang, J. The Development of Fiber Displacement Interferometer and Its Applications. Master’s Thesis, University of Science and Technology of China, Hefei, China, 17 May 2012. [Google Scholar]

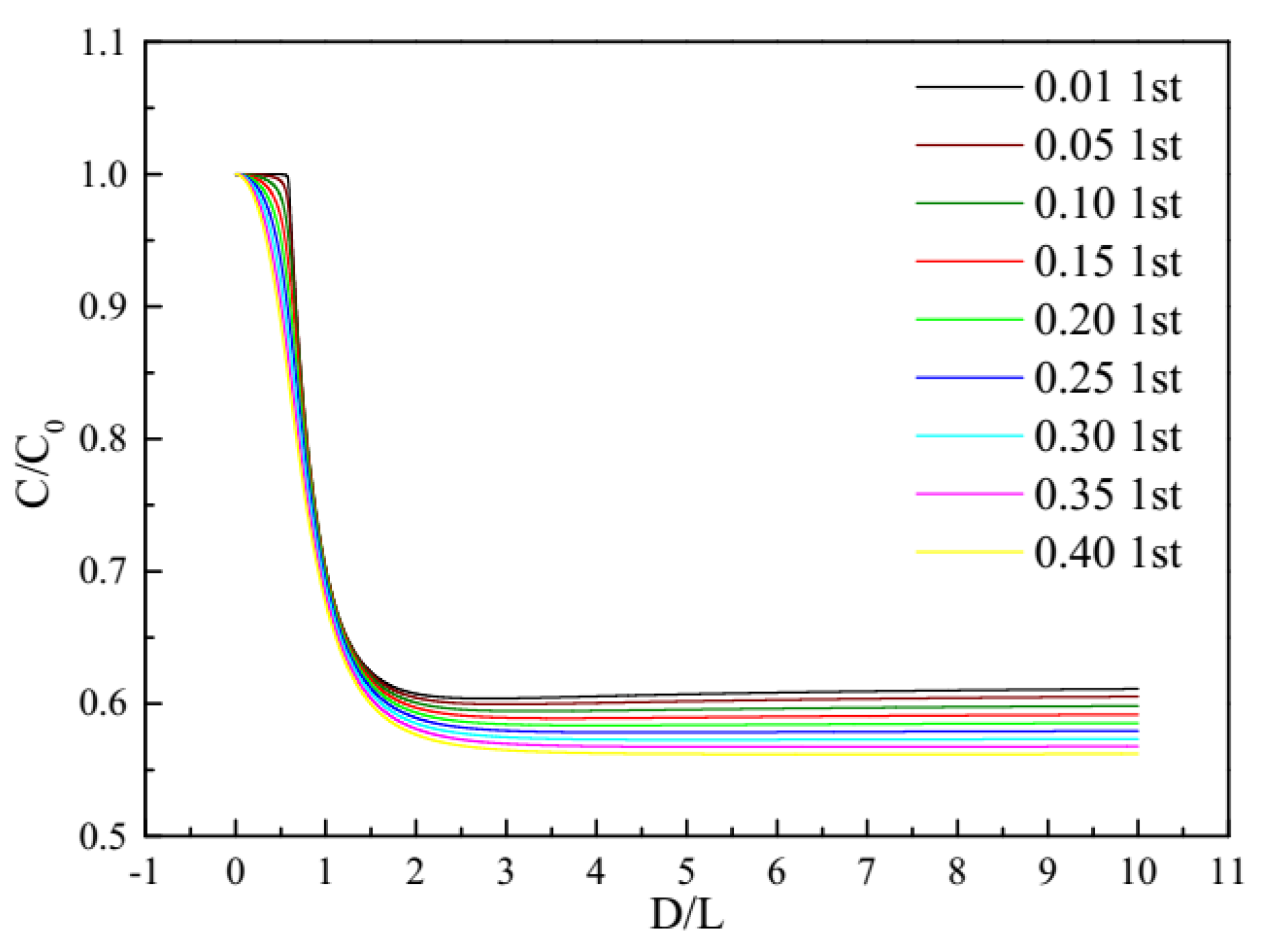
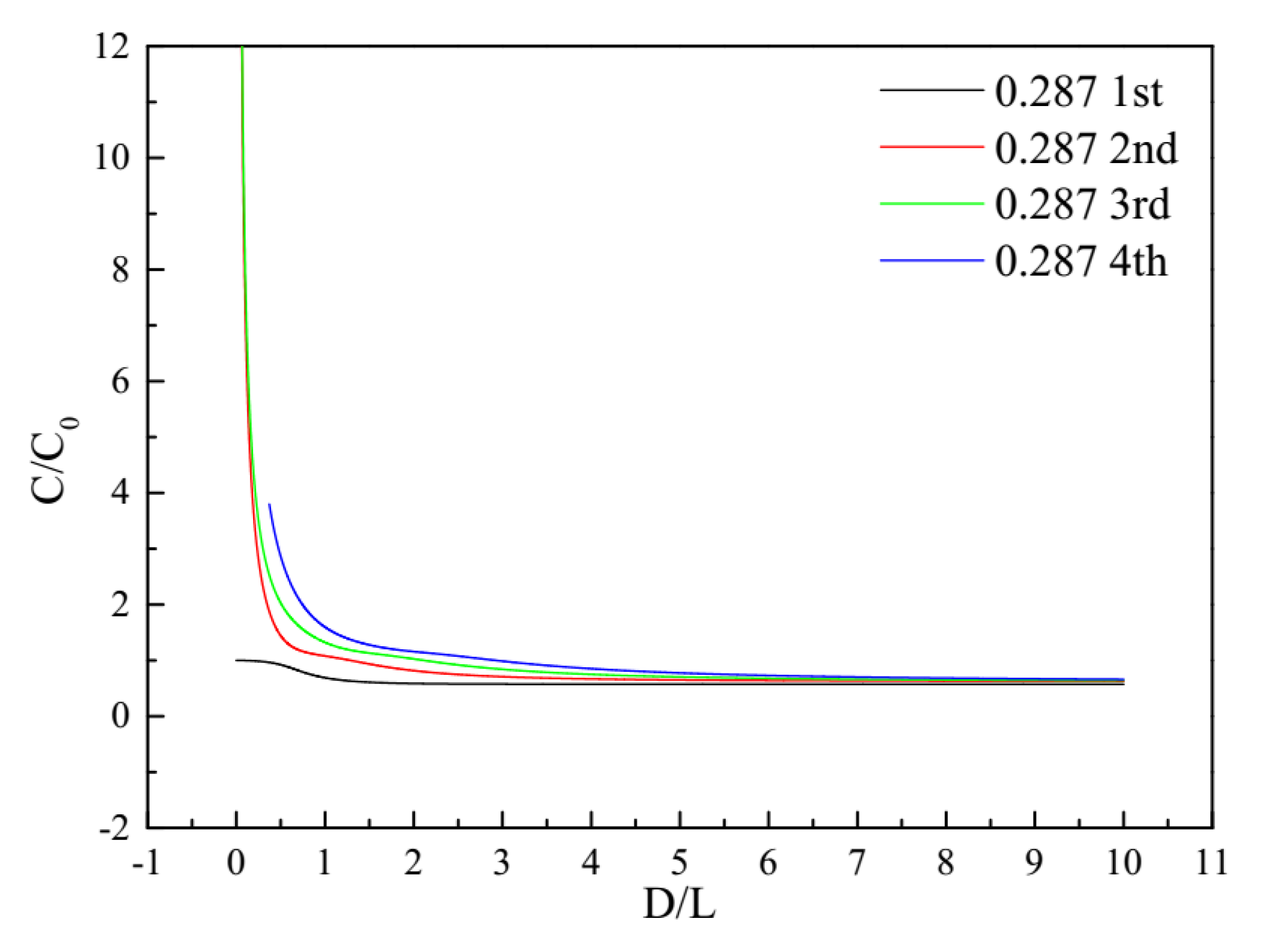
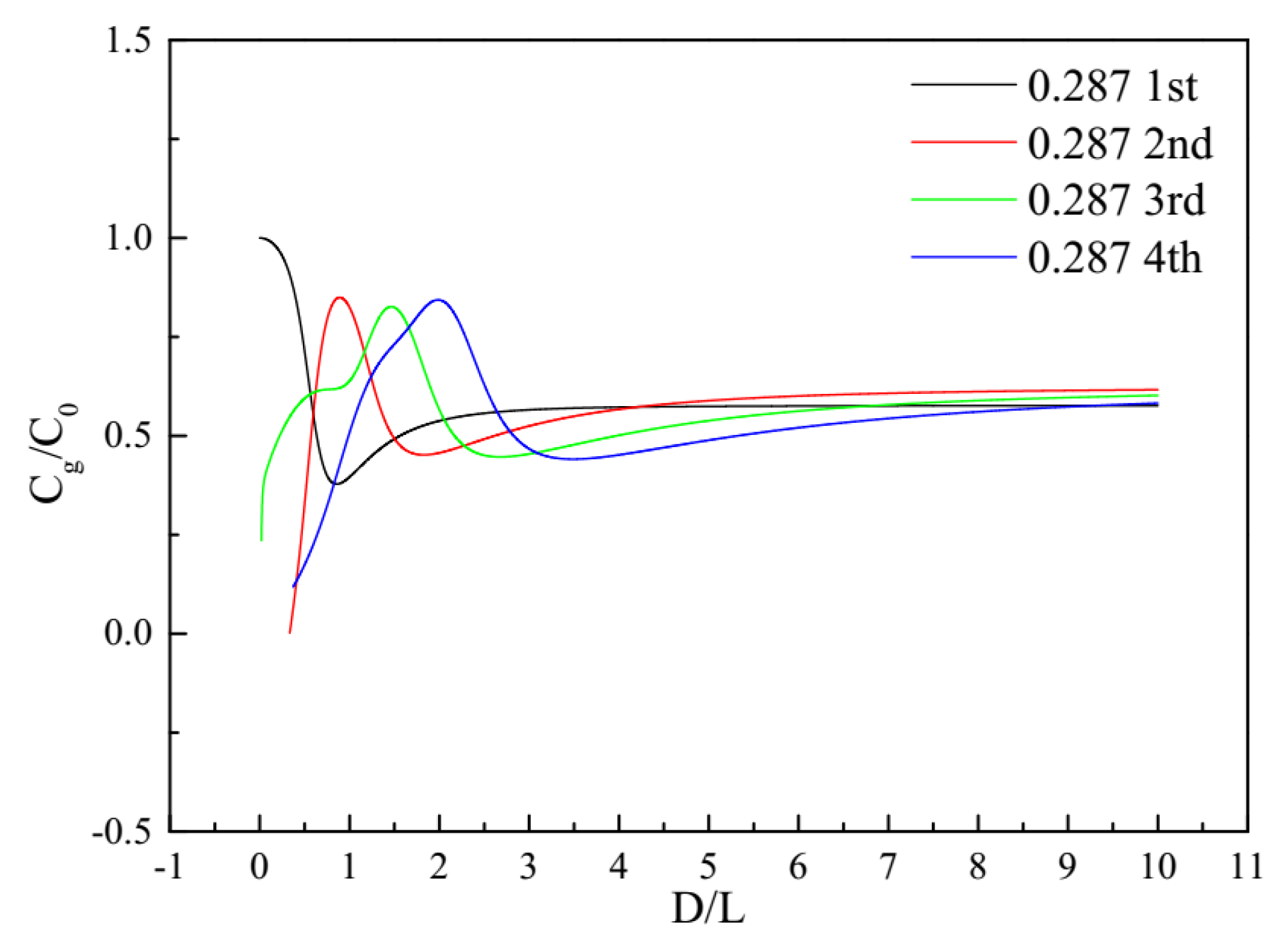
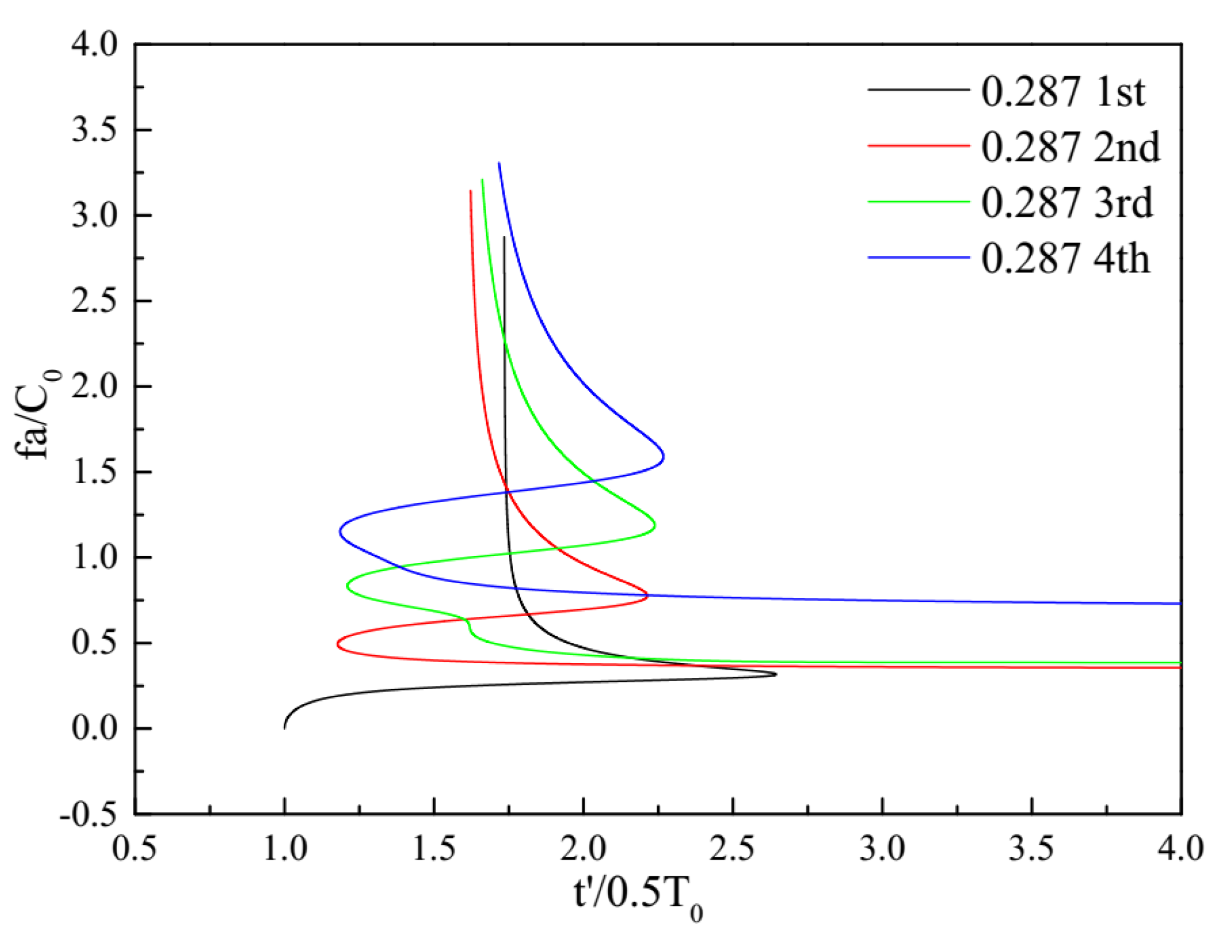


| Parameter | Definition |
|---|---|
| phase velocity | |
| group velocity | |
| longitudinal wave velocity | |
| wavelength | |
| wave number | |
| frequency | |
| angular frequency | |
| diameter of pressure bar | |
| radius of pressure bar | |
| Poisson’s ratio | |
| intermediate parameters | |
| intermediate parameters | |
| Young’s modulus | |
| modulus of rigidity | |
| intermediate parameters | |
| intermediate parameters | |
| composite function based on the Bessel function of the first kind |
| Order | Non-Dimensional Number | Peak Value | Valley Value | Asymptotic Value |
|---|---|---|---|---|
| First | 0 | 0.857 | 10 | |
| 1 | 0.378 | 0.576 | ||
| Second | 0.891 | 1.825 | 10 | |
| 0.850 | 0.452 | 0.616 | ||
| Third | 1.465 | 2.677 | 10 | |
| 0.826 | 0.447 | 0.602 | ||
| Fourth | 1.985 | 3.488 | 10 | |
| 0.843 | 0.441 | 0.583 |
| Number of Bar | Peak Time (ms) | Reflection Period (μs) | Conversion Coefficient (MPa/ms−1) | |
|---|---|---|---|---|
| 01 | 3.666 | 570.42 | 5.2595 | 20.51 |
| 02 | 3.394 | 571.08 | 5.2537 | 20.49 |
| 03 | 3.897 | 570.67 | 5.2577 | 20.51 |
| 04 | 3.612 | 570.46 | 5.2589 | 20.51 |
| 05 | 3.903 | 570.49 | 5.2591 | 20.51 |
| 06 | 3.902 | 570.29 | 5.2610 | 20.52 |
| 07 | 3.637 | 570.29 | 5.2610 | 20.52 |
| 08 | 4.036 | 570.65 | 5.2578 | 20.51 |
| Average | - | 570.54 | 5.2586 | 20.51 |
| standard deviation | - | 0.24 | 0.0022 | 0.01 |
| Order | Lower Frequency Limit /MHz | Upper Frequency Limit /MHz |
|---|---|---|
| First | 0 | 1.0 |
| Second | 0.6 | 1.5 |
| Third | 0.6 | 1.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; He, J.; Zhang, D.; Xu, H.; Shi, G.; Zhang, M.; Liu, W.; Zhang, Y. Local Phase-Amplitude Joint Correction for Free Surface Velocity of Hopkinson Pressure Bar. Appl. Sci. 2020, 10, 5390. https://doi.org/10.3390/app10155390
Yang J, He J, Zhang D, Xu H, Shi G, Zhang M, Liu W, Zhang Y. Local Phase-Amplitude Joint Correction for Free Surface Velocity of Hopkinson Pressure Bar. Applied Sciences. 2020; 10(15):5390. https://doi.org/10.3390/app10155390
Chicago/Turabian StyleYang, Jun, Junhua He, Dezhi Zhang, Haibin Xu, Guokai Shi, Min Zhang, Wenxiang Liu, and Yang Zhang. 2020. "Local Phase-Amplitude Joint Correction for Free Surface Velocity of Hopkinson Pressure Bar" Applied Sciences 10, no. 15: 5390. https://doi.org/10.3390/app10155390
APA StyleYang, J., He, J., Zhang, D., Xu, H., Shi, G., Zhang, M., Liu, W., & Zhang, Y. (2020). Local Phase-Amplitude Joint Correction for Free Surface Velocity of Hopkinson Pressure Bar. Applied Sciences, 10(15), 5390. https://doi.org/10.3390/app10155390




