Nondestructive Evaluation of Solids Based on Deformation Wave Theory

Abstract

The application of a recent field theory of deformation and fracture to nondestructive testing (NDT) is discussed. Based on the principle known as the symmetry of physical laws, the present field theory formulates all stages of deformation including the fracturing stage on the same theoretical basis. The formalism derives wave equations that govern the spatiotemporal characteristics of the differential displacement field of solids under deformation. The evolution from the elastic to the plastic stage of deformation is characterized by a transition from longitudinal (compression) wave to decaying longitudinal/transverse wave characteristics. The evolution from the plastic to the fracturing stage is characterized by transition from continuous wave to solitary wave characteristics. Further, the evolution from the pre-fracturing to the final fracturing stage is characterized by transition from the traveling solitary wave to stationary solitary wave characteristics. In accordance with these transitions, the criterion for deformation stage is defined as specific spatiotemporal characteristics of the differential displacement field. The optical interferometric technique, known as Electronic Speckle-Pattern Interferometry (ESPI), is discussed as an experimental tool to visualize those wave characteristics and the associated deformation-stage criteria. The wave equations are numerically solved for the elastoplastic stages, and the resultant spatiotemporal behavior of the differential displacement field is compared with the experimental results obtained by ESPI. Agreement between the experimental and numerical results validates the present methodology at least for the elastoplastic stages. The solitary wave characteristics in the fracturing stages is discussed based on the experimental results and dislocation theory.

1. Introduction

Structures collapse unexpectedly. Continuous application of external loads, even if their strength is considerably lower than the ultimate strength of the material, causes fractures. The current load level observed or associated deformation data is not reliable information to predict fracture. It is known that fracture is led by a defect and that defects grow in the scale level from the atomistic to macroscopic. Dislocations [1] are typical atomistic defects and their propagation is responsible for the deformation to evolve from the elastic to plastic regime. It is known that in the plastic regime the dislocations react to the stress field and lead to the generation of macroscopic defects. Egorushkin [2] formulates the dynamics of dislocation as a wave phenomenon. However, it is difficult to connect dislocation behaviors and macroscopically observable phenomena. In other words, on the one hand we know that the propagation of dislocation initiates plastic deformation. On the other hand, we cannot identify the initiation of plastic deformation as a macroscopically observable quantity, except as the yield point on the stress–strain curve. From the nondestructive testing (NDT) perspective, it is unrealistic to measure the stress-stain characteristics of test objects in the field. It is desirable to develop a methodology that allows us to diagnose the initiation of plastic deformation and the subsequent evolution of the deformation toward the final fracture.

One immediate problem in such methodological development is that prevailing deformation theories are phenomenological and, thereby, stage specific. Elastic theories [3,4,5] describe the stress strain relationship in the elastic regime. Most plastic deformation theories [6,7] describe plastic behavior by either mathematically modeling the constitutive relation in the plastic regime or formulating the plasticity based on the energy dissipation. Fracture [8] is treated as an independent phenomenon of deformation. This situation makes it difficult to describe the transition from one deformation regime to another.

In this work, we propose that the application of a recent field theory [9] of deformation and fracture can be a solution to the problem. Being based on the physical principle known as the local symmetry of theory [10,11,12] (See Appendix A), this theory has a mechanism to describe deformation and fracture on the same theoretical basis. It formulates all stages of deformation and fracture based on the wave equation derived from the equation of motion that governs the dynamics of a unit volume in a deforming object. Different stages of deformation are characterized by different forms of resistive force that the unit volume exerts in response to the external load. This difference in the resistive force alters some terms of the wave equation yielding different wave solutions. Details about the wave equation and wave solutions will be discussed later in this paper. In short, the elastic stage is represented by non-decaying longitudinal waves, the early stage of plastic deformation is by decaying longitudinal and transverse waves, the developed plastic stage (the pre-fracture stage) is by travelling solitary waves, and the fracturing stage is by standing solitary waves. In all stages, these waves carry the stress energy that is caused by the external load.

These forms of deformation waves in association with the corresponding deformation stages have been observed by several authors. In a tensile experiment of an aluminum alloy specimen, we [13] observed that a transverse displacement wave started to appear near the yield point and decayed towards the final fracture of the specimen. In refs. [14,15,16], the authors identified a solitary-wave like pattern in the displacement field of tensile loaded metal plate specimens and observed that the pattern becomes stationary when the specimen broke. Ref. [17] reports simlar observation of a solitary-wave like pattern in the displacement field for a cyclic loaded metal specimen. Ref. [18] explains these experimentally observed behaviors of the solitary-wave like patterns based on a Korteweg-de Vries (KdV)-type [19] solitary wave solution. The formation of solitary waves from non-solitary waves has also been reported. Ziv and Shmuel [20] discuss the coalescence of longitudinal and shear waves to form shock waves in soft materials. Lints [21] et al. discuss the formation of solitary waves in a carbon fiber reinforced polymer with non-solitary ultrasonic excitation.

The use of the above-mentioned, stage-specific behavior of deformation waves makes the present NDT unique. Various waves are widely used in conventional NDT methods. In these methods, a linear wave is typically applied to the test object as the input and the reflected or transmitted (the output) wave is monitored. The structural or mechanical properties of the object are diagnosed through analysis of the output wave based on a certain property of the wave. Acoustic imaging [22,23] identifies abnormality from the difference in the acoustic impedance, which alters the reflection coefficient for the input wave; hence, making a contrast in the output wave. Scanning Acoustic Microscopy [24,25] uses the interference between the input and reflected ultrasound waves to characterize the property of the subsurface region of a specimen. X-ray diffractometry [26,27] uses diffraction to find the lattice constant of the object material. In relatively new methods, solitary waves are also used as the input wave [28,29,30]. As a nonlinear wave, a solitary wave changes its wave form depending on the material’s property. This feature makes it possible to detect abnormality that linear input waves are unable to detect.

The present NDT algorithm is intrinsically different from these methods in the following sense. Instead of analyzing the output signal that results from a certain input wave, it analyzes the materials’ self-generated deformation waves. In other words, while conventional techniques analyze the material’s response to the input wave, the present method characterizes the material’s response to the applied load as a wave phenomenon. Thus, the observed wave exhibits the dynamics that governs the deformation behavior for the respective stages. By knowing the dynamics for each stage and the associated features of the deformation wave, we can diagnose the current status of deformation and its future trend.

Based on the stage-specific specific behaviors of the deformation wave, we have derived field theoretical criteria of deformation stages [31]. The criteria describe the spatiotemporal behavior of the displacement field in the elastic, plastic, pre-fracture, and fracture stages. In accordance with the above-mentioned form of the displacement wave, the displacement field expressed in the principal coordinates is rotation-free (because the wave is longitudinal) in the elastic stage, rotational (because the wave has transverse component due to the shear strain) in the plastic stage, localized in a small region (because the wave is a solitary wave), but dynamic in the pre-fracture stage, and localized in a small region and static (because the solitary wave becomes standing) in the fracture stage (more detailed descriptions of the characteristics of the displacement field will be discussed later in this paper).

In refs. [31,32], we demonstrated the deformation stage criteria based on these qualitative features of the displacement field. Using the optical interferometric technique known as Electronic Speckle-Pattern Interferometry (ESPI) [33,34,35], we continuously visualized the displacement field of metal plate specimens as the test machine applied a tensile load. With a pre-defined time interval small enough to resolve the stress-strain curve, the ESPI setup displayed the displacement field as full-field, two-dimensional optical interferometric image data. This arrangement is convenient for the diagnosis against the deformation stage criteria because the interferometric fringes, which represent contours of differential displacement components, readily exhibit the qualitative features of the displacement field (rotation-free etc). The diagnosed deformation stages were found to be consistent with the stress–strain characteristic obtained during the same tensile experiment.

In this study, the idea of using the ESPI fringe patterns is extended in order to visualize the wave characteristics of the displacement field. We analyzed the fringe pattern for several consecutive time steps in several deformation stages, and compared the spatiotemporal behavior of the displacement field against numerically generated deformation wave forms. Here, the numerical wave forms were obtained by solving the above-mentioned wave equation without assuming a constitutive model (except for the use of Poisson’s effect). It has been found that the visualized displacement field shows the same spatiotemporal behavior as the numerical wave forms. This allowed us to confirm the validity of the proposed wave-dynamics based diagnosis of deformation status via direct comparison with the wave forms. The aim of this paper is to report our observations in this investigation. The present paper is organized in the following way. Section 2 presents the gist of the field theory, including the deformation stage criteria and the explicit form of the wave equation for all the stages. Section 3 describes the experimental and numerical methods that were used in this study. Section 4 presents the experimental and numerical results and discusses the observations based on the wave dynamics. The semi-quantitative agreement between the experimentally observed displacement field and the numerical result obtained as solutions to the wave equation encourages further investigation of the subject toward the development of more quantitative NDT algorithm based on the present field theory.

2. Field Theory of Deformation and Fracture

2.1. Field Theory Overview

The present field theoretical approach has been derived from the concept of physical mesomechanics. Panin et al. [36] are the first to introduce the concept of mesoscopic scale-level to deformation dynamics and developed physical mesomechanics. In his paradigm of deformation, Panin characterizes plastic deformation as shear instability associated with the finite volume defined as the deformation structural element (DSE). When a deformation enters the plastic regime, the solid gains rotational degrees of freedom in the deformation dynamics and the DSE is the unit volume of material rotations. Applying the concept of the (gauge) field theory [11], he formulates dynamics of plastic deformation as the spatiotemporal behavior of the compensation (gauge) field that accommodates the rotational degree of freedom in the linear (non-rotational) elastic theory.

The present field theory is an extension of Panin’s paradigm to all stages of deformation and fracture. The wave characteristics of the deformation field for each stage of deformation can be summarized, as follows. In the elastic regime, the solid responds to the external force with elastic oscillatory motion that is transferred as a longitudinal wave known as the elastic compression wave. This dynamics is described by Young’s modulus and Poisson’s ratio. In the principal coordinate system, this leads to zero shear components in the distortion tensor. In the plastic regime two things happen. First, the material loses the shear stability, and consequently, the shear components become active in the distortion tensor. In the wave dynamics, this generates a transverse wave. Second, the material exhibits energy damping that is associated with the nonlinear behavior of the velocity filed. This makes the deformation irreversible, causing the longitudinal and transverse waves to decay. In the late stage of plastic deformation (the pre-fracture stage), the material’s elasticity becomes nonuniform. This induces dispersion (as the elasticity is not represented by a single constant), as is the case of the classical dispersion observed in a string on an elastic medium [37] or in a granular chain [38]. When the nonlinear term associated with the above-mentioned energy damping mechanism and the dispersion term of the wave equation satisfy a certain condition, the decaying wave takes the form of a solitary wave that travels carrying the stress energy. Fracture is characterized as the final stage of deformation where the material loses the mechanism to dissipate the stress energy in the form of traveling wave. Consequently, the mechanical wave, at this stage it is a solitary wave, becomes standing and unable to carry the stress energy. As a result, the stress becomes motionless at a certain location of the material. It follows that the generation of discontinuity becomes the only mechanism for the material to balance the energy.

Figure 1 illustrates the gist of the present field theory. The theory postulates that a solid at any stage of deformation possess local elasticity. The dynamics of local elasticity is represented by the deformation gradient tensor $U_{i,j}=\partial x_i^{\prime }/\partial x_j$ that describes Hooke’s law [39]. Here, $x_i^{\prime }$ and $x_j$ represent the coordinates of a reference point, expressed with the local coordinate system, after and before the deformation occurs, respectively. Hooke’s law is orientation preserving [4], because the applied force and the resultant stretch or compression are parallel to each other. In other words, it describes translational dynamics. Continuum mechanics extends Hooke’s law by expressing the compression (stretch) in orthogonal directions to the applied tensile (compressive) force with a Poisson’s ratio. The deformation in the orthogonal directions are parallel to the corresponding orthogonal axis, and hence the dynamics is still translational. The three elliptical shapes in Figure 1 represent three segments inside the same solid object that undergo elastic deformation in their own orientation. Being a tensor describing an orientation preserving phenomenon, the deformation gradient tensor for one segment cannot describe other segments unless they are oriented in the same direction. Figure 1 illustrates the situation, where the three elastic segments are not oriented in the same direction. This means that, in this situation, the elasticity of the three segments cannot be described by a common (global) coordinate system.

Consider how we can describe the elasticity of all the segments commonly with a global coordinate system. A solution is that we align all of the segments to the same orientation by introducing an additional field. This type of field is referred to as a connection (gauge) field [11], as they logically “connect” local dynamics. We can incorporate the dynamics that are associated with the connection field by considering the effect as a potential [11]. In Figure 1, “Potential A” represents this potential. In other words, we incorporate the dynamics associated with difference in the actual orientation among the segments into the effect of the potential and interpret that the three segments are experiencing elastic deformation at the global level. In this fashion, we can formulate the nonlinearity in the plastic regime by finding the dynamics that the connection field obeys. Note that the irreversibility of plastic deformation is not formulated by the connection field. Instead, it is represented by the energy dissipative part of the dynamics of the connection field. By applying the Lagrangian formalism to the dynamics of the connection field, a set of field equations that are discussed in the next section are derived.

2.2. Field Equations

The detailed procedure to derive the field equations is described elsewhere [9,40,41]. In short, it can be described as follows. The first step is to find the Lagrangian associated with the potential $\mathbf{A}$. As clear from its role to rotate the local segments so that they are all aligned in a common orientation and, therefore, the dynamics can be formulaically expressed by Hooke’s law, $\mathbf{A}$ has a dimension of displacement. In general, Lagrangian takes the form of kinetic energy minus potential energy. In the present case, it is natural to interpret that the kinetic energy is associated with the temporal derivative (the velocity) of $\mathbf{A}$. On the other hand, the potential energy depends on the type of the dynamics, as will be discussed below for elasto-plastic dynamics and fracture dynamics. The second step is to derive the field equations by using the Lagrangian in the Euler-Lagrangian equation of motion for the given dynamics. The active terms in the Euler-Lagrangian equation of motion also depends on the type of the dynamics that the system experiences.

2.2.1. Elasto-Plastic Dynamics

A rigorous analysis that is based on the gauge theoretical approach identifies the Lagrangian density for the elasto-plastic dynamics, as follows.

$${\mathcal{L}}_{ep}=\frac{\rho v^2}{2}-\frac{G{\omega }^2}{2}+\frac{G}{c}{j}^0{A}_0+G{j}^i{A}_i$$

(1)

Here, G is the shear modulus, $c=\sqrt{G/\rho }$ is the phase velocity of the wave characteristics, and $j^0$ and $j^i$ are the temporal and spatial components of the charge of symmetry, respectively. $\mathit{v}$ and $\mathit{\omega }$ are related to $\mathit{A}$, as follows.

$$\begin{array}{ccc}\hfill \mathit{v}& =& \dot{\mathit{A}}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\omega }^k& =& \frac{\partial A^j}{\partial x^i}-\frac{\partial A^i}{\partial x^j},\hfill \end{array}$$

(3)

Here, indexes $i,j,k$ represent the spatial coordinate variables.

The Euler–Lagrangian equation of motion in this case is given as follows.

$${\partial }_t\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_t{A}_{\mu }\right)}\right)+{\partial }_x\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_x{A}_{\mu }\right)}\right)-\frac{\partial \mathcal{L}}{\partial A_{\mu }}=0$$

(4)

where $\mu =t,x,y,z$. Substitution of Equation (1) into Equation (4) yields the following field equations.

$$\begin{array}{ccc}\hfill \nabla ·\mathit{v}& =& -j^0\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill \nabla \times \mathit{\omega }& =& -\frac{\rho }{G}\frac{\partial \mathit{v}}{\partial t}-\mathit{j}\hfill \end{array}$$

(6)

Multiplication of G on both-hand sides allows us to rewrite Equation (6) in the following form.

$$\rho \frac{\partial \mathit{v}}{\partial t}=-G(\nabla \times \mathit{\omega })-G\mathit{j}$$

(7)

The left-hand side of Equation (7) is in the form of mass times acceleration. Thus, Equation (7) can be interpreted as an equation of motion. The first and second terms on the right-hand side of Equation (7) can be interpreted as the transverse (shear) force and longitudinal force acting on the unit volume that is represented by density $\rho$ (see Chapter 5 of ref. [9]). Analysis indicates that the longitudinal force takes the following forms in the pure elastic and pure plastic dynamics, respectively.

$$\begin{array}{ccc}\hfill G{\mathit{j}}_e& =& -(\lambda +2G)\nabla (\nabla ·\mathit{\xi })\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill G{\mathit{j}}_p& =& {\sigma }_0\rho (\nabla ·\mathit{v})\mathit{v}\hfill \end{array}$$

(9)

Here, $\lambda$ is the Lamé’s first parameter, ${\sigma }_0$ is a material constant (See Chapter 5 of ref. [9]), $\mathit{\xi }$ is the displacement vector. In Appendix B, conceptual images of the shear force that are represented by $G\nabla \times \mathit{\omega }$ and the longitudinal fore represented by $(\lambda +2G)\nabla (\nabla ·\mathit{\xi })$ are illustrated. ($\mathit{\xi }$ appearing on the right-hand side of Equation (8) is the displacement vector associated with elastic force law and $\mathit{v}$ on the right-hand side of Equation (9) is the temporal derivative of vector potential $\mathit{A}$ whose dimension is displacement. Strictly speaking, the physical meaning of displacement $\mathit{A}$ is different from $\mathit{\xi }$. However, recent theoretical consideration indicates that, formulaically, we can replace $\mathit{A}$ with $\mathit{\xi }$ and interpret it as the total displacement vector (see Appendix C). Hereafter in this paper, $\mathit{\xi }$ is used to represent the displacement vector and $\mathit{v}=\dot{\mathit{\xi }}$).

Equations (8) and (9) indicate that the form of the longitudinal force term differentiates plastic deformation from elastic deformation. When the deformation is elastic, the longitudinal force is proportional to the differential displacement $\nabla ·\mathit{\xi }$, which is interpreted as the three-dimensional stretch or compression of a unit volume. When the deformation is plastic, the longitudinal force is proportional to the velocity through a variable coefficient $(\nabla ·\mathit{v})$. This relation can be interpreted as the proportionality is not connected by a constant but a variable coefficient. These two longitudinal forces are interpreted as material’s resistant force; with the elastic dynamics the unit volume resists the external force exerted by the neighboring unit volume via elastic force (8), and with the plastic dynamics the unit volume resists the external force via the velocity damping force (9). The former force induces traveling waves and the latter force causes the wave to decay. More will be discussed regarding the wave dynamics below.

2.2.2. Fracture Dynamics

The Lagrangian for the fracture dynamics is as follows.

$${\mathcal{L}}_{ep}=\frac{\rho v^2}{2}-\frac{G{\omega }^2}{2}+\frac{G}{c}{j}^0{A}_0+G{j}^i{A}_i+\frac{E}{2}{\left({\partial }_{x_s}^2\xi \right)}^2\left(\delta x_s\Delta x_s\right)$$

(10)

As compared with Lagrangian density (1), expression (10) has the extra term at the end of the right-hand side. This term represents the potential energy that is associated with the secondary spatial derivatives of displacement. Because the first-order derivative of displacement is strain, this term represents the potential energy associated with the spatial gradient of the strain. In the pre-fracturing stage, deformation becomes so nonuniform that the differential strain generates potential energy. In other words, this term represents how nonuniform the deformation field becomes.

In this case, since the Lagrangian density has a term depending on the second-order spatial differential term, the Euler–Lagrangian equation of motion has the extra term.

$${\partial }_t\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_t{A}_{\mu }\right)}\right)+{\partial }_x\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_x{A}_{\mu }\right)}\right)-{\partial }_{xx}\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_{xx}{A}_{\mu }\right)}\right)-\frac{\partial \mathcal{L}}{\partial A_{\mu }}=0$$

(11)

Tensile experiments [14,15,16,17] indicate that under the pre-fracture condition, $(\nabla ·\mathit{v})$ is one-dimensional and oriented at approximately 45${}^{\circ }$ to the tensile axis. Under the one-dimensional condition, the substitution of Equation (10) into Equation (11) yields the following field equation corresponding to (7).

$$\rho \frac{\partial \mathit{v}}{\partial t}=-G(\nabla \times \mathit{\omega })\frac{\lambda +2G}{\rho }\frac{d{\xi }_s}{d{x}_s}-{\sigma }_0\rho \frac{d{v}_s}{d{x}_s}{v}_s-\left(E\delta x_s\Delta x_s\right)\left({\partial }_{x_s}^4\xi \right)$$

(12)

Here, $x_s$ is the axis set along the one-dimensional $(\nabla ·\mathit{v})$. Accordingly, $d{\xi }_s/d{x}_s$ and $d{v}_s/d{x}_s$ in the first and second terms on the right-hand side are the one-dimensional form of $(\nabla ·\mathit{\xi })$ and $(\nabla ·\mathit{v})$ appearing in Equations (8) and (9), respectively. It is reasonable to assume that a fracturing unit volume does not exert elastic resistant force proportional to the volume expansion. When the volume is about to fracture, the resistant force does not increase as the volume stretches. Instead, the surrounding unit volumes that border the fracturing unit volume at $x_s$ and $x_s+\Delta x_s$ exert elastic force proportional to the local stretch occurring within the small region expressed by $\delta x_s$ (in other words, the strain energy is associated with the differential strain, not strain. See Figure 2 and the associated text). The third term on the right-hand side of Equation (12) represents this force. Thus, we can set the first term on the right-hand side of Equation (12) to null and rewrite the equation, as follows.

$$\rho \frac{\partial \mathit{v}}{\partial t}=-{\sigma }_0\rho \frac{d{v}_s}{d{x}_s}{v}_s-\left(E\delta x_s\Delta x_s\right)\left({\partial }_{x_s}^4\xi \right)$$

(13)

As will be discussed later in this paper this assumption is consistent with the experiment.

2.3. Conditions for Deformation Stages and Wave Equations

2.3.1. Linear Elastic Stage

When the deformation dynamics is linear elastic, Hooke’s law and Poisson’s effect are the only governing laws. Under this condition, the dynamics can be expressed in one coordinate system for the entire object. In terms of the concept that is depicted by Figure 1, there is no distinction between the global and local coordinate systems. In this situation, rotation $\mathit{\omega }$ represents rigid-body rotation, as defined by continuum mechanics. The entire entity (in the present context the block for which stress and strain are argued) undergoes a common rotation. Therefore, its spatial dependence is null. The force law is described by means of elastic force proportional to the local stretch or compression. Thus, we can express the linear elastic condition, as follows.

$$\begin{array}{ccc}\hfill \nabla \times \mathit{\omega }& =& 0\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill G\mathit{j}& =& G{\mathit{j}}_e=-(\lambda +2G)(\nabla ·\mathit{\xi })\hfill \end{array}$$

(15)

When the principal axis coordinate system is used to express the dynamics, the corresponding stress and strain tensors are diagonal. They have only normal components and all shear components become null. This is contrastive to the elasto-plastic dynamics, as discussed in the following section. In Appendix D, a short argument is made to show that the same physical elastic deformation raises shear components in the stress and strain tensors when a non-principal axis coordinate system is used.

2.3.2. Elasto-Plastic Stage

The $\nabla \times \mathit{\omega }$ term in field Equation (6) represents shear elastic force. When this force is active, the deformation becomes nonlinear at the global level. Accordingly, in principle, we can define a nonlinear elastic condition. However, tensile experiments [13] indicate that, when the deformation shows a nonlinear behavior represented by $\nabla \times \mathit{\omega }\ne 0$ (the shear component becomes non-zero when expressed in the principal coordinate system), the stress–strain curve exhibits irreversible stretch. Thus, it is reasonable to combine the nonlinear elasticity and plasticity. Accordingly, we express the elasto-plastic condition, as follows.

$$\begin{array}{ccc}\hfill \nabla \times \mathit{\omega }& \ne & 0\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill G\mathit{j}& =& G{\mathit{j}}_p={\sigma }_0\rho (\nabla ·\mathit{v})\mathit{v}\hfill \end{array}$$

(17)

The meaning of condition (16) is straightforwardly understood by recalling that Hooke’s law is orientation preserving, as mentioned earlier in this paper. When different blocks start to undergo linear elastic deformation in their own orientations, as schematically illustrated in Figure 1, it becomes impossible to describe the dynamics at the global level based on an orientation-preserving force law. This is when the vector potential $\mathit{A}$ plays its role as the orientation aligner. Referring to Figure 1, we can argue $\nabla \times \mathit{\omega }$, as follows. Assume that the plane that is illustrated in Figure 1 is the $xy$ plane of a Cartesian coordinate system. The rotation vector $\mathit{\omega }$ for each of the three blocks has only a z component. Under this situation, with the negative sign in front, the force term $-G\nabla \times \mathit{\omega }$ in equation of motion (7) can be interpreted as the elastic resistive force that the material exerts at the boundary of two neighboring unit volumes (see Figure A2a) to oppose the rotational deformation. This resistive force has in-plane components, as shown on the right-hand side of Equation (18), because the rotations that the force opposes are around an out-of-plane axis.

$$\nabla \times \mathit{\omega }=\frac{\partial {\omega }_z}{\partial y}\widehat{i}-\frac{\partial {\omega }_z}{\partial x}\widehat{j}$$

(18)

While condition (16) illustrates the non-linear elastic resistive behavior of plasticity, condition (17) illustrates the linear energy-dissipative behavior of plasticity. Being proportional to the particle velocity $\mathit{v}$, it represents that the material exerts a velocity-damping, longitudinal force as an energy dissipative resistive force. Importantly, the damping coefficient $(\nabla ·\mathit{v})$ is a variable depending on the divergence of the particle velocity vector field. The quantity $(\nabla ·\mathit{v})$ can be interpreted as the rate of the local volume expansion. This variable nature of the damping coefficient has a significant meaning in the late stage of plastic deformation. The higher the volume expansion rate the greater the damping effect. This causes the self-driven nature of the evolution to fracture at this stage of deformation; the higher the volume expansion rate, the more energy dissipative the dynamics becomes. Hence, this makes the energy balance with the external load tend toward irreversible energy consumption as opposed to recoverable elastic energy. Note that this damping force can be interpreted as the energy dissipative resistive force that the material exerts making the resultant deformation irreversible.

2.3.3. Fracturing Stage

When a unit volume is fracturing, the elastic force terms become inactive. It is possible that the velocity damping force is still active in the one-dimensional form used in Equation (13). Thus, we can express the fracture condition, as follows.

$$\begin{array}{ccc}\hfill \nabla \times \mathit{\omega }& =& 0\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill G{j}_s& =& {\sigma }_0\rho \frac{d{v}_s}{d{x}_s}{v}_s\hfill \end{array}$$

(20)

The first fracture condition (19) indicates that when the fracture condition is satisfied the material does not exert elastic resistive force. The second fracture condition (20) indicates that the material exerts energy dissipative force in response to the external load. The second condition is further classified into recoverable fracture and final fracture conditions.

$$\begin{array}{ccc}\hfill & \mathrm{Recoverable}\mathrm{fracture}\mathrm{condition}:& G{j}_s\ne 0,v_s\ne 0\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill & \mathrm{Final}\mathrm{fracture}\mathrm{condition}:& G{j}_s\ne 0,v_s=0\hfill \end{array}$$

(22)

In conditions (21) and (22), $G{j}_s\ne 0$ ensures Newton’s third law. The energy dissipative force $G{j}_s$ is the reaction to the external force. Condition (22) is interpreted as the final fracture condition because of the following argument. In condition (20), if the left-hand side is non-zero and $v_s=0$ on the right-hand side, it follows that $d{v}_s/d{x}_s\to \infty$. This condition means that the particles diverge at the infinite rate from the unit volume, which apparently indicates the generation of material discontinuity. It is interesting to note that material fracture resembles electric discharge of gasses [42]. More specifically, recoverable fracture resembles spark discharge [43] and final fracture resembles arc discharge. Spark discharge in gas media is similar to arc discharge, but it does not cause electrical breakdown of the gas [44]. These resemblances between fractures and electric discharges are not coincidence. Rather, they come from the similarity of the above field equations to Maxwell’s equations of electrodynamics [45]. Appendix E describes spark discharge and discusses the similarity between the present deformation dynamics and Electrodynamics.

2.4. Wave Equations

The wave dynamics of the differential displacement originates in the equation of motion. In this section we derive the wave equation for each stage of deformation.

2.4.1. Linear Elastic Stage

Using linear elastic conditions (14) and (15) and taking the divergence of the resulting equation, we can rewrite the equation of motion (7), as follows.

$$\frac{{\partial }^2(\nabla ·\mathit{\xi })}{\partial t^2}=\frac{\lambda +2G}{\rho }{\nabla }^2(\nabla ·\mathit{\xi })$$

(23)

Equation (23) is the well-known equation of compression waves.

2.4.2. Elasto-Plastic Stage

Substituting Equation (2) for $d\mathit{v}/dt$, Equation (3) for $\mathit{\omega }$ (with the replacement of $\mathbf{A}$ with $\mathit{\xi }$) and using the mathematical identity $\nabla \times (\nabla \times \mathit{\xi })=\nabla (\nabla ·\mathit{\xi })-{\nabla }^2\mathit{\xi }$, we can eliminate $\mathit{\omega }$ from Equation (7) and rewrite it, as follows.

$$\frac{{\partial }^2\mathit{\xi }}{\partial t^2}-\frac{G}{\rho }{\nabla }^2\mathit{\xi }=-\frac{G}{\rho }\nabla (\nabla ·\mathit{\xi })-G\mathit{j}$$

(24)

Using both Equations (8) and (9) for $G\mathit{j}$, we can further rewrite Equation (24), as follows.

$$\frac{{\partial }^2\mathit{\xi }}{\partial t^2}+{\sigma }_0(\nabla ·\mathit{v})\frac{\partial \mathit{\xi }}{\partial t}-\frac{G}{\rho }{\nabla }^2\mathit{\xi }=-\frac{G}{\rho }\nabla (\nabla ·\mathit{\xi })+\frac{\lambda +2G}{\rho }\nabla (\nabla ·\mathit{\xi })$$

(25)

Equation (25) can be viewed as the equation of a wave that travels with the phase velocity $\sqrt{G/\rho }$ and the damping coefficient ${\sigma }_0(\nabla ·\mathit{v})$. The plastic longitudinal force appears as the damping term on the left-hand side. The right-hand side of Equation (25) can be viewed as the source term of the wave equation. Here, the first term originates from the elastic transverse force $G(\nabla \times \mathit{\omega })$ and the second term is the elastic longitudinal force (8). Because both terms have $\nabla (\nabla ·\mathit{\xi })$, we can combine the two terms, which indicates that, when the elastic and plastic dynamics coexist, the overall elastic constant is $\lambda +G$. If the dynamics is purely elastic, the elastic constant is $\lambda +2G$, higher than the elasto-plastic case by G. Thus, introducing the elastic factor $\alpha$ ($0\le \alpha \le 1$), we can rewrite Equation (25) for the elasto-plastic dynamics, as follows.

$$\frac{{\partial }^2\mathit{\xi }}{\partial t^2}+{\sigma }_0(\nabla ·\mathit{v})\frac{\partial \mathit{\xi }}{\partial t}-\frac{G}{\rho }{\nabla }^2\mathit{\xi }=-\frac{G}{\rho }\nabla (\nabla ·\mathit{\xi })+\alpha \frac{\lambda +2G}{\rho }\nabla (\nabla ·\mathit{\xi })$$

(26)

In the elasto-plastic regime, the higher the elastic factor $\alpha$, the more effective the elastic longitudinal force is. Note that, for the purely elastic dynamics, condition (14) drops the third term on the left-hand side and the first term on the right-hand side, and condition (15) drops the second term on the left-hand side and set $\alpha =1$ (because $G\mathit{j}=G{\mathit{j}}_e$ with $G{\mathit{j}}_p=0$). The application of divergence ($\nabla ·$) to the resulting equation yields the linear elastic wave Equation (23).

2.4.3. Fracturing Stage

Using fracture criterion $\nabla \times \mathit{\omega }=0$, one-dimensional $\nabla ·\mathit{v}$ and

$$\frac{\partial {\xi }_s}{\partial x_s}=\frac{\partial {\xi }_s}{\partial t}\frac{dt}{d{x}_s}=\frac{1}{c_s}\frac{\partial {\xi }_s}{\partial t},$$

(27)

we can put Equation (12) in the following form.

$$\rho \left({\partial }_t{v}_s\right)+\left({\sigma }_0\rho \right)v_s\left({\partial }_{x_s}{v}_s\right)+\frac{E\delta x_s\Delta x_s}{c_s}\left({\partial }_{x_s}^3{v}_s\right)=0$$

(28)

Here, $c_s$ is the wave velocity in the direction of $x_s$ axis. Equation (13) is in the form of a wave equation known as the Korteweg-de Vries (KdV) equation [19] that has a solitary wave solution of the following type.

$$v_s=a{\mathrm{sech}}^2\left(b(x_s-c_{w}t)\right)$$

(29)

Here a is the amplitude, b is a shape constant and $c_w$ is the propagation velocity of the solitary wave. The substitution of solution (29) into the wave Equation (28) yields the following relations.

$$\begin{array}{ccc}\hfill c_w& =& \frac{{\sigma }_{0}a}{3}\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill b& =& \left(\frac{{\sigma }_{0}a}{3}\right)\sqrt{\frac{\rho }{4E\delta x_s\Delta x_s}}=c_w\sqrt{\frac{\rho }{4E\delta x_s\Delta x_s}}\hfill \end{array}$$

(31)

A solitary wave, in general, is formed when the nonlinearity and dispersion interact with each other and, consequently, the wave form becomes unchanged as the wave travels [21]. It is interesting to discuss the sources of nonlinearity and dispersion in Equation (28). On the left-hand side of this equation, the second term represents nonlinearity and the last term dispersion. The nonlinear term originates from the energy damping longitudinal force (9), ${\sigma }_0\rho (\nabla ·\mathit{v})\mathit{v}$. This force is apparently nonlinear with respect to the particle velocity $\mathit{v}$. As discussed in Appendix E, this term is analogous to the Ohmic loss in a conductive gas medium, which takes the form proportional to the product of the electric charge density $\rho =ϵ(\nabla ·\mathit{E})$ and the current density $\mathit{J}={\sigma }_e\mathit{E}$.

The dispersive term originates from the last term of the Lagrangian density expression (10), which represents the potential energy that is associated with the spatial gradient of the strain. In a linear elastic medium, the normal stress is the product of a Young’s modulus and normal strain, $E{ϵ}_{xx}$, and the potential energy is determined by the normal strain and the normal stress in this form. When the gradient of the strain becomes significant, the material is no more a continuum represented by a single elastic modulus (if so, the stretch would be uniform). Under a certain condition, the material consists of a hard portion of width $\Delta x$ sandwiched by softer portions of width $\delta x$ [41]. Figure 2 illustrates the situation This situation resembles a string on an elastic medium [37] as the material is represented by two elastic media or a granular chain [38], both are classical examples of dispersive system.

3. Experimental and Numerical Methods

In this and the next sections, we examine the above-discussed conditions of deformation stage in conjunction with the wave characteristics of differential displacement via experiments and numerical analysis. The experiment has been conducted for a plate metal specimen with a monotonic tensile load. An optical interferometric setup recorded the differential displacement field of the specimen continuously until the specimen broke. The above-derived wave equations indicate the type of waves in each stage. However, in realistic situations the boundary conditions are not simple and the actual solution cannot be easily obtained. Thus, in this study, we constructed a simple Finite Element Model (FEM) using the elasto-plastic wave equation as the governing equation, and ran the FEM under a monotonic loading condition. Here, we will compare the resultant differential displacement field with the corresponding experimental results.

3.1. Experimental

Figure 3 illustrates the experimental arrangement. An aluminum alloy plate specimen was mounted on a test machine for a tensile load. An optical interferometric technique, known as the Electronic Speckle-Pattern Interferometry (ESPI), was used to record the differential displacement field. Two sets of optical interferometers were configured. The first set was sensitive to the in-plane displacement component perpendicular to the tensile axis and the second set is sensitive to the in-plane displacement component parallel to the tensile axis. The laser beam (wavelength 660 nm) was split into two beams by a 50% transmissive beam splitter for each interferometer and the two beams were recombined on the specimen surface. The recombined image (the interferogram) was a superposition of two speckle fields formed by the respective beams. The ESPI setup recorded the interferogram continuously with a preset time interval. The CCD camera captured the interferogram of the perpendicular and parallel components individually in order to separate the perpendicular and parallel components. The captured images were sent to computer memory where the image taken at a time step was subtracted from the image taken at a later time step. The subtracted image frame exhibits the so-called fringe patterns that represent contours of differential displacement components. More details about this ESPI technique can be found elsewhere [33,34,35].

3.2. Finite Element Model

In a Cartesian coordinate system in two dimensions, we can express Equation (25), as follows.

$$\begin{array}{c}\hfill \frac{{\partial }^2{\xi }_x}{\partial t^2}+{\sigma }_0(\nabla ·\mathit{v})\frac{\partial {\xi }_x}{\partial t}-\frac{G}{\rho }\left(\frac{{\partial }^2{\xi }_x}{\partial x^2}+\frac{{\partial }^2{\xi }_x}{\partial y^2}\right)=-\frac{G}{\rho }\frac{\partial }{\partial x}\left(\frac{\partial {\xi }_x}{\partial x}+\frac{\partial {\xi }_y}{\partial y}\right)+\alpha \frac{(\lambda +2G)}{\rho }\frac{\partial }{\partial x}\left(\frac{\partial {\xi }_x}{\partial x}+\frac{\partial {\xi }_y}{\partial y}\right)\end{array}$$

(32)

$$\begin{array}{c}\hfill \frac{{\partial }^2{\xi }_y}{\partial t^2}+{\sigma }_0(\nabla ·\mathit{v})\frac{\partial {\xi }_y}{\partial t}-\frac{G}{\rho }\left(\frac{{\partial }^2{\xi }_y}{\partial x^2}+\frac{{\partial }^2{\xi }_y}{\partial y^2}\right)=-\frac{G}{\rho }\frac{\partial }{\partial y}\left(\frac{\partial {\xi }_x}{\partial x}+\frac{\partial {\xi }_y}{\partial y}\right)+\alpha \frac{(\lambda +2G)}{\rho }\frac{\partial }{\partial y}\left(\frac{\partial {\xi }_x}{\partial x}+\frac{\partial {\xi }_y}{\partial y}\right)\end{array}$$

(33)

Using Poisson’s ratio $\nu$, we can rewrite the volume expansion term appearing on the right-hand side in the following form. Here, y is chosen to be the axis along which an external load is applied to the specimen.

$$\frac{\partial {\xi }_x}{\partial x}+\frac{\partial {\xi }_y}{\partial y}=-\nu \frac{\partial {\xi }_y}{\partial y}+\frac{\partial {\xi }_y}{\partial y}$$

(34)

Using Equation (34), canceling common terms from the left and right-hand sides and further simplifying several terms, we can rewrite Equations (32) and (33), as follows.

$$\begin{array}{c}\hfill \frac{{\partial }^2{\xi }_x}{\partial t^2}+{\sigma }_0(\nabla ·\mathit{v})\frac{\partial {\xi }_x}{\partial t}-\frac{G}{\rho }\frac{{\partial }^2{\xi }_x}{\partial y^2}=-\frac{G}{\rho }\frac{{\partial }^2{\xi }_y}{\partial x\partial y}+\alpha \frac{(\lambda +2G)(1-\nu )}{\rho }\frac{{\partial }^2{\xi }_y}{\partial x\partial y}\end{array}$$

(35)

$$\begin{array}{c}\hfill \frac{{\partial }^2{\xi }_y}{\partial t^2}+{\sigma }_0(\nabla ·\mathit{v})\frac{\partial {\xi }_y}{\partial t}-\frac{G}{\rho }\frac{{\partial }^2{\xi }_y}{\partial x^2}=\frac{G\nu }{\rho }\frac{{\partial }^2{\xi }_y}{\partial y^2}+\alpha \frac{(\lambda +2G)(1-\nu )}{\rho }\frac{{\partial }^2{\xi }_y}{\partial y^2}\end{array}$$

(36)

Equation (36) indicates that the longitudinal displacement component travels as longitudinal and transverse waves. The transverse wave characteristics comes from the ${\partial }^2{\xi }_y/\partial x^2$ term on the left-hand side of the equation. The longitudinal wave characteristics comes from the first term on the right-hand side. It is important to note that the quantities multiplied to the secondary spatial derivative (${\partial }^2{\xi }_y/\partial y^2$) term on the right-hand side represents the phase velocity of the longitudinal wave. It depends on the shear modulus G, the Poisson’s ratio $\nu$, the density $\rho$, the degree of the elastic force contribution $\alpha$, and the Lamé’s parameter $\lambda$. The phase velocity of the transverse wave is determined by the quantity multiplied to ${\partial }^2{\xi }_y/\partial x^2$ term on the left-hand side. Hence, the transverse wave velocity only depends on G and $\rho$.

The transverse component ${\xi }_x$ is in a different situation according to Equation (35). While the secondary spatial derivative (${\partial }^2{\xi }_x/\partial y^2$) term on the left-hand side generates transverse wave characteristics, the right-hand side of this equation does not cause wave dynamics, as it does not contain the secondary spatial derivative of ${\xi }_x$. Instead, the entire right-hand side is a function of the secondary spatial derivative of ${\xi }_y$. This indicates that the spatiotemporal behavior of the transverse component depends on that of the longitudinal component.

Thus, we built a two-dimensional FEM using a Partial Differential Equation (PDE) solver in the coefficient form [46], and solved the pair of wave Equations (35) and (36). Figure 4 illustrates the geometry of the numerical model. The load application was simulated by making the entire Boundary 1 displaced in the positive x-direction at a constant rate. Boundary 2 and 3 were the free boundaries. Boundary 4 was fixed in both x and y directions. To assimilate previous experiments [13], we used the set of parameters shown in

Table 1. Elastic conditions.

${\mathit{\sigma }}_0$	G (N/m${}^2$)	$\mathit{\lambda }$ (N/m${}^2$)	$\mathit{\rho }$ (kg/m${}^3$)	$\mathit{\nu }$	$\mathit{\alpha }$	Pulling Rate ($\mathsf{\mu }$m/s)
$1\times {10}^{-8}$	$2.8\times {10}^{-6}$	$4.2\times {10}^{-6}$	1	0.3	1	35

. This combination of G and $\rho$ yields the transverse wave velocity of 10 cm/min., which is of the same order as the experimental values reported in ref. [13]. The pulling rate of 35 $\mathsf{\mu }$m/s is also of the same order as these experiments.

4. Results and Discussions

4.1. Transition from Linear Elastic to Elasto-Plastic Regime

Figure 5 shows the sample fringe patterns obtained with the use of the experimental arrangement (Figure 3) along with the stress-strain characteristics. The specimen was a dog-bone shaped plate of 25 mm in the gauge length, 10 mm in the gauge width and 5 mm in thickness. The material was an industrial Al-Zn-Mg-Cu alloy AA 7075 [47,48]. The base material was solid-solution treated and hardened up to the peak hardness by non-scale precipitates. After being cut into the final size, the specimen was over-aged at 400 ${}^{\circ }$C for 30 min., so that the matrix was softened through coarsening of the precipitates. These treatments were performed to make the alloy macroscopically homogeneous. The specimen was pulled at a constant rate of 1 mm/min.

In Figure 5, the fringe images are paired being labeled u and v. Here, u and v represent the horizontal and vertical differential displacement $u=d{\xi }_x$ and $v=d{\xi }_y$ with reference to Figure 3. The number shown above each pair of images indicates the point on the stress–strain curve. The numbers match those indicated in the stress-strain curve. Apparently, (1) and (2) are in the linear elastic regime of the stress-strain curve, (3)–(5) are in the pre-yield regime, and (6)–(8) are in the post-yield regime. The dark fringes observed in each regime can be argued in conjunction with the linear elastic and elasto-plastic conditions that are discussed above.

(1)–(2)

The u fringes are vertical and linear indicating that $\partial {\xi }_x/\partial y=0$. The v fringes are horizontally parallel at an approximately constant interval, indicating that $\partial {\xi }_y/\partial y=$ constant and $\partial {\xi }_y/\partial x=0$. All of these conditions are consistent with linear elastic condition (14), i.e., shear strain is zero and $\nabla \times \mathit{\omega }=0$. The number of the u fringes is less than the v fringes in accordance with Poisson’s ratio. The number of the u fringes is approximately one over 10 mm and the number of the v fringes is 7 over 25 mm. The Poisson ratio can be estimated as $(1/10)/(7/25)=0.35$. This value is close to a literature value of 0.33 [48].

(3)–(5)

At this stage, the u and v fringes start to show shear strain. The slant features seen in both fringes indicate $\partial {\xi }_x/\partial y\ne 0$ and $\partial {\xi }_y/\partial x\ne 0$, hence elasto-plastic condition (16) is satisfied. Notice that the u fringes are much more horizontal and v fringes are much more vertical as compared with (1) and (2). The u fringes at stage (5) clearly indicate the semi-circular feature (near the right-upper shoulder) that represents a transverse wave, as will be discussed shortly. It is likely that the region near this shoulder undergoes plastic deformation at a higher degree than the rest of the specimen. This is reasonable because the shoulder part of a dog-bone specimen is a spot of stress concentration in general.

(6)–(8)

The u fringes are vertical and slightly curved, and the v fringes are approximately horizontally parallel like the elastic stages (1) and (2). The u fringe pattern indicates that the deformation is still plastic satisfying condition $\nabla \times \mathit{\omega }\ne 0$, but the degree of the plastic deformation is much less than that observed near the right-upper shoulder in (5).

While the v fringes display the same general pattern (horizontally parallel) as the elastic stages, the number of fringes is much higher than the elastic stages. Because the fringe patterns are formed with the same time interval and the pulling rate is constant, the total elongation at this stage is the same as the elastic stage. The much higher number of v fringes indicates that the specimen undergoes compression and stretch. This can be explained, as follows. The v component of the differential displacement exhibits longitudinal wave characteristics as in the elastic stage. However, because the elastic constant is much lower than before the yield point, the wave velocity, which is in the form of the square root of the elastic constant divided by the density, is significantly lower. The frequency of the longitudinal wave is determined by the external load and, therefore, more or less the same as the elastic stage. Consequently, the wavelength is significantly shorter than the elastic stage. This situation results in the higher fringe density. We can intuitively understand that the lower elastic constant shortens the wavelength by imagining pulling two springs of different strengths. First, pull one end of the stronger spring holding the other end stationary. The spring is stretched uniformly. Every part of the spring along its length is elongated at the same time. Now, pull the weaker spring in the same fashion at the same pulling speed. It is easy to imagine that the part of the spring closer to the moving end is stretched first and then the stretching pattern moves towards the other end along the length of the spring. Moreover, as the next section is stretched the first section tends to be compressed due to the recoiling motion of the spring. Consequently, we see a higher number of compression and stretch patterns. In a solid material, the same feature can be observed. The pattern of compression and stretch represents longitudinal wave characteristics. It is well known that the longitudinal wave velocity is the square root of the ratio of the Young’s modulus over density. The longitudinal wave travels at a lower velocity in a softer (less stiff) material. Because the wavelength is proportional to the wave velocity, the softer the material the shorter the wavelength. If the wavelength is shorter for a given material length, a higher number of waves are excited by the pulling action. The higher fringe density that is discussed above corresponds to a lower stiffness.

4.2. Propagation of Elasto-Plastic Wave

Figure 6 shows the propagation of u and v fringe patterns observed in post-yield stages of deformation in the same experiment, as in Figure 5. The three rows of u and v fringe patterns are formed successively with the same interval corresponding to an increment of 0.045% in the normal strain ${ϵ}_{xx}$. Each row represents a specific stage of deformation as indicated as “stage 1” through “stage 3” in the stress–strain curve at the top of Figure 6.

Stage 1 ($2.19\%<{ϵ}_{xx}<2.41\%$)

In stage 1, both u and v patterns travel upward at a constant rate. The u pattern is characterized by two half-circles located at the same horizontal position. The pair of half-circles occupies approximately a quarter of the vertical length of the specimen, and moves upward without changing their shapes. The v pattern is characterized by concentrated horizontal fringes located at approximately the same vertical position of the specimen as the pair of half-circles in the u pattern. The concentrated fringes move together with the pair of the half-circles in the u pattern.

Figure 7 shows numerically obtained differential displacement patterns that result from the FEM computation conducted with the parameters listed in Table 1. The patterns labeled u correspond to the experimental u pattern discussed above, and the ones labeled v correspond to the experimental v patterns. The numerical results show qualitative agreement with the experimental patterns that are shown in Figure 6 in the following sense. (a) the u pattern consists of a pair of half-circles that move upward along the length of the specimen and (b) the v pattern consists of partially concentrated fringes that move in the same direction as the pair of half-circles in the u pattern. The FEM simply solves the wave equations for the horizontal (u) and vertical (v) components of the differential displacement without using a deformation model (except for the Poisson’s effect). The agreement between the experimental and numerical results proves that the u and v fringe patterns observed in stage 1 represent the longitudinal and transverse waves. At $t=t_5$, the numerical u pattern shows another pair of half-circles that are not seen in the experimental result. It is not clear why the second pair does not appear in the experiment.

Stage 2 ($2.86\%<{ϵ}_{xx}<3.08\%$)

In this stage, the u pattern still shows a pair of half-circles moving upward on the specimen. However, the half-circles are not horizontally symmetric, and the pair of half-circles are divided by a group of approximately linear and slanted fringes. The slanted fringes indicate a shear band. The reason for this asymmetry is not fully understood at this time. However, it is interesting to note that the linear pattern possibly represents strong shear deformation and, within this region, the fracture condition (19) is satisfied in the recoverable mode (21). Perfectly-linear fringes make $\omega$ defined by Equation (3) a constant, and therefore $\nabla \times \mathit{\omega }=0$. It is likely that the formation of the slant linear pattern (called the shear band) displaying the recoverable fracture condition is responsible for the sharp stress drop observed in the stress-strain curve in Figure 6. This type of sharp stress drop followed by immediate recovery is known as the serration. Propagation of the half-circle pair repeats a number of times between Stage 2 and Stage 3, where some of them exhibit the symmetric feature, like Stage 1, and others exhibit the asymmetry feature, like Stage 2. The symmetric and asymmetric features alternate in a random fashion. Although clear correlation has not been found between the serration and the formation of shear band at this time, this alternating behavior of the symmetric and asymmetric patterns involving the shear band formation makes us believe that the establishment of the recoverable fracture condition is closely related to the serration.

The shear band (the slanted linear fringe pattern) can be interpreted as displaying the solitary wave solution (29). As mentioned above and confirmed in a number of experiments [14,15,16], the propagation speed of these solitary waves decreases with the development of deformation and the final fracture occurs when the wave becomes stationary. Thus, the slanted linear fringes can be used as an early indicator of deformation behavior in conjunction with the final fracture. The initial propagation speed is proportional to the pulling rate of the specimen. This proportionality has been qualitatively explained based on the field theory [18]. An interesting aspect that is related to this is that the temporal behavior of the decrease in the propagation speed is independent of the pulling rate and obeys a single function of time. Figure 8 [49] shows the propagation speed of shear bands observed in the same type of experiment as above. The material was an aluminum alloy plate (A5083) [47]. The shear band propagation speed is plotted as a function of the elapsed time from the beginning of the tensile loading for five different pulling rates, 3, 1, 0.5, 0.3, and 0.1 mm/min.

Table 2. Various quantities at onset of shear band propagation. Quantities in the top three rows are found directly from experimental data. Quantities in the bottom three rows are evaluated based on theories.

Pulling Rate (mm/min)	3	1	0.5	0.3	0.1
Onset time (s)	6.6	31.1	150.1	456.2	2415
Elongation (mm)	0.55	0.51	1.25	2.28	4.02
Normal strain (%)	2.2	2.0	5.0	9.1	16.1
Dislocation velocity (cm/s)	1.92	7.16$\times {10}^{-1}$	1.77$\times {10}^{-1}$	6.03$\times {10}^{-2}$	1.16$\times {10}^{-2}$
Dislocation density (cm${}^{-2}$)	3.6$\times {10}^4$	3.3$\times {10}^4$	6.6$\times {10}^4$	1.2$\times {10}^5$	2.0$\times {10}^5$
Solitary wave amplitude (mm/min)	11.5	4.29	1.06	0.36	0.07

lists the onset times (when the shear band appears for the first time since the beginning of the tensile loading), the total elongation computed as the product of the pulling rate and the onset time for each pulling rate, and the average normal strain evaluated by dividing the total elongation by the gauge length of 25 mm. Apparently, the shear band starts to appear at different total elongations (i.e., the averaged strain) among different pulling rates.

On the other hand, as indicated by the trend line that is drawn in Figure 8, a single function fits the data for all of the five pulling rates. Numerical curve fitting indicates that a function in the form of $A/(t+B)$ fits the best. Here, A and B are constants and t is the elapsed time. This particular form of the function is of great interest, because the average speed of mobile dislocations, $<v_{md}>$, can be expressed, as follows [1].

$$sinsinglesi<v_{md}>=\frac{L}{(t+t_s)}$$

(37)

Here, L is the average distance between neighboring barriers and $t_s$ is the interaction time with each barrier. The observed good fitting indicates that the shear band is formed in a process that is closely related with mobile dislocation’s dynamics and its propagation speed is strongly related to the amount of the mobile dislocations. This argument is consistent with the prevailing theory regarding the micromechanism [50,51,52,53,54,55,56]. It is also consistent with the above-mentioned (see the paragraph under Equation (18)) self-driven nature of the evolution of deformation to fracture in association with an increase in the volume expansion rate $(\nabla ·\mathit{v})$. The generation of dislocations forms a new source of $(\nabla ·\mathit{v})$.

The function $A/(t+B)$ has the best fit to the experimental data in Figure 8 when $A=280$ mm and $B=8$ s. As the average distance between neighboring barriers for mobile dislocations, 280 mm is unrealistically long. However, notice that the value of this function remains unchanged if the same factor m is multiplied to L, t and $t_s$ as $\mathrm{m}L/(\mathrm{m}t+\mathrm{m}{t}_s)$. This allows for us to make the following hypothesis, i.e., a shear band is formed every time mobile dislocations interact with barriers m times. With this hypothesis, we can estimate the average velocity of mobile dislocations at the onset of shear band propagation by substituting $L=280,t_s=80$, and the onset time that is shown in Table 2 for t into the $<v_{md}>$ expression (37). The fourth row of Table 2 lists the value of $<v_{md}>$ estimated in this fashion for all puling rates.

The dislocation density can be related to the average velocity of mobile dislocation, as follows (See Section 2.3 Dislocation Velocity on p. 17 of ref. [1]).

$$n=\frac{{\dot{\gamma }}_{ex}}{b_B<v_{md}>}$$

(38)

Here, n is the dislocation density ${\dot{\gamma }}_{ex}$ is externally imposed rate of deformation by the tensile machine and $b_B$ is the magnitude of Burger’s vector. Equation (38) indicates that the average velocity of mobile dislocations decreases in proportion to the mobile dislocation density. This explains the decrease in the shear-band propagation velocity with the passage of time for a given pulling rate.

Using the above estimated $<v_{md}>$, the average deformation rate (the tensile machine’s pulling rate divided by the gauge length of the specimen, 25 mm ) and 0.286 nm for $b_B$ (see p. 83 of ref. [47]), we can estimate the dislocation density at the beginning of the shear band propagation for each pulling rate. The results are shown in the fifth row of Table 2. The dislocation density for pulling rates of 3 and 1 mm/min. is close to the initial (before deformation) dislocation density of copper discussed by Suzuki et al. (See p. 25 of ref. [1]). When the pulling rates are lowered to 0.5, 0.3, and 0.1 mm/min., the onset dislocation density increases in this order by factor of two to five. These observations are consistent with the third row of Table 2, which indicates that the onset normal strain also increases in this order. Figure 9 explicitly illustrates that the onset normal strain is approximately equal to the yield strain for pulling rates of 3 and 1 mm/min. and that the onset normal strain lags behind the yield point for pulling rate of 0.3 and 0.1 mm/min., where the amount of lag is greater for 0.1 mm/min.

With the hypothesis that a solitary wave represents a shear band, we can discuss the parameters used in the solitary wave solution (29) semi-quantitatively. The quantity ${\sigma }_0$ appearing in the solitary wave velocity expression (30) has been found in the neighborhood of 300 (See p. 179 of ref. [9]). Using the onset shear band velocity in Figure 8 and ${\sigma }_0=300$, we can estimate the solitary wave amplitude a for each pulling rate, as follows.

$$a=\frac{3c_w}{{\sigma }_0}=\frac{3c_w}{300}$$

(39)

The sixth row of Table 2 shows the value of the solitary wave amplitude evaluated in this fashion in the unit of mm/min. It is seen that the solitary (velocity) wave’s amplitude is of the same order as the pulling rate, which is understandable because the particle velocity is caused by the pulling action of the tensile machine. The observed solitary wave velocity is a factor of four higher than the pulling rate at pulling rates of 3 and 1 mm/min., a factor of two higher at pulling rate 0.5 mm/min., approximately equal to at pulling rate 0.3 mm/min. and 30% lower at pulling rate 0.1 mm/min. We speculate that the reason why the peak particle velocity (the amplitude of the solitary wave) can be higher than the pulling rate is that the formation of a shear band involves a snapping motion of the material. On the formation of a shear band, the material experiences a recoverable partial fracture and this causes the particles on the opposite sides of the partial fracture to recoil sharply, as if a stretched spring breaks. This speculation is consistent with the instantaneous stress drop accompanied by the formation of a shear band, as a number of authors [54,55,56,57] observed. The reduction in the amplitude of solitary wave relative to the pulling rate indicates that the increase in the mobile dislocation density lowers the amplitude of the solitary wave (because the onset mobile dislocation density is higher for the lower pulling rate). The precise mechanism underlying the relation between the solitary wave amplitude and the mobile dislocation density has not been understood at this time.

Solitary wave solution (29) indicates that the width of solitary wave is inversely proportional to parameter b. In refs. [14,57], the authors observed that the shear band width decreased as the tensile deformation advances toward the final fracture. This reduction is understandable, because it is expected that the stress concentration enhances toward the fracture. Equation (31) indicates two possibilities for b to increase; hence, the solitary wave becomes narrow. The first is an increase in $c_w$ and the second is a decrease in Young’s modulus E. These two factors behave oppositely with the development of deformation. As plastic deformation advances, the shear band (solitary wave) velocity $c_w$ decreases as the mobile dislocation density increases (as argued above), and Young’s modulus E also decreases as the stress strain curve flattens. The former reduces b and the latter increases it. Figure 10 plots the change in the shear band width as a function of time. It is seen that the shear band width decreases with time. Moreover, a comparison with Figure 9 indicates that the rate of decrease in the shear band width accelerates when the shear band’s propagation velocity (the slope of the time-shear band position plots) decreases for the last time before the shear band becomes stationary, but not yet stationary. It is possible that, at this point, the mobile dislocation density reaches some critical value that makes the effect of E significantly exceed the effect of $c_w$, resulting in the drastic reduction in the width of the shear band.

The loading curves in Figure 9 show the zigzag behavior of the stress known as the serration. The authors of refs. [54,55,56,57] made thorough analyses on the relation between the appearance of shear bands and serration and found clear correlation between them. Basically, a shear band is formed when the stress drops sharply, and it disappears when the stress rises again. This phenomenon is similar to spark discharge in a gas medium and its recovery. When a local region of the gas medium experiences a spark discharge, the voltage drops sharply as the conductivity rises. As the spark discharge disappears for some mechanism that decreases the number density of free charges, the gas medium recovers from the temporary partial breakdown. In the present context, the free charge ($\nabla ·\mathit{E}$) corresponds to $\nabla ·\mathit{v}$, which, in the one-dimensional form in a shear band, is $\partial v_s/\partial x_s$. The disappearance of a shear band corresponds to the decrease in free charges, and is accompanied by a stress rise that corresponds to the voltage rise. The above-discussed narrowing of the shear band corresponds to the increase in the electric charge density, which triggers the positive feedback (self-enhancing) mechanism (an increase in conductivity increases the charge density that, in turn, increases the conductivity) that leads to the final arc discharge (See Appendix E). The final sharp shear band narrowing corresponds to this self-enhancing effect. If a deforming solid enters this stage, there is no more recovery; the solid will break.

Stage 3 ($18.69\%<{ϵ}_{xx}<18.91\%$)

This is the stage when the stress is at the peak on the stress-strain curve. From this point onward, the stress decreases monotonically until the specimen breaks. In this stage, both the u and v fringe patterns are stationary. At the same time, the shear band pattern becomes more prominent, and the u and v fringes start to be similar to each other.

The similarity between the u and v fringe patterns is very interesting from the field theoretical viewpoint. This condition indicates that u and v can be expressed with the same function $f(x,y)$. Consider the volume expansion and shear strain under this condition.

$$\begin{array}{ccc}\hfill \nabla ·\mathit{\xi }& =& \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill {ϵ}_{xy}& =& \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\hfill \end{array}$$

(41)

Apparently, the two quantities take the identical form. The $(\nabla ·\mathit{v})$ term in the plastic energy dissipative term is the time derivative of the volume expansion.

$$\nabla ·\mathit{v}=\frac{\partial }{\partial t}(\nabla ·\mathit{\xi })$$

(42)

This means that, under this condition, the shear strain causes energy dissipation. This is interesting, because it is consistent with the concept of plastic deformation proposed by Panin [58]; plastic deformation is shear instability. It is also consistent with the the field theoretical interpretation of the onset of plastic deformation discussed above; the deformation transitions from elastic to plastic when the strain tensor expressed in the principal coordinate system starts to have shear components.

In addition, u and v constitute the x and y components of the differential displacement vector at a given point. Having the same x and y components, the differential displacement vector is directed at ${45}^{\circ }$ to the x axis. This is why the linear fringe patterns run in 45${}^{\circ }$ to the tensile axis, or along the maximum shear stress.

Figure 11 shows three stationary u and v patterns observed in Stage 3. Note that the shear band pattern runs from the bottom left to the top right when ${ϵ}_{xx}=18.88\%$, it disappears and, consequently, the half-circle patterns become symmetric when ${ϵ}_{xx}=18.92\%$, and it runs from the bottom right to the top left when ${ϵ}_{xx}=18.94\%$. It seems that approximately 45${}^{\circ }$ is the preferred orientation for the linear fringes to run. Notice that the shear band does not run vertically when the two half-circle patterns are symmetric at ${ϵ}_{xx}=18.92\%$. This is consistent with the above argument regarding the similarity of the u and v fringes (Equations (40) and (41)).

5. Summary and Concluding Remarks

Fringe patterns obtained from ESPI for a tensile experiment are analyzed in detail based on the field theoretical criteria of deformation stages. The wave equations that are derived by the field theory are solved numerically as a two-dimensional finite element model. The numerical results show semi-quantitative but clear agreement with the experimentally observed spatiotemporal behaviors of the differential displacement under elasto-plastic dynamics. This agreement confirms that the displacement field obeys the wave dynamics in the elasto-plastic regime, as predicted by the field theory. The analysis led to the following specific findings.

• The fringe patterns obtained at approximately one-third of the yield strain exhibit the elastic deformation criterion.
• The fringe patterns obtained at 80–90% of the yield strain indicate $\nabla \times \mathit{\omega }\ne 0$, one of the conditions constituting the plastic deformation criterion. The u (the differential displacement component perpendicular to the tensile axis) fringe patterns obtained at approximately 95% of the yield strain show a circular pattern that represents the transverse-wave in the plastic stage. These observations indicate that plastic deformation starts 10–15% prior to the yield point.
• When the normal strain reaches 2.19% past the yield strain of 1.0%, the u and v fringe patterns start to show traveling wave like behaviors. The numerical solutions to the wave equations confirm that these fringe patterns represent the transverse wave characteristics in the u-component and the longitudinal wave characteristics in the v-component of the differential displacement vector. The transverse and longitudinal waves propagate along the length of the specimen at the same speed. From this post-yield stage onward until the stress reaches the peak on the stress-strain curve, the wave motions repeat.
• In the above-mentioned post-yield stage, the u and v fringe patterns are not uniformly distributed along the length of the specimen. This makes the u fringe consist of two half-circle patterns and the v fringe concentrated over approximately half the length of the specimen. The pair of half-circles in the u pattern is initially horizontally symmetric, and it propagates along the specimen length maintaining the half-circle shape. As the stress increases, the semi-circle patterns become asymmetric, and approximately linear slant fringe patterns (shear bands) appear between the asymmetrically located semi-circle patterns. The shear band propagates at the same speed as the semi-circle patterns.
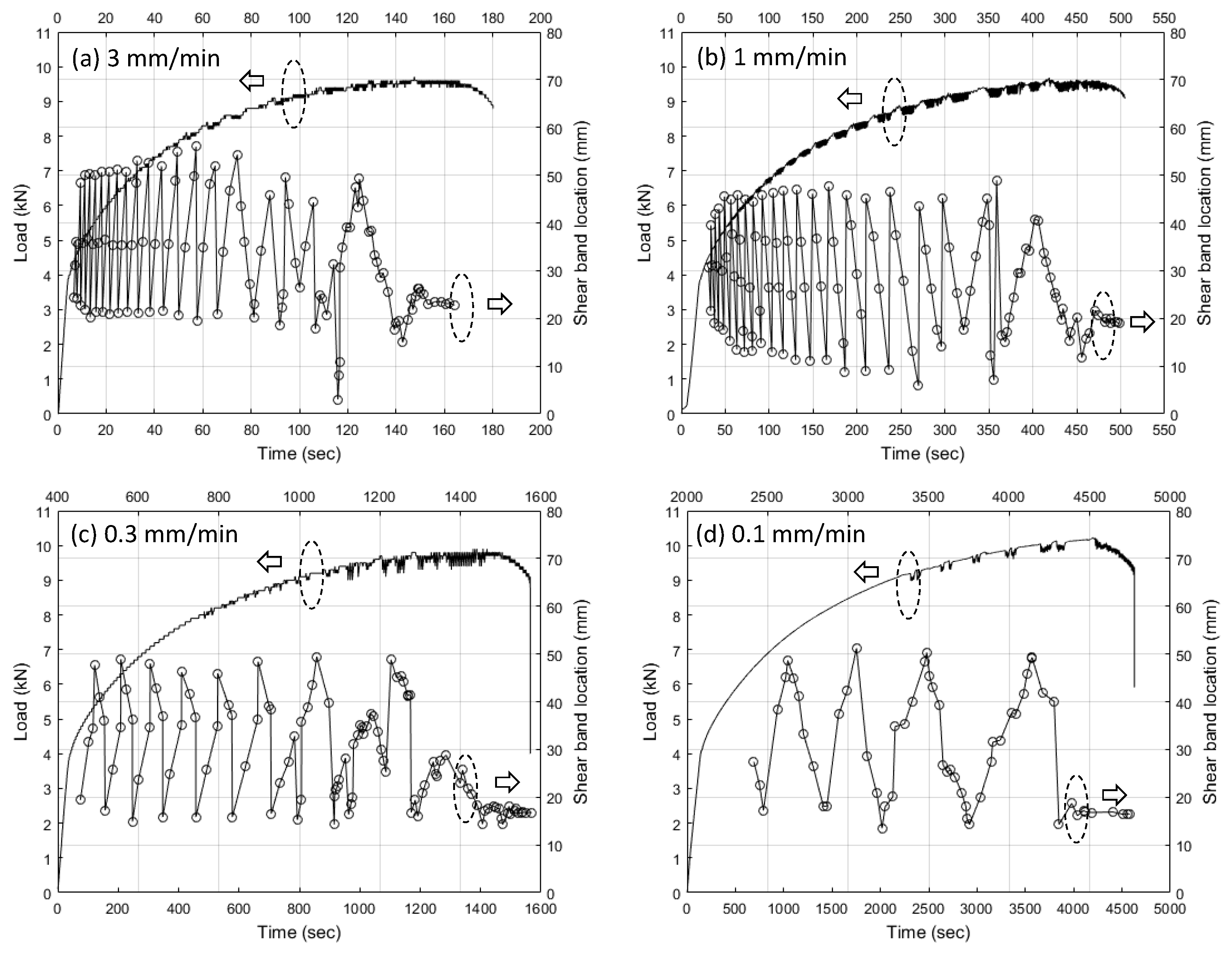
• The shear band propagation speed decreases towards the final fracture as a function of the elapsed time from the beginning of tensile loading. This behavior strongly indicates that the shear band formation and propagation are related to the mobile dislocation dynamics.

The results of this study confirm the usefulness of the present field theoretical approach for diagnosis of deformation status. Especially, when combined with the ESPI for the visualization of displacement field, it provides us with a quick way to make diagnosis. As a possible application of this combination of ESPI and wave dynamic diagnosis, we can consider the use of Artificial Neural Network (ANN) algorithm for an automated diagnostic system. We can use typical fringe patterns for the respective stages in one of the hidden layers of a pattern-recognition type of ANN algorithm [59] to train the system, so that it makes a judgment of a given ESPI fringe image for the stage of deformation. This is on our list of the future plan for this research.