Quantum Turing Machines: Computations and Measurements
Abstract
1. Introduction
Organization of the Paper
2. Quantum Turing Machines
2.1. Plain Configurations
- 1.
- is the current state, where Q is the finite set of the internal states of M.
- 2.
- is the right content of the tape (w.r.t. the head position), where is the tape alphabet of the machine M. If , the symbol is the current symbol, which is the content of the current cell, while is the longest string on the tape ending with a symbol different from □ and whose first symbol (if any) is written in the cell immediately to the right of the current cell. When instead, the right content of the tape, including the current cell, is empty, and the current symbol is □.
- 3.
- is the left content of the tape (w.r.t. the head position). That is, it is either the empty string , or it is the longest string on the tape starting with a symbol different from □, and whose last symbol is written in the cell immediately to the left of the current cell.
- 4.
- i is the address of the current cell.
2.2. Hilbert Space of Configurations
2.3. Transitions of a QTM
2.4. Initial and Final Configurations
2.5. Pre Quantum Turing Machines
- is the set of source states of M, and is a distinguished source state named the initial state of M;
- is the set of target states of M, and is a distinguished target state named the final state of M;
- and have the same cardinality and ;
- is the quantum transition function of M, where .
2.6. Configurations
- is the set of the configurations of M.
- and are the sets of the source and of the target configurations of M, respectively.
- and are the sets of the initial and final configurations of M, respectively.
- is the set of the configurations of M.
2.7. Quantum Configurations
2.8. Time Evolution Operator and QTM
- 1.
- .Let be the configuration obtained by leaving the counter to 0, by replacing the symbol u in the current cell with the symbol v, by moving the head on the d direction, and by setting the machine into the new state p. In detail, if we haveand we definewhere is the quantum transition function of M, and, as already introduced at the end of Section 2.3, is the new configuration obtained from C by changing the current state from q to p, by replacing the current symbol u with v, and by moving the tape head in the direction d.
- 2.
- .Let be the source configuration obtained by decreasing by 1 the counter of C, we define
- 3.
- .Let be the target configuration obtained by increasing by 1 the counter of C, we define
2.9. Computations
- 1.
- ;
- 2.
- .
2.10. Local Conditions for Unitary Evolution
- 1.
- for any
- 2.
- for any with
- 3.
- for any
- 1.
- is the same of the transition function of M for any non-terminal state;
- 2.
- for any terminal state and every current symbol u, has a unique non-null transition, with weight 1, that leaves the current symbol on the tape unchanged, moves the head to the right, and goes into an initial state ; and,
- 3.
- the non-null out transitions from two distinct terminal states lead to two distinct source states, defining in this way a bijection between the set of the target and source states.
2.11. A Comparison with Bernstein and Vazirani’s QTMs: Part 1
- 1.
- the set of configurations coincides with all possible classical configurations, namely all the set ;
- 2.
- no superposition is allowed in the initial q-configuration (it must be a classical configuration with amplitude 1);
- 3.
- given an initial configuration , the q-configuration is the final q-configuration for the computation starting in , when: (i) all of the configurations in are final; (ii) for all , the q-configuration does not contain any final configuration. When this is the case, we also say that the QTM halts in k steps in ;
- 4.
- if a QTM halts, then the tape head is on the start cell of the initial configuration; and,
- 5.
- there is no counter and for every symbol a there is loop from the only final state into the only initial state , which is, for every . Therefore, because of the local unitary conditions (that must hold in the final state too), these are the only outgoing transitions from , and the only incoming ones into . Accordingly, if and if .
3. Quantum Computable Functions
3.1. Probability Distributions
- 1.
- A partial probability distribution (PPD) of natural numbers is a function such that .
- 2.
- If , is a probability distribution (PD).
- 3.
- and denote the sets of all the PPDs and PDs, respectively.
- 4.
- If the set is finite, is finite.
- 5.
- Let be two PPDs, we say that () if and only if for each , ().
- 6.
- Let be a denumerable sequence of PPDs; is monotone if and only if , for each .
3.2. Monotone Sequences of Probability Distributions
- 1.
- exists and it is the supremum of ;
- 2.
- ;
- 3.
- .
3.3. PPD Sequence of a Computation
- 1.
- That when in a final (target) configuration, the machine can only increment the counter; as a consequence, the of final (target) configurations does not change.
- 2.
- That when entering for the first time into a final (target) state, the value of the counter is initialised to 0.
- 3.
- That when in a final (target) configuration , the counter gives the number of steps n since M is looping into the plain configuration .
3.4. Computed Output
- 1.
- There exists a k, such that, for each , is final and .
- 2.
- is a PD.
- 1.
- is finitary. In this case, ; the output of the computation is then a PD and is determined after a finite number of steps;
- 2.
- is not finitary, but . The output is a PD and is determined as a limit; and,
- 3.
- is not finitary, and (the sum of the probabilities of observing natural numbers is ). Not only the result is determined as a limit, but we cannot extract a PD from the output.
3.5. Quantum Partial Computable Functions
- 1.
- A function is partial quantum computable (q-computable) if there exists a QTM M s.t. if and only if .
- 2.
- A q-partial computable function f is quantum total (q-total) if for each , .
4. Observables
Measurement
Given a set of configurations , a measurement observing if a quantum configuration belongs to the subspace generated by gives a positive answer with a probability , equal to the square of the norm of the projection of onto , causing at the same time a collapse of the configuration into the normalised projection ; dually, with probability , it gives a negative answer and a collapse onto the subspace orthonormal to , which is, into the normalised configuration ,
4.1. The Approach of Bernstein and Vazirani
4.2. The Approach of Deutsch
- 1.
- If the result of the measurement of T gives the value 0, collapses (with a probability equal to ) to the q-configurationand the computation continues with .
- 2.
- If the result of the measurement of T gives the value 1, collapses (with probability ) toand, immediately after the collapse, the observer makes a further measurement of the component in order to read-back a final configuration.
4.3. Problems with Deutsch Measurement
- 1.
- . In this case, the tape is measured at an intermediate time between and , and the machine is in an intermediate configuration between and . Because the QTM is defined in terms of the unitary operator , its configurations are well-defined only at time , for . The quantum configuration is therefore unknown and depends on how the unitary operator is physically realised. In any case, in general it differs from .
- 2.
- . In this case the second measurement takes place at time , on the configuration . That implies , since may hold only in the trivial case the unitary operator is the identity and the , for every n.
4.4. Fixing the Measurement Protocol
Once the halt qubit is set to the state , the quantum Turing machine no longer changes the halt qubit or the tape string.
If the relevant outcome of the computation is designed to be written by the program in a restricted part of the tape, this condition can be weakened so that the quantum Turing machine may change the part of the tape string except that part of the tape.
Recently, Linden and Popescu [22] claimed that the halt scheme given in [13] is not consistent with unitarity of the evolution operator. However, their argument applies only to the special case in which the whole tape is required not to change after the halt. As suggested in footnote 11 of [13], the conclusion in [13] can be obtained from the weaker condition for the general case where the tape is allowed to change except for the data slot. Linden and Popescu [22] disregarded this case and hence their conclusion is not generally true.
4.5. Our Approach
- 1.
- first of all, we observe the final states of , forcing the q-configuration to collapse either into the final q-configuration , or into the q-configuration , which does not contain any final configuration;
- 2.
- then, if the q-configuration collapses into , we observe one of these configurations, say , which gives us the observed output , forcing the q-configuration to collapse into the final base q-configuration ;
- 3.
- otherwise, we leave unchanged the q-configuration obtained after the first observation, and we say that we have observed the special value ⊥.
- 1.
- either , and
- 2.
- or , and
- 1.
- a-observed runof M on the initial q-configuration is a sequence s.t.:
- (a)
- ;
- (b)
- , when for some ;
- (c)
- otherwise.
- 2.
- Afinite -observed runof length k is any finite prefix of length of some τ-observed run. Notation: if , then .
- 1.
- either it never obtains a value as the result of an output observation, and then it never reaches a final configuration; and,
- 2.
- or it eventually obtains such a value collapsing the q-configuration into a base final configuration s.t. and , and from that point onward all the configurations of the run are base final configurations s.t. , and all the following observed outputs are equal to n (see Remark 7).
- 1.
- The sequence s.t. , with , is the output sequence of the τ-observed run R.
- 2.
- The observed output of R is the value (notation: ) defined by:
- (a)
- , if for some ;
- (b)
- otherwise.
- 3.
- For any k, the output sequence of the finite τ-observed run is the finite sequence and is its observed output.
- 1.
- For , the probability of the finite τ-observed run is inductively defined by
- (a)
- ;
- (b)
- 2.
- .
- 1.
- for , that is, ;
- 2.
- for , the q-configurations are in two orthonormal subspaces generated by two distinct subsets of .
- 1.
- and , where D is a final plain configuration and . As already seen for , for , we have and . Therefore, , since , for by construction.
- 2.
- . Let , where D is a plain configuration and . By induction on j, it is readily seen that . Thus, .
- 1.
- , for any i. In this case, there is a bijection between the runs of length k and those of length , since each run is obtained from a run with last q-configuration , by appending to R the q-configuration . Moreover, because, by definition, , we can conclude that
- 2.
- , for some i. In this case, every with last q-configuration generates a run of length for every output observation , where is obtained by appending to R. Therefore, let andBy applying Definition 17, we easily check thatThus, by substitution, andsince . □
- 1.
- , for and ; and,
- 2.
- .
5. A Comparison With Bernstein and Vazirani’s QTMs: Part 2
5.1. QTM Transition Graphs
5.2. A Classical Reversible TM With Quantum Behaviour
5.3. A PD Obtained as a Limit
6. Related Works
6.1. On Quantum Extensions of Turing Machines, And of Related Complete Formalisms
- Strictly following the B&V approach, Nishimura and Ozawa [17,24] study the relationship between QTMs and quantum circuits (extending previous results by Yao [25]). They show that there exists a perfect computational correspondence between QTMs and uniform, finitely generated families of quantum circuits. Such a correspondence preserves the quantum complexity classes EQP, BQP, and ZQP.
- Perdrix and Jorrand [26] proposes a new way to deal with quantum extensions of Turing Machines. The basic idea is reminiscent of the quantum-data/classical-control paradigm coined by Selinger [27,28]. In fact, in Perdrix QTM’s, the only quantum component is the tape whereas the control is completely classical.
- Dal Lago, Masini, and Zorzi [3,29,30] extend the quantum-data/classical-control paradigm to a type free quantum -calculus that is proven to be in perfect correspondence with the QTMs of B&V. Following the ideas of the so-called Implicit Computational Complexity, the authors propose an alternative way to deal with the quantum classes EQP, BQP, and ZQP.
6.2. On the Readout Problem
- Myers [31] tries to show that it is not possible to define a truly quantum general computer. The article highlights how the B&V approach fails on truly quantum data. In fact, in such a case, it is impossible to guarantee the synchronous termination of all the computations in superposition. Consequently, the use of a termination bit spoils the quantum superposition of the computation. This defect was well known, and it is for this reason that B&V did not define a general notion of quantum computability, but rather a notion sufficient to solve—in a quantum way—only classical decision problems. Myers’s criticism does not apply to our approach. Our QTMs are fully quantum, and they have an observational protocol of the result that does not depend on the synchronous termination of the computations in superposition.
- In an unpublished note, Kieu and Danos [32] claim that: “For halting, it is desirable of the dynamics to be able to store the output, which is finite in terms of qubit resources, invariantly (that is, unchanged under the unitary evolution) after some finite time when the desirable output has been computed”. Unfortunately, it is not possible to enter into a truly invariant final quantum configuration—only a machine starting in a final configuration and computing the identity can accomplish this constraint. We overcome the problem by introducing a feasible (i.e., correct from a quantum point of view) notion of invariant, w.r.t. the readout, of final configurations. In this way, even if the final configuration changes, the output we read from that configuration does not change.
- In another unpublished note, Linden and Popescu [22] address the problem of how to readout the result of a general quantum computer. The authors write: “We explicitly demonstrate the difficulties that arise in a quantum computer when different branches of the computation halt at different, unknown, times”, implicitly referring to the problems in extending the approach of B&V to general quantum inputs (see again [31], discussed above). In the first part of the work, the authors show that the problem cannot be solved by means of the so-called “ancilla”. The ancilla is an additional information added to the main information encoded by a configuration of the quantum machine. The idea is that, once a final state is reached, the machine keeps modifying the ancilla only. The authors show that the ancilla approach destroys the quantum capabilities of quantum machines, since only classical computations can survive to this treatment of ancilla. Even if reminiscent of the ancilla, our approach is technically different—the problems addressed by Linden and Popescu do not apply—since we carefully tailor the space of the possible configurations of the machines, allowing for the ancilla to play a role only during its final and initial evolution.In the second part of the work, the authors launch a strong attack against the use of termination bit, the solution originally proposed by Deutsch and successively refined by Ozawa [13]. The authors try to argue that the approach that was proposed by Deutsch/Ozawa cannot work. In fact, they show that, even if it is true that once the termination bit is set to 1, it remains firmly with such a value forever, any terminal configuration cannot be frozen, and keeps evolving according to the Hamiltonian of the system. Once again, our proposal does not have the defect depicted in the paper, because, far away to force a final configuration to remain stable, only the readout of a final configuration is stable in our approach.
- Hines [33] shows how to ensure simultaneous coherent halting, provided that termination is guaranteed for a restricted class of quantum algorithms. This kind of approach that is based on coherent halting is intentionally not followed in our paper. Indeed, as previously remarked, we are interested in treating systems which includes, as a particular case, all classical computable functions—we cannot restrict to terminating computations.
- Miyadera and Ohya [34] discuss the notion of probabilistic halting. In particular, “[…] the notion of halting is still probabilistic. That is, a QTM with an input sometimes halts and sometimes does not halt. If one can not get rid of the possibility of such a probabilistic halting, one can not tell anything certain for one experiment since one can not say whether an event of halting or non-halting occurred with probability one or just by accident, say with probability ”. Therefore, they wonder about the existence of any algorithm to decide whether or not a QTM probabilistic halts. With no surprise, they conclude that such an algorithm cannot exist. In fact, because the non-probabilistic halting of a QTM corresponds to the simultaneous halting of all the superposing branchings of its computation, an algorithm deciding the probabilistic halting would decide the simultaneous termination of two classical reversible machines (by combining them into a unique QTM), which is clearly an undecidable problem. In a sense, the question of probabilistic or non-probabilistic halting is irrelevant for our approach. In our QTMs, the result of a computation is defined as a limit, and any computation converges to some result. Accordingly, the only possible readouts that we can get are approximations of such a result. At the same time, because we show that a repeated-measures protocol can retrieve the distribution associated to the output of a computation, we can accept to say that our approach is probabilistic.
7. Conclusions and Further Work
Author Contributions
Funding
Conflicts of Interest
Appendix A. Hilbert Spaces With Denumerable Basis
- 1.
- An inner sumdefined by ;
- 2.
- A multiplication by a scalardefined by ;
- 3.
- An inner productdefined by (observe that the condition implies that converges for every pair of vectors).
- 4.
- The Euclidian norm is defined as .
- 1.
- is a dense subspace of ;
- 2.
- is the (unique! up to isomorphism) completion of .
Appendix A.1. Dirac Notation
| mathematical notion | Dirac notation |
| inner product | |
| vector | |
| dual of vector | |
| i.e., the linear application | |
| defined as | note that |
Appendix B. Implementation of the Counter
Appendix B.1. Extra Symbols
- 1.
- 2.
- 3.
- 1.
- 2.
- 3.
Appendix B.2. Additional Counter Tape
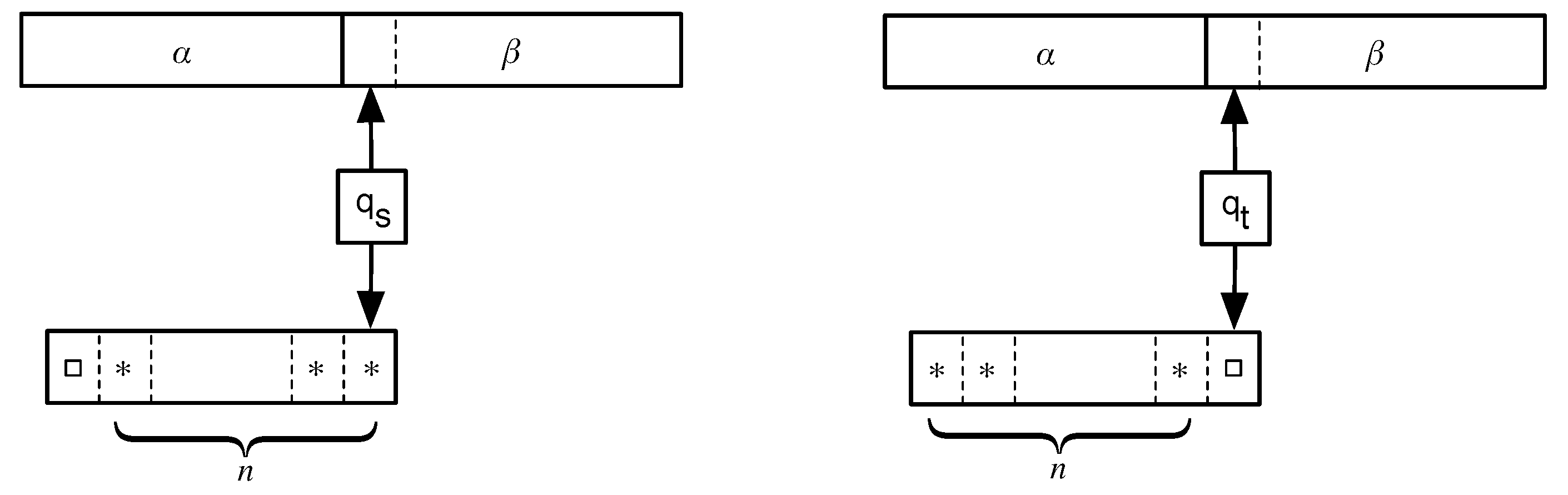
- 1.
- When the machine is in a source state , the counter head is on the rightmost ∗ of the counter tape, if , or on an empty cell, if . If the current counter symbol is a ∗, any transition in the state replaces such a ∗ with a □, and moves the counter head to the left, until the current counter symbol becomes a □, in which case the machine starts its main evolution.
- 2.
- When the machine is in a target state , the counter head is on the first empty cell of the counter tape to the right of the sequence of ∗. Any transition in the state replaces then the □ in the current counter cell with a ∗, and moves the counter head to the right.
- 3.
- When the state is neither a source nor a target state, the counter tape is empty, and any transition leaves the counter tape unchanged.
References
- Backus, J.W. The Syntax and Semantics of the Proposed International Algebraic Language of the Zurich ACM-GAMM Conference. In Proceedings of the 1st International Conference on Information Processing, UNESCO, Paris, France, 15–20 June 1959; pp. 125–132. [Google Scholar]
- McCarthy, J. A Basis for a Mathematical Theory of Computation. In Computer Programming and Formal Systems; Studies in Logic and the Foundations of Mathematics Series, Braffort, P., Hirschberg, D., Eds.; North-Holland Publishing Company, Elsevier B.V.: Amsterdam, The Netherlands, 1963; Volume 35, pp. 33–70. [Google Scholar]
- Dal Lago, U.; Masini, A.; Zorzi, M. Confluence Results for a Quantum Lambda Calculus with Measurements. Electron. Notes Theor. Comput. Sci. 2011, 270, 251–261. [Google Scholar] [CrossRef]
- Dal Lago, U.; Zorzi, M. Wave-Style Token Machines and Quantum Lambda Calculi. In Proceedings of the Third International Workshop on Linearity, LINEARITY 2014, Vienna, Austria, 13 July 2014; Alves, S., Cervesato, I., Eds.; Open Publishing Association: Waterloo, Australia, 2014; Volume 176, pp. 64–78. [Google Scholar] [CrossRef]
- Zorzi, M. On quantum lambda calculi: A foundational perspective. Math. Struct. Comput. Sci. 2016, 26, 1107–1195. [Google Scholar] [CrossRef]
- Viganò, L.; Volpe, M.; Zorzi, M. A branching distributed temporal logic for reasoning about entanglement-free quantum state transformations. Inf. Comput. 2017, 255, 311–333. [Google Scholar] [CrossRef]
- Paolini, L.; Roversi, L.; Zorzi, M. Quantum programming made easy. In Proceedings of the Joint International Workshop on Linearity & Trends in Linear Logic and Applications, Linearity-TLLA@FLoC 2018, Oxford, UK, 7–8 July 2018; Ehrhard, T., Fernández, M., de Paiva, V., de Falco, L.T., Eds.; Open Publishing Association: Waterloo, Australia, 2018; Volume 292, pp. 133–147. [Google Scholar] [CrossRef]
- Masini, A.; Zorzi, M. A Logic for Quantum Register Measurements. Axioms 2019, 8, 25. [Google Scholar] [CrossRef]
- Paolini, L.; Piccolo, M.; Zorzi, M. QPCF: Higher-Order Languages and Quantum Circuits. J. Autom. Reason. 2019, 63, 941–966. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. Ser. A 1985, A400, 97–117. [Google Scholar]
- Benioff, P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys. 1980, 22, 563–591. [Google Scholar] [CrossRef]
- Bernstein, E.; Vazirani, U. Quantum Complexity Theory. SIAM J. Comput. 1997, 26, 1411–1473. [Google Scholar] [CrossRef]
- Ozawa, M. Quantum Nondemolition Monitoring of Universal Quantum Computers. Phys. Rev. Lett. 1998, 80, 631–634. [Google Scholar] [CrossRef]
- Davis, M. Computability and Unsolvability; McGraw-Hill Series in Information Processing and Computers; McGraw-Hill Book Co. Inc.: New York, NY, USA, 1958. [Google Scholar]
- Conway, J.B. A Course in Functional Analysis, 2nd ed.; Graduate Texts in Mathematics Series; Springer: New York, NY, USA, 1990; Volume 96, xvi+399p. [Google Scholar]
- Roman, S. Advanced Linear Algebra, 3rd ed.; Graduate Texts in Mathematics Series; Springer: New York, NY, USA, 2008; Volume 135, xviii+522p. [Google Scholar]
- Nishimura, H.; Ozawa, M. Computational complexity of uniform quantum circuit families and quantum Turing machines. Theor. Comput. Sci. 2002, 276, 147–181. [Google Scholar] [CrossRef]
- Ozawa, M.; Nishimura, H. Local transition functions of quantum Turing machines. Theor. Inform. Appl. 2000, 34, 379–402. [Google Scholar] [CrossRef]
- Bennett, C.H. Logical reversibility of computation. IBM J. Res. Dev. 1973, 17, 525–532. [Google Scholar] [CrossRef]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; Oxford University Press: Oxford, UK, 2007; xii+274p. [Google Scholar]
- Isham, C.J. Lectures on Quantum Theory. Mathematical and Structural Foundations; Imperial College Press: London, UK, 1995; xii+220p. [Google Scholar]
- Linden, N.; Popescu, S. The Halting Problem for Quantum Computers. arXiv 1998, arXiv:quant-ph/9806054. [Google Scholar]
- Ozawa, M. Halting of Quantum Turing Machines. In Unconventional Models of Computation; Springer: Berlin/Heidelberg, Germany, 2002; pp. 58–65. [Google Scholar]
- Nishimura, H.; Ozawa, M. Perfect computational equivalence between quantum Turing machines and finitely generated uniform quantum circuit families. Quantum Inf. Process. 2009, 8, 13–24. [Google Scholar] [CrossRef]
- Yao, A. Quantum Circuit Complexity. In Proceedings of the 34th Annual Symposium on Foundations of Computer Science, Palo Alto, CA, USA, 3–5 November 1993; IEEE Press: Los Alamitos, CA, USA, 1993; pp. 352–360. [Google Scholar]
- Perdrix, S.; Jorrand, P. Classically controlled quantum computation. Math. Struct. Comput. Sci. 2006, 16, 601–620. [Google Scholar] [CrossRef]
- Selinger, P. Towards a Quantum Programming Language. Math. Struct. Comput. Sci. 2004, 14, 527–586. [Google Scholar] [CrossRef]
- Selinger, P.; Valiron, B. A lambda calculus for quantum computation with classical control. Math. Struct. Comput. Sci. 2006, 16, 527–552. [Google Scholar] [CrossRef]
- Dal Lago, U.; Masini, A.; Zorzi, M. On a Measurement-Free Quantum Lambda Calculus with Classical Control. Math. Struct. Comput. Sci. 2009, 19, 297–335. [Google Scholar] [CrossRef]
- Dal Lago, U.; Masini, A.; Zorzi, M. Quantum implicit computational complexity. Theor. Comput. Sci. 2010, 411, 377–409. [Google Scholar] [CrossRef]
- Myers, J.M. Can a universal quantum computer be fully quantum? Phys. Rev. Lett. 1997, 78, 1823–1824. [Google Scholar] [CrossRef]
- Kieu, T.D.; Danos, M. The Halting problem for universal quantum computers. arXiv 1998, arXiv:quant-ph/9811001. [Google Scholar]
- Hines, P. Quantum circuit oracles for Abstract Machine computations. Theor. Comput. Sci. 2010, 411, 1501–1520. [Google Scholar] [CrossRef]
- Miyadera, T.; Ohya, M. On Halting Process of Quantum Turing Machine. Open Syst. Inf. Dyn. 2005, 12, 261–264. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrini, S.; Martini, S.; Masini, A. Quantum Turing Machines: Computations and Measurements. Appl. Sci. 2020, 10, 5551. https://doi.org/10.3390/app10165551
Guerrini S, Martini S, Masini A. Quantum Turing Machines: Computations and Measurements. Applied Sciences. 2020; 10(16):5551. https://doi.org/10.3390/app10165551
Chicago/Turabian StyleGuerrini, Stefano, Simone Martini, and Andrea Masini. 2020. "Quantum Turing Machines: Computations and Measurements" Applied Sciences 10, no. 16: 5551. https://doi.org/10.3390/app10165551
APA StyleGuerrini, S., Martini, S., & Masini, A. (2020). Quantum Turing Machines: Computations and Measurements. Applied Sciences, 10(16), 5551. https://doi.org/10.3390/app10165551





