Influence of Blade Leading-Edge Shape on Rotating-Stalled Flow Characteristics in a Centrifugal Pump Impeller

Featured Application

This study can be applied to turbomachinery flow cases for energy loss study and flow-induced noise evaluation.

Abstract

Rotating stall, which is a common phenomenon in turbomachinery, strongly relates to the flow rate condition. In centrifugal impellers, rotating stall was induced by the incidence angle on blade leading-edge at partial-load. The blade leading-edge shape also influences the rotating stall because of the subtle change of local flow-field. In this study, the influence of blade leading-edge shape on rotating-stalled flow characteristics was studied in a six-blade centrifugal pump impeller. The stall pattern was “alternating”: Three passages were stalled, three passages were well-behaved, and the stalled and well-behaved passages occurred alternately. The stalled flow characteristics can be studied without the interruption of stall cell movement. Four types of blade leading-edge (blunt, sharp, ellipse, and round) were numerically compared based on the initial typical impeller and the numerical–experimental verification. The numerical comparison shows that the leading-edge shape has a strong influence on the stalled flow pattern, velocity, pressure, turbulence kinetic energy, and flow-induced noise inside impellers. The blunt and sharp leading-edge impellers had a similar internal pattern; the ellipse and round leading-edge impellers were also similar in the internal flow-field. Pressure pulsation analysis showed more obvious differences among these impellers. The main frequency and the pulsation peak–peak values were completely different because of the slight leading-edge shape differences. It revealed the impact of leading-edge geometry on the transient flow-field change under the same incidence angle conditions. It also provided reference for influencing or controlling the rotating stall by blade profile design.

1. Introduction

When designing a pump impeller, two main targets need special considerations. Firstly, operation efficiency at design load is important. Secondly, reliability at off-design load is also crucial, because the pump usually operates off from the design condition [1]. The puzzle of how to improve the pump efficiency at design load has been solved with many typical methods in the past decades [2]. The current works are applying these methods for specific cases [3,4,5]. On the contrary, flow inside pump impeller under off-design conditions are treated as uncontrollable. The internal flow becomes complex at off-design load, especially at partial-load, with noise, vibration, and other undesirable phenomena [6,7]. These phenomena would affect the stability and security of the pump unit, and even cause faults.

Under the design flow rate condition Q = Q_d, flow is along the impeller blade geometry with high efficiency. From design load to partial load, the incidence angle becomes higher and higher and causes undesirable flow on the blade suction side [8]. Typically, the undesirable flow develops in three steps. Firstly, small-scale flow separation occurs on the blade suction side [9]. Secondly, backflow occurs at both the inlet and outlet of the impeller. Passage blockage happens and brings vibration and efficiency drop [10]. Thirdly, the inlet and outlet backflow structures expand and block the entire passage [11]. Among them, the second stage, which may cover the flow rate from 0.3 to 0.8 Q_d, is complex and important, because pumps usually operate in this flow rate range with partial passage blockage. Emmons [12] used “rotating stall” to describe this complex changing blockage and distinguish it against “surge”. In actual pumps and compressors, impeller eccentricity or asymmetricity may exist due to installation, manufacturing, and instantaneous flow destabilization [13]. Affected by the eccentricity or asymmetricity, the blocked flow turns into neighboring passages, as shown in Figure 1a. In the neighboring passage rotational, turned flow strikes the suction surface and diminishes part of the stall cell. In the neighboring passage, counter-rotational, turned flow strikes the pressure surface and increases the scale of the stall cell. The asymmetric distribution of stall cell moves counter-rotationally during impeller rotation. It makes the flow regime more complicated.

Many researchers studied the rotation stall mechanism and influences [14,15,16,17]. Because of the compressibility of the fluid medium, people mainly focused on the rotating stall in aerodynamic turbomachines like compressors. Cumpsty [18] studied the mechanism of rotating stall and explained the partial passage blockage as an adaptability of small flow rate. Cossar et al. [19] experimentally tested the rotating stall in axial-flow compressors. The stall cell was found starting from the trailing-edge and developing to the leading-edge. Experiences show that the rotating stall is relative to the incidence angle at the leading-edge and the flow distortion at inlet [20,21]. The counter-rotational movement of the stall cell [12] is found relative to the impeller rotation. The stall frequency will be 1/5~1/2 impeller rotating frequency in different cases [19]. Based on the mechanism studies, Weigl [22], Day [23], Behnken et al. [24], and Suder et al. [25] investigated the controlling method of rotating stall, using different methods in the past. The sound generated by the rotating stall was also studied by Mongeau et al. [26]. Low-frequency noise from the impeller was found to be relative to the rotating stall. Currently, researchers still focus on the rotating stall phenomenon in turbomachinery, which has complicated flow characteristics [27,28,29]. In pumps which usually transport incompressible fluids, researchers have also studied the rotating stall characteristics. Krause et al. [30] studied the rotating stall in a radial pump and provided time-resolved particle image velocimetry (PIV) measurements in the impeller passages. A spatially stable stall cell was found in the passage and analyzed on its frequency. Sinha [17] studied the flow structure during onset and developed states of rotating stall in centrifugal pump’s guide vane. The movement and frequency of rotating stall was discussed. Takamine et al. [31] discussed the diffuser rotating stall in a three-stage centrifugal pump, and the mechanism of the widen onset range of rotating stall was well explained. Pedersen et al. [32] showed a static alternating stall pattern in a centrifugal pump by PIV and laser Doppler velocimetry (LDV) measurements. In the six-blade impeller, three stalled and three un-stalled passages were observed, as shown in Figure 1b. The well-behaved passages and stalled passages occurred alternately and were cite-fixed without periodically moving.

Above all, the rotating stall in pumps were also strongly related to the local flow around the blade leading-edge, which was mainly the incidence angle. The leading-edge shape also influences the local flow field [33,34]. However, there is a lack of discussion on the influence of leading-edge shape on rotating stall. Thus, in this study, numerical simulation was conducted to compare the rotating stall characteristics for different leading-edge geometries, based on the experimental measurement by Pedersen et al. [32], at partial-load of a centrifugal pump impeller. The velocity, turbulence kinetic energy, pressure pulsation, and noise are discussed in detail.

2. Pump Impeller Object

In this study, the impeller investigated by Pedersen et al. [32] was used as the studied object. Its design flow rate, Q_d, is 3.06 kg/s, and its angular rotating speed is ω = 725 r/min (revolution per minute). This is a typical pump impeller with six untwisted blades (blade number Z = 6) and widely studied by researchers [35,36]. In this case, the quarter partial-load condition Q = 0.25 Q_d, which is about 0.76 kg/s, was analyzed. As shown in Figure 2, the impeller inlet radius is R₁ = 35.5 mm, the impeller outlet radius is R₂ = 95 mm, the impeller leading-edge width is b₁ = 13.8 mm, and the impeller trailing-edge width is b₂ = 5.8 mm. For single stage simulation, the impeller domain was modeled with inlet and outlet extension. The inlet extension is e₁ = 0.5 R₂, and the outlet extension is e₂ = 0.125 R₂.

3. Numerical Modeling and Setup

3.1. Turbulence and Acoustic Modeling

In this case, the Reynolds-Averaged Navier–Stokes (RANS) equations were used for turbulence flow. The zonal-mixed turbulence model SST (Shear Stress Transport) k-ω model [37] was applied. Its k equation and ω equation can be expressed as follows:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho u_{i}k\right)}{\partial x_i}=P-\frac{\rho k^{3/2}}{l_{k-\omega }}+\frac{\partial }{\partial x_i}\left[\left(\mu +{\sigma }_k{\mu }_t\right)\frac{\partial k}{\partial x_i}\right]$$

(1)

$$\frac{\partial \left(\rho \omega \right)}{\partial t}+\frac{\partial \left(\rho u_i\omega \right)}{\partial x_i}=C_{\omega }P-\beta \rho {\omega }^2+\frac{\partial }{\partial x_i}\left[\left({\mu }_l+{\sigma }_{\omega }{\mu }_t\right)\frac{\partial \omega }{\partial x_i}\right]+2\left(1-F_1\right)\frac{\rho {\sigma }_{\omega 2}}{\omega }\frac{\partial k}{\partial x_i}\frac{\partial \omega }{\partial x_i}$$

(2)

where t denotes the time, ρ the density, u the velocity, and x the coordinate. P is the production term, μ is the dynamic viscosity, μ_t is the turbulent eddy viscosity, σ is the model constants, C_ω is the coefficient of the production term, and l_k-ω is the turbulence scale. F₁ is the zonal mixture function, which is used to combine the standard k-ε model and Wilcox’s k-ω model.

To improve the sensitivity of streamline curvature and system rotation, the Spalart–Shur correction [38] was also applied, accompanied by the SST k-ω turbulence model. It adds the correction term f_r1 as a multiplier on the production term P_k. Moreover, f_r1 has its specific limiters:

$$f_{r1}=\max \left[0,1+C_s\left(f_r^{*}\right)\right]$$

(3)

$$f_r^{*}=\max \left[\min \left(f_{rot},1.25\right),0\right]$$

(4)

$$f_{rot}=\left(1+C_{r1}\right)\frac{2r^{*}}{1+r^{*}}\left[1-C_{r3}{\tan }^{-1}\left(C_{r2}\widehat{r}\right)\right]-C_{r1}$$

(5)

where C_s is the correction scaling factor. The constants C_r1, C_r2, and C_r3 are equal to 1.0, 2.0, and 1.0. The remaining functions are defined as follows:

$$r^{*}=\frac{S}{\Omega }$$

(6)

$$\Omega =\sqrt{2{\Omega }_{ij}{\Omega }_{ij}}$$

(7)

$$\widehat{r}=\frac{2{\Omega }_{ik}{S}_{jk}}{\Omega B^3}\left[\frac{D{S}_{ij}}{Dt}+\left({\epsilon }_{imn}{S}_{jn}+{\epsilon }_{jmn}{S}_{in}\right){\Omega }_m^{rot}\right]$$

(8)

$$B^2=\max \left(S^2,0.09{\omega }^2\right)$$

(9)

where Ω^rot is the rotation rate of the reference frame, and DS_ij/D_t is the Lagrangian derivative of the strain rate tensor.

In this study, the Lighthill acoustic analogy method was used to analyze the near-field of noise in the pump impellers. Proudman [39] introduced a sound power calculation method for the flow-induced noise:

$$W_A={\alpha }_{\epsilon }\rho \epsilon M_t^5$$

(10)

where α_ε is a constant which can be valued as 0.1, ρ is the density, ε is the eddy dissipation rate, and M_t can be expressed as follows:

$$M_t=\frac{\sqrt{2k_{2D}}}{c}$$

(11)

where c is the sound speed, which is 1500 m/s in water. Thus, the sound power level, L_sp, can be calculated as follows:

$$L_{sp}=10 {\log }_{10}\left(\frac{W_A}{W_{ref}}\right)$$

(12)

where W_ref is the reference sound power in water, which is about 6.7 × 10⁻¹⁹ W/m³.

3.2. Computational Fluid Dynamics Setup

Computational fluid dynamics (CFD) method was used for flow simulation. The impeller domain shown in Figure 3a was discretized by tetrahedral unstructured mesh elements. The mesh number was checked to balance the simulation accuracy and the time-cost. The residual of the hydraulic efficiency was checked for determining the final mesh scheme. The mesh schemes with about 0.16, 0.32, 0.60, 1.5, and 3.1 million nodes (different leading-edge shape has similar but different mesh node number) are checked by monitoring the residual of the hydraulic efficiency for less than 1%. As an example, the mesh check detail of the initial leading-edge impeller is shown in Figure 3b and

Table 1. Mesh independence check details.

No.	Mesh Node Number of Initial Impeller	Residual of Hydraulic Efficiency
1	159,836	-
2	323,332	2.53%
3	602,024	1.32%
4	1,500,322	0.951%
5	3,112,086	0.217%

. After checking, we see the meshes for different leading-edge impellers have about 1.5 million nodes and 6.0 million elements. Figure 3 shows the schematic map of mesh.

Based on the domain, three types of boundaries are given:

(a)

Velocity inlet was given on the inlet boundary. The velocity value depends on the flow rate Q = 0.25 Q_d. On this boundary, pressure followed the Neumann condition;

(b)

Pressure outlet was given on the outlet boundary. The average static pressure was 0 Pa, based on the environment pressure of 1 Atm. On this boundary, velocity followed the Neumann condition;

(c)

No-slip walls were set on the solid walls, including the blade, hub, and shroud.

The fluid medium is set as water at 20 °C. Steady state simulation was conducted before transient simulation. The maximum iteration number was 1000 for steady state, with convergence criteria of RMS (root mean square) value less than 1 × 10⁻⁵. The transient simulation was conducted because the flow was continually changing during rotation. A total of 360 time-steps were set for each revolution. The maximum iteration number for each time-step was 10 for transient state with convergence criteria of RMS value less than 1 × 10⁻⁵.

4. Computational–Experimental Result Verification

Computational fluid dynamics (CFD) method was used for predicting the flow field in centrifugal pump impellers with different leading-edge shapes. To have an accurate computational result, a computational–experimental result verification was conducted at first. The relative velocity, V, vectors on the spanwise 50% surface, the contour of turbulence kinetic energy (k_2D) on the spanwise 50% surface, and the relative radial velocity (V_r/U₂) distribution on the spanwise 50% surface at R = 0.9 R₂ were compared. U₂ denotes the rotational linear velocity at R = R₂.

Figure 4 shows the CFD predicted relative velocity (V) vectors on the spanwise 50% surface. It can be compared with the experimental data by Pederson et al. in Ref. [32]. The alternate stall pattern, which includes three well-behaved and three stalled passages, can be observed in the impeller. The symbols “A” and “B”—“A” denotes the well-behaved passage, and “B” denotes the stalled passage—were drawn on this figure. CFD simulation captured the flow separation at leading-edge on the blade suction side and the backflow near the outlet in the B passage. The large-scale “vortex” flow was also found in the middle of the B passage. These undesirable flow structures were also measured in the experiment.

Figure 5 shows the CFD-predicted contour of turbulence kinetic energy (k_2D) on the spanwise 50% surface, compared with the experimental data in Ref. [32]. There were three high k_2D cites captured. Firstly, a high k_2D cite occurred at the leading-edge flow separation region in the B passage. Secondly, a high k_2D cite occurred on the blade suction side in the middle of the A passage. Thirdly, a high k_2D cite generated at the impeller outlet in the B passage. These three high k_2D cites were also captured in the experiment, which proved the CFD simulation to be relatively accurate. However, there is a deviation that shows the experimental k_2D value at the impeller outlet was stronger than CFD simulation. In this computational case, only the impeller domain was considered. In the experimental study of Reference [32], a vaned-diffuser was set downstream to the impeller. The intensity of k_2D would be influenced by the vaned-diffuser. In this study, the main target was to compare the internal flow among different leading-edge impellers. Thus, the CFD simulation can be considered correct and accurate.

To have a better comparison near impeller outlet, the radial velocity, which represents the flow direction, was compared at R = 0.9 R₂. Figure 6 compares the relative radial velocity, V_r/U₂, distribution on the spanwise 50% surface at R = 0.9 R₂. Generally, the distribution laws were similar between the CFD data and the experimental data. In detail, in the A passages, the radial velocity from the CFD simulation was larger than that from by experimental test. In the middle of the B passages, the CFD-predicted radial velocity was higher than that of the experimental data. These two differences might also be influenced by the downstream vaned-diffuser and may have changed the local velocity intensity.

Above all, the CFD simulation in this study correctly predicted the internal flow in the centrifugal pump impeller. The predictions of velocity and turbulence kinetic energy were reasonable and reliable. Thus, the CFD simulations can be used for further comparisons among different leading-edge impellers.

5. Leading-Edge Reshaping

To compare the influence of different leading-edge shapes, the initial impeller [32] was reshaped on the leading-edge, as shown in Figure 7. The blunt, sharp, round, and ellipse leading-edges were created step by step. Firstly, the initial leading-edge geometry was extended along the meanline and its perpendicular direction. The blunt leading-edge was created, and its width was L_LE. Secondly, we cut the two sides off by S_LE = 0.5 L_LE, to create the sharp leading-edge. Thirdly, the leading-edge geometry was changed to be an arc and generated the round leading-edge, whose radius was R_LE = 0.5 L_LE. Finally, the arc of the round leading-edge was changed to an elliptical arc and generated the ellipse leading-edge, whose long axis is a_LE = 2 L_LE, and short axis b_LE = L_LE.

6. Comparative Results and Analysis

6.1. Alternating Stall Patterns

The internal flow patterns were predicted by CFD simulation. Figure 8 indicates the streamlines in the impellers with different leading-edge shape on the spanwise 50% plane. As in the situation in the initial impeller, the alternating stall patterns were observed in the blunt, sharp, ellipse, and round impellers. As indicated by “A”, there were three well-behaved passages in each impeller. As indicated by “B”, three stalled passages also existed in each impeller. The A and B passages distributed alternately. The backflow regions in the blade passages, which are indicated by red-dash circles, had relative fixed cites during impeller rotation.

Differences were found when comparing the pattern in different impellers. In the blunt and sharp leading-edge impellers, the B passages were completely blocked by undesirable flow characters. Two backflow regions were generated in the B passages. The smaller one was located between two blades’ leading-edge, and the larger one blocked the passage from the middle passage to the trailing-edge. The A passages were smooth, without obvious blockage. In the ellipse and round impellers, the B passages were almost blocked by undesirable flow characters with two equal-scale backflow regions. One was located from the leading-edge to middle passage, and the other was located from the middle passage to trailing-edge. The A passages were also slightly blocked with a small backflow region near the blade suction side in the middle passage.

6.2. Impeller Performances

Considering the difference of streamline patterns in different impellers, it is necessary to compare the impeller performance based on the initial impeller [32]. Figure 9 compares the difference in pump head, as an example of the performance. The pump impeller head, H, can be calculated as follows:

$$H=\frac{\mathrm{\Delta }{p}_{total}}{\rho g}$$

(13)

where Δp_total is the difference of total pressure in stationary frame between the impeller outlet and inlet, ρ is the density of fluid medium, and g is the acceleration of gravity. As shown in Figure 9, H_ini is the CFD-predicted head of the initial impeller. The H values of the blunt and sharp impellers were lower than the initial impeller by 0.21% and 0.33%, respectively. The H values of the ellipse and round impellers were higher than those of the initial impeller by 1.31% and 1.54%, respectively.

Figure 10 comparatively shows the hydraulic efficiency of different impellers. The hydraulic efficiency η can be calculated as follows:

$$\eta =\frac{\rho gQH}{M\omega }$$

(14)

where Q is the flow rate; M is the total torque on blades, impeller hub, and shroud; and ω is the rotational angular speed of impeller. The η values were between 0.901 and 0.905. The differences were very slight. The ellipse impeller has the highest value, η = 0.905, which is also higher than the initial impeller (η = 0.904). Generally, the hydraulic efficiency has no obvious law among these impellers.

6.3. Contours of Flow-Field under Alternating Stall

6.3.1. Pressure Coefficient C_p

Based on the alternating stall pattern and the differences among different impellers, the flow-field was also compared by plotting relevance parameters in contours. Firstly, the pressure distributions in the impellers were important. The dimensionless pressure coefficient, C_p, was used:

$$C_p=\frac{p-p_{\infty }}{\rho gH}-\frac{V_{\infty }^2}{2gH}$$

(15)

where p is pressure, p_∞ is the reference pressure on the impeller inlet boundary, and V_∞ is the reference velocity on the impeller inlet boundary.

Figure 11 shows the contour of the pressure coefficient, C_p, on the spanwise 50% surface. Caused by the backflow region near leading-edge, the wide low-pressure region occurred at the inlet of B passages in the blunt and sharp impellers. The pressure value near the leading-edge in the A passages was at a relative high level, because all of the fluid smoothly flowed into A passages. Differently, the low-pressure region near the leading-edge is much narrower in the ellipse and round impellers. However, local pressure-drop can be found on the suction side of every blade’s leading-edge. It means that leading-edge flow separation also happened in the A passages in the ellipse and round impellers. This is why backflow “vortex” also exists in the A passages.

6.3.2. Turbulence Kinetic Energy (k_2D)

Figure 12 shows the contour of turbulence kinetic energy, k_2D, on the spanwise 50% surface in these impellers. It is found that high k_2D region covered the B passages’ inlet in all the impellers. In the blunt and sharp impellers, the k_2D values at the A passages’ inlet were small. In the ellipse and round impellers, a high k_2D region can be observed at the A passages’ inlet, near the suction surface. The high k_2D region covered nearly half of the A passages’ inlet. Thus, it can be recognized that high k_2D region and flow blockage were relative to the backflow characteristics.

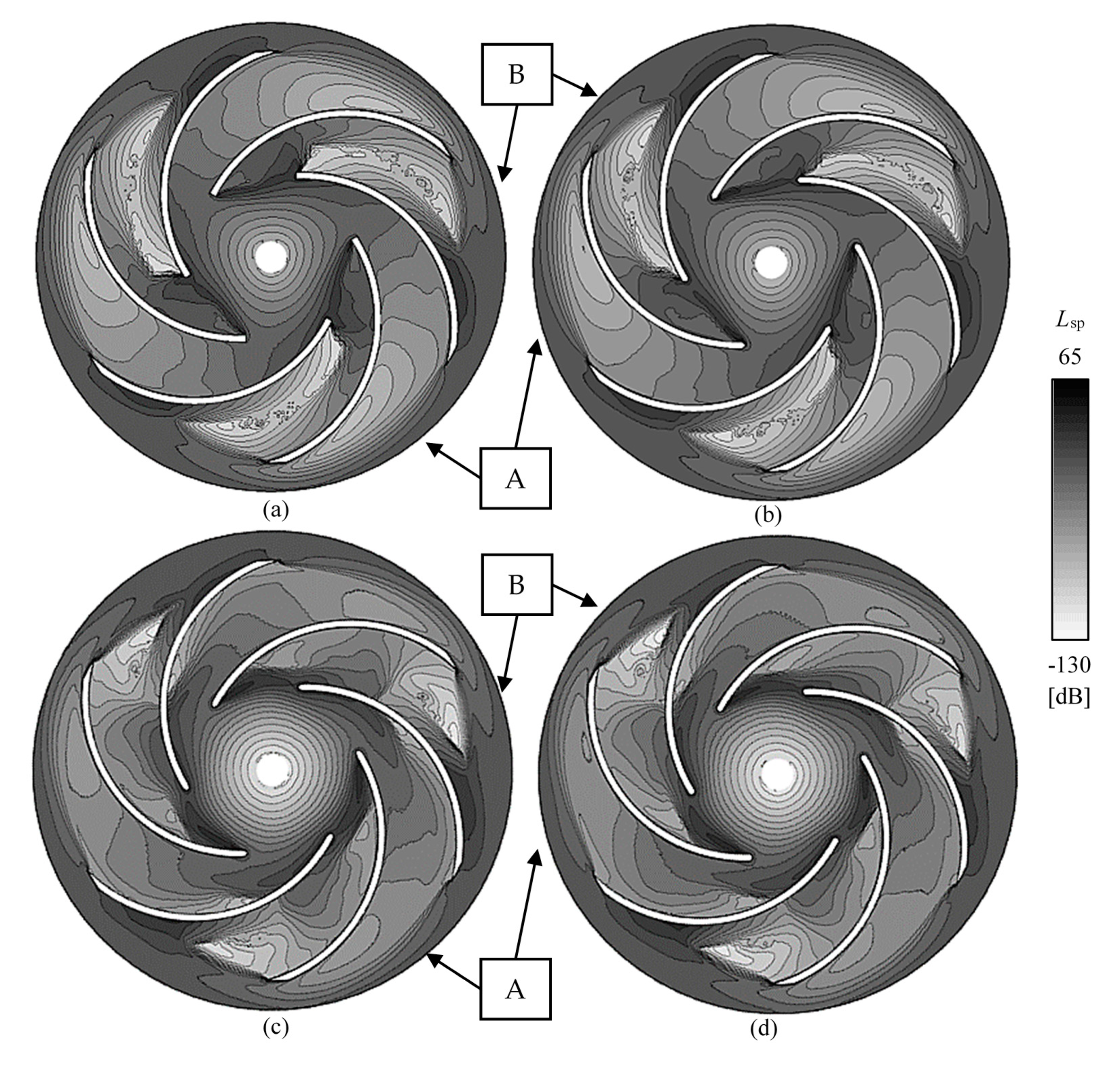
6.3.3. Sound Power Level (L_sp)

Figure 13 shows the contour of the flow-induced sound power level, L_sp, on the spanwise 50% surface in these impellers. According to Equation (10) to Equation (12), the sound power level was dominated by the turbulence kinetic energy when sound speed was a constant. Comparing Figure 13 to Figure 12, we see that the high noise was induced by high turbulence kinetic energy. In the blunt and sharp impellers, the L_sp value near the blade leading-edge was higher than that in the ellipse and round impellers. However, high L_sp regions can be found in the A passages in the ellipse and round impellers, due to the high k_2D regions’ existence.

6.4. Pressure Pulsations

Considering the cite-fixed alternating stall and its different performances in different blade passages of these different impellers, the pressure pulsations were monitored and analyzed. As shown in Figure 14, three monitoring points were set in an A passage: P_Ain, P_Amid, and P_Aout. At the same time, three monitoring points were set in the neighbor B passage: P_Bin, P_Bmid, and P_Bout. The pressure pulsations were monitored for more than 10 revolutions, as they became stable or rotating-periodic in changing. The time-domain data were handled by the fast Fourier transform (FFT) method with Hanning window. The time-domain and frequency-domain plots are shown below.

Figure 15 shows the pressure pulsations in the blunt leading-edge impeller. Periodic variation was obvious on the time-domain plot. In the A passage, the pressure pulsation amplitude is relatively high, with peak–peak values of about 5 × 10⁻⁶ Pa, on P_Ain and P_Amid. On P_Aout, the pressure pulsation amplitude decreased to a lower level. In the B passage, the pressure pulsation amplitude is relatively high, with peak–peak values larger than 6 × 10⁻⁶ Pa, on P_Bin. Because of the blockage and strong backflow, the pressure pulsation amplitude on P_Bmid and P_Bout became much lower.

The frequency-domain plot shows the frequencies on each point. These points were all dominated by frequency f_mb, which is 9.67 Hz. This frequency was about 4/5 rotating frequency. Frequency 5 f_mb can be found in the A passage. Another frequency of 370 Hz was obvious on P_Amid and was widened to a band of 350~380 Hz. Frequencies 3 and 5 f_mb can be found in the B passage. On P_Bin and P_Bmid, 3 and 5 f_mb frequencies were both obvious. On P_Bout, 5 f_mb was obvious. Another frequency band of 140~200 Hz was found on P_Bin. It disappeared on P_Bmid and P_Bout.

Figure 16 shows the pressure pulsations in the sharp leading-edge impeller. The waveform of the pressure pulsations was also periodic. The peak–peak value on P_Bin was the largest among the six monitoring points. It was about 1.2 × 10⁻³ Pa. The peak–peak values on the other five points were about 4 × 10⁻⁴ Pa~5 × 10⁻⁴ Pa. Generally, the pressure pulsation intensity in the sharp leading-edge impeller was approximately 100 times that of the blunt leading-edge impeller.

As shown in Figure 16b, the frequency of pressure pulsation in the sharp leading-edge impeller was dominated by three frequencies. Firstly, the main frequency (with the highest amplitude) was f_ms = 0.81 Hz on all six points. Moreover, f_ms is about 0.067 rotating frequency. Secondly, there was a vice frequency of about 2 f_ms. Thirdly, the frequency of about 3 f_ms was also obvious in the A passage. The frequency of about 3 f_ms was widened to a band of 3.2 ~4.9 Hz, which was about 4~6 f_ms in the B passage.

When comparing the pressure pulsation characteristics between the blunt impeller and sharp impeller, we can find differences on both the peak–peak values and the frequency values. Even though the instantaneous flow patterns in the blunt and sharp impellers were similar, the slight change of leading-edge shape can strongly influence the pressure pulsation that represented the subtle change of flow field.

Figure 17 shows the pressure pulsations in the ellipse leading-edge impeller. Based on the waveform, it was observed that the pressure pulsation peak–peak values became much higher than in the blunt and sharp impellers. The peak–peak values were especially high on P_Bin and P_Bmid, as they were about 1.2 × 10⁻² Pa and 1.0 × 10⁻² Pa, respectively. The peak–peak values on the other points were about 3 × 10⁻³ Pa~5 × 10⁻³ Pa, which were also higher than in the blunt and sharp impellers.

As in the sharp leading-edge impeller, there were also three obvious frequencies. Firstly, the main frequency was f_me = 2.41 Hz, which was approximately 1/5 rotating frequency. The second and third dominant frequencies were 2 and 3 f_me, which are also indicated on Figure 17. Another low-frequency band can be observed on all the points, especially on P_Amid, P_Bin, and P_Bmid. This low-frequency band covered about 0.2~1.4 Hz.

Figure 18 shows the pressure pulsations in the round leading-edge impeller. The peak–peak value on P_Amid was around 1.8 × 10⁻² Pa, which was the highest among the six points. The peak–peak value was around 1.0 × 10⁻² Pa on P_Bin and much smaller on the other four points. Generally, in the A passage, pressure pulsation was high in the middle of the passage. In the B passage, pressure pulsation was high in the inlet and decreased gradually from the inlet to middle-passage to outlet.

According to the frequency-domain plot, the main frequency on all six points was f_mr = 1.00 Hz, which was 0.083 rotating frequency. However, a wide frequency band covered around the main frequency. The band was approximately from 0.33 to 1.35 Hz. Another peak, 3.33 Hz, can be found on the frequency-domain plot.

The instantaneous flow patterns in the ellipse and round leading-edge impellers were similar. However, the frequency of pressure pulsation characteristics was different. The main frequencies were also different, as listed in

Table 2. Main/dominant frequency value in the impellers with different leading-edge shape.

Leading-Edge Shape	Main Frequency fm (Hz)	fm/frt (Rotating Frequency)
Blunt	9.67	0.8
Sharp	0.81	0.067
Ellipse	2.41	0.2
Round	1.00	0.083

. Comparing among all the four types of impellers, the blunt leading-edge impeller had the smallest amplitude of pressure pulsation but a noisier frequency pattern. On the contrary, the ellipse and round had the strongest pulsation amplitudes, but the frequency pattern is relatively pure.

Table 3. Obviously seen frequencies and frequency bands in different leading-edge shape impellers.

Leading-Edge Shape	Obvious Frequencies/Frequency Bands
Blunt	fmb, 3 fmb, 5 fmb, 14.5~20.7 fmb and 36.2~39.3 fmb
Sharp	fms, 2 fms, 3 fms and 4~6 fms
Ellipse	fme, 2 fme, 3 fme
Round	0.33~1.35 fmr (including 1.0 fmr)

shows the obvious frequencies or frequency bands on the frequency-domain plots of all the four leading-edge types of impellers. These obvious frequencies and frequency bands are denoted by their main frequency values: f_mb, f_ms, f_me, and f_mr. As shown in Table 3, the obvious frequencies or bands are complex, with five parts in the blunt leading-edge impeller. The 5 parts are f_mb, 3 f_mb, 5 f_mb, 14.5~20.7 f_mb and 36.2~39.3 f_mb. In the sharp leading-edge impeller, it is also complex with 4 obvious frequencies or bands that f_ms, 2 f_ms, 3 f_ms and 4~6 f_ms which are relatively ordered. In the ellipse leading-edge impeller, the obvious frequencies or bands becomes purer with only 3 very ordered parts that f_me, 2 f_me, 3 f_me. In the round leading-edge impeller which is the most hydrodynamic, there is only one obvious frequency band that 0.33~1.35 f_mr which includes the main frequency of 1.0 f_mr. Generally, Table 2 and Table 3 reveal the difference of the subtle transient change of flow field induced by different leading-edge shapes.

7. Conclusions

By comparing the flow pattern, impeller performance, internal flow field distribution, and pressure pulsation, the following conclusions can be drawn:

(1)

At partial-load (0.25 Q_d in this study), incoming flow struck on the blade leading-edge on the pressure surface. Flow separation happened on the blade suction surface and induced the passage blockage. In this case, an alternating stall pattern was found in the impellers. In the six blade passages, three passages were well-behaved, and three passages were stalled (flow-blockage caused by backflow structures). The well-behaved and stalled passages distributed alternately and cite-fixed during rotation.

(2)

Leading-edge shape strongly influenced the alternating stall pattern and showed differences. In the blunt and sharp leading-edge impellers, the leading-edge geometry had sudden turned corners. Flow direction suddenly changed at the corner with large-scale separation. The stalled passages were completely blocked. Fluid went into the well-behaved passages. The flow pattern in the well-behaved passages was very smooth, without undesired flow structures, meaning that only three passages were accessible. In the ellipse and round leading-edge impellers, the geometry continually changed on the arc or elliptical-arc without sudden turning. The backflow scale in the stalled passages was smaller with slight accessibility because the leading-edge separation was not so strong. The flow rate in the well-behaved passages became smaller, and some backflow “vortex” structures occurred on the blade suction side.

(3)

Because of the difference of the leading-edge shape, the internal flow field became different. In the blunt and sharp leading-edge impellers, an extremely low-pressure region occurred at the inlet of the stalled passage. The pressure at the inlet of the wall-behaved passage was on a higher level. A high turbulence kinetic energy region occurred mainly in the stalled passage due to strong leading-edge separation. In the ellipse and round leading-edge impellers, a small-scale low-pressure region occurred on each blade’s leading-edge. The pressure distribution near the blade inlet was somehow averaged. A high turbulence kinetic energy region occurred in both the well-behaved passages and the stalled passages. It revealed the flow instability in all the blade passages of the ellipse and round leading-edge impellers.

(4)

The flow pattern in the blunt leading-edge impeller was similar to that in the sharp leading-edge impeller. Moreover, the flow pattern in the ellipse leading-edge impeller was similar to that in the round leading-edge impeller. However, the pressure pulsation characteristics in the four types of impellers were completely different. In the blunt leading-edge impeller, frequency of 9.67 Hz dominated. The amplitude of pressure pulsation on the monitoring points was up to about 6 × 10⁻⁶ Pa. In the sharp leading-edge impeller, a frequency of 0.81 Hz dominated. The amplitude of pressure pulsation on the monitoring points was up to about 1.2 × 10⁻³ Pa. In the ellipse leading-edge impeller, frequency of 2.41 Hz dominated. The amplitude of pressure pulsation on the monitoring points was up to about 1.2 × 10⁻² Pa. In the round leading-edge impeller, a frequency of 1.00 Hz dominated. The amplitude of pressure pulsation on the monitoring points was up to about 1.8 × 10⁻² Pa.

Above all, blade leading-edge shape strongly influenced the rotating stall behavior of the centrifugal pump impeller. For fixed blades, the flow angle and blade angle are unchanged under a specific flow rate condition. At this time, the difference of leading-edge shape may cause differences on velocity field, pressure field, turbulence kinetic energy, flow-induced noise, and pressure pulsations. In the stability or flow-control design of the centrifugal pump, especially at partial-load, the determination of the leading-edge shape will be crucial. A reasonable leading-edge geometry will be helpful for reducing undesirable flow characteristics and enhancing the flow stability.