Study of the Effect of Exploiting 3D Semantic Segmentation in LiDAR Odometry
Abstract
:1. Introduction
2. Related Work
3. Methodology
3.1. Data
3.2. Input Configurations
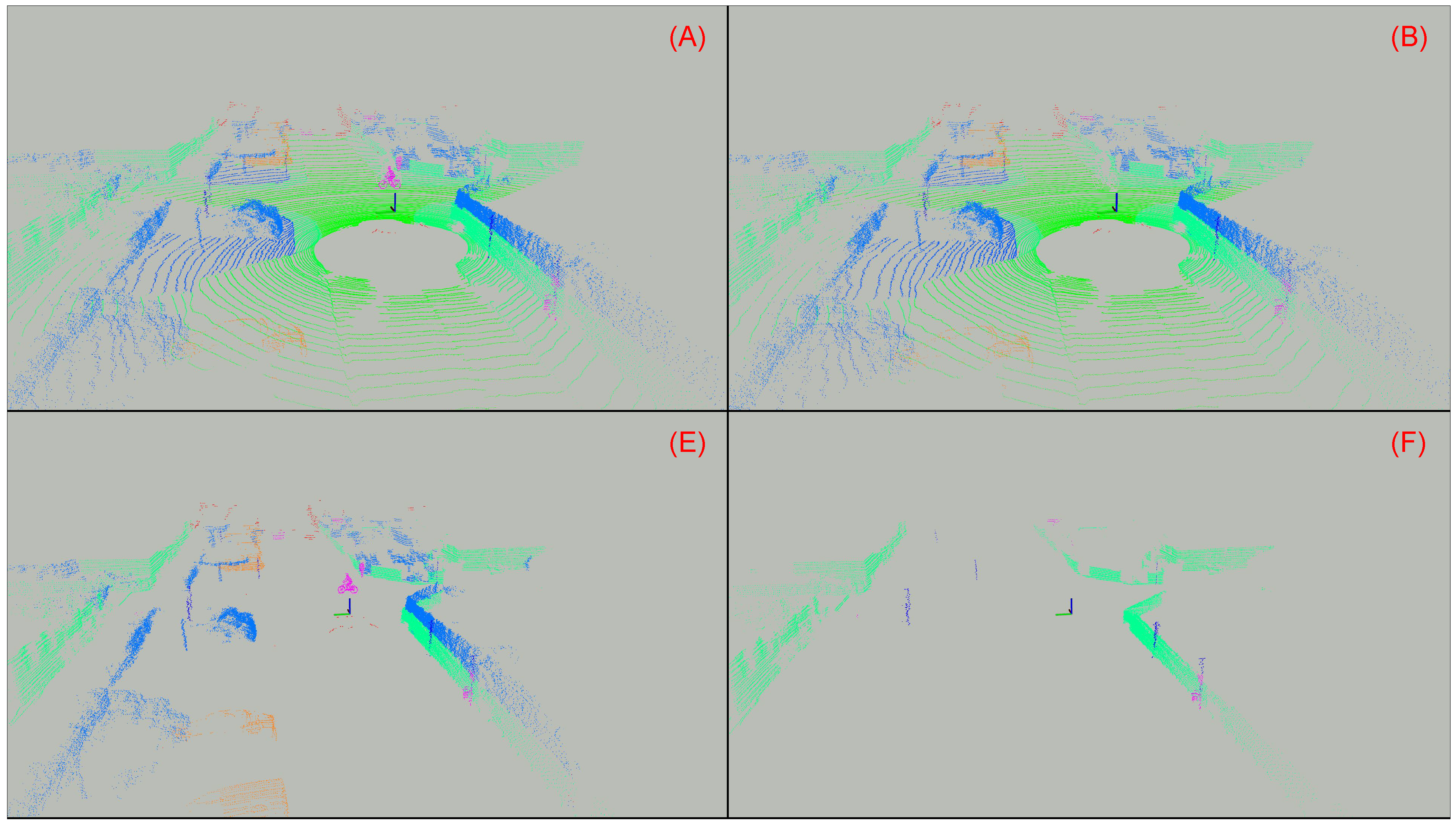
- (A)
- Raw: Raw original point cloud from the KITTI dataset. This configuration serves as the baseline for the comparison.
- (B)
- Dynamic: Remove all dynamic objects from the point cloud, i.e., vehicles and pedestrians. As stated in other works (e.g., [8]), dynamic objects are a source of spurious correspondences in the matching, leading to erroneous estimations.
- (C)
- Dynamic Vehicles: Remove only dynamic vehicles from the point cloud. The only difference between this configuration and the previous one is that pedestrians are not removed from the point cloud. The hypothesis that motivates this configuration is that, due to their smaller size and lower velocity, the contribution of pedestrians to the error may be negligible.
- (D)
- Far: Remove all points that are far from the vehicle. All points p with a distance m are removed from the point cloud. This configuration is motivated by the fact that LiDAR point clouds are dense and rich in details in close distances, but become more sparse over the distance, thus far points may introduce more noise to the system.
- (E)
- Ground: Remove the ground points. Removing the ground from the point cloud may have some advantages, but also some disadvantages. On the one hand, the rings of the LiDAR sensor that lay on the ground (assuming it is planar) will always have the same appearance. This should result in a misconceiving of the translation part because all those points will have the same coordinates in different frames, even if the vehicle was moving. On the other hand, ground points may be helpful for the rotation part, particularly for pitch and roll angles.
- (F)
- Structures: Leave only points from structures, such as buildings, and objects, such as poles and traffic signs. This test case is proposed to analyze what would happen if only the truly static and structured objects from the scene are kept. Everything is removed from the point cloud, including static vehicles, vegetation and the ground.
3.3. Odometry Algorithm
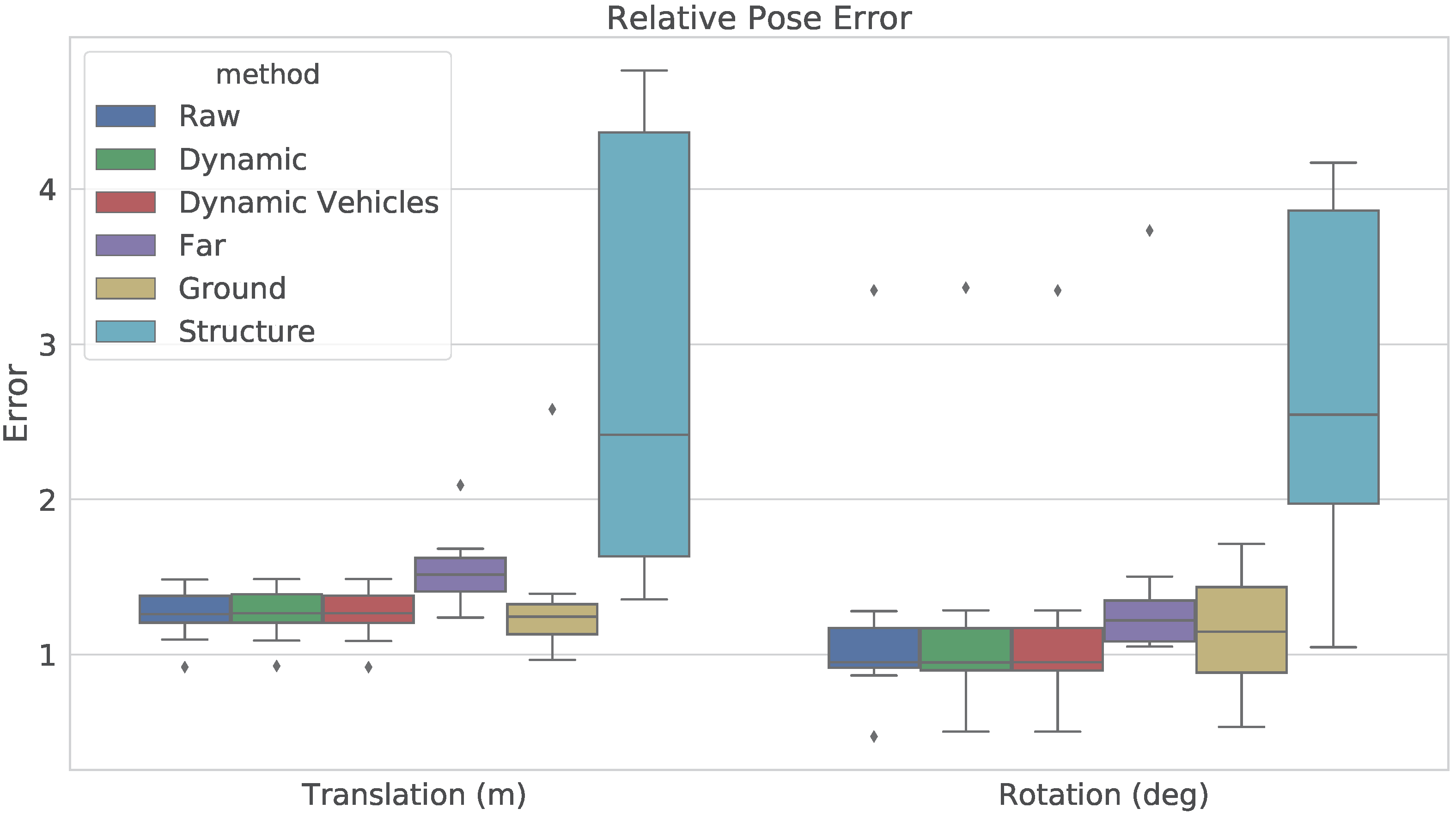
3.4. Evaluation Metrics
4. Results and Discussion
4.1. Results
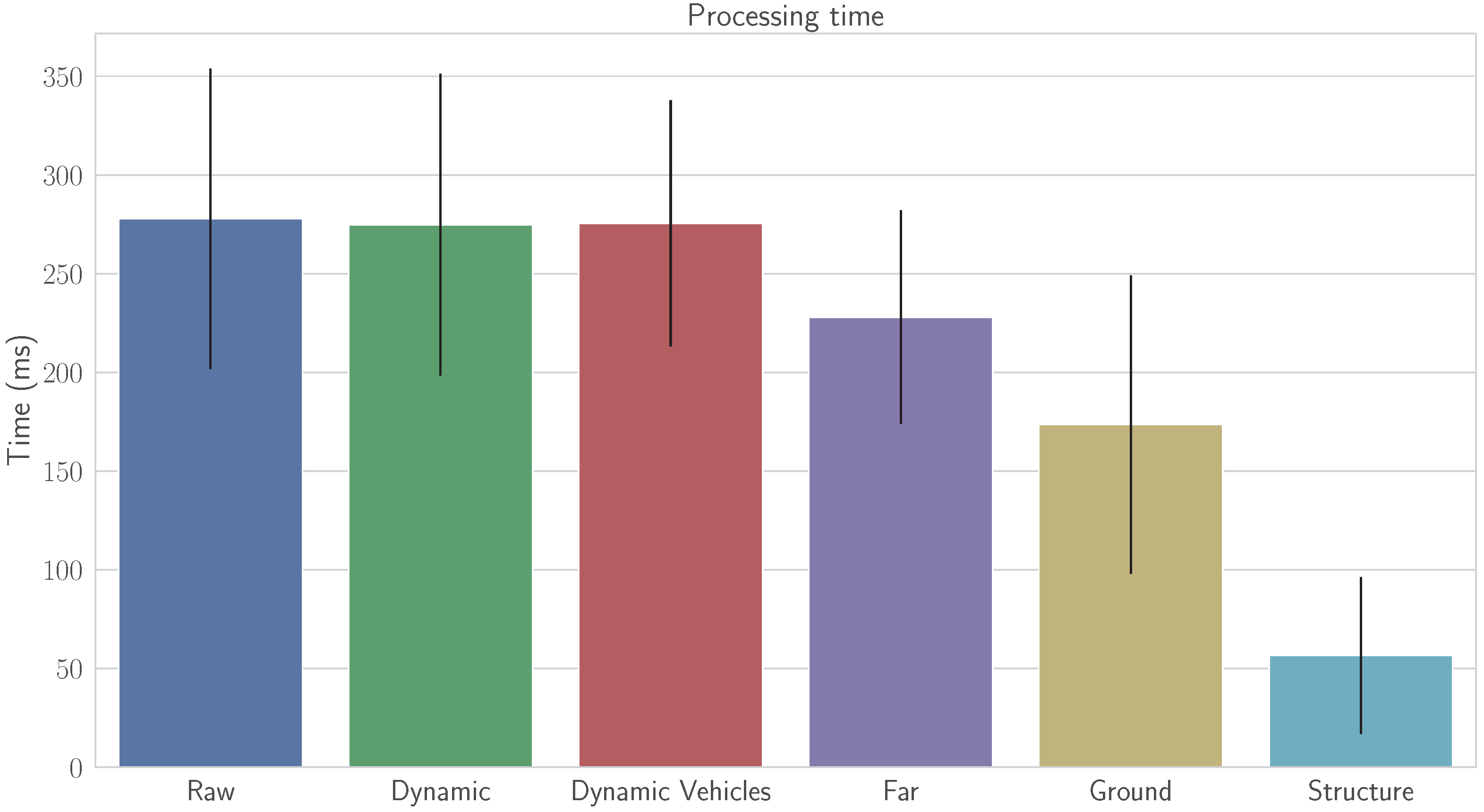
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arnold, E.; Al-Jarrah, O.Y.; Dianati, M.; Fallah, S.; Oxtoby, D.; Mouzakitis, A. A Survey on 3D Object Detection Methods for Autonomous Driving Applications. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3782–3795. [Google Scholar] [CrossRef] [Green Version]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Stachniss, C.; Gall, J. SemanticKITTI: A Dataset for Semantic Scene Understanding of LiDAR Sequences. In Proceedings of the IEEE/CVF International Conf. on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics Science and Systems (RSS), Berkeley, CA, USA, 12–16 July 2014. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Fraundorfer, F. Visual odometry. Part I: The First 30 Years and Fundamentals. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, J.; He, X.; Ye, C. DLO: Direct LiDAR Odometry for 2.5D Outdoor Environment. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 774–778. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.; Wang, Y.; Ding, X.; Tang, L.; Huang, S.; Xiong, R. 3D LiDAR-Based Global Localization Using Siamese Neural Network. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1380–1392. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Deschaud, J.E. IMLS-SLAM: Scan-to-Model Matching Based on 3D Data. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2480–2485. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Singh, S. Visual-lidar Odometry and Mapping: Low-drift, Robust, and Fast. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181. [Google Scholar] [CrossRef]
- Neuhaus, F.; Koß, T.; Kohnen, R.; Paulus, D. MC2SLAM: Real-Time Inertial Lidar Odometry Using Two-Scan Motion Compensation. In Proceedings of the German Conference on Pattern Recognition 2018 (LNCS), Stuttgart, Germany, 9–12 October 2019; Volume 11269, pp. 60–72. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Chen, X.; Milioto, A.; Palazzolo, E.; Giguere, P.; Behley, J.; Stachniss, C. SuMa++: Efficient LiDAR-based Semantic SLAM. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4530–4537. [Google Scholar]
- Chen, S.W.; Vicentim Nardari, G.; Lee, E.S.; Qu, C.; Liu, X.; Romero, R.A.F.; Kumar, V. SLOAM: Semantic Lidar Odometry and Mapping for Forest Inventory. IEEE Robot. Autom. Lett. 2020, 5, 612–619. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Chen, S.; Wang, C.; Li, X.; Wen, C.; Cheng, M.; Li, J. LO-Net: Deep Real-Time Lidar Odometry. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 8473–8482. [Google Scholar] [CrossRef] [Green Version]
- Valente, M.; Joly, C.; De La Fortelle, A. An LSTM network for real-time odometry estimation. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1434–1440. [Google Scholar] [CrossRef] [Green Version]
- Laboshin, L. Open-source implementation of Laser Odometry and Mapping (LOAM). Available online: https://github.com/laboshinl/loam_velodyne (accessed on 22 July 2020).
- Grupp, M. Evo: Python Package for the Evaluation of Odometry and SLAM. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 22 July 2020).
- Kümmerle, R.; Steder, B.; Dornhege, C.; Ruhnke, M.; Grisetti, G.; Stachniss, C.; Kleiner, A. On measuring the accuracy of SLAM algorithms. Auton. Robots 2009, 27, 387–407. [Google Scholar] [CrossRef] [Green Version]
- Lu, F.; Milios, E. Globally Consistent Range Scan Alignment for Environment Mapping. Auton. Robots 1997, 4, 333–349. [Google Scholar] [CrossRef]
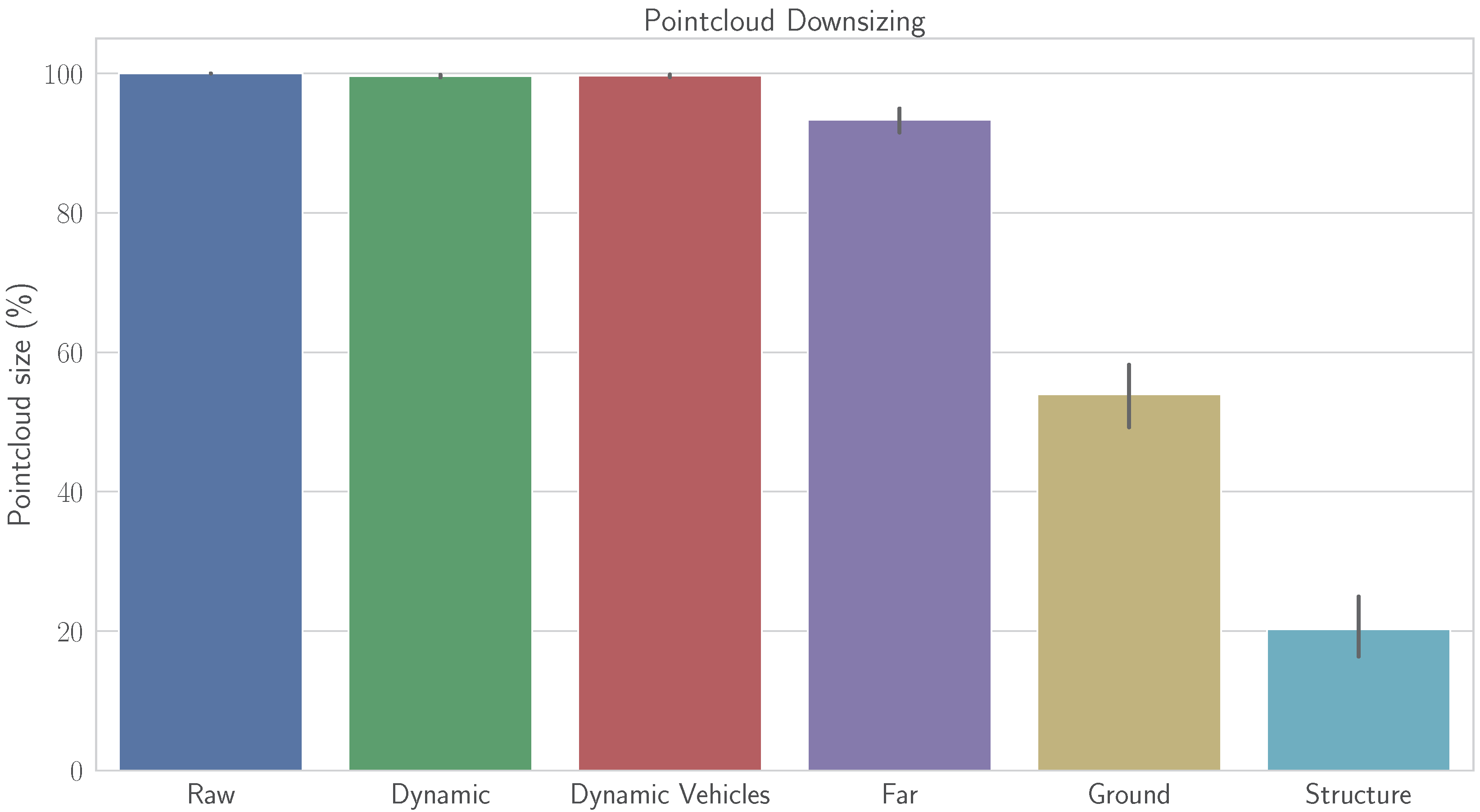

| Configuration | |||||||
|---|---|---|---|---|---|---|---|
| Sequence | A | B | C | D | E | F | |
| Translation ( ) | 00 (Urban) | 21.8 (18.5) | 21.3 (17.4) | 22.1 (18.4) | 41.2 (36.4) | 26.8 (26.2) | 36.6 (26.2) |
| 01 (Highway) | 95.5 (69.1) | 93.6 (67.9) | 93.4 (67.6) | 770.9 (569.1) | 97.4 (71.6) | 41.0 (34.4) | |
| 02 (Urban) | 142.3 (115.6) | 143.3 (116.1) | 142.9 (115.4) | 179.4 (143.3) | 91.5 (65.0) | 16 656 (12 752) | |
| 03 (Country) | 4.8 (3.5) | 4.7 (3.4) | 4.7 (3.4) | 6.2 (5.0) | 3.8 (2.5) | 15.8 (16.5) | |
| 04 (Country) | 2.8 (2.0) | 3.0 (1.9) | 3.0 (1.9) | 17.1 (3.9) | 2.7 (1.3) | 5.4 (5.8) | |
| 05 (Country) | 12.2 (9.6) | 12.1 (9.6) | 12.3 (9.7) | 22.2 (20.8) | 10.0 (8.7) | 8.6 (8.3) | |
| 06 (Urban) | 2.8 (1.9) | 2.8 (1.9) | 2.8 (1.7) | 4.3 (1.9) | 1.6 (0.8) | 4.5 (6.1) | |
| 07 (Urban) | 2.8 (1.7) | 2.8 (1.7) | 2.8 (1.7) | 4.1 (2.0) | 2.5 (1.2) | 7.3 (3.7) | |
| 08 (Urban) | 35.6 (30.2) | 35.0 (30.0) | 35.0 (30.0) | 72.0 (59.3) | 34.2 (29.4) | 202.3 (162.2) | |
| 09 (Urban) | 15.6 (9.0) | 15.3 (8.8) | 15.5 (9.0) | 28.6 (17.9) | 17.1 (9.4) | 2672 (1725) | |
| 10 (Country) | 12.9 (7.5) | 12.9 (7.5) | 12.9 (7.5) | 12.9 (7.6) | 5.5 (2.4) | 141.2 (85.1) | |
| Rotation ( ) | 00 (Urban) | 6.0 (3.5) | 5.6 (3.3) | 6.2 (3.6) | 11.7 (7.0) | 7.8 (5.1) | 11.7 (4.0) |
| 01 (Highway) | 4.3 (1.8) | 4.2 (1.6) | 4.1 (1.6) | 19.3 (19.6) | 3.1 (1.7) | 4.3 (1.6) | |
| 02 (Urban) | 31.0 (21.8) | 31.2 (21.9) | 31.1 (21.8) | 38.2 (25.8) | 19.6 (11.8) | 118.9 (44.6) | |
| 03 (Country) | 1.9 (0.8) | 1.9 (0.8) | 1.9 (0.8) | 2.5 (1.0) | 1.5 (0.6) | 3.7 (2.5) | |
| 04 (Country) | 0.7 (0.3) | 0.8 (0.3) | 0.8 (0.3) | 2.9 (0.8) | 0.8 (0.2) | 6.3 (8.3) | |
| 05 (Country) | 3.9 (2.1) | 3.9 (2.1) | 3.9 (2.1) | 7.5 (4.6) | 3.6 (2.0) | 4.4 (2.4) | |
| 06 (Urban) | 1.4 (0.6) | 1.3 (0.6) | 1.3 (0.6) | 1.8 (0.7) | 1.2 (0.6) | 2.5 (1.1) | |
| 07 (Urban) | 1.7 (0.7) | 1.7 (0.8) | 1.7 (0.7) | 2.3 (1.1) | 1.8 (0.6) | 4.9 (1.8) | |
| 08 (Urban) | 7.4 (4.0) | 7.3 (3.9) | 7.3 (4.0) | 14.4 (7.2) | 7.1 (3.9) | 81.3 (32.7) | |
| 09 (Urban) | 3.7 (1.8) | 3.6 (1.7) | 3.7 (1.8) | 6.9 (3.6) | 4.1 (1.8) | 123.0 (40.4) | |
| 10 (Country) | 2.6 (1.0) | 2.6 (1.0) | 2.6 (1.0) | 3.2 (1.6) | 1.6 (0.8) | 30.3 (5.2) | |
| Configuration | |||||||
|---|---|---|---|---|---|---|---|
| Sequence | A | B | C | D | E | F | |
| Translation ( ) | 00 (Urban) | 1.38 (0.87) | 1.39 (0.85) | 1.38 (0.85) | 1.52 (0.73) | 1.26 (0.79) | 2.89 (1.72) |
| 01 (Highway) | 5.93 (14.58) | 5.93 (14.90) | 5.97 (14.99) | 430.36 (472.06) | 9.83 (23.05) | 1.78 (0.75) | |
| 02 (Urban) | 7.68 (22.98) | 7.71 (23.05) | 7.66 (22.92) | 9.28 (27.71) | 2.58 (5.00) | 45.84 (32.42) | |
| 03 (Country) | 0.92 (0.44) | 0.93 (0.45) | 0.92 (0.44) | 1.29 (0.49) | 0.97 (0.48) | 4.69 (2.41) | |
| 04 (Country) | 1.25 (0.31) | 1.27 (0.31) | 1.27 (0.31) | 2.09 (2.26) | 1.39 (0.37) | 4.37 (5.13) | |
| 05 (Country) | 1.26 (0.53) | 1.26 (0.54) | 1.26 (0.54) | 1.44 (0.59) | 1.16 (0.57) | 1.44 (0.80) | |
| 06 (Urban) | 1.21 (0.43) | 1.21 (0.43) | 1.20 (0.43) | 1.41 (0.52) | 1.12 (0.48) | 1.36 (0.75) | |
| 07 (Urban) | 1.10 (0.59) | 1.09 (0.59) | 1.09 (0.59) | 1.24 (0.59) | 1.23 (0.68) | 2.42 (1.40) | |
| 08 (Urban) | 1.48 (0.70) | 1.49 (0.70) | 1.49 (0.71) | 1.68 (0.81) | 1.34 (0.72) | 4.77 (5.84) | |
| 09 (Urban) | 1.28 (0.41) | 1.27 (0.42) | 1.28 (0.42) | 1.62 (0.55) | 1.11 (0.48) | 60.84 (23.32) | |
| 10 (Country) | 1.44 (0.52) | 1.43 (0.52) | 1.43 (0.52) | 1.59 (0.48) | 1.28 (0.59) | 1.63 (1.36) | |
| Rotation ( ) | 00 (Urban) | 1.28 (0.76) | 1.29 (0.76) | 1.28 (0.75) | 1.36 (0.68) | 1.46 (0.70) | 4.10 (1.85) |
| 01 (Highway) | 0.92 (0.77) | 0.89 (0.71) | 0.89 (0.69) | 30.77 (23.92) | 0.82 (0.52) | 1.05 (0.63) | |
| 02 (Urban) | 3.35 (7.18) | 3.37 (7.21) | 3.35 (7.18) | 3.73 (7.29) | 1.71 (1.80) | 79.58 (54.90) | |
| 03 (Country) | 0.92 (0.34) | 0.92 (0.33) | 0.92 (0.33) | 1.25 (0.40) | 0.90 (0.35) | 3.62 (2.31) | |
| 04 (Country) | 0.47 (0.25) | 0.50 (0.22) | 0.50 (0.22) | 1.08 (0.54) | 0.53 (0.28) | 7.18 (8.05) | |
| 05 (Country) | 1.00 (0.58) | 1.01 (0.58) | 1.01 (0.58) | 1.19 (0.69) | 1.32 (0.65) | 2.34 (0.92) | |
| 06 (Urban) | 0.87 (0.41) | 0.86 (0.41) | 0.86 (0.41) | 1.05 (0.41) | 0.87 (0.54) | 1.6 (0.79) | |
| 07 (Urban) | 1.08 (0.46) | 1.08 (0.46) | 1.07 (0.46) | 1.09 (0.48) | 1.69 (0.63) | 4.17 (1.30) | |
| 08 (Urban) | 1.26 (0.69) | 1.26 (0.69) | 1.27 (0.69) | 1.50 (0.81) | 1.41 (0.66) | 9.50 (13.50) | |
| 09 (Urban) | 0.91 (0.52) | 0.91 (0.51) | 0.91 (0.52) | 1.33 (0.64) | 1.15 (0.59) | 100.13 (54.49) | |
| 10 (Country) | 0.95 (0.59) | 0.95 (0.60) | 0.95 (0.60) | 1.08 (0.59) | 1.02 (0.57) | 2.55 (3.82) | |
| Sequence | Metric | |||
|---|---|---|---|---|
| APE (Trans.) | APE (Rot.) | RPE (Trans.) | RPE (Rot.) | |
| 00 (Urban) | B (Dynamic) | B (Dynamic) | E (Ground) | A (Raw) |
| 01 (Highway) | F (Structure) | E (Ground) | F (Structure) | E (Ground) |
| 02 (Urban) | E (Ground) | E (Ground) | E (Ground) | E (Ground) |
| 03 (Country) | E (Ground) | E (Ground) | C (Dyn. Vehicles) | E (Ground) |
| 04 (Country) | E (Ground) | A (Raw) | A (Raw) | A (Raw) |
| 05 (Country) | F (Structure) | E (Ground) | E (Ground) | A (Raw) |
| 06 (Urban) | E (Ground) | E (Ground) | E (Ground) | C (Dyn. Vehicles) |
| 07 (Urban) | E (Ground) | A (Raw) | C (Dyn. Vehicles) | C (Dyn. Vehicles) |
| 08 (Urban) | E (Ground) | E (Ground) | E (Ground) | B (Dynamic) |
| 09 (Urban) | B (Dynamic) | B (Dynamic) | E (Ground) | B (Dynamic) |
| 10 (Country) | E (Ground) | E (Ground) | E (Ground) | B (Dynamic) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, F.M.; Guindel, C.; Armingol, J.M.; García, F. Study of the Effect of Exploiting 3D Semantic Segmentation in LiDAR Odometry. Appl. Sci. 2020, 10, 5657. https://doi.org/10.3390/app10165657
Moreno FM, Guindel C, Armingol JM, García F. Study of the Effect of Exploiting 3D Semantic Segmentation in LiDAR Odometry. Applied Sciences. 2020; 10(16):5657. https://doi.org/10.3390/app10165657
Chicago/Turabian StyleMoreno, Francisco Miguel, Carlos Guindel, José María Armingol, and Fernando García. 2020. "Study of the Effect of Exploiting 3D Semantic Segmentation in LiDAR Odometry" Applied Sciences 10, no. 16: 5657. https://doi.org/10.3390/app10165657
APA StyleMoreno, F. M., Guindel, C., Armingol, J. M., & García, F. (2020). Study of the Effect of Exploiting 3D Semantic Segmentation in LiDAR Odometry. Applied Sciences, 10(16), 5657. https://doi.org/10.3390/app10165657







