Cost-Sensitive Ensemble Feature Ranking and Automatic Threshold Selection for Chronic Kidney Disease Diagnosis
Abstract
:1. Introduction
- We propose an automatic cost-sensitive threshold selection heuristic that takes into account both the worth of a set of features and the overall accumulated cost.
- Decision tree-based classifiers performed favorably on the resulting features on a benchmark CKD dataset.
- The features could also yield higher average accuracy with more sophisticated classification structures, which shows that these features present high generalizability.
2. Literature Review
3. Proposed Methodology
3.1. Data Preprocessing
3.2. Classifier-Ensemble
3.3. Combiner
- Ensemble-1 produces multiple feature weightages obtained from individual feature scoring functions. In this case, the task of combiner is to consolidate the individual feature weightages into a consolidated score. The final scores are obtained by taking the average across multiple scoring functions as shown in Equation (1):
- Ensemble-2 deals with multiple partial solutions in the form of feature subsets. In this case, each scoring function produces an independent ranked list. A threshold operation is applied to each list. Subsequently, three different subsets are produced. All the subsets are combined by taking the majority voting scheme. In our case, as the ensemble is comprised of 3 scoring functions, therefore the majority voting is effectively translated into the selection of a feature that is present into at least 2/3rd of the subsets.
| Algorithm 1 Ensemble-1 |
| Input: Dataset D, Cost vector Cv, List of scoring functions N Output: Selected feature set S 1: Begin 2: foreach m in N do: 3: IL[m] = score_function(m, D) //N=3 i.e., DT, RF, GBT 4: endfor 5: L = average (IL) // using Equation (1) 6: *L = sort(L) // *L, is sorted in descending order 7: foreach f in *L do: 8: Acc_Cost (f) = Cv(f) //using Equation (2), cost accumulation based on all the elements in *L up to ‘f’ 9: *L.cost[f] = Acc_Cost (f) //accumulated cost assignment 10: endfor 11: T = intersection (*L) // where *L.score < *L.cost 12: S = retained (*L, T) // retained features in *L after applying T 13: return S 14: End |
| Algorithm 2 Ensemble-2 |
| Input: Dataset D, Cost vector Cv, List of scoring functions N Output: Selected feature set S 1: Begin 2: foreach m in N do: 3: L[m] = score_function(m, D) //same as Algorithm 1 4: *L[m] = sort(L[m]) //separate list for each scoring function ‘m’ 5: foreach f in *L[m] do: 6: Acc_Cost(f) = Cv(f) //same as Algorithm 1 7: *L[m].cost = Acc_Cost (f) //accumulated cost assignment for ‘m’ 8: endfor 9: T = intersection (*L) //same as Algorithm 1 10: Sm = retained (*L, T) //feature subset is obtained for ‘m’ 11: endfor 12: S = combine( //using majority vote scheme 13: return S 14: End |
3.4. Feature Cost Aggregator
3.5. Threshold and Feature Subset Selector
4. Experimentation
4.1. Dataset Description
4.2. Experimental Setup
- True Positive (TP): denotes positive instances predicted as positive.
- True Negative (TN): denotes negative instances predicted as negative.
- False Positive (FP): denotes negative instances predicted as positive.
- False Negative (FN): denotes positive instances predicted as negative.
5. Results and Analysis
5.1. Baseline Results
5.2. Feature Weightage Calculation and Feature Subset Acquisition
- Decision Tree Score: Features are scored through the CART decision tree classifier. The blue line in Figure 6 shows the feature weightage (FW) in the decreasing order of their importance while the orange line denotes accumulated cost (Cscore). Both values are normalized. The point of intersection between FW and Cscore is found around feature number 5 as shown in Figure 6.
- Random Forest Score: The second scoring function is based on random forest. The blue line in Figure 7 shows the feature weightage (FW) while the orange line denotes accumulated cost (Cscore). Both the values are normalized. The point of intersection between FW and Cscore can be observed around feature number 9 as shown in Figure 7.
- Gradient Boosted Trees Score: The last scoring function is based on GBT. The blue line in Figure 8 shows the feature weightage (FW) while the orange line denotes accumulated cost (Cscore). Both the values are normalized. The point of intersection between FW and Cscore is around feature number 3 as shown in Figure 8.
5.3. Ensemble-1 Results
5.4. Ensemble-2 Results
5.5. Comparison with Other Similar Approaches
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CKD | Chronic Kidney Disease |
| FW | Feature Weightage |
| CScore | Cost Score |
| KNN | K-Nearest Neighbor |
| SVM | Support Vector Machine |
| RF | Random Forest |
| ANN | Artificial Neural Network |
| PCA | Principal Component Analysis |
| GA | Genetic Algorithm |
| CART | Classification And Regression Trees |
| GBT | Gradient Boosted Trees |
| UCI | University of California, Irvine |
| AUC | Area under Receiver Operating Characteristics Curve |
| TP | True Positive |
| TN | True Negative |
| FP | False Positive |
| FN | False Negative |
References
- Kidney Disease: Improving Global Outcomes (KDIGO) Transplant Work Group. KDIGO clinical practice guideline for the care of kidney transplant recipients. Am. J. Transplant. Off. J. Am. Soc. Transplant. Am. Soc. Transpl. Surg. 2009, 9, S1. [Google Scholar] [CrossRef] [PubMed]
- Kellum, J.A.; Lameire, N. KDIGO AKI Guideline Work Group Diagnosis, evaluation, and management of acute kidney injury: A KDIGO summary (Part 1). Crit. Care 2013, 17, 204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, J.I.; Baek, H.; Jung, H.H. Prevalence of chronic kidney disease in korea: The korean national health and nutritional examination survey 2011–2013. J. Korean Med. Sci. 2016, 31, 915–923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Q.-L.; Rothenbacher, D. Prevalence of chronic kidney disease in population-based studies: Systematic review. BMC Public Health 2008, 8, 117. [Google Scholar] [CrossRef] [Green Version]
- Moyer, V.A.; Force, U.P.S.T. Screening for prostate cancer: U.S. Preventive Services Task Force recommendation statement. Ann. Intern. Med. 2012, 157, 120–134. [Google Scholar] [CrossRef] [Green Version]
- Álvaro, S.; Queiroz, A.C.M.D.S.; Da Silva, L.D.; Costa, E.D.B.; Pinheiro, M.E.; Perkusich, A. Computer-Aided Diagnosis of Chronic Kidney Disease in Developing Countries: A Comparative Analysis of Machine Learning Techniques. IEEE Access 2020, 8, 25407–25419. [Google Scholar] [CrossRef]
- Itani, S.; Lecron, F.; Fortemps, P. Specifics of medical data mining for diagnosis aid: A survey. Expert Syst. Appl. 2019, 118, 300–314. [Google Scholar] [CrossRef]
- Ogunleye, A.A.; Qing-Guo, W. XGBoost Model for Chronic Kidney Disease Diagnosis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 1. [Google Scholar] [CrossRef]
- Khan, B.; Naseem, R.; Muhammad, F.; Abbas, G.; Kim, S. An Empirical Evaluation of Machine Learning Techniques for Chronic Kidney Disease Prophecy. IEEE Access 2020, 8, 55012–55022. [Google Scholar] [CrossRef]
- Cios, K.J.; Krawczyk, B.; Cios, J.; Staley, K.J. Uniqueness of Medical Data Mining: How the New Technologies and Data They Generate are Transforming Medicine. arXiv 2019, arXiv:1905.09203. [Google Scholar]
- Salekin, A.; Stankovic, J. Detection of Chronic Kidney Disease and Selecting Important Predictive Attributes. In Proceedings of the 2016 IEEE International Conference on Healthcare Informatics (ICHI), Chicago, IL, USA, 4–7 October 2016; pp. 262–270. [Google Scholar]
- Zhou, Q.; Zhou, H.; Li, T. Cost-sensitive feature selection using random forest: Selecting low-cost subsets of informative features. Knowl.-Based Syst. 2016, 95, 1–11. [Google Scholar] [CrossRef]
- Min, F.; Liu, Q. A hierarchical model for test-cost-sensitive decision systems. Inf. Sci. 2009, 179, 2442–2452. [Google Scholar] [CrossRef]
- Vasquez-Morales, G.R.; Martinez-Monterrubio, S.M.; Moreno-Ger, P.; Recio-Garcia, J.A. Explainable Prediction of Chronic Renal Disease in the Colombian Population Using Neural Networks and Case-Based Reasoning. IEEE Access 2019, 7, 152900–152910. [Google Scholar] [CrossRef]
- Qin, J.; Chen, L.; Liu, Y.; Liu, C.; Feng, C.; Chen, B. A Machine Learning Methodology for Diagnosing Chronic Kidney Disease. IEEE Access 2020, 8, 20991–21002. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for feature selection: A review and future trends. Inf. Fusion 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Tsai, C.-F.; Hsiao, Y.-C. Combining multiple feature selection methods for stock prediction: Union, intersection, and multi-intersection approaches. Decis. Support Syst. 2010, 50, 258–269. [Google Scholar] [CrossRef]
- Polat, H.; Mehr, H.D.; Cetin, A. Diagnosis of Chronic Kidney Disease Based on Support Vector Machine by Feature Selection Methods. J. Med. Syst. 2017, 41, 55. [Google Scholar] [CrossRef]
- Taradeh, M.; Mafarja, M.; Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Fujita, H. An evolutionary gravitational search-based feature selection. Inf. Sci. 2019, 497, 219–239. [Google Scholar] [CrossRef]
- Seijo-Pardo, B.; Bolón-Canedo, V.; Alonso-Betanzos, A. On developing an automatic threshold applied to feature selection ensembles. Inf. Fusion 2019, 45, 227–245. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Sanchez-Marono, N.; Alonso-Betanzos, A. An ensemble of filters and classifiers for microarray data classification. Pattern Recognit. 2012, 45, 531–539. [Google Scholar] [CrossRef]
- Almansour, N.A.; Syed, H.F.; Khayat, N.R.; Altheeb, R.K.; Juri, R.E.; Alhiyafi, J.; Alrashed, S.; Olatunji, S.O. Neural network and support vector machine for the prediction of chronic kidney disease: A comparative study. Comput. Biol. Med. 2019, 109, 101–111. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, X.; Zhang, Z. Clinical risk assessment of patients with chronic kidney disease by using clinical data and multivariate models. Int. Urol. Nephrol. 2016, 48, 2069–2075. [Google Scholar] [CrossRef] [PubMed]
- Serpen, A.A. Diagnosis Rule Extraction from Patient Data for Chronic Kidney Disease Using Machine Learning. Int. J. Biomed. Clin. Eng. 2016, 5, 64–72. [Google Scholar] [CrossRef] [Green Version]
- Al-Hyari, A.Y.; Al-Taee, A.M.; Al-Taee, M.A. Clinical decision support system for diagnosis and management of chronic renal failure. In Proceedings of the 2013 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies, Amman, Jordan, 3–5 December 2013; pp. 1–6. [Google Scholar]
- Ani, R.; Sasi, G.; Sankar, U.R.; Deepa, O.S. Decision support system for diagnosis and prediction of chronic renal failure using random subspace classification. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics, Jaipur, India, 21–24 September 2016; pp. 1287–1292. [Google Scholar]
- Tazin, N.; Sabab, S.A.; Chowdhury, M.T. Diagnosis of Chronic Kidney Disease using effective classification and feature selection technique. In Proceedings of the 2016 International Conference on Medical Engineering, Health Informatics and Technology, Dhaka, Bangladesh, 17–18 December 2016; pp. 1–6. [Google Scholar]
- Cahyani, N.; Muslim, M.A. Increasing Accuracy of C4. 5 Algorithm by Applying Discretization and Correlation-based Feature Selection for Chronic Kidney Disease Diagnosis. J. Telecommun. Electron. Comput. Eng. (JTEC) 2020, 12, 25–32. [Google Scholar]
- Seijo-Pardo, B.; Bolón-Canedo, V.; Alonso-Betanzos, A. Testing Different Ensemble Configurations for Feature Selection. Neural Process. Lett. 2017, 46, 857–880. [Google Scholar] [CrossRef]
- Lal, T.N.; Chapelle, O.; Weston, J.; Elisseeff, A. Embedded methods. In Feature Extraction; Springer: Berlin/Heidelberg, Germany, 2008; pp. 137–165. [Google Scholar]
- Jain, D.; Singh, V. Feature selection and classification systems for chronic disease prediction: A review. Egypt. Inform. J. 2018, 19, 179–189. [Google Scholar] [CrossRef]
- Ali, M.; Ali, S.I.; Kim, H.; Hur, T.; Bang, J.; Lee, S.; Kang, B.H.; Hussain, M. uEFS: An efficient and comprehensive ensemble-based feature selection methodology to select informative features. PLoS ONE 2018, 13, e0202705. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Sanchez-Marono, N.; Alonso-Betanzos, A. A review of feature selection methods on synthetic data. Knowl. Inf. Syst. 2012, 34, 483–519. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. Recent advances and emerging challenges of feature selection in the context of big data. Knowl.-Based Syst. 2015, 86, 33–45. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Golawala, M.; Van Hulse, J. An empirical study of learning from imbalanced data using random forest. In Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence, Patras, Greece, 29–31 October 2007; Volume 2, pp. 310–317. [Google Scholar]
- Mejia-Lavalle, M.; Sucar, E.; Arroyo, G. Feature selection with a perceptron neural net. In Proceedings of the International Workshop on Feature Selection for Data Mining, Bethesda, MA, USA, 22 April 2006; pp. 131–135. [Google Scholar]
- Seijo-Pardo, B.; Bolón-Canedo, V.; Alonso-Betanzos, A. Using data complexity measures for thresholding in feature selection rankers. In Proceedings of the Spanish Association for Artificial Intelligence, Salamanca, Spain, 14–16 September 2016; pp. 121–131. [Google Scholar]
- Willett, P. Combination of Similarity Rankings Using Data Fusion. J. Chem. Inf. Model. 2013, 53, 1–10. [Google Scholar] [CrossRef]
- Seijo-Pardo, B.; Bolón-Canedo, V.; Alonso-Betanzos, A. Using a feature selection ensemble on DNA microarray datasets. In Proceedings of the ESANN. European Symposium on Artificial Neural Networks, Bruges, Belgium, 27–29 April 2016. [Google Scholar]
- Osanaiye, O.; Cai, H.; Choo, K.-K.R.; Dehghantanaha, A.; Xu, Z.; Dlodlo, M.E. Ensemble-based multi-filter feature selection method for DDoS detection in cloud computing. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 130. [Google Scholar] [CrossRef] [Green Version]
- Chiew, K.-L.; Tan, C.L.; Wong, K.; Yong, K.S.; Tiong, W.-K. A new hybrid ensemble feature selection framework for machine learning-based phishing detection system. Inf. Sci. 2019, 484, 153–166. [Google Scholar] [CrossRef]
- Kurt, I.; Türe, M.; Kurum, T. Comparing performances of logistic regression, classification and regression tree, and neural networks for predicting coronary artery disease. Expert Syst. Appl. 2008, 34, 366–374. [Google Scholar] [CrossRef]
- Sathe, S.; Aggarwal, C.C. Nearest Neighbor Classifiers Versus Random Forests and Support Vector Machines. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 1300–1305. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2019; Available online: http://archive.ics.uci.edu/ml (accessed on 5 May 2020).
- Mierswa, I.; Klinkenberg, R. RapidMiner Studio (9.2) [Data Science, Machine Learning, Predictive Analytics]. 2018. Available online: https://rapidminer.com/ (accessed on 30 June 2020).
- CHART Based Feature Weightage. 2020. Available online: http://www.myexperiment.org/workflows/5148.html (accessed on 30 June 2020).
- Gradient Boosting Trees Based Feature Weightage. 2020. Available online: http://www.myexperiment.org/workflows/5149.html (accessed on 30 June 2020).
- Random Forest Based Feature Weightage. 2020. Available online: http://www.myexperiment.org/workflows/5150.html (accessed on 30 June 2020).
- Kendall, M.G. Rank Correlation Methods; American Psychological Association: Washington, DC, USA, 1948. [Google Scholar]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaud. Sci. Nat. 1901, 37, 547–579. [Google Scholar]











| Technique | Merits | De-Merits |
|---|---|---|
| Filter |
|
|
| Wrapper |
|
|
| Embedded |
|
|
| Function Name | Input | Output | Purpose |
|---|---|---|---|
| score_function () | m: Feature scoring function i.e., DT, RF, GBT D: dataset | List: feature weightage based on ‘m’ on ‘D’ for each feature ‘f’ | To quantify the merit of the feature set based on different scoring functions |
| average () | List: an object containing feature list | Average of different feature scores obtained from ‘N’ scoring functions for each feature ‘f’ | To obtain a single value describing the merit of each feature |
| sort () | List: an object containing feature list | Obtain a re-ordered list based on feature’s weightage | To place more important features earlier in the list |
| intersection () | List: an object containing sorted feature list | θ: intersection point | To employ θ in feature subset selection. θ is a point of intersection where a feature’s score/weightage is less than that of its accumulated cost |
| retained () | List: an object containing sorted feature list θ: intersection point | List: a subset of features | Final solution in the case of Algorithm 1. For Algorithm 2, a partial solution is obtained for each ‘m’ |
| combine () | List: a list of partial solutions in the form of feature subsets | List: selected features that qualified the majority voting constraint | Final solution in the case of Algorithm 2 |
| Subset 1 | Subset 2 | Subset 3 | Feature ID | Frequency |
|---|---|---|---|---|
| 3 | 19 | 3 | 3 | 3 |
| 6 | 18 | 19 | 19 | 3 |
| 20 | 3 | 20 | 18 | 3 |
| 19 | 15 | 4 | 20 | 2 |
| 7 | 5 | 22 | 4 | 2 |
| 16 | 8 | 18 | 15 | 2 |
| 22 | 14 | 23 | 22 | 2 |
| 18 | 2 | 12 | 23 | 2 |
| 4 | 1 | 21 | 7 | 1 |
| 23 | 9 | 11 | 16 | 1 |
| ID | Attribute | Cost | Description | ID | Attribute | Cost | Description |
|---|---|---|---|---|---|---|---|
| 1 | Age <age: numerical> | 1 | In years | 13 | Sodium <sod: numerical> | 4.2 | mEq/L |
| 2 | Blood Pressure <bp: numerical> | 1 | Mm/Hg | 14 | Potassium <pot: numerical> | 50 | mEq/L |
| 3 | Specific Gravity <sg: numerical> | 1 | 1.005, 1.010, 1.015, 1.020, 1.025 | 15 | Hemoglobin <hemo: numerical> | 2.65 | Gms |
| 4 | Albumin <al: numerical> | 26 | 0–5 | 16 | Packed Cell Volume <pcv: numerical> | 2.62 | Integer valued |
| 5 | Sugar <su: categorical> | 21 | 0–5 | 17 | White Blood Cells Count <wc: numerical> | 31 | cells/cumm |
| 6 | Red Blood Cells <rbc: categorical> | 40 | 1: Normal, 0: Abnormal | 18 | Red Blood Cells Count <rc: numerical> | 31 | millions/cmm |
| 7 | Pus Cell <pc: categorical> | 31 | 1: Normal, 0: Abnormal | 19 | Hypertension <htn: categorical> | 1 | 1: Yes, 0: No |
| 8 | Pus Cell Clumps <pcc: categorical> | 31 | 1: Present, 0: Absent | 20 | Diabetes Mellitus <dm: categorical> | 19.4 | 1: Yes, 0:No |
| 9 | Bacteria <ba: categorical> | 51 | 1: Present, 0: Absent | 21 | Coronary Artery Disease <cad: categorical> | 51 | 1: Yes, 0: No |
| 10 | Blood Glucose Random <bgr: numerical> | 21 | mgs/dl | 22 | Appetite <appet: categorical> | 1 | 1: Good, 0: Poor |
| 11 | Blood Urea <bu: numerical> | 12.85 | mgs/dl | 23 | Pedal Edema <pe: categorical> | 1 | 1: Yes, 0: No |
| 12 | Serum Creatinine <sc: numerical> | 15 | mgs/dl | 24 | Anemia <ane: categorical> | 28.64 | 1: Yes, 0: No |
| Method | Parameters |
|---|---|
| Naïve Bayes (NB) | N/A |
| Logistic Regression (LG) | N/A |
| Deep Learning (DL) | Layers: 4 Hidden Layer size: 50 each Activation: Rectifier, Softmax |
| Decision Tree (CART) | Impurity measure: Gini index Maximal depth: 4 |
| Random Forest (RF) | Number of trees: 20 Maximal depth: 7 |
| Gradient Boosted Trees (GBT) | Number of trees 20 Maximal depth: 7 Learning rate: 0.100 |
| Support Vector Machine (SVM) | Gamma: 0 C: 10 |
| Models | Accuracy | Precision | Recall | Specificity | F-Measure | AUC | Cost |
|---|---|---|---|---|---|---|---|
| NB | 62.3 ± 2.0% | 62.3 ± 2.0% | 100.0 ± 0.0% | 0.0 ± 0.0% | 76.6 ± 1.5% | 0.908 ± 0.09 | 475.36 |
| LG | 84.3 ± 6.6% | 83.2 ± 5.8% | 94.3 ± 9.3% | 66.9 ± 14.0% | 88.2 ± 5.6% | 0.952 ± 0.58 | |
| DL | 89.5 ± 2.3% | 85.4 ± 2.8% | 100.0 ± 0.0% | 72.8 ± 5.7% | 92.1 ± 1.6% | 1.0 ± 0.0 | |
| DT | 87.7 ± 4.8% | 97.3 ± 3.7% | 90.4 ± 10.5% | 95.6 ± 6.1% | 93.3 ± 4.5% | 0.966 ± 0.03 | |
| RF | 89.5 ± 3.5% | 83.9 ± 3.6% | 100.0 ± 0.0% | 66.4 ± 11% | 91.2 ± 2.2% | 0.998 ± 0.004 | |
| GBT | 73.8 ± 5.8% | 86.2 ± 6.9% | 100.0 ± 0.0% | 71.4 ± 15.6% | 92.5 ± 4.0% | 1.0 ± 0.0 | |
| SVM | 92.2 ± 9.0% | 71.8 ± 8.1% | 97.2 ± 3.8% | 35.8 ± 20.7% | 82.4 ± 5.6% | 0.844 ± 0.12 | |
| Average | 82.75 ± 4.8% | 81.44 ± 4.7% | 97.41 ± 3.3% | 58.41 ± 10.4% | 88.07 ± 3.5% | 0.952 ± 0.04 |
| DT and RF | RF and GBT | GBT and DT |
|---|---|---|
| −0.17 | −0.09 | 0.22 |
| Scoring Function | List | Selected Features |
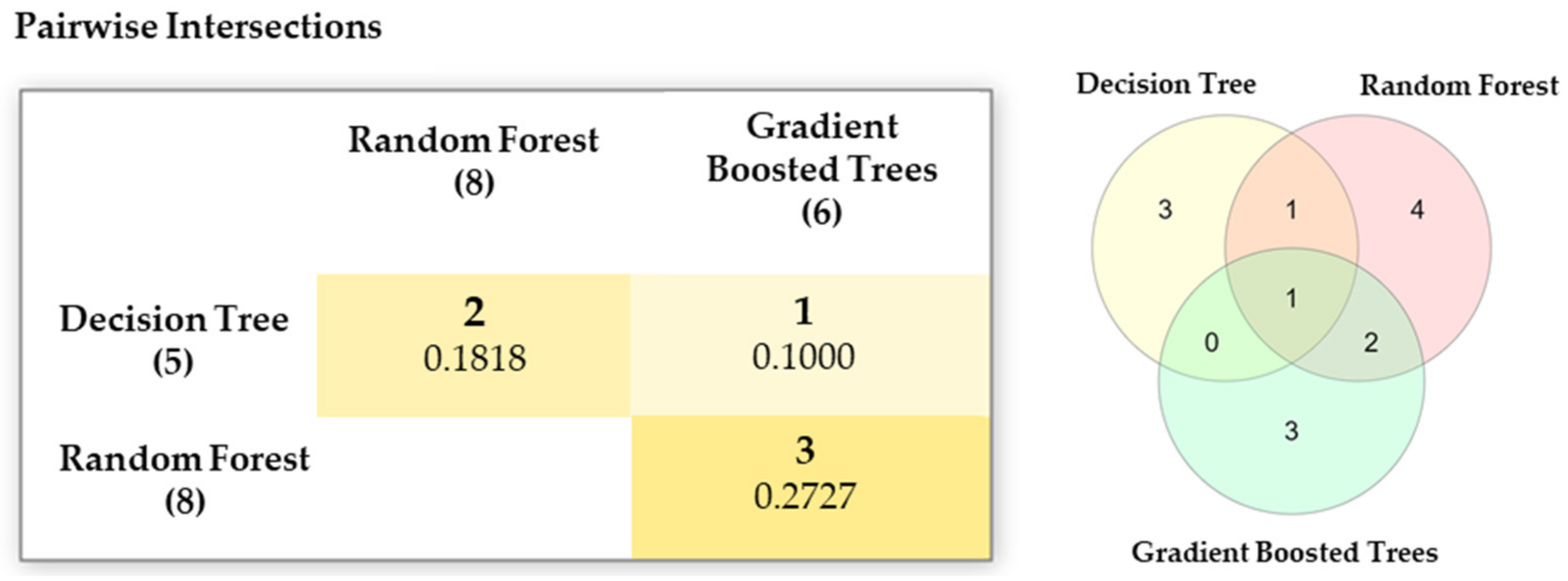
|---|---|---|
| Decision Tree | L1 | 15, 6, 17, 24, 5 |
| Random Forest | L2 | 20, 19, 18, 6, 15, 3, 22, 9 |
| Gradient Boosted Trees | L3 | 6, 19, 4, 20, 14, 11, 3 |
| Scoring Function | Average Accuracy | Average Precision | Average Recall | Average Specificity | Average F-Measure | Average AUC | Cost |
|---|---|---|---|---|---|---|---|
| DT Only | 71.95 ± 3.44% | 70.21 ± 2.94% | 99.01 ± 1.28% | 27.32 ± 7.05% | 81.78 ± 2.27% | 0.937 ±0.056 | 123.29 |
| RF Only | 96.01 ± 2.64% | 95.30 ± 2.71% | 98.78 ± 1.91% | 90.42 ± 5.92% | 96.98 ± 2.25% | 0.995 ± 0.006 | 197.05 |
| GBT Only | 85.24 ± 3.88% | 84.71 ± 4.58% | 98.34 ± 2.14% | 63.22 ± 13.18% | 90.25 ± 3.01% | 0.941 ± 0.05 | 150.25 |
| Models | Accuracy | Precision | Recall | Specificity | F-Measure | AUC | Cost |
|---|---|---|---|---|---|---|---|
| NB | 98.25 ± 2.92% | 95.72 ± 3.81% | 98.78 ± 1.64% | 91.94 ± 7.55% | 97.14 ± 2.21% | 0.995 ± 0.006 | 95.05 |
| LG | 99.10 ± 1.90% | 98.80 ± 2.80% | 100.0 ± 0.0% | 97.50 ± 5.60% | 99.40 ± 1.40% | 1.0 ± 0.0 | |
| DL | 97.40 ± 2.40% | 96.10 ± 3.60% | 100.0 ± 0.0% | 93.10 ± 6.40% | 98.0 ± 1.90% | 1.0 ± 0.0 | |
| DT | 89.40 ± 4.0% | 87.70 ± 5.20% | 97.10 ± 3.90% | 76.40 ± 12.3% | 92.10 ± 2.80% | 0.975 ± 0.03 | |
| RF | 98.30 ± 2.4% | 97.50 ± 3.4% | 100.0 ± 0.0% | 95.0 ± 6.805 | 98.70 ± 1.80% | 1.0 ± 0.0 | |
| GBT | 95.70 ± 4.3% | 93.80 ±6.1 % | 100 ± 0.0% | 88.30 ± 11.9% | 96.70 ± 3.20% | 1.0 ± 0.0 | |
| SVM | 95.60 ± 3.1% | 96.20 ±5.6 % | 97.20 ± 3.8% | 93.30 ± 9.90% | 96.50 ± 2.40% | 0.993 ± 0.009 | |
| Average | 96.25 ± 2.82% | 95.72 ± 3.81% | 98.78 ± 1.64% | 91.94 ± 7.55% | 97.14 ± 2.21% | 0.995 ± 0.006 |
| Scoring Functions | Averaged Accuracy | Averaged Precision | Averaged Recall | Averaged Specificity | Averaged F-Measure | Averaged AUC | Cost |
|---|---|---|---|---|---|---|---|
| DT Only | 71.95 ± 3.44% | 70.21 ± 2.94% | 99.01 ± 1.28% | 27.32 ± 7.05% | 81.78 ± 2.27% | 0.937 ±0.056 | 123.29 |
| RF Only | 96.01 ± 2.64% | 95.30 ± 2.71% | 98.78 ± 1.91% | 90.42 ± 5.92% | 96.98 ± 2.25% | 0.995 ± 0.006 | 197.05 |
| GBT Only | 85.24 ± 3.88% | 84.71 ± 4.58% | 98.34 ± 2.14% | 63.22 ± 13.18% | 90.25 ± 3.01% | 0.941 ± 0.05 | 150.25 |
| DT-RF | 93.78 ± 3.04% | 95.29 ± 4.90% | 95.31 ± 6.50% | 91.41 ± 9.00% | 95.04 ± 2.57% | 0.99 ± 0.02 | 143.69 |
| DT-GBT | 91.40 ± 2.27% | 91.89 ± 3.01% | 96.01 ± 4.36% | 83.79 ± 5.61% | 93.59 ± 1.89% | 0.95 ± 0.02 | 162.54 |
| GBT-RF | 93.39 ± 2.70% | 91.53 ± 4.07% | 99.19 ± 1.47% | 83.80 ± 8.19% | 95.04 ± 1.96% | 1.00 ± 0.01 | 172.05 |
| Ensemble-1 | 96.26 ± 2.93% | 95.73 ± 3.81% | 98.79 ± 1.64% | 91.94 ± 7.56% | 97.14 ± 2.21% | 1.00 ± 0.01 | 95.05 |
| Scoring Function | List | Selected Features | Frequency |
|---|---|---|---|
| Decision Tree | L1 | 15, 6, 17, 24, 5 | 6:3, 3:2, 15:2, 19:2, 20:2, 1:1, 2:1, 4:1, 5:1, … |
| Random Forest | L2 | 20, 19, 18, 6, 15, 3, 22, 9 | |
| Gradient Boosted Trees | L3 | 6, 19, 4, 20, 14, 11, 3 | |
| Ensemble-2 | *L | 6, 15, 20, 19, 3 |
| Models | Accuracy | Precision | Recall | Specificity | F-measure | AUC | Cost |
|---|---|---|---|---|---|---|---|
| NB | 96.5 ± 3.60% | 100.0 ± 0.0% | 94.40 ± 6.0% | 100.0 ± 0.0% | 97.0 ± 3.20% | 1.0 ± 0.0 | 64.05 |
| LG | 96.5 ± 2.0% | 100.0 ± 0.0% | 94.50 ± 3.10% | 100.0 ± 0.0% | 97.10 ± 1.60% | 0.997 ± 0.007 | |
| DL | 100.0 ± 0.0% | 100.0 ± 0.0% | 100.0 ± 0.0% | 100.0 ± 0.0% | 100.0 ± 0.0% | 1.0 ± 0.0 | |
| DT | 93.90 ± 6.60% | 100.0 ± 0.0% | 90.40 ±10.50% | 100.0 ± 0.0% | 94.70 ± 5.9% | 0.952 ± 0.052 | |
| RF | 98.30 ± 2.40% | 97.40± 3.50% | 100.0 ± 0.0% | 95.30 ± 1.80% | 98.70 ± 1.8% | 0.998 ± 0.004 | |
| GBT | 100.0 ± 0.0% | 100.0 ± 0.0% | 100.0 ± 0.0% | 100.0 ± 0.0% | 100.0 ± 0.0% | 1.0 ± 0.0 | |
| SVM | 95.70 ± 4.30% | 98.70 ± 3.0% | 94.50 ± 7.60% | 97.80 ± 5.0% | 96.30 ± 3.70% | 0.961 ± 0.057 | |
| Average | 97.27 ± 2.92% | 99.44± 0.92% | 96.25 ± 3.88% | 99.01 ± 1.64% | 97.68 ± 2.31% | 0.986 ± 0.017 |
| Case | Averaged Accuracy | Averaged Precision | Averaged Recall | Averaged Specificity | Averaged F-Measure | Averaged AUC | Cost |
|---|---|---|---|---|---|---|---|
| Intersection | 62.30 ± 2.0% | 62.30 ± 2.0% | 100.0 ± 0.0% | 0.0 ± 0.0% | 76.80 ± 1.50% | 0.56 ± 0.03 | 31 |
| Union | 89.77 ± 2.43% | 89.56 ± 2.99% | 97.61 ± 3.01% | 76.96 ± 6.94% | 92.77 ± 1.81% | 0.98 ± 0.01 | 317.54 |
| Multi-intersection | 97.27 ± 2.70% | 99.44 ± 0.93% | 96.26 ± 3.89% | 99.01 ± 1.64% | 97.69 ± 2.31% | 0.99 ± 0.02 | 64.05 |
| Method | Averaged Accuracy | Averaged Precision | Averaged Recall | Averaged Specificity | Averaged F-Measure | Averaged AUC | Cost |
|---|---|---|---|---|---|---|---|
| [8] | 83.29 ± 5.07% | 82.65 ± 5.82% | 97.20 ± 3.34% | 60.04 ± 12.11% | 88.55 ± 3.75% | 0.934 ± 0.50 | 167.31 |
| [15] | 92.64 ± 2.74% | 93.5 ± 2.45% | 97.38 ± 3.02% | 84.68 ± 5.44% | 94.41 ± 2.15% | 0.987 ± 0.01 | 141.10 |
| [17] | 90.0 ± 2.80% | 90.71 ± 2.57% | 97.22 ± 2.60% | 78.25 ± 4.31% | 93.07 ± 2.22% | 0.979 ± 0.02 | 193.70 |
| [18] | 85.74 ± 2.44% | 84.92 ± 2.91% | 99.40 ± 1.0% | 62.94 ± 4.84% | 90.75 ± 1.82% | 0.918 ± 0.02 | 236.11 |
| [22] | 93.41 ± 3.27% | 94.24 ± 3.04% | 96.61 ± 3.34% | 88.20 ± 6.21% | 95.0 ± 2.64% | 0.981 ± 0.02 | 272.20 |
| [32] | 87.37 ± 3.40% | 86.84 ± 3.47% | 98.62 ± 1.50% | 68.87 ± 9.18% | 92.95 ± 2.42% | 0.976 ± 0.03 | 136.72 |
| [40] | 90.51 ± 3.24% | 89.54 ± 4.18% | 98.6 ± 1.80% | 80.60 ± 8.20% | 93.31 ± 2.42% | 0.994 ± 0.02 | 91 |
| Ensemble-1 | 96.26 ± 2.92% | 95.72 ± 3.81% | 98.76 ± 1.64% | 91.94 ± 7.55% | 97.14 ± 2.21% | 0.995 ± 0.006 | 95.05 |
| Ensemble-2 | 97.27 ± 2.70% | 99.44 ± 0.82% | 96.25 ± 3.88% | 99.01 ± 1.64% | 97.68 ± 2.31% | 0.986 ± 0.01 | 64.05 |
| Method | Statistical Difference |
|---|---|
| [8] | ± |
| [15] | º |
| [17] | º |
| [18] | º |
| [22] | º |
| [32] | º |
| [40] | º |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran Ali, S.; Ali, B.; Hussain, J.; Hussain, M.; Satti, F.A.; Park, G.H.; Lee, S. Cost-Sensitive Ensemble Feature Ranking and Automatic Threshold Selection for Chronic Kidney Disease Diagnosis. Appl. Sci. 2020, 10, 5663. https://doi.org/10.3390/app10165663
Imran Ali S, Ali B, Hussain J, Hussain M, Satti FA, Park GH, Lee S. Cost-Sensitive Ensemble Feature Ranking and Automatic Threshold Selection for Chronic Kidney Disease Diagnosis. Applied Sciences. 2020; 10(16):5663. https://doi.org/10.3390/app10165663
Chicago/Turabian StyleImran Ali, Syed, Bilal Ali, Jamil Hussain, Musarrat Hussain, Fahad Ahmed Satti, Gwang Hoon Park, and Sungyoung Lee. 2020. "Cost-Sensitive Ensemble Feature Ranking and Automatic Threshold Selection for Chronic Kidney Disease Diagnosis" Applied Sciences 10, no. 16: 5663. https://doi.org/10.3390/app10165663





