Quantitative Evaluation of the Spatial Variation of Surface Soil Properties in a Typical Alluvial Plain of the Lower Yellow River Using Classical Statistics, Geostatistics and Single Fractal and Multifractal Methods
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
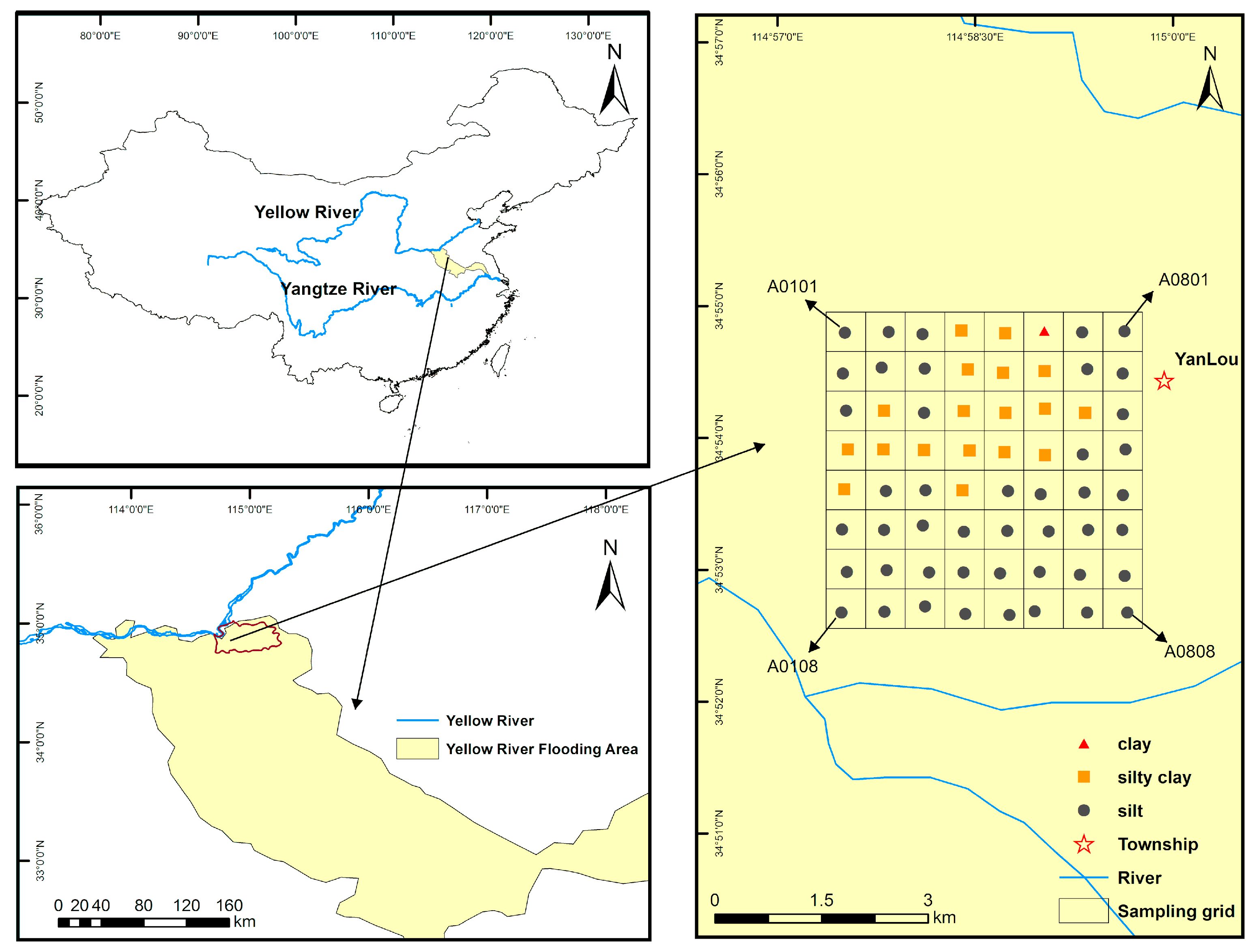
2.1. Site Description
2.1.1. Geographical Location
2.1.2. Sampling and Indoor Experiment
2.1.3. Mesh Generation
2.2. Research Methods
2.2.1. Geostatistics and Fractal Method
2.2.2. Multifractal Method
3. Results
3.1. Classical Statistical Features
3.2. Geostatistical Analysis
3.3. Single Fractals
3.4. Multifractal Analysis
4. Discussion
4.1. Influencing Factors of Variability
4.2. Comparison of Research Methods
5. Conclusions
- 1.
- The results of classical statistics show that the silt content, bulk density and saturated water content in the study area have weak variation; the clay content has medium variation; and the sand content and saturated hydraulic conductivity have strong variation. The variability of the six soil properties is quite different. The order of variability is sand > Ks > clay > silt > θs > γ, and the variation coefficient is consistent with the result of the generalised fractal dimension, ΔD(q) (q > 0).
- 2.
- The geostatistical results (isotropy) after logarithmic transformation show that the nugget coefficient of the silt content in the study area is 0.002, so the silt content has a strong spatial autocorrelation. Its range is also the smallest, which indicates that the scale range of its spatial continuity is the smallest. The nugget coefficients of the other five kinds of soil properties are all between 0.4 and 0.5, which can be considered moderate spatial autocorrelation. The nugget coefficient can also reflect the spatial variability of soil properties to some degree, and the order from the largest to the smallest is Ks > sand > γ > clay > θs > silt.
- 3.
- The single fractal (isotropy) shows that the relationship of the fractal dimension, D, is Ks > silt >θs > γ > sand > clay. According to the meaning of D, the larger the fractal dimension value, the smaller the variability, which shows that the variables after considering the spatial position factor (lag distance) have different statistical characteristics from the variables themselves. The fractal dimension, D, can be used as a simple and direct parameter to measure the relationship between the lag and variogram. However, due to the small sample capacity and lag distance calculation, the low accuracy leads to substantial limitations in practical application.
- 4.
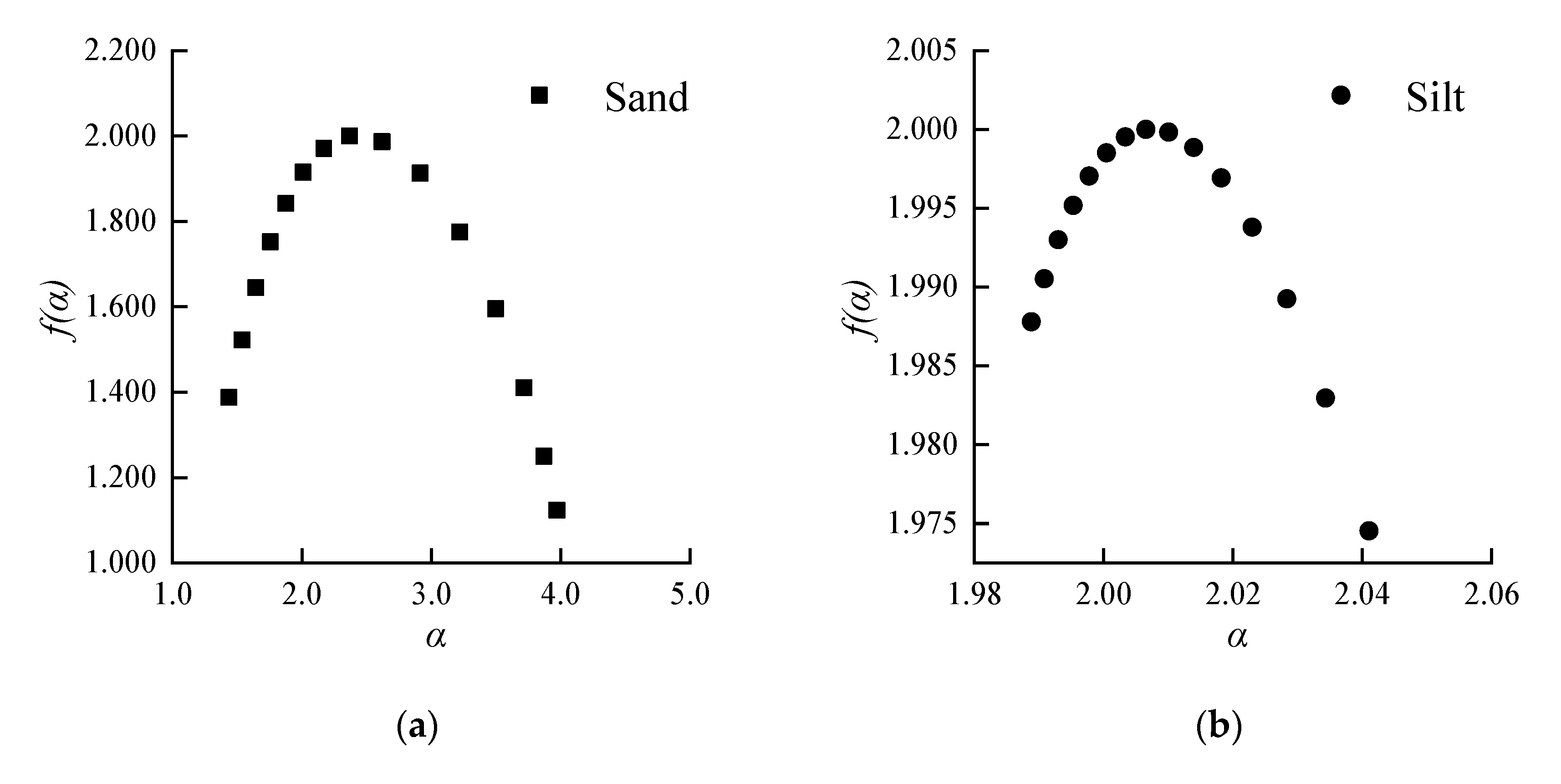
- The six soil properties in the study area have multifractal characteristics to different degrees. According to the multifractal spectrum curve, the relationship between the spectrum width, Δα, and the soil properties shows that different soil properties have different variability. The relationship order of Δα is Ks > clay > sand > silt > θs > γ. The symmetry of the multifractal spectrum curve can reflect the distribution dominance of variables. The content of sand, silt, clay and saturated hydraulic conductivity are obviously “left hook”, and the spatial variation is mainly dominated by small-value data. Δf values of bulk density and saturated water content are less than zero, which shows that the multifractal spectrum is “right hook”, and its variability is mainly dominated by large-value data. The multifractal method does not need to consider the normality of the data. It has higher accuracy than geostatistics and single fractal analysis and has obvious advantages in the quantitative characterisation of local characteristics and extreme values.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gohardoust, M.R.; Sadeghi, M.; Ahmadi, M.Z.; Jones, S.B.; Tuller, M. Hydraulic conductivity of stratified unsaturated soils: Effects of random variability and layering. J. Hydrol. 2017, 546, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Caniego, F.J.; Espejo, R.; Martın, M.A.; José, S. Multifractal scaling of soil spatial variability. Ecol. Model. 2005, 182, 291–303. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Zhu, Y.; Li, B.; Wang, P. Application of fractal theory on pedology: A Review. Chin. J. Soil Sci. 2017, 48, 227–234. [Google Scholar]
- Lv, Y.; Li, B.; Cui, Y. Micro-scale spatial variability of soil nutrients under different plant communities. Sci. Agric. Sin. 2006, 39, 1581–1588. [Google Scholar]
- Li, X.; Zhang, S.; Wang, Z.; Zhang, H. Spatial variability and pattern analysis of soil properties in Dehui City of Jilin Province. J. Geogr. Sci. 2004, 49, 989–997. [Google Scholar]
- Eghball, B.; Hergert, G.W.; Lesoing, G.W.; Ferguson, R.B. Fractal analysis of spatial and temporal variability. Geoderma 1999, 88, 349–362. [Google Scholar] [CrossRef]
- Burrough, P.A. Multiscale sources of spatial variation in soil. I. The application of fractal concepts to nested levels of soil variation. Eur. J. Soil Sci. 1983, 34, 577–597. [Google Scholar] [CrossRef]
- Blagoveschensky, Y.N.; Samsonova, V.P. Fractal and the statistical analysis of spatial distributions of Fe-Mn concretions in soddy-podsolic soils. Geoderma 1999, 88, 265–282. [Google Scholar] [CrossRef]
- Cunha, J.M.; Campos, M.C.C.; Gaio, D.C.; Nogueira, J.S.; Soares, M.D.R.; Silva, D.M.P.; Oliveira, I.A. Fractal analysis in the description of soil particle-size distribution under different land-use patterns in Southern Amazonas State, Brazil. Afr. J. Agric. Res. 2016, 11, 2032–2042. [Google Scholar]
- Marinho, M.A.; Pereira, M.W.M.; Vázquez, E.V.; Lado, M.; González, A.P. Depth distribution of soil organic carbon in an Oxisol under different land uses: Stratification indices and multifractal analysis. Geoderma 2017, 287, 126–134. [Google Scholar] [CrossRef]
- Zeleke, T.B.; Si, B.C. Scaling relationships between saturated hydraulic conductivity and soil physical properties. Soil Sci. Soc. Am. J. 2005, 69, 1691–1702. [Google Scholar] [CrossRef]
- Eghball, B.; Schepers, J.S.; Negahban, M. Spatial and temporal variability of soil nitrate and corn yield: Multifractal analysis. Agron. J. 2003, 95, 339–346. [Google Scholar]
- Liu, J.; Ma, X.; Zhang, Z. Multifractal study on spatial variability of soil water and salt and its scale effect. Trans. Chin. Soc. Agric. Eng. 2010, 26, 81–86. [Google Scholar]
- Brito, W.B.M.; Campos, M.C.C.; Mantovanelli, B.C.; Cunha, J.M.d.; Franciscon, U.; Soares, M.D.R. Spatial variability of soil physical properties in Archeological Dark Earths under different uses in southern Amazon. Soil Tillage Res. 2018, 182, 103–111. [Google Scholar] [CrossRef]
- Ma, Y.; Minasny, B.; Welivitiya, W.D.P.; Malone, B.P.; Willgoose, G.R.; McBratney, A.B. The feasibility of predicting the spatial pattern of soil particle-size distribution using a pedogenesis model. Geoderma 2019, 241, 195–205. [Google Scholar] [CrossRef]
- Zou, X.; Zhang, Z.; Wu, M.; Wan, Y. Spatial variability of particle size distribution at slope scalein Bashang region of Hebei province. Sci. Soil. Water. Conserv. 2019, 17, 44–53. [Google Scholar]
- Qiao, J.; Zhu, Y.; Jia, J.; Huang, L.; Shao, M. Spatial variation and simulation of the bulk density in a deep profile (0–204 m) on the Loess Plateau, China. Catena 2018, 164, 88–95. [Google Scholar] [CrossRef]
- Yu, D.; Jia, X.; Huang, L.; Shao, M.; Wang, J. Spatial variation of soil bulk density in different soil layers in the loess area and simulation. Acta Pedol. Sin. 2019, 56, 57–66. [Google Scholar]
- Li, S.; Zhang, J.; Zhang, W.; Xiao, L. Study of spatial variability and stochastic modeling of surface soil permeability. Rock Soil Mech. 2009, 30, 300–304. [Google Scholar]
- Guo, L.; Li, Y.; Li, M.; Ren, X.; Liu, C.; Zhu, D. Multifractal study on spatial variability of soil hydraulic properties of Lou Soil. Trans. Chin. Soc. Agric. Mach. 2011, 42, 56–64. [Google Scholar]
- Bagarello, V.; Baiamonte, G.; Caia, C. Variability of near-surface saturated hydraulic conductivity for the clay soils of a small Sicilian basin. Geoderma 2019, 340, 133–145. [Google Scholar] [CrossRef]
- Godoy, V.A.; Zuquette, L.V.; Gómez-Hernández, J.J. Spatial variability of hydraulic conductivity and solute transport parameters and their spatial correlations to soil properties. Geoderma 2019, 339, 59–69. [Google Scholar] [CrossRef]
- Soto, M.A.A.; Chang, H.K.; van Genuchten, M.T. Fractal-based models for the unsaturated soil hydraulic functions. Geoderma 2017, 306, 144–151. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, W.; Wang, L.; Liu, Y.; Liu, Y.; Feng, Q. Relationship between soil water content and soil particle size on typical slopes of the Loess Plateau during a drought year. Sci. Total Environ. 2019, 648, 943–954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guan, X.; Yang, P.; Lv, Y. Analysis on spatial variability of soil properties based on multifractal theory. J. Basic Sci. Eng. 2011, 19, 712–720. [Google Scholar]
- Gwenzi, W.; Hinz, C.; Holmes, K.; Phillips, I.R.; Mullins, I.J. Field-scale spatial variability of saturated hydraulic conductivity on a recently constructed artificial ecosystem. Geoderma 2011, 166, 43–56. [Google Scholar] [CrossRef]
- Kong, D.; Wang, L.; Liu, J.; Fu, Q. Scale effect of spatial variability of cropland soil water content in black soil region. J. Hydraul. Eng. 2017, 48, 608–612. [Google Scholar]
- Liu, J.; Zhang, S.; Ren, G.; Fu, Q.; Zhang, L.; Liu, L.; Li, J.; Yu, K.; Xu, Q. Influence of rainfall on spatial variability of soil moisture in corn farmland under straw return condition. J. Basic Sci. Eng. 2019, 27, 768–779. [Google Scholar]
- Chen, S.; Wang, N.; Yan, F.; Zou, X. Horizontal variability and autocorrelation of soil organic matter at different soil layers inestuarine wetland. Chin. J. Ecol. 2019, 38, 2805–2812. [Google Scholar]
- Wang, Z.; Sun, J.; Jiang, Q.; Fu, Q.; Lin, B.; He, X. Spatial distribution characteristics and influencing factors of organicmatter in black soil region of the Songnen Plain. J. Northeast. Agric. Univ. 2019, 50, 54–62. [Google Scholar]
- General Institute of Water Resources and Hydropower Planning and Design, Ministry of Water Resources. Standards for Geotechnical Testing Method (GB/T 50123-2019); China Water&Power Press: Beijing, China, 2019. [Google Scholar]
- Ministry of Construction of the People’s Republic of China. Code for Investigation of Geotechnical Engineering (GB5002-2001); China Architecture & Building Press: Beijing, China, 2009. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Burrough, P.A. Fractal dimensions of landscapes and other environmental data. Nature 1981, 294, 240–242. [Google Scholar] [CrossRef]
- Renyi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Chhabra, A.; Jensen, R.V. Direct determination of the f(α) singularity spectrum. Phys. Rev. Lett. 1989, 62, 1327–1330. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wu, T.; Yu, Z. Geometrical characteristics of singularity spectra of multifractals II-Partition Function Definition. J. East. China Univ. Sci. Technol. 2000, 26, 62–67. [Google Scholar]
- Zhang, N.; Zhang, D.; Qu, Z.; Lv, S.; Liu, Q. Spatial variability of soil organic matter at different sampling scales in Inner MongoliaHetao irrigation area. Chin. J. Ecol. 2016, 35, 74–84. [Google Scholar]
- Zeleke, T.B.; Si, B.C. Characterizing scale-dependent spatial relationships between soil properties using multifractal techniques. Geoderma 2006, 134, 440–452. [Google Scholar] [CrossRef]
- Cheng, Q. Multifractal and Geostatisic methods for characterzing local structure and singularity properities of exploration geochemical anomalies. Earth Sci. J. China Univ. Geosci. 2001, 26, 161–166. [Google Scholar]


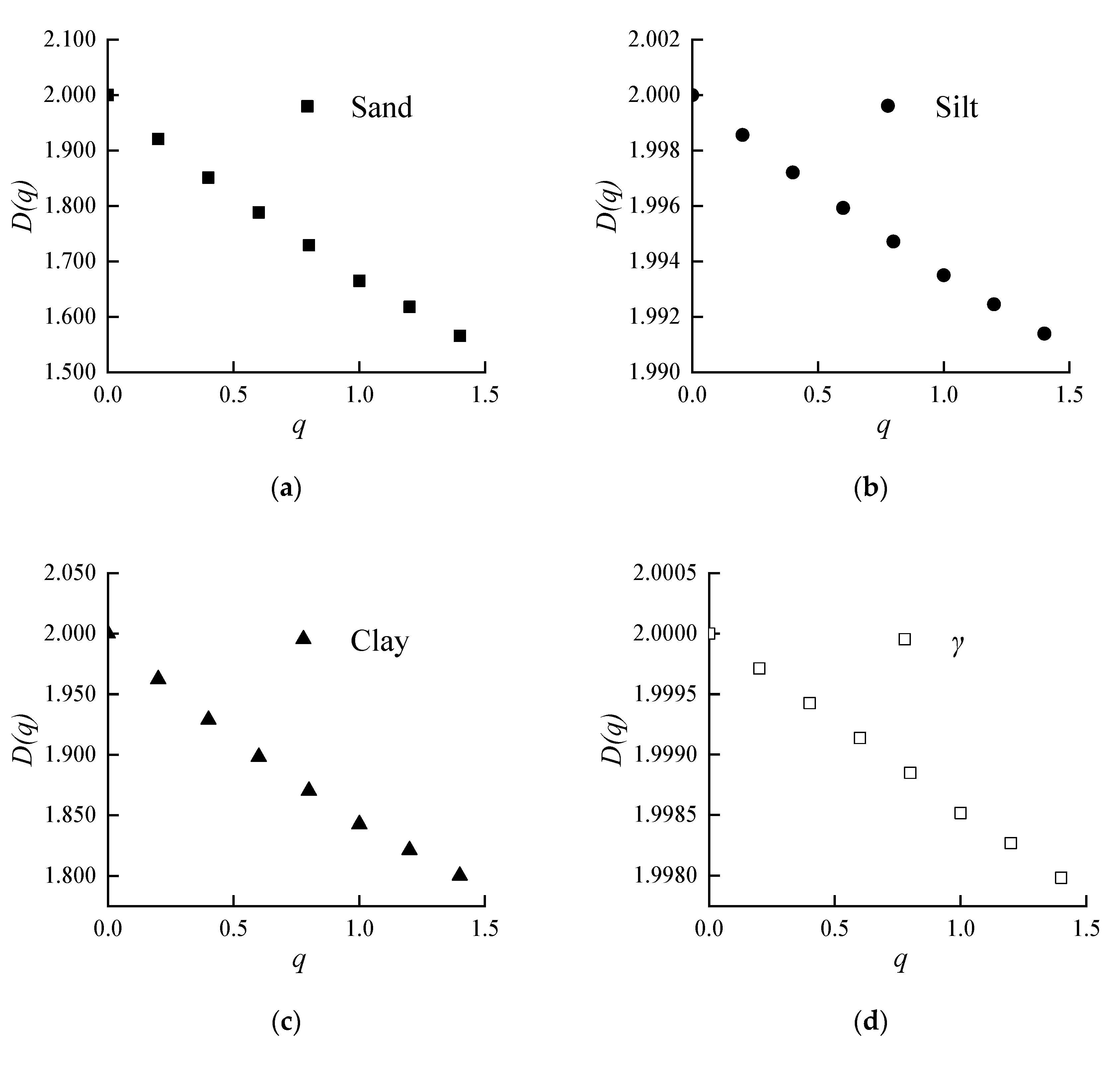

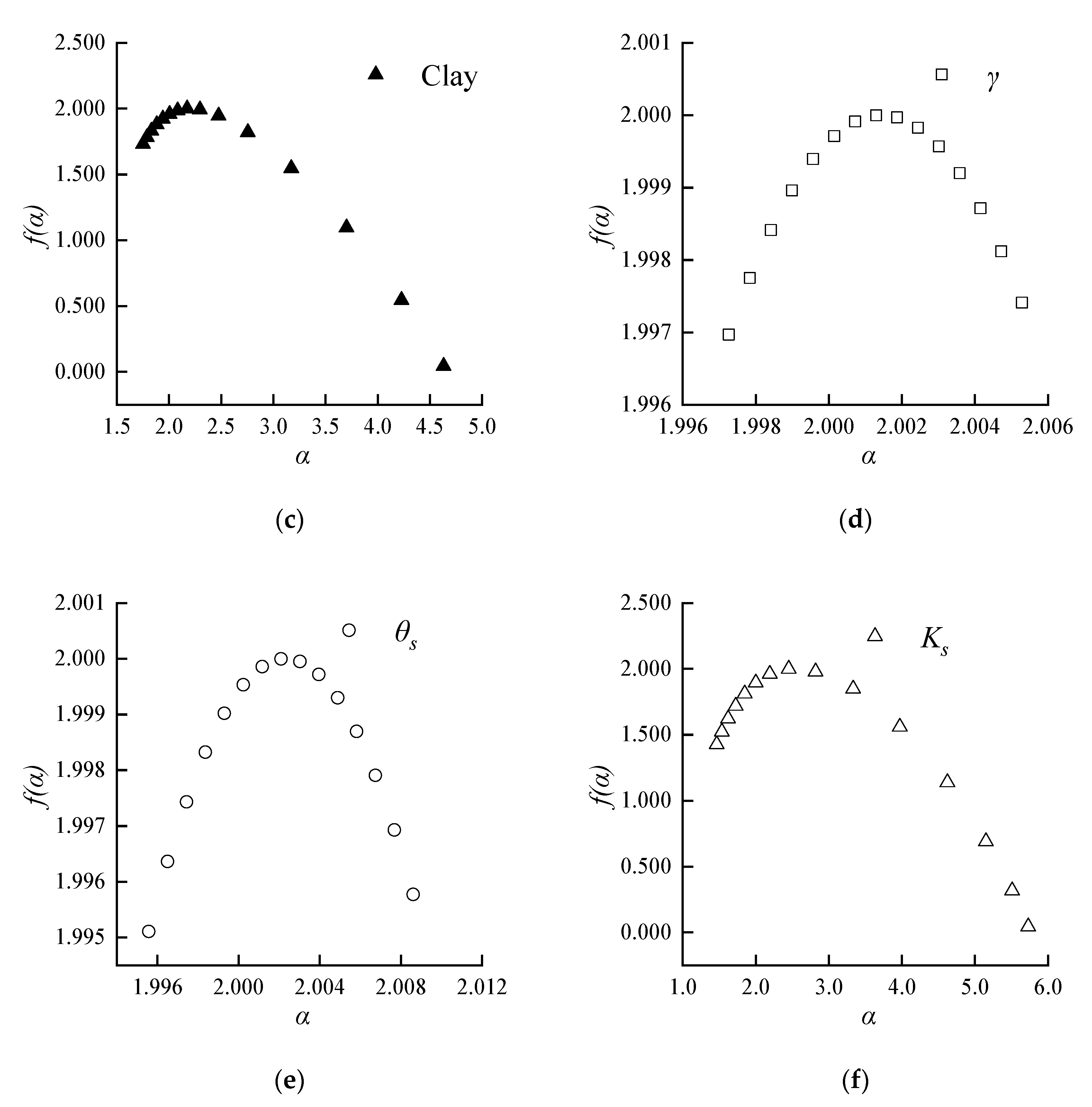
| Soil Property | Symbol | Particle Size | Test Method |
|---|---|---|---|
| Sand | \ | 0.075~2mm | Sieve analysis |
| Silt | \ | 0.005~0.075mm | Densimeter method |
| Clay | \ | <0.005mm | Densimeter method |
| Bulk density | γ | \ | Ring knife method |
| Saturated water content | θs | \ | Drying method |
| Saturated hydraulic conductivity | Ks | \ | Variable head test method |
| Soil Property | Minimum | Maximum | Mean | Standard Deviation | Cv (%) |
|---|---|---|---|---|---|
| Sand (%) | 0.10 | 66.70 | 7.05 | 10.54 | 149.58 |
| Silt (%) | 33.20 | 95.70 | 81.42 | 10.50 | 12.89 |
| Clay (%) | 0.10 | 42.90 | 11.40 | 9.16 | 80.32 |
| γ 1 (N·m−3) | 12,055.20 | 16,056.00 | 14,049.35 | 948.95 | 6.75 |
| θs 2 (cm3·cm−3) | 34.47 | 53.24 | 42.53 | 4.00 | 9.41 |
| Ks 3 (10−4cm·s−1) | 0.01 | 28.31 | 4.70 | 5.76 | 122.63 |
| Soil Property | Geostatistical Analysis (Isotropy) | |||||
|---|---|---|---|---|---|---|
| Model | C0 1 | C0 + C 2 | C0/C0 + C 3 | Range(m) | R2 | |
| Sand | Gaussian | 0.24450 | 0.49500 | 0.494 | 4094.57 | 0.886 |
| Silt | Exponential | 0.00001 | 0.00401 | 0.002 | 1119.00 | 0.713 |
| Clay | Gaussian | 0.10870 | 0.24340 | 0.447 | 5097.43 | 0.969 |
| γ | Gaussian | 0.00045 | 0.00095 | 0.468 | 1913.92 | 0.759 |
| θs | Linear | 0.00119 | 0.00185 | 0.402 | 3051.46 | 0.661 |
| Ks | Spherical | 0.27110 | 0.54320 | 0.499 | 2173.00 | 0.504 |
| Sand | Silt | Clay | γ | θs | Ks | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| D | R2 | D | R2 | D | R2 | D | R2 | D | R2 | D | R2 |
| 1.832 | 0.817 | 1.932 | 0.590 | 1.786 | 0.972 | 1.838 | 0.767 | 1.899 | 0.572 | 1.944 | 0.478 |
| Soil Properties | αmin1 | f(αmin) 2 | αmax3 | f(αmax) 4 | Δα 5 | Δf 6 |
|---|---|---|---|---|---|---|
| Sand | 1.4385 | 1.3878 | 3.9716 | 1.1239 | 2.5331 | 0.2639 |
| Silt | 1.9888 | 1.9878 | 2.0410 | 1.9745 | 0.0522 | 0.0133 |
| Clay | 1.7514 | 1.7318 | 4.6308 | 0.0439 | 2.8749 | 1.6879 |
| γ | 1.9973 | 1.9970 | 2.0053 | 1.9974 | 0.0080 | −0.0004 |
| θs | 1.9956 | 1.9951 | 2.0086 | 1.9958 | 0.0130 | −0.0007 |
| Ks | 1.4648 | 1.4271 | 5.7296 | 0.0438 | 4.2648 | 1.3833 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, J.; He, Y.; Zhao, G.; Li, Z.; Yuan, Q.; Liu, L. Quantitative Evaluation of the Spatial Variation of Surface Soil Properties in a Typical Alluvial Plain of the Lower Yellow River Using Classical Statistics, Geostatistics and Single Fractal and Multifractal Methods. Appl. Sci. 2020, 10, 5796. https://doi.org/10.3390/app10175796
Zhan J, He Y, Zhao G, Li Z, Yuan Q, Liu L. Quantitative Evaluation of the Spatial Variation of Surface Soil Properties in a Typical Alluvial Plain of the Lower Yellow River Using Classical Statistics, Geostatistics and Single Fractal and Multifractal Methods. Applied Sciences. 2020; 10(17):5796. https://doi.org/10.3390/app10175796
Chicago/Turabian StyleZhan, Jiang, Yujiang He, Guizhang Zhao, Zhiping Li, Qiaoling Yuan, and Lili Liu. 2020. "Quantitative Evaluation of the Spatial Variation of Surface Soil Properties in a Typical Alluvial Plain of the Lower Yellow River Using Classical Statistics, Geostatistics and Single Fractal and Multifractal Methods" Applied Sciences 10, no. 17: 5796. https://doi.org/10.3390/app10175796





