An Automatic Shadow Compensation Method via a New Model Combined Wallis Filter with LCC Model in High Resolution Remote Sensing Images
Abstract
:1. Introduction
2. Related Works
- (1)
- By taking full advantage of Wallis filter with adjustable coefficients for contrast and brightness enhancement as well as the useful LCC model in shadow compensation, we propose a compensation model by introducing two useful intensity and stretching coefficients based on Wallis filtering and LCC model. The capability of enhancing the contrast and brightness is strengthened significantly. Then it can be applied to shadow compensation more effectively.
- (2)
- Customize the shadow compensation model for the pixels in each shadow region by automatic parameter calculation and a compensation combination strategy. First, the compensation parameters are calculated using automatic feature points selection and matching for each shadow area. Then, the local window information of every pixel is considered by the combination strategy. Then, the adaptive compensation model is implemented so that they are suitable to recover the shaded information more flexibly and evenly.
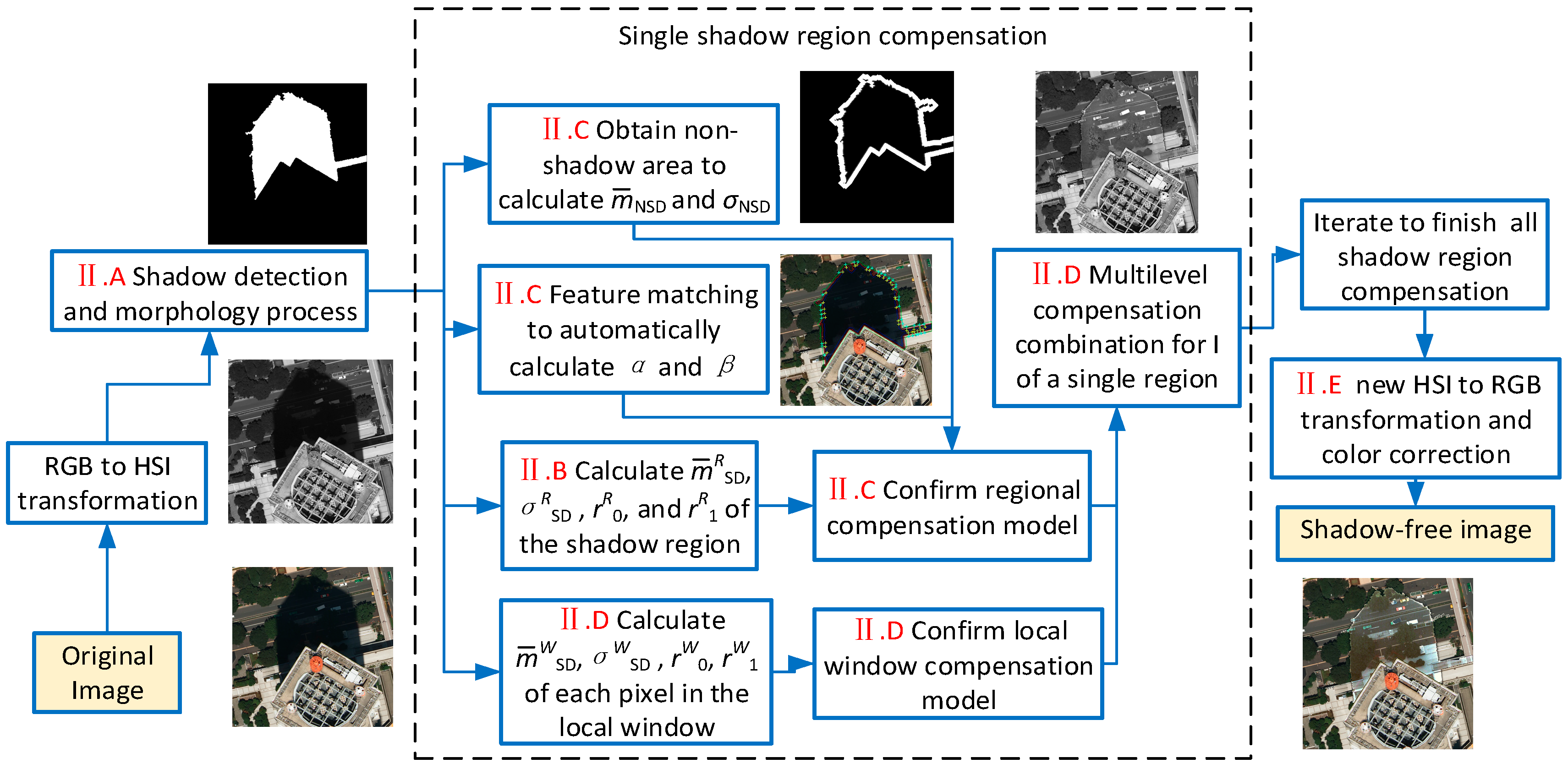
3. Materials and Methods
3.1. Shadow Detection
3.2. Shadow Compensation Model Based on Wallis Filter and LCC Model
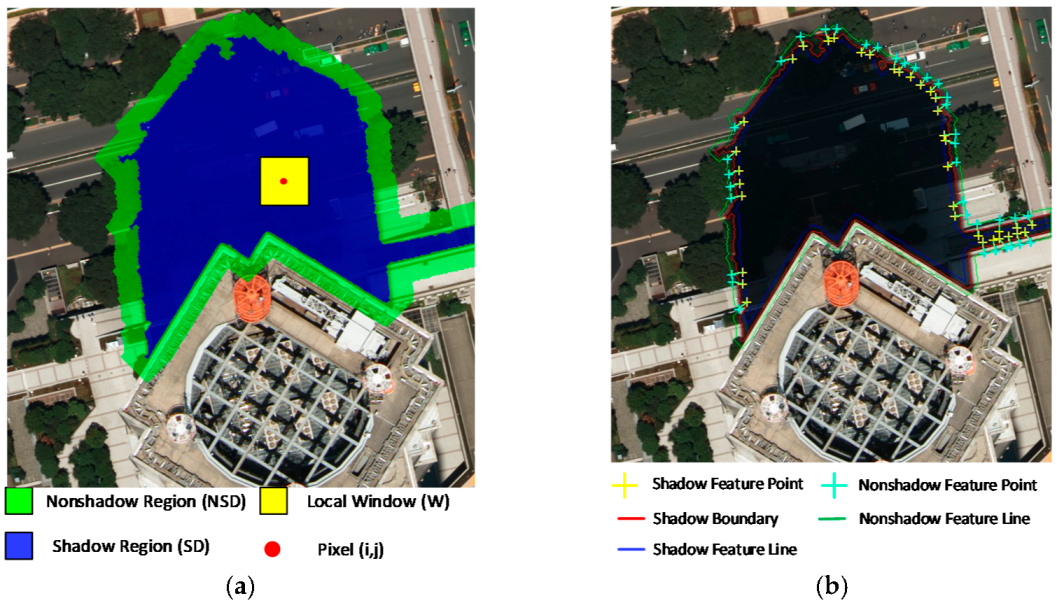
3.3. Automatic Parameter Calculation Method
3.4. Final Combination with the Local Window Information
4. Experimental Results
4.1. Dataset Description and Parameters Setting
4.2. Precision Evaluation Criteria
4.3. Qualitative Comparison
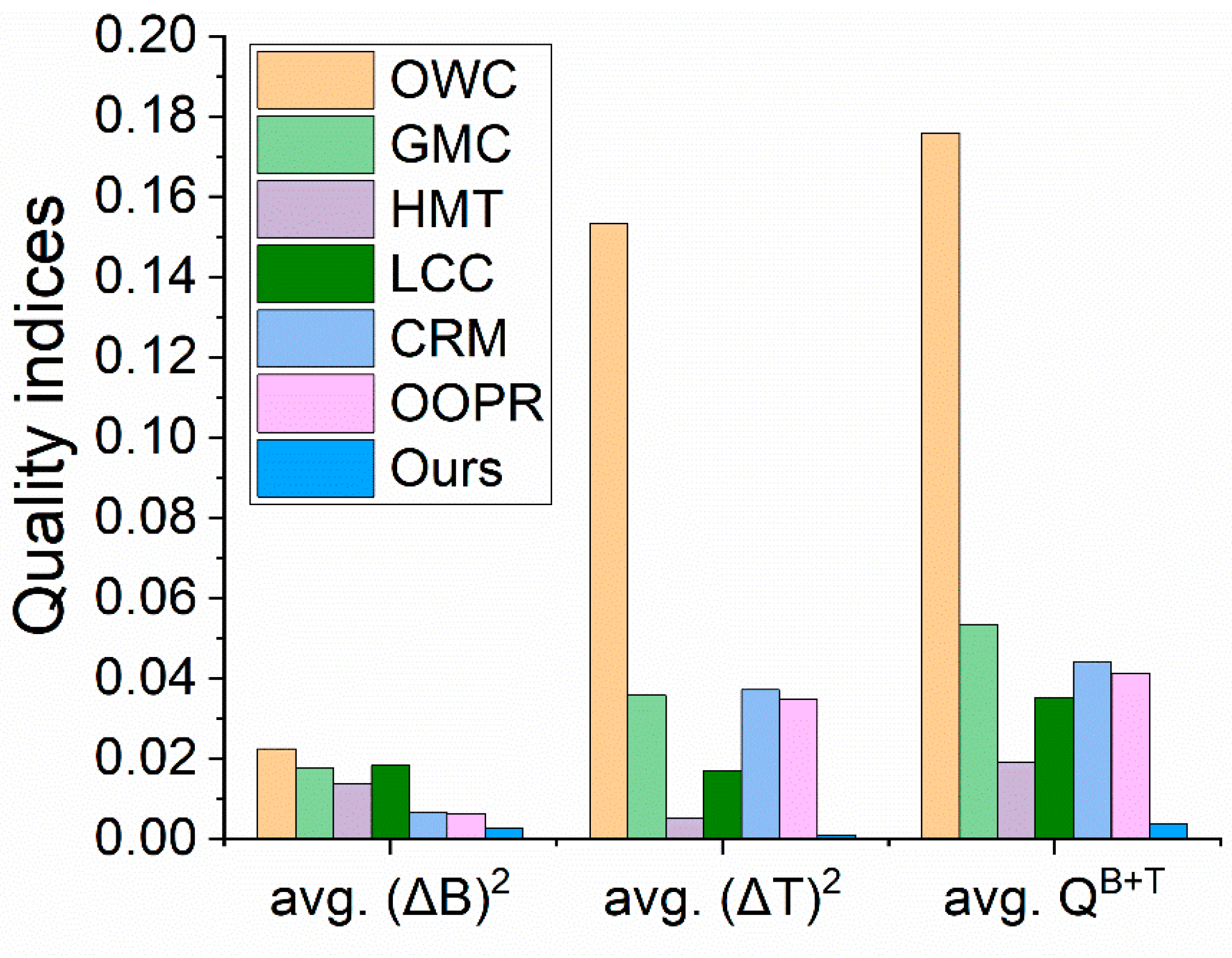
4.4. Quantitative Comparison
4.5. Time Computation
5. Discussions
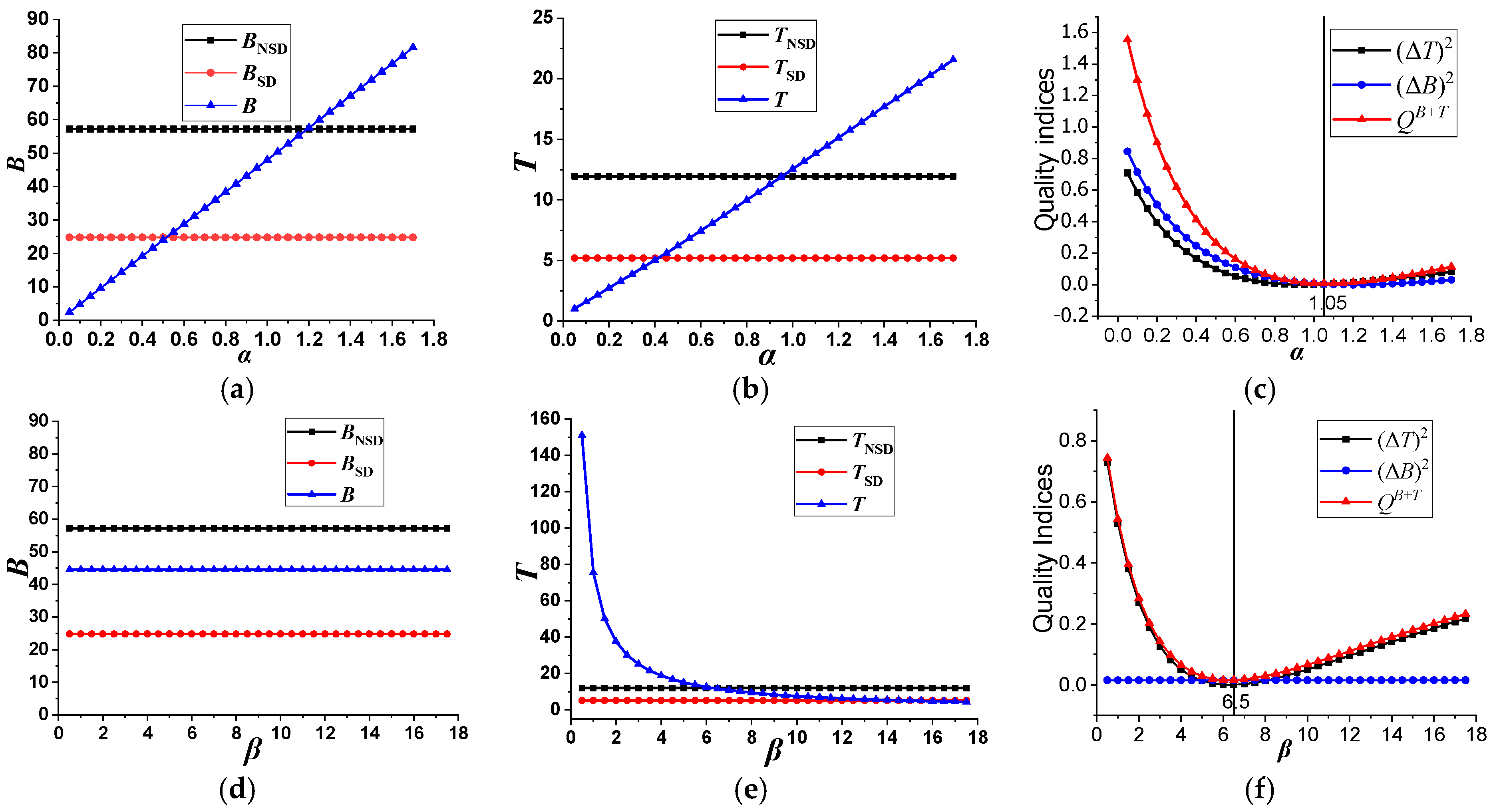
5.1. The Positive Impact of α and β on the Proposed Model
5.2. The Effectiveness of the Automatic Strategy for α and β Calculation
5.3. Validation for Color Correction
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mostafa, Y. A review on various shadow detection and compensation techniques in remote sensing images. Can. J. Remote Sens. 2017, 43, 545–562. [Google Scholar] [CrossRef]
- Chai, D.; Newsam, S.; Zhang, H.K.; Qiu, Y.; Huang, J. Cloud and cloud shadow detection in Landsat imagery based on deep convolutional neural networks. Remote Sens. Environ. 2019, 225, 307–316. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Li, H.; Xia, G.; Gamba, P.; Zhang, L. Multi-feature combined cloud and cloud shadow detection in GaoFen-1 wide field of view imagery. Remote Sens. Environ. 2017, 191, 342–358. [Google Scholar] [CrossRef] [Green Version]
- Lv, Z.Y.; Liu, T.F.; Zhang, P.; Benediktsson, J.A.; Lei, T.; Zhang, X. Novel adaptive histogram trend similarity approach for land cover change detection by using bitemporal very-high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9554–9574. [Google Scholar] [CrossRef]
- Gao, X.; ang, M.; Yang, Y.; Li, G. Building Extraction From RGB VHR Images Using Shifted Shadow Algorithm. IEEE Access 2018, 6, 22034–22045. [Google Scholar] [CrossRef]
- Sarabandi, P.; Yamazaki, F.; Matsuoka, M.; Kiremidjian, A. Shadow detection and radiometric restoration in satellite high resolution images. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’04), Anchorage, AK, USA, 20–24 September 2004; pp. 3744–3747. [Google Scholar]
- Wang, S.; Wang, Y. Shadow detection and compensation in high resolution satellite image based on retinex. In Proceedings of the 2009 Fifth International Conference on Image and Graphics, Xi’an, China, 20–23 September 2009; pp. 209–212. [Google Scholar]
- Jobson, D.J.; Rahman, Z.-U.; Woodell, G.A. Properties and performance of a center/surround retinex. IEEE Trans. Image Process. 1997, 6, 451–462. [Google Scholar] [CrossRef]
- Ma, H.; Qin, Q.; Shen, X. Shadow segmentation and compensation in high resolution satellite images. In Proceedings of the IGARSS 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 8–11 July 2008; pp. II-1036–II-1039. [Google Scholar]
- Liu, J.; Fang, T.; Li, D. Shadow detection in remotely sensed images based on self-adaptive feature selection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 5092–5103. [Google Scholar]
- Tiwari, K.C.S.; Kurmi, Y. Shadow detection and compensation in aerial images using MATLAB. Int. J. Comput. Appl. 2015, 119, 5–9. [Google Scholar] [CrossRef]
- Wang, W. Study of Shadow Processing’s Method High-Spatial Resolution RS Image. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2008. [Google Scholar]
- Liu, W.; Yamazaki, F. Object-based shadow extraction and correction of high-resolution optical satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1296–1302. [Google Scholar] [CrossRef]
- Luo, S.; Li, H.; Shen, H. Shadow removal based on clustering correction of illumination field for urban aerial remote sensing images. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 485–489. [Google Scholar]
- Tsai, V.J. A comparative study on shadow compensation of color aerial images in invariant color models. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1661–1671. [Google Scholar] [CrossRef]
- Jian, Y.; He, Y.; Caspersen, J. Fully constrained linear spectral unmixing based global shadow compensation for high resolution satellite imagery of urban areas. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 88–98. [Google Scholar]
- Nair, V.; Ram, P.G.K.; Sundararaman, S. Shadow detection and removal from images using machine learning and morphological operations. J. Eng. 2019, 2019, 11–18. [Google Scholar] [CrossRef]
- Vicente, T.F.Y.; Hoai, M.; Samaras, D. Leave-one-out kernel optimization for shadow detection and removal. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 682–695. [Google Scholar] [CrossRef] [PubMed]
- Zigh, E.; Belbachir, M.F.; Kadiri, M.; Djebbouri, M.; Kouninef, B. New shadow detection and removal approach to improve neural stereo correspondence of dense urban VHR remote sensing images. Eur. J. Remote Sens. 2015, 48, 447–463. [Google Scholar] [CrossRef]
- Ibrahim, I.; Yuen, P.; Hong, K.; Chen, T.; Soori, U.; Jackman, J.; Richardson, M. Illumination invariance and shadow compensation via spectro-polarimetry technique. Opt. Eng. 2012, 51. [Google Scholar] [CrossRef] [Green Version]
- Roper, T.; Andrews, M. Shadow modelling and correction techniques in hyperspectral imaging. Electron. Lett. 2013, 49, 458–459. [Google Scholar] [CrossRef]
- Wan, C.Y.; King, B.A.; Li, Z. An Assessment of Shadow Enhanced Urban Remote Sensing Imagery of a Complex City-Hong Kong. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences XXII ISPRS Congress, Melbourne, Australia, 25 August 2012; pp. 177–182. [Google Scholar]
- Mo, N.; Zhu, R.; Yan, L.; Zhao, Z. Deshadowing of urban airborne imagery based on object-oriented automatic shadow detection and regional matching compensation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 585–605. [Google Scholar] [CrossRef]
- Luo, S.; Shen, H.; Li, H.; Chen, Y. Shadow removal based on separated illumination correction for urban aerial remote sensing images. Signal Process. 2019, 165, 197–208. [Google Scholar] [CrossRef]
- Wang, C.; Xu, H.; Zhou, Z.; Deng, L.; Yang, M. Shadow detection and removal for illumination consistency on the road. IEEE Trans. Intell. Veh. 2020. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, D.; Jing, L.; Shi, P. Shadow information recovery in urban areas from very high resolution satellite imagery. Int. J. Remote Sens. 2007, 28, 3249–3254. [Google Scholar] [CrossRef]
- Mostafa, Y.; Abdelwahab, M.A. Corresponding regions for shadow restoration in satellite high-resolution images. Int. J. Remote Sens. 2018, 39, 7014–7028. [Google Scholar] [CrossRef]
- Liang, D.; Kong, J.; Hu, G.; Huang, L. The removal of thick cloud and cloud shadow of remote sensing image based on support vector machine. Acta Geod. Cartogr. Sin. 2012, 41, 225–231+238. [Google Scholar]
- Zhang, H.Y.; Sun, K.M.; Li, W.Z. Object-oriented shadow detection and removal from urban high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6972–6982. [Google Scholar] [CrossRef]
- Friman, O.; Tolt, G.; Ahlberg, J. Illumination and shadow compensation of hyperspectral images using a digital surface model and non-linear least squares estimation. In Proceedings of the Image and Signal Processing for Remote Sensing XVII 2011, Prague, Czech Republic, 26 October 2011; pp. 81800Q–81808Q. [Google Scholar]
- Gao, X.; Wan, Y.; Yang, Y.; He, P. Automatic shadow detection and automatic compensation in high resolution remote sensing images. Acta Autom. Sin. 2014, 40, 1709–1720. [Google Scholar]
- Huang, X.; Zhang, L. Morphological building/shadow index for building extraction from high-resolution imagery over urban areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 161–172. [Google Scholar] [CrossRef]
- Jiménez, L.I.; Plaza, J.; Plaza, A. Efficient implementation of morphological index for building/shadow extraction from remotely sensed images. J. Supercomput. 2017, 73, 482–494. [Google Scholar] [CrossRef]
- Otsu, N. Threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.; Chen, X.; Zhong, L.; Zhou, M.; Shi, Y.; Duan, Y. Improved wallis dodging algorithm for large-scale super-resolution reconstruction remote sensing images. Sensors 2017, 17, 623. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Li, X.; Duan, F.; Wang, J.; Ou, Y. An efficient seam elimination method for UAV images based on wallis dodging and gaussian distance weight enhancement. Sensors 2016, 16, 662. [Google Scholar] [CrossRef]













| Image Name | Quality Index | SD | NSD | OWC | GMC | HMT | LCC | CRM | OOPR | Ours |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | B | 36.2754 | 63.1889 | 58.7920 | 62.0299 | 63.2713 | 62.7771 | 73.4417 | 77.7327 | 63.7444 |
| T | 5.1839 | 14.4409 | 5.7489 | 9.3673 | 11.3595 | 9.2900 | 8.2844 | 13.2295 | 14.2704 | |
| QB+T | — | — | 0.1866 | 0.0455 | 0.0143 | 0.0471 | 0.0790 | 0.0126 | 0.0001 | |
| 2 | B | 57.9359 | 85.1085 | 83.2481 | 82.4600 | 91.8727 | 86.9860 | 97.1427 | 94.9559 | 87.5762 |
| T | 7.8907 | 16.2861 | 9.6110 | 13.0989 | 13.8274 | 11.0122 | 10.2769 | 11.7217 | 15.0647 | |
| QB+T | — | — | 0.0666 | 0.0120 | 0.0081 | 0.0374 | 0.0555 | 0.0295 | 0.0017 | |
| 3 | B | 37.0008 | 74.3142 | 61.5478 | 73.1817 | 72.7659 | 66.7924 | 86.1723 | 76.8533 | 71.7967 |
| T | 4.9003 | 23.7773 | 4.8980 | 11.3497 | 19.7813 | 17.5462 | 21.9928 | 10.3542 | 21.7824 | |
| QB+T | — | — | 0.4423 | 0.1252 | 0.0085 | 0.0256 | 0.0070 | 0.1549 | 0.0022 | |
| 4 | B | 56.9910 | 150.1633 | 124.6353 | 116.4057 | 133.0205 | 124.2297 | 155.2552 | 160.0377 | 149.8764 |
| T | 10.8680 | 20.6191 | 13.3118 | 17.8083 | 21.3499 | 13.3118 | 35.5466 | 21.3857 | 21.0447 | |
| QB+T | — | — | 0.0550 | 0.0214 | 0.0040 | 0.0553 | 0.0709 | 0.0013 | 0.0001 | |
| 5 | B | 24.6591 | 91.9680 | 65.7744 | 71.3056 | 73.0492 | 68.0745 | 81.7099 | 89.3095 | 82.5732 |
| T | 5.5742 | 22.1672 | 10.4184 | 16.5486 | 22.1398 | 19.0862 | 15.6511 | 17.7781 | 23.2122 | |
| QB+T | — | — | 0.1576 | 0.0371 | 0.0131 | 0.0279 | 0.0332 | 0.0123 | 0.0034 | |
| 6 | B | 23.4614 | 107.7722 | 72.7422 | 63.7967 | 80.8888 | 74.7187 | 129.5133 | 66.2398 | 96.0105 |
| T | 10.5629 | 21.5307 | 11.1936 | 20.7145 | 25.6043 | 21.1387 | 44.5303 | 20.5617 | 23.9488 | |
| QB+T | — | — | 0.1374 | 0.0661 | 0.0278 | 0.0329 | 0.1296 | 0.0575 | 0.0062 | |
| A | B | 52.7057 | 148.7910 | 107.6152 | 109.4551 | 121.2661 | 113.6874 | 105.1475 | 127.9258 | 131.1461 |
| T | 6.7169 | 16.9851 | 9.5116 | 13.4378 | 18.8517 | 15.5673 | 12.6911 | 11.0926 | 17.1362 | |
| QB+T | — | — | 0.1053 | 0.0368 | 0.0131 | 0.0198 | 0.0505 | 0.0497 | 0.0040 | |
| B | B | 52.0459 | 149.1248 | 113.8646 | 117.4061 | 136.1765 | 127.4515 | 107.5620 | 140.2063 | 139.5191 |
| T | 4.0803 | 13.4322 | 5.3878 | 8.4708 | 13.9667 | 12.0483 | 10.5662 | 8.7642 | 13.8181 | |
| QB+T | — | — | 0.2007 | 0.0655 | 0.0024 | 0.0091 | 0.0405 | 0.0452 | 0.0013 | |
| C | B | 50.3020 | 136.3924 | 116.0753 | 105.9343 | 121.3617 | 112.6049 | 142.1750 | 135.7543 | 135.5174 |
| T | 7.0388 | 21.5283 | 8.5362 | 11.9807 | 19.4671 | 15.5198 | 25.8519 | 13.6585 | 21.2531 | |
| QB+T | — | — | 0.1932 | 0.0970 | 0.0059 | 0.0354 | 0.0088 | 0.0500 | 0.0001 | |
| D | B | 54.6436 | 142.2926 | 105.7497 | 120.4303 | 121.9426 | 114.5220 | 115.9803 | 142.4835 | 129.9071 |
| T | 4.9285 | 15.2054 | 5.9959 | 10.2507 | 15.7802 | 14.1726 | 10.9094 | 10.5155 | 15.3493 | |
| QB+T | — | — | 0.2104 | 0.0448 | 0.0063 | 0.0129 | 0.0374 | 0.0332 | 0.0021 | |
| E | B | 22.1513 | 90.6838 | 72.6012 | 71.6895 | 81.1097 | 76.1222 | 73.8717 | 91.9199 | 88.5145 |
| T | 2.8182 | 20.4905 | 8.7832 | 14.8224 | 20.3036 | 18.6539 | 16.3324 | 11.4661 | 20.5716 | |
| QB+T | — | — | 0.1722 | 0.0394 | 0.0031 | 0.0098 | 0.0232 | 0.0798 | 0.0002 | |
| F | B | 22.1948 | 116.9342 | 84.3402 | 71.4961 | 95.5993 | 87.6406 | 112.3088 | 86.5574 | 102.5739 |
| T | 6.4213 | 18.4400 | 7.3065 | 14.6794 | 21.0539 | 17.7352 | 30.7426 | 16.6335 | 17.2710 | |
| QB+T | — | — | 0.2132 | 0.0710 | 0.0145 | 0.0209 | 0.0630 | 0.0249 | 0.0054 | |
| Average QB+T | — | — | 0.1915 | 0.0581 | 0.0099 | 0.0268 | 0.0557 | 0.0500 | 0.0021 | |
| Image Name | Shadow Rate (%) | Length × Width (pixel) | OWC (s) | GMC (s) | HMT (s) | LCC (s) | CRM (s) | OOPR (s) | Ours (s) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50.563 | 823×576 | 0.075 | 0.033 | 0.034 | 0.179 | 4.627 | 1.102 | 0.893 |
| 2 | 38.979 | 686×601 | 0.076 | 0.038 | 0.033 | 0.082 | 1.650 | 0.889 | 0.677 |
| 3 | 45.893 | 894×634 | 0.143 | 0.065 | 0.064 | 0.159 | 2.336 | 1.604 | 1.338 |
| 4 | 26.783 | 1437×937 | 0.297 | 0.172 | 0.186 | 0.375 | 33.469 | 5.034 | 4.688 |
| 5 | 22.352 | 937×1437 | 0.186 | 0.105 | 0.108 | 0.234 | 20.276 | 1.903 | 1.641 |
| 6 | 27.077 | 1004×1188 | 0.263 | 0.129 | 0.129 | 0.269 | 32.886 | 1.525 | 1.264 |
| α = 0.5 | α = 0.75 | α = 1 | α = 1.25 | |
|---|---|---|---|---|
| β = 10 |  |  |  |  |
 |  |  |  |
| β = 5 | β = 10 | β = 15 | β = 20 | |
|---|---|---|---|---|
| α = 0.95 |  |  |  |  |
 |  |  |  |
| Area Name | α Automatic Value | β Automatic Value | α Ideal Value | β Ideal Value |
|---|---|---|---|---|
| 1 | 1.295 | 1.036 | 1.35 | 1 |
| 2 | 1.264 | 0.926 | 1.3 | 1 |
| 3 | 1.091 | 9.831 | 1.1 | 10 |
| 4 | 1.0863 | 6.321 | 1.05 | 6.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Ran, S.; Gao, X.; Wang, M.; Li, X. An Automatic Shadow Compensation Method via a New Model Combined Wallis Filter with LCC Model in High Resolution Remote Sensing Images. Appl. Sci. 2020, 10, 5799. https://doi.org/10.3390/app10175799
Yang Y, Ran S, Gao X, Wang M, Li X. An Automatic Shadow Compensation Method via a New Model Combined Wallis Filter with LCC Model in High Resolution Remote Sensing Images. Applied Sciences. 2020; 10(17):5799. https://doi.org/10.3390/app10175799
Chicago/Turabian StyleYang, Yuanwei, Shuhao Ran, Xianjun Gao, Mingwei Wang, and Xi Li. 2020. "An Automatic Shadow Compensation Method via a New Model Combined Wallis Filter with LCC Model in High Resolution Remote Sensing Images" Applied Sciences 10, no. 17: 5799. https://doi.org/10.3390/app10175799
APA StyleYang, Y., Ran, S., Gao, X., Wang, M., & Li, X. (2020). An Automatic Shadow Compensation Method via a New Model Combined Wallis Filter with LCC Model in High Resolution Remote Sensing Images. Applied Sciences, 10(17), 5799. https://doi.org/10.3390/app10175799






