Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Modeling
2.2. Analytical Analysis
2.2.1. Analytical Solutions for the Stator without Windings
2.2.2. Analytical Solutions for the Stator with Windings
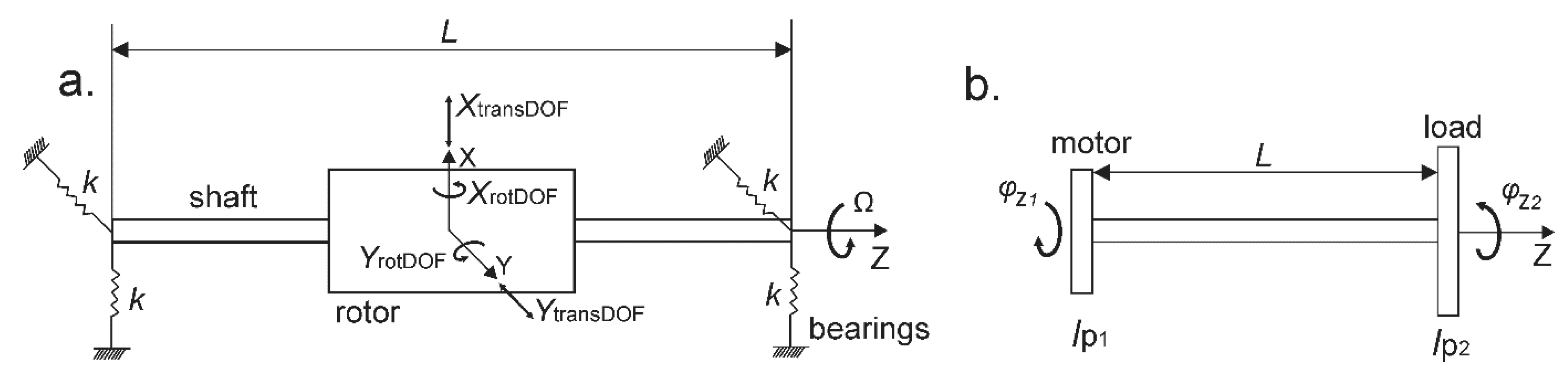
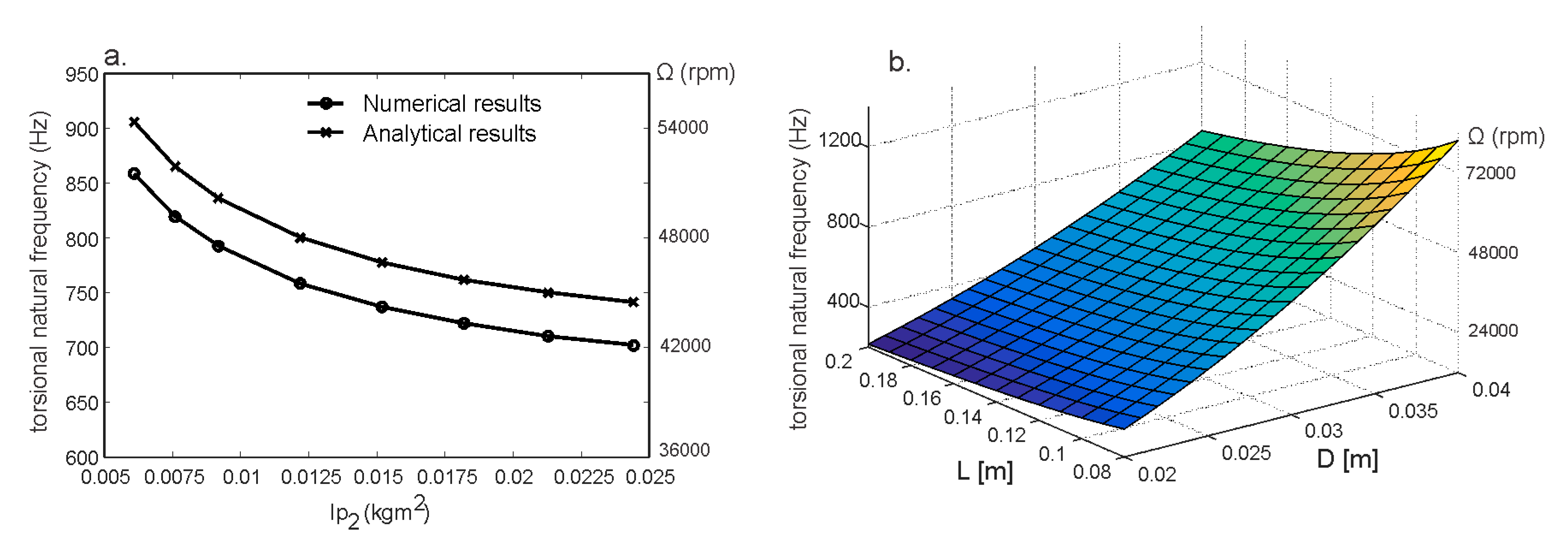
2.2.3. Analytical Calculation of Rotor Critical Speeds, Whirl Natural Frequencies and Torsional Natural Frequencies
2.2.4. Calculation of Torsional Natural Frequencies
2.3. Experimental Measurements
3. Results and Discussion
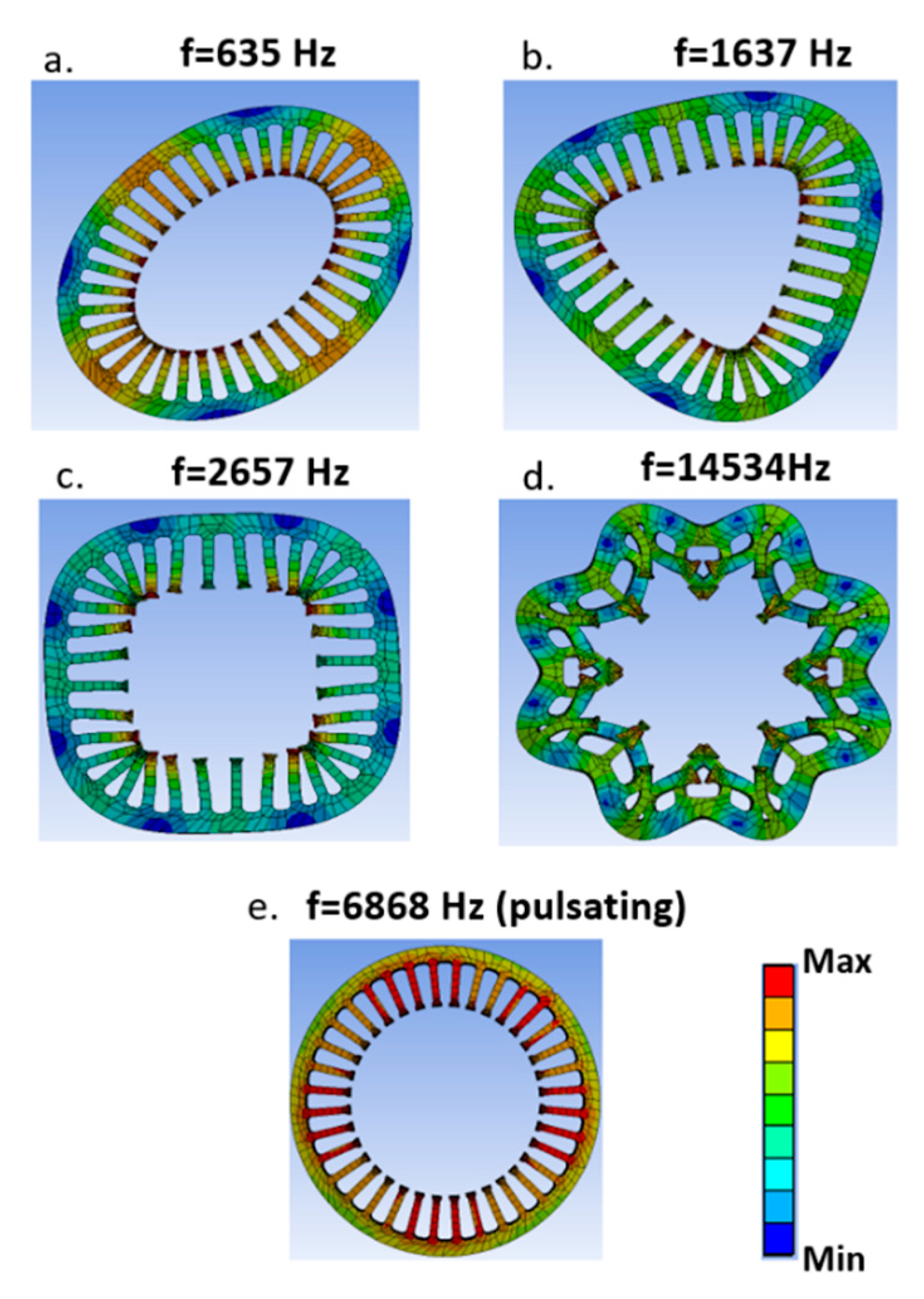
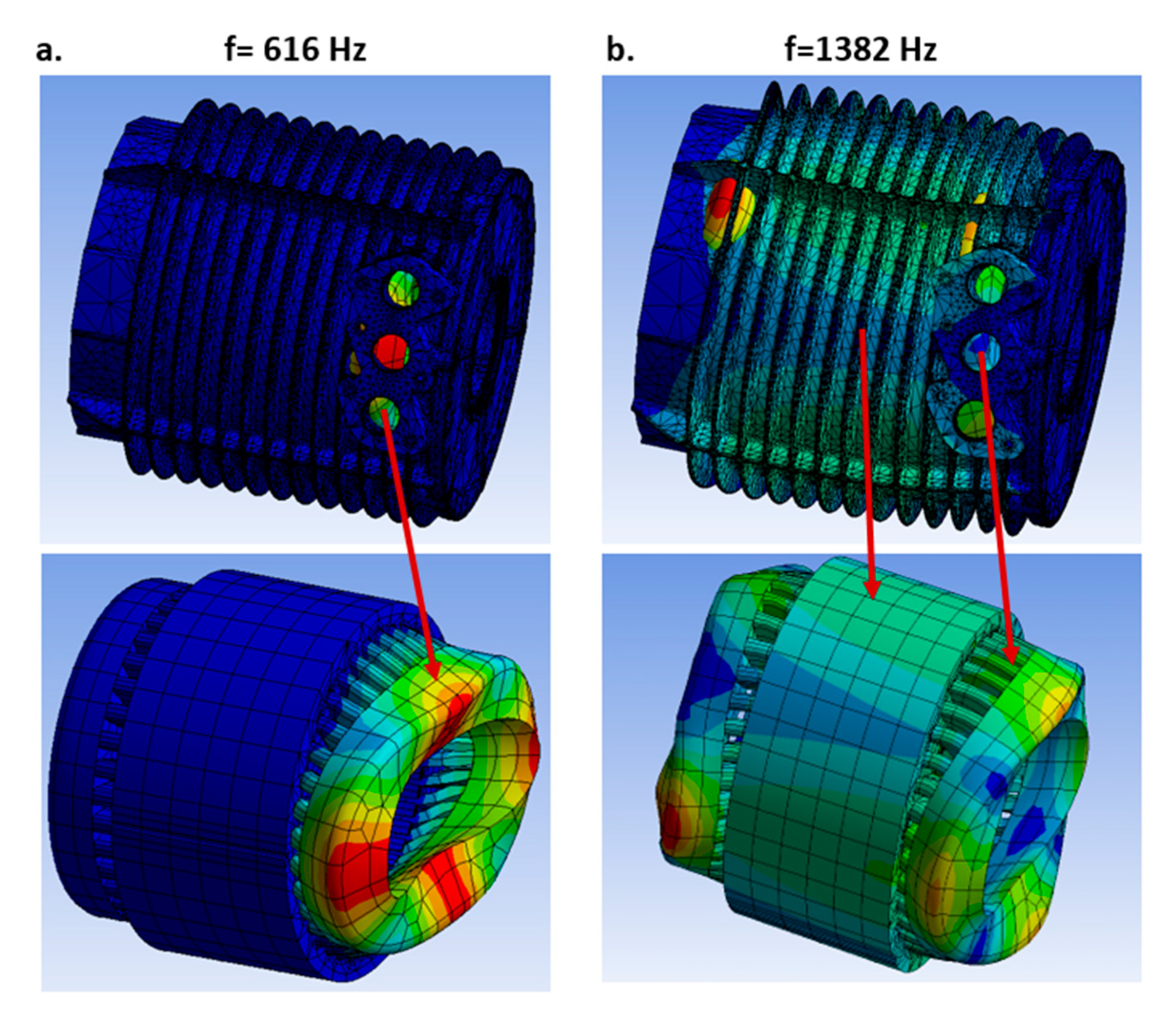
3.1. Natural Frequencies and Modal Shapes of the Stator with and without Windings
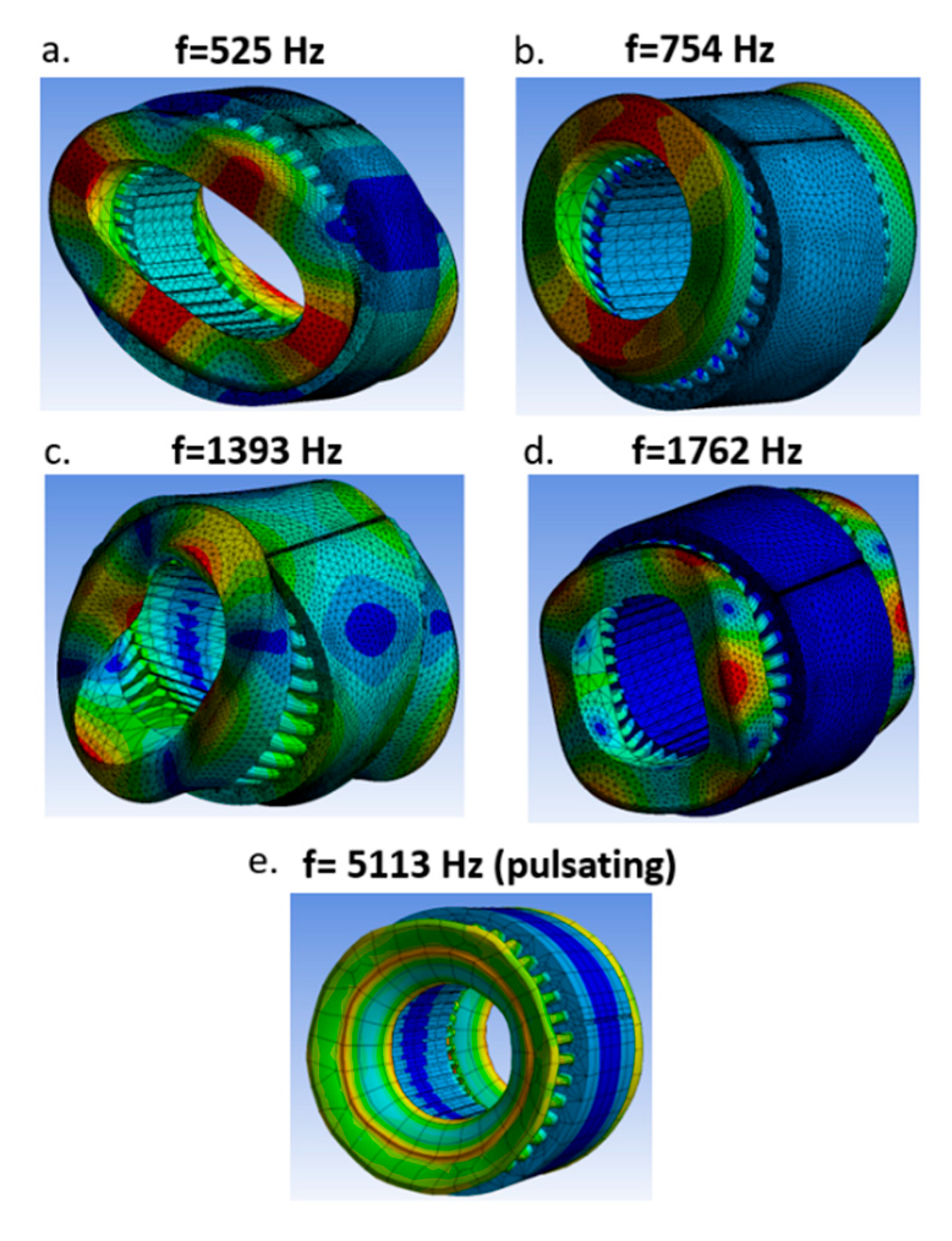
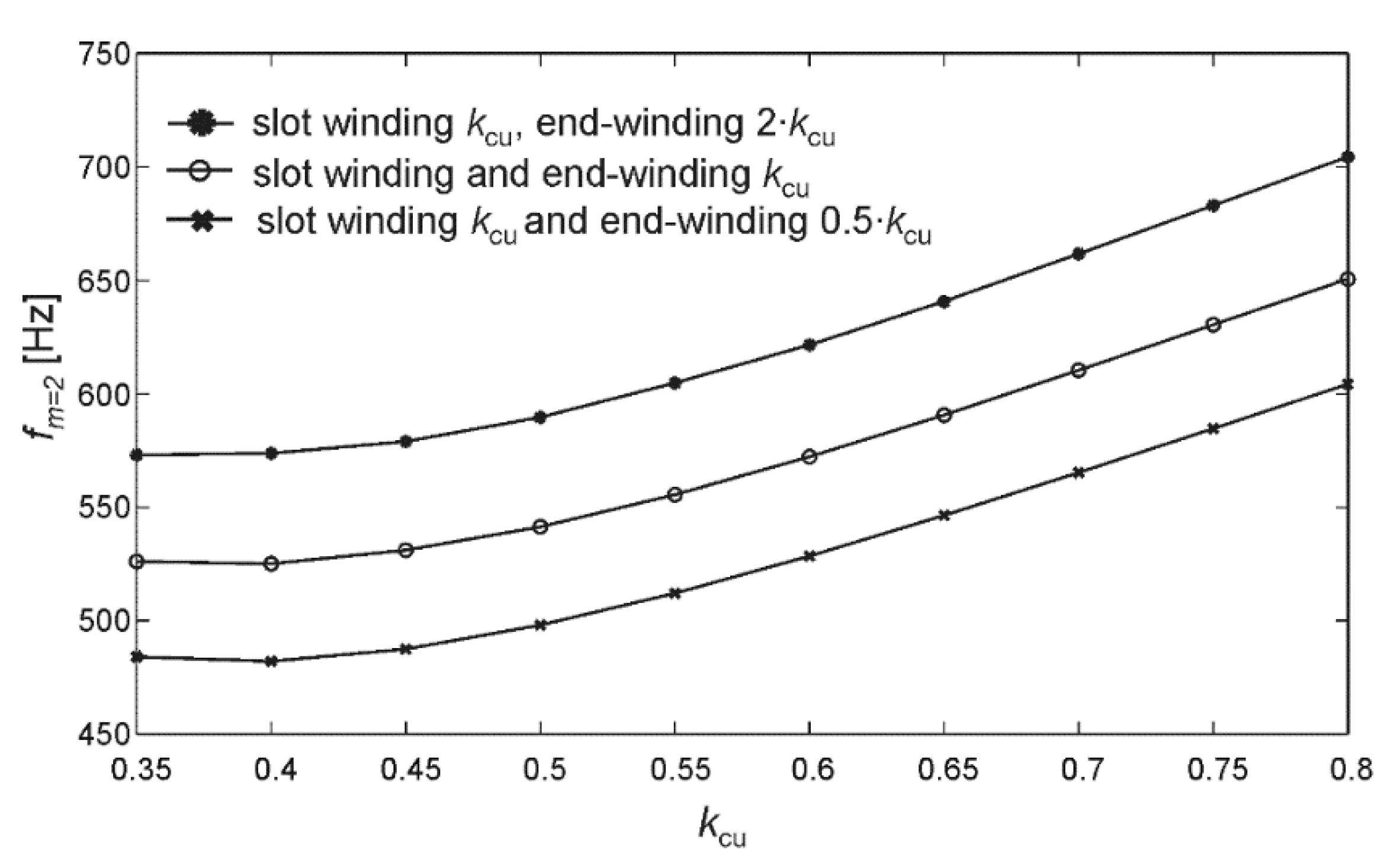
3.2. Influence of Motor Frame/Housing on Natural Frequencies and Modal Shapes
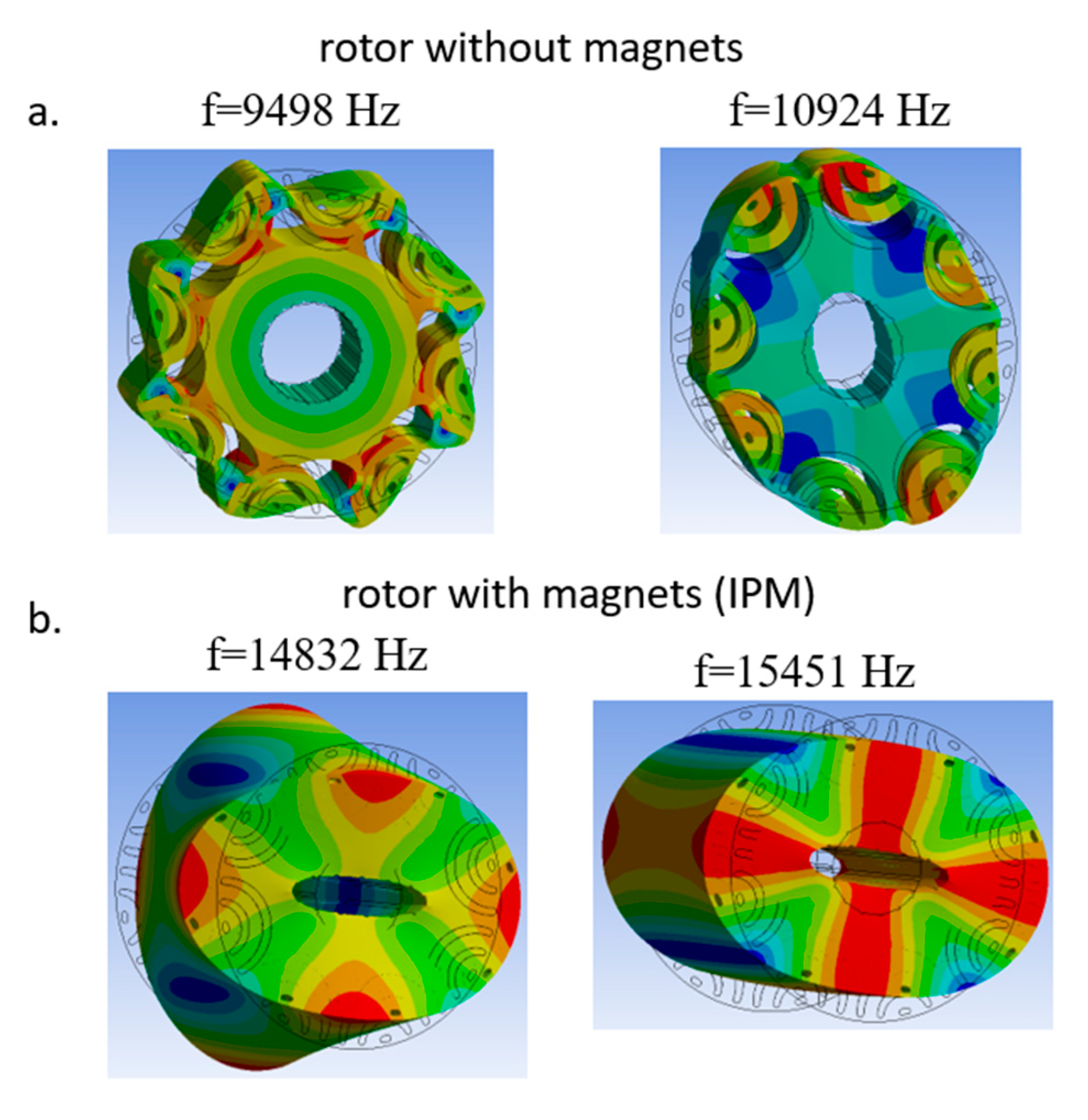
3.3. Modal Analysis of the IPM Rotor Configuration
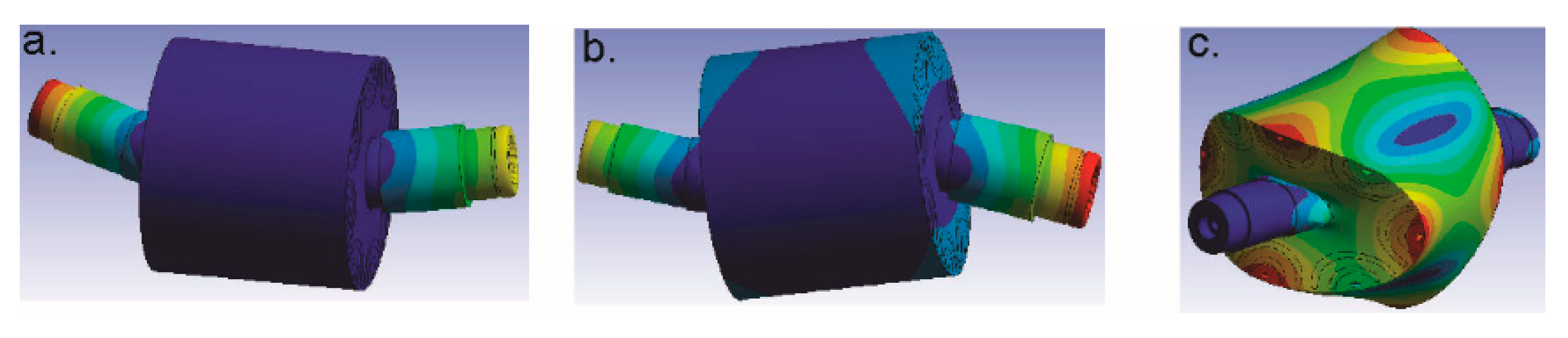
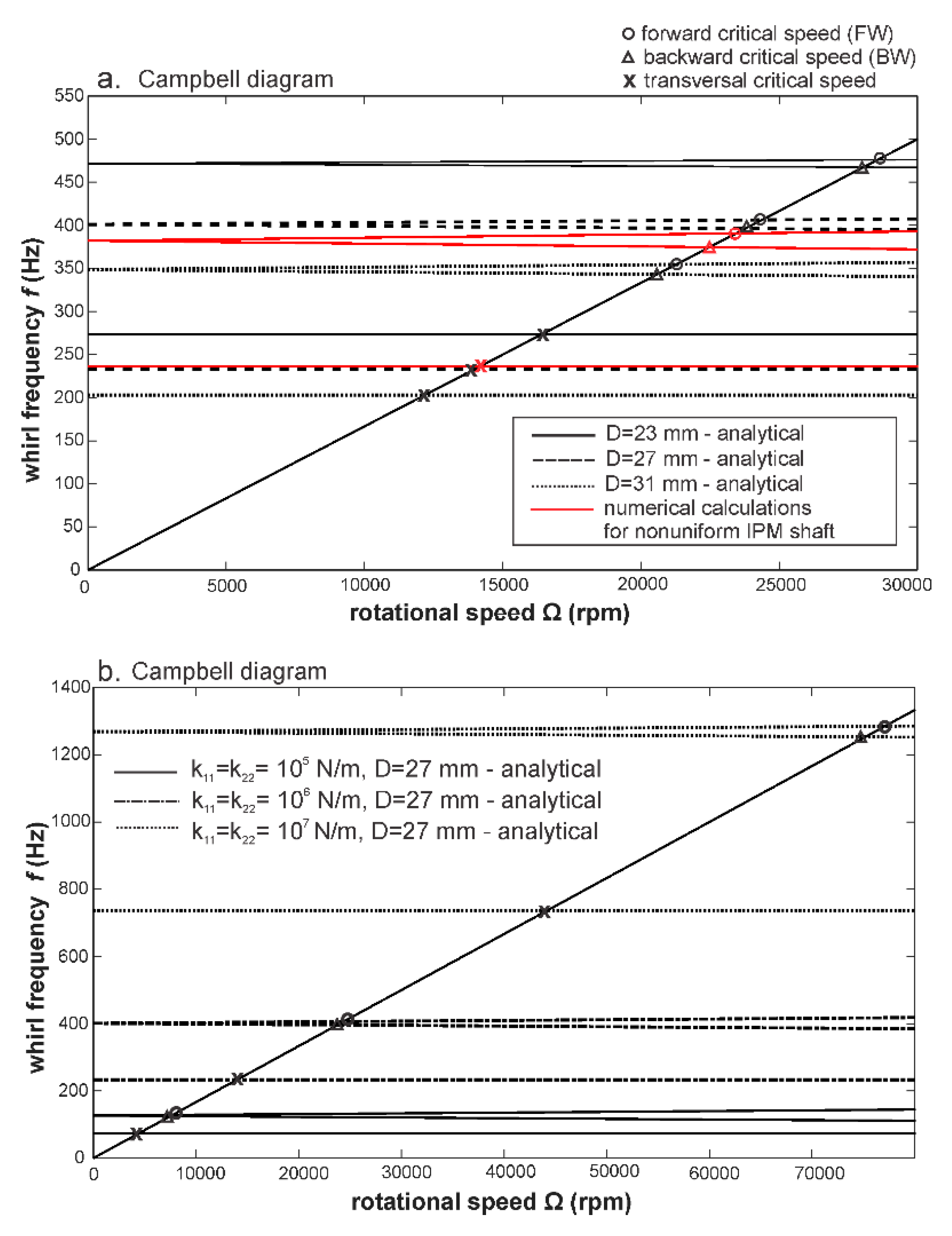
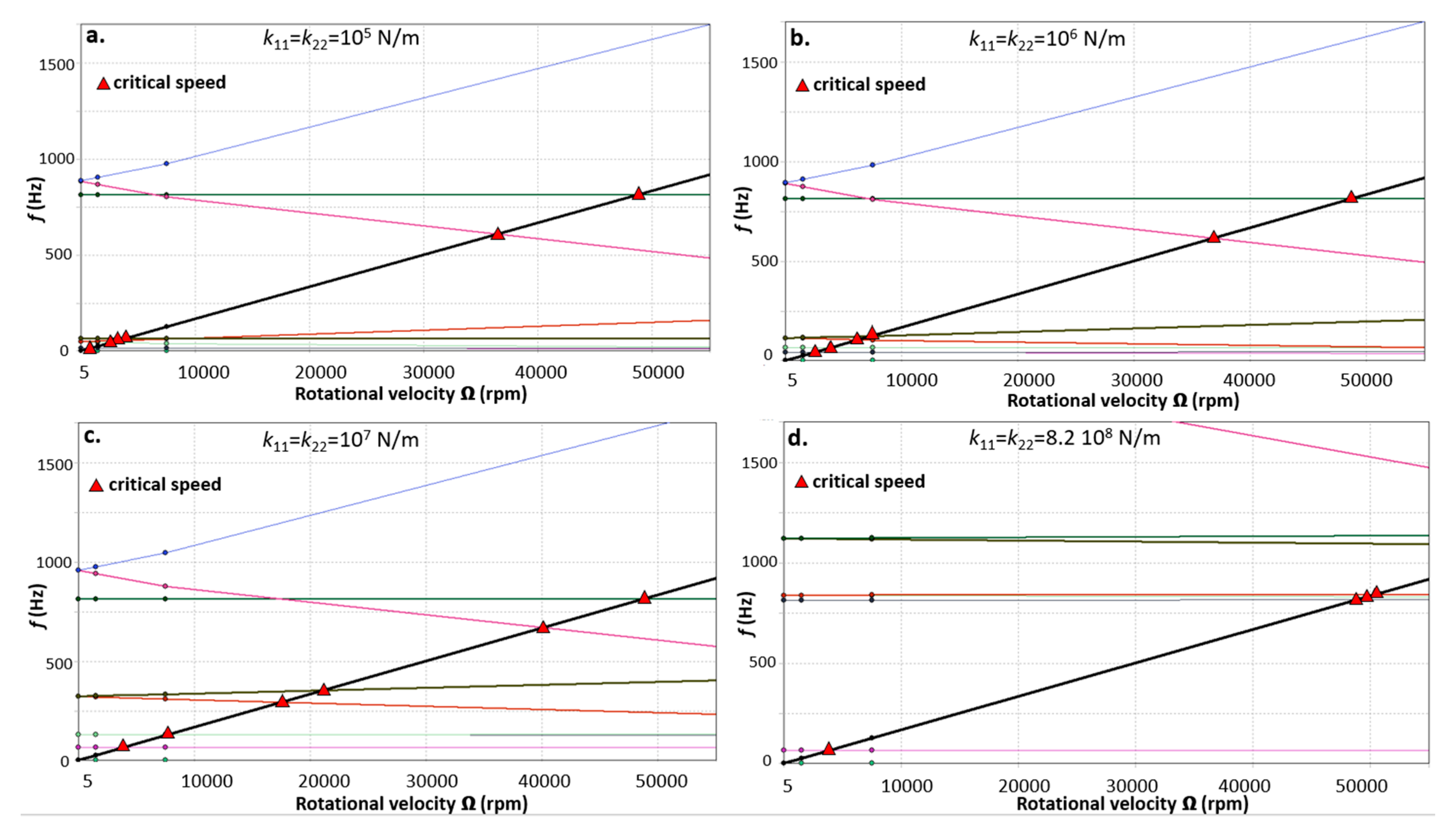
3.4. Results of the Rotordynamic Analysis
4. Conclusions
- The presence of the permanent magnets results in higher natural frequencies of the IPM rotor configuration compared to the natural frequencies of the rotor without magnets. This finding can be useful for robust design of the IPM rotor as well as for the design of synchronous reluctance machines’ rotors without magnets. This is also important for the IMP machine fault detection since the natural frequencies of the rotor with mechanically damaged magnets (and/or partially demagnetized magnets) may be altered (i.e., lower natural frequencies and/or additional natural frequencies might be detected due to the damage).
- The numerical modeling approach presented in this study proposes a simplified but accurate modeling of the slot winding and end-winding as a solid object with equivalent mechanical properties of the composite material (i.e., conductor and insulations). The proposed model was successfully validated with experimental measurements. The advantage of such a modeling approach is the reduction of the computational time needed for numerical simulations.
- When an equal fill factor kcu is applied for both end winding and slot winding, the numerically calculated and experimentally measured natural frequencies of the stator with windings differed by 4.7%. This finding might be particularly important when coupling mechanical analysis with magnetic and thermal analysis of the electrical machine, since the kcu of the end windings is usually difficult to determine.
- The presence of the slot windings and end-winding decreases the natural frequency of the stator assembly. This finding can be also important for analysis of mechanical vibrations imposed by insertion of mechanical supporting structures in order to reduce the mechanical vibrations of the whole stator assembly.
- The presence of the motor housing results in the higher natural frequencies of the motor assembly. The numerical modal analysis of the stator assembly with housing revealed that certain natural frequencies of the end-windings were excited even though the mechanical vibrations of the motor housing/frame (dictated by mechanical vibration of the stator) were not observed/detected, which is important in prevention of premature damage of windings.
- The rotor dynamic analysis, taking into account the gyroscopic effect, showed that the bearings with higher stiffness contribute to the increase of the critical speeds and their elimination from the operation range of the analyzed IMP rotor. The models show that a strong bifurcation was present due to the presence of the rotor with magnets compared to the rotor-dynamic shaft only. The calculated torsional critical speeds of the IPM rotor are significantly higher compared to the maximum operational speed, confirming the safe design of the IPM rotor analyzed in this study. The proposed rotor-dynamic numerical models of the IPM rotors were successfully validated with the analytical solutions.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Bearingsk 11 = k12 = 105 N/m | Bearingsk 11 = k12 = 106 N/m | Bearingsk 11 = k12 = 107 N/m | Bearingsk 11 = k12 = 8.2·108 N/m NN3006KTN/SP | ||||
|---|---|---|---|---|---|---|---|
| Critical Speed Ω (rpm) | Whirl Dir. | Critical Speed Ω (rpm) | Whirl Dir. | Critical Speed Ω (rpm) | Whirl Dir. | Critical Speed Ω (rpm) | Whirl Dir. |
| 1751 | BW | 5520.5 | FW | / | / | / | / |
| 1751 | FW | 5520.9 | BW | / | / | / | / |
| 7256.6 | BW * | 7256.7 | BW | 7256.7 | BW | 7256.7 | BW |
| 6080.8 | BW | 11,256 | BW | 17,003 | BW | 63,246 | BW |
| 14,373 | FW | 25,319 | FW | 17,005 | FW | 64,372 | FW |
| / | / | / | / | 32,130 | BW | / | / |
| / | / | / | / | 72,766 | FW | / | / |
| Bearingsk 11 = k12 = 105 N/m | Bearingsk 11 = k12 = 106 N/m | Bearingsk 11 = k12 = 107 N/m | Bearingsk 11 = k12 = 8.2·108 N/m NN3006KTN/SP | ||||
|---|---|---|---|---|---|---|---|
| Critical Speed Ω [(rpm) | Whirl Dir. | Critical Speed Ω (rpm) | Whirl Dir. | Critical Speed Ω (rpm) | Whirl Dir. | Critical Speed Ω (rpm) | Whirl Dir. |
| 842 | BW | / | / | / | / | / | / |
| 844 | FW | / | / | / | / | / | / |
| 2646 | BW | 2493 | BW | / | / | / | / |
| 3138 | FW | 2511 | FW | / | / | / | / |
| 3790 | BW | 3790 | BW | 3790 | BW | 3790 | BW |
| 48,774 | FW | 6245 | BW | 7721 | BW | 48,774 | BW |
| 36,476 | BW | 7378 | FW | 7776 | FW | 49,683 | FW |
| / | / | 48,774 | FW | 17,541 | BW | 50,393 | BW |
| / | / | 36,800 | BW | 21,138 | FW | / | / |
| / | / | / | / | 48,774 | FW | / | / |
| / | / | / | / | 40,084 | BW | / | / |
References
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Appl. 2014, 61, 2946–2959. [Google Scholar]
- Huang, Z.; Le, Y. Rotordynamics modelling and analysis of high-speed permanent magnet electrical machine rotors. IET Electr. Power Appl. 2018, 12, 1104–1109. [Google Scholar]
- Breznik, M.; Goričan, V.; Hamler, A.; Čorović, S.; Miljavec, D. Analysis and identification of influential phenomena on iron losses in embedded permanent magnet synchronous machine. J. Electr. Eng. 2017, 68, 23–30. [Google Scholar]
- Ramarathnam, S.; Mohammed, A.K.; Bilgin, B.; Sathyan, A.; Dadkhah, H.; Emadi, A. A Review of Structural and Thermal Analysis of Traction Motors. IEEE Trans. Transp. Electrif. 2015, 1, 255–265. [Google Scholar] [CrossRef]
- Delaere, K.; Iadevaia, M.; Heylen, W.; Sas, P.; Hameyer, K.; Beimans, R. Statistical energy analysis of acoustic noise and vibration for electric motors: transmission from air gap field to motor frame. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting (Cat. No.99CH36370), Phoenix, AZ, USA, 3–7 October 1999. [Google Scholar]
- Ishikawa, T. Analysis of Natural Frequency, Radial Force and Vibration of Induction Motors Fed by PWM Inverter, Edited volume: Induction Motors - Modelling and Control; Rui Esteves, Araújo, Ed.; IntechOpen Limited: London, UK, 2012. [Google Scholar]
- Anwar, M.N.; Husain, I. Radial Force Calculation and Acoustic Noise Prediction in Switched Reluctance Machines. IEEE Trans. Ind. Appl. 2000, 36, 1589–1597. [Google Scholar]
- Tang, Z.; Pillay, P.; Omekanda, A.M.; Li, C.; Cetinkaya, C. Young’s Modulus for Laminated Machine Structures with Particular Reference to Switched Reluctance Motor Vibrations. IEEE Trans. Ind. Appl. 2004, 40, 748–754. [Google Scholar] [CrossRef]
- Pupadubsin, R.; Steven, A.; Widmer, J.D.; Mecrow, B.C. Mechanical Material Properties for Structural Simulation Model of Switched Reluctance Machines. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016. [Google Scholar]
- Jordan, H. Geräuscharme Elektromotoren: Lärmbildung und Lärmbeseitigung bei Elektromotoren; Essen: Girardet, Germany, 1950. [Google Scholar]
- Lecointe, J.P.; Romary, R.; Brudny, J.F.; Czapla, T. Five methods of stator natural frequency determination: Case of induction and switched reluctance machines. Mech. Syst. Signal. Process. 2004, 18, 1133–1159. [Google Scholar] [CrossRef]
- Cai, W.; Pillay, P.; Tang, Z. Impact of stator windings and end-bells on resonant frequencies and mode shapes of switched reluctance motors. IEEE Trans. Ind. Appl. 2002, 38, 1027–1036. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Fahimi, B. Prediction of acoustic noise in switched reluctance motor drives. IEEE Trans. Energy Convers. 2014, 29, 250–258. [Google Scholar] [CrossRef]
- Corovic, S.; Benedetic, R.; Miljavec, D. Modal Analysis of Different Stator Configurations to Mitigate Electromagnetically Excited Audible Noise and Vibrations of Switched Reluctance Motors. ACES J. 2017, 32, 1089–1097. [Google Scholar]
- Hong, D.K.; Woo, B.C.; Koo, D.H. Rotordynamics of 120 000 r/min 15 kW Ultra High Speed Motor. IEEE Trans. Mag. 2009, 45, 2831–2834. [Google Scholar] [CrossRef]
- Swanson, E.; Powell, C.D.; Weissman, S. A practical review of rotating machinery critical speeds and modes. Sound Vib. 2005, 39, 10–17. [Google Scholar]
- Genta, G. ibration of Structures and Machines, 3rd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Wang, Q.; Feese, T.D.; Pettinato, B.C. Torsional Natural Frequencies: Measurement vs. Prediction. In Proceedings of the Forty-Second Turbomachinery Symposium, Houston, TX, USA, 30 September–3 October 2013. [Google Scholar]
- Kalita, M.; Kakoty, S.K. Analysis of whirl speeds for rotor-bearing systems supported on fluid film bearings. Mech. Syst. Sig. Process. 2004, 18, 1369–1380. [Google Scholar] [CrossRef]
- Friswell, M.; Penny, J.; Garvey, S.; Lees, A. Free Lateral Response of Simple Rotor Models. In Dynamics of Rotating Machines; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2010; pp. 76–123. [Google Scholar]
- Friswell, M.; Penny, J.; Garvey, S.; Lees, A. Axial and Torsional Vibration. In Dynamics of Rotating Machines; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2010; pp. 383–419. [Google Scholar]
- Tiwari, R. Rotor Systems: Analysis and Identification; CRC Press Taylor&Francis Group, LLC: New York, NY, USA, 2018. [Google Scholar]
- Badshah, S.; Naeem, A.; Rafique, A.F.; Haq, I.U.; Malik, S.A. Numerical Study on the Critical Frequency Response of Jet Engine Rotors for Blade-Off Conditions against Bird Strike. Appl. Sci. 2019, 9, 5568. [Google Scholar] [CrossRef] [Green Version]
- Spagnol, J.; Wu, H.; Yang, C. Application of Non-Symmetric Bending Principles on Modelling Fatigue Crack Behaviour and Vibration of a Cracked Rotor. Sci. Appl. Sci. 2020, 10, 717. [Google Scholar] [CrossRef] [Green Version]
- Mudau, T.; Field, R.M. Rotordynamic Analysis of the AM600 Turbine-Generator Shaftline. Energies 2018, 11, 3411. [Google Scholar] [CrossRef] [Green Version]
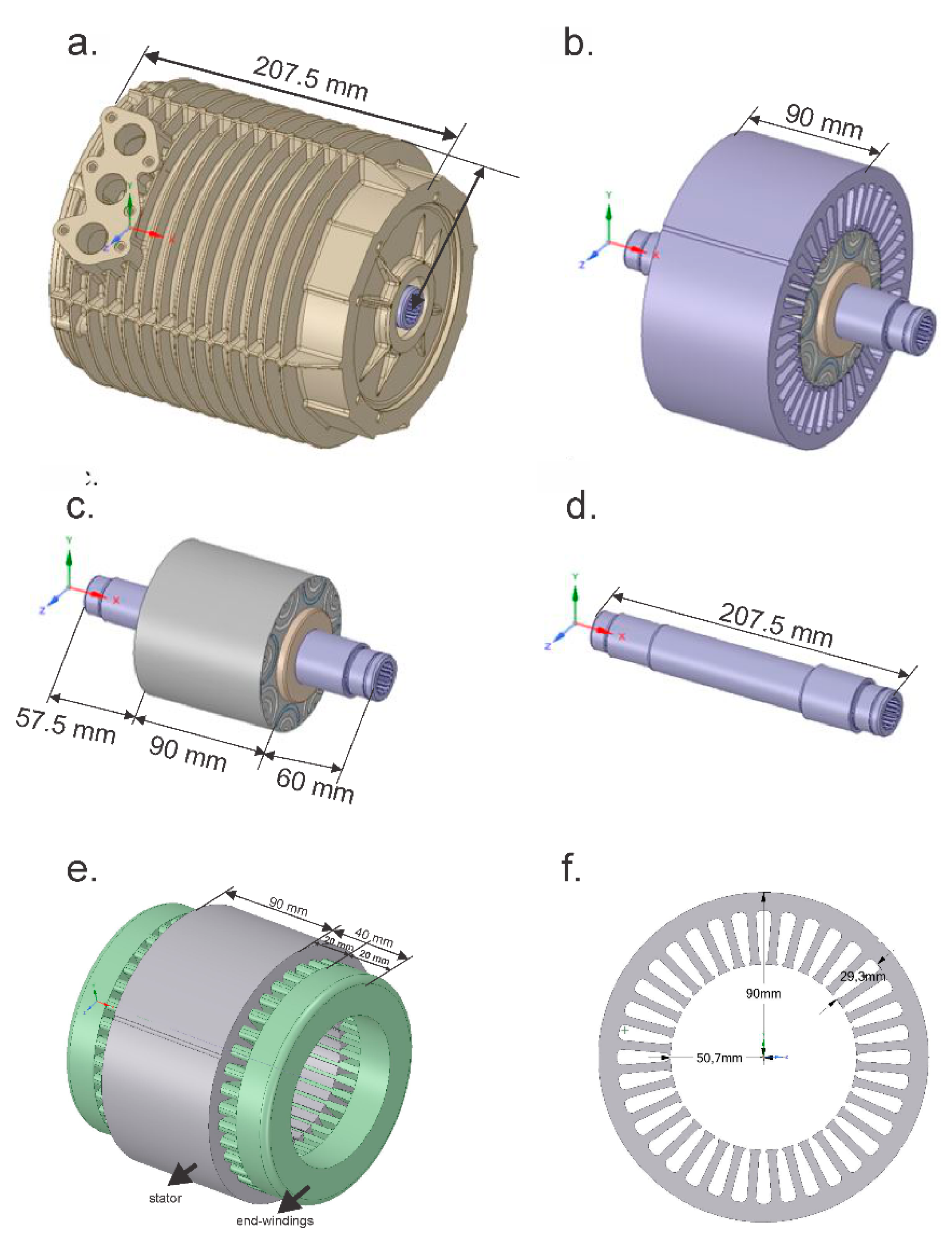




| Stator Length | 90 mm |
|---|---|
| Inner Radius of the Stator | 50.7 mm |
| Outer Diameter of the Stator | 90 mm |
| Stator Teeth Length | 29.3 mm |
| Number of Stator Slots | 36 |
| Height of the End Windings | 40 mm |
| Rotor Length | 90 mm |
| Rotor Outer Radius | 50 mm |
| Rotor Inner Radius | 15.5 mm |
| Length of the Shaft | 207.5 mm |
| The Motor Component | Material | Mass Density ρ ([kg/m3) | Young’s Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|---|
| Stator | M270-35A | 7650 | 2 × 1011 | 0.3 |
| Rotor | M270-35A | 7650 | 2 × 1011 | 0.3 |
| Permanent Magnets | NdFeB | 7500 | 1.6 × 1011 | 0.24 |
| Shaft | Steel [Ansys Built-in Library] | 7850 | 2 × 1011 | 0.3 |
| The Slot Windings and the End-Windings | Equivalent Mechanical Properties of the Cooper and the Insulation [9] | 4373 | 4.97 × 108 | 0.343 |
| Motor Frame/Housing, Back and Front End Cover | Aluminum Alloy [Ansys Built-in Library] | 2770 | 7.1 × 1010 | 0.33 |
| *** | f (Hz), m = 2 | f (Hz), m = 3 | f (Hz), m = 4 | f (Hz), m = 0 | f (Hz), m = 8 |
|---|---|---|---|---|---|
| Experiments | 625.6 | 1593 | 2652 | / | / |
| Numerical, FEM | 635 | 1637 | 2657 | 6868 | 14,534 |
| Analytical, Equation (8) | 613 | 1734 | 3325 | 6775 | 14,285 |
| *** | f (Hz), m = 2 | f (Hz) | f [Hz] | f (Hz), m = 0 |
|---|---|---|---|---|
| Experiments | 500.5 | 695.8 | 1315.3 | / |
| Numerical, FEM | 525 | 754 | 1393 | 5113 |
| Analytical, Equation (11) | 458.7 | / | / | 5066.4 |
| Critical Speed | Transversal Ω [(rpm) | FW Rotational Ω (rpm) | BW Rotational Ω (rpm) |
|---|---|---|---|
| Analytical-Uniform IPM Shaft D = 27mm | 13,990 | 24,400 | 23,780 |
| Numerical-Uniform IPM Shaft D = 27mm | 13,790 | 24,336 | 23,741 |
| Numerical-Non-Uniform IPM Shaft 23 mm ≤ D ≤ 31 mm (Dmean = 27 mm) | 14,184 | 23,417 | 22,479 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čorović, S.; Miljavec, D. Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study. Appl. Sci. 2020, 10, 5881. https://doi.org/10.3390/app10175881
Čorović S, Miljavec D. Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study. Applied Sciences. 2020; 10(17):5881. https://doi.org/10.3390/app10175881
Chicago/Turabian StyleČorović, Selma, and Damijan Miljavec. 2020. "Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study" Applied Sciences 10, no. 17: 5881. https://doi.org/10.3390/app10175881
APA StyleČorović, S., & Miljavec, D. (2020). Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study. Applied Sciences, 10(17), 5881. https://doi.org/10.3390/app10175881





