Characteristic Analysis and Co-Validation of Hydro-Mechanical Continuously Variable Transmission Based on the Wheel Loader
Abstract
1. Introduction
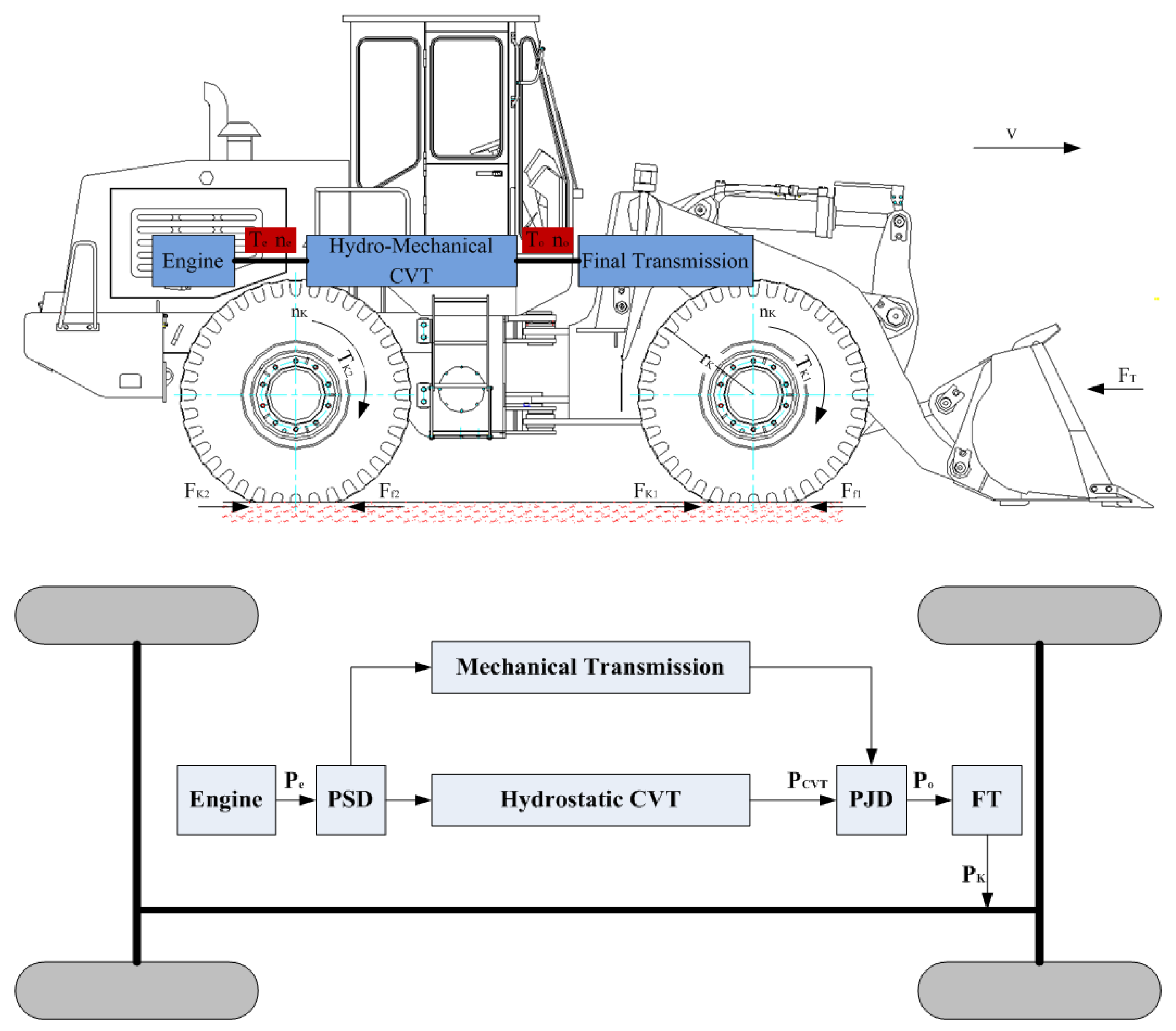
2. Analysis of the Wheel Loader Characteristics
2.1. Force Characteristics
2.2. Velocity Characteristics
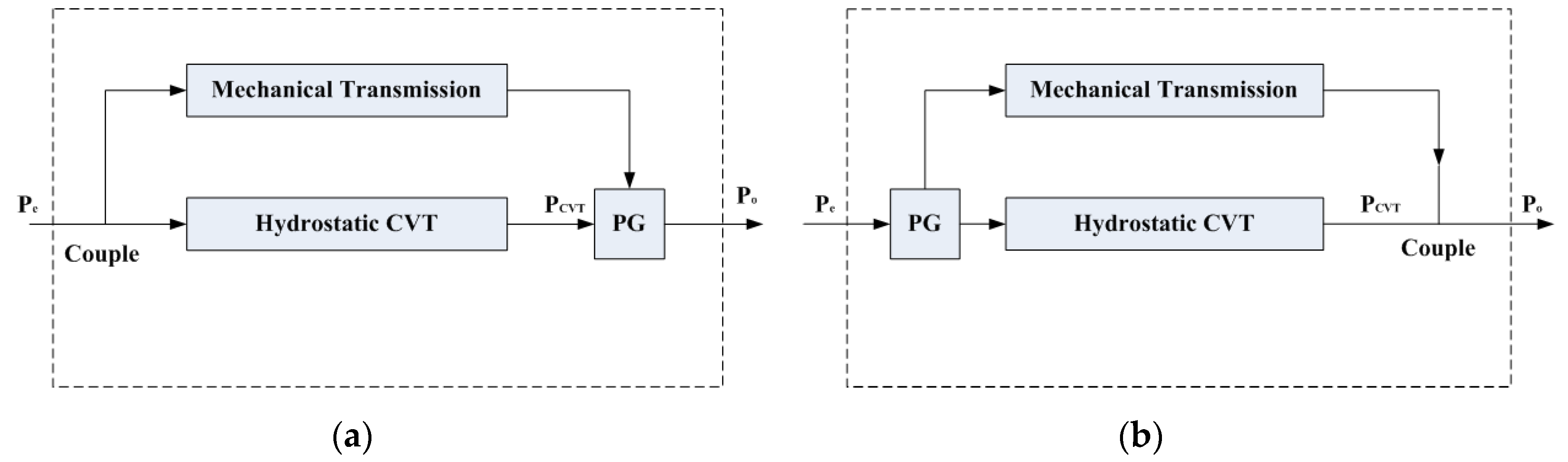
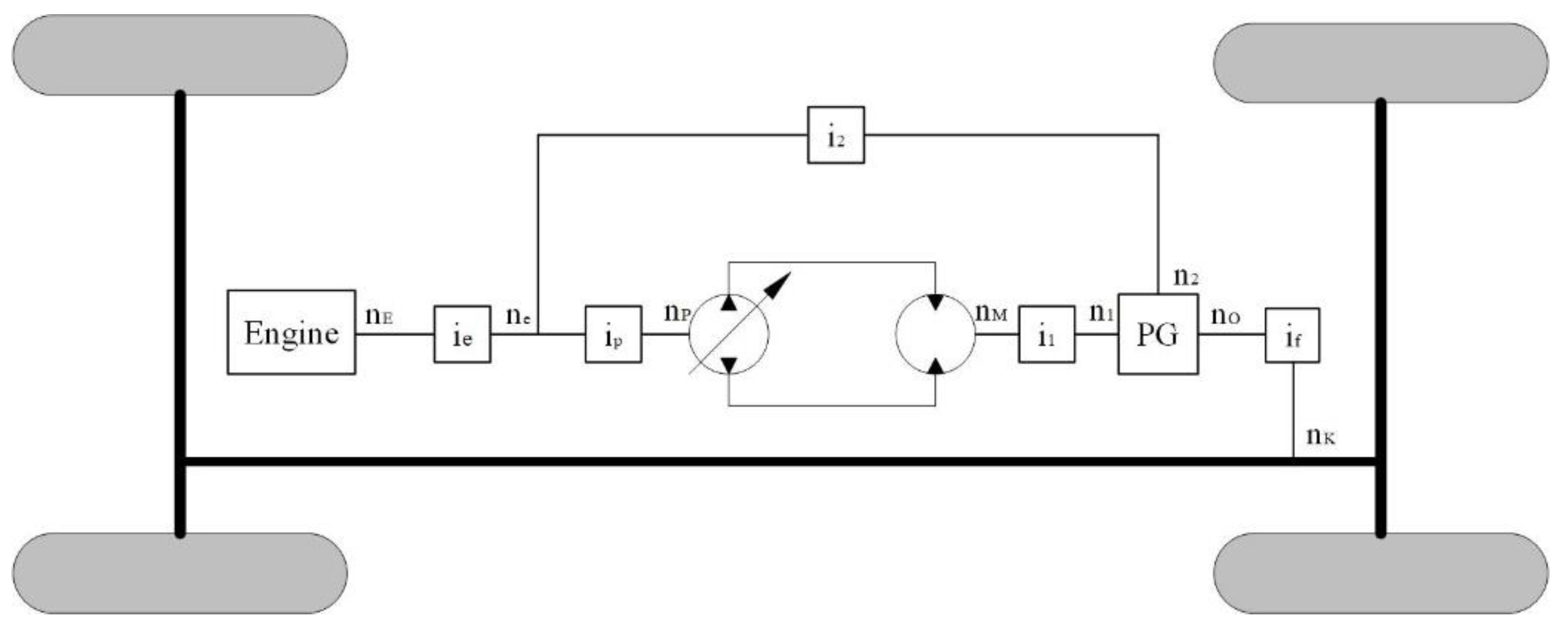
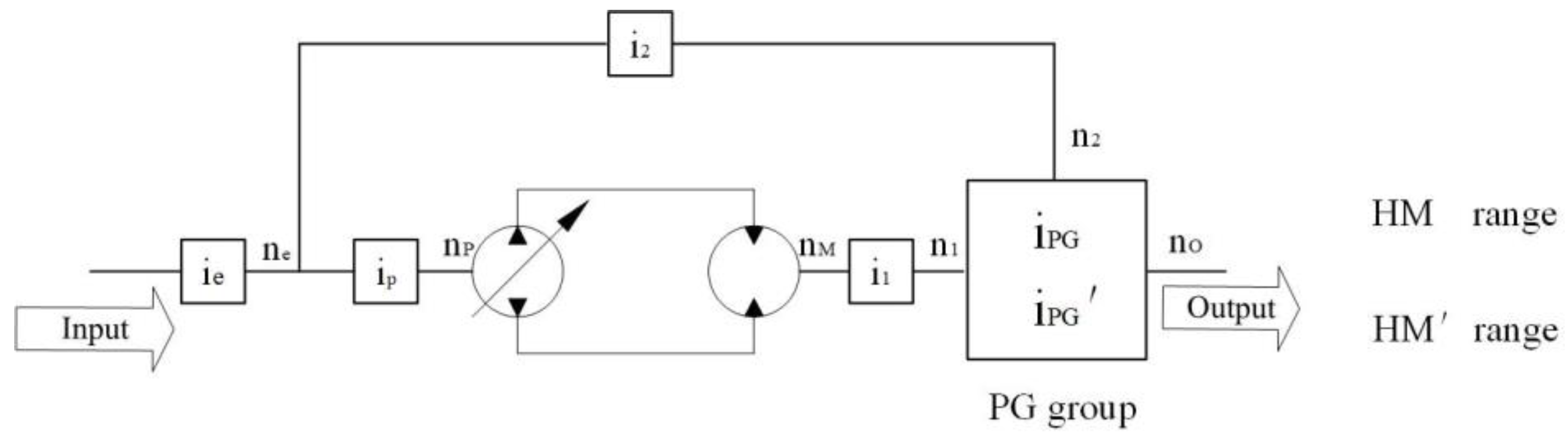
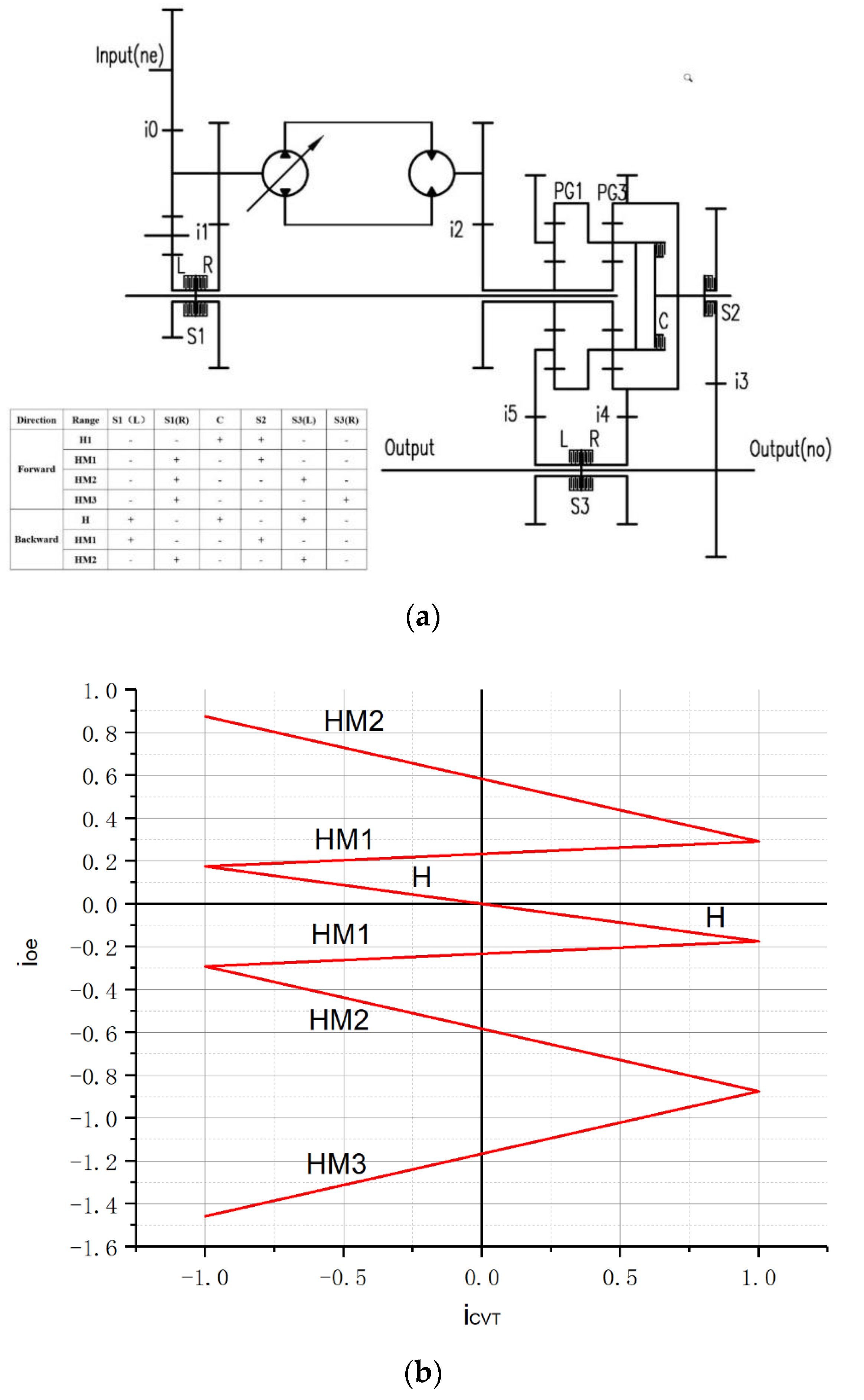
2.2.1. Types of HMCVT
- H range, where the transmission has only hydrostatic power.
- HM range, with forward transmission of the PG.
- HM’ range, with reverse transmission of the PG.
2.2.2. Velocity Characteristics
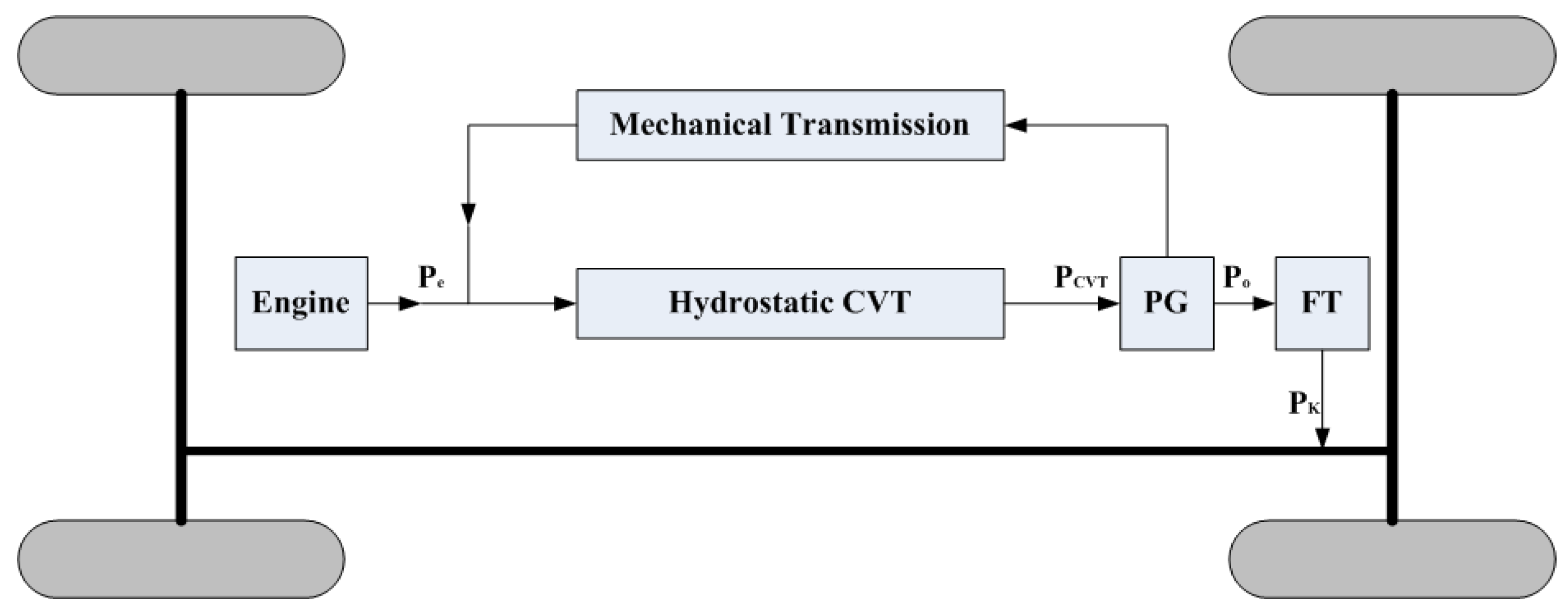
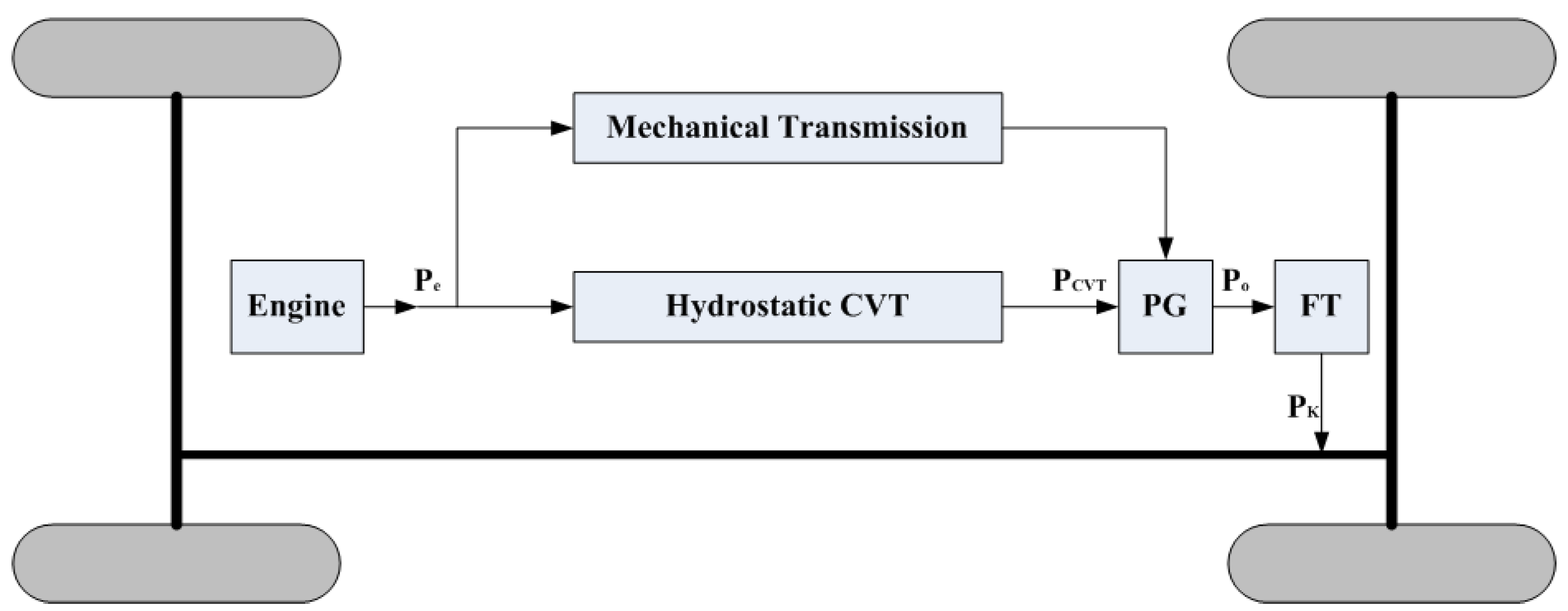
2.3. Power Characteristics
3. The Factors Influencing the Proportion of Hydrostatic Power
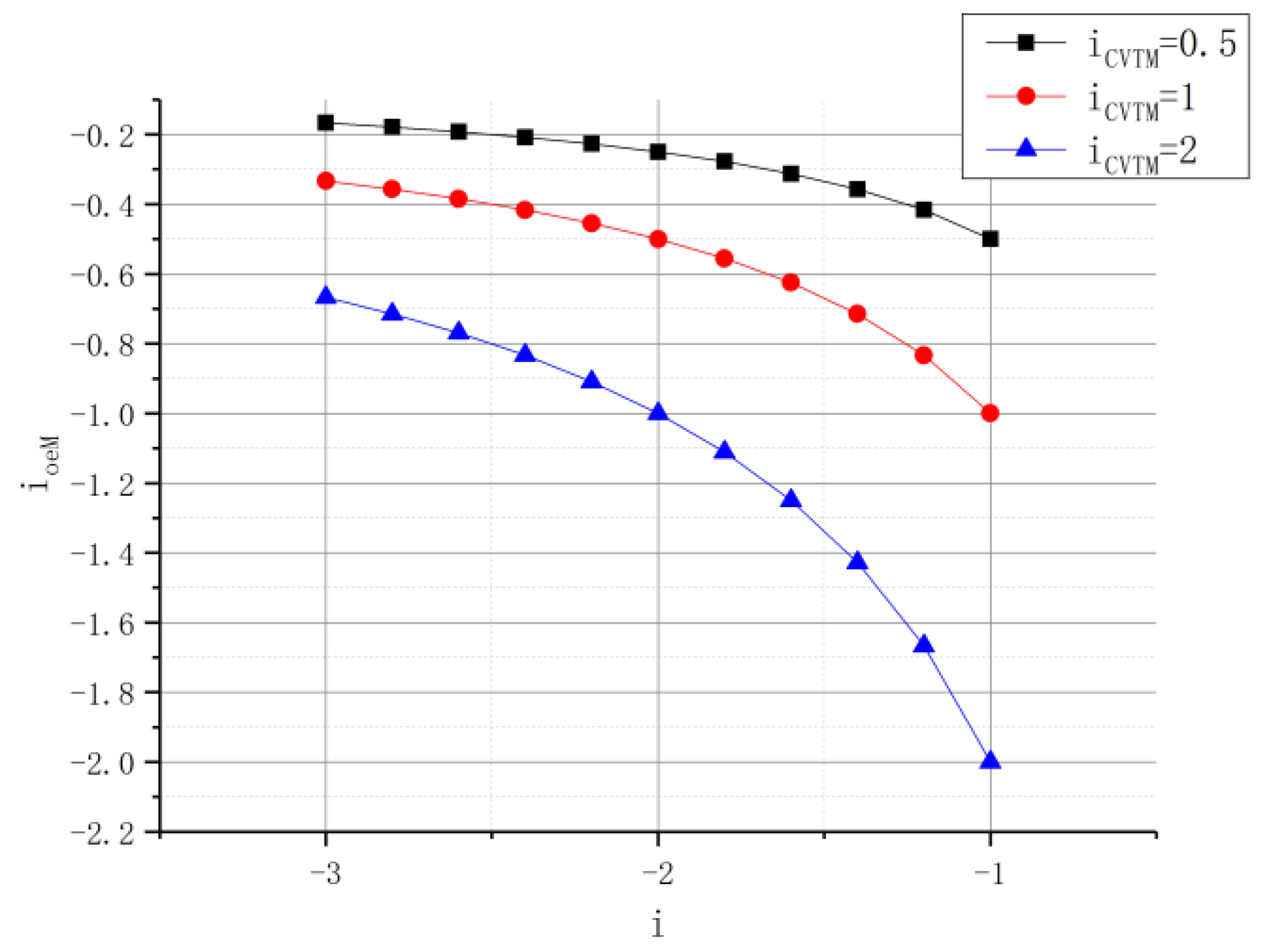
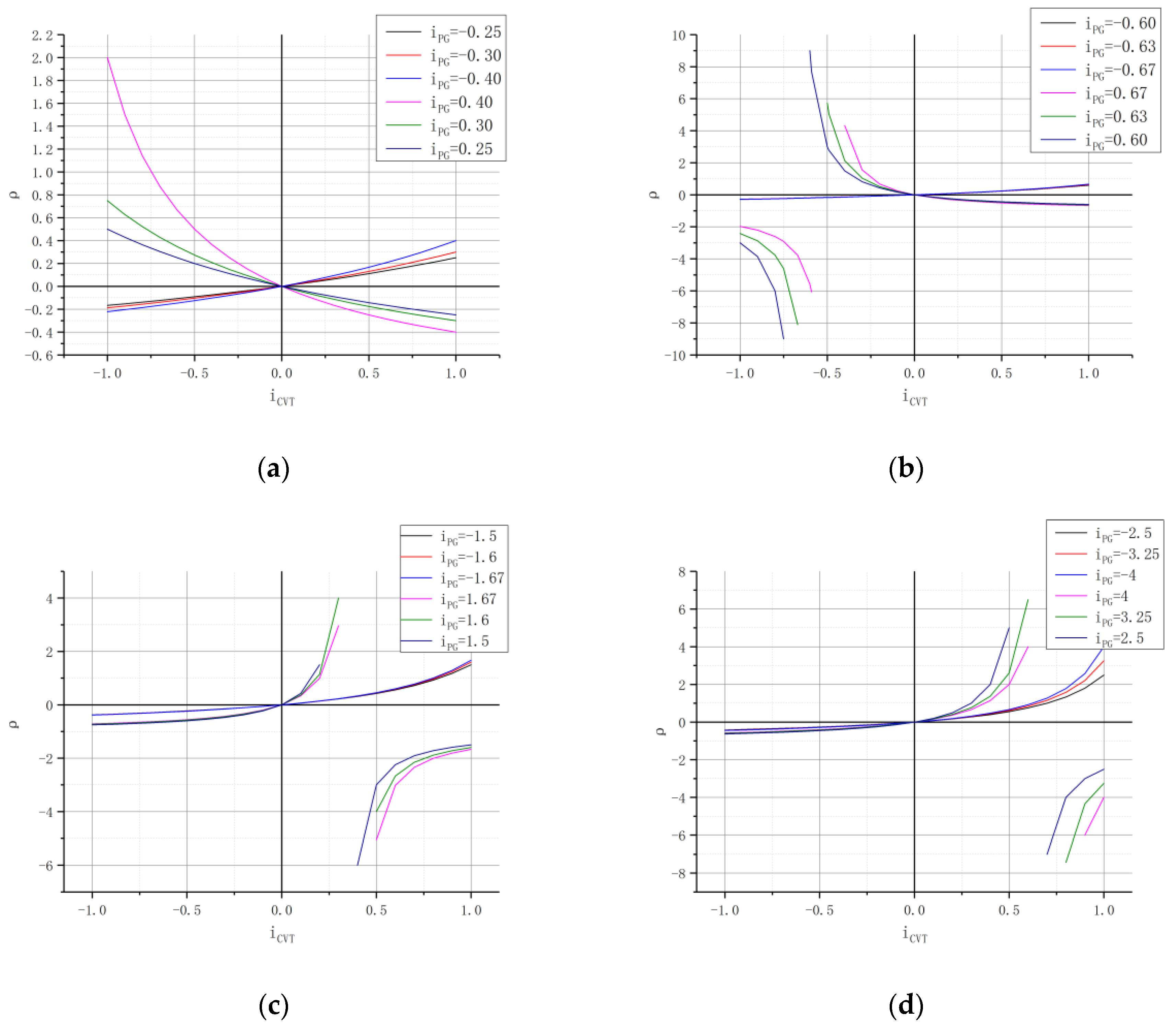
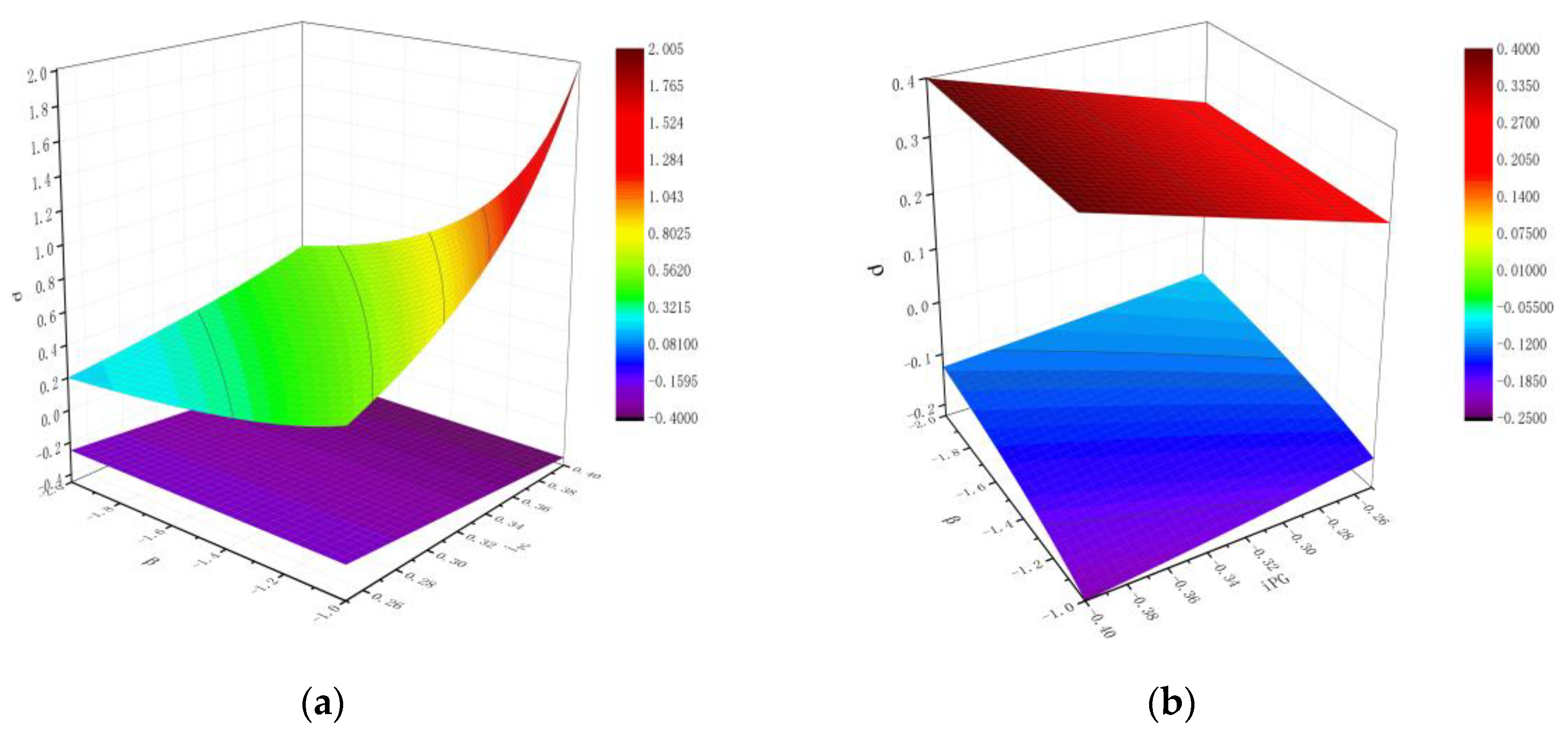
- To realize the same speed shift connection between the H range and hydro-mechanical range, as you can see from Equation (23) and Figure 9, when , increases with the increase of and decreases with the increase of .
- As can be seen from Equation (19), under certain conditions of , increases with the increase of and decreases with the increase of . So, matching patterns a and b have better torque characteristics than matching patterns c and d in Table 2.
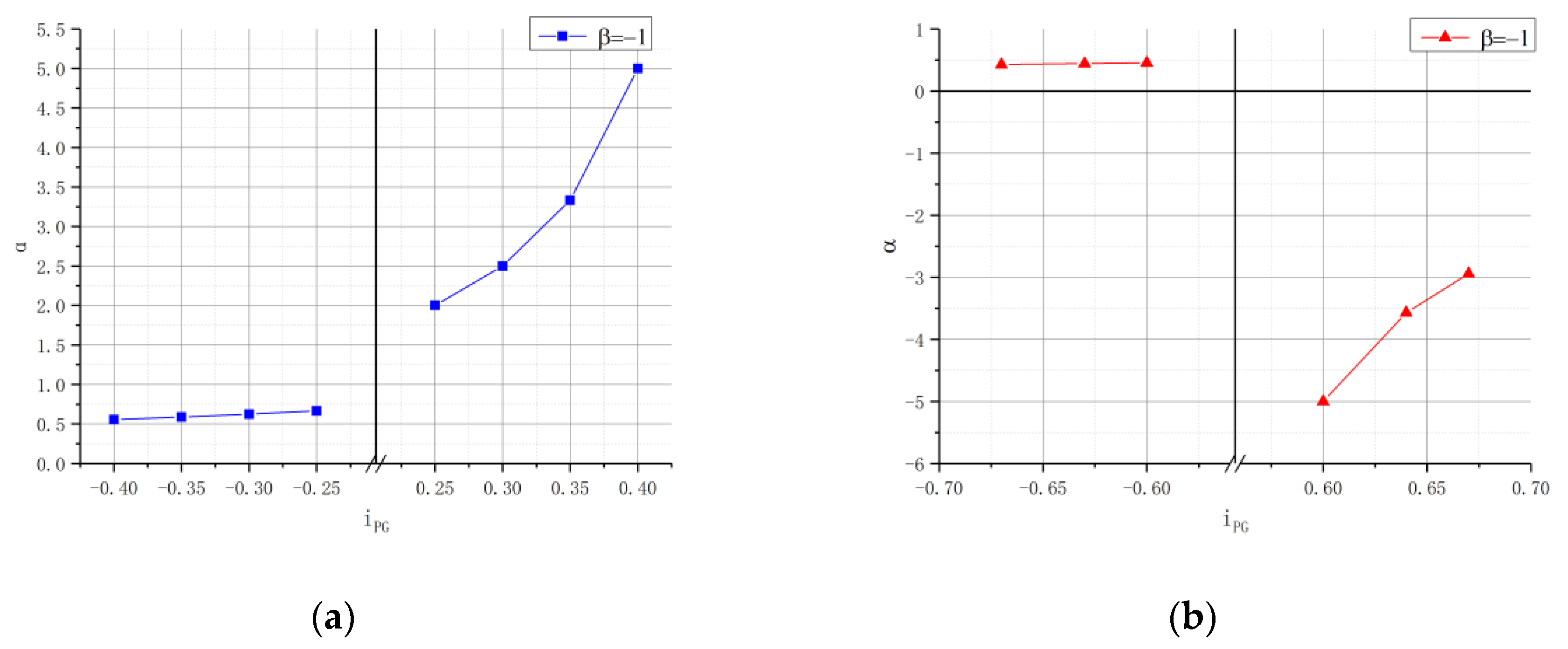
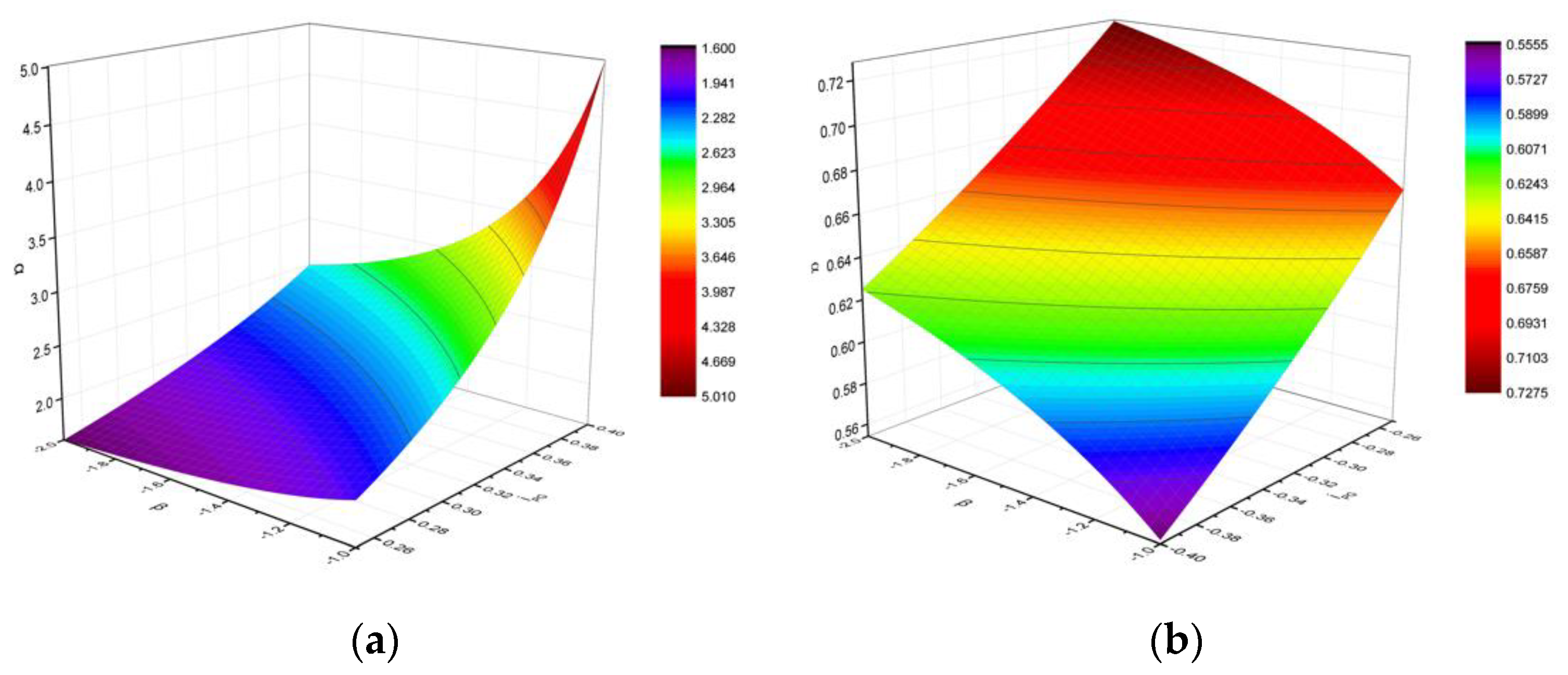
- From Equation (28) and Figure 10, the range of transmission ratio, increases with the increase of , and Schemes 2, 4, and 6 exist as because of .
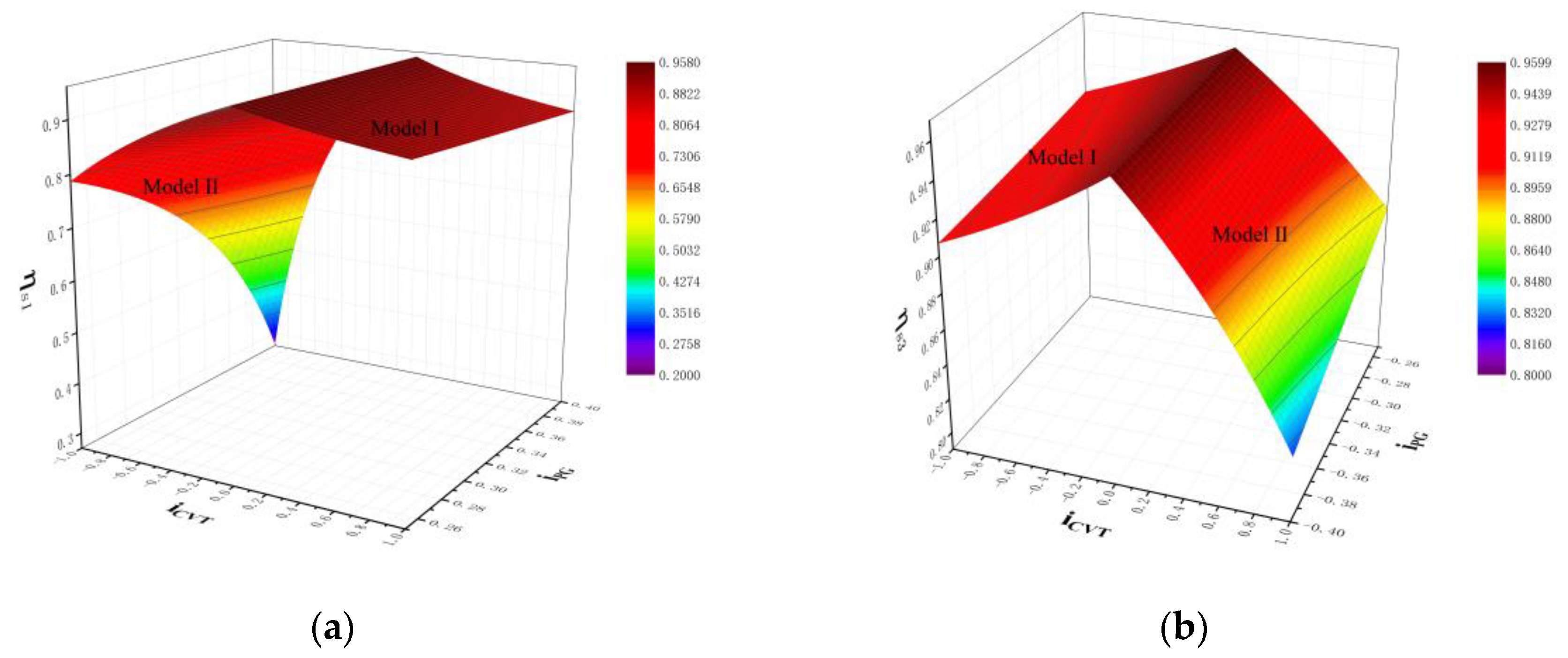
- From the Equations (26), (27), (29), and Figure 11, and are independent of , and only related to . Schemes 2, 4, and 6 exist as the work condition with the lowest transmission efficiency because mechanical transmission occurs in backward power recirculation, i.e., , as shown in Figure 6. The transmission efficiency of matching patterns b, c, and d are lower than matching pattern a because and mechanical transmission occurs even in backward power recirculation, as shown in Figure 6. Therefore, the efficiency of HMCVT is significantly reduced.
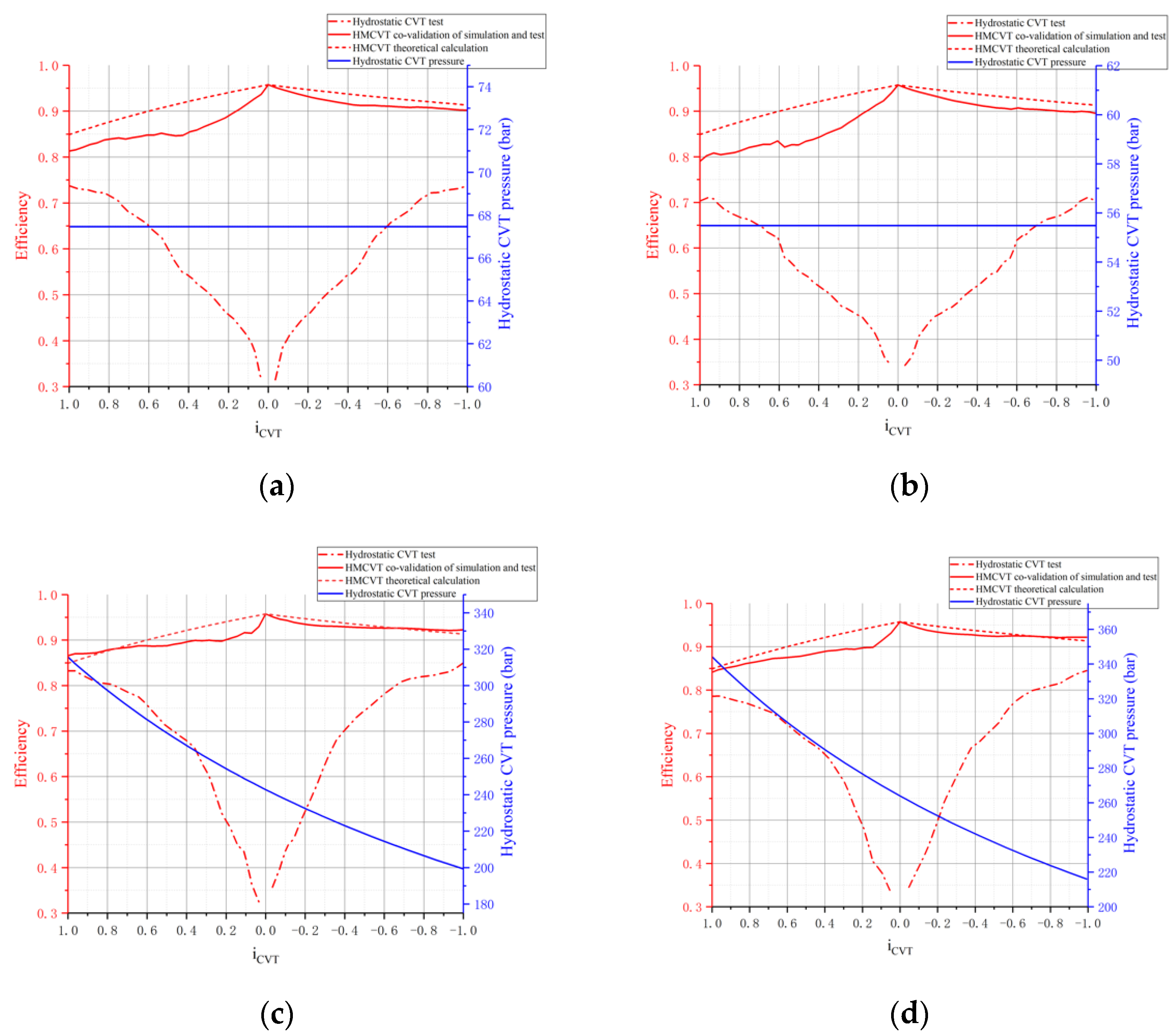
4. The Efficiency Analysis of the Matching Pattern A
Theoretical Calculation
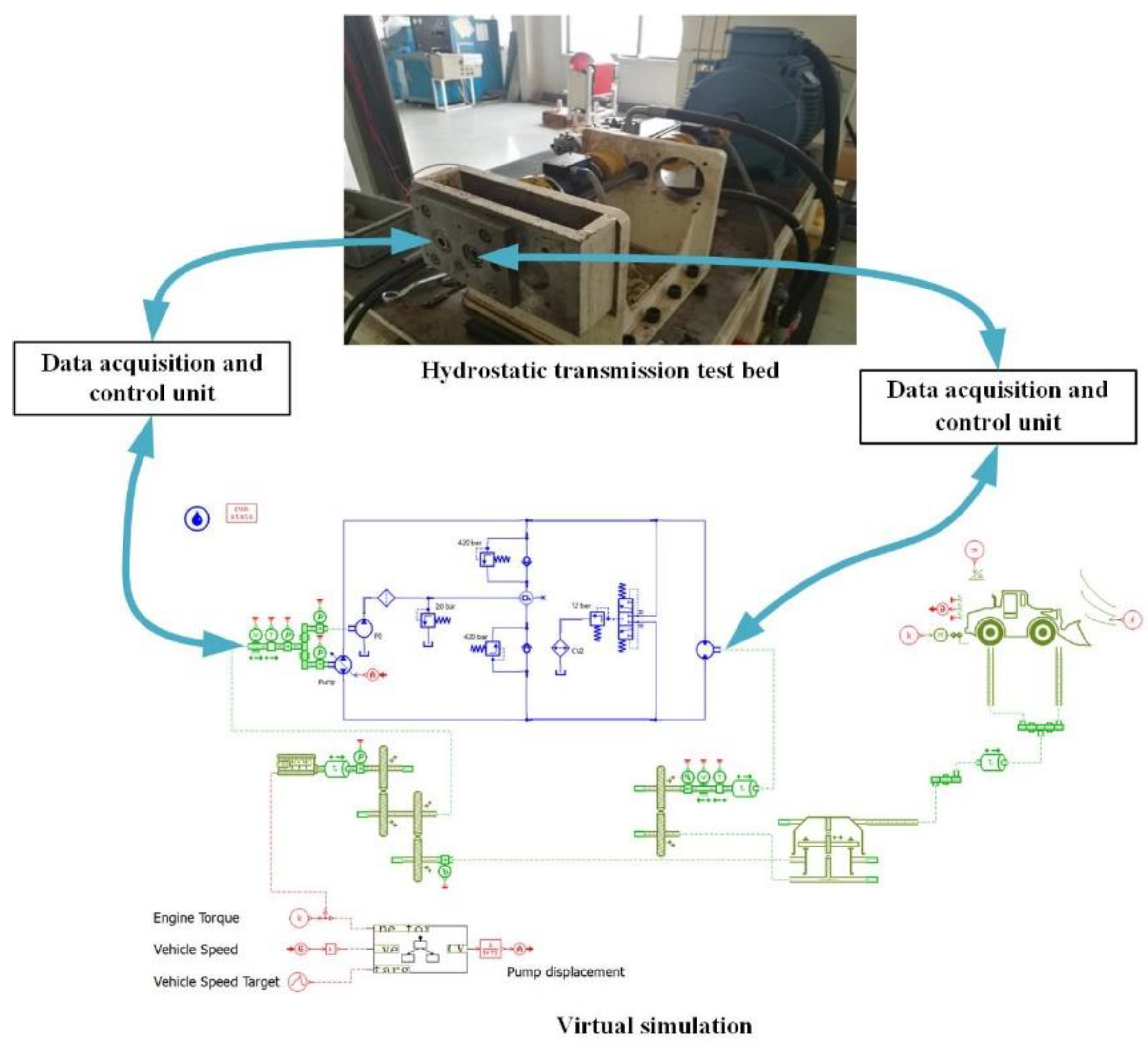
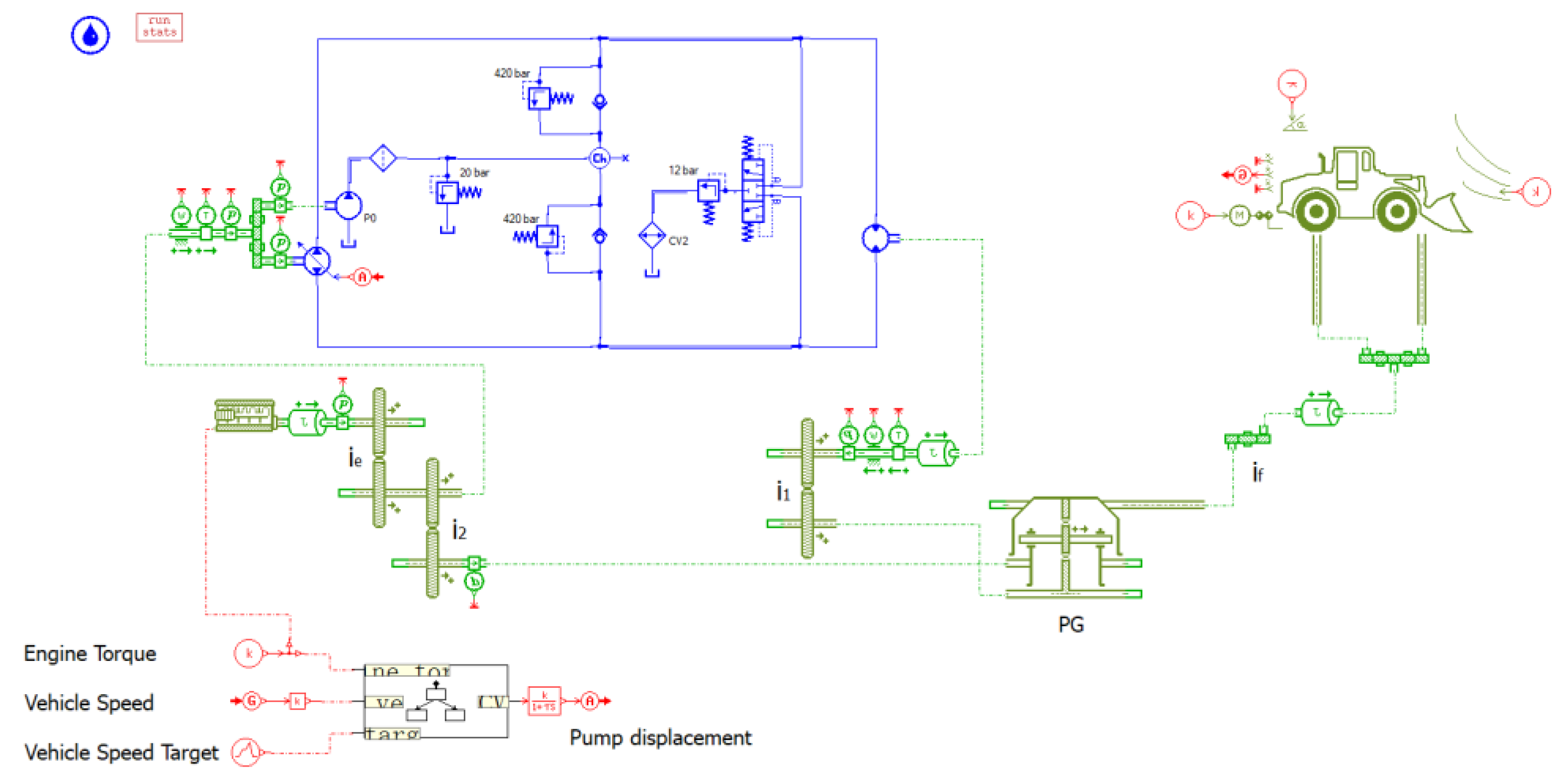
5. Co-Validation of Simulation and Test
5.1. The Method of Co-Validation
5.2. The Application of Test and Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HMCVT | Hydro-Mechanical Continuously Variable Transmission |
| CVT | Continuously Variable Transmission |
| PSD | Power-Split Device |
| PJD | Power Junction Device |
| FT | Final Transmission |
| PG | Planetary Gear train |
| VP | Variable Displacement Hydraulic Pump |
| FM | Fixed Displacement Hydraulic Motor |
| Driving force of the wheel loader | |
| Rolling resistance of the wheel loader | |
| Air resistance of the wheel loader | |
| Ramp resistance of the wheel loader | |
| Inertia force of the wheel loader | |
| Total weight of the wheel loader | |
| Transmission ratio of the whole transmission system. | |
| The transmission ratio between engine and shaft e | |
| The transmission ratio between shaft e and pump | |
| Transmission ratio between motor and shaft 1 of PG | |
| Transmission ratio between shaft e and shaft 2 of PG | |
| Transmission ratio between output shaft and shaft 1 | |
| Transmission ratio of Hydrostatic CVT | |
| Transmission ratio of HMCVT | |
| Transmission ratio between PG output shaft and the wheel | |
| Engine speed | |
| Shaft e speed | |
| Pump shaft speed | |
| Motor shaft speed | |
| Shaft 1 speed of PG | |
| Shaft 2 speed of PG | |
| Output shaft speed of PG | |
| Wheel speed | |
| Pump displacement | |
| Motor displacement | |
| Shaft 1 torque of PG | |
| Shaft 2 torque of PG | |
| Output shaft torque of PG | |
| Motor shaft torque | |
| Driving torque of wheel loader | |
| Engine torque | |
| The range of transmission ratio, | |
| The range of | |
| Wheel loader velocity | |
| Radius of wheel | |
| Proportion of hydrostatic power in total power | |
| Output power of HMCVT | |
| Driving power | |
| Hydrostatic CVT power | |
| Mechanical Transmission power | |
| PG characteristic coefficient | |
| Efficiency of mode Ⅰ | |
| Efficiency of mode Ⅱ | |
| Volumetric efficiency of Hydrostatic CVT | |
| Mechanical efficiency of Hydrostatic CVT | |
| Volumetric efficiency of VP | |
| Mechanical efficiency of VP | |
| Total efficiency of VP | |
| Volumetric efficiency of FM | |
| Mechanical efficiency of FM | |
| Total efficiency of FM | |
| Hydrostatic CVT efficiency | |
| Efficiency of gear set 1 | |
| Efficiency of gear set 2 | |
| Efficiency of gear set p | |
| Efficiency between shaft 2 and shaft 1 of PG | |
| Efficiency between shaft 1 and output shaft of PG | |
| Efficiency between shaft 2 and output shaft of PG | |
| HMCVT efficiency of scheme 1 | |
| HMCVT efficiency of scheme 3 |
References
- Liu, X.; Sun, D.; Qin, D.; Liu, J. Achievement of Fuel Savings in Wheel Loader by Applying Hydrodynamic Mechanical Power Split Transmissions. Energies 2017, 10, 1267. [Google Scholar]
- Zhang, Q.; Sun, D.; Qin, D. Optimal parameters design method for power reflux hydro-mechanical transmission system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 233, 585–594. [Google Scholar] [CrossRef]
- Oledzki, J.W. Split power hydro-mechanical transmission with power circulation. J. Chin. Inst. Eng. 2018, 41, 333–341. [Google Scholar] [CrossRef]
- Dana Rexroth Transmission System. HVT R2 Hydromechanical Variable Transmission. Available online: http://www.danarexroth.com/_content/HVT_R2_SpecSheet.pdf (accessed on 18 February 2019).
- Dana Rexroth Transmission System. HVT R3 Hydromechanical Variable Transmission. Available online: http://www.danarexroth.com/_content/HVT_R3_SpecSheet.pdf (accessed on 18 February 2019).
- ZF Friedrichshafen AG. ZF cPOWER. Available online: https://www.zf.com/products/media/industrial/construction/downloads_1/new/see.think.act._cPower.pdf (accessed on 17 March 2019).
- Liebherr-Werk Bischofshofen GmbH. Job Report Wheel Loader L566 XPower. Available online: https://www.liebherr.com/external/products/products-assets/265798/Einsatzbericht%20L%20566%20XPower%20RBS%20Kiesgewinnung%20GmbH.pdf (accessed on 17 March 2019).
- Ince, E.; Guler, M.A. Design and Analysis of a Novel Power-Split Infinitely Variable Power Transmission System. J. Mech. Des. 2019, 141, 054501. [Google Scholar] [CrossRef]
- Xiong, S.; Wilfong, G.; Lumkes, J. Components Sizing and Performance Analysis of Hydro-Mechanical Power Split Transmission Applied to a Wheel Loader. Energies 2019, 12, 1613. [Google Scholar] [CrossRef]
- Liu, F.X.; Wu, W.; Hu, J.B.; Yuan, S.H. Design of multi-range hydro-mechanical transmission using modular method. Mech. Syst. Signal. Proc. 2019, 126, 1–20. [Google Scholar] [CrossRef]
- Macor, A.; Rossetti, A. Optimization of hydro-mechanical power split transmissions. Mech. Mach. Theory 2011, 46, 1901–1919. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, Z.; Dai, F. Research on HMCVT Efficiency Model Based on the Improved SA Algorithm. Math. Probl. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Rossetti, A.; Macor, A. Multi-objective optimization of hydro-mechanical power split transmissions. Mech. Mach. Theory 2013, 62, 112–128. [Google Scholar] [CrossRef]
- Cammalleri, M.; Rotella, D. Functional design of power-split CVTs: An uncoupled hierarchical optimized model. Mech. Mach. Theory 2017, 116, 294–309. [Google Scholar] [CrossRef]
- Rotella, D.; Cammalleri, M. Direct analysis of power-split CVTs: A unified method. Mech. Mach. Theory 2018, 121, 116–127. [Google Scholar] [CrossRef]
- Rotella, D.; Cammalleri, M. Power losses in power-split CVTs: A fast black-box approximate method. Mech. Mach. Theory 2018, 128, 528–543. [Google Scholar] [CrossRef]
- Rossetti, A.; Macor, A. Continuous formulation of the layout of a hydromechanical transmission. Mech. Mach. Theory 2019, 133, 545–558. [Google Scholar] [CrossRef]
- Carl, B.; Ivantysynova, M.; Williams, K. Comparison of Operational Characteristics in Power Split Continuously Variable Transmissions; Technical Paper 2006-01-3468; SAE Technical Papers: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, L.; Zeng, F. Reverse design and characteristic study of multi-range HMCVT. IOP Conf. Ser. Mater. Sci. Eng. 2017, 231, 012178. [Google Scholar] [CrossRef]
- Zhu, Z.; Gao, X.; Cao, L.; Cai, Y.; Pan, D. Research on the shift strategy of HMCVT based on the physical parameters and shift time. Appl. Math. Model. 2016, 40, 6889–6907. [Google Scholar] [CrossRef]
- Mingzhu, Z.; Dongyang, B.; Quansheng, W. Research of HMCVT speed change law based on optimal productivity. In Proceedings of the 2015 4th International Conference on Sustainable Energy and Environmental Engineering, Shenzhen, China, 20–21 December 2015; pp. 844–849. [Google Scholar]
- Zhou, Z.; Zhang, J.; Xu, L.; Guo, Z. Modeling and simulation of hydro-mechanical continuously variable transmission system based on Simscape. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems (ICAMechS), Beijing, China, 22–24 August 2015; pp. 397–401. [Google Scholar]
- Bae, M.H.; Bae, T.Y.; Choi, S.K. The Critical Speed Analysis of Gear Train for Hydro-Mechanical Continuously Variable Transmission. J. Drive Control 2017, 14, 71–78. [Google Scholar] [CrossRef]
- Linares, P.; Méndez, V.; Catalán, H. Design parameters for continuously variable power-split transmissions using planetaries with 3 active shafts. J. Terramech. 2010, 47, 323–335. [Google Scholar] [CrossRef]






| Scheme | Transmission Sketch | Range of Values | |
|---|---|---|---|
| 1 | 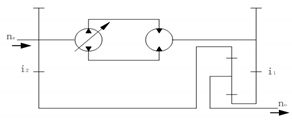 | 0.2 to 0.4 | |
| 2 |  | 0.6 to 0.8 | |
| 3 | 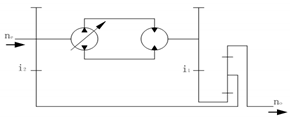 | −0.67 to −0.25 | |
| 4 | 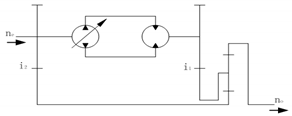 | 1.25 to 1.67 | |
| 5 |  | −4 to −1.5 | |
| 6 |  | 2.5 to 5 |
| Pattern | Scheme | Sketch | Property | ||
|---|---|---|---|---|---|
| a | 1 |  | Forward deceleration | 0.25 to 0.4 | |
| 3 |  | Reverse deceleration | −0.25 to −0.4 | ||
| b | 2 | 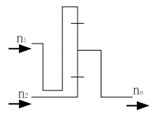 | Forward deceleration | 0.6 to 0.67 | |
| 3 |  | Reverse deceleration | −0.6 to −0.67 | ||
| c | 4 | 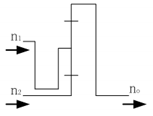 | Forward acceleration | 1.5 to 1.67 | |
| 5 | 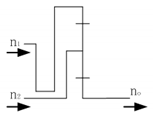 | Reverse acceleration | −1.5 to −1.67 | ||
| d | 6 |  | Forward acceleration | 2.5 to 4 | |
| 5 | 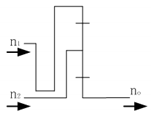 | Reverse acceleration | −2.5 to −4 |
| Parameters | Value |
|---|---|
| Rated power, /Rated speed, | 162 kW/2000 rpm |
| Maximum torque, /Engine speed | 853 N·m /1500 rpm |
| Vehicle mass | 16,500 kg |
| Rated load | 50 kN |
| VP Maximum displacement | 80 mL/r |
| FM displacement | 80 mL/r |
| Maximum pressure | 42 MPa |
| Working Condition | Power (kW)/Torque (N·m) | Speed (rpm) |
|---|---|---|
| Engine rated power, | 162/- | 2000 |
| Engine maximum torque | -/853 | 1500 |
| Engine medium torque | -/400 | 2000 |
| Vehicle full load, | -/16,480 | 2000 |
| Vehicle no-load, | -/11,880 | 2000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, L.; Dai, H.; Zeng, Q.; Sun, Z.; Tian, M. Characteristic Analysis and Co-Validation of Hydro-Mechanical Continuously Variable Transmission Based on the Wheel Loader. Appl. Sci. 2020, 10, 5900. https://doi.org/10.3390/app10175900
Wan L, Dai H, Zeng Q, Sun Z, Tian M. Characteristic Analysis and Co-Validation of Hydro-Mechanical Continuously Variable Transmission Based on the Wheel Loader. Applied Sciences. 2020; 10(17):5900. https://doi.org/10.3390/app10175900
Chicago/Turabian StyleWan, Lirong, Hanzheng Dai, Qingliang Zeng, Zhiyuan Sun, and Mingqian Tian. 2020. "Characteristic Analysis and Co-Validation of Hydro-Mechanical Continuously Variable Transmission Based on the Wheel Loader" Applied Sciences 10, no. 17: 5900. https://doi.org/10.3390/app10175900
APA StyleWan, L., Dai, H., Zeng, Q., Sun, Z., & Tian, M. (2020). Characteristic Analysis and Co-Validation of Hydro-Mechanical Continuously Variable Transmission Based on the Wheel Loader. Applied Sciences, 10(17), 5900. https://doi.org/10.3390/app10175900





