Safe Proximity Operation to Rotating Non-Cooperative Spacecraft with Complex Shape Using Gaussian Mixture Model-Based Fixed-Time Control
Abstract
1. Introduction
- (1)
- A novel GMM-based potential function is proposed, which can depict obstacle constraints of arbitrary targets with complex shape and provide attraction force to the desired position and repulsive force to avoid collision to the components of target spacecraft.
- (2)
- A compound controller is designed for ultra-close-range safe proximity based on GMM and FTC method, which can guarantee not only collision avoidance, but also fixed-time convergence to the desired state.
2. Problem Statement
2.1. Mathematical Preliminaries
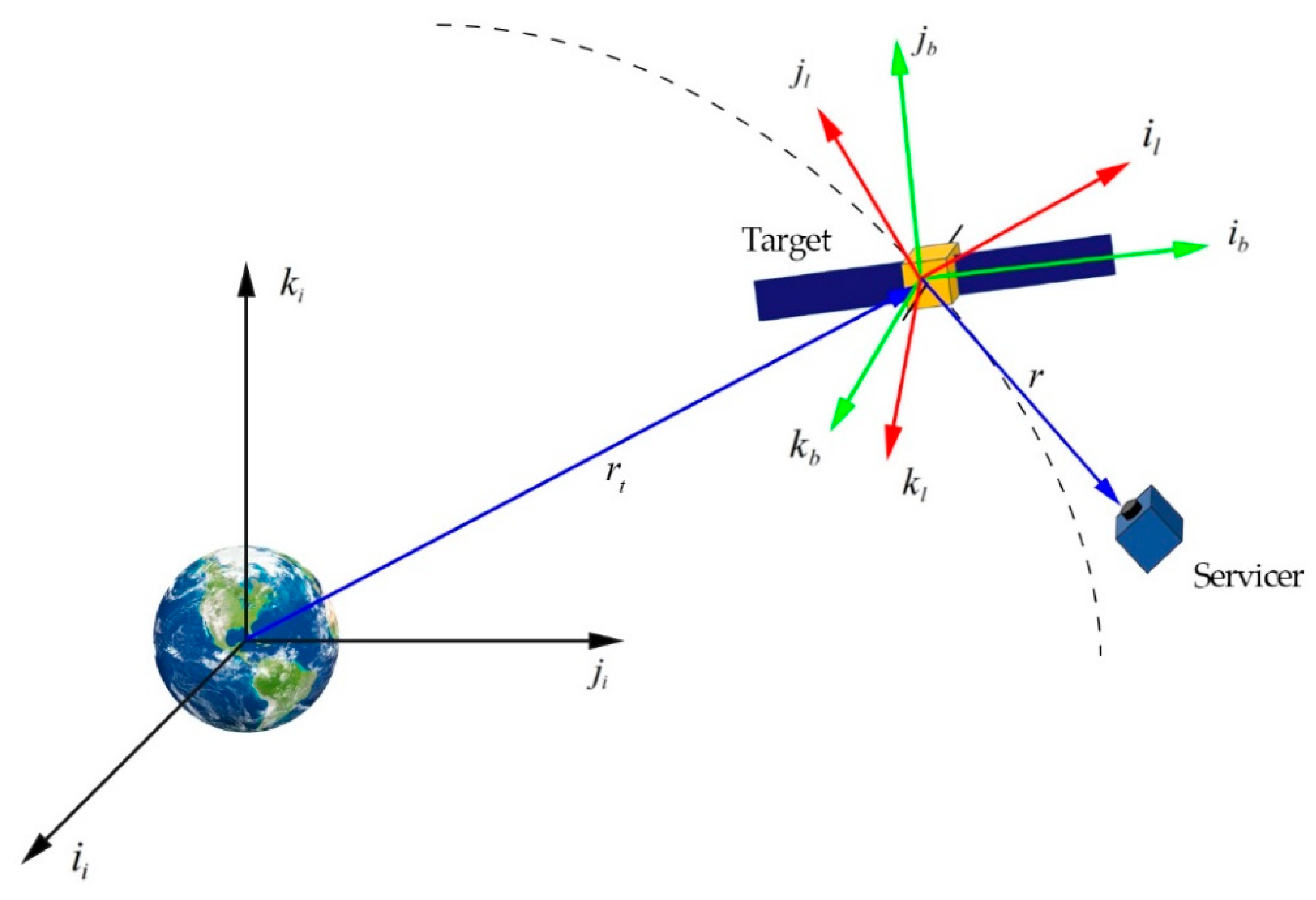
2.2. Coordinate Frames
2.3. Translational Relative Dynamics
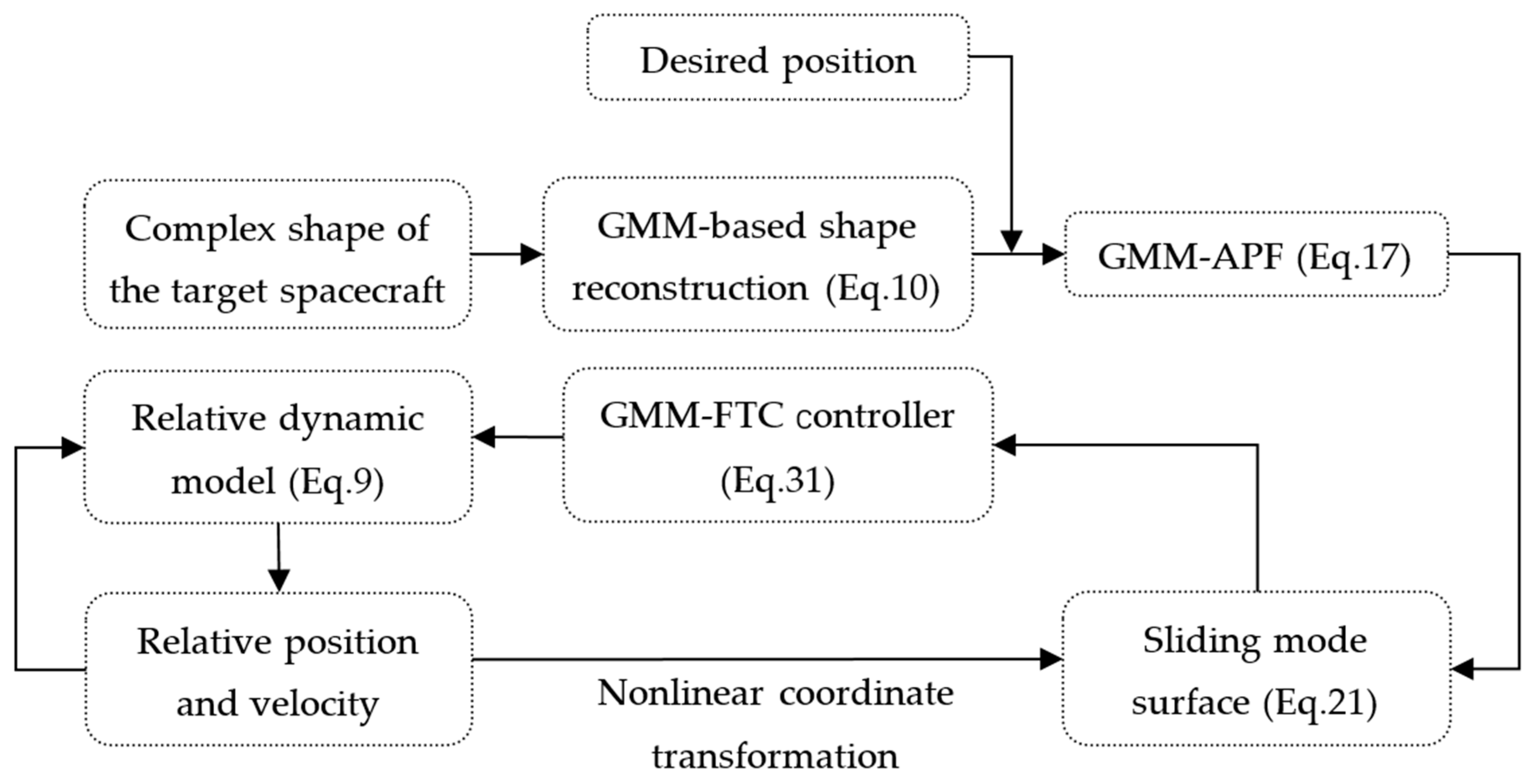
3. Main Methodologies
3.1. GMM-Based APF Design
- (1)
- Set the initial parameters .
- (2)
- E-step: Calculate the probability that each data comes from sub-model j, based on above parameters.
- (3)
- M-step: Calculate the next generation parameters as follows,
- (4)
- Iterate the E-step and M-step until satisfying the condition in Equation (15). is small positive constant, and the superscript k means the kth calculation.
- (1)
- Set the initial K means.
- (2)
- Calculate the Euclidean distance between and each mean (j = 1, 2, …, K), then, dividing to the nearest cluster center, i.e., mean and recording as .
- (3)
- Recalculate each cluster center by the data in same cluster.
- (4)
- Iterate the steps (2) and (3) until , is the distortion function of K-means, written as
3.2. GMM-Based Fixed-Time Controller Design
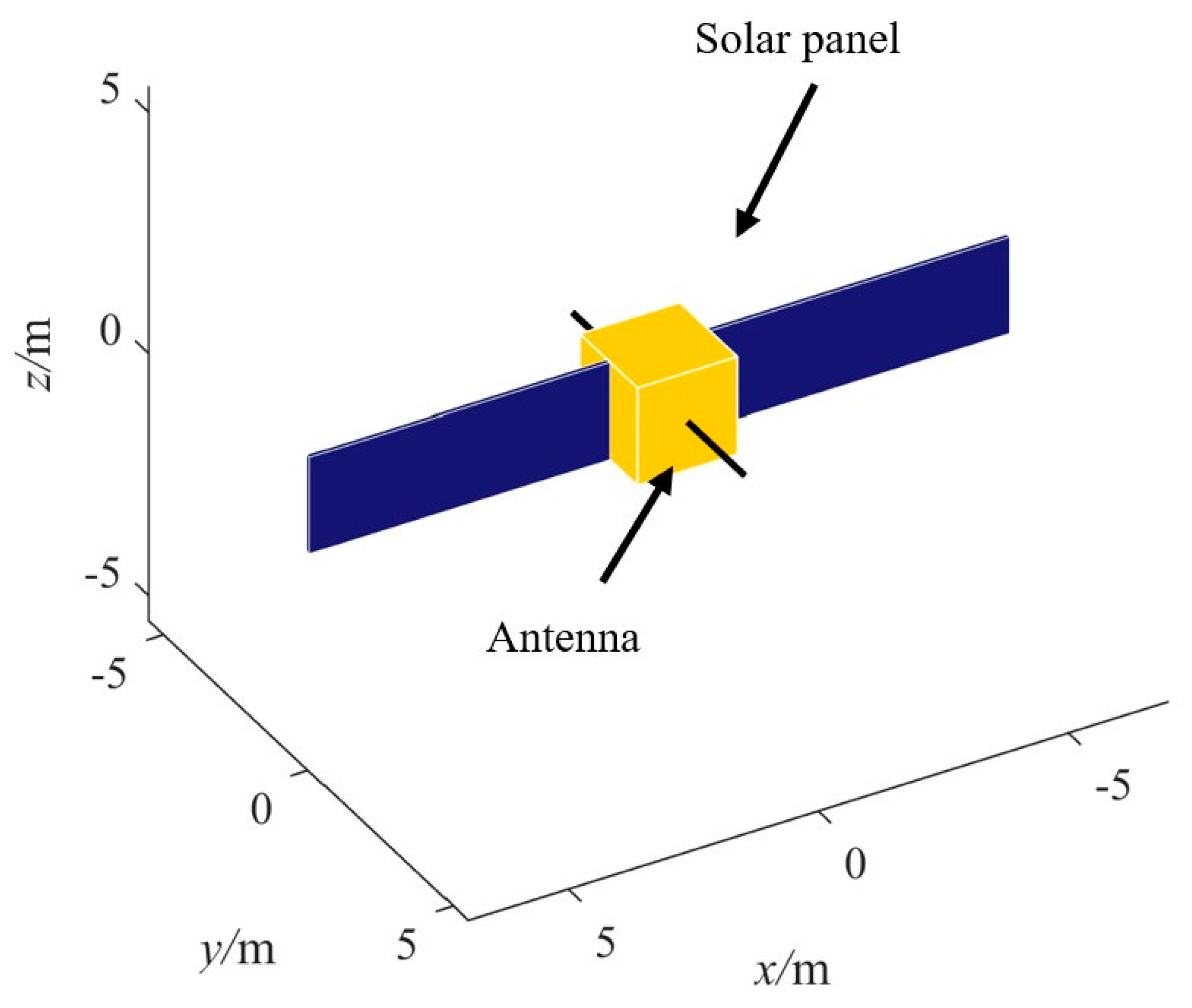
4. Numerical Simulation
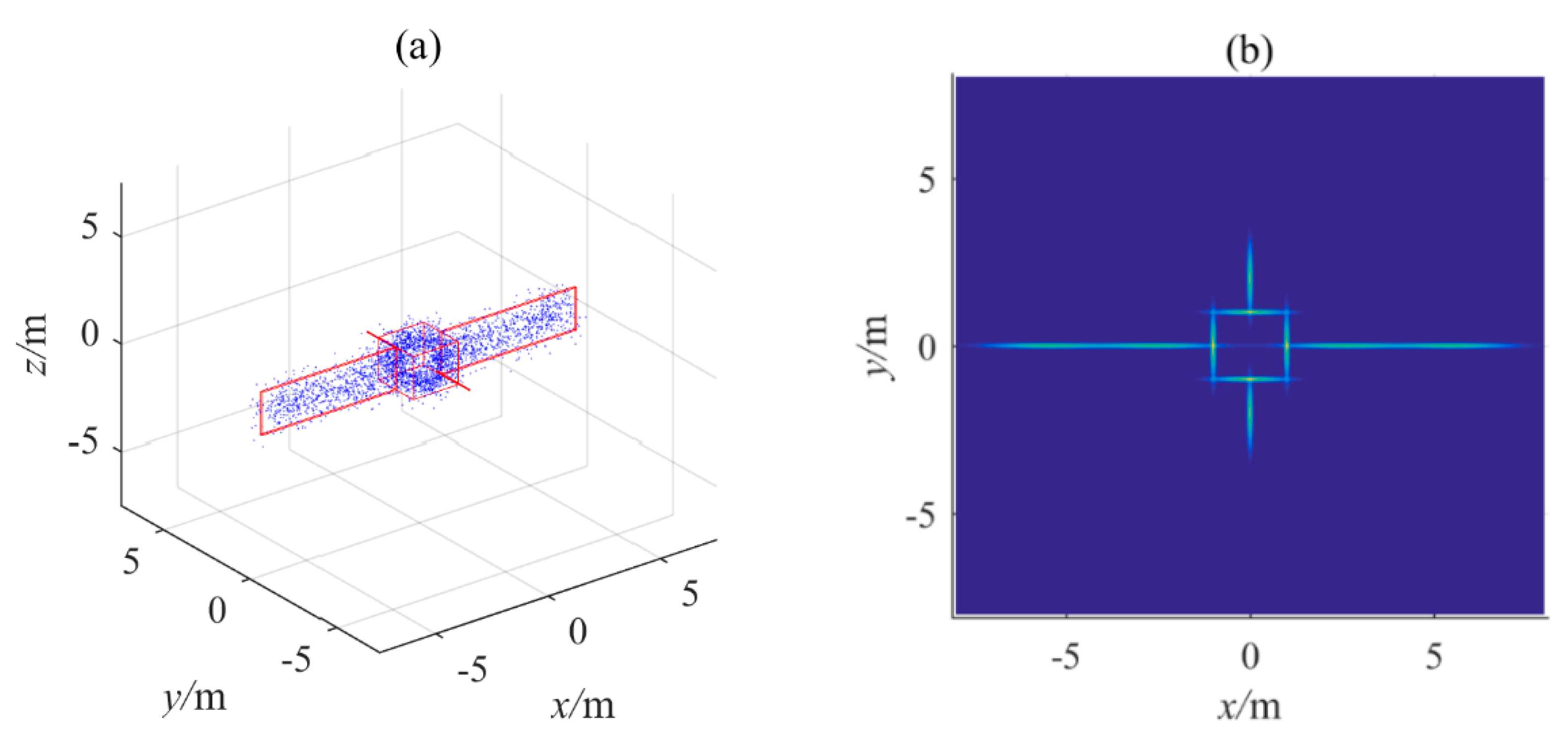
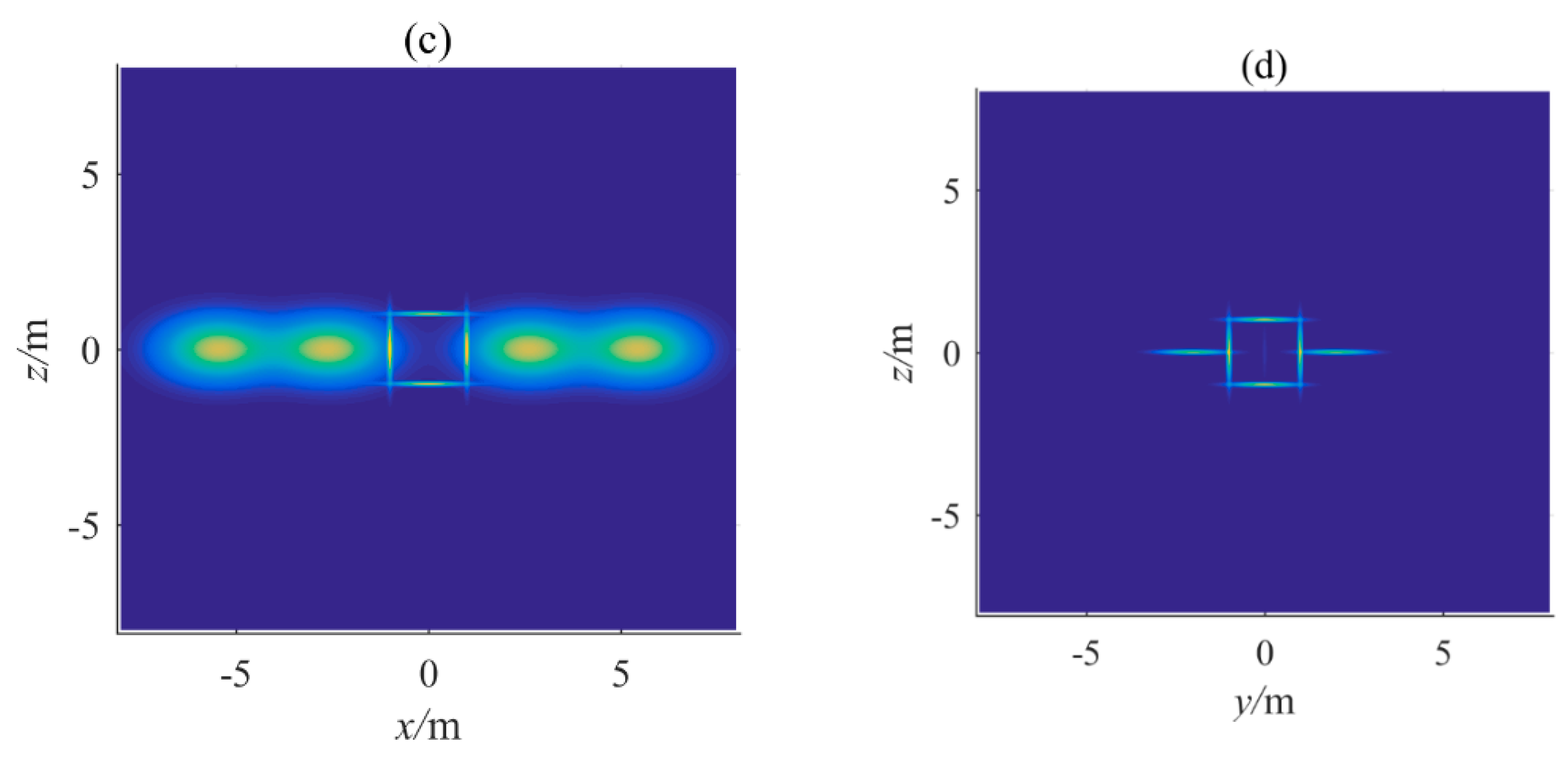
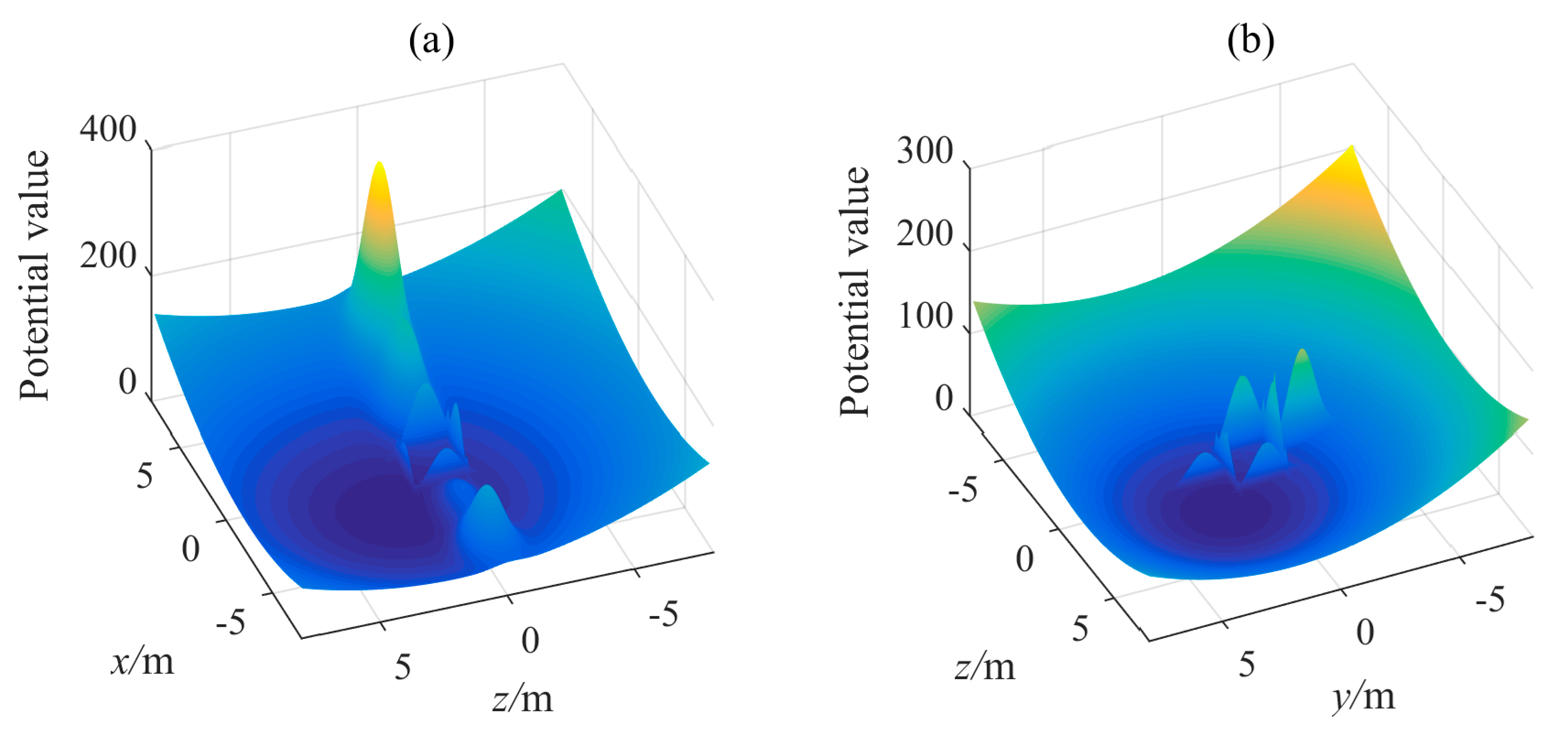
4.1. GMM-Based Artificial Potential Function Simulation
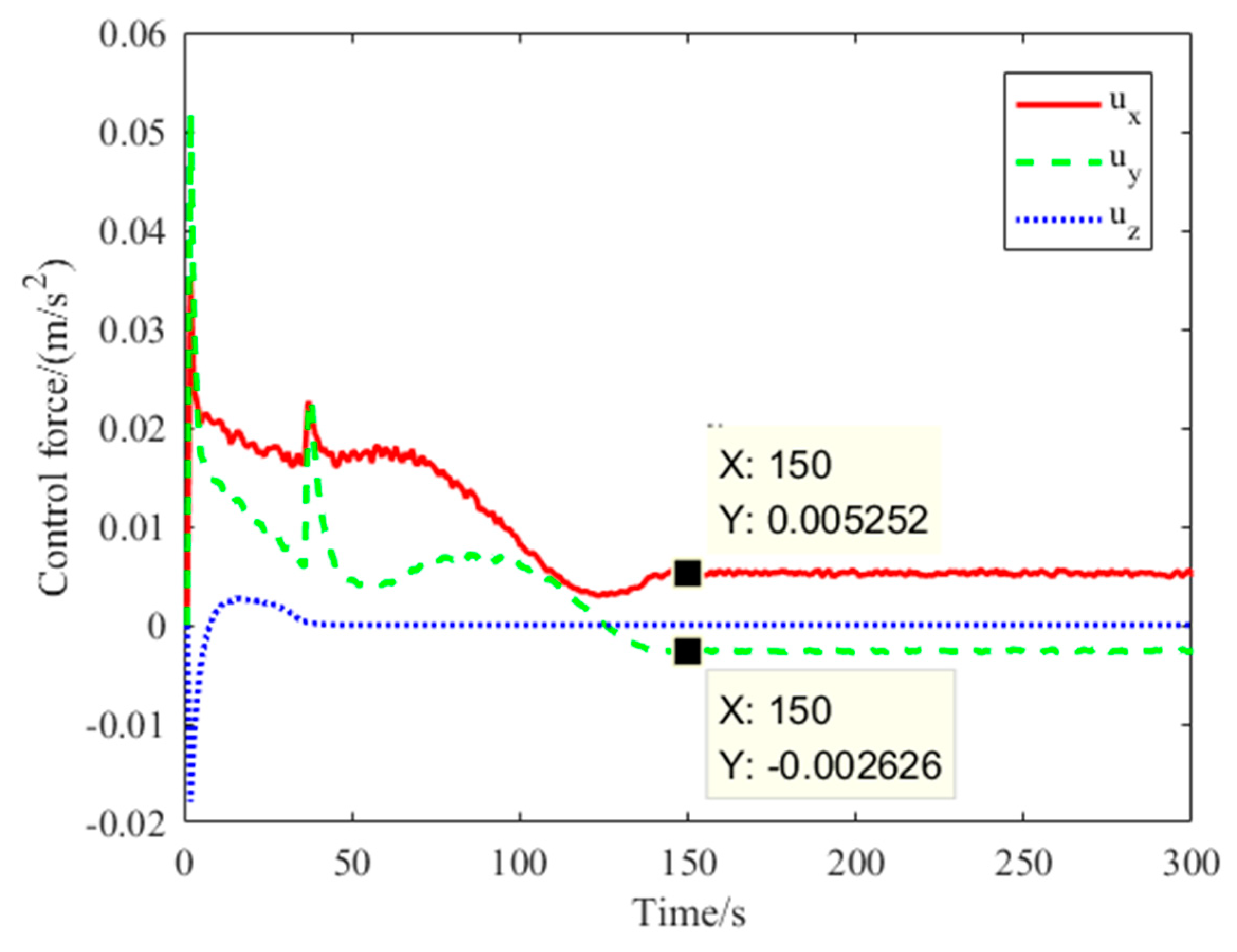
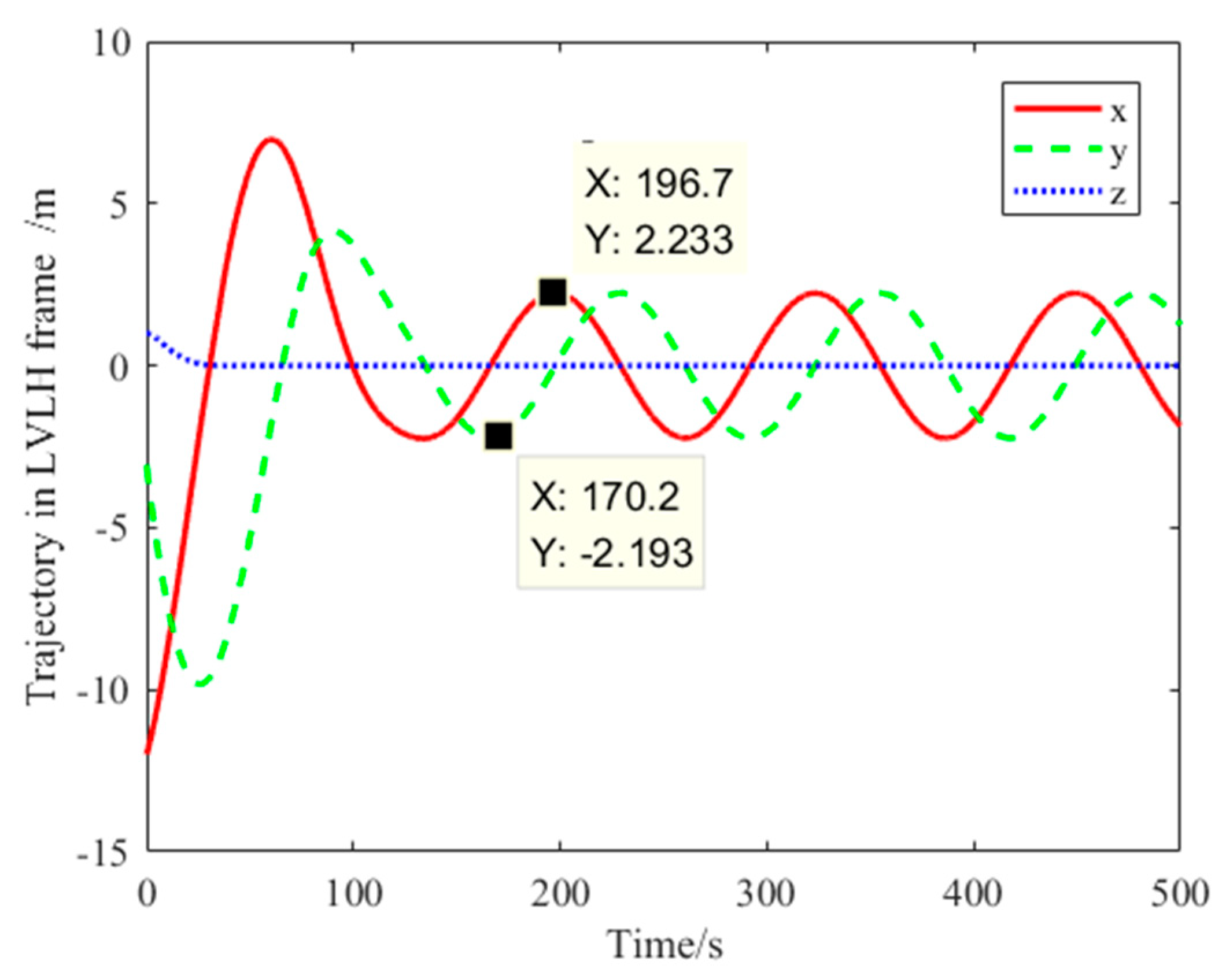
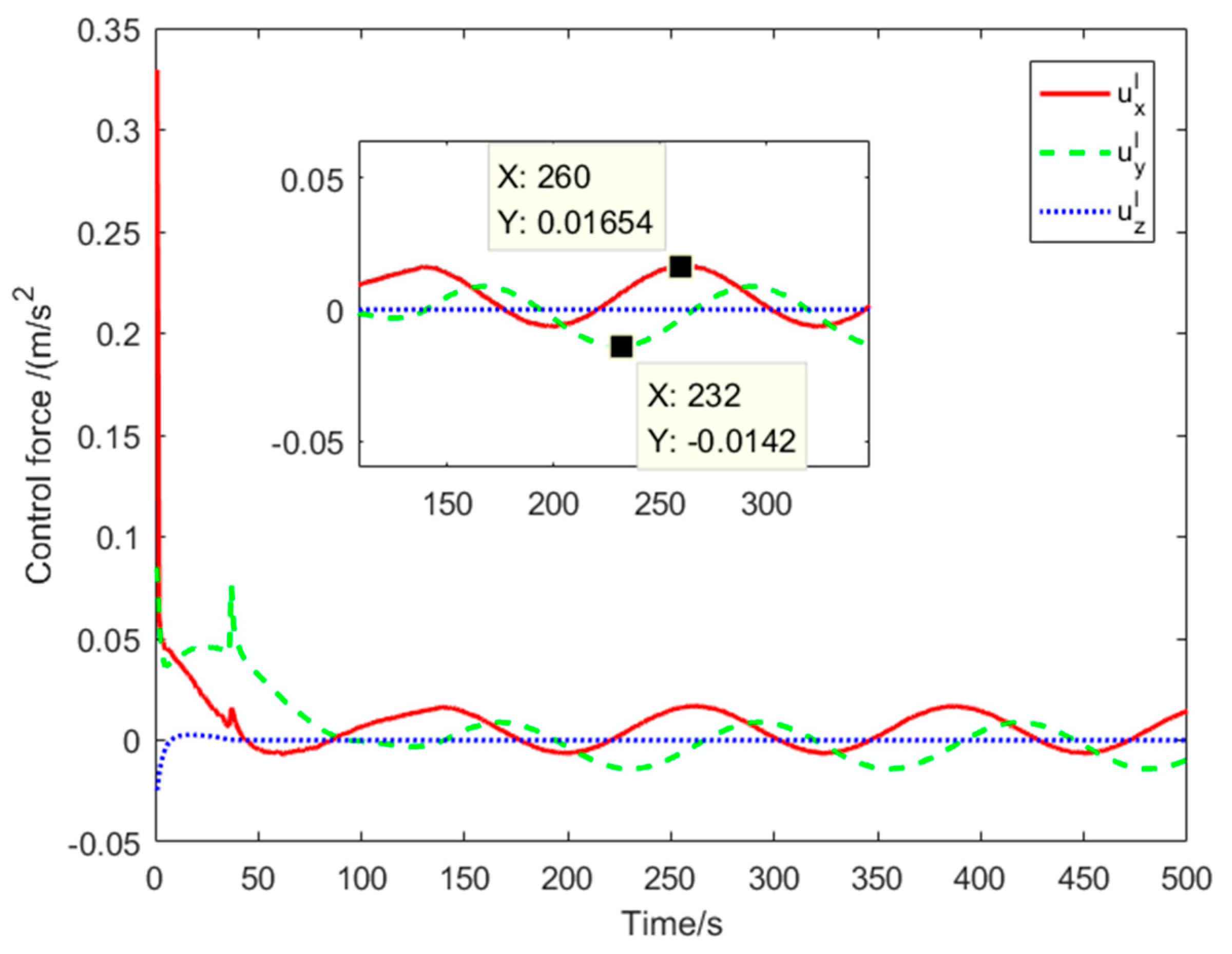
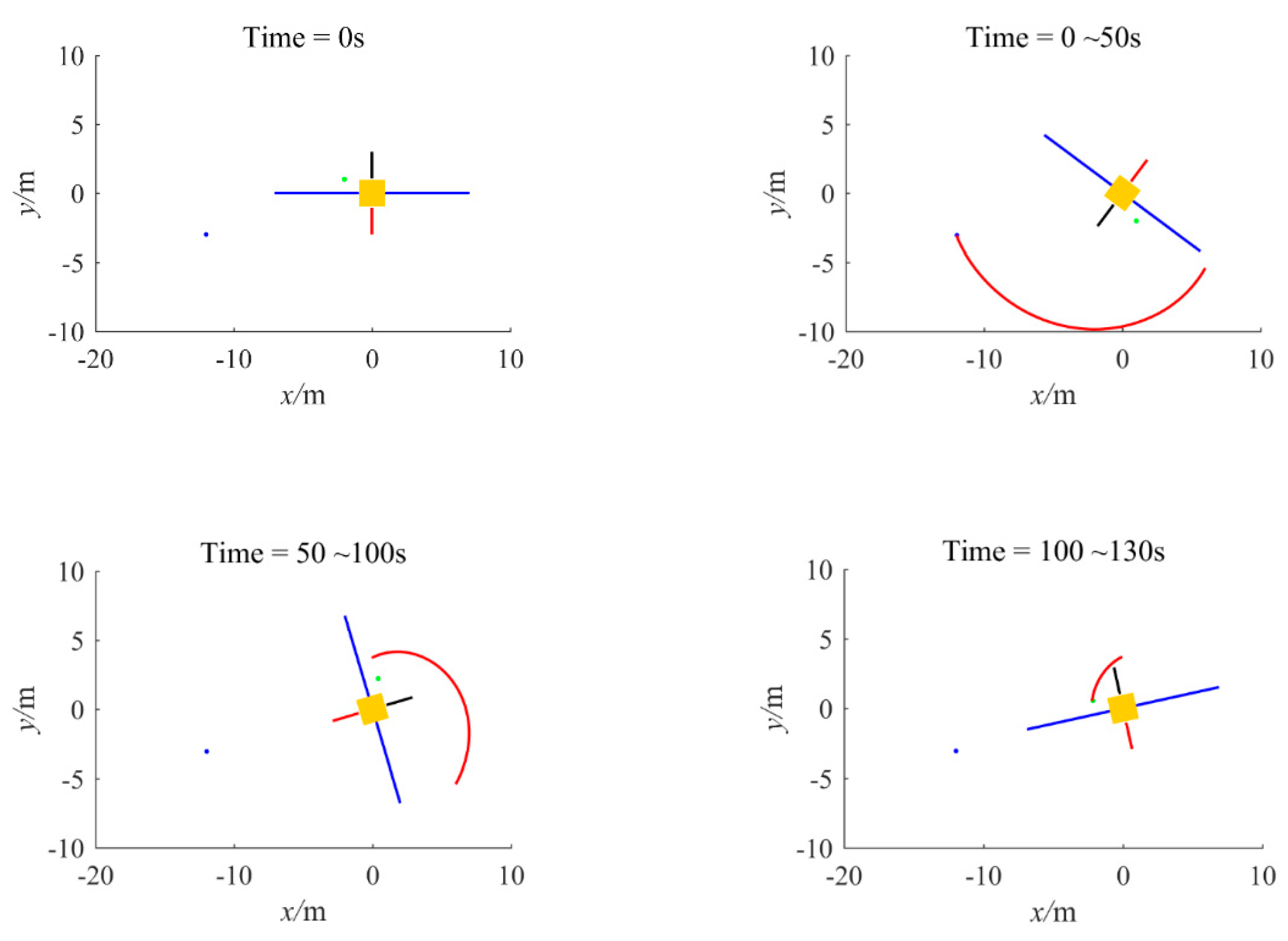
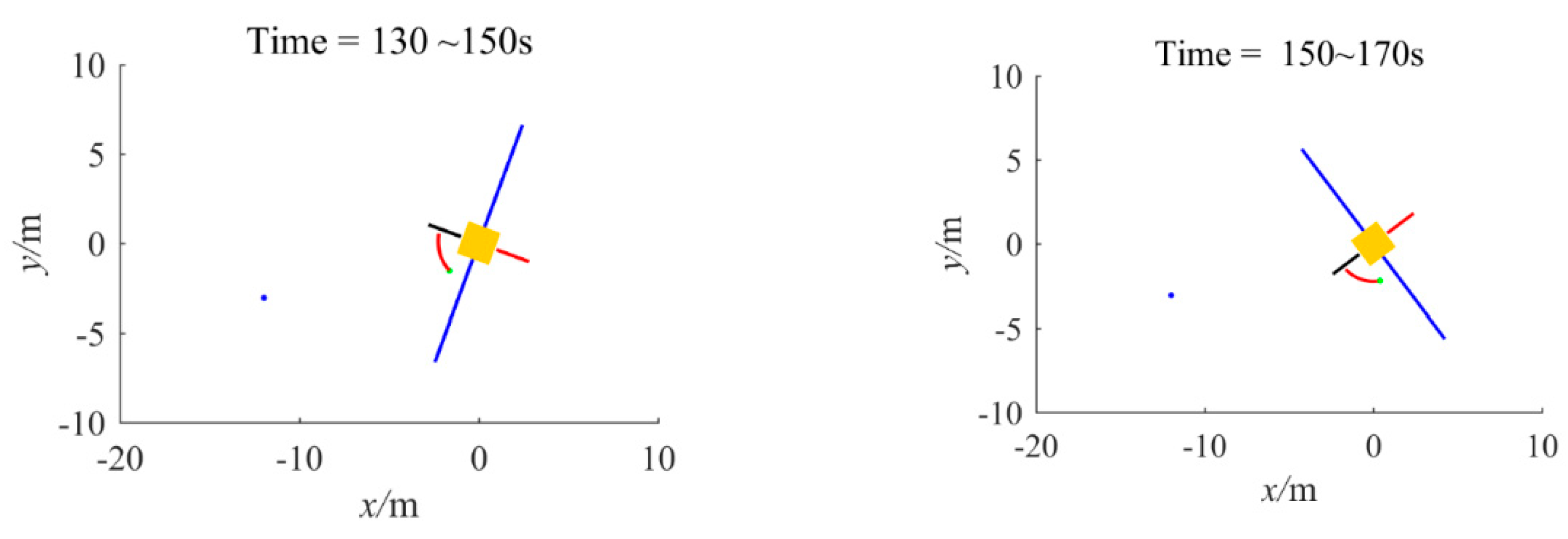
4.2. GMM-FTC Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roscoe, C.W.T.; Westphal, J.J.; Mosleh, E. Overview and GNC design of the CubeSat Proximity Operations Demonstration (CPOD) mission. Acta Astronaut. 2018, 153, 410–421. [Google Scholar] [CrossRef]
- Aglietti, G.S.; Taylor, B.; Fellowes, S.; Salmon, T.; Retat, I.; Hall, A.; Chabot, T.; Pisseloup, A.; Cox, C.; Mafficini, A. The active space debris removal mission RemoveDebris. Part 2: In orbit operations. Acta Astronaut. 2020, 168, 310–322. [Google Scholar] [CrossRef]
- Biesbroek, R.; Innocenti, L.; Wolahan, A.; Serrano, S.M. e.Deorbit—ESA’s active debris removal mission. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–21 April 2017; p. 10. [Google Scholar]
- Zappulla, R.; Park, H.; Virgili-Llop, J.; Romano, M. Real-Time Autonomous Spacecraft Proximity Maneuvers and Docking Using an Adaptive Artificial Potential Field Approach. IEEE Trans. Control Syst. Technol. 2019, 27, 2598–2605. [Google Scholar] [CrossRef]
- McCamish, S.; Romano, M.; Yun, X. Autonomous Distributed Control Algorithm for Multiple Spacecraft in Close Proximity Operations. AIAA Guid. Navig. Control Conf. Exhib. 2007, 5, 6857. [Google Scholar]
- Cao, L.; Qiao, D.; Xu, J. Suboptimal artificial potential function sliding mode control for spacecraft rendezvous with obstacle avoidance. Acta Astronaut. 2018, 143, 133–146. [Google Scholar] [CrossRef]
- Li, Q.; Yuan, J.; Wang, H. Sliding mode control for autonomous spacecraft rendezvous with collision avoidance. Acta Astronaut. 2018, 151, 743–751. [Google Scholar] [CrossRef]
- Li, X. Non-cooperative autonomous rendezvous and docking using artificial potentials and sliding mode control. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1171–1184. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, D.; Biggs, J.D.; Sun, Z. Finite-time relative orbit-attitude tracking control for multi-spacecraft with collision avoidance and changing network topologies. Adv. Space Res. 2019, 63, 1161–1175. [Google Scholar] [CrossRef]
- Dong, H.; Hu, Q.; Akella, M.R. Safety control for spacecraft autonomous rendezvous and docking under motion constraints. Caterer 2017, 207, 1680–1692. [Google Scholar] [CrossRef]
- Zagaris, C.; Romano, M. Reachability analysis of planar spacecraft docking with rotating body in close proximity. J. Guid. Control Dyn. 2018, 41, 1416–1422. [Google Scholar] [CrossRef]
- Ventura, J.; Ciarcià, M.; Romano, M.; Walter, U. Fast and near-optimal guidance for docking to uncontrolled spacecraft. J. Guid. Control Dyn. 2017, 40, 3138–3154. [Google Scholar] [CrossRef]
- Ma, Z.; Ma, O.; Shashikanth, B.N. Optimal control for spacecraft to rendezvous with a tumbling satellite in a close range. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4109–4114. [Google Scholar]
- Boyarko, G.; Yakimenko, O.; Romano, M. Optimal rendezvous trajectories of a controlled spacecraft and a tumbling object. J. Guid. Control Dyn. 2011, 34, 1239–1252. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Y.; Xu, Z. Optimal guidance and collision avoidance for docking with the rotating target spacecraft. Adv. Space Res. 2019, 63, 3223–3234. [Google Scholar] [CrossRef]
- St. John-Olcayto, E.; McInnes, C.; Ankersen, F. Safety-critical autonomous spacecraft proximity operations via potential function guidance. In Proceedings of the AIAA Infotech@ Aerospace 2007 Conference and Exhibition, Chicago, IL, USA, 7–10 May 2007; p. 2895. [Google Scholar]
- Badawy, A.; McInnes, C.R. On-orbit assembly using superquadric potential fields. J. Guid. Control Dyn. 2008, 31, 30–43. [Google Scholar] [CrossRef]
- Feng, L.-C.; Bai, Y.-Z.; Chen, X.-Q. Collision-free trajectory planning for spacecraft close-range proximity via potential sigmoid function. J. Beijing Inst. Technol. (Engl. Ed.) 2016, 25, 43594. [Google Scholar] [CrossRef]
- Liu, J.; Li, H. Artificial Potential Function Safety and Obstacle Avoidance Guidance for Autonomous Rendezvous and Docking with Noncooperative Target. Math. Probl. Eng. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Zhang, D.; Song, S.; Pei, R.; Duan, G. Ellipse cissoid-based potential function guidance for autonomous rendezvous and docking with non-cooperative target. J. Astronaut. 2010, 31, 2259–2268. [Google Scholar]
- Qing, N. Safety Guidance and Control for Spacecraft Close Proximity Maneuvers; National University of Defense Technology: Changsha, Hunan, China, 2016. [Google Scholar]
- Vittaldev, V.; Russell, R.P. Space Object Collision Probability Using Multidirectional Gaussian Mixture Models. J. Guid. Control Dyn. 2016, 39, 2163–2169. [Google Scholar] [CrossRef]
- Vishwajeet, K.; Singla, P. Adaptive Split/Merge-Based Gaussian Mixture Model Approach for Uncertainty Propagation. J. Guid. Control Dyn. 2018, 41, 603–617. [Google Scholar] [CrossRef]
- Vittaldev, V.; Russell, R.P.; Linares, R. Spacecraft uncertainty propagation using Gaussian mixture models and Polynomial chaos expansions. J. Guid. Control Dyn. 2016, 39, 2615–2626. [Google Scholar] [CrossRef]
- Rommel, C.; Bonnans, F.; Martinon, P.; Gregorutti, B. Gaussian mixture penalty for trajectory optimization problems. J. Guid. Control Dyn. 2019, 42, 1857–1862. [Google Scholar] [CrossRef]
- Eckart, B. Compact Generative Models of Point Cloud Data for 3D Perception. Ph.D. Thesis, Carnegie Mellon University Pittsburgh, Pittsburgh, PA, USA, 2017. [Google Scholar]
- Wang, G.; Schultz, L.; Qi, J. Statistical Image Reconstruction for Muon Tomography Using a Gaussian Scale Mixture Model. IEEE Trans. Nucl. Sci. 2009, 56, 2480–2486. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, Y.; Xing, J.; Radice, G.; Ni, Q.; Chen, X. Equal-collision-probability-curve method for safe spacecraft close-range proximity maneuvers. Adv. Space Res. 2018, 62, 2599–2619. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Dechao, R.; Yangwei, O.; Qing, N.; Yuzhu, B. Multi-Equal-Collision-Probability-Cure Method for Convex Polygon-shape Spacecraft Safe Proximity Manoeuvres. J. Navig. 2019, 72, 405–429. [Google Scholar]
- Liu, Y.; Liu, X.-P.; Li, X.-H. Survey on finite-time control for nonlinear systems. Control Theory Appl. 2020, 37, 1–12. [Google Scholar]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Zuo, Z.; Han, Q.-L.; Ning, B. An Overview of Recent Advances in Fixed-Time Cooperative Control of Multiagent Systems. IEEE Trans. Ind. Inform. 2018, 14, 2322–2334. [Google Scholar] [CrossRef]
- Liu, X.; Liao, X. Fixed-time stabilization control for port-Hamiltonian systems. Nonlinear Dyn. 2019, 96, 1497–1509. [Google Scholar] [CrossRef]
- Chen, Q.; Xie, S.; Sun, M.; He, X. Adaptive Nonsingular Fixed-Time Attitude Stabilization of Uncertain Spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2937–2950. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-Time Attitude Control for Rigid Spacecraft With Actuator Saturation and Faults. IEEE Trans. Control Syst. Technol. 2016, 24, 1892–1898. [Google Scholar] [CrossRef]
- Shi, X.-N.; Zhang, Y.-A.; Zhou, D.; Zhou, Z.-G. Global fixed-time attitude tracking control for the rigid spacecraft with actuator saturation and faults. Acta Astronaut. 2019, 155, 325–333. [Google Scholar] [CrossRef]
- Ton, C.; Petersen, C. Continuous Fixed-Time Sliding Mode Control for Spacecraft with Flexible Appendages. IFAC-Pap. 2018, 51, 1–5. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, W.; Li, C.; Li, D.; Ma, G. Hovering control for spacecraft in relative orbit based on fixed-time stabilization theory. J. Harbin Inst. Technol. 2016, 48, 26–31. [Google Scholar]
- Hu, Q.; Chen, W.; Guo, L. Fixed-Time Maneuver Control of Spacecraft Autonomous Rendezvous With a Free-Tumbling Target. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 562–577. [Google Scholar] [CrossRef]
- Huang, Y.; Jia, Y. Adaptive Fixed-Time Six-DOF Tracking Control for Noncooperative Spacecraft Fly-Around Mission. IEEE Trans. Control Syst. Technol. 2019, 27, 1796–1804. [Google Scholar] [CrossRef]
- Tschauner, J.; Hempel, P. Optimale beschleunigungsprogramme fur das rendezvous-manover. Astronaut. Acta. 1964, 10, 296–307. [Google Scholar]
- Clohessy, W.; Wiltshire, R. Terminal guidance system for satellite rendezvous. J. Aerosp. Sci. 1960, 27, 653–658. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Li, B. An Experiment of K-Means Initialization Strategies on Handwritten Digits Dataset. Intell. Inf. Manag. 2018, 10, 43–48. [Google Scholar]




| j | |||
|---|---|---|---|
| 1 | 8.302 × 10−2 | ||
| 2 | 8.302 × 10−2 | ||
| 3 | 8.302 × 10−2 | ||
| 4 | 8.302 × 10−2 | ||
| 5 | 8.302 × 10−2 | ||
| 6 | 8.302 × 10−2 | ||
| 7 | 4.193 × 10−4 | ||
| 8 | 4.193 × 10−4 | ||
| 9 | 1.256 × 10−1 | ||
| 10 | 1.252 × 10−1 | ||
| 11 | 1.252 × 10−1 | ||
| 12 | 1.252 × 10−1 |
| j | |||
|---|---|---|---|
| 1 | 8.295 × 10−2 | ||
| 2 | 8.295 × 10−2 | ||
| 3 | 8.302 × 10−2 | ||
| 4 | 8.302 × 10−2 | ||
| 5 | 8.300 × 10−2 | ||
| 6 | 8.302 × 10−2 | ||
| 7 | 4.196 × 10−4 | ||
| 8 | 4.196 × 10−4 | ||
| 9 | 1.287 × 10−1 | ||
| 10 | 1.279 × 10−1 | ||
| 11 | 1.221 × 10−1 | ||
| 12 | 1.225 × 10−1 |
| Parameters | Value |
|---|---|
| diag{3 × 10−1 3 × 10−1 3 × 10−1} | |
| diag{1 × 10−2 1 × 10−2 1 × 10−2} | |
| 0.6 | |
| 1.5 | |
| diag{5 × 10−2 5 × 10−2 5 × 10−2} | |
| diag{1 × 10−2 1 × 10−2 1 × 10−2} | |
| diag{3 × 10−4 1.0 × 10−4 1.0 × 10−4} | |
| M | diag{6 × 10−1 6 × 10−1 4 × 10−1} |
| P | diag{8 × 10−1 8 × 10−1 8 × 10−1} |
| Elements | Value | Units |
|---|---|---|
| Semi-major axis, a | 6878.14 | km |
| Eccentricity, e | 0.01 | |
| Inclination, i | 45 | deg |
| Longitude of the ascending node, | 0 | deg |
| Argument of perigee, | 0 | deg |
| Initial true anomaly, | 0 | deg |
| Parameters | Value | Units |
|---|---|---|
| Initial relative position, | m | |
| Initial relative velocity, | m/s | |
| Desired relative position, | m | |
| Desired relative velocity, | m/s | |
| Angular velocity of target spacecraft, | rad/s | |
| Angular acceleration of target spacecraft, | rad/s2 | |
| Initial attitude of target spacecraft, | rad |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Bai, Y.; Zhao, Y.; Chen, Z.; Sheng, T. Safe Proximity Operation to Rotating Non-Cooperative Spacecraft with Complex Shape Using Gaussian Mixture Model-Based Fixed-Time Control. Appl. Sci. 2020, 10, 5986. https://doi.org/10.3390/app10175986
Chen R, Bai Y, Zhao Y, Chen Z, Sheng T. Safe Proximity Operation to Rotating Non-Cooperative Spacecraft with Complex Shape Using Gaussian Mixture Model-Based Fixed-Time Control. Applied Sciences. 2020; 10(17):5986. https://doi.org/10.3390/app10175986
Chicago/Turabian StyleChen, Rong, Yuzhu Bai, Yong Zhao, Zhijun Chen, and Tao Sheng. 2020. "Safe Proximity Operation to Rotating Non-Cooperative Spacecraft with Complex Shape Using Gaussian Mixture Model-Based Fixed-Time Control" Applied Sciences 10, no. 17: 5986. https://doi.org/10.3390/app10175986
APA StyleChen, R., Bai, Y., Zhao, Y., Chen, Z., & Sheng, T. (2020). Safe Proximity Operation to Rotating Non-Cooperative Spacecraft with Complex Shape Using Gaussian Mixture Model-Based Fixed-Time Control. Applied Sciences, 10(17), 5986. https://doi.org/10.3390/app10175986




