Application of Machine Learning in the Control of Metal Melting Production Process
Abstract
1. Introduction
2. Machine Learning
2.1. Neural Networks (NN)
2.2. Support Vector Regression (SVR)
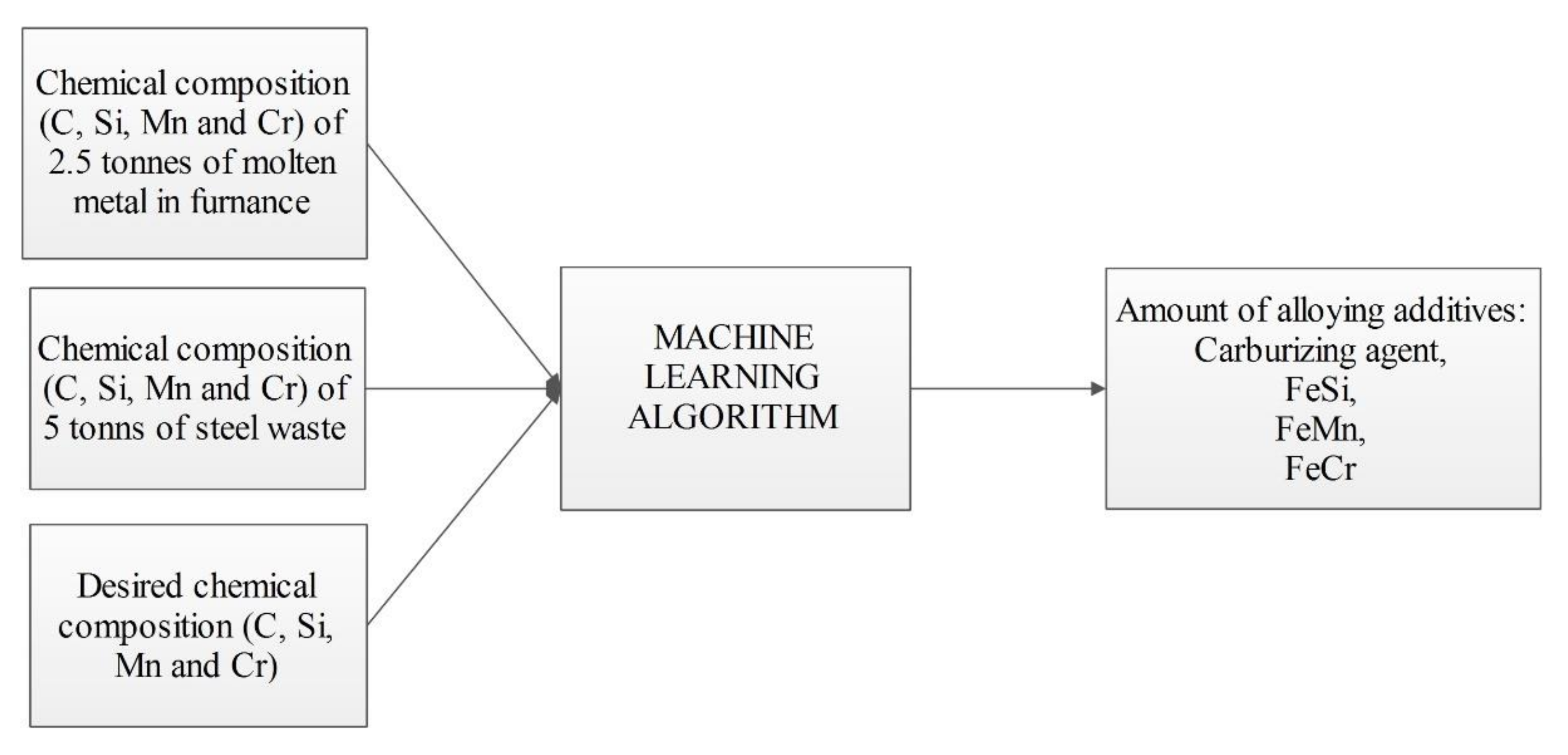
3. Metal Melting: Experimental Setup and Data Collection
4. Control of Metal Melting Process
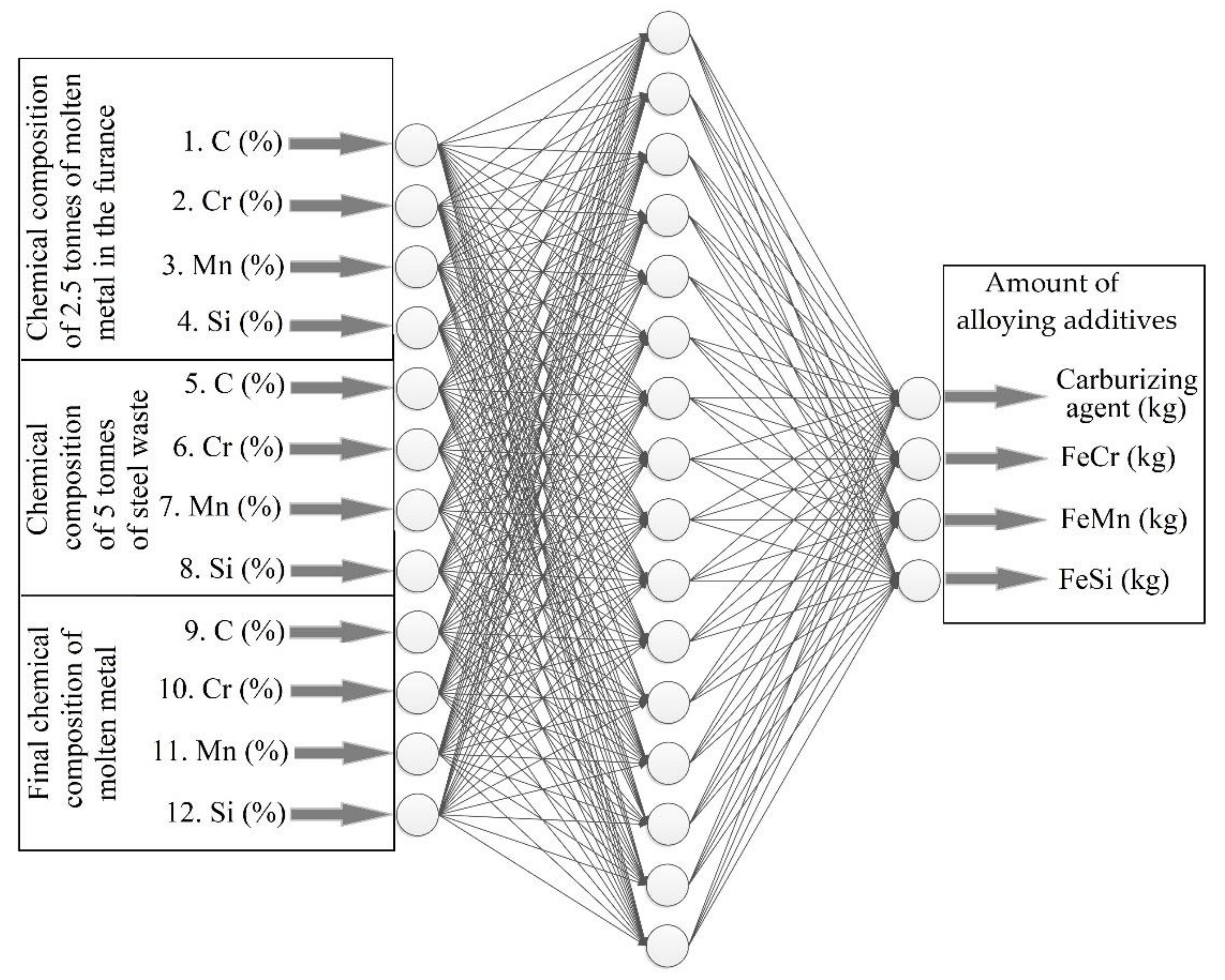
4.1. Neural Network Control of Metal Melting Process
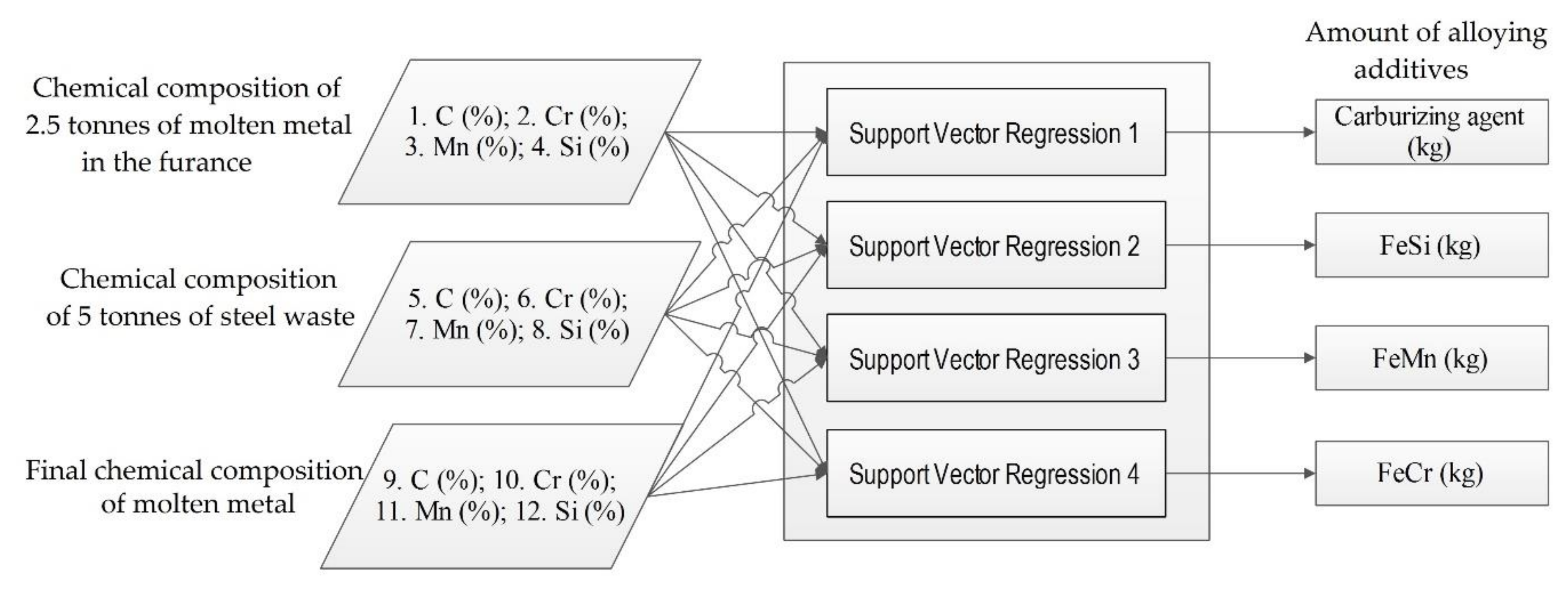
4.2. Support Vector Regression Control of the Metal Melting Process
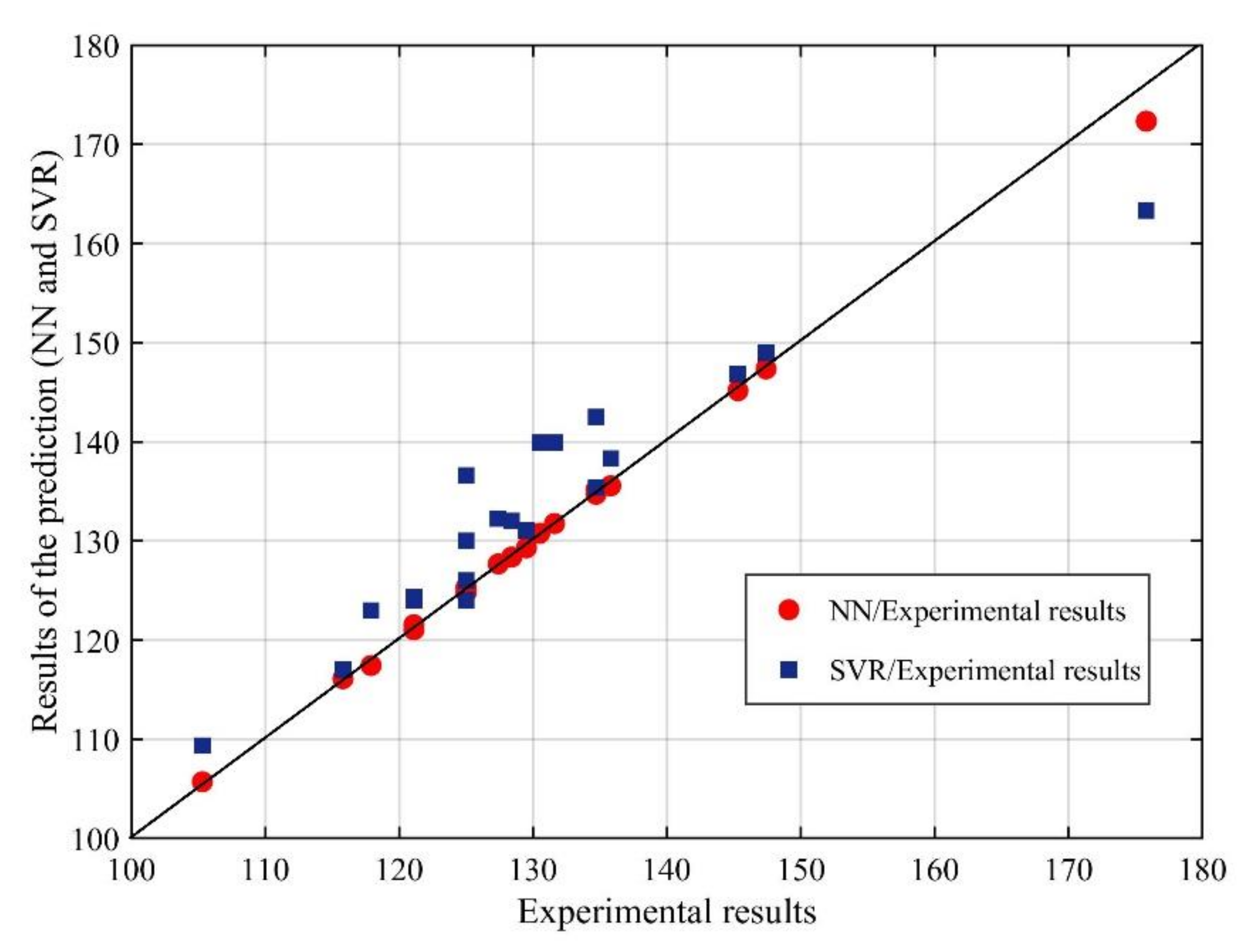
4.3. Discussion of Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bouhouche, S.; Boucherit, M.S.; Lahreche, M.; Bast, J. Modeling of ladle metallurgical treatment using neural networks. Arab. J. Sci. Eng. 2004, 29, 65–81. [Google Scholar]
- Fernandez, M.M.J.; Cabal, A.C.; Montequin, R.V.; Balsera, V.J. Online estimation of electric arc furnace tap temperature by using fuzzy neural networks. Eng. Appl. Artif. Intell. 2008, 21, 1001–1012. [Google Scholar] [CrossRef]
- Anupam, D.; Maiti, J.; Banerjee, R.N. Process control strategies for a steel making furnace using ANN with Bayesian regularization and ANFIS. Expert Syst. Appl. 2010, 37, 1075–1085. [Google Scholar] [CrossRef]
- Karunakar, B.D.; Datta, L.G. Prevention of defects in castings using back propagation neural networks. Int. J. Adv. Manuf. Technol. 2008, 39, 1111–1124. [Google Scholar] [CrossRef]
- Surekha, B.; Kaushik, L.K.; Panduy, A.K.; Vundavilli, P.R.; Parappagoudar, M.B. Multi-objective optimization of green sand mould system using evolutionary algorithms. Int. J. Adv. Manuf. Technol. 2012, 58, 9–17. [Google Scholar] [CrossRef]
- Chen, W.J.; Lin, C.X.; Chen, Y.T.; Lin, J.R. Optimization design of a gating system for sand casting aluminium A356 using a Taguchi method and multi-objective culture-based QPSO algorithm. Adv. Mech. Eng. 2016, 8, 1–14. [Google Scholar] [CrossRef]
- Dučić, N.; Ćojbašić, Ž.; Manasijević, S.; Radiša, R.; Slavković, R.; Milićević, I. Optimization of the gating system for sand casting using genetic algorithm. Int. J. Met. 2017, 11, 255–265. [Google Scholar] [CrossRef]
- Tsoukalas, V. An adaptive neuro-fuzzy inference system (ANFIS) model for high pressure die casting. Proc. Inst. Mech. Eng. Part. B J. Eng. Manuf. 2011, 225, 2276–2286. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, R. An intelligent system for low-pressure die-cast process parameters optimization. Int. J. Adv. Manuf. Technol. 2013, 65, 517–524. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, R.; Wang, G.; Sun, L.; Zhang, Z.; Li, Q. Breakout prediction for continuous casting using genetic algorithm based back propagation neural network model. Int. J. Model. Identif. Control 2012, 16, 199–205. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Liu, Y.; Du, F.; Yao, M.; Zhang, X. A particle swarm approach for optimization of secondary cooling process in slab continuous casting. Int. J. Heat Mass Transf. 2016, 93, 250–256. [Google Scholar] [CrossRef]
- Sata, A.; Ravi, B. Comparison of some neural network and multivariate regression for predicting mechanical properties of investment casting. J. Mater. Eng. Perform. 2014, 23, 2953–2964. [Google Scholar] [CrossRef]
- Pattnaik, S.; Kumar, M.S. Optimization of the investment casting process using genetic algorithm. Comput. Intell. Data Min. 2014, 2, 201–208. [Google Scholar] [CrossRef]
- Kurra, S.; Hifzur, N.; Srinivasa, R.; Amit, R.P.; Gupta, K. Modeling and optimization of surface roughness in single point incremental forming process. J. Mater. Res. Technol. 2015, 4, 304–313. [Google Scholar] [CrossRef]
- Choa, S.; Asfoura, S.; Onar, A.; Kaundinyaa, N. Tool breakage detection using support vector machine learning in a milling process. Int. J. Mach. Tools Manuf. 2005, 45, 241–249. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal. Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Kankar, K.P.; Sharma, C.S.; Harsha, P.S. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, K.; Yua, T.; Fang, M. Reliable multi-objective optimization of high-speed WEDM process based on Gaussian process regression. Int. J. Mach. Tools Manuf. 2008, 48, 47–60. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; Orlando, D.J. Neural Network Design, 2nd ed.; Hagan, M., Ed.; Oklahoma State University: Stillwater, OK, USA, 2014. [Google Scholar]
- Hagan, T.M.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; pp. 119–166. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; Technical Report; Department of Computer Science and Information Engineering, University of National Taiwan: Taipei, Taiwan, 2003; pp. 1–12. [Google Scholar]



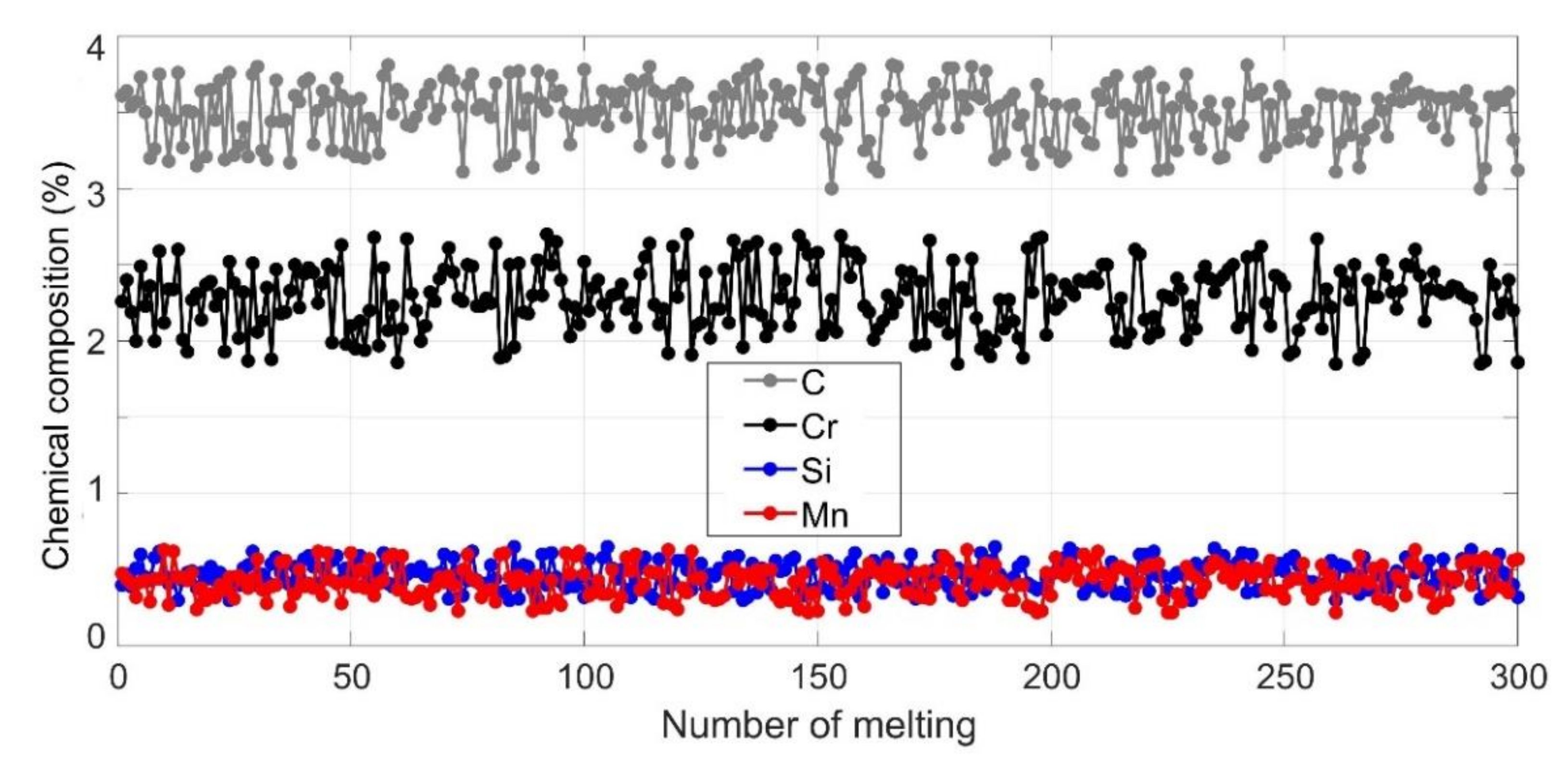
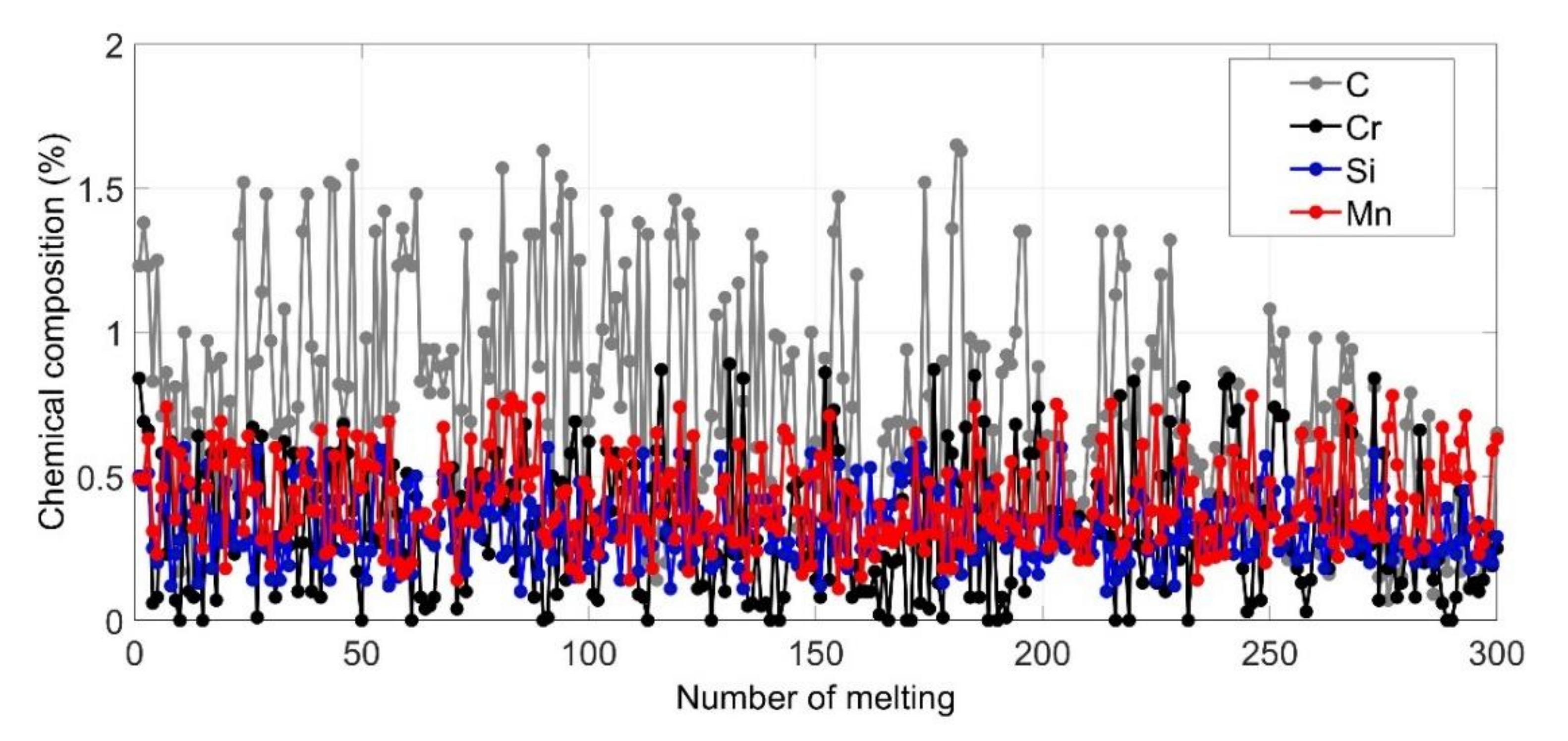
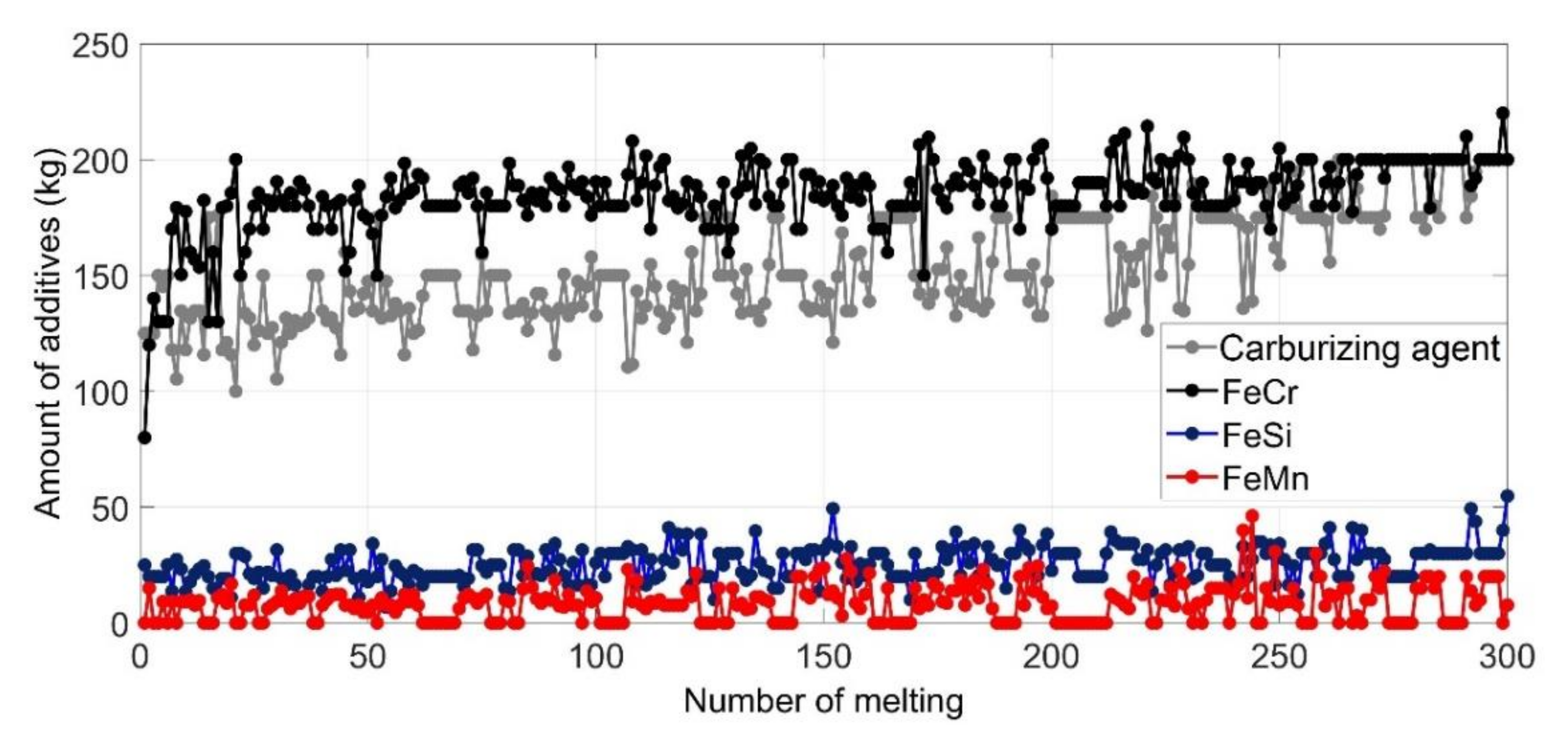
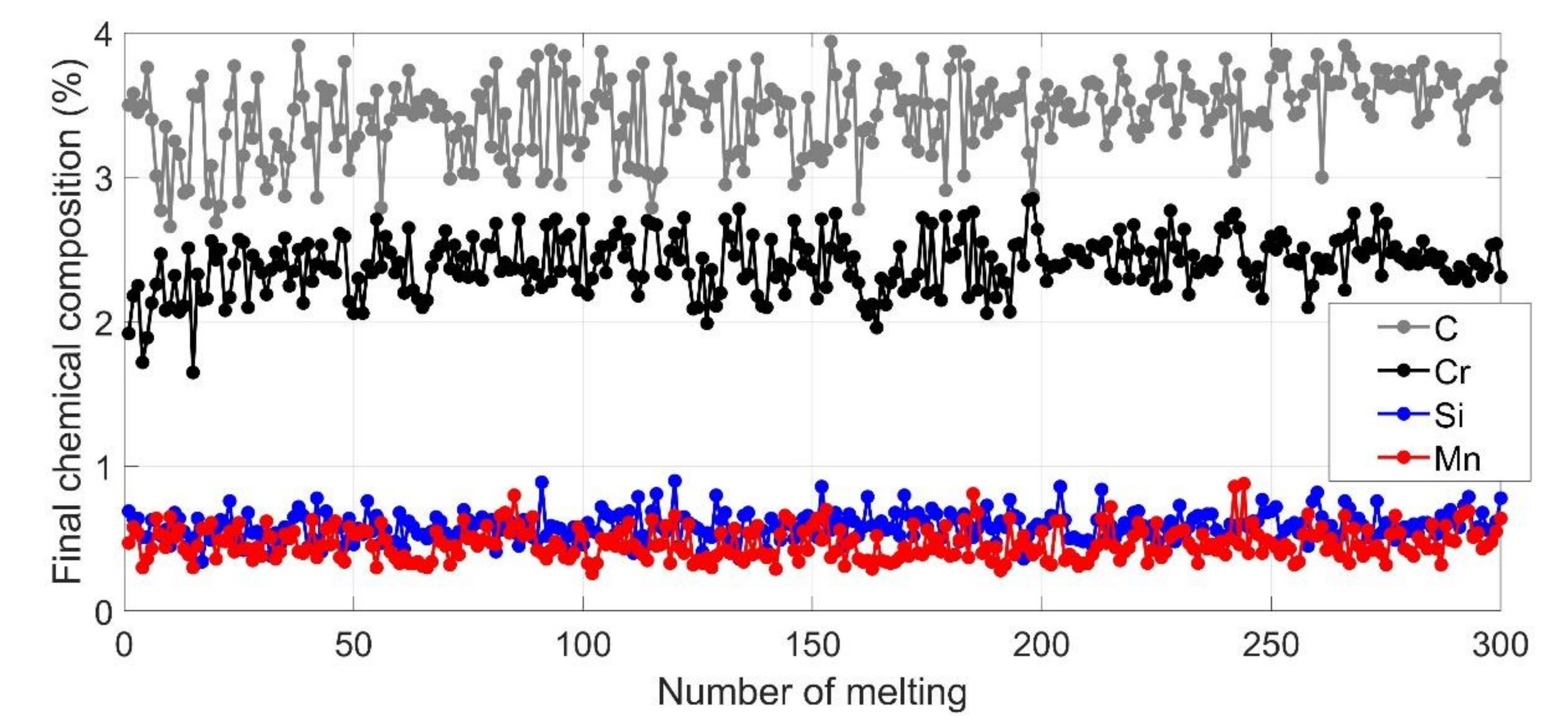
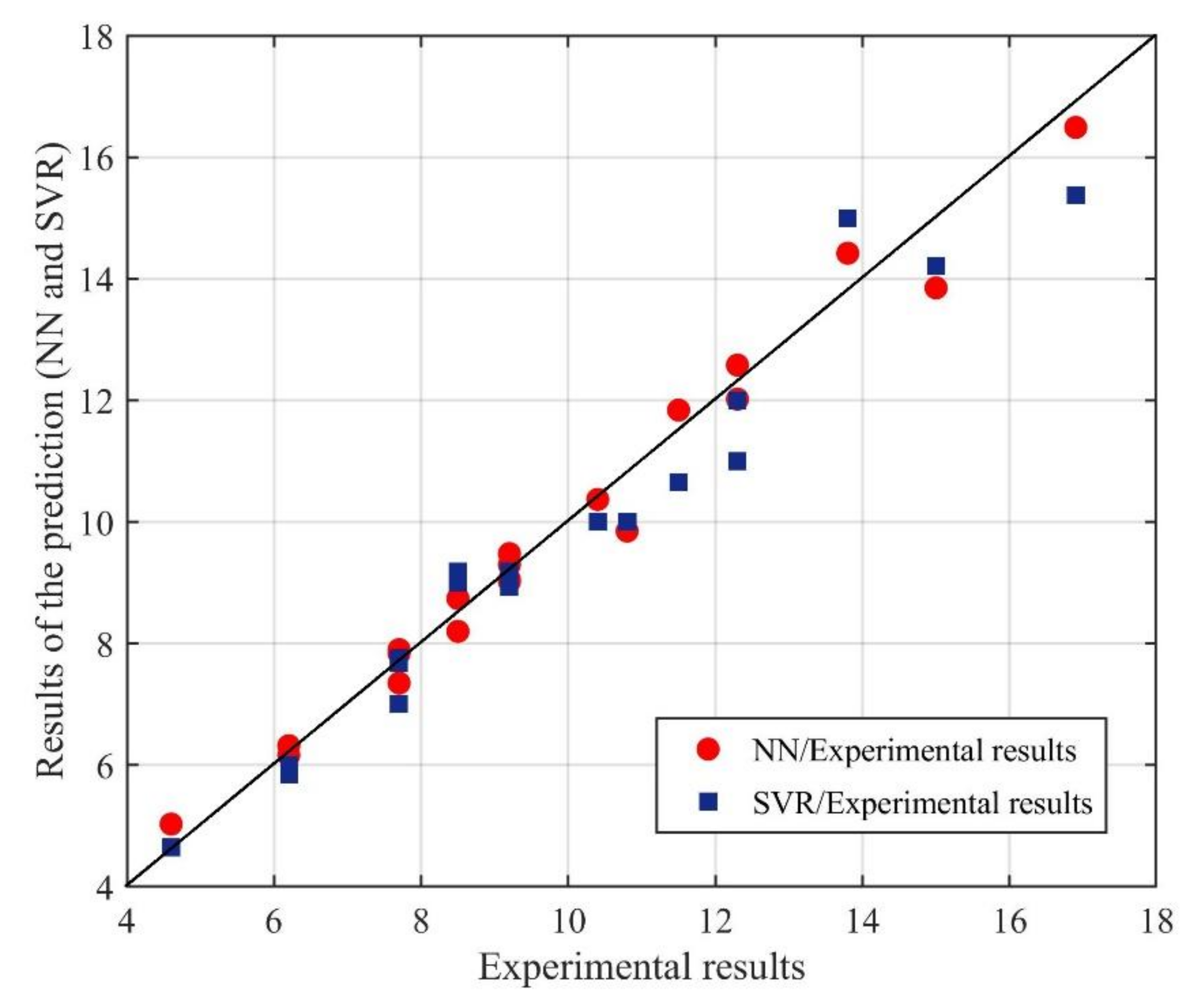
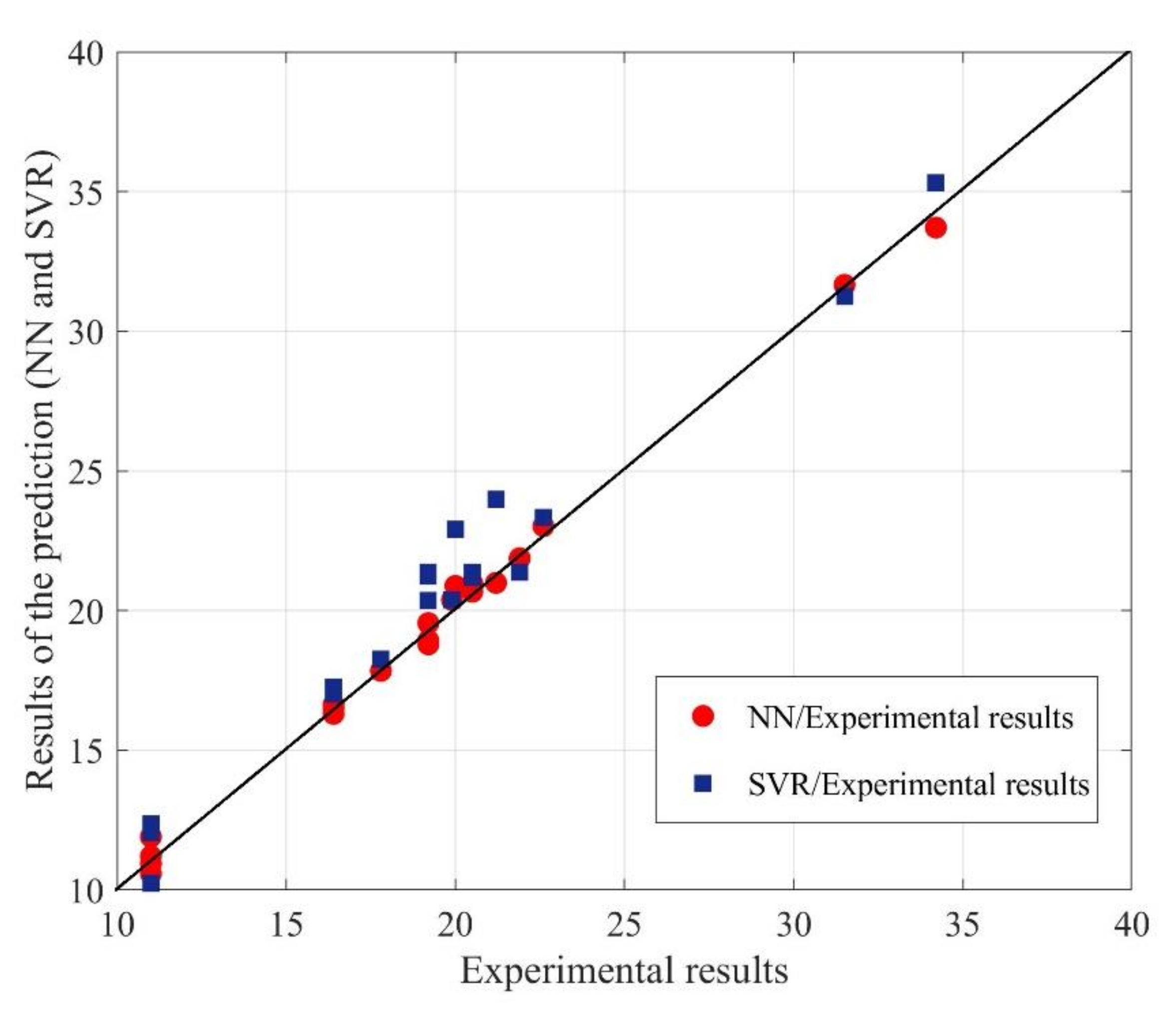
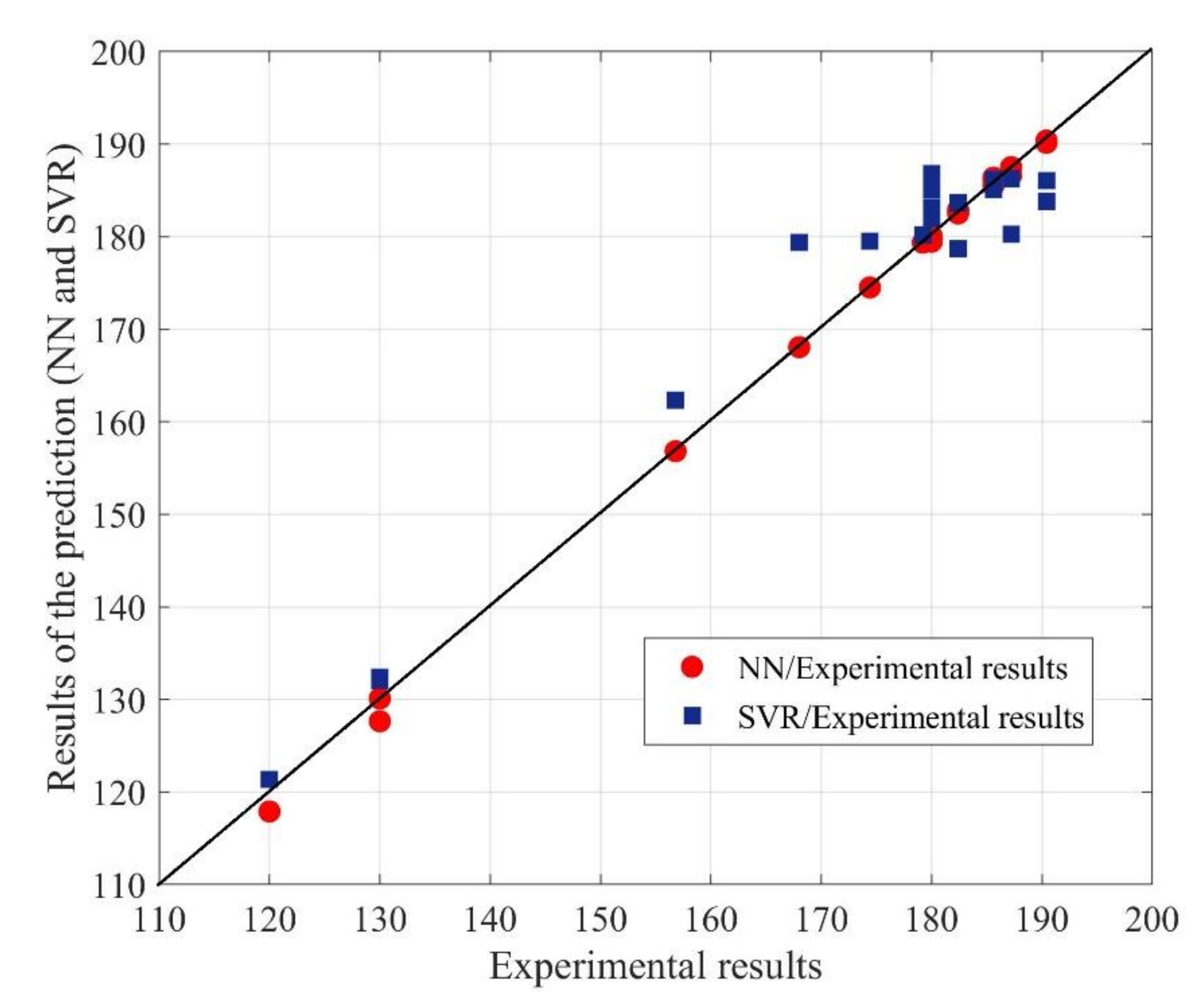
| NN Model (Input-Hidden-Output) | Mean Squared Error |
|---|---|
| 12-14-4 | 0.23 |
| 12-15-4 | 0.31 |
| 12-18-4 | 0.28 |
| 12-16-4 | 0.16 |
| 12-12-4 | 0.25 |
| Carburizing Agent (kg) | FeCr (kg) | FeMn (kg) | FeSi (kg) | |
|---|---|---|---|---|
| Mean error (%) | 0.47 | 0.51 | 3.31 | 1.88 |
| Max. error (%) | 1.97 | 1.92 | 9.42 | 8.18 |
| Models | C | Mean Squared Error (mse) | ||
|---|---|---|---|---|
| Case 1 | Support Vector Regression 1 | 6 | 0.02 | 0.88 |
| Support Vector Regression 2 | 6 | 0.02 | 0.98 | |
| Support Vector Regression 3 | 6 | 0.02 | 0.75 | |
| Support Vector Regression 4 | 6 | 0.02 | 0.65 | |
| Case 2 | Support Vector Regression 1 | 10 | 0.005 | 0.45 |
| Support Vector Regression 2 | 10 | 0.005 | 0.47 | |
| Support Vector Regression 3 | 10 | 0.005 | 0.42 | |
| Support Vector Regression 4 | 10 | 0.005 | 0.38 | |
| Case 3 | Support Vector Regression 1 | 32 | 0.12 | 0.84 |
| Support Vector Regression 2 | 32 | 0.12 | 1.13 | |
| Support Vector Regression 3 | 32 | 0.12 | 0.95 | |
| Support Vector Regression 4 | 32 | 0.12 | 0.48 |
| Carburizing Agent (kg) | FeCr (kg) | FeMn (kg) | FeSi (kg) | |
|---|---|---|---|---|
| Mean error (%) | 3.39 | 2.05 | 4.81 | 6.65 |
| Max. error (%) | 9.29 | 6.77 | 10.57 | 14.56 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dučić, N.; Jovičić, A.; Manasijević, S.; Radiša, R.; Ćojbašić, Ž.; Savković, B. Application of Machine Learning in the Control of Metal Melting Production Process. Appl. Sci. 2020, 10, 6048. https://doi.org/10.3390/app10176048
Dučić N, Jovičić A, Manasijević S, Radiša R, Ćojbašić Ž, Savković B. Application of Machine Learning in the Control of Metal Melting Production Process. Applied Sciences. 2020; 10(17):6048. https://doi.org/10.3390/app10176048
Chicago/Turabian StyleDučić, Nedeljko, Aleksandar Jovičić, Srećko Manasijević, Radomir Radiša, Žarko Ćojbašić, and Borislav Savković. 2020. "Application of Machine Learning in the Control of Metal Melting Production Process" Applied Sciences 10, no. 17: 6048. https://doi.org/10.3390/app10176048
APA StyleDučić, N., Jovičić, A., Manasijević, S., Radiša, R., Ćojbašić, Ž., & Savković, B. (2020). Application of Machine Learning in the Control of Metal Melting Production Process. Applied Sciences, 10(17), 6048. https://doi.org/10.3390/app10176048








