Characteristic Test and Electromagnetic Analysis of Regenerative Hybrid Electrodynamic Damper for Vibration Mitigation and Monitoring of Stay Cables
Abstract
1. Introduction
2. Analytical Investigation of Electromagnetic Damper Model
2.1. Magnetic Circuit and Operating Point
2.2. Induced Voltage and Machine Constant
2.3. Winding Properties and Damping Force
3. Characteristics Test of Electromagnetic Dampers
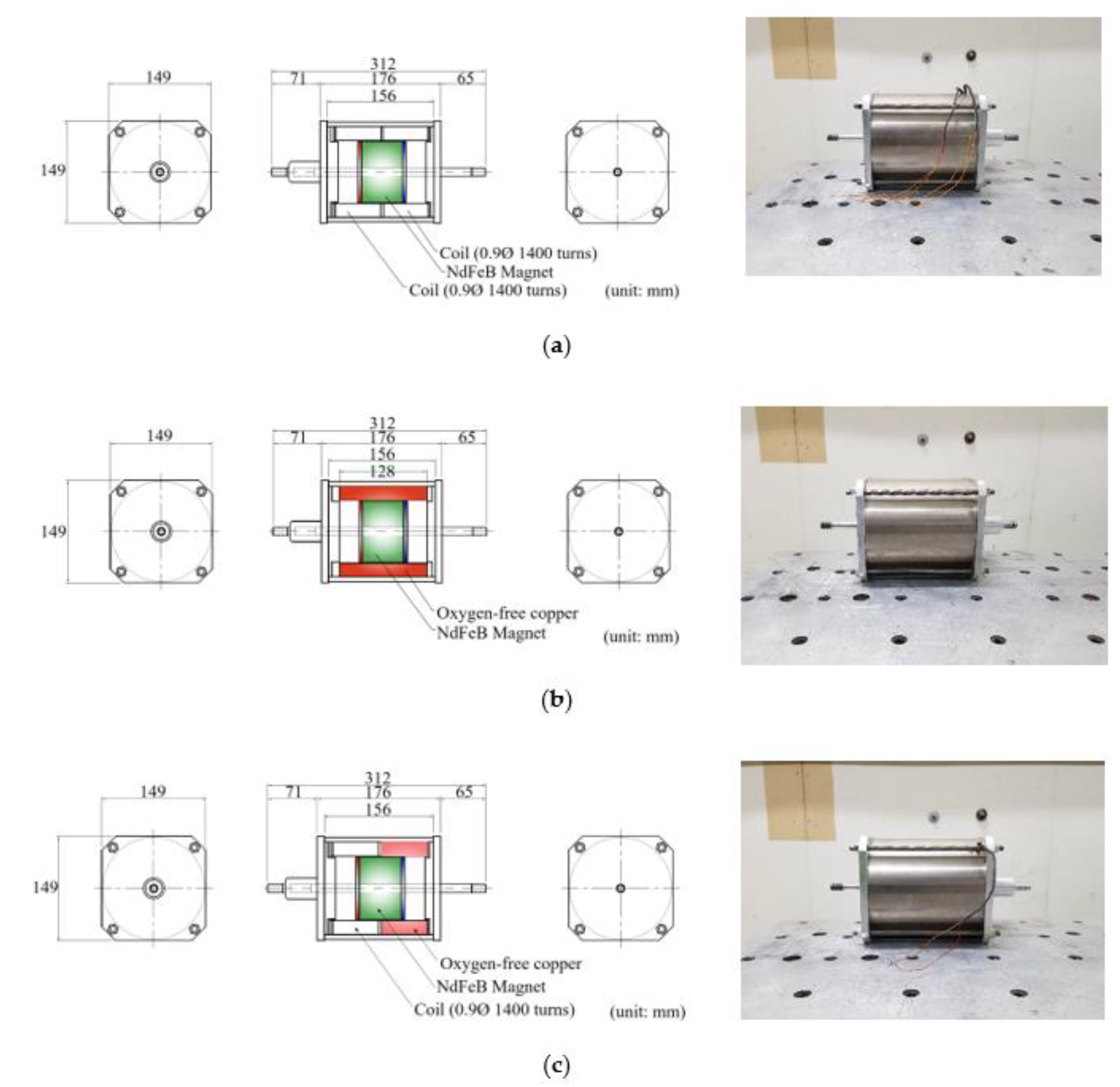
3.1. Structural Properties
3.2. Test Conditions
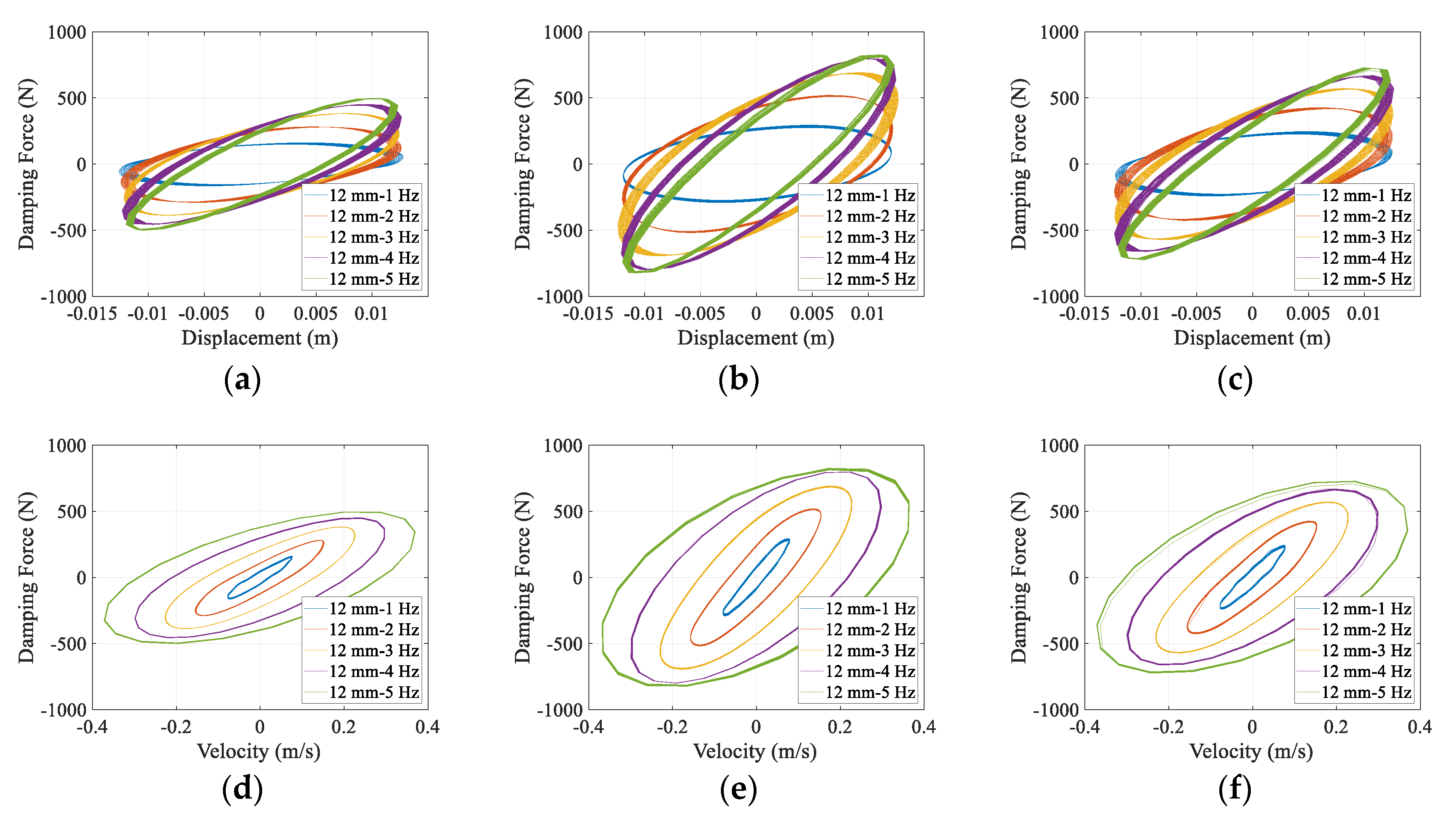
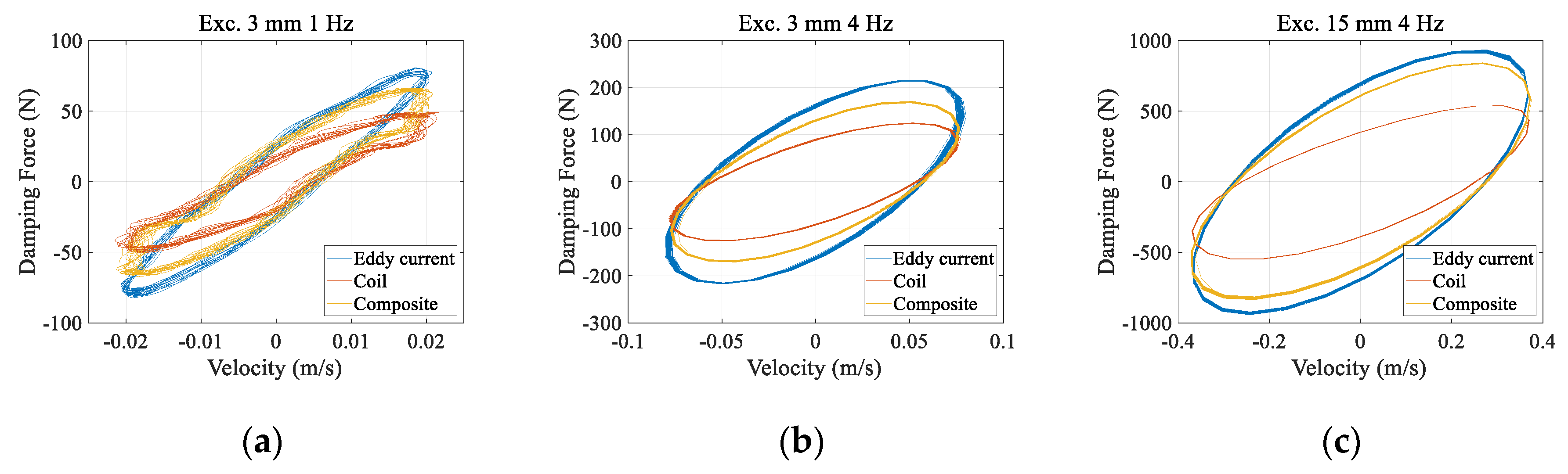
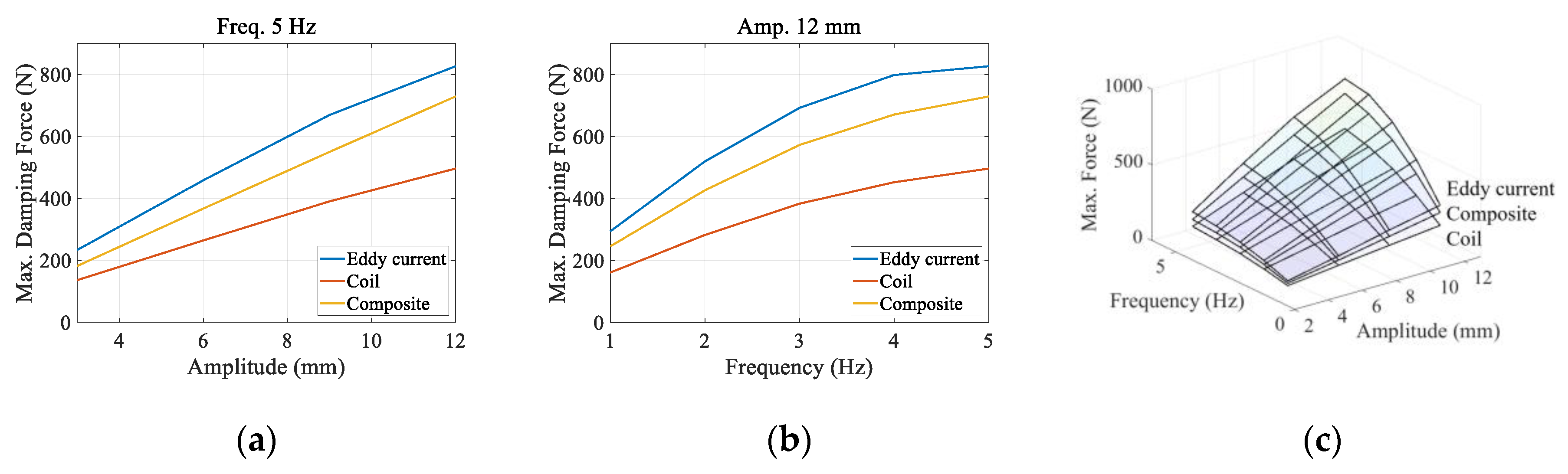
3.3. Comparative Analysis of Test Results
4. Electromagnetic Analysis of the Proposed Damper
4.1. Design Orientation and Model Configuration
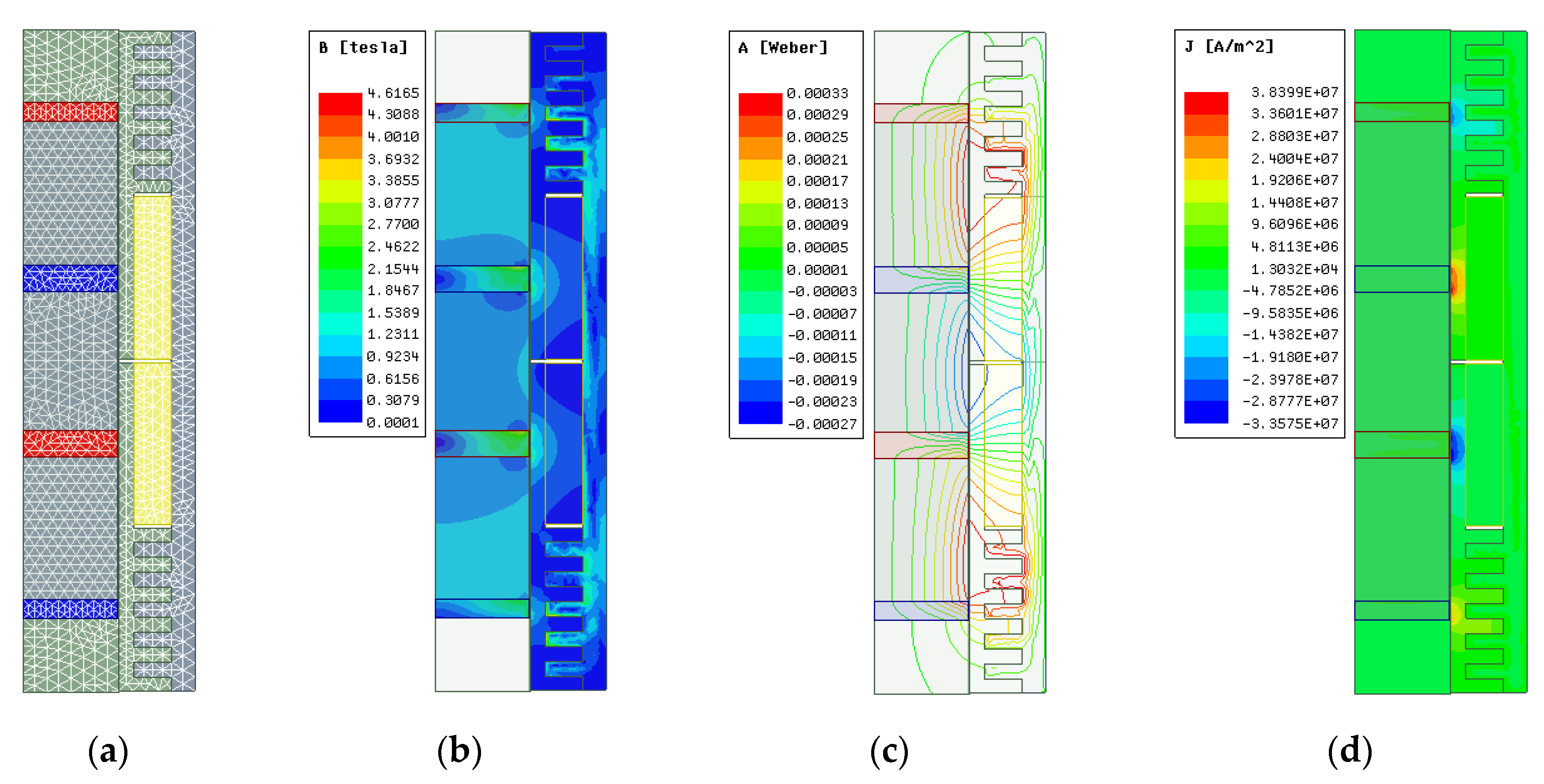
4.2. Analysis Conditions
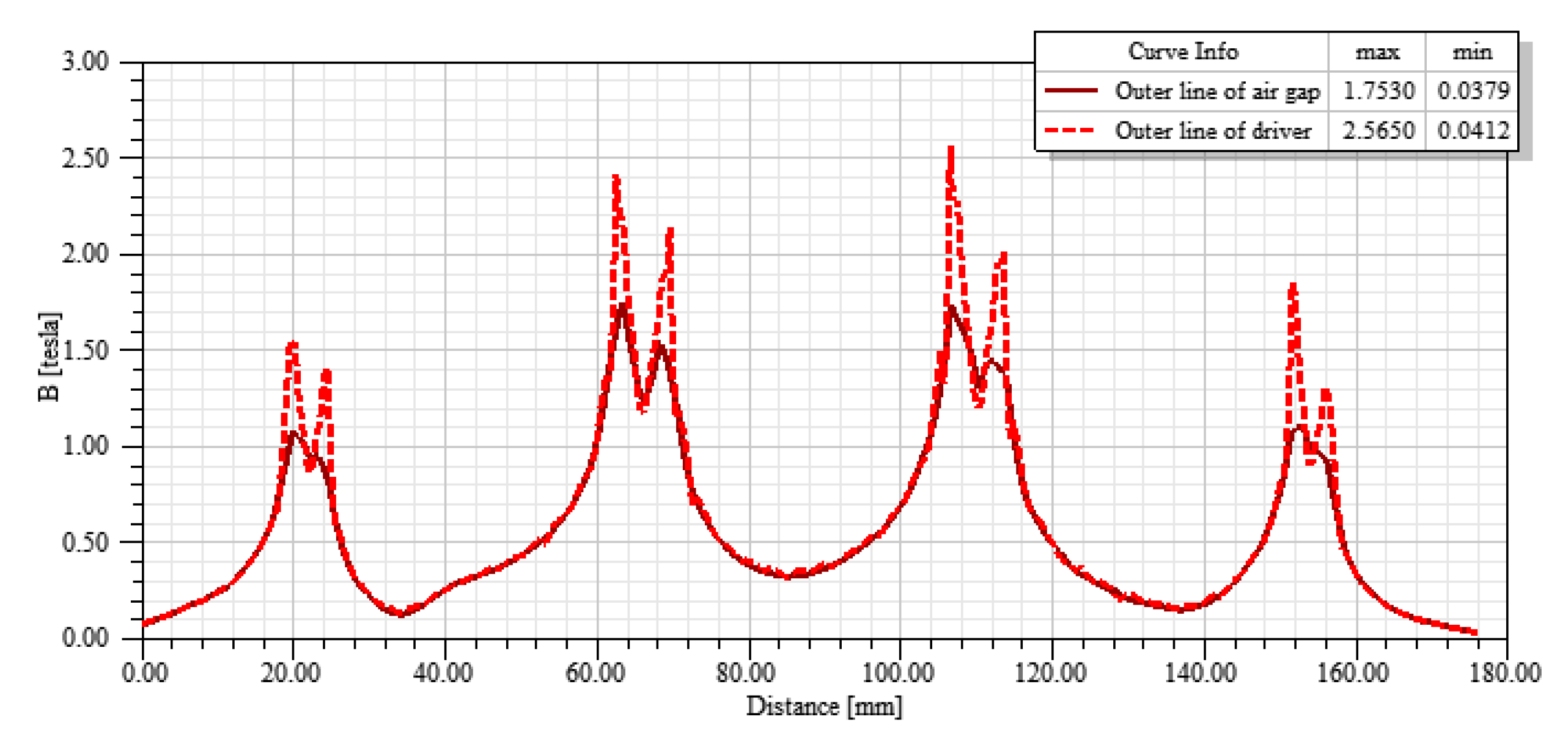
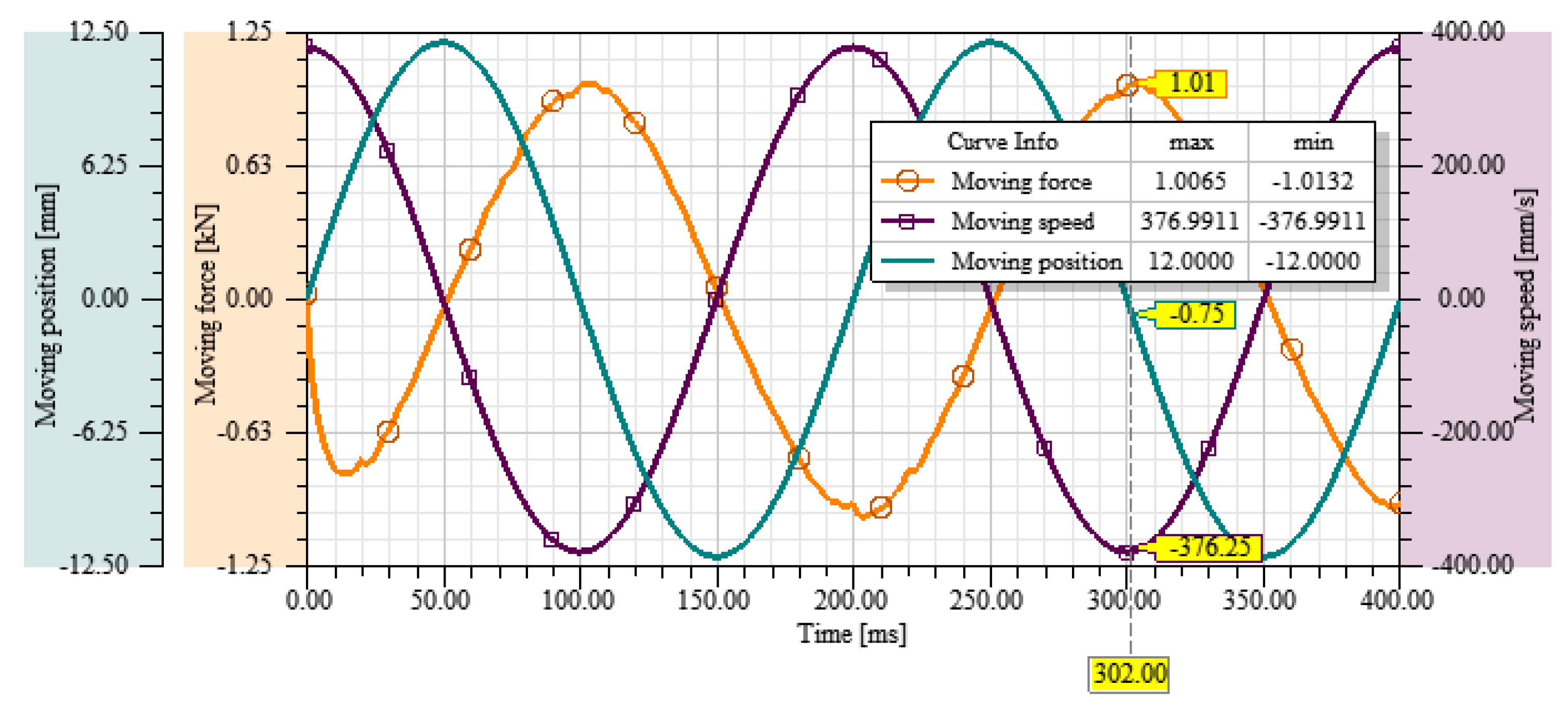
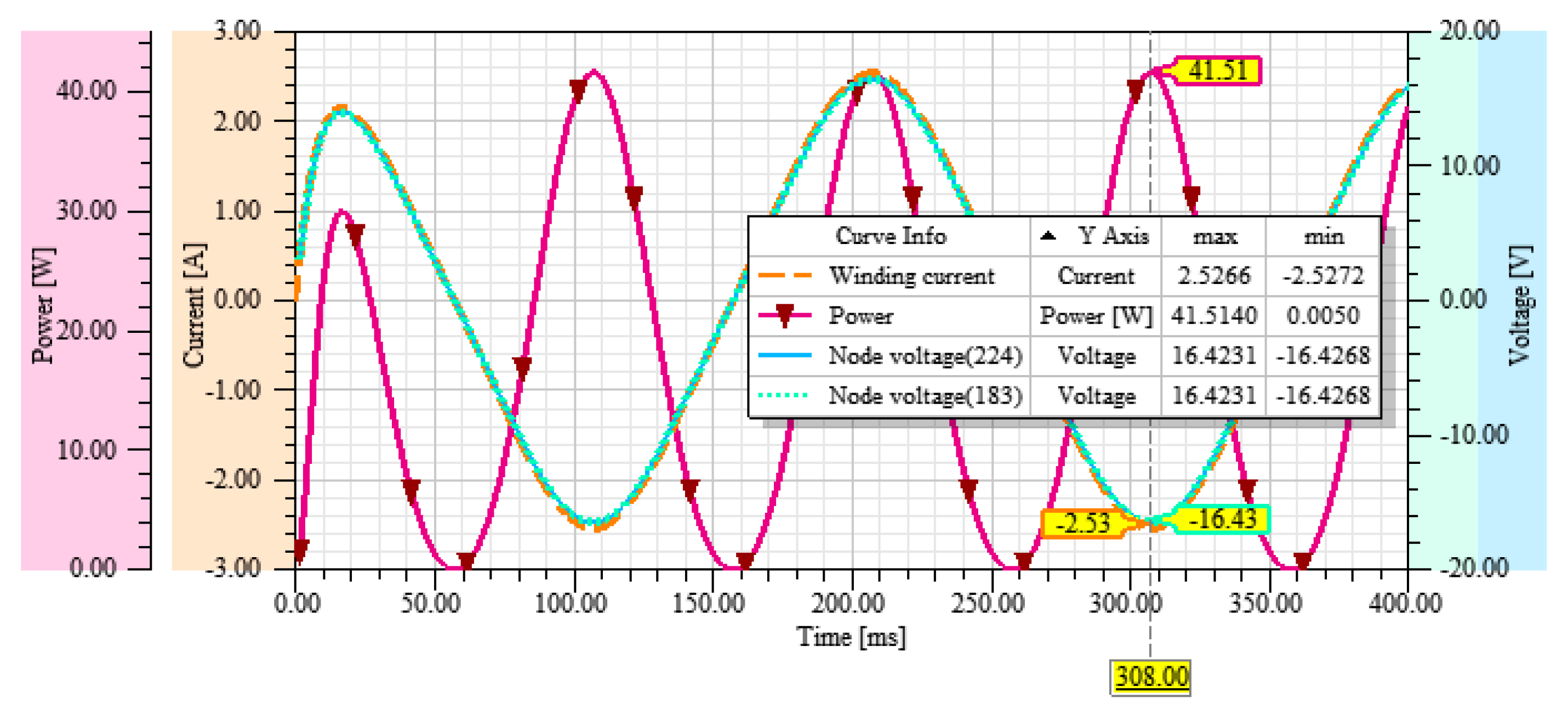
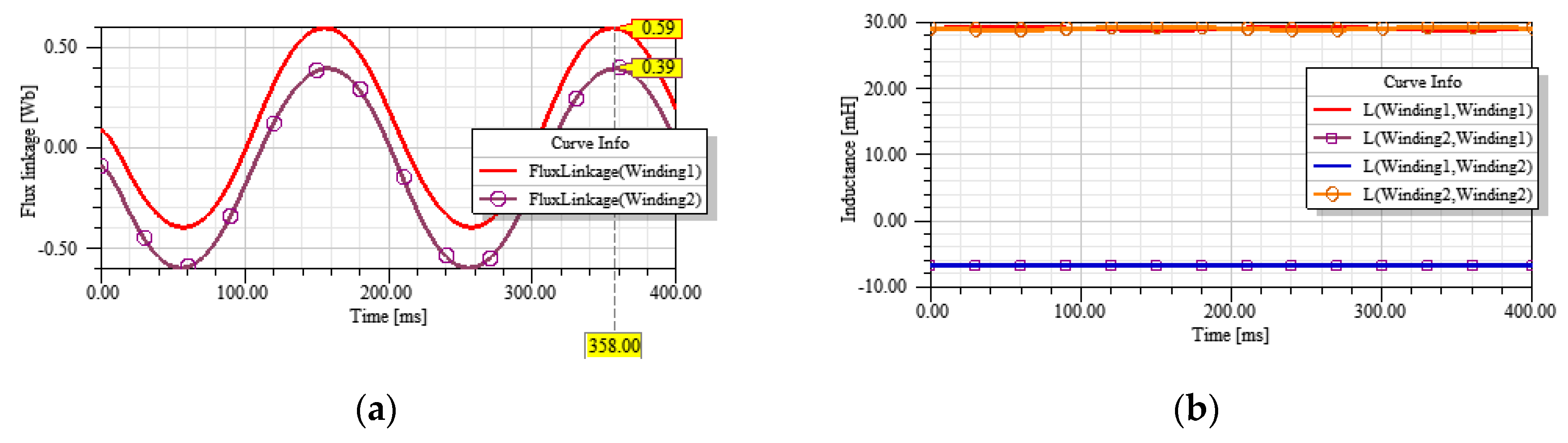
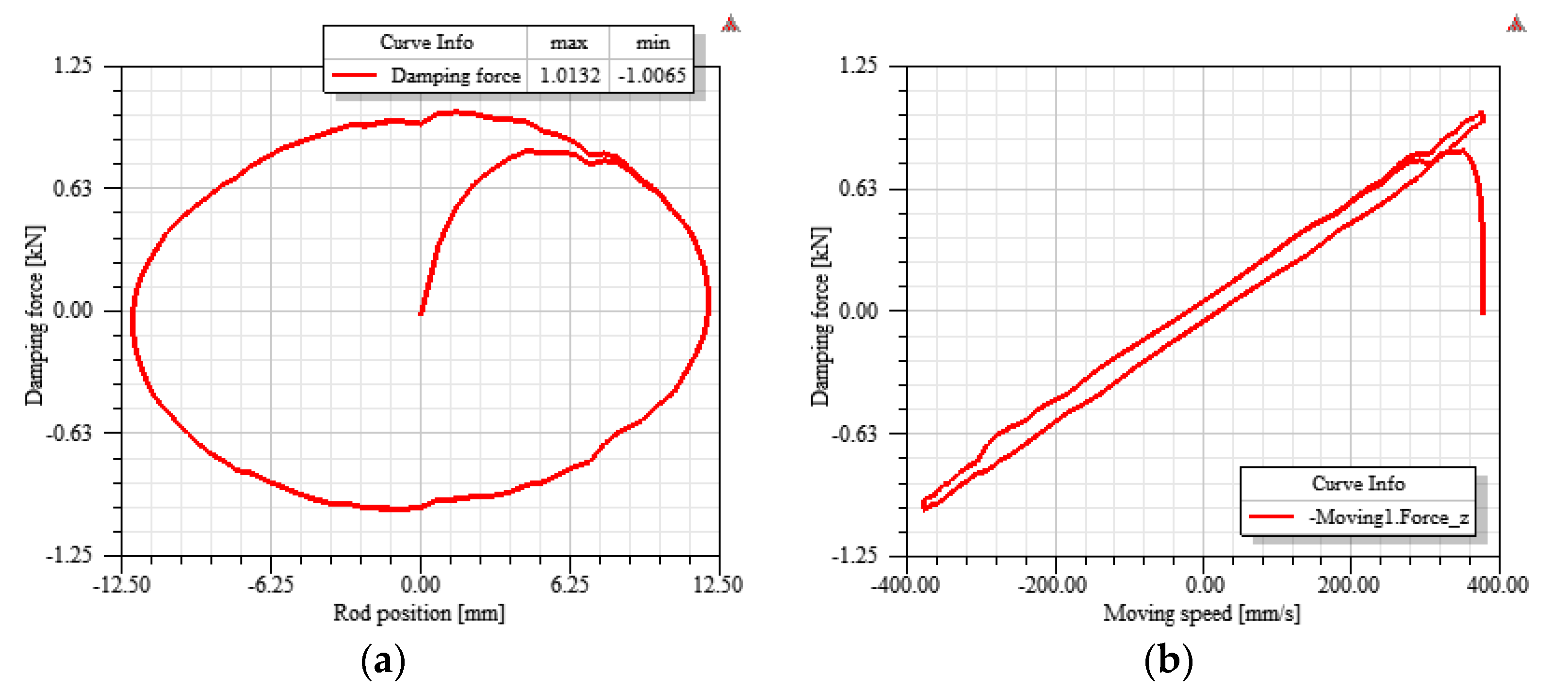
4.3. Analysis Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, S.; Park, J.; Kim, H.K. Damping Identification and Serviceability Assessment of a Cable-Stayed Bridge Based on Operational Monitoring Data. J. Bridge Eng. 2017, 22, 04016123. [Google Scholar] [CrossRef]
- Park, K.J.; Hwang, E.S. Assessment of Vibration Serviceability for Steel Cable-Stayed Bridges Using GNSS Data. Int. J. Steel Struct. 2016, 16, 1251–1262. [Google Scholar] [CrossRef]
- Li, H.; Ou, J. The state of the art in structural health monitoring of cable-stayed bridges. J. Civ. Struct. Health Monit. 2016, 6, 43–67. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, C.; Cai, C.S.; Jiang, X.; Xiong, W. Corrosion fatigue analysis of stay cables under combined loads of random traffic and wind. Eng. Struct. 2020, 206, 110153. [Google Scholar] [CrossRef]
- Park, C. Detail Planning Research Project on Super-Long Span Cable Bridge; Korea Expressway Corporation: Seongnam, Korea, 2008; p. 688. [Google Scholar]
- Wang, J.; Howe, D.; Jewell, G.W. Analysis and Design Optimization of an Improved Axially Magnetized Tubular Permanent-Magnet Machine. IEEE Trans. Energy Convers. 2004, 19, 289–295. [Google Scholar] [CrossRef]
- Ebrahimi, B.; Khamesee, M.B.; Golnaraghi, M.F. Feasibility Study of an Electromagnetic Shock Absorber with Position Sensing Capability. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008. [Google Scholar]
- Wang, Z.; Hua, G. Feasibility Study of Passive Electromagnetic Dampers for Vibration Control of Stay Cables. Appl. Mech. Mater. 2013, 438–439, 1141–1144. [Google Scholar] [CrossRef]
- Jamshidi, M.; Chang, C.C.; Bakhshi, A. Self-powered hybrid electromagnetic damper for cable vibration mitigation. Smart Struct. Syst. 2017, 20, 285–301. [Google Scholar] [CrossRef]
- Zuo, L.; Chen, X.; Nayfeh, S. Design and Analysis of a New Type of Electromagnetic Damper With Increased Energy Density. J. Vib. Acoust. 2011, 133, 041006. [Google Scholar] [CrossRef]
- Palomera-Arias, R. Passive Electromagnetic Damping Device for Motion Control of Building Structures. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices-Materials, Analysis, and Applications, 1st ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Zhang, C.; Chen, Z.; Wang, L. An investigation on the field strength and loading rate dependences of the hysteretic dynamics of magnetorheological dampers. Mech. Time-Depend. Mater. 2014, 19, 61–74. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, C.; Li, A. Experimental Investigation on the Mechanical Properties of Curved Metallic Plate Dampers. Appl. Sci. 2020, 10, 269. [Google Scholar] [CrossRef]
- Dominguez, A.; Sedaghati, R.; Stiharu, I. Modelling the hysteresis phenomenon of magnetorheological dampers. Smart Mater. Struct. 2004, 13, 1351–1361. [Google Scholar] [CrossRef]
- Jung, H.Y. Feasibility Study of Multifunctional Electromagnetic Damper for Vibration Control of Cable and Energy Harvesting. Ph.D. Thesis, Korea Advanced Institute of Science and Technology, Daejeon, Korea, 2018. [Google Scholar]
- Jung, H.Y.; Kim, I.H.; Jung, H.J. Feasibility Study of the Electromagnetic Damper for Cable Structures Using Real-Time Hybrid Simulation. Sensors 2017, 17, 2499. [Google Scholar] [CrossRef] [PubMed]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; John Wiley & Sons Ltd.: Chichester, UK, 1997. [Google Scholar]
- Zhao, Z.; Zhang, R.; Jiang, Y.; De Domenico, D.; Pan, C. Displacement-Dependent Damping Inerter System for Seismic Response Control. Appl. Sci. 2019, 10, 257. [Google Scholar] [CrossRef]
- Kim, J.B.; Jeong, S.S. Characteristics of linear reciprocating motor applying ferrite magnet. In Proceedings of the KIEE Summer Conference 2017, Jeollanam-do, Korea, 12–14 July 2017. [Google Scholar]
- Lee, J.; Lee, J.; Ha, J.I. On-line Tracking of Harmonic Torque Feedforward for Torque Ripple Reduction of PMSM. In Proceedings of the Power Electronics Annual Conference, Seoul, Korea, 22 November 2019. [Google Scholar]
- Kye, S. Regenerative Hybrid Electrodynamic Damper for Stay Cables. Ph.D. Thesis, Korea Advanced Institute of Science and Technology, Daejeon, Korea, 2020. [Google Scholar]
- Jung, S.J.; Lee, J. Characteristic Analysis and Test of IPMSM for e-4WD of the Hybrid Electric Vehicle. Trans. Korean Inst. Electr. Eng. 2016, 65, 777–784. [Google Scholar] [CrossRef]
- Glinka, T.; Bernatt, J. Asynchronous slip-ring motor synchronized with permanent magnets. Arch. Electr. Eng. 2017, 66, 199–206. [Google Scholar] [CrossRef]
- Basak, A.; Shirkoohi, G.H. Computation of magnetic field in DC brushless linear motors built with NdFeB magnets. IEEE Trans. Magn. 1990, 26, 948–951. [Google Scholar] [CrossRef]
- Park, Y.B.; Kim, J.W.; Lee, J.S. Study on Magnetic Property for Test Coil and Permanent Magnet. J. Korean Magn. Soc. 2016, 26, 154–158. [Google Scholar] [CrossRef]
- Kim, C.E.; Lee, S.H. Design and Analysis of Permanent Magnet Double-Sided Linear Synchronous Motor with Perpendicular Arrangement. J. Korean Inst. IIIum. Electr. Install. Eng. 2013, 27, 62–73. [Google Scholar] [CrossRef]
- Bianchi, N. Analytical Field Computation of a Tubular Permanent-Magnet Linear Motor. IEEE Trans. Magn. 2000, 36, 3798–3801. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J. Magnetic Force Enhancement Using Air-Gap Magnetic Field Manipulation by Optimized Coil Currents. Appl. Sci. 2019, 10, 104. [Google Scholar] [CrossRef]
- Pan, Q.; He, T.; Xiao, D.; Liu, X. Design and Damping Analysis of a New Eddy Current Damper for Aerospace Applications. Lat. Am. J. Solids Struct. 2016, 13, 1997–2011. [Google Scholar] [CrossRef][Green Version]
- Kim, R.E.; Seo, J.M.; Rhyu, S.H. Design and analysis of Permanent Magnet Motor without Shoes of Stator Teeth Considering Cogging Torque Reduction. In Proceedings of the 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016. [Google Scholar]
- Kim, J.M.; Cho, H.W.; Jang, S.M.; Jo, J.M.; Han, Y.J. Design and Characteristics Analysis on Linear Synchronous Motor with Long Stator and Phase Concentrated Winding. Trans. Korean Inst. Electr. Eng. 2014, 63, 54–62. [Google Scholar] [CrossRef][Green Version]
- Tomczuk, B.; Schroder, G.; Waindok, A. Finite-Element Analysis of the Magnetic Field and Electromechanical Parameters Calculation for a Slotted Permanent-Magnet Tubular Linear Motor. IEEE Trans. Magn. 2007, 43, 3229–3236. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, D.; Yan, X. Computation of Transient Thrust Force in a Tubular Linear Motor for Pumping Unit. In Proceedings of the 2008 World Automation Congress, Hawaii, HI, USA, 28 September–2 October 2008. [Google Scholar]
- Kye, S.; Jung, H.-J.; Jung, H.-Y. Experimental Investigation on a Cable Structure Equipped with an Electrodynamic Damper and Its Monitoring Strategy through Energy Harvesting. Sensors 2019, 19, 2631. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, X.; Li, L.; Wang, M. Analysis of Flux Linkage and Detent Force for a Modular Tubular Permanent Magnet Synchronous Linear Motor With Large Slots. IEEE Trans. Energy Convers. 2019, 34, 1532–1541. [Google Scholar] [CrossRef]
- Palomera-Arias, R.; Connor, J.J.; Ochsendorf, J.A. Feasibility study of passive electromagnetic damping systems. J. Struct. Eng. 2008, 134, 164–170. [Google Scholar] [CrossRef]
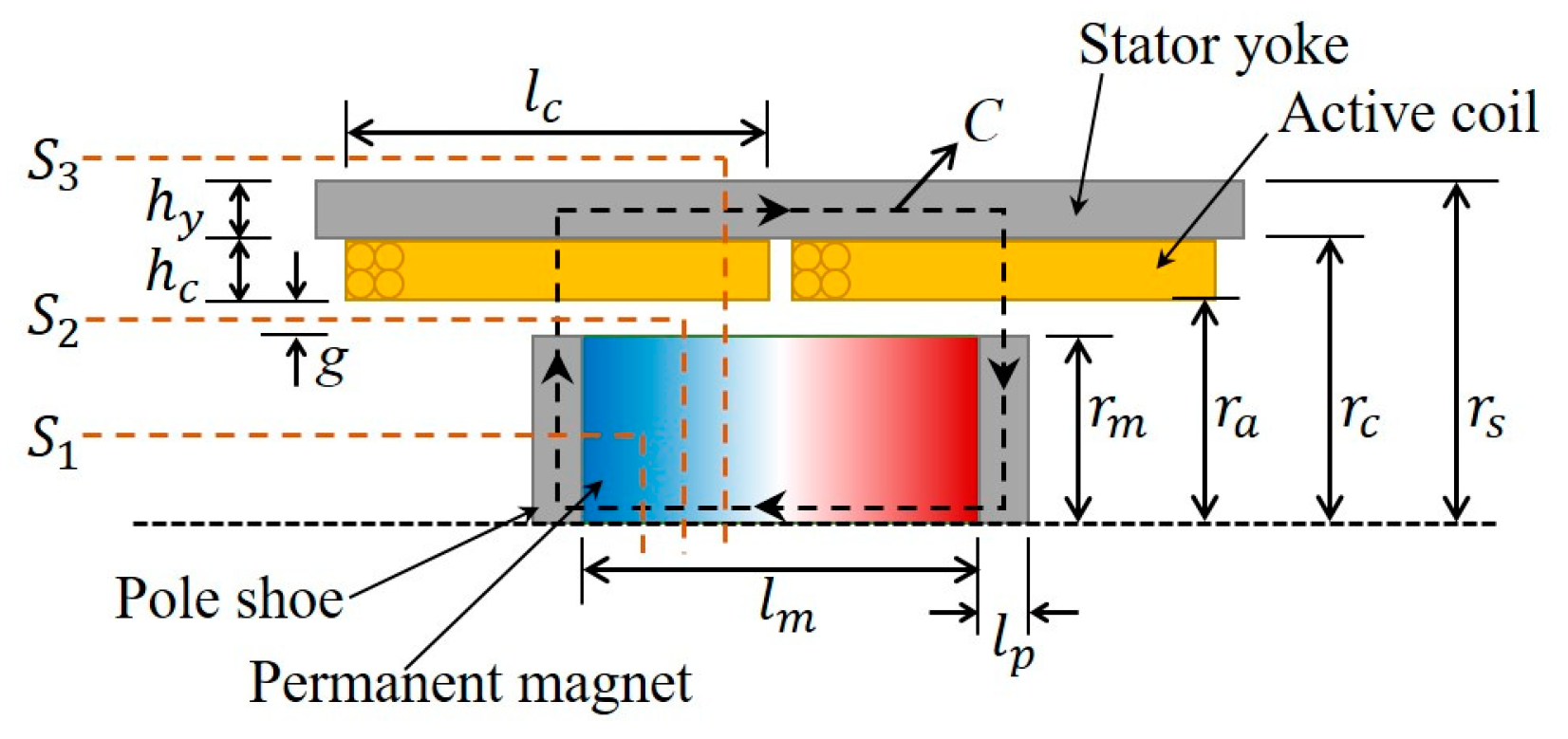




| Name | Symbol | Description |
|---|---|---|
| Magnet length | Actual length of the magnet (smaller than the pole pitch) | |
| Pole shoe thickness | Length excluding the magnetic length in the pole pitch | |
| Coil length | Axial length of each armature coil | |
| Mover radius | Outer radius of the magnet or pole pieces | |
| Armature radius | Inside radius of the armature | |
| Winding radius | Outside radius of the armature coil | |
| Stator yoke radius | Outside radius of the armature shell | |
| Air gap | Distance between the mover and armature windings | |
| Coil height | Height of the armature coil section | |
| Yoke thickness | Armature shell thickness |
| Name | Symbol | Value | Name | Symbol | Value |
|---|---|---|---|---|---|
| Magnet length | 0.06 m | Number of poles | 2 | ||
| Pole shoe thickness | 0.01 m | Wire diameter | 0.009 m | ||
| Air gap | 0.001 m | Coil turns | 1400 | ||
| Coil height | 0.02 m | Coil resistance | 27 Ω | ||
| Yoke thickness | 0.02 m | - | - | - |
| Type | Freq. | 4 Hz | 5 Hz | 6 Hz | 7 Hz | Remarks | |
|---|---|---|---|---|---|---|---|
| Amp. | |||||||
| Eddy current | 3 mm | 215.19 | 234.14 | 242.49 | 240.66 | - | |
| 6 mm | 421.47 | 458.95 | - | - | - | ||
| 9 mm | 615.98 | 669.36 | - | - | - | ||
| 12 mm | 798.31 | 826.67 | - | - | - | ||
| 15 mm | 935.05 | - | - | - | 100% | ||
| Coil | 3 mm | 125.22 | 136.64 | 144.81 | 145.25 | - | |
| 6 mm | 238.09 | 264.73 | - | - | - | ||
| 9 mm | 351.25 | 390.60 | - | - | - | ||
| 12 mm | 452.56 | 496.52 | - | - | - | ||
| 15 mm | 538.26 | - | - | - | 60% | ||
| Composite | 3 mm | 170.91 | 182.43 | - | - | - | |
| 6 mm | 335.91 | 367.56 | - | - | - | ||
| 9 mm | 506.64 | 550.21 | - | - | - | ||
| 12 mm | 670.79 | 729.11 | - | - | - | ||
| 15 mm | 842.62 | - | - | - | 88% | ||
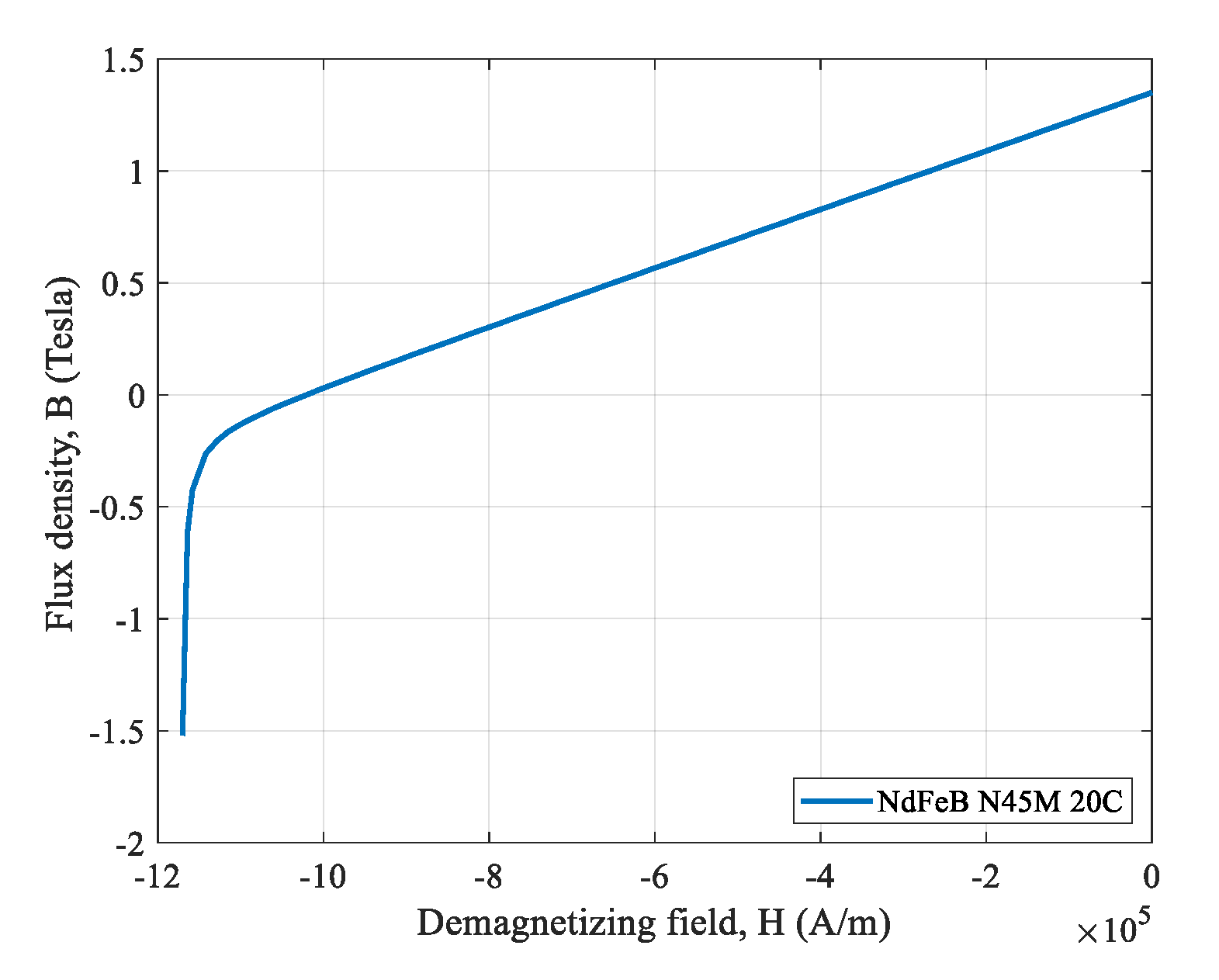
| Characteristics | Description | Values | Units |
|---|---|---|---|
| Br | Residual induction | 1.35 | T |
| Hc | Coercivity | −1,074,295.87 | A/m |
| BHmax | Maximum energy product | 36,2574.85 | J/m3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kye, S.; Jung, H.-J. Characteristic Test and Electromagnetic Analysis of Regenerative Hybrid Electrodynamic Damper for Vibration Mitigation and Monitoring of Stay Cables. Appl. Sci. 2020, 10, 6078. https://doi.org/10.3390/app10176078
Kye S, Jung H-J. Characteristic Test and Electromagnetic Analysis of Regenerative Hybrid Electrodynamic Damper for Vibration Mitigation and Monitoring of Stay Cables. Applied Sciences. 2020; 10(17):6078. https://doi.org/10.3390/app10176078
Chicago/Turabian StyleKye, Seungkyung, and Hyung-Jo Jung. 2020. "Characteristic Test and Electromagnetic Analysis of Regenerative Hybrid Electrodynamic Damper for Vibration Mitigation and Monitoring of Stay Cables" Applied Sciences 10, no. 17: 6078. https://doi.org/10.3390/app10176078
APA StyleKye, S., & Jung, H.-J. (2020). Characteristic Test and Electromagnetic Analysis of Regenerative Hybrid Electrodynamic Damper for Vibration Mitigation and Monitoring of Stay Cables. Applied Sciences, 10(17), 6078. https://doi.org/10.3390/app10176078





