A Personalised Emotion-Based Model for Relaxation in Virtual Reality
Abstract
:1. Introduction
2. Related Work
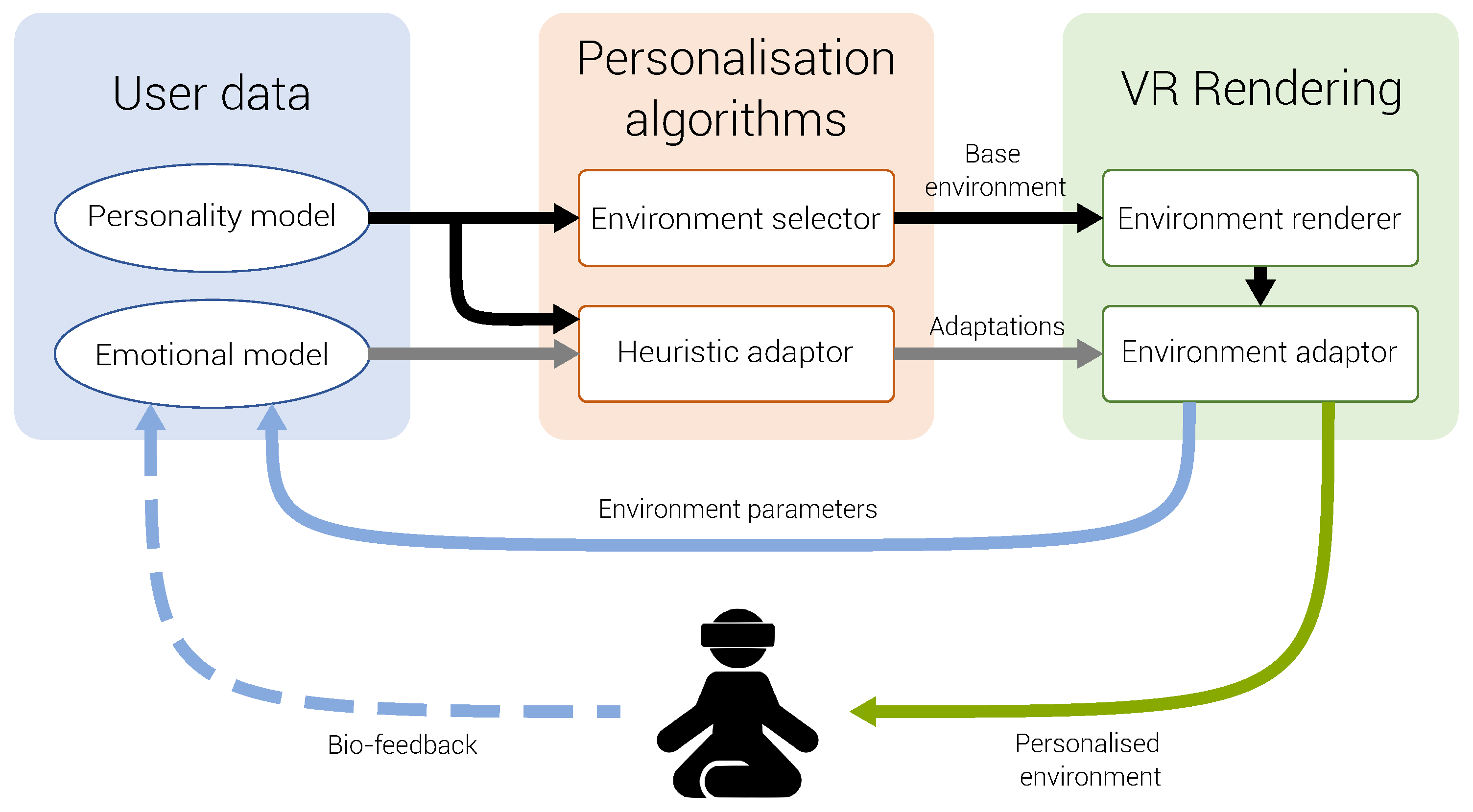
3. Methodology
3.1. Personality Model
3.2. Emotional Model
3.3. Heuristic Adaptor
4. Use Case Implementation
4.1. Personalisation Model and Environment Selector
4.2. Emotional Model
- dog
- fire
- natural lighting
- artificial lighting
- controlled breathing on
- controlled breathing off
- music
- light colour
5. Experimental Evaluation
5.1. Simulating Users
5.2. Results
5.2.1. Performance Analysis
5.2.2. Adaptation Order
5.3. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network. |
| HMD | Head Mounted Display. |
| ICU | Intensive Care Unit. |
| MILP | Mixed Integer Linear Programming. |
| MINLP | Mixed Integer Non-Linear Programming. |
| SVM | Support Vector Machine. |
| VE | Virtual Environment. |
| VR | Virtual Reality. |
| WHO | World Health Organisation. |
References
- Varvogli, L.; Darviri, C. Stress Management Techniques: Evidence-based procedures that reduce stress and promote health. Health Sci. J. 2011, 5, 74–89. [Google Scholar]
- Bell, A.S.; Rajendran, D.; Theiler, S. Job stress, wellbeing, work-life balance and work-life conflict among Australian academics. E J. Appl. Psychol. 2012, 8, 25–37. [Google Scholar] [CrossRef]
- Skakon, J.; Nielsen, K.; Borg, V.; Guzman, J. Are leaders’ well-being, behaviours and style associated with the affective well-being of their employees? A systematic review of three decades of research. Work Stress 2010, 24, 107–139. [Google Scholar] [CrossRef]
- Kinman, G.; Wray, S. Taking Its Toll: Rising Stress Levels in Further Education UCU Stress Survey 2014; University and College Union: London, UK, 2015. [Google Scholar] [CrossRef]
- Carder, M.; Turner, S.; McNamee, R.; Agius, R. Work-related mental ill-health and ’stress’ in the UK (2002–2005). Occup. Med. 2009, 59, 539–544. [Google Scholar] [CrossRef] [Green Version]
- Hanser, S.B. Music Therapy and Stress Reduction Research. J. Music Ther. 1985, 22, 193–206. [Google Scholar] [CrossRef]
- Steptoe, A.; Kivimäki, M. Stress and cardiovascular disease. Nat. Rev. Cardiol. 2012, 9, 360–370. [Google Scholar] [CrossRef]
- Schure, M.B.; Christopher, J.; Christopher, S. Mind-Body Medicine and the Art of Self-Care: Teaching Mindfulness to Counseling Students Through Yoga, Meditation, and Qigong. J. Couns. Dev. 2008, 86, 47–56. [Google Scholar] [CrossRef]
- Trappey, A.; Trappey, C.V.; Chang, C.M.; Kuo, R.R.; Lin, A.P.; Nieh, C. Virtual Reality Exposure Therapy for Driving Phobia Disorder: System Design and Development. Appl. Sci. 2020, 10, 4860. [Google Scholar] [CrossRef]
- Pizzoli, S.F.M.; Mazzocco, K.; Triberti, S.; Monzani, D.; Alcañiz Raya, M.L.; Pravettoni, G. User-Centered Virtual Reality for Promoting Relaxation: An Innovative Approach. Front. Psychol. 2019, 10, 479. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, A.; Sepúlveda-Muñoz, D.; Gil-Agudo, A.; de los Reyes Guzmán, A. Serious Game Platform with Haptic Feedback and EMG Monitoring for Upper Limb Rehabilitation and Smoothness Quantification on Spinal Cord Injury Patients. Appl. Sci. 2020, 10, 963. [Google Scholar] [CrossRef] [Green Version]
- Lee, L.N.; Kim, M.J.; Hwang, W.J. Potential of Augmented Reality and Virtual Reality Technologies to Promote Wellbeing in Older Adults. Appl. Sci. 2019, 9, 3556. [Google Scholar] [CrossRef] [Green Version]
- Valmaggia, L.R.; Latif, L.; Kempton, M.J.; Rus-Calafell, M. Virtual reality in the psychological treatment for mental health problems: An systematic review of recent evidence. Psychiatry Res. 2016, 236, 189–195. [Google Scholar] [CrossRef] [Green Version]
- Emmelkamp, P.M.G. Effectiveness of cybertherapy in mental health: A critical appraisal. Stud. Health Technol. Inform. 2011, 167, 3–8. [Google Scholar]
- Meyerbröker, K.; Emmelkamp, P.M. Virtual reality exposure therapy in anxiety disorders: A systematic review of process-and-outcome studies. Depress. Anxiety 2010, 27, 933–944. [Google Scholar] [CrossRef]
- Sekhavat, Y.A.; Nomani, P. A Comparison of Active and Passive Virtual Reality Exposure Scenarios to Elicit Social Anxiety. Int. J. Serious Games 2017, 4, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Powers, M.B.; Emmelkamp, P.M. Virtual reality exposure therapy for anxiety disorders: A meta-analysis. J. Anxiety Disord. 2008, 22, 561–569. [Google Scholar] [CrossRef]
- Opriş, D.; Pintea, S.; García-Palacios, A.; Botella, C.; Szamosközi, Ş.; David, D. Virtual reality exposure therapy in anxiety disorders: A quantitative meta-analysis: Virtual Reality Exposure Therapy. Depress. Anxiety 2012, 29, 85–93. [Google Scholar] [CrossRef]
- Shah, L.B.I.; Torres, S.; Kannusamy, P.; Chng, C.M.L.; He, H.G.; Klainin-Yobas, P. Efficacy of the Virtual Reality-Based Stress Management Program on Stress-Related Variables in People With Mood Disorders: The Feasibility Study. Arch. Psychiatr. Nurs. 2015, 29, 6–13. [Google Scholar] [CrossRef]
- Soyka, F.; Leyrer, M.; Smallwood, J.; Ferguson, C.; Riecke, B.E.; Mohler, B.J. Enhancing stress management techniques using virtual reality. In Proceedings of the ACM Symposium on Applied Perception— SAP ’16, Anaheim, CA, USA, 22–23 July 2016; pp. 85–88. [Google Scholar] [CrossRef]
- Gerber, S.M.; Jeitziner, M.M.; Wyss, P.; Chesham, A.; Urwyler, P.; Müri, R.M.; Jakob, S.M.; Nef, T. Visuo-acoustic stimulation that helps you to relax: A virtual reality setup for patients in the intensive care unit. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Anderson, A.P.; Mayer, M.D.; Fellows, A.M.; Cowan, D.R.; Hegel, M.T.; Buckey, J.C. Relaxation with Immersive Natural Scenes Presented Using Virtual Reality. Aerosp. Med. Hum. Perform. 2017, 88, 520–526. [Google Scholar] [CrossRef]
- Hyland, M.E.; Halpin, D.M.; Blake, S.; Seamark, C.; Pinnuck, M.; Ward, D.; Whalley, B.; Greaves, C.J.; Hawkins, A.L.; Seamark, D. Preference for different relaxation techniques by COPD patients: Comparison between six techniques. Int. J. Chronic Obstr. Pulm. Dis. 2016, 11, 2315–2319. [Google Scholar] [CrossRef] [Green Version]
- Graffam, S.; Johnson, A. A comparison of two relaxation strategies for the relief of pain and its distress. J. Pain Symptom Manag. 1987, 2, 229–231. [Google Scholar] [CrossRef]
- Macnamara, C.L.; Cvejic, E.; Parker, G.B.; Lloyd, A.R.; Lee, G.; Beilharz, J.E.; Vollmer-Conna, U. Personalised relaxation practice to improve sleep and functioning in patients with chronic fatigue syndrome and depression: Study protocol for a randomised controlled trial. Trials 2018, 19, 371. [Google Scholar] [CrossRef] [Green Version]
- Maples-Keller, J.L.; Bunnell, B.E.; Kim, S.J.; Rothbaum, B.O. The Use of Virtual Reality Technology in the Treatment of Anxiety and Other Psychiatric Disorders. Harv. Rev. Psychiatry 2017, 25, 103–113. [Google Scholar] [CrossRef]
- Garcia-Ceja, E.; Riegler, M.; Nordgreen, T.; Jakobsen, P.; Oedegaard, K.J.; Tørresen, J. Mental health monitoring with multimodal sensing and machine learning: A survey. Pervasive Mob. Comput. 2018, 51, 1–26. [Google Scholar] [CrossRef]
- Egger, M.; Ley, M.; Hanke, S. Emotion Recognition from Physiological Signal Analysis: A Review. Electron. Notes Theor. Comput. Sci. 2019, 343, 35–55. [Google Scholar] [CrossRef]
- Healey, J.; Picard, R. Detecting Stress During Real-World Driving Tasks Using Physiological Sensors. IEEE Trans. Intell. Transp. Syst. 2005, 6, 156–166. [Google Scholar] [CrossRef] [Green Version]
- Miranda, D.; Calderón, M.; Favela, J. Anxiety detection using wearable monitoring. In Proceedings of the 5th Mexican Conference on Human-Computer Interaction—MexIHC ’14, Oaxaca, Mexico, 3–5 November 2014; pp. 34–41. [Google Scholar] [CrossRef]
- Lee, M.S.; Lee, Y.K.; Pae, D.S.; Lim, M.T.; Kim, D.W.; Kang, T.K. Fast Emotion Recognition Based on Single Pulse PPG Signal with Convolutional Neural Network. Appl. Sci. 2019, 9, 3355. [Google Scholar] [CrossRef] [Green Version]
- Domínguez-Jiménez, J.; Campo-Landines, K.; Martínez-Santos, J.; Delahoz, E.; Contreras-Ortiz, S. A machine learning model for emotion recognition from physiological signals. Biomed. Signal Process. Control 2020, 55, 101646. [Google Scholar] [CrossRef]
- Steimer, T. The biology of fear- and anxiety-related behaviors. Dialogues Clin. Neurosci. 2002, 4, 231–249. [Google Scholar]
- Sims, C.R. Rate–distortion theory and human perception. Cognition 2016, 152, 181–198. [Google Scholar] [CrossRef] [Green Version]
- Smolders, K.C.; de Kort, Y.A. Bright light and mental fatigue: Effects on alertness, vitality, performance and physiological arousal. J. Environ. Psychol. 2014, 39, 77–91. [Google Scholar] [CrossRef]
- Luenberger, D.G.; Ye, Y. Linear and Nonlinear Programming; International Series in Operations Research & Management Science; Springer International Publishing: Cham, Switzerland, 2016; Volume 228. [Google Scholar] [CrossRef]
- Manav, B. Color-emotion associations and color preferences: A case study for residences. Color Res. Appl. 2007, 32, 144–150. [Google Scholar] [CrossRef]
- Dana Lynn, C. Hearth and Campfire Influences on Arterial Blood Pressure: Defraying the Costs of the Social Brain through Fireside Relaxation. Evol. Psychol. 2014, 12, 147470491401200. [Google Scholar] [CrossRef]
- Friedmann, E.; Son, H. The Human–Companion Animal Bond: How Humans Benefit. Vet. Clin. N. Am. Small Anim. Pract. 2009, 39, 293–326. [Google Scholar] [CrossRef]
- Suied, C.; Drettakis, G.; Warusfel, O.; Viaud-Delmon, I. Auditory-Visual Virtual Reality as a Diagnostic and Therapeutic Tool for Cynophobia. Cyberpsychol. Behav. Soc. Netw. 2013, 16, 145–152. [Google Scholar] [CrossRef] [Green Version]
- Paulus, E.; Yusuf, F.; Suryani, M.; Suryana, I. Development and Evaluation on Night Forest Virtual Reality as Innovative Nyctophobia Treatment. J. Phys. Conf. Ser. 2019, 1235, 012003. [Google Scholar] [CrossRef] [Green Version]
- Heyse, J.; Jonge, T.D.; Torres Vega, M.; Backere, F.D.; De Turck, F. A personalized Virtual Reality Experience for Relaxation Therapy. In Proceedings of the 2019 Eleventh International Conference on Quality of Multimedia Experience (QoMEX), Berlin, Germany, 5–7 June 2019; pp. 1–3. [Google Scholar] [CrossRef] [Green Version]













| Full Name | Notation | Indoor | Outdoor | Description |
|---|---|---|---|---|
| Artificial light | x | Artificial light coming from light bulbs in the ceiling of the room. | ||
| Natural light | x | x | Natural light coming from the sun and moon. | |
| Light colour | x | The colour of the artificial light. The available colors are white and blue and any mixture of these two. | ||
| Fire | x | A simulation of a campfire. This also generates some artificial light. | ||
| Dog | x | x | A dog playing around. The dog can be either playing around further away or be near the user. | |
| Music | x | x | Some relaxation music or sounds are playing in the background. These are birds sounds for the indoor environments and soothing music for the indoor environments. | |
| Controlled breathing | x | An visual aid for a controlled breathing exercise is shown. |
| No. | Question | Possible Answers |
|---|---|---|
| 1 | Would you prefer an indoor or outdoor environment to relax? | [indoor, outdoor] |
| 2 | Could the presence of water help you to relax? | [yes, no] |
| 3 | Are you afraid of heights? | [yes, no] |
| 4 | What is you favourite season? | [summer, winter] |
| 5 | How does having a calm campfire nearby make you feel? | {relaxed, anxious} |
| 6 | How do you feel when a dog is in your presence? | {relaxed, anxious} |
| 7 | How does darkness make you feel? | {relaxed, anxious} |
| 8 | How do you find classical relaxation music? | {very relaxing, not relaxing at all} |
| 9 | Blue light gives you a relaxed feeling, do you agree? | {agree, disagree} |
| 10 | How afraid do you feel right now? | {not at all, very much} |
| 11 | How stressed do you feel right now? | {not at all, very much} |
| 12 | How aroused do you feel right now? | {not at all, very much} |
| Range | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| Id | Environment | Optimal Intensity | Description | |||||
|---|---|---|---|---|---|---|---|---|
| dg | py | nl | al | lc | ms | |||
| User | indoor | 0.9 | n/a | 0.9 | 0.9 | 0.9 | 0.9 | Dog lover; Afraid of darkness; Likes music and blue light. |
| User | outdoor | 0.9 | 0.9 | 0.9 | n/a | n/a | 0.9 | Dog lover; Afraid of darkness; Likes music and fire. |
| User | indoor | 0.5 | n/a | 0.5 | 0.5 | 0.5 | 0.5 | Neutral towards every adaptation. |
| User | outdoor | 0.5 | 0.5 | 0.5 | n/a | n/a | 0.5 | Neutral towards every adaptation. |
| User | indoor | 0.1 | n/a | 0.1 | 0.1 | 0.1 | 0.1 | Afraid of dogs; Loves darkness; Dislikes music and blue light. |
| User | outdoor | 0.1 | 0.1 | 0.1 | n/a | n/a | 0.1 | Afraid of dogs and fire; Loves darkness; Dislikes music. |
| User | indoor | 0.0 | n/a | 0.1 | 0.1 | 0.7 | 0.9 | Afraid of dogs; Loves darkness, music and blue light. |
| User | outdoor | 0.0 | 0.7 | 0.1 | n/a | n/a | 0.9 | Afraid of dogs; Loves darkness, music and fire. |
| User | indoor | 1.0 | n/a | 0.8 | 0.8 | 0.1 | 0.3 | Dog lover; Afraid of darkness; Dislikes music and blue light. |
| User | outdoor | 1.0 | 0 | 0.8 | n/a | n/a | 0.3 | Dog lover; Afraid of darkness and fire; Dislikes music. |
| User | indoor | 0.6 | n/a | 0.4 | 0.4 | 0.8 | 0.1 | Likes blue light; Dislikes music. |
| User | outdoor | 0.6 | 0.8 | 0.4 | n/a | n/a | 0.1 | Loves fire; Dislikes music. |
| No. | Sequence | Average Relaxation | Final Relaxation | |||
|---|---|---|---|---|---|---|
| 1 | dg | nl | ms | py | 0.894 | 1 |
| 2 | dg | nl | py | ms | 0.890 | 1 |
| 3 | nl | dg | ms | py | 0.884 | 1 |
| 4 | dg | ms | nl | py | 0.881 | 1 |
| 5 | nl | dg | py | ms | 0.880 | 1 |
| 6 | ms | dg | nl | py | 0.875 | 1 |
| 7 | nl | ms | dg | py | 0.874 | 1 |
| 8 | nl | py | dg | ms | 0.865 | 1 |
| 9 | dg | py | nl | ms | 0.864 | 1 |
| 10 | ms | nl | dg | py | 0.861 | 1 |
| 11 | dg | ms | py | nl | 0.856 | 1 |
| 12 | nl | ms | py | dg | 0.855 | 1 |
| 13 | nl | py | ms | dg | 0.855 | 1 |
| 14 | dg | py | ms | nl | 0.850 | 1 |
| 15 | py | dg | nl | ms | 0.850 | 1 |
| 16 | ms | dg | py | nl | 0.850 | 1 |
| 17 | py | nl | dg | ms | 0.844 | 1 |
| 18 | ms | nl | py | dg | 0.842 | 1 |
| 19 | py | dg | ms | nl | 0.836 | 1 |
| 20 | ms | py | dg | nl | 0.836 | 1 |
| 21 | py | nl | ms | dg | 0.834 | 1 |
| 22 | py | ms | dg | nl | 0.831 | 1 |
| 23 | ms | py | nl | dg | 0.825 | 1 |
| 24 | py | ms | nl | dg | 0.820 | 1 |
| No. | Sequence | Average Relaxation | Final Relaxation | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | lc | dg | ms | cb | nl | al | 0.782 | 1.000 |
| … | ||||||||
| 72 | ms | nl | dg | cb | lc | al | 0.736 | 1.000 |
| 73 | lc | dg | ms | cb | al | nl | 0.793 | 0.996 |
| … | ||||||||
| 221 | dg | nl | al | cb | ms | lc | 0.759 | 0.982 |
| … | ||||||||
| 276 | ms | al | nl | dg | cb | lc | 0.751 | 0.982 |
| 277 | dg | al | lc | ms | cb | nl | 0.793 | 0.972 |
| … | ||||||||
| 360 | al | ms | nl | dg | cb | lc | 0.745 | 0.972 |
| 361 | lc | nl | ms | al | cb | dg | 0.719 | 0.858 |
| … | ||||||||
| 528 | cb | ms | al | nl | dg | lc | 0.622 | 0.858 |
| 529 | lc | nl | al | cb | dg | ms | 0.720 | 0.848 |
| … | ||||||||
| 660 | cb | al | ms | nl | dg | lc | 0.621 | 0.848 |
| 661 | al | lc | nl | ms | cb | dg | 0.719 | 0.838 |
| … | ||||||||
| 720 | al | cb | ms | nl | dg | lc | 0.644 | 0.838 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heyse, J.; Torres Vega, M.; De Jonge, T.; De Backere, F.; De Turck, F. A Personalised Emotion-Based Model for Relaxation in Virtual Reality. Appl. Sci. 2020, 10, 6124. https://doi.org/10.3390/app10176124
Heyse J, Torres Vega M, De Jonge T, De Backere F, De Turck F. A Personalised Emotion-Based Model for Relaxation in Virtual Reality. Applied Sciences. 2020; 10(17):6124. https://doi.org/10.3390/app10176124
Chicago/Turabian StyleHeyse, Joris, Maria Torres Vega, Thomas De Jonge, Femke De Backere, and Filip De Turck. 2020. "A Personalised Emotion-Based Model for Relaxation in Virtual Reality" Applied Sciences 10, no. 17: 6124. https://doi.org/10.3390/app10176124
APA StyleHeyse, J., Torres Vega, M., De Jonge, T., De Backere, F., & De Turck, F. (2020). A Personalised Emotion-Based Model for Relaxation in Virtual Reality. Applied Sciences, 10(17), 6124. https://doi.org/10.3390/app10176124







