Optimal Scheduling Strategy of Building Integrated Photovoltaic Microgrid Considering Virtual Energy Storage

Abstract

Building integrated photovoltaic (BIPV) is one of the most efficient ways to utilize renewable energy in buildings. However, the stochastic characteristic of PV power generation and load challenges the optimal dispatch of the BIPV. This paper proposes an optimal scheduling strategy of BIPV microgrid considering virtual energy storage (VES), which intends to further improve the operating economy of a BIPV microgrid. Firstly, existing research findings and gaps in this research area were analyzed. Then, the mathematical model of each unit in the system was created, meanwhile, the air conditioner-based VES (ACVES) model and electric water heater-based VES (EWHVES) model are built by exploiting the heat/cold storage capability of building and the electric water heater, respectively. Next, the optimal scheduling model considering the VES is designed. Finally, the optimal scheduling model is solved by CPLEX to obtain the optimal scheduling strategy that reduces the operating cost of the system. Simulation results demonstrate that the proposed strategy can reduce the operating cost of the system. Furthermore, the VES shows the potential to replace the battery energy storage system.

1. Introduction

In recent years, with the increasing demand for energy, fossil fuel shortage and environmental aggravation are becoming more and more serious. Renewable energy can effectively solve the above issues as potential alternatives to fossil fuel, which have wide attention [1,2]. Building integrated photovoltaic (BIPV) is a system that integrates building and photovoltaic (PV) power generation by deploying photovoltaic arrays on the surface of a building, which intends to harvest power that is used for the building. Recently, BIPV is one of the most efficient ways to utilize renewable energy. In Europe, the potential of BIPV is estimated at more than 22% of the expected 2030 electricity demand, and other countries, including India, China, and Brazil, consider it to be an important option for generating electricity [3]. Government bodies in Germany, Spain, and France are promoting the BIPV by executing feed-in tariff systems, other developed countries such as Japan, USA, Australia have adopted financial subsidies as the main policy to develop BIPV [4]. The microgrid system based on BIPV shows the advantage of easy to control and with high energy utilization rate, which can provide reliable and high-quality electric energy for the electrical equipment in building [5]. Therefore, BIPV has become one of the most widely used forms of renewable energy in buildings. However, there is often a mismatch between the peak of photovoltaic (PV) generation and the pinnacle of the electricity demand for the building’s power system. More specifically, peak PV generation occurs at noon, while peak load demand generally occurs at other time-spans of a day [6]. Thus, the benefits of BIPV microgrid is reduced due to the phenomenon of solar curtailment or selling electricity to the main grid at a lower price. Furthermore, PV power generation shows the characteristics of randomness and intermittence, which may affect the stable operation and real-time power balance of the main grid [7]. The above problems can be effectively solved by installing a battery energy storage system. However, the battery shows the disadvantages of high investment cost and short life span [8]. Therefore, the concept of virtual energy storage (VES) has been widely researched. As a generalized form of energy storage, VES intends to make the controllable loads show a similar regulation function with the traditional energy storage system through proper dispatch of some controllable loads. For instance, an air conditioner (AC) can convert electrical energy into heat/cold energy that stored in buildings, and an electric water heater (EWH) can convert electrical energy into a heater that is stored in the water tank of EWH. The stored heat/cold energy could be changed by regulating the working states of these controllable loads. Therefore, these controllable loads can be treated as VES equipment in a microgrid. The working state of these controllable loads can be directly controlled by a dispatching center or guided by economic measures (e.g., real-time electricity price). Generally, the power consumption of AC accounts for 30–55% of the whole building [9], EWH and refrigerators are also essential electrical appliances in every home, hence VES has a wide range of applications. For example, in residential communities, the controllable loads of AC, refrigerators, and EWH can be aggregated and regulated by smart meters to provide VES utility. In commercial buildings, central AC and EWH can also be directly controlled to provide VES utility. On the premise of ensuring user comfort and privacy, VES shows great practical value as they can bring huge social and economic benefits. The optimal scheduling of the microgrid, considering controllable load, is also known as demand response (DR).

DR is a significant way for the new-generation energy systems to cope with the randomness and intermittence of renewable energy generation as well as load fluctuation. On the one hand, DR can effectively reduce the peak load of the power system and delay the investments required for new generation units and transmission lines. On the other hand, DR can improve the consumption of renewable energy and reduce the adjustment and start-up/shut-down costs of thermal power units during the off-peak periods [10]. Generally, there are two kinds of DR, such as price-based DR and incentive-based DR [11]. The research content of this paper belongs to price-based DR. Existing research on DR mainly focuses on two aspects: the optimal operation of the power system considering DR, and the optimal strategy for customers to participate in DR according to external signals [10].

In this paper, firstly, the ACVES model and EWHVES model are built by exploiting the heat/cold storage capability of building and the electric water heater, respectively. In a building, due to the insulating properties of the building walls, the heat exchange between the interior and exterior is a slow process, the indoor temperature will not change rapidly relative to the electrical characteristics. Thus, during periods of low electricity prices, it is possible to increase the power consumption of AC to provide more cool/warm air to the building, which can be used in the following time intervals with higher electricity prices and thus reduce the total costs. Thus, the AC can be operated through mimicking the charging and discharging characteristics of a storage system, while meeting the indoor comfort requirements. Similarly, based on the good thermal insulation of the water heater tank, the power consumption of the water heater is increased during the low electricity price period, and the excess hot water is stored in the water tank for usage during the high electricity price period. Based on the above analysis, the ACVES and EWHVES model is built in this paper. Then, the optimal scheduling model considering the VES is established. The objective function is built through considering the system’s optimal scheduling, which aims at the lowest daily operating cost of the BIPV microgrid. The comprehensive constraints are also considered in the optimal model, which includes the constraints of each unit device and the operating constraints of the microgrid, such as the charging/discharging power and capacity constraints of the batteries, indoor temperature comfort zone constraints, power balance constraints, etc. Finally, CPLEX is applied to solve the optimal scheduling model.

In this paper, in order to improve the operation efficiency of BIPV microgrid, an optimal scheduling strategy of BIPV microgrid considering virtual energy storage (VES) is proposed. The main objectives of this paper are as follows:

• The potential of VES is exploited to make them play a role similar to the battery storage system.
• The differences of charging/discharging characteristics between VES and battery storage system are analyzed and compared.
• The differences of AC and EWH that participate in the VES control are analyzed and compared.
• The performance of the proposed strategy is verified with different case studies for all the four different seasons.

2. Literature Review

Demand-side controllable loads (e.g., air conditioners, water heaters, and refrigerators, etc.) have the characteristics of large power consumption, rapid response, and flexibility. According to Zhang [12], a high-precision AC load aggregation model is established based on the second-order equivalent thermal parameter (ETP) model of the AC load, meanwhile, the AC cluster control strategy is designed to provide various demand response services such as frequency adjustment and peak shaving. According to Wang [13], the AC load is equivalent to a VES device base on the second-order equivalent thermal parameter model of the AC load, which improves the matching characteristics of the system, reduces the discharge depth and increases the life of the battery. However, model parameters based on the ETP are not easy to obtain, which increases the complexity of research. The relationship between the amount of cooling supplied by the AC, the heat storage capacity of the building, and the dissipation of cooling is established according to the law of conservation of energy, the continuous change characteristic curve of the temperature in the AC room is obtained in the work of Peppanen [14]. The AC load modeling principle based on energy conservation is simple and does not require parameter identification. This paper uses this method to model the AC load and further establishes its VES model. According to Hao [15], a type of first-order explicit equation is utilized to describe the thermal dynamic modes of the EWH, and the optimal scheduling problem of EWH is solved using linear integer planning to reduce the system dispatch costs. In the work of Diao [16], a comprehensive model of the EWH is built, which switches between a one-node model and a two-node model depending on the situation and test its responses. According to Cheng [17], a VES model of a domestic refrigerator is developed based on its thermodynamic model, its control algorithm using the grid frequency as a regulation signal is proposed to mitigate the impact of uncertainties of DR. The aforementioned literature models typical controllable loads on the demand side and validates their utility for independent participation in DR. However, in actual situations, the demand side generally coexists with multiple controllable loads, and they can participate together to provide DR services.

In a residential microgrid, the floor radiant heating/cooling system is modeled as a VES system, and the operating cost of the residential microgrid is effectively reduced through optimal scheduling of the microgrid [18]. In a combined cooling, heating, and power microgrid, the VES of the building is considered in the optimal scheduling model, which improves the economic and environmental operational benefits [19]. In a hybrid energy microgrid, a VES system based on AC and buildings is established, and the daily operating cost of the microgrid is reduced through the charging/discharging management of the VES system [20]. With the increasing penetration of BIPV in urban commercial buildings, it is practical significance to improve the operating economics of BIPV microgrid. However, little literature has considered VES in BIPVmicrogrid to enhance its economics.

Therefore, in this paper, both the ACVES and EWHVES models were built and integrated into BIPV microgrid’s optimal scheduling model. Through proper control of these devices, they can operate as VES that with similar functions of a battery storage system, i.e., transferring energy among each time interval based on the price signals. Thus, the operation cost of a BIPV microgrid can be further reduced with the proposed control strategy.

3. BIPV Microgrid System

The structure of the BIPV microgrid system is shown in Figure 1.

The system is connected to the main grid. PV is the distributed generation in the system. The PV units are connected to the system via a smart inverter to increase the utilization of PV power and maximize the benefits of PV [21,22]. The battery is the energy storage equipment in the system. The loads in the system are divided into controllable loads and uncontrolled loads. Controllable loads include AC and EWH, which provide the VES effect for the system. Uncontrolled loads include lighting, computers, monitoring equipment, etc. The hot water demand is supplied by the EWH. The heat power and cold power are provided by AC. They all meet the demands of the system through a centralized supply.

The generated power of the PV depends on solar irradiance and the terminal voltage [23]. The PV power generation works in the maximum power point tracking (MPPT) mode, which is combined with one-cycle control method, its output power is described as follow [24]:

$$P_{\mathrm{pv}}=\frac{U_{\mathrm{o}}^2}{R_{\mathrm{s}}}(K+\frac{K_{\mathrm{g}}{T}_{\mathrm{s}}}{R_1{C}_1}-\frac{U_{\mathrm{c}}{T}_{\mathrm{s}}}{U_{\mathrm{g}}{R}_1{C}_1})$$

(1)

where $U_{\mathrm{g}}$ is the output voltage of PV. $U_{\mathrm{o}}$ is the effective value of grid-connected voltage of PV. $R_{\mathrm{s}}$ is the sampling resistance. $T_{\mathrm{s}}$ is the clock cycle of the flip-flop. K, $K_{\mathrm{g}}$, $U_{\mathrm{c}}$, $R_1$,$C_1$ are the parameters of one-cycle control.

Battery mathematic model can be represented as:

$$\left\{\begin{array}{c}\mathrm{charge}:{\mathrm{E}}_{b,t}=(1-\lambda )\times E_{\mathrm{b},t-1}+P_{\mathrm{b},t}\times \Delta t\times {\eta }_{\mathrm{bch}}\\ \mathrm{discharge}:{\mathrm{E}}_{b,t}=(1-\lambda )\times E_{\mathrm{b},t-1}+P_{\mathrm{b},t}\times \Delta t\times \frac{1}{{\eta }_{\mathrm{bdis}}}\end{array}\right.$$

(2)

where $E_{b,t}$ is the amount of energy stored in the battery. $P_{\mathrm{b},t}$ is the charging/discharging power of the battery. $\Delta t$ is the simulation time step. ${\eta }_{\mathrm{bch}}$ and ${\eta }_{\mathrm{bdis}}$ are the charging/discharging efficiency of the battery. $\lambda$ is the self-discharge rate of the battery. The monthly self-discharge rate of lead–acid batteries is about 3%, which can be ignored in daily optimal scheduling of microgrid [25].

AC consumes electric energy to meet the demand of heat and cold. Its mathematic model can be given as:

$$Q_{\mathrm{ec}}=P_{\mathrm{ec}}\times {\eta }_{\mathrm{ec}}$$

(3)

where $Q_{\mathrm{ec}}$ represents the output cold or heat power of AC. $P_{\mathrm{ec}}$ is the electrical power consumed by the AC. ${\eta }_{\mathrm{ec}}$ is the energy efficiency ratio of AC.

EWH consumes electric energy to provide hot water for the system. Its mathematic model is described as:

$$Q_{\mathrm{h}}=P_{\mathrm{h}}\times {\eta }_{\mathrm{h}},$$

(4)

where $Q_{\mathrm{h}}$ represents the output heat power of EWH. $P_{\mathrm{h}}$ is the electrical power consumed by the EWH. ${\eta }_{\mathrm{h}}$ is the energy efficiency ratio of EWH.

4. VES Model

4.1. ACVES Model

AC pumps cool or warm air into the building to change the indoor temperature, and the building has a certain heat and cold storage capacity, so the AC has VES effect. According to the conservation of energy, taking the summer cooling scenario as an example, the heat balance equation is described as [26]:

$$\rho \times C\times V\times \frac{\mathrm{d}{T}_{\mathrm{in}}}{\mathrm{d}\tau }=Q_{\mathrm{in}}+Q_{\mathrm{wall}}+Q_{\mathrm{win}}+Q_{\mathrm{sc}}-Q_{\mathrm{ec}}$$

(5)

where $Q_{\mathrm{wall}}=k_{\mathrm{wall}}\times F_{\mathrm{wall}}\times \left(T_{\mathrm{out}}-T_{\mathrm{in}}\right)$, $Q_{\mathrm{win}}=k_{\mathrm{win}}\times F_{\mathrm{win}}\times \left(T_{\mathrm{out}}-T_{\mathrm{in}}\right)$, $Q_{\mathrm{sc}}=I\times F_{\mathrm{win}}\times SC$. The left side of Equation (5) represents the change of indoor heat, the right side represents the various factors that cause the change. $\rho$ is the air density. C is the specific heat capacity of air. V is the volume of indoor air. $Q_{\mathrm{in}}$ is the indoor heat source, which comes from people and electric equipment. $Q_{\mathrm{wall}}$ is the heat transferred from the exterior walls of the building to its interior. $k_{\mathrm{wall}}$ is the heat transfer coefficient of the exterior walls, which indicates the heat passing through the exterior walls every second in case of the indoor and outdoor temperature difference is 1 Celsius in the steady-state. $F_{\mathrm{wall}}$ is the area of the exterior walls of the building. $T_{\mathrm{out}}$ is the outdoor temperature. $T_{\mathrm{in}}$ is the indoor temperature. $Q_{\mathrm{win}}$ is the heat transferred from building exterior windows to the interior. $k_{\mathrm{win}}$ is the heat transfer coefficient of the exterior windows, which means that during heat transfer steadily, the heat passing through the exterior windows every second when indoor and outdoor temperature difference is 1 Celsius. $F_{\mathrm{win}}$ is the area of the exterior windows of the building. $Q_{\mathrm{sc}}$ is the heat transferred from solar radiation. I is the solar radiation power, which means the heat received per square meter per second when the exterior windows of the building are perpendicular to the light. $SC$ is the shading coefficient and its value is related to the shading device [27].

Equation (5) shows that the indoor temperature can be regulated by adjusting the output cold/heat power of the AC can change. When the system did not adopt VES, AC maintains the indoor temperature at the set point. When the VES is employed, the working model of AC is changed, the indoor temperature can be adjusted within a certain rang by AC, which is the human body’s comfortable temperature zone. So the power consumed by AC is controllable, which makes the AC express the charging/discharging characteristic of the battery. Thus, the ACVES could participate in the economic optimal scheduling of microgrid like the battery. Define the charging/discharging power of ACVES as follows:

$$P_{\mathrm{ves}\_\mathrm{ec}}=P_{\mathrm{ec}\_\mathrm{ne}}-P_{\mathrm{ec}\_\mathrm{re}},$$

(6)

where $P_{\mathrm{ves}\_\mathrm{ec}}$ is the charging/discharging power of ACVES. $P_{\mathrm{ec}\_\mathrm{ne}}$ is the power consumed by AC when the VES method is not adopted. $P_{\mathrm{ec}\_\mathrm{re}}$ is the power consumed by AC when the VES method is adopted.

4.2. EWHVES Model

EWH is an important demand response resource [28]. The tank of EWH has good thermal insulation. Therefore, when the electricity price is low or the PV generates a lot of power, more water is heated and stored in the tank, which will be used at the time of high electricity price or peak power consumption. So, the EWH plays a similar role as the battery. While the hot water is stored in the tank, there is a phenomenon of heat dissipation. Assuming that the amount of heat stored in the hot water storage tank at time t is $E_{\mathrm{h},t}$, and the loss coefficient is $\delta$, the next time $E_{\mathrm{h},t+1}$ is described as:

$$E_{\mathrm{h},t+1}=(1-\delta )\times E_{\mathrm{h},t},$$

(7)

where $\delta$ is affected by the ambient temperature and the hot water temperature in the tank. $\delta$ ranges from 1.44% to 2.76%, its value in this article is set as 2% [29].

Modeling EWH as a VES equipment, define the charging/discharging power of EWHVES as follows:

$$P_{\mathrm{ves}\_\mathrm{h}}=P_{\mathrm{h}\_\mathrm{ne}}-P_{\mathrm{h}\_\mathrm{re}}$$

(8)

where $P_{\mathrm{ves}\_\mathrm{h}}$ is the charging/discharging power of EWHVES. $P_{\mathrm{h}\_\mathrm{ne}}$ is the power consumed by EWH when EWHVES isn’t adopted. $P_{\mathrm{h}\_\mathrm{re}}$ is the power consumed by EWH when employ VES.

5. Optimal Scheduling Model of BIPV Microgrid

5.1. Constraints

The system power balance constraint is given as:

$$P_{\mathrm{grid}}+P_{\mathrm{pv}}+P_{\mathrm{b}}=P_{\mathrm{ec}}+P_{\mathrm{h}}+P_{\mathrm{load}},$$

(9)

where $P_{\mathrm{grid}}$ is the power exchanged between the system and the main grid, $P_{\mathrm{grid}}\ge 0$ means system purchase electricity from main grid, $P_{\mathrm{grid}}<0$ means system sell electricity to main grid. $P_{\mathrm{load}}$ is the power consumed by the uncontrollable loads.

The heat dissipation and temperature change in the building is a slowly changing process. Differentiating Equation (5), the building heat balance equation could be expressed by the difference equation:

$$\rho \times C\times V\times \left(T_{\mathrm{in},t}-T_{\mathrm{in},t-1}\right)=\Delta t\times \left[Q_{\mathrm{in}}+Q_{\mathrm{wall}}+Q_{\mathrm{win}}+Q_{\mathrm{sc}}-Q_{\mathrm{ec}}\right].$$

(10)

Indoor temperature constraint is described as:

$$T_{\mathrm{in}\_\min }\le T_{\mathrm{in}}\le T_{\mathrm{in}\_\max }$$

(11)

where $T_{\mathrm{in}\_\min }$ and $T_{\mathrm{in}\_\max }$ is the upper and lower limits of indoor temperature, which will directly affect the comfort of indoor person and VES effect.

The upper and lower power constraints of system equipment are described as:

$$\left\{\begin{array}{c}{P}_{\mathrm{grid}\_\min }\le P_{\mathrm{grid}}\le P_{\mathrm{grid}\_\max }\\ P_{\mathrm{b}\_\min }\le P_{\mathrm{b}}\le P_{\mathrm{b}\_\max }\\ P_{\mathrm{ec}\_\min }\le P_{\mathrm{ec}}\le P_{\mathrm{ec}\_\max }\\ P_{\mathrm{h}\_\min }\le P_{\mathrm{h}}\le P_{\mathrm{h}\_\max }\end{array}\right.$$

(12)

The upper and lower capacity constraints of System equipment are described as:

$$\left\{\begin{array}{c}{E}_{\mathrm{b}\_\min }\le E_{\mathrm{b}}\le E_{\mathrm{b}\_\max }\\ E_{\mathrm{h}\_\min }\le E_{\mathrm{h}}\le E_{\mathrm{h}\_\max }\end{array}\right.,$$

(13)

where $P_{\mathrm{grid}\_\min }$ and $P_{\mathrm{grid}\_\max }$ is the lower and upper limits of power exchange between the system and the main grid. $P_{\mathrm{b}\_\min }$ and $P_{\mathrm{b}\_\max }$ is the lower and upper limits of charging/discharging power of battery. $P_{\mathrm{ec}\_\min }$, $P_{\mathrm{ec}\_\max }$, $P_{\mathrm{h}\_\min }$ and $P_{\mathrm{h}\_\max }$ are the lower and upper limits of power consumption of AC and EWH respectively.$E_{\mathrm{b}\_\min }$, $E_{\mathrm{b}\_\max }$, $E_{\mathrm{h}\_\min }$ and $E_{\mathrm{h}\_\max }$ are the lower and upper limits of energy storage capacity of battery and tank.

5.2. The Objective Function

This article aims at the minimum daily operating cost of the system, meanwhile, it also considers the comfort of the staff in the building. Therefore, the objective function contains three parts; the first is the economic cost, including the cost of power purchase from the main grid and the maintenance cost of each equipment in the system, the second is the penalty caused by the comfort decrease of the staff, the last is the revenue of selling electricity to the main grid. In summary, the objective function of the system is developed as:

$$C=min\sum _{t=1}^N\left(C_1+C_2+C_3-C_4\right)$$

(14)

where $C_1$ is the cost of purchasing power. When $P_{\mathrm{grid}}\ge 0$, $C_1=c_{\mathrm{grid}}\times \left|P_{\mathrm{grid},t}\right|\times \Delta t$. When $P_{\mathrm{grid}}<0$, $C_1=0$. $c_{\mathrm{grid}}$ is the real-time electricity price. $C_2=c_{\mathrm{pv}}\times P_{\mathrm{pv},t}+c_{\mathrm{b}}\times \left|P_{\mathrm{b},t}\right|+{\mathrm{c}}_{\mathrm{ec}}\times P_{\mathrm{ec},t}+c_{\mathrm{h}}\times P_{\mathrm{h},t}$, which is the maintenance cost of each device in the system. $c_{\mathrm{pv}}$, $c_{\mathrm{b}}$, $c_{\mathrm{ec}}$ and $c_{\mathrm{h}}$ is the operating and maintenance cost of PV, battery, AC, and EWH per hour per kilowatt, respectively. $C_3=\gamma \times \left|T_{\mathrm{in},t}-T_{\mathrm{set},t}\right|$, which is the penalty term of staff comfort. $\gamma$ is the penalty factor. $T_{\mathrm{set},t}$ is the temperature setting of AC without VES. $C_4$ is the revenue from selling electricity to the main grid. When $P_{\mathrm{grid}}<0$, $C_4=0.2\times c_{\mathrm{grid}}\times \left|P_{\mathrm{grid},t}\right|\times \Delta t$. When $P_{\mathrm{grid}}\ge 0$, $C_4=0$. Set the price of electricity sold to main grid at 0.2 times the real-time price.

In this paper, we first establish the mathematical model of each unit in the system according to its working principle and describe its operating state. For example, the mathematical model of a battery accurately describes the charging/discharging process of the battery, and ACVES accurately describes the heat transfer process inside and outside the building. These models precisely describe the changes in their state and provide an approximate simulation of their actual operation. Each unit in the microgrid has physical operating limits, such as the maximum capacity of the battery. At the same time, the operation of the system also has various constraints, such as the power balance constraints, heat transfer balance constraints inside and outside the building, and comfort constraints for indoor staff. The system has to operate within these constraints and achieve its optimization goals. For this purpose, this paper develops an optimal scheduling model of the system, which contains a set of constraints and an economic objective function. It should be noted that the optimization model proposed in this paper can also be applied and modified by similar studies. For example, the VES model and control strategy can also be applied to a hybrid AC/DC microgrid that contains more dispatchable loads and distributed generators. Furthermore, the ancillary services, such as fast frequency response, can also be provided through proper control of the VES in an AC microgrid.

6. Case Data and Simulation Results

6.1. Case Data

In this paper, an office building in a certain region was taken as an example to conduct day-ahead optimal scheduling for the BIPV microgrid, and the dispatch interval is 1 h. In order to obtain the energy consumption data inside the building, the building energy consumption model is established by the software DEST. The model is established as a three-story office building, its long side equal to 30 meters, wide side equal to 20 meters and each floor is 3.3 m high. The solar photovoltaic panels are installed on the roof and the south-facing window sunshade. Other relevant parameters are shown in

Table 1. Parameters of building.

Parameters	${\mathit{K}}_{\mathbf{wall}}$/(W/m2·K)	${\mathit{K}}_{\mathbf{win}}$/(W/m2·K)	${\mathit{F}}_{\mathbf{wall}}$/(m2)	${\mathit{F}}_{\mathbf{wall}}$/(m2)
Value	1.092	2.800	1000	450

[30].

In this paper, a series of relevant data including real-time electricity price, PV generation power, light intensity, building electrical load demand, cold/heat load demand, and hot water load demand were obtained from the DEST result report and an open-source website Elia [31]. These data were appropriately processed and used for the simulation analysis in this paper.

Table 2. Parameters of microgrid operation.

Parameters	Upper Limit	Lower Limit
$P_{\mathrm{pv}}$/kW	125	0
$P_{\mathrm{h}}$/kW	25	0
$P_{\mathrm{ec}}$/kW	25	0
$P_{\mathrm{b}}$/kW	30	−30
$P_{\mathrm{grid}}$/kW	150	−150
$E_{\mathrm{b}}$/(kWh)	160	20
$E_{\mathrm{h}}$/(kWh)	20	0

and

Table 3. Parameters of microgrid equipment.

Parameters	Magnitude
$c_{\mathrm{b}}$/($/(kWh))	0.0038
$c_{\mathrm{ec}}$/($/(kWh))	0.0017
$c_{\mathrm{h}}$/($/(kWh))	0.0017
$c_{\mathrm{pv}}$/($/(kWh))	0.0140
${\eta }_{\mathrm{ec}}$	3.80
${\eta }_{\mathrm{h}}$	3.80
${\eta }_{\mathrm{bch}}$	0.95
${\eta }_{\mathrm{bdis}}$	0.95

list related parameters of the microgrid operation and equipment. The inlet water temperature of the EWH is 25 Celsius, the outlet water temperature is 75 Celsius, which is injected into the water tank. The maximum capacity of the water heater tank is 1300 L, and the maximum temperature of the water stored in the tank is 75 Celsius. Therefore the equivalent heat capacity of tank is 20 kWh approximately. The AC coverage area in the building is about 1300 ${\mathrm{m}}^2$. The air density is 1.2 $\mathrm{kg}/{\mathrm{m}}^3$.

6.2. Optimal Scheduling Result Analysis

This paper first takes the summer cooling scenario as an example for simulation. In the scenario, four cases are established: case 1: VES is not considered; case 2: Only EWHVES is considered; case 3: only ACVES is considered; case 4: both EWHVES and ACVES are considered. Then, in order to verify the effectiveness of the strategy proposed in this paper, simulations are performed in different seasons.

6.2.1. The Summer Cooling Scenario Data

Real-time electricity prices can effectively guide the user’s behavior of electricity consumption [32]. The typical daily real-time electricity price changes in this region in summer are shown in Figure 2.

Solar radiation passing through the windows changes the indoor temperature. The heat transferred to the interior of the building is determined by solar radiation power, window area and shading coefficient. Considering the angle of solar exposure and visor, the shading coefficient is set as 0.3. The variation curves of solar radiation power and outdoor temperature in summer are shown in Figure 3.

Set the office building from 8:00 to 21:00 as working hours. The cold/heat load and hot water load demand generated during working hours. The PV generation, load demand and indoor heat source heating of the day-ahead prediction are shown in Figure 4.

6.2.2. The Summer Cooling Scenario Simulation Analysis

Case 1: VES is not considered

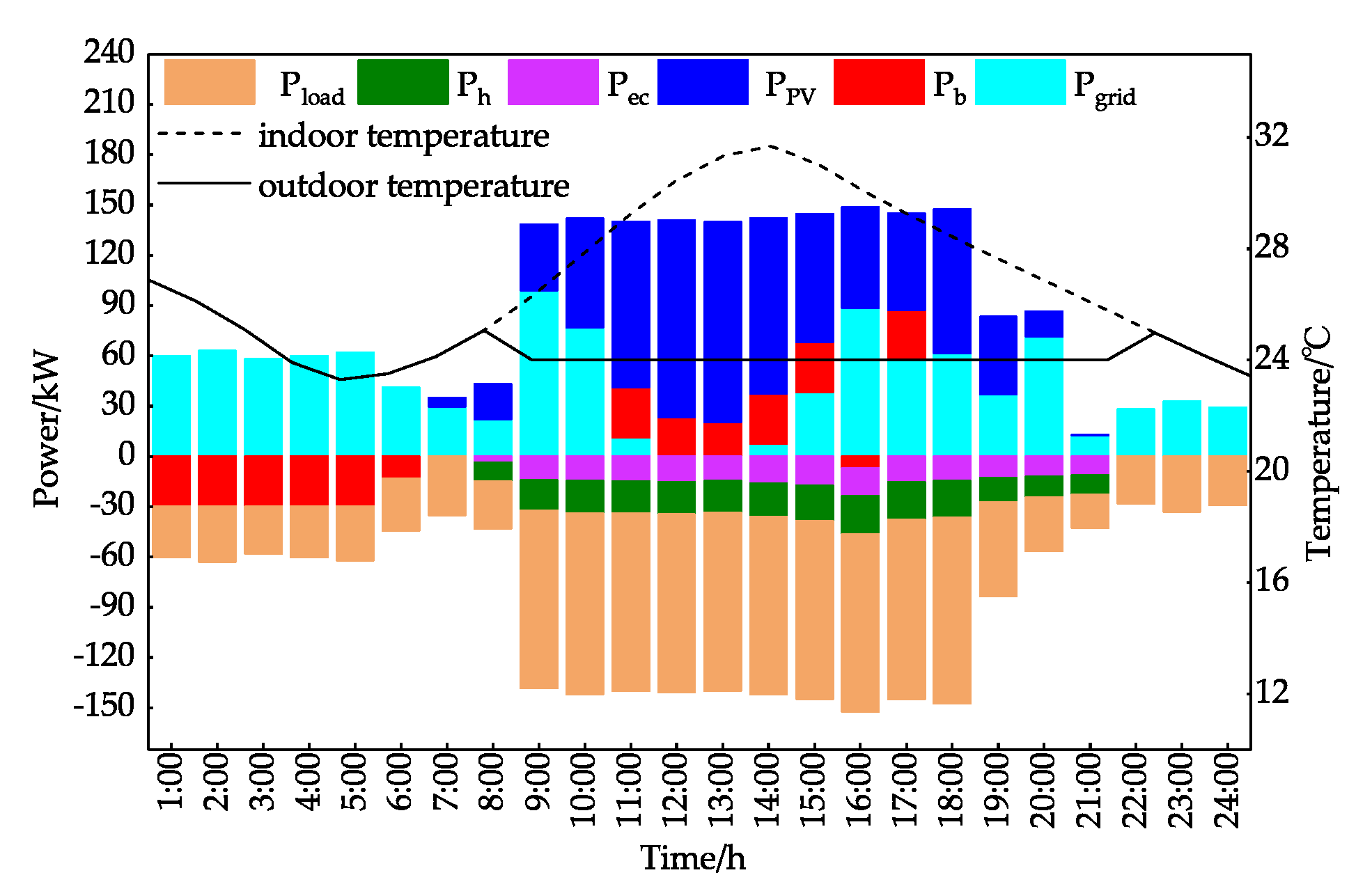
VES is not adopted in the system, which means that the AC injects cool air into the building to maintain the indoor temperature at 24 Celsius, and the water heater adopts a ready-to-use model, not equipped with a tank. Figure 5 depicts the optimal scheduling results in the summer.

In Figure 5, the power ≥0 represents the output power of PV, battery and the main grid. The power <0 represents the power consumed by loads, the charging power of the battery and the power sold to the main grid. Figure 5 shows that during non-working hours, due to the low electricity price, the system purchases electricity from the main grid to meet the electrical load demand in the building and charges the battery. During working hours, PV generator provides power for the system, the cost of purchasing electricity is reduced. Most of the working time, the battery is in the discharge state, but at 16:00, because the price of electricity is relatively lower than the adjacent time, the battery is charged. The cost of running the system in a day when VES is not considered is $165.06.

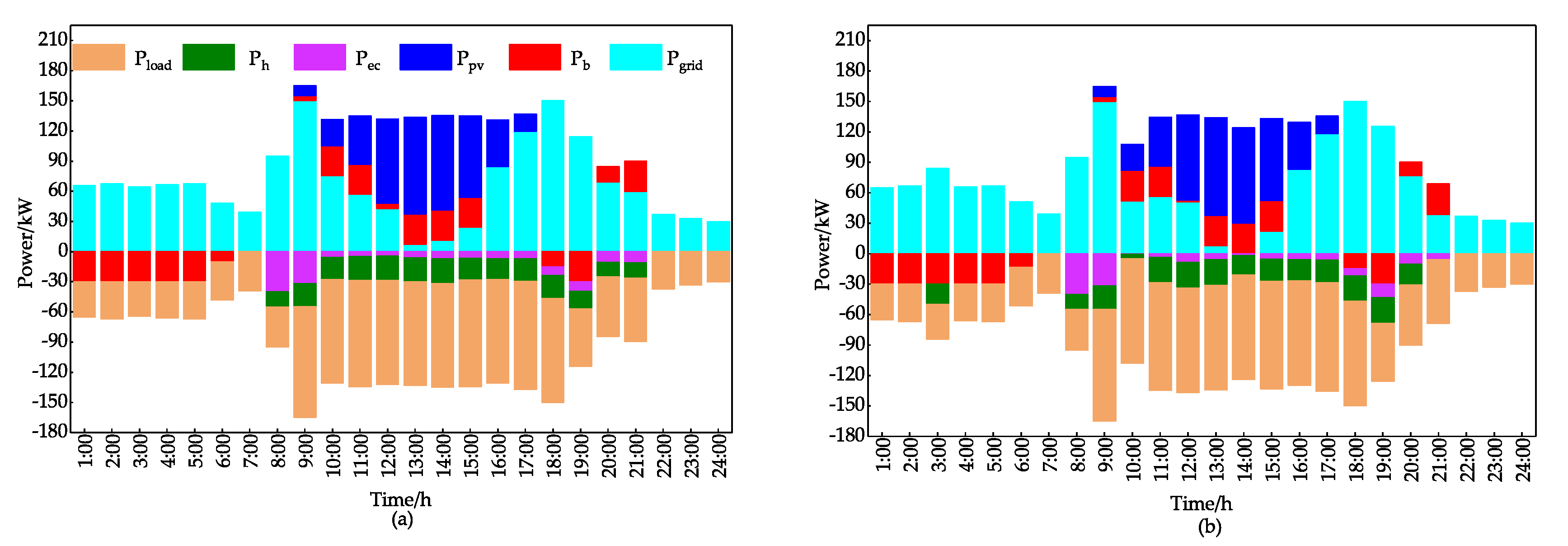
Case 2: Only EWHVES is considered

As shown in Figure 6, which plots the optimal scheduling result of BIPV microgrid when only EWHVES is considered in summer.

As can be seen from Figure 6, at 3:00, due to the low electricity price, the EWH works and inject hot water into the tank for use during the working hours. At 11:00, due to the high electricity price, the power exchanged between the system and the main grid changes to 0, which reduces the system’s electricity cost. Figure 7 shows the EWHVES and battery charging/discharging power and their state of charge.

As shown in Figure 7, power ≤0 represents charging, and power >0 represents discharging. During non-working hours, the electricity price is low, both the battery and the WHVES are charged, meanwhile, both reach the maximum state of charge. During the working period, the battery discharges. Due to its limited capacity, the EWHVES is in a discharged state at a high electricity price time, and in a charged state at low electricity price time. As mentioned above, both of them charge when the electricity price is low, and discharge when the electricity price is high, which play the role of peak load shaving. The BIPV microgrid costs $152.46 operating a day when only the EWHVES is adopted, which reduces 7.63% than that in case of without VES.

In order to prove that the EWHVES can replace the battery to a certain extent, reduce part of the capacity of the battery to simulation, the result shows that when reducing 78 kWh capacity of the battery, the system has the same cost as the scene where the VES is not considered.

Case 3: Only ACVES is considered

The AC is turned on only during working hours. The indoor temperature is adjusted from the original fixed 24 Celsius to the upper and lower limit of 22–26 Celsius. The penalty factor of user comfort is 0.1. The optimal scheduling results of BIPV microgrid adopts ACVES is shown in Figure 8.

As the figure above shows, at 11:00 and 17:00 with higher electricity price, the AC only consumes little electric energy to keep the room temperature in the comfort zone, which plays the role of peak load shaving and reduces the operating cost of the system. The BIPV microgrid costs $152.46 a day when only ACVES is considered, which is 5.67% less than the operating cost of the microgrid without VES. The charging/discharging of ACVES and indoor/outdoor temperature variation are shown in Figure 9.

AS can be seen in Figure 9, at 10:00 and 16:00 with higher electricity price, the ACVES is charged and the indoor temperature drops to 22 Celsius, next moment, the ACVES is discharged and the indoor temperature rises to 26 Celsius. The ACVES is charged when the electricity price is low, and discharged when the electricity price is high, playing a similar role to the battery. In order to illustrate that ACVES can supersede battery, reduce the certain capacity of battery to simulation, the result shows that when reducing 61 kWh capacity of the battery, the system has the same cost as the scene that the VES is not considered.

Compared with the EWH, the AC only need to adjust the indoor temperature to achieve VES, additional equipment is not required. However, ACVES is affected by weather, indoor temperature zone, building parameters and other factors, which cannot be quantified its capacity specifically. Moreover, the ACVES can only play its role in winter and summer, cannot provide stable VES utility. The WHVES is less affected by the external environment, and the energy storage utility is stable, but in the early stage of system construction, the tank equipment needs to be invested.

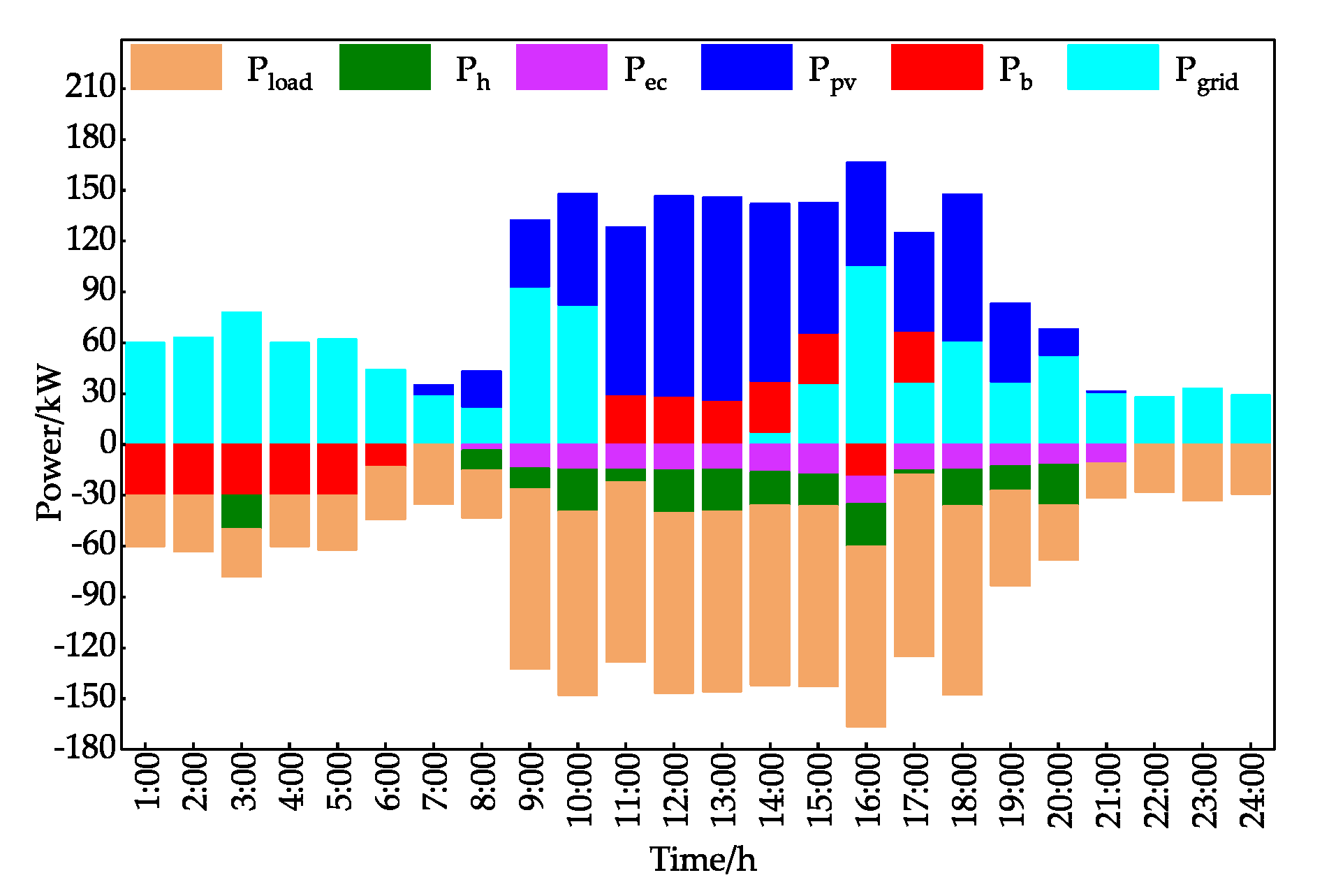
Case 4: Both EWHVES and ACVES are considered

In order to maximize the effectiveness of VES, the two types of VES are integrated into the BIPV microgrid for optimal scheduling. The results are shown in Figure 10.

The system costs $144.69 to operating for a day, which is 12.34% less than the operating cost of the microgrid without VES. We reduced the capacity of the battery and set the system to have the same daily operating cost as the system without VES. The simulation results show that VES has the effect of 115 kWh of battery capacity. The operating cost of the system under four scenarios is shown in

Table 4. Daily operating costs of the system under 4 scenarios.

Scenarios	Cost/$	Economize/$
Without VES	165.06	/
EWHVES	152.46	12.60
ACVES	155.70	9.36
EWHVES and ACVES	144.69	20.37

.

Table 4 summarizes the cost of the system under four scenarios. It is clear that VES can reduce the operating cost of the system. When two kinds of VES are integrated into the system, the cost saved is not the linear superposition of the effect when they participate in the system separately.

6.3. Simulations Result and Analysis in Different Seasons

To verify the effectiveness of the proposed strategy, this paper selects the typical days in spring, autumn, and winter for simulation. The data source is the same as that in summer.

The simulation results in the spring are shown in Figure 11. In the spring, the AC is only turned on and heated at the lower temperatures of 8:00, 9:00, 20:00, and 21:00 due to the pleasant outdoor temperature. When VES is considered, the power consumed by the AC is further elevated due to the lower electricity price at the 8:00, and the building stores cool air for usage at the 9:00. In general, VES utility is provided by EWHVES primarily in the spring to reduce the operating costs of the system.

The simulation results in autumn are shown in Figure 12. In the autumn, the AC generally works on heating mode due to the lower temperatures. From 12:00 to 13:00, the outside temperature is comfortable and thus the AC is turned off. At 8:00, when the outside temperature is low, the AC works at its full capacity to raise the temperature in the building.

The simulation results in winter are shown in Figure 13. In the winter, PV generation decreases due to low irradiation, and the system purchases more power to increase the temperature in the building. Thus, the operating costs in winter are relatively high. At 8:00 and 9:00, the temperature in the building is very low, and thus the AC works at its full capacity to raise the temperature. In the following several hours, the solar radiation and the indoor heat sources can provide heat to the room. Thus, the air conditioner operates at lower power to maintain the indoor temperature within a comfort zone. Furthermore, with increased demand for hot water during the winter months, EWHVES offers more virtual energy storage utility.

Table 5. Daily operating costs of the system under 4 seasons.

Seasons	Without VES/$	With VES/$	Cost Reduction with VES
Spring	226.01	218.02	3.54%
Summer	165.06	144.69	12.34%
Autumn	228.71	214.84	6.06%
Winter	257.27	246.51	4.18%

shows the operating costs of the system under different seasons.

From Table 5, it can be seen that the proposed strategy is effective in reducing the operating costs of the system in all four seasons. Among them, the lowest operating costs are incurred during the summer months due to the high volume of photovoltaic generation. VES works best in the summer because the AC show great potential to provide VES in the summer.

7. Discussion

With the increasing penetration of BIPV in urban buildings, it is increasingly important to optimize the operation of a BIPV microgrid. This paper proposes an optimal scheduling strategy for BIPV microgrid considering multiple VES. The simulation results validate the effectiveness of the proposed strategy and provide ideas for future research.

Most of the existing literature studies focus on the participation of a single controllable load in the optimal scheduling of a microgrid, improving the operation economy of a microgrid or providing frequency response service, etc. In practice, controllable loads such as AC, EWH, and refrigerators often participate in demand response together. Therefore, in this paper, two VES models, i.e., ACVES and EWHVES, are developed and integrated into the optimal scheduling of a BIPV microgrid. At the same time, the charging/discharging characteristics between ACVES and EWHVES, EWHVES and battery were analyzed and compared. Thus, the integrated research of ACVES and EWHVES fills the gap and enriches the existing literature. Simulation results in different studies demonstrate that both ACVES and EWHVES are effective in reducing the operating cost of the system. When ACVES participated alone in the optimal scheduling of the system during the summer scenario, the operating costs were reduced by 5.67%, and indoor temperature comfort was maintained. A similar research approach to analyze the ACVES utility is also applied in [19], which shows similar results of this paper. When EWHVES participated alone in the optimal scheduling of the system in the summer scenario, the operating cost was reduced by 7.63%, which is in consistent with the findings shown in [15]. In this paper, there are two main new insights: (1) both ACVES and EWHVES can effectively reduce the operating cost of the system, and when they participate together, the cost reduction is not a linear superposition of their effects when they participate alone; (2) both ACVES and EWHVES play a similar role of battery energy storage system, but they show different energy storage principles due to different VES characteristics.

The simulations in this paper are based on day-ahead forecast data, and due to the forecast errors, the day-ahead planned operation strategy differs from the actual situation of the microgrid’s intra-day operation. The solution to this issue is either improving the forecast accuracy or performing intraday optimal scheduling.

In future work, we will study more VES characteristics of controllable loads and aggregate them together to provide VES utility. Besides, based on their different VES characteristics (e.g., storage quality, VES charging/discharging power, response speed, etc.) and our optimization goals (e.g., reduction of operating costs, providing frequency response, etc.), we will set their charging/discharging priorities to maximize the VES utility. In addition, we consider integrating VES into intraday optimal scheduling using methods such as model predictive control to cope with forecast uncertainty in real-time. In addition, how to aggregate massively different controllable loads and design their control algorithms to provide VES utility can also be a research point. At last, we will also research how to develop incentives for more controlled loads in homes and commercial buildings to provide VES utility, while ensuring user comfort and privacy.

8. Conclusions

An optimal scheduling strategy of BIPV microgrid considering VES is proposed in this paper. Firstly, the ACVES model and EWHVES model are built by exploiting the heat/cold storage capability of the building and the electric water heater, respectively. The ACVES and EWHVES are integrated into BIPVmicrogrid as flexible and controllable units for optimal scheduling. Then the optimal scheduling model containing the system operation constraints and the objective function is established. At last, the CPLEX solver is used to solve the proposed day-ahead optimal scheduling model, and the following main conclusions can be derived with the simulation analysis.

• The integration of both ACVES and EWHVES into the optimal scheduling model of the BIPV microgrid can effectively reduce the operating cost of the system by managing the charging/discharging of the VES in different seasons. When two kinds of VES are integrated together into the system, the cost saved is not the linear superposition of the effect when they participate in the system separately.
• Compared with ACVES, EWHVES shows more stable VES utility. The VES utility of EWHVES is primarily affected by the capacity of the water heater’s tank. The VES utility of ACVES is affected by a number of factors such as outdoor temperature, solar radiation, indoor heat sources, and seasonal variations. However, the ACVES shows great potential to provide VES utility in the summer.
• Through proper control of VES, the investment cost of the energy storage system can be significantly reduced. At the same time, the VES can replace the energy storage system and perform a similar function when its capacity is curtailed or the energy storage system fails.

The main contribution of this paper includes:

• An optimal scheduling strategy of BIPV microgrid considering VES is proposed, which provides new approaches to further improve its operating economy.
• The VES characteristics of ACVES and EWHVES are compared and analyzed to provide a reference for designing a better strategy in future work.
• This paper validates the effectiveness of VES in day-ahead optimization scheduling in different seasons, which provides a basis for its participation in real-time optimization scheduling.
• During the summer months, the operating costs of the system are significantly reduced due to the sufficient amount of PV power generation, and VES is also effective in reducing the operating costs of the system in different seasons, which can effectively promote government departments to formulate a series of policies to promote the development of BIPV and VES.