Parametric Estimation and Constraint Programming-Based Planning and Simulation of Production Cost of a New Product ^†

Abstract

Currently-used decision support solutions allow decision makers to estimate the cost of developing a new product, its production, and promotion, and compare the estimated cost to the target cost. However, these solutions are inadequate for supporting simulations of identifying conditions, by which the specific cost is reached. The proposed approach provides a framework for searching for possible variants towards reaching the target production cost. This paper is concerned with a prototyping problem of product development described in terms of a constraint satisfaction problem. The proposed method uses parametric estimation to identify relationships between variables, and constraint programming to search for project completion variants within the company’s resources and project requirements. The results of an experiment indicate that constraint programming provides effective search strategies for finding admissible solutions. Consequently, the proposed approach allows decision makers to obtain alternative scenarios within the limits imposed by the production process. In this, it outperforms current methods dedicated to the support of evaluating the total cost of a new product. The declarative approach presented in this paper is used to model the production cost; however, it can be effortlessly extended to other aspects of product development (e.g., product reliability).

1. Introduction

The new product development (NPD) process belongs to crucial processes in contemporary companies, which have to compete in a saturated market and by short product life cycles. Successful implementation of NPD projects affects the company’s profitability and survival. Unfortunately, many NPD projects either fail completely, miss the deadline, or exceed the budget. According to a Project Management Institute (PMI) study, some of the most common causes of project failure include changes in priorities within a company and limited resources. There are a few reasons why project duration and cost may be exceeded [1,2]: use of static and inflexible methods, use of low-end software solutions that lack features related to the entire NPD process, failure to align with the company’s goals and strategies, weak executive support, and poor communication. The last three reasons depend on organizational issues, whereas the first two refer to technical support for improving project performance. The goal of this study was to design a method for supporting decision makers in searching for alternative project completion scenarios.

Currently-used software solutions dedicated to project planning provide information on the estimated cost of a project [3]. If the company’s resources (e.g., financial, human) are not sufficient to develop an NPD project according to schedule, then the decision makers may be interested in obtaining information on alternative project completion variants. Additionally, they may find the estimated cost of NPD unacceptable. Current software solutions, however, fail to support project managers in reviewing the possibilities of project performance so that the preferred NPD cost is achieved given the company’s resources and project requirements. The proposed approach fills in this gap and is geared towards specifying foundations for developing a decision support system dedicated to solving project prototyping problems. The aim of this paper is to elaborate an approach for planning and simulating NPD project completion, in which factors related to research and development (R&D), production, and sales promotion are involved. As the production cost usually constitutes the majority of the total cost in the process of product placement in the market, this study mainly focuses on the field of production. The proposed approach aims to identify the cost of R&D, production, and promotion at the early phase of an NPD project in order to select the most promising NPD project.

The current project planning methods represent the procedural approach, in which an NPD model is built for a specific problem, and the process of designing the model ends when the structure of the model is sufficient to solve the given problem. By contrast, in the declarative approach a single NPD model is developed, which can be used to formulate various NPD-related decision problems. A declarative representation of an NPD model allows to use effective techniques for reducing the search space of admissible solutions. This is particularly important when many decision variables with large domains have to be selected for simulations. There exist declarative simulation modeling methods that can be used to increase the efficiency of identifying alternative NPD project performance variants. By using a declarative representation of an NPD model, a decision maker can perform simulations for an entire set of admissible solutions. Consequently, the decision maker obtains more alternative NPD project performance scenarios than they would using a traditional scenario analysis, which includes the basic, optimistic, and pessimistic variants. Moreover, the decision maker may obtain variants of NPD project performance that they would never come up with themselves. This is particularly important in multi-project environments, in which resources are shared.

In this study, a project prototyping problem is formulated in terms of a constraint satisfaction problem and implemented using constraint programming techniques. This study develops previous research [4] towards using the declarative approach to search for variants of project completion within production cost constraints. The novelty of this research is twofold: (1) specifying an NPD project model and company’s resources as a set of variables and constraints; (2) designing a method for solving the project prototyping method. The proposed method uses parametric estimation to identify complex relationships among data, and constraint programming to effectively search for possible solutions. Consequently, the proposed approach is more adaptable to new conditions related to project performance than other currently used methods.

The paper is organized as follows: Section 2 provides a literature review on new product development, cost estimation techniques and constraint programming. In Section 3 a prototyping problem of product development is formulated as a constraint satisfaction problem (CSP). A method for searching variants that meet the desirable production cost is presented in Section 4. An illustrative example of the proposed approach is presented in Section 5. Finally, a conclusion is drawn and directions of future research are indicated in Section 6.

2. Literature Review

2.1. New Product Development

New product development begins with the identification of market needs and ends with introducing a new product on the market. Intermediate phases of the NPD process are variously distinguished in the literature. Ulrich and Eppinger [5] proposed the following phases of the NPD process: planning, concept development, system-level design, detail design, tests and refinement, and production ramp-up. In turn, Crawford and Benedetto [6] distinguished phases in the NPD model such as opportunity identification and selection, concept generation, concept evaluation, development of a new product, and launch. After introducing a product in the market, the next phase of product life cycle is sales and accompanying activities related to production and promotion. If a new product has been successfully launched in the market, the production phase generates the majority of costs in the total cost of the product life cycle. Figure 1 illustrates cumulative cash flows (sales revenue, costs, and corresponding profit/loss).

The potential of a new product can be measured as the comparison of predicted cash inflows with outflows within a given period of time. Consequently, there is a need to predict sales and costs of product development, production, and promotion. Sales forecasting and cost estimation depend on available data regarding similar previous NPD projects. If a new product belongs to the existing product line, then analogical models can be used to cost estimation. In turn, if a company develops an entirely new product, then analytical models are more useful for evaluating sales or costs of the new product.

Cumulative costs include the cost of product development, production, and promotion. The cost of NPD occurs before launching a new product on the market. The production cost appears in the NPD phase by manufacturing prototypes of a new product, and it lasts until the end of product life cycle. In turn, the advertising and promotional cost can begin before launching a new product, and it usually takes place in the first phase of sales. The comparison of alternative new products requires the prediction of product lifespan, sales, and costs. The evaluation of the potential of new products can also include the discount rate (as in the NPV method) towards reflecting opportunity cost of capital and inflation in the investment period.

2.2. Cost Estimation Techniques

Empirical studies indicate that the size of a project team and the project budget are key structural variables affecting the quality of the NPD process and success of the project [7]. An investigation of new product forecasting practices in industrial companies shows that the most popular techniques include customer/market research, looks-like analysis, trend line analysis, moving average, scenario analysis, and multi-attribute models [8,9]. To a lesser extent, companies use forecasting techniques related to nonlinear regression, expert systems, neural, and neuro-fuzzy networks [8,10].

Cost estimation techniques can be divided into the following groups [11,12]: intuitive, analogical, parametric, and analytical. Intuitive methods use past experience of an estimator. Analogical methods estimate the cost of new products using similarity to previous products. Parametric methods estimate the cost of a new product from parameters that significantly influence the cost. In turn, analytical methods estimate the cost of a product by decomposing product development into elementary tasks with the known cost.

Parametric estimation techniques may be based on regression analysis [13,14], artificial neural networks [15,16], fuzzy logic systems [17,18], or hybrid systems such as neuro-fuzzy systems [16,19] and genetic fuzzy systems [20,21]. Engineering approaches are predicated on a detailed analysis of product features and the manufacturing process. For example, the cost of a new product is calculated in this approach as the sum of the resources used to design and produce each component of the product (e.g., raw materials, labor, equipment). As a result, the engineering approach is best used in the final phases of product development, in which the product and the manufacturing process are well defined.

2.3. Constraint Programming Techniques

A project prototyping problem can be formulated as a CSP by specifying constraints and variables. CSPs, which are combinatorial problems, are solved with the use of constraint programming (CP) [22,23]. CP includes consistency techniques and systematic search strategies that are crucial to improving the search efficiency in solving the CSPs [23,24]. Consequently, CP provides an appropriate framework for developing decision-making software to support identification of project completion alternatives.

Constraint programming consists of two phases: first, the problem is specified in terms of constraints, and then it is solved. The specification of a problem by means of constraints is very flexible because constraints can be added, removed, or modified [24]. The goal of CP is to develop efficient domain-specific methods to be used instead of general methods. They can be employed to develop more efficient constraint solvers, constraint propagation algorithms, and search algorithms. Consequently, CP is a powerful paradigm for solving combinatorial search problems, in which the user declaratively states the constraints on feasible solutions for a set of decision variables [25].

The advantages of using CP refer to declarative problem modeling, propagation of the effects of decisions by means of efficient algorithms, and the search for optimal solutions. The specific search methods and constraint propagation algorithms used in CP allow to significantly reduce the search space. Consequently, CP is suitable for modeling complex problems related to scheduling [26,27], manufacturing [28,29], resource allocation [30,31], supply chain problems [32,33,34], and others. In the context of an NPD project, the CP paradigm has been used in areas such as design and product configuration [35,36], project scheduling [37,38], and project prototyping [39]. Although the use of CP to project selection and scheduling problems has been widely discussed in the literature, the NPD project prototyping problem has not been considered thus far.

3. Problem Formulation

The project prototyping problem is a problem in which alternative NPD project completion scenarios are searched for, taking into account the adopted constraints. This study is concerned with searching for project completion variants that meet the desired NPD cost. In the traditional approach to project evaluation, when the decision maker finds a specific cost unacceptable the project is rejected. However, if the project is important from a strategic point of view, the decision maker is interested in prerequisites that must be met to achieve the desired cost threshold. The proposed approach consists of identifying all possible project performance scenarios (variants) that meet constraints related to project objectives, project budget, human resources, machines, etc. Figure 2 compares the traditional approach to project evaluation (Figure 2a) with the proposed approach in which variants within the target project performance are searched for (Figure 2b). The traditional approach may be considered as a project prototyping problem stated in a forward form, whereas the approach presented in this study can be viewed as the same type of problem stated in an inverse form.

The proposed approach allows the decision maker to identify the prerequisites that must be met for the project to attain the desired performance level given the specified constraints, variables, and relationships between these variables. The number of possible project performance variants depends on what constraints and variable domains are considered and the granularity of decision variables. Relationships between variables can be identified on the basis of previous experiences with similar projects and represented as if-then rules. Then, they may be used to predict the potential of a project (the traditional approach), or to test whether there exist alternative project completion scenarios that could deliver the desired project performance (the proposed approach). The use of CSP to the formulation of the project prototyping problem offers significant flexibility of the proposed approach. The addition/removal of variables or constraints to/from CSP causes a simultaneous recalculation and a new set of possible solutions.

The present project prototyping approach requires the specification of variables, their domains, and constraints. This allows to identify all available solutions, if there are any. The prototyping problem can be easily expressed as a CSP which can be described in the following form [28]:

(V, D, C)

(1)

where V is a finite set of n variables {V₁, V₂, …, V_n}, D is a finite set of discrete domains {D₁, D₂, …, D_n} related to variables V, and C is a finite set of constraints {C₁, C₂, …, C_m} that restrict the values of the variables and link them.

Each constraint is treated as a predicate that can be seen as an n-relation defined by Cartesian product D₁ × D₂ × … × D_n. The solution to the CSP is a vector (D_1i, D_2k, …, D_nj) related to the assessment of the values of each variable that satisfy all constraints C. Generally, constraints may be specified using analytical and/or logical formulas.

The variables are associated with the company’s resources and the NPD project. Characteristically, the variables (V₄, …, V₁₆), which are purported to affect costs (V₁, …, V₃), are controllable by a company and can be simulated to identify a set of their values that satisfy all constraints and ensure the desired level of a specific cost. The following set of variables for estimating the NPD, production, and promotional cost were proposed:

• V₁—NPD cost (in thousand €),
• V₂—unit production cost (in €),
• V₃—advertising and promotional cost (in thousand €),
• V₄—number of R&D employees involved in product design,
• V₅—number of R&D employees involved in prototype tests,
• V₆—duration of product design (in months),
• V₇—duration of prototype tests (in months),
• V₈—number of prototype tests (in hundreds),
• V₉—number of product components,
• V₁₀—amount of materials needed to manufacture a unit of a new product,
• V₁₁—amount of energy needed to manufacture a unit of a new product,
• V₁₂—assembly time for a unit of a new product,
• V₁₃—processing time for a unit of a new product,
• V₁₄—number of workplace units needed for assembling and processing a new product,
• V₁₅—duration of advertising and promotional campaign of a new product,
• V₁₆—number of potential receivers of advertising and promotional campaign,
• V₁₇—sales volume,
• V₁₈—production cost (in thousand €),
• V₁₉—desirable margin (in €),
• V₂₀—product price (in €),
• V₂₁—sales revenue of a new product (in thousand €).

There are the following constraints regarding the available quantity of resources in a company and technical parameters of a new product: NPD project budget (PB, in thousand €), total number of R&D employees involved in an NPD project (TE), deadline for launching the new product into the market (LD, in months), time needed to manufacture a unit of a new product (MT), and advertising and promotional budget (AB, in thousand €). The set of constraints and relationships is as follows:

V₁ ≤ PB

(2)

V₄ + V₅ ≤ TE

(3)

V₆ + V₇ ≤ LD

(4)

V₁₂ + V₁₃ ≤ MT

(5)

V₃ ≤ AB

(6)

V₂ ∙ V₁₇ = V₁₈

(7)

V₂ + V₁₉ ≤ V₂₀

(8)

V₁ + V₃ + V₁₈ ≤ V₂₁

(9)

The model formulated as an CSP incorporates the technical parameters of the new product that refer to the planned project performance and the available resources. The problem is solved by searching for answers to the following questions:

•

What is the cost of product development (including unit production cost)?

•

What values should the variables have to reach the desirable level of the cost?

A project prototyping problem can be expressed as a CSP and then be solved with the use of specific techniques such as constraint propagation and variable distribution. Constraint propagation applies constraints to prune the search space. Propagation techniques aim to reach a certain level of consistency, and accelerate the search procedures to reduce the size of the search tree [28]. The values of the variables excluded by constraints are removed from their domains. A CSP may be effectively solved with the use of CP techniques. The declarative nature of CP is particularly useful in applications where it is enough to state what has to be solved without saying how to solve it [28]. As CP uses specific search methods and constraint propagation algorithms, it allows to considerably reduce the search space. Consequently, CP is suitable for modeling and solving complex problems.

4. The Proposed Method for Planning and Simulation of Production Cost

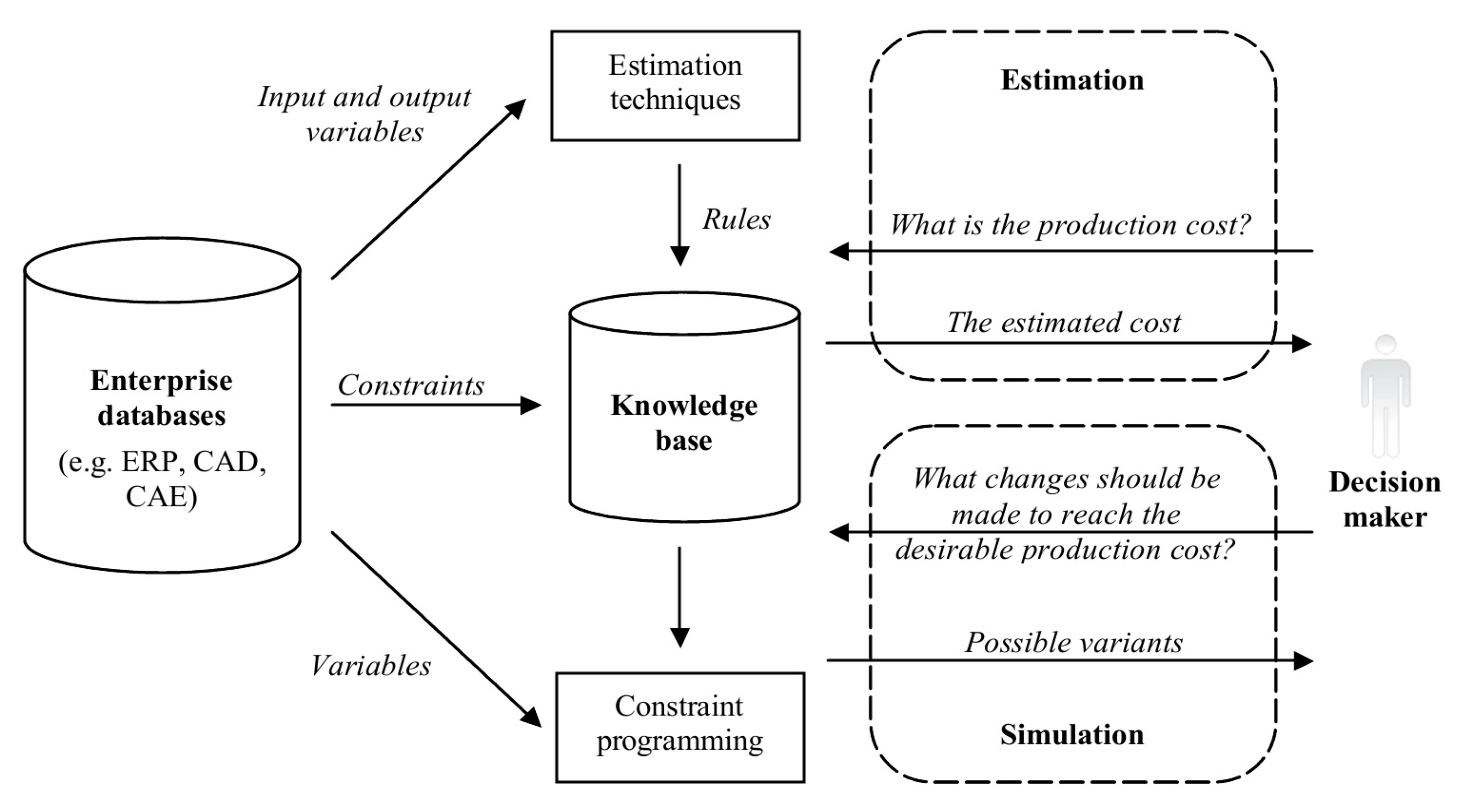
The proposed method consists of the following phases: (1) collecting data from previous projects that are similar to the new project, (2) identifying relationships between variables, (3) estimating the production cost, and, if needed, (4) searching for variants that allow to obtain the desired cost. Figure 3 shows a framework for the proposed decision support system that uses parametric estimation techniques to identify relationships and constraint programming to reduce the search space and test the possibility of reaching the desired production cost.

In the first phase, the data is collected from enterprise databases, for example related to information systems such as enterprise resource planning (ERP), computer-aided design (CAD), and computer-aided engineering (CAE). This requires the use of some project management standards, including project performance planning, monitoring, control, and appropriate project planning and execution techniques. The use of the proposed approach requires the access to the sufficient amount of data related to the past NPD projects that can be outdated, which causes the need to consider the delay aspect. The applicability of the proposed method depends on whether or not the following data management procedures are used: the enterprise adjusts the common project management standards to its needs, distinguishes phases in the NPD process, uses standards for specifying tasks in an NPD project and for project portfolio management, measures the success of new products on corporate financial performance, uses the results of a financial performance analysis to improve the effectiveness of NPD projects, registers performance and metrics of NPD projects, uses a primary schedule for monitoring performance in NPD projects, and uses the defined procedure to allocate employees to NPD projects.

In the second phase of the proposed method, cause-and-effect relationships are identified and then used to estimate the cost of product development, and search for a desirable outcome of an NPD project. The input variables should impact the cost and be controlled by a company, such as the number of project team members, product components, and prototype tests. A set of variables, their domains, and constraints constitute a CSP, which provides a framework for finding the value of the NPD, production and promotional cost (the third phase), and, if that is unacceptable, the values of variables at which the desired cost of a new product can be achieved (the fourth phase).

In the third phase, the cost is estimated using the parametric models based on linear regression and artificial neural networks. The quality of the obtained results is compared using the root mean square errors. The data set is divided into learning and testing sets to verify the quality of the learned neural network. The small errors in the testing set exhibit good predictive abilities of the learned network.

The fourth phase of the proposed method refers to the search for possible solutions to achieve the desired cost. The size of the search space depends on the number of variables analyzed, the range of decision variable domains, and the constraints that link the variables and limit the set of possible solutions. An exhaustive search always finds a solution if one exists, but its performance is proportional to the number of admissible solutions. Therefore, an exhaustive search tends to grow very quickly as the size of the problem increases, which limits its usage in solving many practical problems. Consequently, more effective methods for searching the space and finding possible solutions are needed. This study proposes a CP that can be used to efficiently solve a project prototyping problem modelled as a CSP. Figure 4 shows a framework for solving this problem in the inverse form.

The proposed approach includes three stop/go conditions. The first stop/go condition checks whether there exists a solution for a set of decision variables, given the specified input and output variables, their domains, and constraints. If such a solution exists, then it is verified whether a number of solutions is acceptable for the user or not. If not, the granularity of the solution is increased. Furthermore, changes in granularity are related to scaling domains and significantly affect the effectiveness of the CP application (e.g., the production cost specified in 1000 euros provides a smaller number of solutions than when specified in single euros). If there is any solution, the possibility of extending the domains related to the selected decision variables is tested. Finally, if the domains of the selected decision variables cannot be changed, the last stop condition leads to the empty solution set.

5. An Example of Using the Proposed Method

5.1. Cost Estimation of a New Product

The relationships between the input and output variables (V₁, V₂, V₃) have been identified with the use of parametric estimation techniques such as the artificial neuron networks (ANNs), linear regression (LR), and compared with the average. The use of ANNs offers advantages over ability to learn and identification of complex nonlinear relationships. The dataset used in the analysis included 25 completed NPD projects that featured products in the same line as the investigated project. The data were divided into two sets—learning (20 cases) and testing (five cases)—to evaluate the quality of the estimating model. The relationships between the input and output variables are determined using the data related to the previous NPD projects to estimate the cost of product development. The set of input variables is obtained taking into account the significant impact of an input variable on an output variable, as well as the possibility of their controllability by a company and the access to the data through the past specifications of NPD projects. There are the following relationships between input variables and costs: the NPD cost (V₁) depends on {V₄, …, V₉}, the unit production cost (V₂) depends on {V₉, …, V₁₄}, and the advertising and promotional cost (V₃) depends on {V₁₅, V₁₆}.

In this study, a multilayer feed-forward ANN has been trained according to the back-propagation algorithm and weights optimized according to the Levenberg-Marquardt algorithm (LM) and gradient descent momentum with adaptive learning rate algorithm (GDX). The neural network structure has been determined in an experimental way, by the comparison of a learning set and testing set for the different number of layers and hidden neurons. The root mean square errors (RMSEs) have been calculated as the average of 50 iterations for each structure of a neural network with a number to the extent of 30 hidden neurons.

Table 1. A comparison of root mean square errors (RMSEs) for estimation models.

Data Set	Model	V1	V2	V3
	ANN LM	0.005	0.001	0.003
Learning	ANN GDX	0.521	0.051	0.118
	LR	0.637	0.072	0.142
	Average	1.312	0.134	0.326
	ANN LM	0.496	0.067	0.129
Testing	ANN GDX	0.602	0.049	0.085
	LR	0.913	0.106	0.138
	Average	1.826	0.180	0.548

presents the RMSEs calculated in the learning and testing set using the different parametric models for estimating the cost of NPD (V₁), production (V₂), and promotion (V₃).

The ANNs trained according to the LM algorithm obtained the least RMSEs in the learning set. However, the least RMSEs in the testing set was calculated using the ANNs trained according to the GDX algorithm (for V₂ and V₃) and LM algorithm (for V₁). The trained ANN is used to estimate the unit production cost for the following values of input variables: V₉ = 45, V₁₀ = 830, V₁₁ = 55, V₁₂ = 25, V₁₃ = 15, V₁₄ = 7. The estimated unit production cost reaches 24.5 €, and the total production cost 970 thousand € in the two-year projected period of product life cycle. In turn, the NPD cost reaches 190 thousand €, and the advertising and promotional cost 150 thousand €.

Let us assume that the estimated unit production cost does not satisfy the decision maker who is interested in reducing this cost to 24 €. To check whether these expectations can be fulfilled, the problem is reformulated into an inverse problem in which such values of input variables are sought to ensure the desired level of the unit production cost.

5.2. Simulation for Identifying the Desired Level of Costs

The example consists of two steps presented in Figure 4: (1) a basic variant for the originally selected decision variables, their domains, and constraints; and (2) an extension of the domains of the selected decision variables.

5.2.1. The Basic Variant

Let us assume that the decision maker is interested in reducing the unit production cost to 24 €. To test whether there exist solutions, the problem under consideration is reformulated into an inverse problem. A solution to the inverse problem is sought using constraint programming, which requires that decision variables, their domains, and constraints, including relationships between variables (e.g., their mutual impact on one another), are specified. The domains for the considered variables are as follows: D₉ = {45}, D₁₀ = {830}, D₁₁ = {54, 55, 56}, D₁₂ = {24, 25}, D₁₃ = {14, 15}, and D₁₄ = {7}. The domains include only integer numbers and the simulation step is related to the increase of these numbers by one for each variable separately. As a result, all available solutions, referring to all numbers in the domains, are sought.

The inverse problem is implemented in Mozart/Oz software, which is a multiparadigm programming language. Mozart/Oz contains most of the major programming paradigms, including logic, functional, imperative, object-oriented, concurrent, constraint, and distributed programming. The major strengths of Mozart/Oz are related to its constraint and distributed programming components, which are able to effectively solve many practical problems, for example, timetabling and scheduling problems [40].

Table 2. A set of possible solutions.

Variant	Values of Variables	V2
1	V9 = 45, V10 = 830, V11 = 55, V12 = 25, V13 = 15, V14 = 7	24.00
2	V9 = 45, V10 = 830, V11 = 54, V12 = 25, V13 = 15, V14 = 7	23.97
3	V9 = 45, V10 = 830, V11 = 56, V12 = 24, V13 = 15, V14 = 7	23.98
4	V9 = 45, V10 = 830, V11 = 55, V12 = 24, V13 = 15, V14 = 7	23.95
5	V9 = 45, V10 = 830, V11 = 54, V12 = 24, V13 = 15, V14 = 7	23.82
6	V9 = 45, V10 = 830, V11 = 56, V12 = 25, V13 = 14, V14 = 7	23.99
7	V9 = 45, V10 = 830, V11 = 55, V12 = 25, V13 = 14, V14 = 7	23.96
8	V9 = 45, V10 = 830, V11 = 54, V12 = 25, V13 = 14, V14 = 7	23.93

presents eight possible solutions (variants of the production process) that take into account the specified constraints and variables. The minimal unit production cost appears for the values of variables in the fifth variant.

The changes presented in Table 2 regard three variables V₁₁, V₁₂, and V₁₃. The set of possible solutions informs the decision maker what changes may be incorporated into the production process to reduce the unit production cost.

Let us assume that the decision maker’s expectations regarding the unit production cost decrease from 24 to 22 €. There is no solution by the indicated domains that satisfies this new value of the preferred cost. This triggers the next step in the problem solving procedure, i.e., testing whether it is possible to extend the domains related to the selected variables.

5.2.2. Extension of Variable Domains

This step of the procedure of solving the inverse form of the problem involves selecting variables whose domains can be extended. As a result of domain extension, the problem is solved again for new domains assigned to some variables, all other conditions being equal. The set of domains is as follows: D₉ = {45}, D₁₀ = {800, …, 850}, D₁₁ = {50, …, 60}, D₁₂ = {20, …, 30}, D₁₃ = {10, …, 20}, and D₁₄ = {7}. The remaining constraints are the same as in the basic variant. An extension of domains for four variables causes an increase in the number of choice nodes in the explored search tree. Consequently, there is a need to use an effective technique to search the space of admissible solutions.

Table 3. A comparison of strategies for variable distribution.

Distribution Strategy	Number of Nodes Checked	Depth	Time [s]
ES	67,880	65	5.25
CP Naïve	32,852	48	1.41
CP First-fail	32,852	48	1.16
CP Split	32,852	48	1.07

presents the results of searching for an admissible solution for different strategies of variable distribution. Different strategies of variable distribution in the constraint programming with exhaustive search (ES) are compared with regard to the number of nodes checked, depth, and the time needed to find solutions. The calculations were tested on an IntelCore (tm) i5-8300H 2.3-4GHz, RAM 8 GB platform.

The results show that the application of the constraint programming reduces the computational time, which is especially important when there is a larger number of possible solutions. The user can obtain the entire set of solutions or one optimal solution. The extension of variable domains can generate many very similar solutions. The number of solutions can be reduced through considering only the minimum and maximum values of domains. Then, the decision maker can develop the scenario analysis towards the preferable direction to recognize all scenarios ensuring the desired cost. Constraint programming techniques allow to use strategies related to constraint propagation and variable distribution, significantly reducing the set of admissible solutions and the average computational time, improving in this way the interactive properties of a decision support system.

6. Conclusions

The declarative approach proposed in the present paper for NPD project prototyping is an alternative to current methods, which only estimate the cost of NPD, production, and promotion. In the proposed project prototyping method, all possible project completion scenarios are sought, if any. These variants inform the decision maker whether an NPD project can be completed based on the company’s resources and within project requirements. Businesses with limited resources need to invest extra effort in managing NPD projects. This approach is especially useful to this type of firms (e.g., ones that have a limited project budget), as it allows them to check whether a project can be completed under the specified constraints (e.g., the desired level of the unit production cost). Consequently, there is a need to develop a decision support system for searching possible variants of the cost reduction. The proposed model encompasses areas related to a product and a company’s resources. These areas were described in terms of a CSP that includes sets of decision variables, their domains, and constraints. The project prototyping problem is a problem in which answers to queries about the estimated cost and the values of input variables that ensure the desired level of cost are searched for. The results of this research include not only the possibility of verification to reach the desired level of the cost, but it can also be developed towards identifying the possible variants of project completion. The presented method can be used to verify the possibility of completing an NPD project at the target time, and to specify the resources needed to the reduction of project duration. This is one of the most important issues related to the new product development process. The problem presented in this paper refers to the project prototyping problem that is stated in an inverse form, i.e., the possible variants are sought to ensure the desirable level of production cost. However, it is also possible to use the proposed approach in other areas, for example, in project scheduling, product configuration, resource allocation, and supply chain problems.

The results show that the application of a CP improves the search efficiency in the context of the project prototyping problem, especially when there are a larger number of admissible solutions. Moreover, this study presents the use of artificial neural networks to identify the relationships for estimating costs within a product life cycle. The identified relationships are stored in a knowledge base and used to generate alternative variants of manufacturing a new product. If decision makers find that the cost related to product development is unacceptable, they can use the identified variants as a support tool in identifying the impact of input variables on an output variable (e.g., the unit production cost) under the specified constraints. The drawback of the proposed approach is that sufficient amounts of data on similar past NPD projects need to be collected, and several parameters must be specified to build and train an artificial neural network. Moreover, the limitation of the presented study is the selection of input variables that significantly affect the cost of a new product and are controllable by a company, as well as the time needed to analyze all solutions by the decision maker. In the case of an enormous number of admissible solutions, the granularity of domain can be increased or the minimum and maximum values of domain can be taken into account in the calculations. In our future work, we would like to verify the proposed approach in project-oriented companies in different business sectors. We also plan to extend the application of the presented approach by incorporating the warranty cost in the total product development cost.