Abstract
The presented paper reveals an innovative device which is the Tuned Particle Impact Damper (TPID). The damper enables the user change the dynamical features of the vibrating system thanks to rapidly tuning the volume of the container where the grains are locked. The effectiveness of proposed semi-active damping methodology was confirmed in experiments on vibrations of a cantilever beam excited by kinematic rule. Various damping characteristics captured for different volumes of the grains container and mass of granular material are presented. It is confirmed that the proposed TPID device allowed for efficient attenuation of the beam’s vibration amplitude in the range of its resonant frequency vibrations.
1. Introduction
Devices that are able to attenuate unwanted mechanical vibrations have interested researches and engineers for several decades. In the everyday engineering applications we can distinguish various types of vibration damper designs. The most popular passive shock absorbers constructions consist of viscous properties of elastomers or more or less sophisticated fluids or gels. Nowadays, it seems that so called Particles Impact Dampers (PID) start to play an increasingly important role in the field of vibrations damping. The classical PID principle of operation lies in inelastic collisions of loose particles enclosed in the specially designed container or cavities. The Energy dissipation mechanism is additionally related to the frictional contact of grains and the container casing. The PID device connected to the vibrating element or structure absorbs a part of global kinetic energy of the investigated system and reduces its vibrations amplitudes. The effectiveness of such a damping strategy mainly results from coupling of friction and impact phenomenon. The energy dissipation process in the most commonly used damping devices is generally related either to the friction phenomenon or previously mentioned visco-elastic material deformations. Such mechanisms increase the operating temperature and also the wear of material resulting in decreasing of damping properties. Considering the aforementioned limitations, the use of granular dampers in which the influence of temperature and material degradation is less important seems to be particularly interesting. The additional advantages of PIDs are: they can perform in a very wide range of frequencies, they can be made of recycled materials, economical aspect, the global mass of the system with grains moving in the internal cavity is generally lower than the initial. All the previously mentioned features of PIDs cause that such devices are very often applied in dynamic systems working in harsh environments. The adjustment of damping properties in a considered group of shock absorbers is limited and consists of choosing the right kind, consistency, shape and size of grains for the given application.
In world literature a significant number of studies have been carried out in the field of granular dampers analysis. They are mainly focused on efficiency ([1,2,3,4]), optimization ([5,6,7]), applications ([8,9,10,11]) and modeling ([12,13,14]). An interesting problem is discussed in Reference [15] where Particles Impact Damper is treated as a double pendulum striking element. It is confirmed that such an object is especially effective to attenuate vibrations of various slender elements. Various excitation rules and PID parameters are taken into account in experimental studies. Other papers suggest, that the PID can be a part of alternative energy harvesting device [16]. In this case the classical grains are replaced by a moving magnet forming the previously mentioned original energy harvester. Taking into account damping of vibrations of elements operating in an extreme environment, the reliability and durability of devices are extremely important. The typical example of such an environment is aerospace engineering, where PIDs are especially popular. It is presented in Reference [17] that attenuation of vibrations of highly sensitive electric circuits can be achieved by PIDs. Application of granular damping seems to also be optimal solution in the case of taking-off or landing of spacecrafts. Various modifications of classical PID designs are also investigated in recently published papers. In Reference [18], the authors propose an innovative solution for the semi-active Tuned Liquid Column Damper (sTLCD). Such a device is connected to the base structure using the spring with controlled stiffness. The efficiency of the considered system is discussed and different control algorithms are taken into consideration in the paper. Applied control strategies enabled the authors to effectively tune the frequency of a structure. The proposed solution is especially interesting in civil engineering where the increased danger of earthquakes exists. A lot of papers dealing with granular damping discuss various modeling approaches and problems encountered in the laboratory tests. Also experimentally determined damping characteristics are presented and discussed in detail ([19,20,21]).
Despite the apparent simplicity of the PIDs fundamental working rule it can be concluded, that capturing the real behavior of the discussed group of devices is rather complex. Previously mentioned papers generally simplify the PIDs modelling process to the 1 or 2 Degrees of Freedom (DOF) problems incorporating additionally external forces or equivalent damping parameters. In Reference [22] or Reference [23] the complex dynamics of vibrating sphere particles is compared to the dense gas flow. Such a solution allows to represent the damping characteristics by formulas dependent on: a mass ratio, volume ratio, restitution coefficient and excitation frequency. The different approach to the PIDs modelling problems can be observed in Reference [24] or Reference [25], where the sophisticated numerical software is used to capture the real laboratory test results. In Reference [24] an interesting original technique to predict the harmonic response of particle damping structure based on ANSYS software is discussed. Other approach basing on Discreet Element Method (DEM) is investigated in Reference [25] where the energy dissipation problems of harmonically excited elements are solved numerically. To solve the classical inverse problem consisting of calibrating the selected model parameters basing on the real response of the PID device various numerical optimization techniques are taken into consideration. In Reference [26] the damper parameters are captured using Artificial Neural Networks. The efficiency of proposed methodology was compared with two other popular parameters identification methods - Feed Forward Back Propagation Network and Radial Basis Function. An interesting practical engineering application of PIDs in the automotive industry is presented in Reference [27] where a granular damper is used as a sound absorber. It is confirmed that such a device is also suitable for increasing the driving comfort of the passengers. Granular dampers are also used in suppression of vibrations in centrifugal field of gear transmission ([28]). In such a case the tightly packed loose material is placed in specially designed holes in the gears. The reliability of PIDs is validated by the comparison of real response of the system with the numerical DEM simulations. The other grain based damping of vibration techniques being the alternative to the discussed PIDs are so called Chain Dampers ([29,30]) or Vibro-Impact Nonlinear Energy Sinks ([31,32,33]). Application of various PIDs seems to be especially interesting in the controlling nonlinear dynamics of slender and light objects resulted from the unknown disturbances. Typical examples of such structures are wind turbines ([34,35]).
Reference [36] describes the effective damping of rail vibrations by adding a TPID consisting of Tuned Absorber Mass and Impact Ball. The mathematical model, experiments and simulations are introduced to establish the optimal damping parameters for the system. In the mentioned paper, the authors analyze the effectiveness of the structure by separating the components of the damper. Reference [37] provides the literature review over PID dampers. It presents various technical solutions and modelling methods. They describe typical applications of the TPIDs, which however allow to change the parameters of the attenuator, but require a significant human involvement aspect. In Reference [38] a simple mathematical model of the vibrating system including TPID damper described as a 2-DOF system is presented. The shock absorber model is mainly described by two coupled parameters: equivalent damping and equivalent mass. Reference [39] presents the construction of a damper named TPID. The gap (free volume of the system) can be manually changed by the threaded lid. The research takes into account experiments, simulations and focuses on comparing three types of dampers: Particle Dampers, Tuned Particles Dampers and Tuned Mass Dampers. Determining the effectiveness of attenuation ability depending on the various excitation frequency and grains mass is also discussed.
In the previous paper of the authors [40], the initial TPID concept was discussed. Preliminary study is presented and discussed. In contrast to Reference [40], in this paper, the authors present a significantly greater number of experimental results conducted for free and kinematically excited vibrations. Based on the recent results it possible to determine the effectiveness of the TPID damper to attenuate vibrations depending on the application of various grains material, variable mass of particles and container volume and the excitation frequency. The main novelty of this paper is the presentation of several different TPID intermediate states during a dynamic strategy of changing the container volume. A mathematical model based on a nonlinear–exponential control function has been proposed. A verification of the real system response and numerical simulations is additionally provided.
The authors of this paper state, that Tuned Particle Impact Dampers can be competitive to other more sophisticated and expensive control schemes for industrial wind turbines such as proportional integral derivative regulators. The overview of PID literature presented in the Introduction section includes mainly passive damping strategies. The dynamics of attenuated by loose materials structures can be basically controlled by grains volume ratio, mass of the granular material or the coefficient of restitution. Although it was shown that PIDs are competitive to other damping techniques, up to this point granular dampers could not be used as a part of semi-active damping strategies. In this paper the authors propose an innovative Tuned Particles Impact Damping device. Its novelty consists of the possibility to rapidly change the volume of the compartment where the grains are encapsulated. This solution enables the implementation of a completely new adaptive-passive strategy of semi-active vibration damping. The paper is divided into several sections. In the next one the idea of the Tuned Particles Impact Damper is presented. In the third and fourth Sections the original test stand and experimental results are discussed respectively. The paper is completed with a Conclusion Section where the summary and the perspective research are revealed.
2. Idea of the Tuned Particles Impact Damper
Popular granular vibrations attenuators are devices introducing additional damping to the system. Dynamic properties of such structures depend on many parameters, where the most important are: size, shape and volume of the container, filling ratio of granular media, grains features like density, shape and roughness. All previous studies related to the application of PIDs in dynamic systems assumed that changing of damping properties can be achieved by passive adjusting of previously mentioned parameters. Taking into consideration the advantages of semi-active methods of damping of vibrations over classical passive strategies the authors decided to improve the classical PIDs and introduce the Tuned Particles Impact Damper (TPID) enabling the user to adjust in the damping properties.
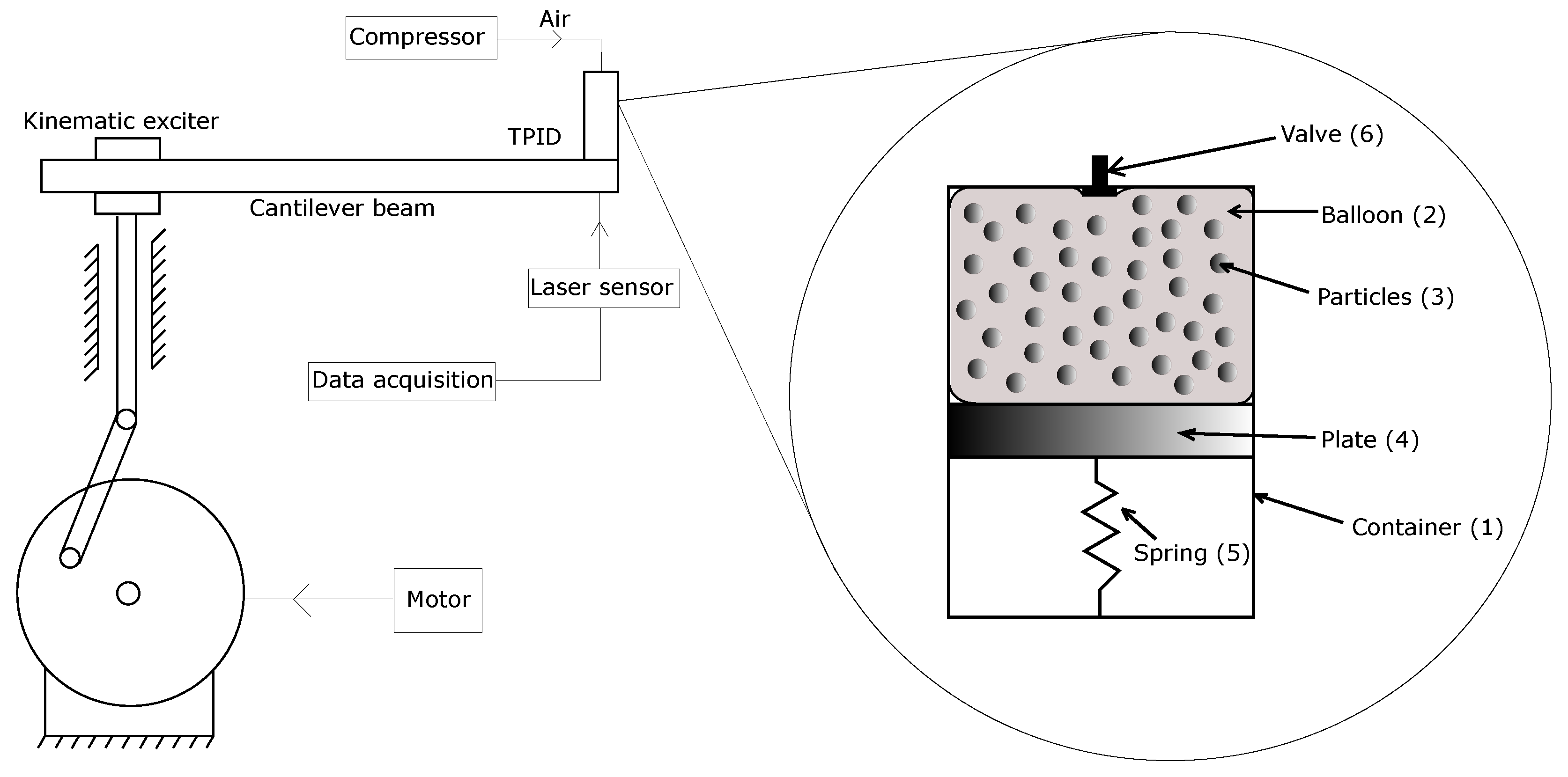
The present paper focuses on the revealing the extraordinary features of the TPID device prototype, where rapid changes of the volume container allow for adjusting the damping characteristics of the system aimed in reducing the effects of temporary external excitations. The simplified idea of investigated TPID prototype and scheme of experimental setup is presented in Figure 1.
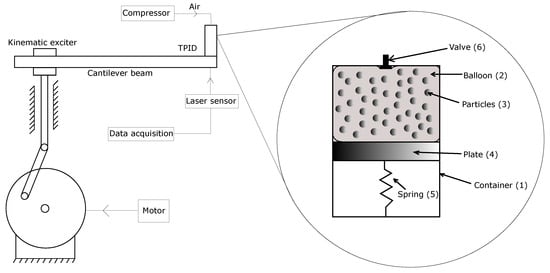
Figure 1.
Scheme of the tests stand and the Tuned Particles Impact Damper (TPID) prototype.
The TPID can be treated as an additional device that can be mounted onto (eventually into) various mechanical systems to control their dynamical features, mainly to reduce their mechanical vibrations. The TPID prototype considered in this paper consists of the container (1) having a varying volume of the range ( [dm]; [dm]). This volume can be controlled by the balloon (2) located inside the container. The balloon in its initial state is deflated and closely encapsulates the loose granular material (3) placed inside of it. In such a case the grains can be treated as a concentrated mass located in a selected place of the system. At the same time discs (4) connected with springs (5) limit the container volume to value. The balloon is additionally equipped with a valve (6), the end of which protrudes from the container, enabling connection of the external pump. Changing the pressure inside the balloon expands it causing the movement of the disc and increasing the operating volume of the container. At this stage the granular material starts to vibrate which results in two main phenomenon: inelastic collisions between single grains and interaction with the casing. A further inflating of the balloon causes reaching the volume of the device. The rapid changes of the TPID operating volume of the TPID device is a novel mechanism enabling adaptive-passive or in future semi-active damping of vibrations strategies. The additional advantages of the proposed TPID prototype are its uncomplicated design, high strength of its components and finally environmental friendliness.
3. Test Stand
To reveal the extraordinary features of the TPID prototype, the special laboratory test stand was designed (Figure 2). It was aimed to conduct the research on the kinematically excited cantilever beam equipped with the TPID device. Various TPID damper parameters were taken into consideration during the experiments. In the first stage of empirical investigations, to fully understand the features of the investigated system the values of TPID such as the volume of container, mass of the grains or type of granular material were systematically changed. Subsequently, the tip of the vibrated beam amplitudes for the resonant range were measured for the various parameters configuration.

Figure 2.
Test stand.
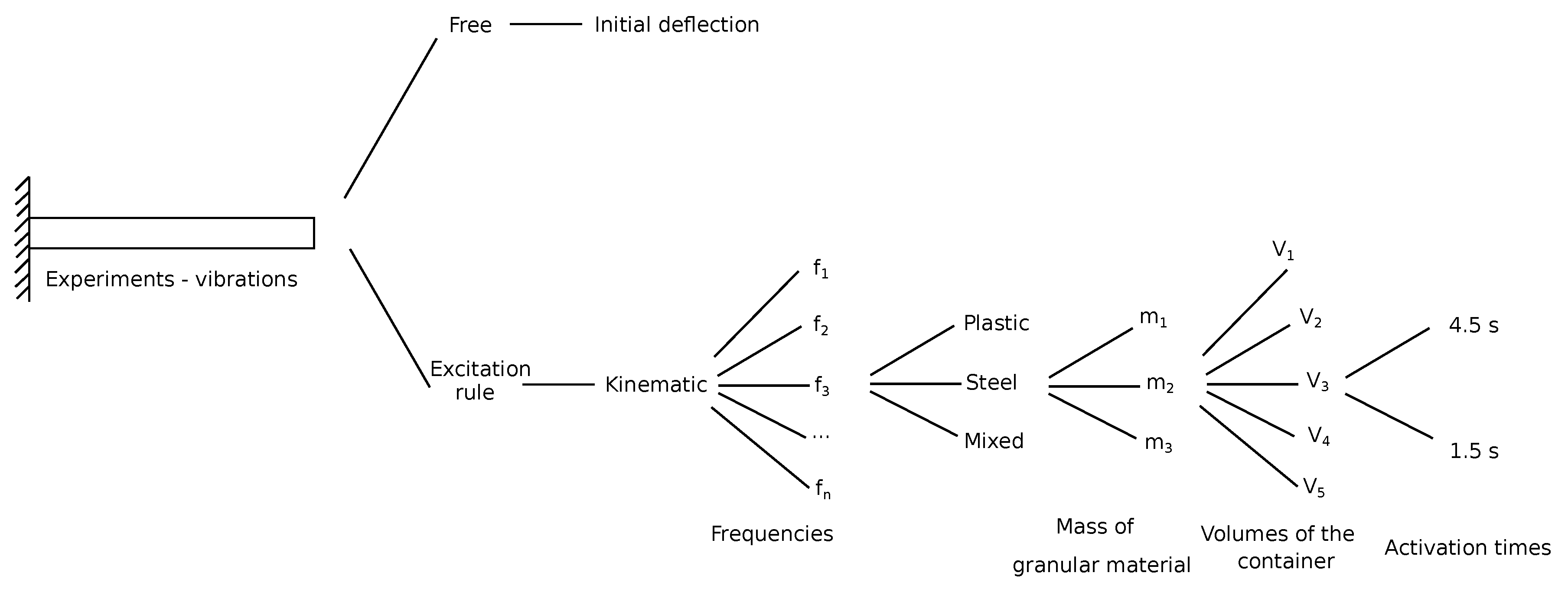
The features of the investigated system, including the geometry of the grains and the dimensions of the test stand, are presented in Table 1. The range of laboratory tests included three different granular media (Figure 3). The spherical shape of particles having diameter [mm] were tested in laboratory tests. Additionally, five different filling ratios (grains volume to total volume) were taken into account. At the current stage of investigations the authors did not concern the wear of grains material process and its influence on the damping properties of the device. The whole research plan is presented in Figure 4.

Table 1.
Parameters used in experiments.

Figure 3.
The investigated grains. (a) Plastic particles; (b) Steel particles; (c) Mixed particles.
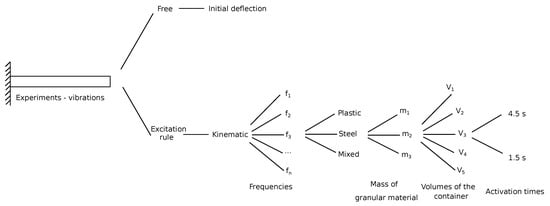
Figure 4.
Research plan.
The measuring system consisted of LabJack and National Instruments data acquisition cards. The beam tip displacements were measured by Emron laser sensor and additional accelerometer located at the end of the beam. The signals were recorded on a personal computer with dedicated recording and analyzing software. The previously mentioned beam was clamped in a special handle and mounted in the individually designed exciter (Figure 2). A special arrangement of gears, belt transmissions and eccentric disks were transforming the rotary movement of the electric rotor into a reciprocating movement of the exciter. The kinematic excitation rule including variable frequencies (up to 60 Hz) and fixed amplitude level (±5 mm) were considered. The data was sampled at 0.5 kHz.
For rapid changes of the rubber balloon volume the compressor equipped with pressure sensors was used. The volume changing of the TPID compartment consisted of inflating and deflating the balloon that tightly filled the working chamber of the granular shock absorber. Recorded data were analyzed in the SageMath environment based on Phyton programing language.
4. Experiments
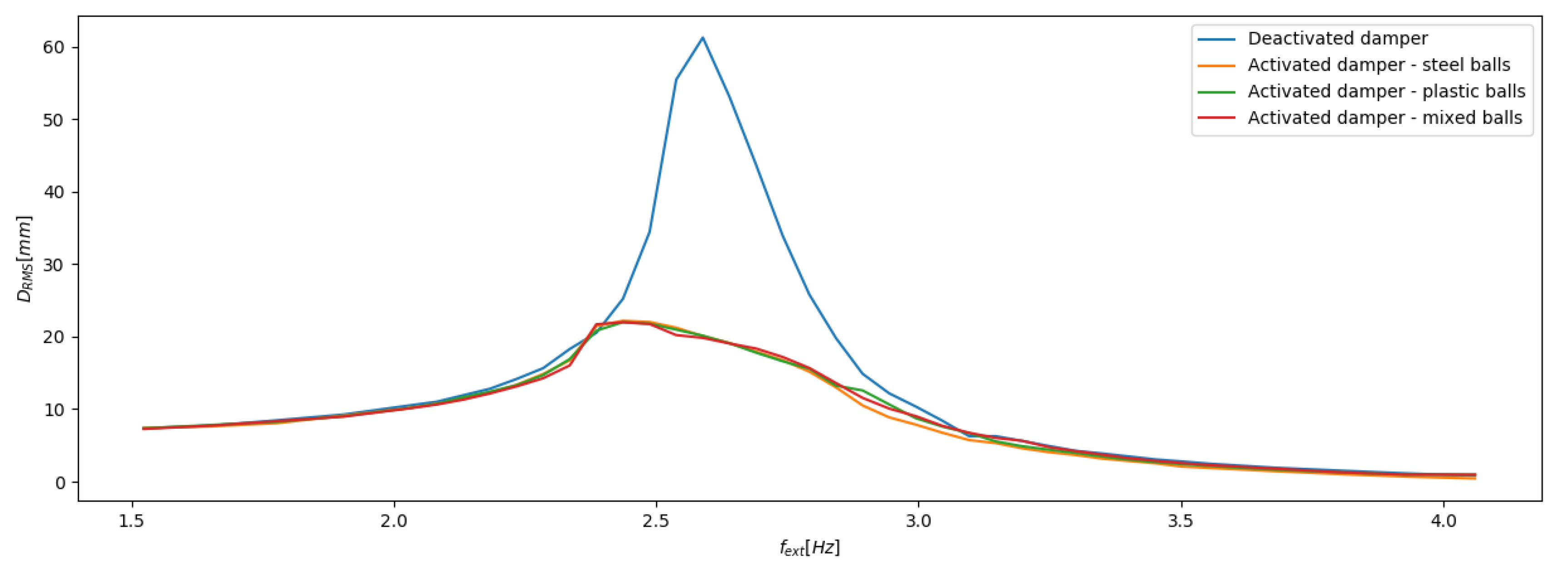
In the laboratory tests the authors focused on determining original damping characteristics for various operating parameters of the TPID device presented in Table 2. The impact of changeable volume of the container is specially underlined. The main objectives of laboratory tests were to confirm the usefulness of introduced granular damping strategy and to reveal the innovative adaptive-passive method for attenuation of the investigated beam vibrations. Several excitation frequencies were taken into account in experimental research. The whole variety of applied frequencies covered the range before and after the resonance. Various vibration acceleration spectra acquired for different kinds of granular materials were determined. The effectiveness of the proposed solution is especially visible for the resonant frequency where the activation and deactivation of the TPID device caused reasonable changes in the recorded amplitudes of the vibrated beam.

Table 2.
Root Mean Square (RMS) of the displacement for various masses of the grains.
4.1. The Influence of Container Volume and Mass of Particles
Five various volumes of the container were investigated in the laboratory tests. The lowest value corresponds to the fully compacted grains. Such a case results in loading of the system by the concentrated mass of the grains. The dissipative properties of TPID element is then reduced to the minimum. For the maximum value of volume the vibrating grains can freely collide between each other. Also the impacts of particles and walls of the container is observable, which results in increased dissipative properties of the granular damper. Three different compositions of the particles were tested. Consequently, three various masses were included in the described experiments. Typical laboratory tests results are depicted in Figure 5 and Figure 6. Root Mean Square (RMS) values of the beam tip displacements (1) for various operating parameters were determined to reveal the recorded response of the considered system. Additionally the RMS data are presented in Table 2.
where —maximum displacement amplitude in “i” cycle of vibration, —frequency of excitation, j—case number, n—number of amplitude values in each case.
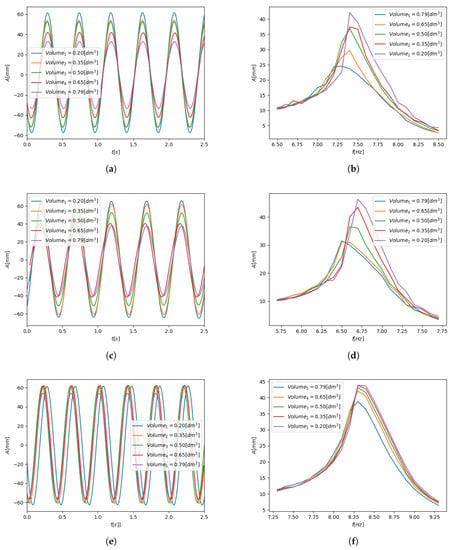
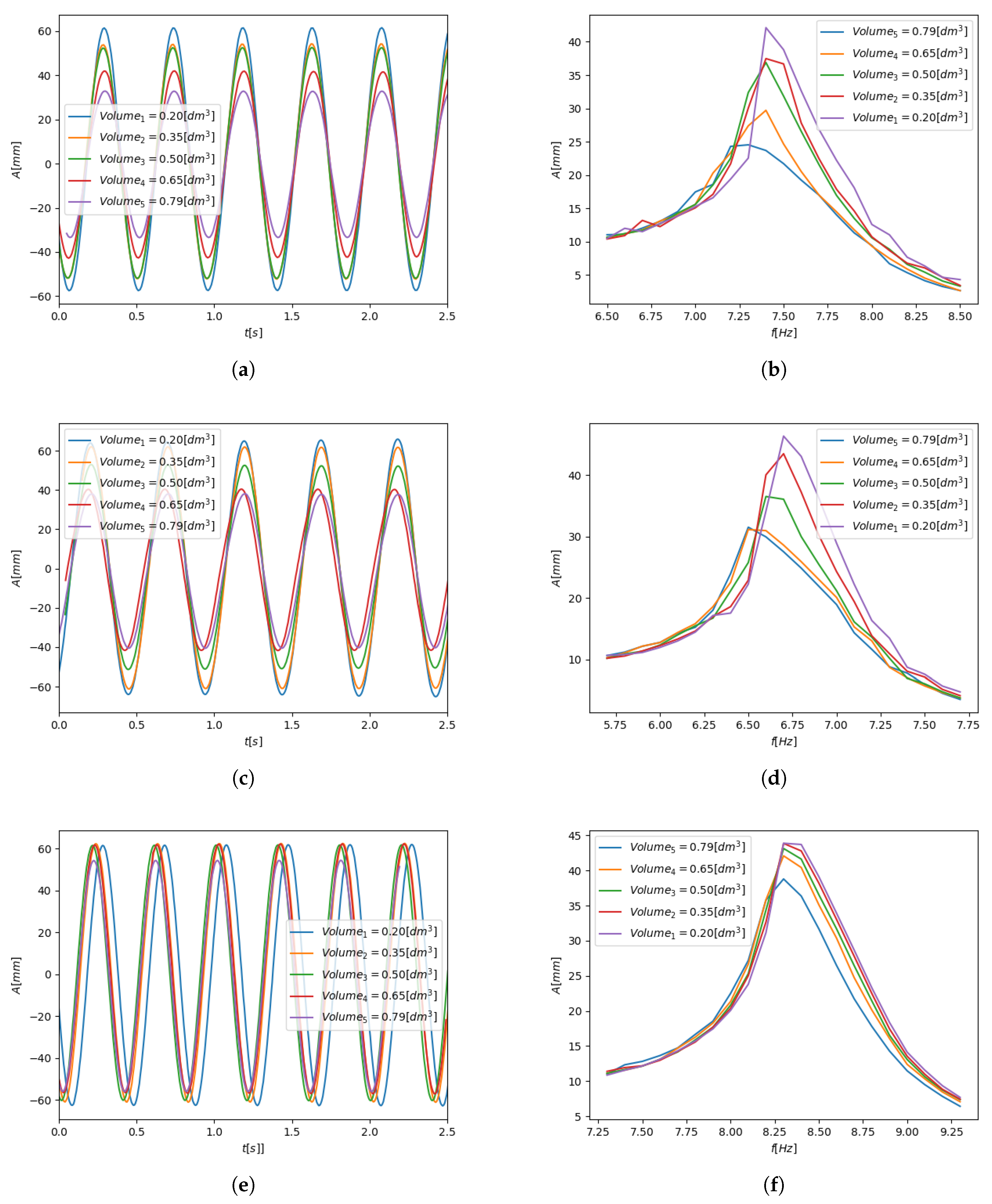
Figure 5.
Displacement waveforms (a,c,e) and RMS values (b,d,f) for various granular grains compositions. (a) Displacements of the beam—; (b) RMS of beam displacements—; (c) Displacements of the beam—; (d) RMS of beam displacements—; (e) Displacements of the beam—; (f) RMS of beam displacements—.
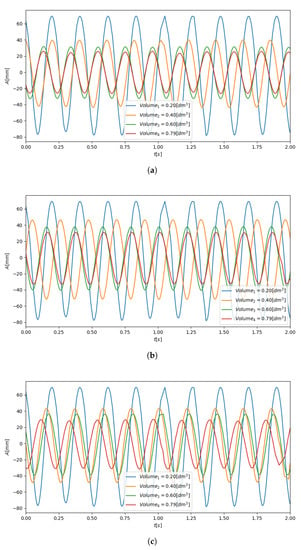
Figure 6.
Displacement waveforms for various composition of the grains. (a) Beam displacements—steel grains; (b) Beam displacements—plastic grains; (c) Beam displacements—mixed grains.
Diagrams depicted in Figure 5a,c,e illustrate the effect of variable container volume for three types (masses) of granular materials. The selection of appropriate mass of particles is of first importance. This parameter can not be easily changed in the presented TPID prototype. At this stage of the research it was assumed, that the total mass of the particles () was 5%, 10% and 20% of the whole system mass (). The second and the most important aspect is the volume of the container, controlled by the volume of the inflatable balloon placed inside the casing.
Data depicted in Figure 5 confirm that changing the volume of the container may lead to reduction of the resonance amplitudes. Lower number of particles (lower mass) is related to limited number of “intergranular” collisions what obviously decreases the dissipative properties of the TPIDs (Figure 5c,e). In Figure 5a,b it can be observed that the RMS amplitude for the case where the particles mass is 10% of the total mass of the system and for the lowest container volume () was 42.5 mm. The value of the considered parameter for the maximum volume of the container () was 22.5 mm, which can be described as a reduction of vibrations by 53%. Lower damping properties were observed for the remaining two cases of the particles mass. In experimental studies, in which the granular mass was 20% of the mass of the entire system, the recorded RMS amplitudes for minimal and maximal volumes were 46.3 mm and 31.5 mm respectively. Analyzing the presented data, it turns out that the system vibration amplitude decreased by 32%. In a situation where the TPID damper worked with the use of granules with a mass equal to only 5%, the reduction of system vibrations was much lower than in the first two cases and amounted to 12%. Analyzing the RMS amplitude for all cases also including the intermediate values of the damper volume, it can be observed that the amplitudes of the system response change nonlinearly, and thus the vibration damping effectiveness is also nonlinear as a function of the TPID damper working space variation. Switching “on” and “off” processes, which involves increasing the initial value of the operating volume slightly changes the natural frequencies of the considered system. This phenomenon is presented in Figure 5b,d,f. Nonlinear contact forces occur during collisions between the granules and the damper container. In the considered mechanical systems they are coupled with changes in the dynamics of the structure. The authors of Reference [7] show that changing (increasing) the gap volume in the PID damper results in two main phenomena: initially the reduction of the system’s frequency is observable, but after exceeding some specific volume threshold value the increase in the natural frequency of the system is noticed. The reason is the response of the grains movement, the occurrance contact forces and their duration in relation to the moving damped system. In the previously mentioned paper such an effect of changing the natural frequency is explained by a change of the effective mass. In the first range, the effective mass of the system increases, and after exceeding the specified value of the gap, the effective mass decreases. The structure which we proposed is evidently operating in the first described range. Such an observation shows some similarities between TPID and Tuned Mass Dampers. It can be stated that the proposed design of novel TPID device ensures all the advantages of classical PIDs [12], [41] or [3].
4.2. The Influence of the Grains Material
In this section, the authors focus on the influence of the grains material on the response of investigated system. In Figure 6a–c various displacement waveforms in the resonant range of the beam vibrations are depicted. At this stage four different volumes of the TPID compartment and three compositions of grains (steel, plastic and particles mixture) were taken into account. In the experiments the constant mass of the grains equal 10% of the dampened system was assumed. Such an approach resulted in slightly different volume of the loose material applied in TPID and in consequences the changeable number of particles involved in the collisions.
Analyzing the data presented in Figure 6a it can be stated, that for the steel particles the energy dissipation process is effective (more than 50% efficiency) even for small volumes of the damper compartments. The main disadvantage of this type of material is significantly reduced controlling process of the system dynamics. Changing the volume from the to causes a reduction of the displacement amplitudes by approximately 20%. A different phenomenon was observed for plastic grains (Figure 6b). In this case even the slightly changed volume of the damper compartment resulted in changing the damping properties of the system. Increasing the volume value from [dm] to [dm] causes decreasing of the displacement amplitude by app. 30%. Additionally, inflating the balloon to [dm] is connected to further decreasing of the amplitudes up to 50%. Applying the volume of the compartment reduces the value of recorded amplitudes by up to 70%. Plastic grains seem to be a much more interesting material for the purpose of controlling the dynamics of the investigated beam. Pumping the balloon, resulting in a gradual change in the volume of the operating space of the damper allows for a smooth change of its damping properties and allows for the application of this type of material in an effective strategy of semi-active vibration attenuation. For the steel-plastic composition of the grains (Figure 6c) experimental results are quite similar to the previously mentioned case illustrated in Figure 6b. Recorded amplitudes for the [dm] volume are slightly lower for grains mixture than for the pure plastic particles. In the contrary the amplitudes observed for [dm] are to some extent higher for the granular material combination. Although the dissipative properties of the TPID device in the case of fully inflated balloon ( of the compartment) seem to be independent on the type of used granular material (Figure 7), the plastic particles appear to be the optimal solution from the controlling point of view.
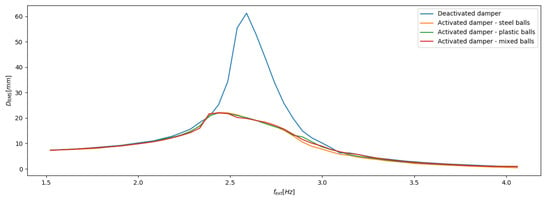
Figure 7.
RMS of displacements for various grains materials.
4.3. Spectrum Analysis
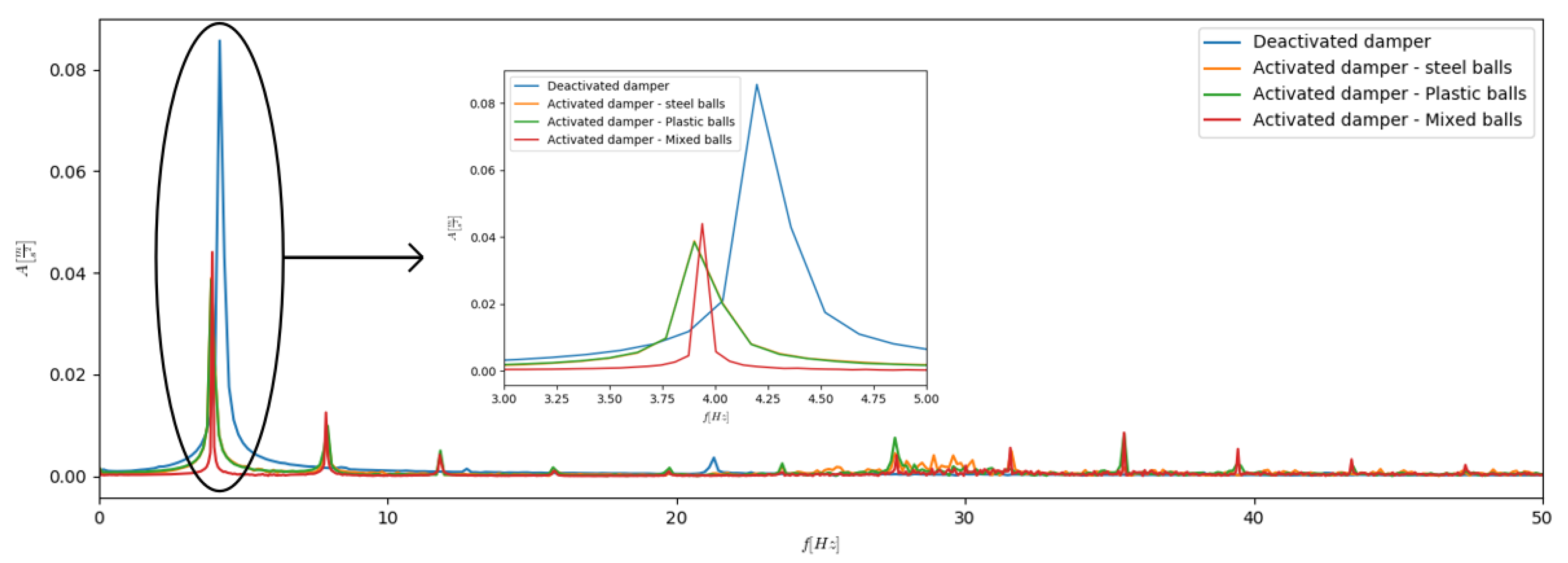
In the literature, it is hard to find the spectral analysis for the vibrated objects dampened by the PIDs. Such a situation results from the fact, that generally PIDs are passively calibrated to attenuate vibrations in the resonant range. In this paper the authors present an innovative Tuned Particles Impact Damping strategy, therefore the spectrum analysis seems to provide important information about the dynamics of the considered system. In Figure 8 the typical spectral analysis obtained for the constant mass of particles (10% of the whole system) and various granular materials is depicted. The maximal volume of the TPID compartment corresponding to the best damping properties of the device was taken into consideration. As the reference result the spectrum for the switched “off” state (minimal volume of the device) is presented.
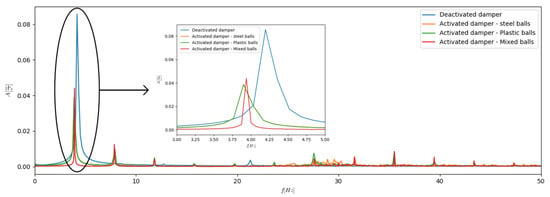
Figure 8.
Exemplary spectrum analysis.
Detailed analysis of the data depicted in Figure 8 revealed the significant decreasing of the acceleration amplitudes of the first component. Additionally in the zoomed region the shifting phenomenon of natural frequencies is observable. Similar phenomenon is observed for Tuned Mass Damper class of devices. Moreover, the complex character of intergranular collisions and multiple contacts between the grains and walls of the TPID casing results in insignificant increases of subsequent component amplitudes. This observation seems to be the only disadvantage of the proposed damper prototype. Nevertheless, it is worth emphasizing that the proposed solution is mainly intended for systems operating close to the first resonance frequency range. In Figure 8 the authors presented the whole spectrum including the higher frequencies. The basic intention of the authors was to focus on the first harmonic as the TPID devices are developed to work effectively in devices that will be subjected to such frequencies. The presented spectrum shows that the change of the material and the filling ratio also affect the higher harmonics but it is less important from the engineering point of view.
5. Modelling
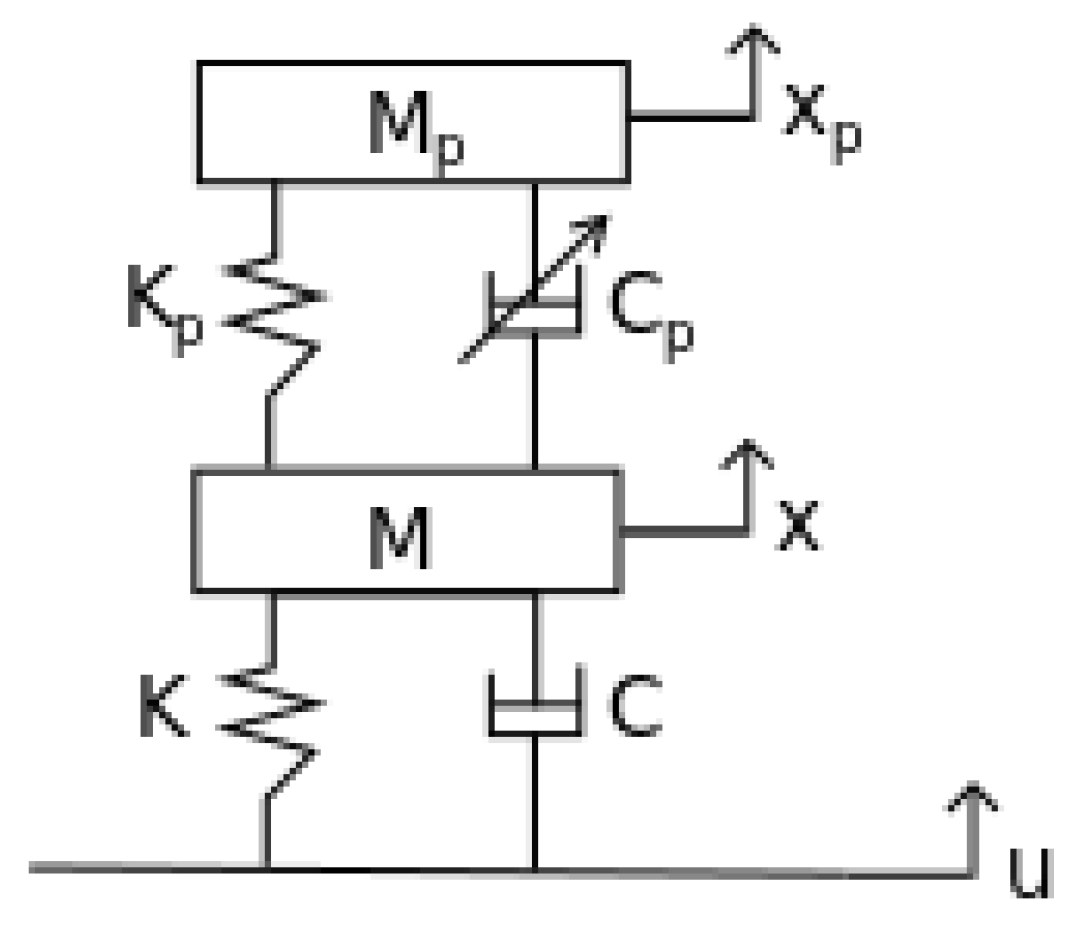
At the initial stage of TPID investigation the 2-DOF linear model (Figure 9), described by equations of motion (2) has been selected to capture the real behavior of the considered system. The authors want to emphasize the dynamics of the tested object in the resonant range for the TPID being in switched “on” and “off” states.
where M—reduced mass of the system (mass of the container included), —mass of particles, K—beam stiffness, C—beam damping, —TPID stiffness, —controllable TPID damping.
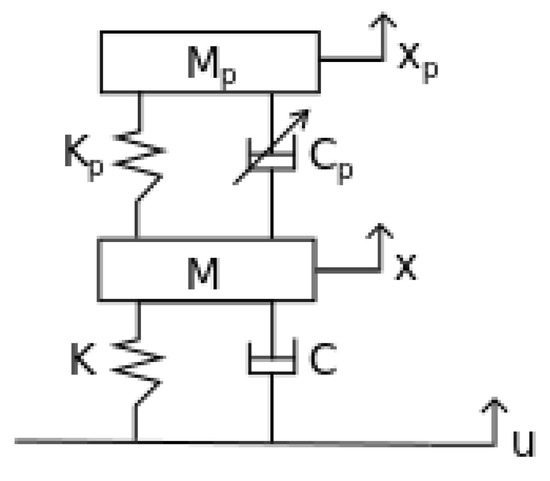
Figure 9.
Mathematical model.
K, C and M parameters were identified for free vibrations of the investigated cantilever beam in separate experimental tests. It was assumed that the value of parameter is constant during laboratory tests and results from the attachment of the container to the beam. It was calibrated basing on the experiments conducted for the fully compacted particles that is, for the lowest volume value () of the TPID container. The parameter values depend on the type of inelastic collisions between single particles and the character of their mutual contact with the container. In the paper it is assumed that variations of this parameter are the function of the TPID operation volume and can be described as:
where -damping parameter for the fully opened TPID device (volume of the container is ), activation function (4), -initial damping in the system (considered as the “intergranular” friction forces acting in the switched “off” state).
The parameter was determined for the test conducted in a fully turned “on” state. It involves the maximal number of collisions between loose material and container. On the contrary, the parameter value was captured for the minimal value of the container volume. Although the mathematical model (Figure 2) seems to be simple, its complexity lies in the previously mentioned complex phenomenon related to not fully understood interactions between internal particles. The confirmation of this fact is the data depicted in Figure 10 where the logarithmic damping decrement for the investigated beam free vibrations is illustrated. In Figure 10a,b the damping characteristics for various particles masses and different container volumes are presented respectively. The characteristics have been obtained on the basis of supplementary experiments. They consisted of measurements of free vibrations of the considered beam initially deflected at the free right end by 30 mm. The release of the deflected beam was achieved by burning out a thin thread attached to the tip of the element.
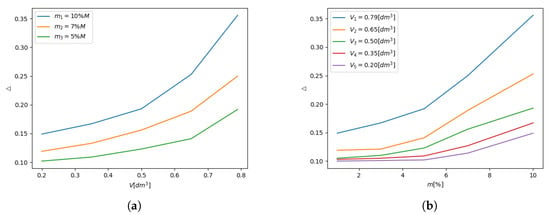
Figure 10.
Logarithmic damping decrement. (a) Variable particles mass; (b) Variable container volume.
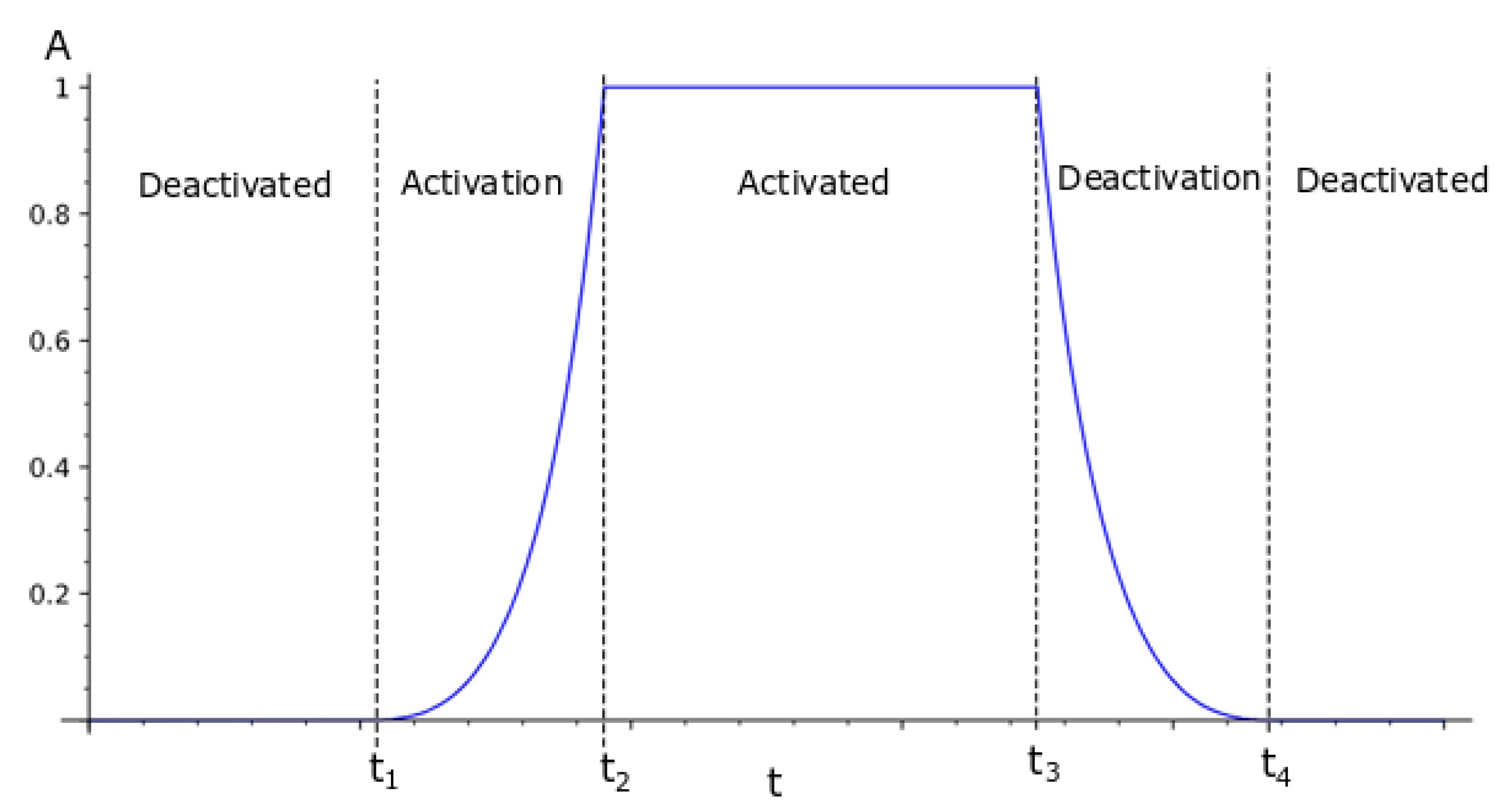
Basing on data presented in Figure 10 it can be stated that the higher mass of grains results in a more efficient energy dissipation process. Similarly, the higher volume of the TPID compartment is related to the more effective vibrations attenuation. The next problem is encountered during the volume changing of the compartment, that is, inflating and deflating of the internal balloon. These transition processes are not fully recognized yet, therefore the authors proposed exponential functions to reproduce them (Figure 11). The function (4) takes 0 value for the deflated balloon (the grains are compacted and can be treated as a concentrated mass). In the contrary, for the volume of the container the activation function takes a value of 1.
where —arbitrary coefficient ( was assumed during numerical simulations), —the activation and deactivation time (at this stage of investigations it was assumed that inflating and deflating times of the balloon were the same) and coefficients because simplifying the formula (4) for cases or , .
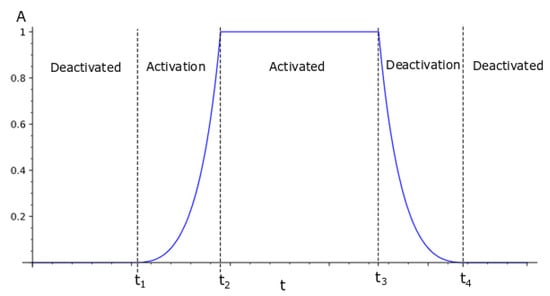
Figure 11.
Activation function .
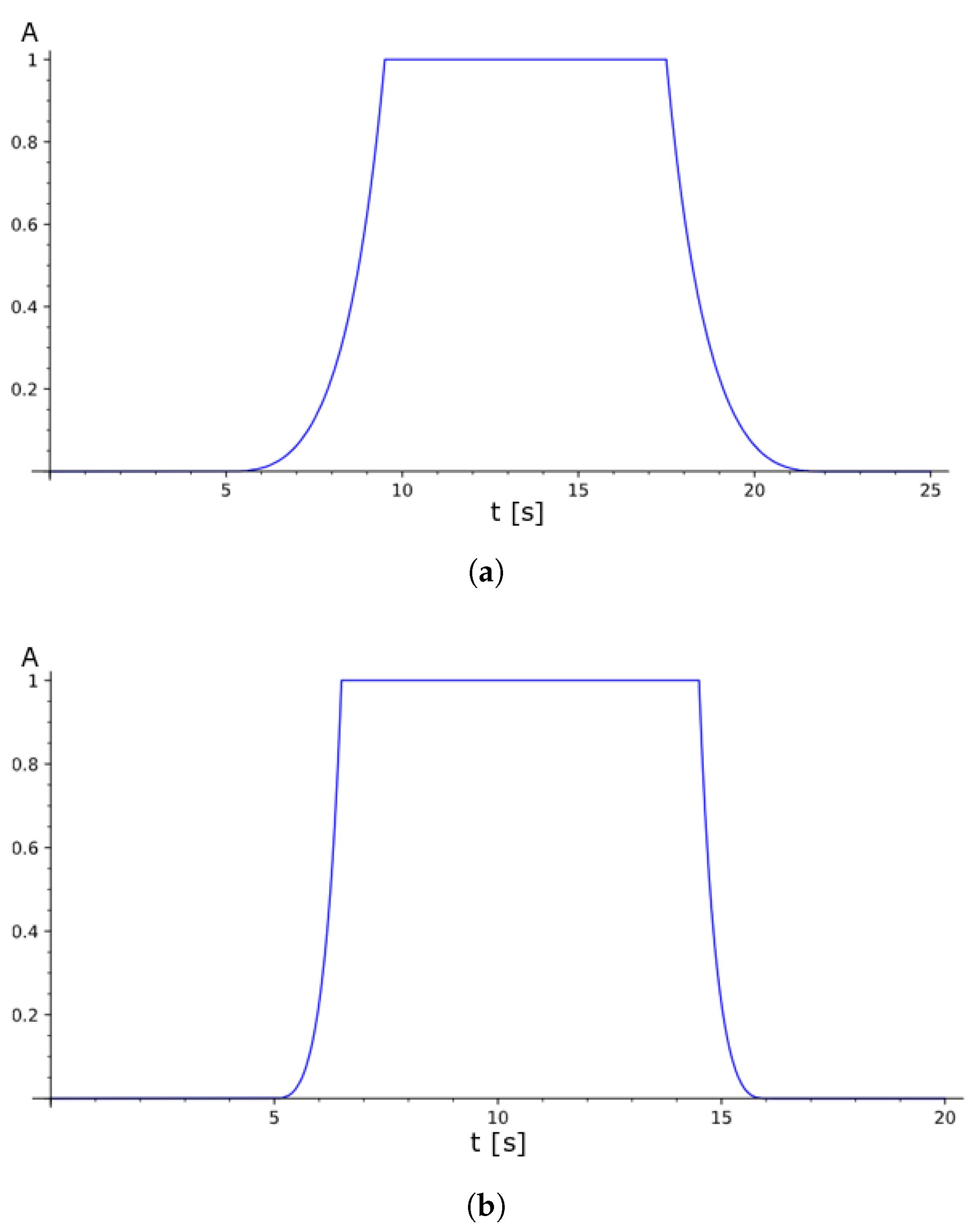
In the experiments, two various forms of activation functions were taken into consideration (Figure 12a,b). They corresponded to changes in the compartment volumes from to in s and s respectively. The investigated beam tip waveforms for the resonant range of excitations are depicted in Figure 13. For all described cases the plastic particles were involved. Two various numbers of grains corresponding to 10% and 5% of the total mass of the beam were taken into account. Additionally, different activation times, according to the data depicted in Figure 12, were applied in the experiments. Moreover, in Figure 13 the numerical simulation results are verified with the real response of the system.
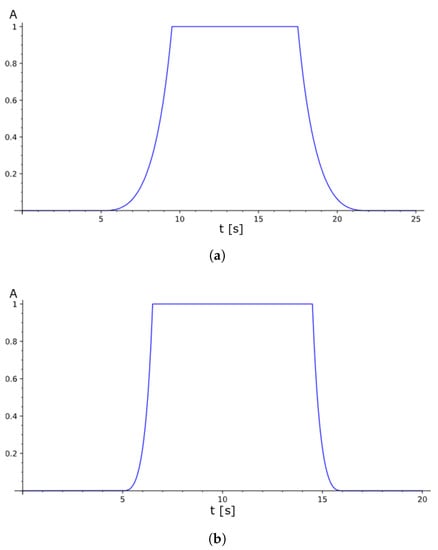
Figure 12.
A proposition of activation functions. (a) s; (b) s.
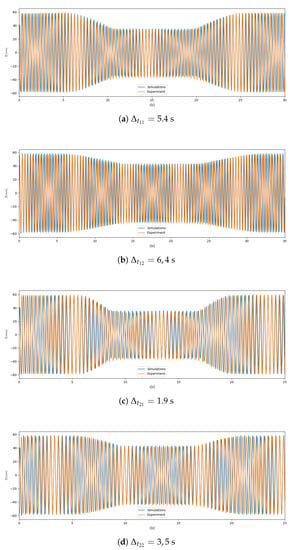
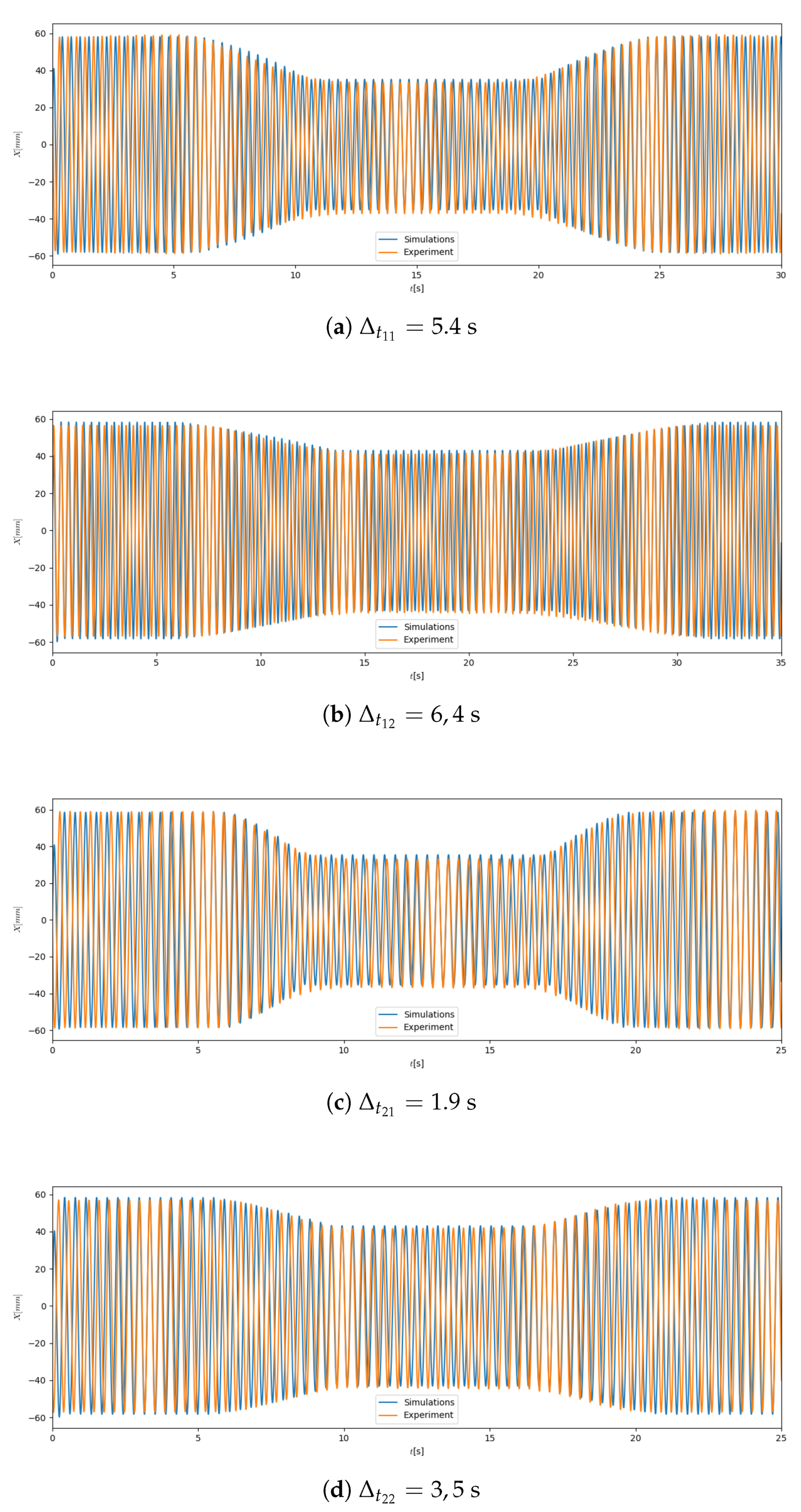
Figure 13.
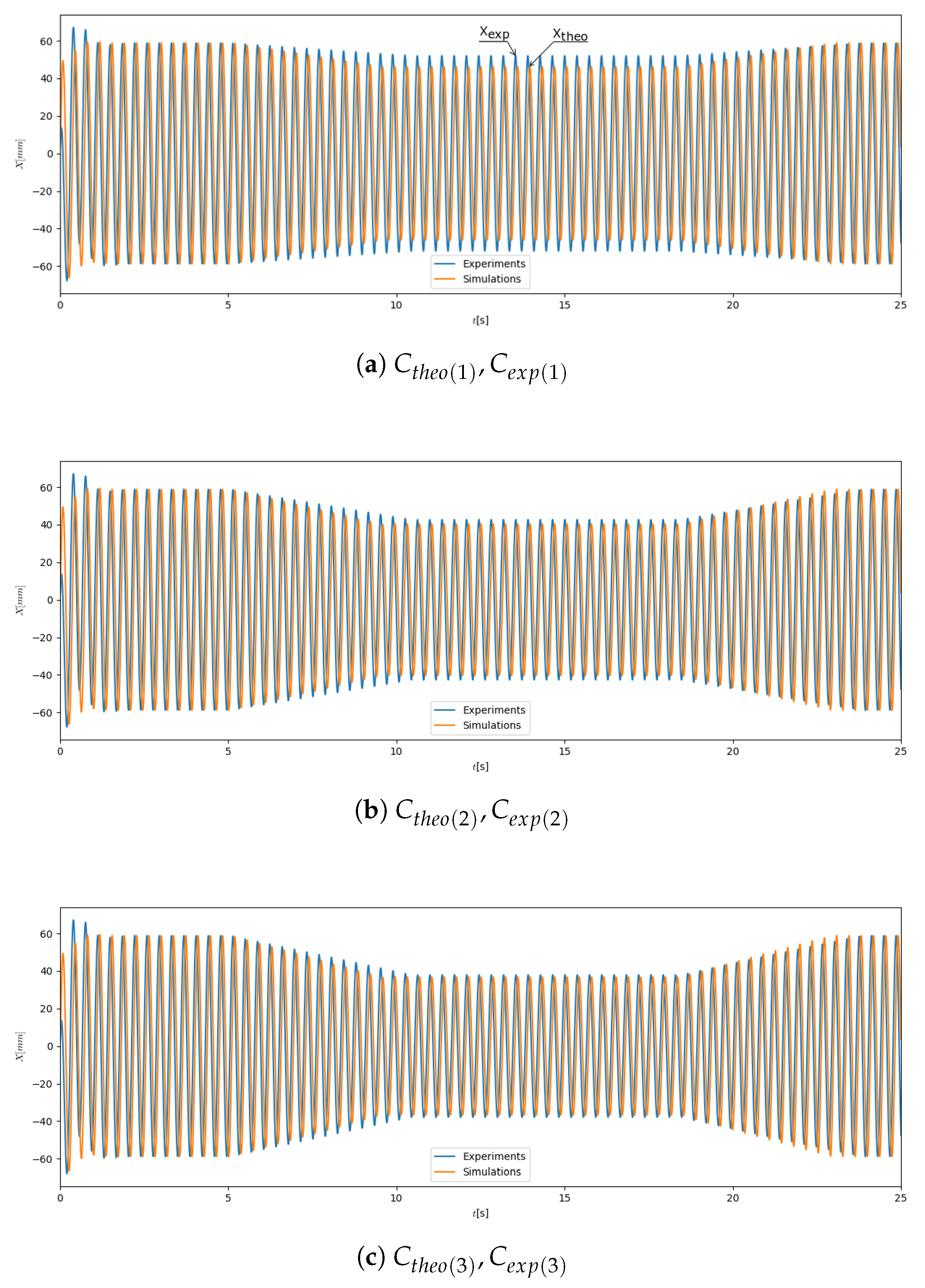
Verification of experimental and numerical data for various operational parameters: (a) 10% mass of grains, 4.5 s activation time; (b) 5% mass of grains, 4.5 s activation time; (c) 10% of grains, 1.5 s activation time; (d) 5% mass of grains, 1.5 s activation time.
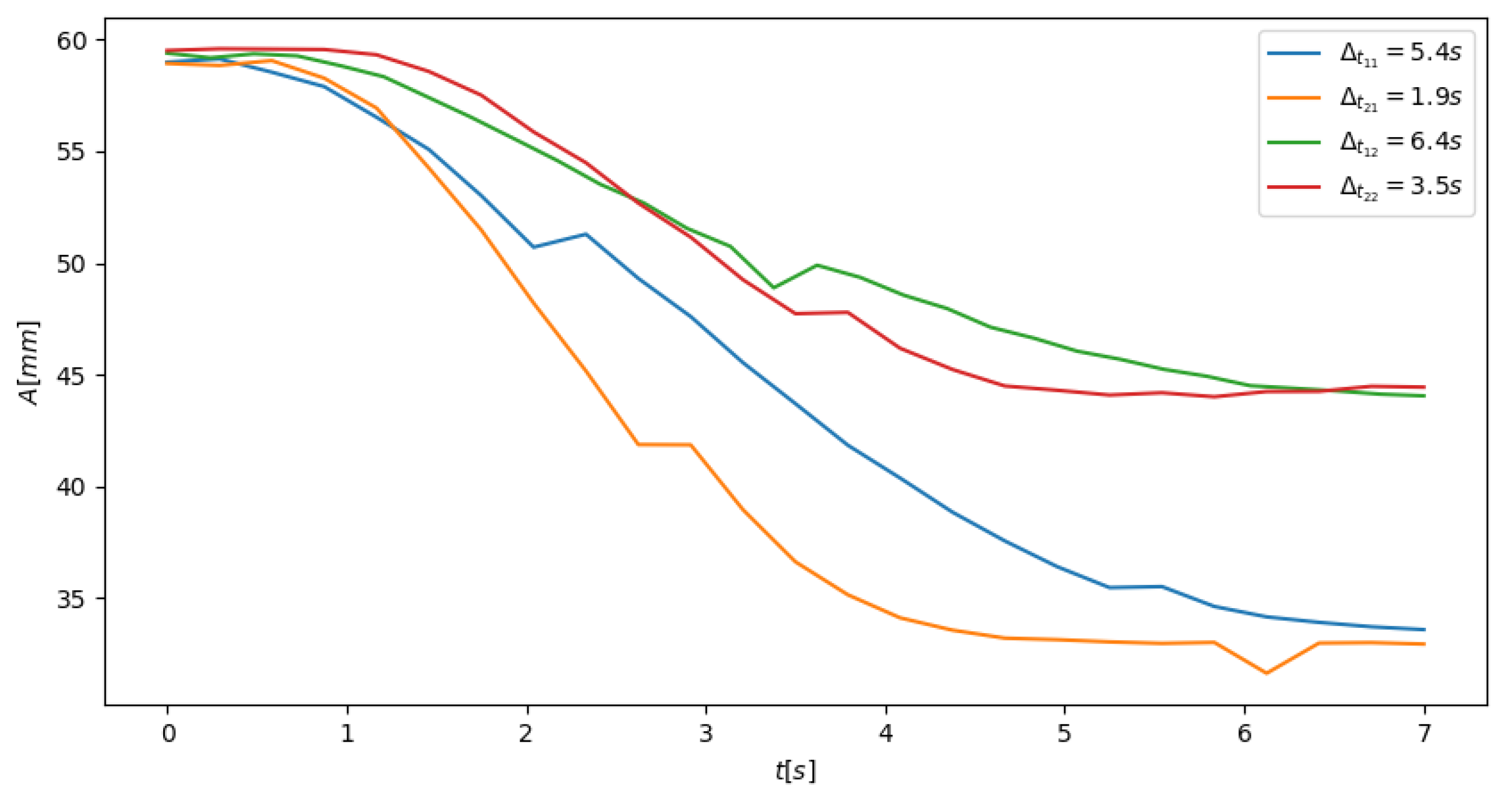
The data depicted in Figure 13 reveal interesting information. It is evident that the activation of the TPID device significantly reduced the resonant vibration amplitudes. The efficiency of granular damper is strongly dependent on the number (mass) of particles being involved in the damping process. On the basis of Figure 12 it can be observed that the larger amount of granular media increased the dissipative properties of the system. Changing the mass of the grains from 5% of the total mass into 10% increased the damping properties of considered device by 35%. This phenomenon is apparent for both damper activation times. The detailed analysis of data depicted in Figure 13 also revealed some damping inertia of the system. For the case of larger amount of particles and applied activation time s (resulted from inflating the balloon to the maximal volume) the time necessary for the recorded waveforms stabilization was 5.4 s (Figure 13d). Similarly to stabilize the vibrations of the beam dampened by lower number of particles (5% of the total mass) the same activation function s was required. Such observations were also valid for the shorter activation time s. The damping inertia for this case was s and s for larger and smaller amount of particles respectively. It is worth emphasizing that the transition from the TPID deactivated into fully activated state was relatively smooth. There were no uncontrolled increases in vibration amplitudes during the balloon pumping process. Figure 14, which depicts the envelopes of registered waveforms for various parameters of the investigated TPID prototype, can be a transparent summary of the experimental work carried out in the paper.
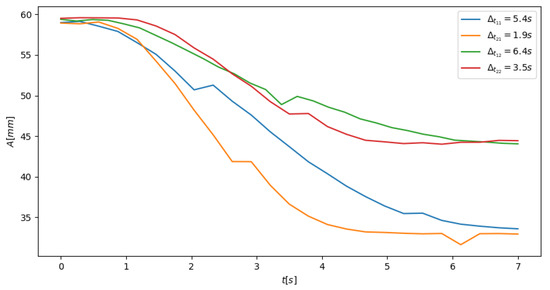
Figure 14.
Envelopes of recorded waveforms for various operating parameters.
It is worth emphasizing that the proposed mathematical model of the system is quite reliable. The verification between real experimental responses of the vibrated beam and numerical simulations being carried out on the basis of Equations (2)–(4) revealed a satisfactory convergence (Figure 13). The differences between real and theoretical waveforms for the “turned on” and “turned off” states are negligible.
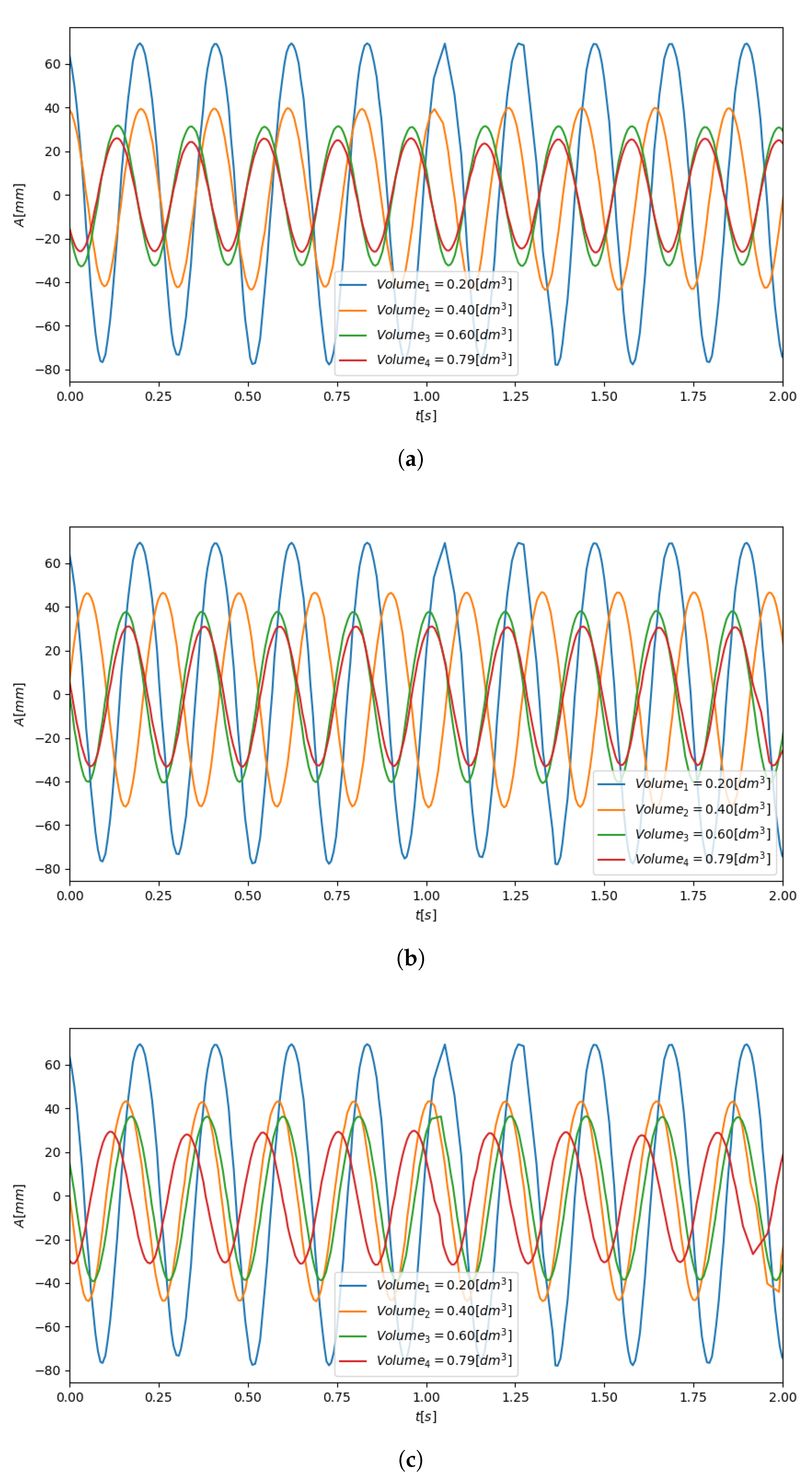
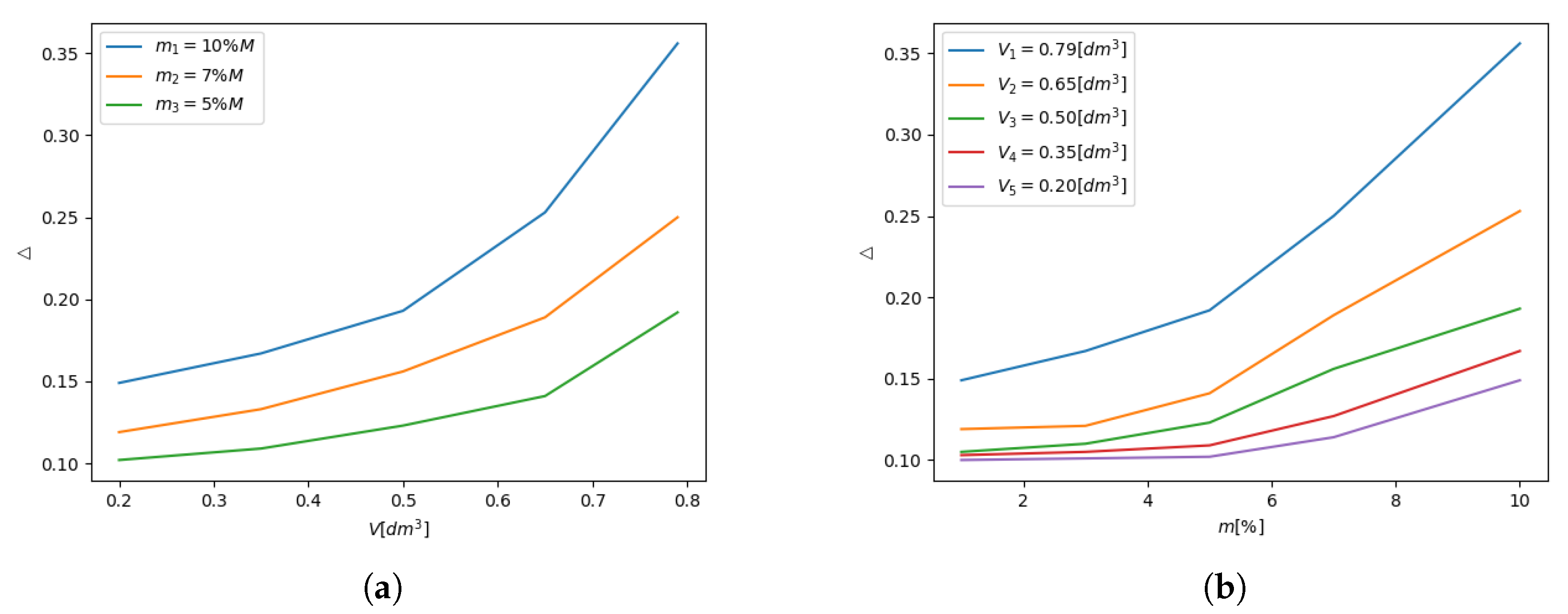
In the next stage of a research the authors examined responses of the kinematically excited cantilever beam for various volumes of the TPID container (excluding turned “on” and “off” states). Three various volumes of the device corresponding to volumes equal to , and [dm] were taken into account. Plastic grains having the mass equal 10% of the total mass of the system were involved in the tests. The registered waveforms are presented in Figure 15. In Figure 15 also the numerical simulation results, derived from Equations (2)–(4) are presented. Knowing the temporary volume value of the TPID device the corresponding damping coefficient value was calculated Equation (3). Basing on data depicted in Figure 15 it can be stated that the model is capable to capture the real behavior of the dampened system. To calculate the quantitative difference between the theoretical and experimental responses the parameter has been introduced (5)

Figure 15.
Waveforms for various values of the container volume: (a) [dm]; (b) [dm]; (c) [dm].
The parameter value decreases for higher values of the container volume (Figure 15). The list of values of the considered parameter is presented in Table 3.

Table 3.
Error parameter values for various volumes of the TPID compartment.
6. Conclusions
The novelty of the proposed TPID device is the application of a special balloon, that has variable volume and is filled with granules. Through inflating and deflating the previously mentioned balloon, the TPID device volume is shifted in a controlled manner, enabling the rapid change of its damping parameters—the volume ratio of particles and container. Damping properties of granules made of plastic, steel and their combinations have been experimentally tested. In addition, tests were carried out for various cases of the container filling ratio and grains mass for the full range of excitation frequencies (before, in resonance and after resonance ranges). Experiments confirmed that the proposed TPID damper structure retains the advantages of standard PID devices ([3,5,7,22]). It was also observed that the type of grains material strongly affects the damping properties of the granular damper. The particles are characterized by various physical parameters, for example, Young’s modulus. Differences in values of the particles restitution coefficient cause changes in the grains movement and collisions character. They also result in different values of contact forces. Basing on detailed analyses of experimental data the authors concluded that the plastic particles allow for a wide range of controllability and tuning of the system response.
Another parameter that significantly influences the dissipative properties of investigated TPID prototype is the mass of the particles. Laboratory tests revealed that increasing the mass of granular material being involved in inelastic collisions inside the PID container improved the damping features of the prototype. Obviously some specific threshold value for the number of particles being involved in the damping process exist. Exceeding this value will cause the limitations of free space for intergranular impacts and consequently will lead to decreasing the dissipative properties of the system. This complex phenomenon, dependent not only on the filling ratio of the TPID, but also on the shape of grains and container and materials involved in contacts, was not discussed in the paper. Assuming too low a mass of granular materials (insufficient number of particles) will not provide the desired vibrations attenuation effect.
The authors assumed that the Young’s modulus is the main parameter of granular material that affects the damping properties. Defining in an empirical way the energy dissipation components is a challenging task. At the current stage of investigations the authors did not conducted such tests. The shape and changeable in time volume of the container make the described problem more complicated. The TPID container was developed by the 3D printing technique. The applied filament material is much softer than the grains material. The problem of investigating the container’s material influence on the global damping properties of the system (TPID effectiveness) is important and requires carrying out additional and time-consuming studies. Also crucial from the operational point of view effects of grains degradation or temperature changes were not discussed in the paper.
The biggest advantage of the proposed TPID prototype is the possibility of adjusting its damping characteristics according to various types of temporary excitations. Discussed proposition by simply adding the expandable balloon to the classical PID device enabled the user to fully control the volume of the grains casing (by the external pump) and in fact transformed the passive PID device into the innovative semi-active TPID damper.
In the modeling section the simple 2DOF linear mathematical model was adopted. To capture nonlinearities of the real system resulted from the inelastic character of collisions inside the granular media the exponential activation function was proposed. The function confirmed its reliability not only for the “on” and “off” states of the TPID but also allowed us to achieve satisfactory results for various transient states of the device being inflated. The biggest differences between the model and the real object did not exceed 6.5%.
In the authors’ opinion, the proposed TPID construction opens new perspectives for the innovative semi-active, inexpensive and environmental friendly damping of vibrations strategies.
Author Contributions
Conceptualization, M.Ż. and R.Z.; methodology, M.Ż. and R.Z.; software, M.Ż.; validation, M.Ż. and R.Z.; formal analysis, M.Ż.; investigation, M.Ż.; resources, R.Z.; data curation, M.Ż.; writing–original draft preparation, M.Ż.; writing–review and editing, R.Z.; visualization, M.Ż.; supervision, R.Z.; project administration, M.Ż. and R.Z.; funding acquisition, M.Ż. and R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by GRANT WEWNĘTRZNY DLA PRACOWNIKÓW POLITECHNIKI WARSZAWSKIEJ WSPIERAJĄCY PROWADZENIE DZIAŁALNOŚCI NAUKOWEJ W DYSCYPLINIE INŻYNIERIA MECHANICZNA, grant number 504/04555/1150/43.090048.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fu, B.; Jiang, H.; Wu, T. Comparative studies of vibration control effects between structures with particle dampers and tuned liquid dampers using substructure shake table testing methods. Soil Dyn. Earthq. Eng. 2019, 121, 421–435. [Google Scholar] [CrossRef]
- Gnanasambandham, C.; Stender, M.; Hoffmann, N.; Eberhard, P. Multi-scale dynamics of particle dampers using wavelets: Extracting particle activity metrics from ring down experiments. J. Sound Vib. 2019, 454, 1–13. [Google Scholar] [CrossRef]
- Marhadi, K.S. Particle impact damping: Effect of mass ratio, material, and shape. J. Sound Vib. 2005, 283, 433–448. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, B.; Tian, A.; Wei, D.; Jiang, X. Prediction methods for the damping effect of multi-unit particle dampers based on the cyclic iterations of a single-unit particle damper. J. Sound Vib. 2019, 443, 341–361. [Google Scholar] [CrossRef]
- Snoun, C.; Trigui, M. Design parameters optimization of a particles impact damper. Int. J. Interact. Des. Manuf. 2018, 12, 1283–1297. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Zheng, Z.; Mo, L.; Wu, C. Parametrical optimization of particle dampers based on particle swarm algorithm. Appl. Acoust. 2020, 160, 107083. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, T.; Wang, X.; Fang, J. Rheology behavior and optimal damping effect of granular particles in a non-obstructive particle damper. J. Sound Vib. 2016, 364, 30–43. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, Z.; Chen, T.; Liu, H.; Zhang, K. Discrete element method model of electromagnetic particle damper with a ferromagnetic end cover. J. Sound Vib. 2019, 446, 211–224. [Google Scholar] [CrossRef]
- Junling, C.; Christos, G. Tuned rolling-ball dampers for vibration control in wind turbines. J. Sound Vib. 2013, 332, 5271–5282. [Google Scholar] [CrossRef]
- Xiao, W.; Lu, D.; Song, L.; Guo, H.; Yang, Z. Influence of particle damping on ride comfort of mining dump truck. Mech. Syst. Signal Process. 2020, 136, 106509. [Google Scholar] [CrossRef]
- Zhang, Z.; Staino, A.; Basu, B.; Nielsen, S.R. Performance evaluation of full-scale tuned liquid dampers (TLDs) for vibration control of large wind turbines using real-time hybrid testing. Eng. Struct. 2016, 126, 417–431. [Google Scholar] [CrossRef]
- Du, Y.; Wang, S. Modeling the fine particle impact damper. Int. J. Mech. Sci. 2010, 52, 1015–1022. [Google Scholar] [CrossRef]
- Yüzbasioglu, T.; Aramendiz, J.; Fidlin, A. On the numerical simulations of amplitude-adaptive impact dampers. J. Sound Vib. 2020, 468, 115023. [Google Scholar] [CrossRef]
- Vinayaravi, R.; Kumaresan, D.; Jayaraj, K.; Asraff, A.; Muthukumar, R. Experimental investigation and theoretical modelling of an impact damper. J. Sound Vib. 2013, 332, 1324–1334. [Google Scholar] [CrossRef]
- Egger, P.; Caracoglia, L. Analytical and experimental investigation on a multiple-mass-element pendulum impact damper for vibration mitigation. J. Sound Vib. 2015, 353, 38–57. [Google Scholar] [CrossRef]
- Afsharfard, A. Application of nonlinear magnetic vibro-impact vibration suppressor and energy harvester. Mech. Syst. Signal Process. 2018, 98, 371–381. [Google Scholar] [CrossRef]
- Veeramuthuvel, P.; Shankar, K.; Sairajan, K. Application of particle damper on electronic packages for spacecraft. Acta Astronaut. 2016, 127, 260–270. [Google Scholar] [CrossRef]
- Sonmez, E.; Nagarajaiah, S.; Sun, C.; Basu, B. A study on semi-active Tuned Liquid Column Dampers (sTLCDs) for structural response reduction under random excitations. J. Sound Vib. 2016, 362, 1–15. [Google Scholar] [CrossRef]
- Sánchez, M.; Manuel Carlevaro, C. Nonlinear dynamic analysis of an optimal particle damper. J. Sound Vib. 2013, 332, 2070–2080. [Google Scholar] [CrossRef]
- Sánchez, M.; Pugnaloni, L.A. Effective mass overshoot in single degree of freedom mechanical systems with a particle damper. J. Sound Vib. 2011, 330, 5812–5819. [Google Scholar] [CrossRef]
- Lei, X.; Wu, C. Optimizing parameter of particle damping based on (Leidenfrost) effect of particle flows. Mech. Syst. Signal Process. 2018, 104, 60–71. [Google Scholar] [CrossRef]
- Djemal, F.; Chaari, R.; Gafsi, W.; Chaari, F.; Haddar, M. Passive vibration suppression using ball impact damper absorber. Appl. Acoust. 2019, 147, 72–76. [Google Scholar] [CrossRef]
- Yao, B.; Chen, Q.; Xiang, H.; Gao, X. Experimental and theoretical investigation on dynamic properties of tuned particle damper. Int. J. Mech. Sci. 2014, 80, 122–130. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, C.; Zhang, Y. A novel technique to predict harmonic response of Particle-damping structure based on ANSYS® secondary development technology. Int. J. Mech. Sci. 2018, 144, 877–886. [Google Scholar] [CrossRef]
- Yin, Z.; Su, F.; Zhang, H. Investigation of the energy dissipation of different rheology behaviors in a non-obstructive particle damper. Powder Technol. 2017, 321, 270–275. [Google Scholar] [CrossRef]
- Veeramuthuvel, P.; Shankar, K.; Sairajan, K.; Machavaram, R. Prediction of Particle Damping Parameters Using RBF Neural Network. Procedia Mater. Sci. 2014, 5, 335–344. [Google Scholar] [CrossRef]
- Hu, L.; Shi, Y.; Yang, Q.; Song, G. Sound reduction at a target point inside an enclosed cavity using particle dampers. J. Sound Vib. 2016, 384, 45–55. [Google Scholar] [CrossRef]
- Xiao, W.; Li, J.; Wang, S.; Fang, X. Study on vibration suppression based on particle damping in centrifugal field of gear transmission. J. Sound Vib. 2016, 366, 62–80. [Google Scholar] [CrossRef]
- Gharib, M.; Ghani, S. Free vibration analysis of linear particle chain impact damper. J. Sound Vib. 2013, 332, 6254–6264. [Google Scholar] [CrossRef]
- Gharib, M.; Karkoub, M.; Ghamary, M. Numerical investigation of Linear Particle Chain impact dampers with friction. Case Stud. Mech. Syst. Signal Process. 2016, 3, 34–40. [Google Scholar] [CrossRef]
- Farid, M.; Gendelman, O. Response regimes in equivalent mechanical model of strongly nonlinear liquid sloshing. Int. J.-Non Mech. 2017, 94, 146–159. [Google Scholar] [CrossRef]
- Gendelman, O. Analytic treatment of a system with a vibro-impact nonlinear energy sink. J. Sound Vib. 2012, 331, 4599–4608. [Google Scholar] [CrossRef]
- Gendelman, O.; Alloni, A. Forced System with Vibro-impact Energy Sink: Chaotic Strongly Modulated Responses. Procedia IUTAM 2016, 19, 53–64. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Sarkar, S.; Staino, A. Improved reliability of wind turbine towers with active tuned mass dampers (ATMDs). J. Sound Vib. 2018, 419, 103–122. [Google Scholar] [CrossRef]
- Hussan, M.; Rahman, M.S. Multiple tuned mass damper for multi-mode vibration reduction of offshore wind turbine under seismic excitation. Ocean. Eng. 2018, 160, 449–460. [Google Scholar] [CrossRef]
- Jin, J.; Yang, W.; Koh, H.I.; Park, J. Development of tuned particle impact damper for reduction of transient railway vibrations. Appl. Acoust. 2020, 169, 107487. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.; Masri, S.F.; Lu, X. Particle impact dampers: Past, present, and future. Struct. Control. Health Monit. 2018, 25, e2058. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, T.; Wang, X.; Fang, J. A model of Tuned Particle Damper. In Proceedings of the 22nd International Congress on Sound and Vibration, Florence, Italy, 12–16 July 2015. [Google Scholar]
- Zhang, K.; Xi, Y.; Chen, T.; Ma, Z. Experimental studies of tuned particle damper: Design and characterization. Mech. Syst. Signal Process. 2018, 99, 219–228. [Google Scholar] [CrossRef]
- Zurawski, M.; Zalewski, R.; Chilinski, B. Concept of an Adaptive-Tuned Particles Impact Damper. J. Theor. Appl. Mech. 2020, 58, 811–816. [Google Scholar] [CrossRef]
- Dehghan-Niri, E.; Zahrai, S.M.; Rod, A.F. Numerical studies of the conventional impact damper with discrete frequency optimization and uncertainty considerations. Sci. Iran. 2012, 19, 166–178. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).