Learning Optimal Time Series Combination and Pre-Processing by Smart Joins

Abstract

In industrial applications of data science and machine learning, most of the steps of a typical pipeline focus on optimizing measures of model fitness to the available data. Data preprocessing, instead, is often ad-hoc, and not based on the optimization of quantitative measures. This paper proposes the use of optimization in the preprocessing step, specifically studying a time series joining methodology, and introduces an error function to measure the adequateness of the joining. Experiments show how the method allows monitoring preprocessing errors for different time slices, indicating when a retraining of the preprocessing may be needed. Thus, this contribution helps quantifying the implications of data preprocessing on the result of data analysis and machine learning methods. The methodology is applied to two case studies: synthetic simulation data with controlled distortions, and a real scenario of an industrial process.

1. Introduction and Description of the Problem

In machine learning there are several steps to follow in order to perform model construction. Many of them, such as feature selection, feature extraction and model training, are based on mathematical optimization. However, the initial preprocessing is often not explicitly and quantitatively optimized.

In preprocessing, one of the main steps consists of obtaining all the features that will be used in model generation. The features can come from different origins and joining all the data adequately can be hard. The specific case of working with time series has the advantage of the use of a temporal reference system, a timeline that enables merging the observations. Nevertheless, each feature has its own sampling, and all of them should be resampled to construct a single multi-variate time series in a synchronized way.

This resampling is done by feature, and, depending on the application objectives, different characteristics of data joining methods should be taken into account. Examples of objective measures of preprocessing quality might be based on measures of distortion and on the information lost in the process. Further considerations might be related to the causal nature of the resulting system, or to the amount of delay (or anticipation, in case of being shifted to a prior time instance) applied to the different original series to synchronize them.

Note that these properties can have different degrees of practical importance depending on the application domain. On the one hand, in the case of real-time prediction, data anticipation can imply the need of waiting for a new data entrance, resulting a big delay in the prediction; obviously a data prediction approach based on time series analysis could be used to avoid this problem, using a correction method in case a significant difference between predicted and real values is detected. On the other hand, information loss and data distortion can have a significant impact on the predictive power of the model.

1.1. Background

In the context of SQL database engines [1], a time series is a sequence of data values measured at successive, though not necessarily regular, points in time (https://cloud.ibm.com/docs/sql-query?topic=sql-query-ts_intro—IBM Cloud SQL Query documentation). Each entry in a time series is called an observation. Each observation comprises a timetick that indicates when the observation was made, and the data recorded for that observation. The set of timeticks defines a temporal base or temporal reference system for the series.

A temporal join is a join operation that operates on time series data. It produces a single array time series based on the original input data and the new temporal reference system.

This section introduces a range of common SQL joining methodologies. Specifically, the following methods will be introduced: left join, nearest join, forward join and backward join. Notably, the outer join is not contemplated, as the obtained results are the same as those from other selected methods (backward join or forward join) depending on the selection of a function for filling in Non-Available (NA) values (ffill or bfill).

In order to simplify the explanation of these methods, a specific example will be used, together with terminology from the documentation of the widely adopted pandas (https://pandas.org—Python data analysis and manipulation tool) data analysis library. Suppose that sensor data $y\left(t_O\right)$ is acquired with the temporal reference system $t_O$ as shown in

Table 1. Problem definition. (a) Captured data. (b) Desired temporal reference system.

(a)
${\mathit{t}}_{\mathit{O}}$	$\mathit{y}$
10:00	$y_1$
10:02	$y_2$
10:16	$y_3$
10:27	$y_4$
(b)
${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00
10:15
10:30

a. For model learning, suppose the temporal reference system $t_D$ shown in Table 1b is required.

Finally, suppose the function $\mathit{ffill}$ is selected for filling NA values, and that this function operates by forward-filling such NA values with the nearest prior known data value.

1.1.1. Left Join

The left join method takes only samples from y that are synchronized with $t_D$, in other words, only data that originally had the desired time is used.

Table 2. Result of left join. (a) After applying the join. (b) After filling Non-Available (NA) values.

(a)
${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00	$y_1$
10:15	NA
10:30	NA
(b)
${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00	$y_1$
10:15	$y_1$
10:30	$y_1$

a shows the application of a left join to the example. After filling NA values, the results shown in Table 2b are obtained.

In this particular example, three samples from y are not taken into account in the joined dataset. In this sense, part of the information in the original data is lost.

1.1.2. Nearest Join

A nearest join takes into account the nearest known available data from y. Results from the join are shown in

Table 3. Result nearest join.

${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00	$y_1$
10:15	$y_3$
10:30	$y_4$

.

Depending on the distribution of y, future knowledge of future data can be added to the past in a non-causal manner. In the example, the joined series at 10:15 uses data from 10:16.

1.1.3. Forward Join

In a forward join, samples of $t_D$ that are not available in $t_O$ are selected using subsequent matches from y. Results from the join are shown in

Table 4. Result of forward join. (a) After applying the join. (b) After filling NA values.

(a)
${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00	$y_1$
10:15	$y_3$
10:30	NA
(b)
${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00	$y_1$
10:15	$y_3$
10:30	$y_3$

a, and after filling NA values in Table 4b.

1.1.4. Backward Join

In a backward join, samples of $t_D$ that are not available in $t_O$ are selected using the nearest prior match. Results from the join are shown in

Table 5. Result of backward join.

${\mathit{t}}_{\mathit{D}}$	$\widehat{\mathit{y}}$
10:00	$y_1$
10:15	$y_2$
10:30	$y_4$

.

Given the above existing methods, the remainder of this paper considers the problem of locally selecting an optimal method by the optimization of a quantitative measure of the quality of the obtained joined series.

1.2. Paper Contributions and Structure

We consider that the need to define an operational mechanism to align multiple time series with a different time base by optimizing of a cost function that can be defined by the user is not adequately addressed in the present literature. In this sense, the contributions put forward by this paper include:

• The idea that the preprocessing steps in a machine learning workflow can be subject to an optimization procedure that is similar to the one used with e.g., an empirical risk estimate in the actual model learning step.
• The idea that a join operation among tables representing time series with different time bases as operated by e.g., a SQL database engines can be learned based on previous data records.
• A specific algorithm and implementation for a method meant to align multiple time series with different time bases.

The rest of the paper is structured as follows. Section 2 introduces the state of the art approaches. The methodology and a proposed solution are explained in Section 3. Section 4 provides a description of the case studies, whereas Section 5 shows the results of those case studies. Finally, conclusions and future work are presented in Section 6.

2. State of the Art

A number of contributions have been put forward in the literature that deal with the need to align of time series. On the one hand, such a need could stem from the fact that the time series described related phenomena with “warped” temporal aspects (as in Dynamic Time Warping). On the other hand, such a need could depend on the fact that the time series suffer from the effects of different decimation processes (as in the literature related to Dynamic Processes).

In the first group, Folgado et al. [2] considered an extension of Dynamic Time Warping based on a distance which characterized the degree of time warping between two sequences meant for applications where the timing factor is essential, and proposed a Time Alignment Measurement, which delivered similarity information on the temporal domain.

Morel et al. [3] extended Dynamic Time Warping to sets of signals. A significant point with respect to the topic of the present paper is the definition of a tolerance that takes into account the admissible variability around the average signal.

One of the nearest related topics is trying to solve, at the same time, several goals, or to deal with several constraints in parallel. In this sense, there are some works which tackle scheduling problems; a review of this type of models in a practical problem related to flow shop scheduling is presented by Sun et al. [4]. The authors stated that that heuristic and meta-heuristic methods and hybrid procedures were proven much more useful than other methods in large and complex situations.

Tawhid and Savsani [5] proposed a novel multi-objective optimization algorithm named multi-objective sine–cosine algorithm (MO-SCA) which was based on the search technique of the sine–cosine algorithm. They ended obtaining different non-discriminatory levels to preserve the diversity among the set of solutions.

Task scheduling is another problem related to this paper requiring multi-objective optimization paradigms. Zuo et al. [6] presented a solution based on an Ant Colony approach to deal with Cloud Computing computational load and storage minimization. In the same direction, Zahedi et al. [7] presented an approach related to vehicle routing for goods distributions in emergency situations. The data from a 2017 big earthquake in India was used, considering the demands heterogeneity and dynamics, distribution planning of goods and routing of vehicles simultaneously by means of a genetic algorithm.

Finally, regarding forecasting, Yang et al. [8] presented a system based on a dual decomposition strategy and multi-objective optimization for electricity price forecasting with the goal of balancing electricity generation and consumption. Data pre-processing was fundamental in the selected time window.

3. Proposed Solution: Smart Join

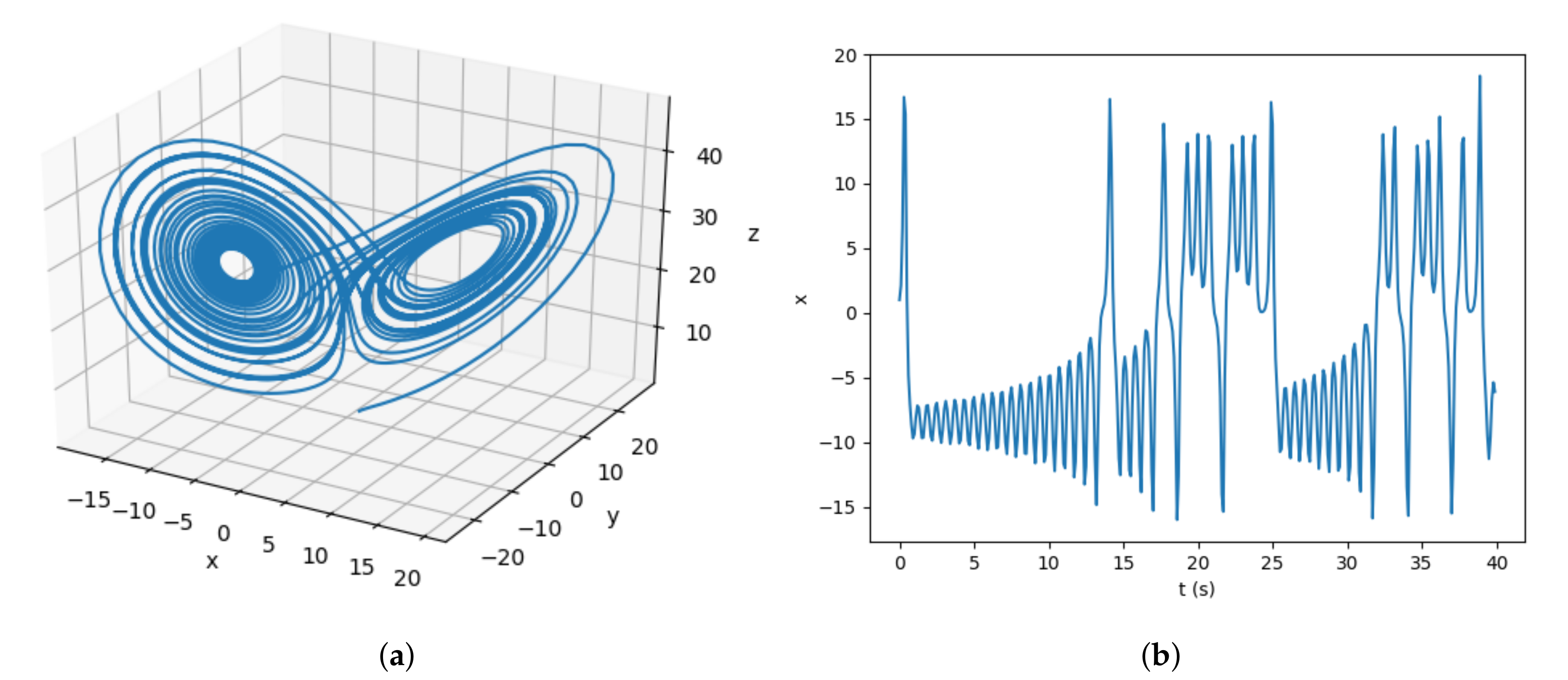
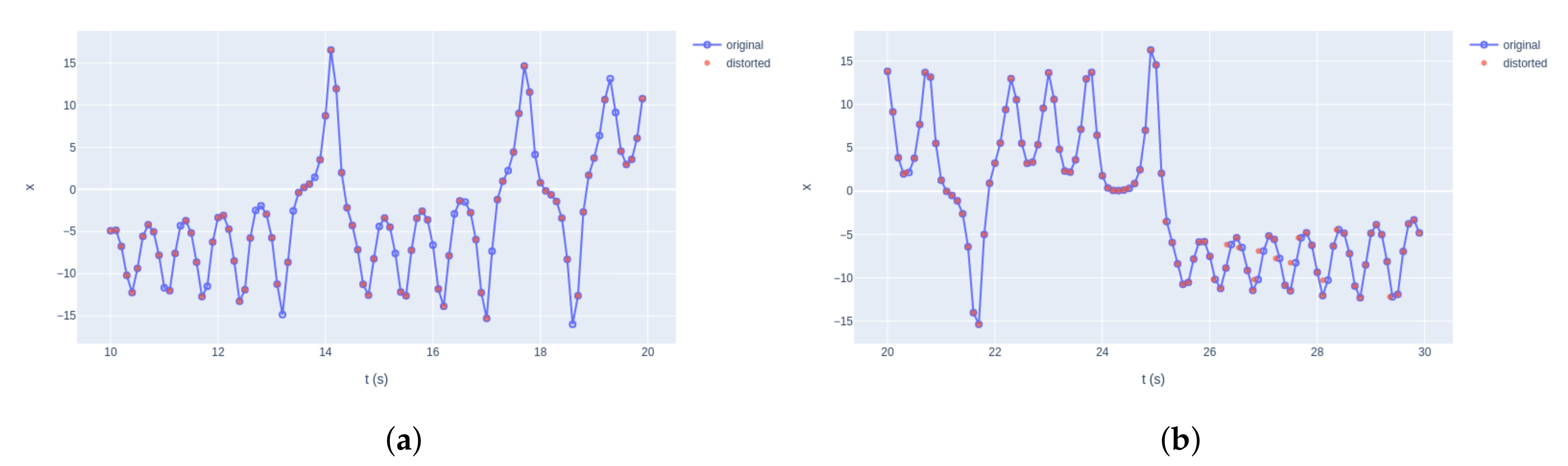
In this paper, a smart join method based on an optimization process is proposed. The aim of this optimization problem is to select the method that minimizes the errors of the resampling process for each feature.

First, a detailed explanation is presented in Section 3.1 and an example of application is shown afterwards in Section 3.2.

3.1. Description of The Methodology

The general concept of the methodology of the smart join is explained next:

• First, the joining model is fitted using training data; in other words, the optimal joining solution of the process is obtained. This needs to be done for each feature separately.
• Then, resampled data is predicted by applying the selected join method to the test data.
• Finally, the model is validated using resampling error.

Suppose we have a time series slice y of the selected feature that needs to be resampled to be joined with a desired time index. First of all, the fit method is used in order to obtain the “optimal” join method. The inputs needed for the join are the original time series slice (y with the original time index) and the desired time index. Other optional parameter can be a fill NA function as it can affect selecting the “optimal” method. Then, another slice of the same feature (z) is used for the testing by the use of the method score. Finally, the optimal joined method is used for resampling other time slices of the features with the predict method. The structure of the different methods can be depicted as in Figure 1.

The fitting process to find an optimal joining model could be mathematically represented as follows:

Suppose we have the time series $y\left(t_O\right)$ where $t_O=[t_{O1},t_{O2},\cdots ,t_{Om}]$ is the initial temporal reference system. Let j be a join method from the available methods set J ($\mathit{left},\mathit{backward},\mathit{forward},\mathit{nearest}$). We need to obtain a new time series $\widehat{y}(t_D;j,y)$ with the desired temporal reference system $t_D=[t_{D1},t_{D2},\cdots ,t_{Dn}]$. The smart join algorithm aims to find the optimal join method $j\in J=\{\mathit{left},\mathit{backward},\mathit{forward},\mathit{nearest}\}$ that minimizes an error function $E(y,\widehat{y})$. The parameters for applying the smart join method are the function meant to fill unavailable measurement values $f\in F=\{\mathit{None},\mathit{bfill},\mathit{ffill},\mathit{nearest}\}$. In case of not being specified, default values will be used (in which case $f=\mathit{None}$). The possible values of the imputation function f are $\mathit{None}$ (not filling NA values), $\mathit{bfill}$ (using subsequent value that is nearest) and $\mathit{ffill}$ (using prior value that is nearest). The optimization problem is defined as:

$$\underset{j\in J}{arg\; min}E(y,\widehat{y})$$

(1)

With respect to the second contribution put forward by the present paper, the error function $E(y,\widehat{y})$ proposed is defined by Equation (2).

$$\begin{array}{cc}\hfill E(y,\widehat{y})=& w_1·\mathit{NaEl}\left(\widehat{y}\right)+w_2·\mathit{MissEl}(y,\widehat{y})+w_3·\mathit{DelEl}(y,\widehat{y})\hfill \\ \hfill & +w_4·\mathit{DelT}(y,\widehat{y})+w_5·\mathit{AntEl}(y,\widehat{y})+w_6·\mathit{AntT}(y,\widehat{y})\hfill \\ \hfill & +w_7·\mathit{Diff}(y,\widehat{y}),\hfill \end{array}$$

(2)

where $w_i>0$ with $i\in \{1,2,\cdots ,7\}$ and ${\sum }_{i=1}^7{w}_i=1$ are the weights for the total error calculation and, in case of not being specified, their default value is $w_i=1/7\forall i$.

In the following paragraphs, each function that takes part in the error $E(y,\widehat{y})$ is presented. Suppose $k\in \{1,2,\cdots ,n\}$ and $l\in \{1,2,\cdots ,m\}$ indicate the index of elements in $\widehat{y}$ and y respectively.

$\mathit{NaEl}\left(\widehat{y}\right)$ represents the percentage of NA elements of $\widehat{y}$ after the application of f. NA values can be problematic in machine learning applications implying for example the need to remove data points with NA value on the model training process or the impossibility to predict an output value using the trained model.

$$\mathit{NaEl}\left(\widehat{y}\right)=\frac{{\sum }_{k=1}^n{s}_k}{n},\mathrm{where}{s}_k=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\widehat{y}}_k\mathrm{is}\mathrm{NA}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(3)

$\mathit{MissEl}(y,\widehat{y})$ is the percentage of elements from y that are not used in $\widehat{y}$. This value is related to the lost of information from the original time series due to the resampling needed.

$$\mathit{MissEl}(y,\widehat{y})=\frac{{\sum }_{l=1}^m{x}_l}{m},\mathrm{where}{x}_l=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{y}_l\notin \widehat{y}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(4)

$\mathit{DelEl}(y,\widehat{y})$ indicates the percentage of delayed elements. If most of the data points from y are delayed, the reality for the machine learning model is displaced. Depending on the application environment, taking decisions supported by the machine learning system that could not adequately represent the current situation can be problematic.

$$\mathit{DelEl}(y,\widehat{y})=\frac{{\sum }_{k=1}^n{d}_k}{n},\mathrm{where}{d}_k=\left\{\begin{array}{cc}1\hfill & \mathrm{if}({\widehat{y}}_k=y_l)\mathrm{and}(t_{Dk}>t_{Ol})\forall l\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

$\mathit{DelT}(y,\widehat{y})$ is the maximum difference in time between a delayed element used in $\widehat{y}$ and its original time position normalized by the time window of y. Whereas the previous case considers the frequency of delayed elements, $\mathit{DelT}(y,\widehat{y})$ takes into account the magnitude of the displacement.

$$\mathit{DelT}(y,\widehat{y})=\frac{max\left(e_k\right)}{t_{Om}-t_{O1}},\mathrm{where}{e}_k=\left\{\begin{array}{cc}{t}_{Dk}-t_{Ol}\hfill & \mathrm{if}({\widehat{y}}_k=y_l)\mathrm{and}(t_{Dk}>t_{Ol})\forall l\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

$\mathit{AntEl}(y,\widehat{y})$ and $\mathit{AntT}(y,\widehat{y})$ are equivalent functions but in this case for anticipated elements.

$$\mathit{AntEl}(y,\widehat{y})=\frac{{\sum }_{k=1}^n{a}_k}{n},\mathrm{where}{a}_k=\left\{\begin{array}{cc}1\hfill & \mathrm{if}({\widehat{y}}_k=y_l)\mathrm{and}(t_{Dk}<t_{Ol})\forall l\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(7)

and

$$\mathit{AntT}(y,\widehat{y})=\frac{max\left(b_k\right)}{t_{Om}-t_{O1}},\mathrm{where}{b}_k=\left\{\begin{array}{cc}{t}_{Ol}-t_{Dk}\hfill & \mathrm{if}({\widehat{y}}_k=y_l)\mathrm{and}(t_{Dk}<t_{Ol})\forall l\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

On the one side, the use of anticipated data is equivalent to the use of future information for prediction and results can be misleading and the used approximation should be sound enough to deal with value forecasting. On the other side, using future data could imply a need to wait for the arrival of a new observation to be able to make a prediction, or a correction would be needed once the predicted value and the real one are compared.

Finally $\mathit{Diff}(y,\widehat{y})$ calculates the difference between the two time series (original and resampled). This value could represent the magnitude of the distortion committed due to the need of a joined data with synchronized temporal reference system.

$$\mathit{Diff}(y,\widehat{y})=\frac{\mathrm{mean}\left(\mathrm{abs}(y_{inter}-{\widehat{y}}_{inter})\right)}{max\left(y\right)-min\left(y\right)},$$

(9)

where $y_{inter}$ and ${\widehat{y}}_{inter}$ are obtained by means of linear interpolation of time series y and $\widehat{y}$ respectively for time values in $t_O\bigcup t_D$.

Each part of the sum of the error calculation Equations (3)–(9) is normalized to guarantee that the result is in range $[0,1]$ so different errors are comparable between them.

The fitting method can be seen graphically in Figure 2.

Validating the joined method in different time slices of the time series is crucial. If the slice of data used to train the joining model is adequately selected, the errors should be similar in different time windows. Depending on the stability of the feature, retraining may be required as the optimal join method could not be the most adequate during all time period. Furthermore, selecting the desired temporal reference system ($t_D$) has equal importance as it should be the same for all the features, in order to be able to construct a database with all the features used by the model. Although the error calculation and the optimal joining methodology is chosen separately per feature, the desired temporal reference system is a common input of all the optimization problems and its selection affects to all the features.

3.2. Application Example

The current subsection introduces an illustrative example of the application of the proposed method to a dataset from a simple piecewise function. Suppose that the piecewise function is sampled irregularly in order to save memory applying two criteria:

• The system checks every minute if the value of the data point has changed enough according to a pre-established criterion (in this particular case, a difference with the prior data point higher than 0.5) to save that data point.
• Every minute the system also checks the difference in time with the last saved data point and if this difference is greater than or equal to four minutes it saves the last available data point.

The original piecewise function and the saved data using these criteria are shown in Figure 3.

Suppose that the desired time reference system corresponds to $t_d=\{1,3,5,\cdots ,33\}$. Results after the application of different joining methods are shown in Figure 4. Error values used in the optimization of the Smart Join methodology are shown in

Table 6. Error values for different join methods in the application example.

Method	$\mathit{NaEl}\left(\widehat{\mathit{y}}\right)$	$\mathit{MissEl}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{DelEl}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{DelT}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{AntEl}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{AntT}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{Diff}(\mathit{y},\widehat{\mathit{y}})$
left	0.882	0.818	0.0	0.0	0.0	0.0	1.0
nearest	0.0	0.0	0.471	0.031	0.412	0.031	0.045
forward	0.0	0.091	0.0	0.0	0.882	0.094	0.092
backward	0.0	0.091	0.882	0.094	0.0	0.0	0.084

.

Because the input for the algorithm is the received data, when default weights in the error function are used ($w_i=1/7\forall i$), the minimal error is obtained by the nearest join (see Figure 4b). However, if knowledge about the irregular sampling approach used by the system is introduced by penalizing the anticipation of data points (for example with $w_5=w_6=2/9\mathrm{and}{w}_1=w_2=w_3=w_4=w_7=1/9$), the optimal join method is backward join. Figure 4d shows that the data points obtained by the backward join as a result of taking into account this extended description of the data sampling mechanism are the ones that are the closest to the real piecewise function.

Having established the significance of the measure of quality of a joining method, in the remainder of this contribution we leverage mathematical optimization techniques on training data to automatically determine which of the joining methods is most adequate for a given time series.

4. Experimental Setup

Two experiments were used in order to show the usefulness of the proposed smart join methodology.

The first one is a controlled application from simulated data and working with a unique time series to resample. Different distortion methods were applied to the data in order to have a practical use case with known theoretical result.

The second case is an application from an industrial chemical process. The aim of showing this example is to demonstrate the performance of the smart join method in a real scenario and the importance of adequately selecting the joining method and its implications.

4.1. Experiments on Synthetic Data

The experiments on synthetic data are carried out on the $x,y,z$ 3D curve generated in time t by a Lorenz system (originally a simplified model for atmospheric convection) [9].

$$\begin{array}{cc}\hfill \frac{dx}{dt}& =\sigma (y-x)\hfill \\ \hfill \frac{dy}{dt}& =x(\rho -z)-y\hfill \\ \hfill \frac{dz}{dt}& =xy-\beta z\hfill \end{array}$$

(10)

with parameters $\sigma =10,\rho =28$ and $\beta =8/3$ and initial conditions $x\left(0\right)=y\left(0\right)=z\left(0\right)=1$ and $t\in [0,40]$. The time sampling interval selected for the time series was $0.1$ time units.

The simulated data can be observed in Figure 5a. To apply the smart join methodology only dimension x was used. The time series is shown in Figure 5b.

In order to generate a distorted version of this time series in a controlled manner, some distortion methods were applied, inspired by from the work of Kreindler and Lumsden [10], which will be described later in the section.

This controlled experiment setup was used to demonstrate how errors change depending on the join method and on the type of distortion that is applied to each time window. The distortions have been selected in order to represent usual problems such as missing data or delays in receiving data points.

The series was divided into four parts of equal size. In the first part ($t\in (0,10]$) the time series remains unaltered. In the range $t\in (10,20]$, 20% randomly selected data points were removed. This distortion can be seen in Figure 6a. In the remaining part of the time series, 20% of data were shifted forward (in $t\in (20,30]$) or backward (in $t\in (30,40]$). The shifted quantity was selected by a random uniform variable, guaranteeing that data points cannot be disordered. In other words, the maximum possible shifted quantity was set by the sampling frequency value of the original simulation data. The distortion effect generated in the time series can be observed in Figure 6b.

The difference between modified and original data can be seen in Figure 7.

4.2. Experiments on Real Industrial Dataset

The efficient management and the energy optimization of distillation units [11,12] in terms of both product quality and energy efficiency in both the petro-chemical and in the sustainable sector pose a great challenge to process and control engineers because of their complexity. The management, optimization and fault analysis of such units all require accurate process models, which in recent years have started to be generated directly from the data available in SCADA Historian databases by using machine learning methods [13,14,15] whose performance depends on the availability of properly pre-processed multi-variate data.

Suppose that the system captures and stores real-time sensor-based data. In this particular case, each sensor writes values in the database only when there is a significant change in the values of data. The decision on the significance of the difference between data points is based on the scale of each feature. The aim of this data recording strategy is reducing data volume. Consequently, if a feature becomes unstable the writing frequency augments drastically.

For machine learning applications, an alignment between features is needed. Each feature should be resampled to obtain a common desired temporal reference system previous to any feature extraction/selection algorithm application. Depending on the feature and the application system, the optimal joining method can be different.

Figure 8 shows the initial sampling for different features. Each column represents a feature and each row an hour time window. The number of samples is counted per hour and feature, and represented by the colour.

Figure 8 shows how, depending on the feature the frequency of data availability can be constant or variable, and the quantity of samples can be very different among features. For example, the feature with id 14 changes drastically from very low frequency to high frequency only in a couple of hours. The data points for this particular feature are shown in Figure 9, where the frequency change is observable.

In this particular case, the desired time sampling interval is selected to be 15 min.

5. Experimental Results

This section presents experimental results for the aforementioned case studies.

5.1. Results on Synthetic Data

For synthetic data, different time series joining methods were used separately and the error, defined by Equation (2), was calculated for each method using windows of $t\in (p,p+2]$ with $p\in \{0,2,\cdots ,38\}$. The selected values for the parameters of smart join methodology were $w_i=1/7\forall i$ (i.e., the same importance for all different functions taking part in the error calculation) and the imputation function was $f=\mathit{ffill}$.

Table 7. Results on synthetic data, in bold the method with minimal error (multiple solutions are possible).

t Range	Backward Join	Forward Join	Left Join	Nearest Join	Theoretical
0–2	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	all
2–4	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	all
4–6	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	all
6–8	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	all
8–10	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	0.00$\times {10}^0$	all
10–12	4.56$\times {10}^{-2}$	4.56$\times {10}^{-2}$	4.56$\times {10}^{-2}$	5.32 $\times {10}^{-2}$	none
12–14	5.08$\times {10}^{-2}$	5.08$\times {10}^{-2}$	5.08$\times {10}^{-2}$	5.08$\times {10}^{-2}$	none
14–16	3.35 $\times {10}^{-2}$	2.77$\times {10}^{-2}$	3.35 $\times {10}^{-2}$	4.06 $\times {10}^{-2}$	none
16–18	4.55 $\times {10}^{-2}$	4.55 $\times {10}^{-2}$	4.55 $\times {10}^{-2}$	5.35$\times {10}^{-2}$	none
18–20	4.36$\times {10}^{-2}$	4.83 $\times {10}^{-2}$	4.36$\times {10}^{-2}$	4.36$\times {10}^{-2}$	none
20–22	1.89$\times {10}^{-2}$	3.61 $\times {10}^{-2}$	3.61 $\times {10}^{-2}$	1.89$\times {10}^{-2}$	backward
22–24	1.50$\times {10}^{-2}$	3.61 $\times {10}^{-2}$	3.61 $\times {10}^{-2}$	1.50$\times {10}^{-2}$	backward
24–26	1.67$\times {10}^{-2}$	3.61 $\times {10}^{-2}$	3.61 $\times {10}^{-2}$	1.67$\times {10}^{-2}$	backward
26–28	7.69$\times {10}^{-2}$	1.21 $\times {10}^{-1}$	1.92 $\times {10}^{-1}$	9.39 $\times {10}^{-2}$	backward
28–30	3.61 $\times {10}^{-2}$	5.86 $\times {10}^{-2}$	5.86 $\times {10}^{-2}$	3.00$\times {10}^{-2}$	backward
30–32	5.75 $\times {10}^{-2}$	3.55$\times {10}^{-2}$	7.22 $\times {10}^{-2}$	4.44 $\times {10}^{-2}$	forward
32–34	5.04 $\times {10}^{-2}$	2.72$\times {10}^{-2}$	5.04 $\times {10}^{-2}$	2.72$\times {10}^{-2}$	forward
34–36	8.90 $\times {10}^{-2}$	5.26$\times {10}^{-2}$	1.11 $\times {10}^{-1}$	5.26$\times {10}^{-2}$	forward
36–38	4.44 $\times {10}^{-2}$	2.86$\times {10}^{-2}$	4.44 $\times {10}^{-2}$	2.86$\times {10}^{-2}$	forward
38–40	3.61 $\times {10}^{-2}$	1.99$\times {10}^{-2}$	3.61 $\times {10}^{-2}$	1.99$\times {10}^{-2}$	forward

shows the error values per method and time window. The optimal solution (minimum error) is marked in bold. An additional column labelled “theoretical” represents the theoretically optimal solution. Thus, the obtained optimal solution in each time window can be compared and contrasted with the theoretical solution. In Figure 10 numerical results are shown graphically.

As per Table 7, the optimal joining method (the one that has minimal error in each window) depends on the controlled distortion introduced. The proposed methodology is capable of obtaining as one of the optimal available results the theoretical solution. On the one hand, for $t\in (0,10]$, the data was already available for the needed temporal reference system and for that reason all the methods were able to obtain a 0.0 value error. On the other hand, for $t\in (10,20]$, as data points are removed randomly, there was no optimal theoretical solution, as from known data points the joining method should not be able to reconstruct the time series. For this range, the optimal solution for the joining method depends on $\mathit{Diff}(y,\widehat{y})$, i.e., the distortion introduced is comparable to the one obtained with the lineal interpolation result. For $t\in (20,30]$ and $t\in (30,40]$ the optimal theoretical solutions were backward and forward join, respectively. However, in multiple windows, the nearest join method obtained the same solution as the theoretically optimal method, as the shifted data points ($t_{Ol}$ introduced in the smart join system) are the nearest ones to the desired data points ($t_{Dk}$ output temporal reference system).

5.2. Results on Real Industrial Datasets

With respect to the real dataset, all features had a common sampling distribution after the joining as per Figure 11. In this case, the common sampling distribution was represented by having the same colour by row for all the features (represented by columns). Furthermore, as the selected temporal reference system ($t_D$) had a constant sampling interval, the figure results in constant colour (four data points for each feature each hour).

In Figure 12 the original time series (y) and the one obtained from the joining methodology ($\widehat{y}$) are shown for making a visual comparison. Both time series (y and $\widehat{y}$) had similar appearance until 16:00 where the feature became unstable. Due to the selected time sampling and the joins considered for finding the optimum being the ones operated by SQL database engines, only a data point near the needed sampling was selected.

Figure 13 shows the alignment distortion for the feature with id 14. Negative values in this misalignment imply that anticipated time data were used in the join, whereas positive values imply delayed time. The difference in the alignment could imply delays in prediction if anticipated data were used in the join or did not really have updated information of the process in order to make an adequate decision. In this particular case as the original time sampling initially writes nearly each 20 min and the desired time sampling is every 15 min, delays or anticipations of nearly 8 min become common. In the last part of the original time series, as data were available every minute or two, the delays or anticipations are drastically reduced for the joined time series.

Figure 14 shows used and unused points from the original time series in the join time series. Depending on the application the lost information could have a great impact. For time later that 16:00, as the selected time sampling ($t_D$) is slower than the dynamic of the original time series, a lot of data points are unused in the joining process, losing the information provided by those data points showed in blue in the figure. In some cases, different aggregation methods or rolling windows could be more adequate to use the data that otherwise will be lost.

The difference between the original time series and the joined one can help optimize the time sampling for a specific application. At the top of Figure 15 both the time series used for error calculation in part of $Diff(y,\widehat{y})$ (${\widehat{y}}_{interp}$ and $y_{interp}$, i.e., generated by linear interpolation of time series y and $\widehat{y}$ in order to have common data sampling distribution ($t_O\bigcup t_D$)) are shown, while the lower diagram shows the absolute error value calculated at each point. For a comparison of how the frequency selection can affect the desired time sampling, a similar diagram with a desired sampling frequency modified from 15 min to one minute is shown in Figure 16. In both figures, as initially the original time series has constant values, there is no difference between both interpolated time series. However, as time passes by and the time series becomes unstable, the difference is remarkable. This error is greater in Figure 15, as the desired time sampling frequency is slower than the real dynamic of the feature and data is not linear.

In

Table 8. Error values for the nearest joining method for different requested sampling frequencies.

Frequency	$\mathit{NaEl}\left(\widehat{\mathit{y}}\right)$	$\mathit{MissEl}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{DelEl}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{DelT}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{AntEl}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{AntT}(\mathit{y},\widehat{\mathit{y}})$	$\mathit{Diff}(\mathit{y},\widehat{\mathit{y}})$
1	0.0	0.494	0.333	0.007	0.667	0.006	0.004
5	0.0	0.851	0.322	0.007	0.678	0.005	0.036
10	0.0	0.903	0.315	0.007	0.685	0.005	0.054
15	0.0	0.921	0.333	0.007	0.667	0.004	0.058

the effect in the error of different selections of desired sampling frequency are shown for comparison.

6. Conclusions and Future Work

Standard data analysis pipelines often include resampling, interpolation and aggregation steps that are not optimized in the model learning procedure.

This paper introduced the definition of an optimization problem for data preprocessing, and in particular for data joining processes that imply a need for data resampling. The defined problem has been addressed by a method designed to efficiently solve it. The case studies introduced have demonstrated the applicability of the proposed method to time series data, using standard SQL-like data joining primitives as a basis to be optimized upon. The first case study, with simulated data and controlled distortions, means to provide insight into the methodology and its applicability. In the second experiment, the proposed methodology is applied in a real scenario, showing the impact of the decisions taken in the preprocessing step on the learning of data-based models.

Furthermore, the paper proposed an error function for its use in the optimization problem of joining time series. This error function allows comparisons across different features and time slices, which is needed to select among different join methods or to monitor their quality on different time series slices. As errors are comparable, selecting the optimal solution or knowing when there is a need for retraining is possible. Moreover, using the input parameters (w and f) of the proposed error function allows adapting the function to an adequate solution for different applications.

The approach presented in this paper has several new paths to follow as future works: on the one hand, the approach could be improved, adding automatic selection of the time window size, or applying B-Spline mode approximations of the missing values; on the other hand, the benefits of the proposed Smart Join method should be quantified on a diverse range of real world applications. Energy consumption, storage and production, supply transportation and storage management are candidates towards this end.