DC-MMD-GAN: A New Maximum Mean Discrepancy Generative Adversarial Network Using Divide and Conquer
Abstract
:1. Introduction
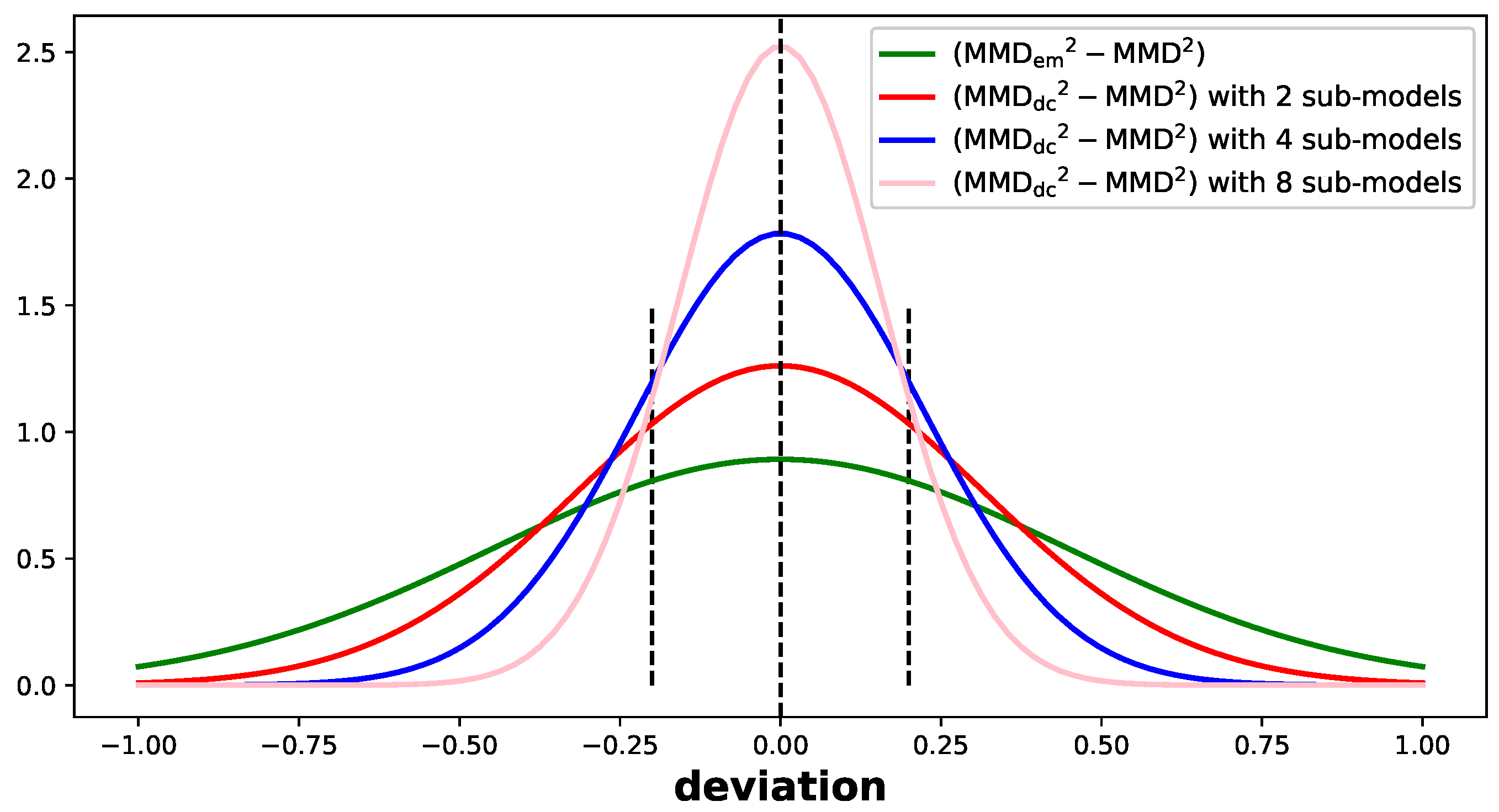
- Based on the deviation between empirical estimate and expected value in [16], we analyze and find that the large deviation exists in original MMD-GANs, which shows that sample size used in each training iteration is not sufficient to make precise evaluation.
- We propose DC-IPM-GANs, a novel method to constrain the loss function to tight bound on the deviation between empirical estimate and expected value of MMD. Compared to the original MMD-GANs, the loss function of DC-MMD-GANs with tighter deviation bound can measure the distance between generated distribution and target distribution more precisely, and provide more precise gradients for updating networks, which accelerates the training process. The multiple sub-models DC-MMD-GANs occupy multiple distributed computing resources. Compared to expanding the batch size on original MMD-GANs directly, the training score of DC-MMD-GANs is close to the score of MMD-GANs using less time.
- Experimental results show that DC-MMD-GANs can be trained efficiently compared to the original MMD-GANs.
2. Related Work
2.1. MMD
2.2. GANs
2.3. MMD-GANs
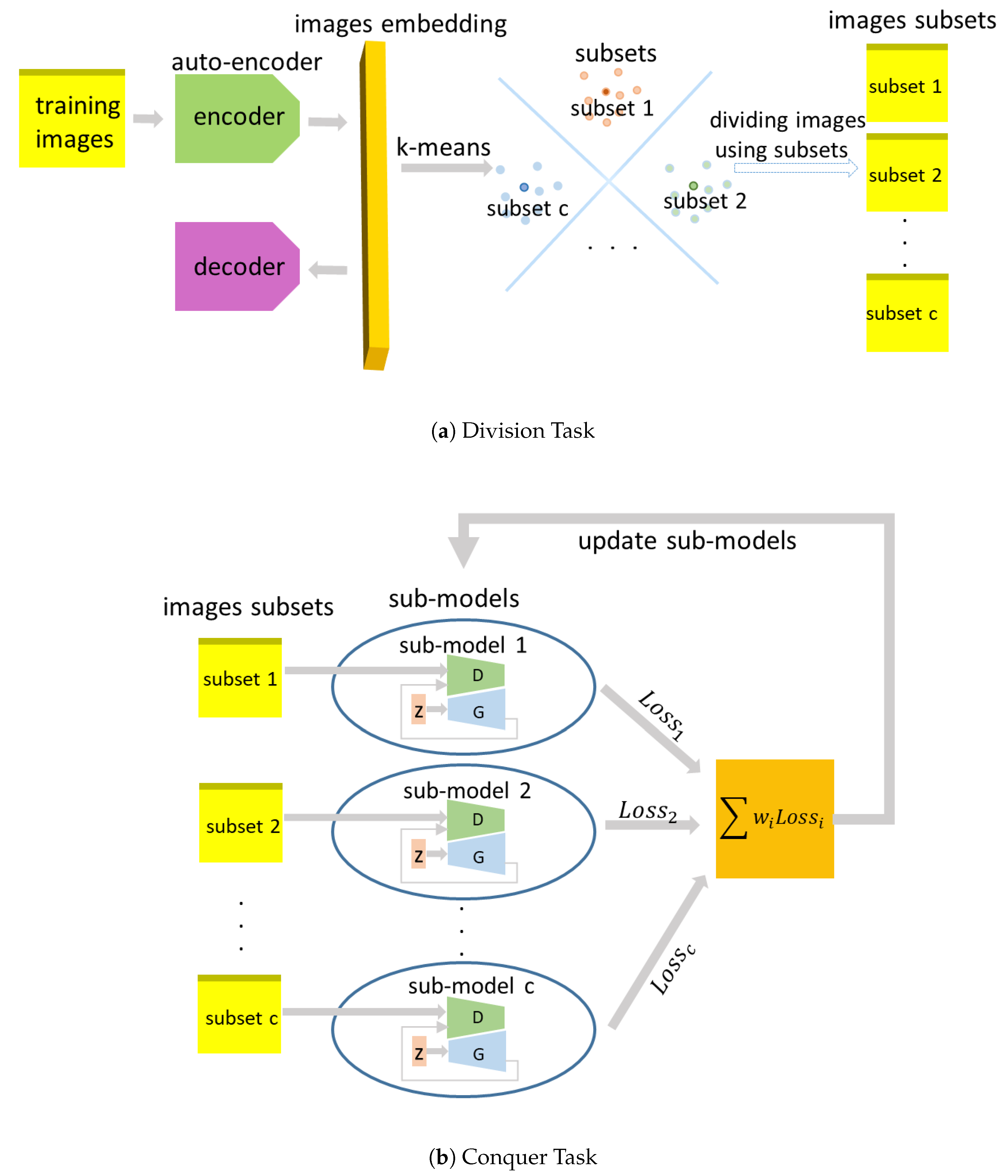
3. Divide and Conquer MMD-GANs
- Each subset of training images divided by k-means owns minimum distance in embedding space. The correlation between each subset is reduced. between each subset gets bigger. and are different batches of training images of different subset. According to Equation (5), the third term in will be reduced, which is the cross term between different subsets and cannot be obtained due to independent sub-model. From this perspective, auto-encoder and k-means help to reduce the loss of information of training images during training process.
- Each subset of training images is used to train on one sub-model. All training images are learned more quickly compared with the baseline model.
- According to different cluster of embeddings, we divide images into subsets, which can be viewed as different categories. Divided subsets contain different information of clustered embeddings, which is shown to improve training of GANs [32]. A pre-trained model such as the combination of auto-encoder and k-means is shown to be benefit for generator to produce high-quality images [33].
4. Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Generative Adversarial Nets, Montréal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Arjovsky, M.; Bottou, L. Towards Principled Methods for Training Generative Adversarial Networks. arXiv 2017, arXiv:1701.04862. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of Wasserstein GANs. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5767–5777. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive growing of GANs for improved quality, stability, and variation. arXiv 2017, arXiv:1710.10196. [Google Scholar]
- Nowozin, S.; Cseke, B.; Tomioka, R. f-GAN: Training generative neural samplers using variational divergence minimization. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 271–279. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, S.; Zhang, L.; Fu, J. Adversarial transfer learning for cross-domain visual recognition. Knowl. Based Syst. 2020, 204, 106258. [Google Scholar] [CrossRef]
- Müller, A. Integral probability metrics and their generating classes of functions. Adv. Appl. Probab. 1997, 29, 429–443. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Mroueh, Y.; Li, C.L.; Sercu, T.; Raj, A.; Cheng, Y. Sobolev GAN. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Genevay, A.; Peyre, G.; Cuturi, M. Learning Generative Models with Sinkhorn Divergences. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Canary Islands, Spain, 9–11 April 2018; pp. 1608–1617. [Google Scholar]
- Mroueh, Y.; Sercu, T.; Goel, V. McGAN: Mean and Covariance Feature Matching GAN. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2527–2535. [Google Scholar]
- Bińkowski, M.; Sutherland, D.; Arbel, M.; Gretton, A. Demystifying MMD GANs. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Li, C.L.; Chang, W.C.; Cheng, Y.; Yang, Y.; Póczos, B. MMD GAN: Towards deeper understanding of moment matching network. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2203–2213. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Hsieh, C.J.; Si, S.; Dhillon, I. A divide-and-conquer solver for kernel support vector machines. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 566–574. [Google Scholar]
- Hsieh, C.J.; Si, S.; Dhillon, I.S. Fast prediction for large-scale kernel machines. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Montréal, BC, Canada, 8–13 December 2014; pp. 3689–3697. [Google Scholar]
- Tandon, R.; Si, S.; Ravikumar, P.; Dhillon, I. Kernel ridge regression via partitioning. arXiv 2016, arXiv:1608.01976. [Google Scholar]
- Si, S.; Hsieh, C.J.; Dhillon, I.S. Memory efficient kernel approximation. J. Mach. Learn. Res 2017, 18, 682–713. [Google Scholar]
- Fukumizu, K.; Gretton, A.; Lanckriet, G.R.; Schölkopf, B.; Sriperumbudur, B.K. Kernel choice and classifiability for RKHS embeddings of probability distributions. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 14–18 June 2009; pp. 1750–1758. [Google Scholar]
- Sriperumbudur, B.K.; Gretton, A.; Fukumizu, K.; Schölkopf, B.; Lanckriet, G.R. Hilbert space embeddings and metrics on probability measures. J. Mach. Learn. Res. 2010, 11, 1517–1561. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Paul Smolley, S. Least squares generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2794–2802. [Google Scholar]
- Mroueh, Y.; Sercu, T. Fisher GAN. In Proceedings of the International Conference on Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2513–2523. [Google Scholar]
- Li, Y.; Swersky, K.; Zemel, R. Generative moment matching networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1718–1727. [Google Scholar]
- Sutherland, D.J.; Tung, H.Y.; Strathmann, H.; De, S.; Ramdas, A.; Smola, A.; Gretton, A. Generative models and model criticism via optimized maximum mean discrepancy. arXiv 2016, arXiv:1611.04488. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X.; Chen, X. Improved Techniques for Training GANs. In Proceedings of the International Conference on Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2234–2242. [Google Scholar]
- Dziugaite, G.K.; Roy, D.M.; Ghahramani, Z. Training generative neural networks via maximum mean discrepancy optimization. arXiv 2016, arXiv:1505.03906. [Google Scholar]
- Arbel, M.; Sutherland, D.; Bińkowski, M.; Gretton, A. On gradient regularizers for MMD GANs. In Proceedings of the International Conference on Advances in Neural Information Processing Systems, Montréal, BC, Canada, 3–8 December 2018; pp. 6700–6710. [Google Scholar]
- Wang, W.; Sun, Y.; Halgamuge, S. Improving MMD-GAN Training with Repulsive Loss Function. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zaremba, W.; Gretton, A.; Blaschko, M. B-test: A Non-parametric, Low Variance Kernel Two-sample Test. In Proceedings of the International Conference on Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 755–763. [Google Scholar]
- Grinblat, G.L.; Uzal, L.C.; Granitto, P.M. Class-splitting generative adversarial networks. arXiv 2017, arXiv:1709.07359. [Google Scholar]
- Zhang, H.; Xu, T.; Li, H.; Zhang, S.; Wang, X.; Huang, X.; Metaxas, D.N. StackGAN: Text to photo-realistic image synthesis with stacked generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5907–5915. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Bengio, Y.; Mesnil, G.; Dauphin, Y.; Rifai, S. Better mixing via deep representations. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 552–560. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 3730–3738. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral normalization for generative adversarial networks. arXiv 2018, arXiv:1802.05957. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the International Conference on Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6626–6637. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the International Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]







| Model | CelebA | CIFAR-10 |
|---|---|---|
| SMMD-GAN with batch size = 64 | 14.70 h | 0.73 h |
| 2-sub-models DC-SMMD-GAN with batch size = 32 | 7.80 h | 0.53 h |
| 4-sub-models DC-SMMD-GAN with batch size = 16 | 5.10 h | 0.41 h |
| 8-sub-models DC-SMMD-GAN with batch size = 8 | 3.60 h | 0.34 h |
| MMD-GAN with batch size = 64 | 18.10 h | 0.90 h |
| 2-sub-models DC-MMD-GAN with batch size = 32 | 9.75 h | 0.61 h |
| 4-sub-models DC-MMD-GAN with batch size = 16 | 6.10 h | 0.47 h |
| 8-sub-models DC-MMD-GAN with batch size = 8 | 4.50 h | 0.40 h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Zhong, Y.; Liu, X.; Li, Q.; Han, S. DC-MMD-GAN: A New Maximum Mean Discrepancy Generative Adversarial Network Using Divide and Conquer. Appl. Sci. 2020, 10, 6405. https://doi.org/10.3390/app10186405
Zhou Z, Zhong Y, Liu X, Li Q, Han S. DC-MMD-GAN: A New Maximum Mean Discrepancy Generative Adversarial Network Using Divide and Conquer. Applied Sciences. 2020; 10(18):6405. https://doi.org/10.3390/app10186405
Chicago/Turabian StyleZhou, Zhaokun, Yuanhong Zhong, Xiaoming Liu, Qiang Li, and Shu Han. 2020. "DC-MMD-GAN: A New Maximum Mean Discrepancy Generative Adversarial Network Using Divide and Conquer" Applied Sciences 10, no. 18: 6405. https://doi.org/10.3390/app10186405






