An Approach on Velocity and Stability Control of a Two-Wheeled Robotic Wheelchair
Abstract
:1. Introduction
2. System Description
3. Modeling of Two-Wheeled Robotic Wheelchair
3.1. Conventional Method
3.2. Proposed Method
4. Controller Design
4.1. Conventional Method
4.2. Proposed Method
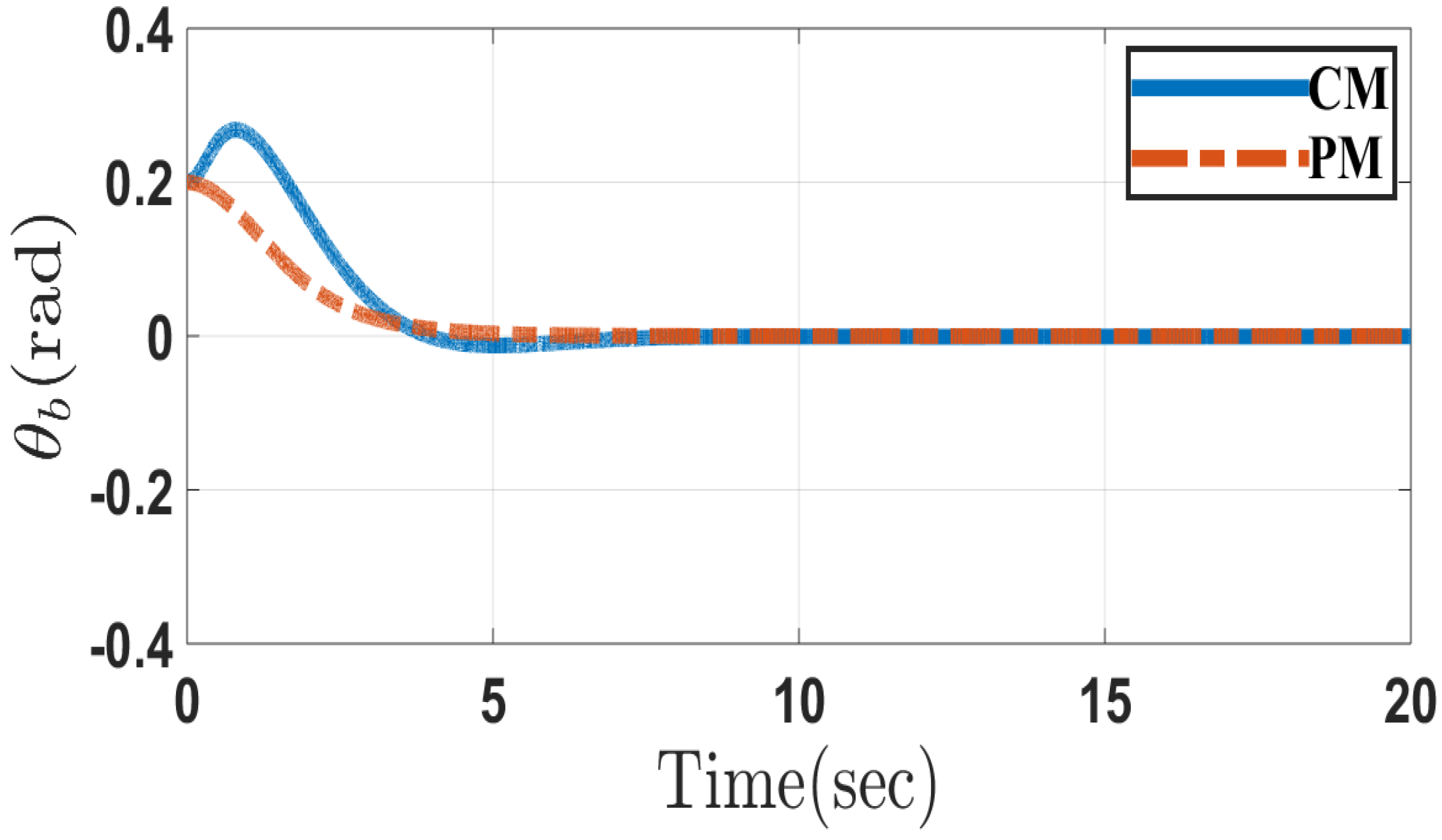
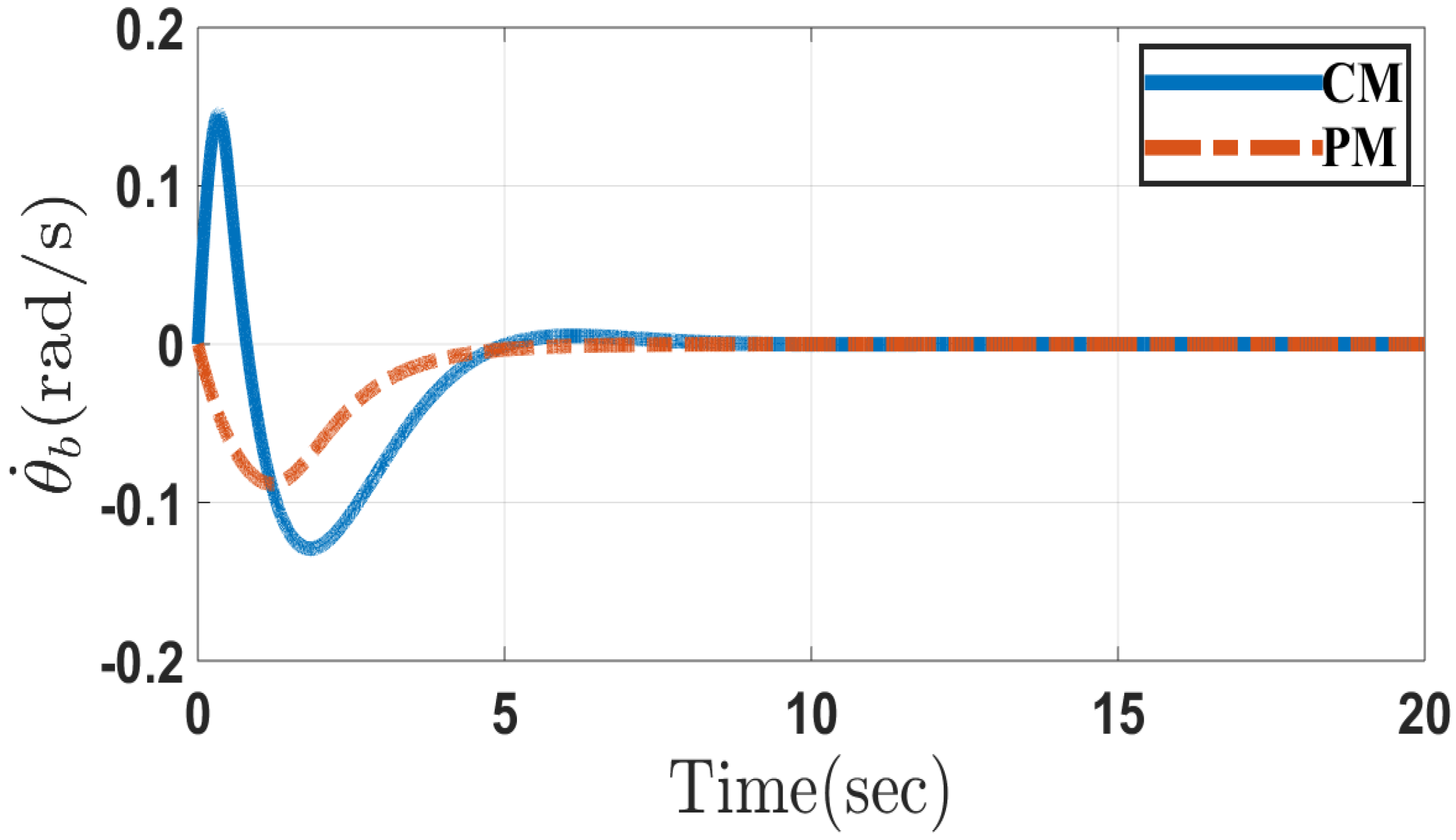
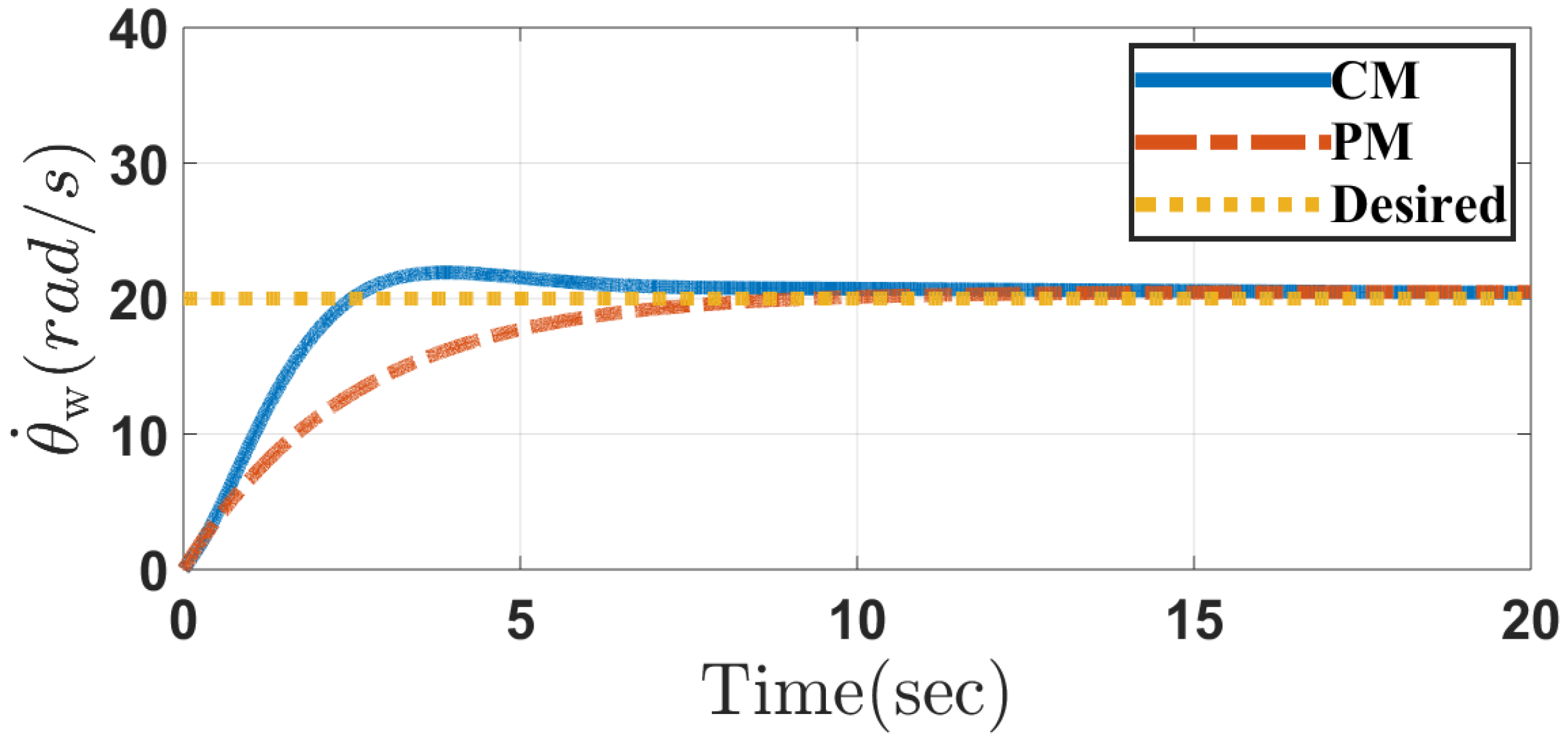
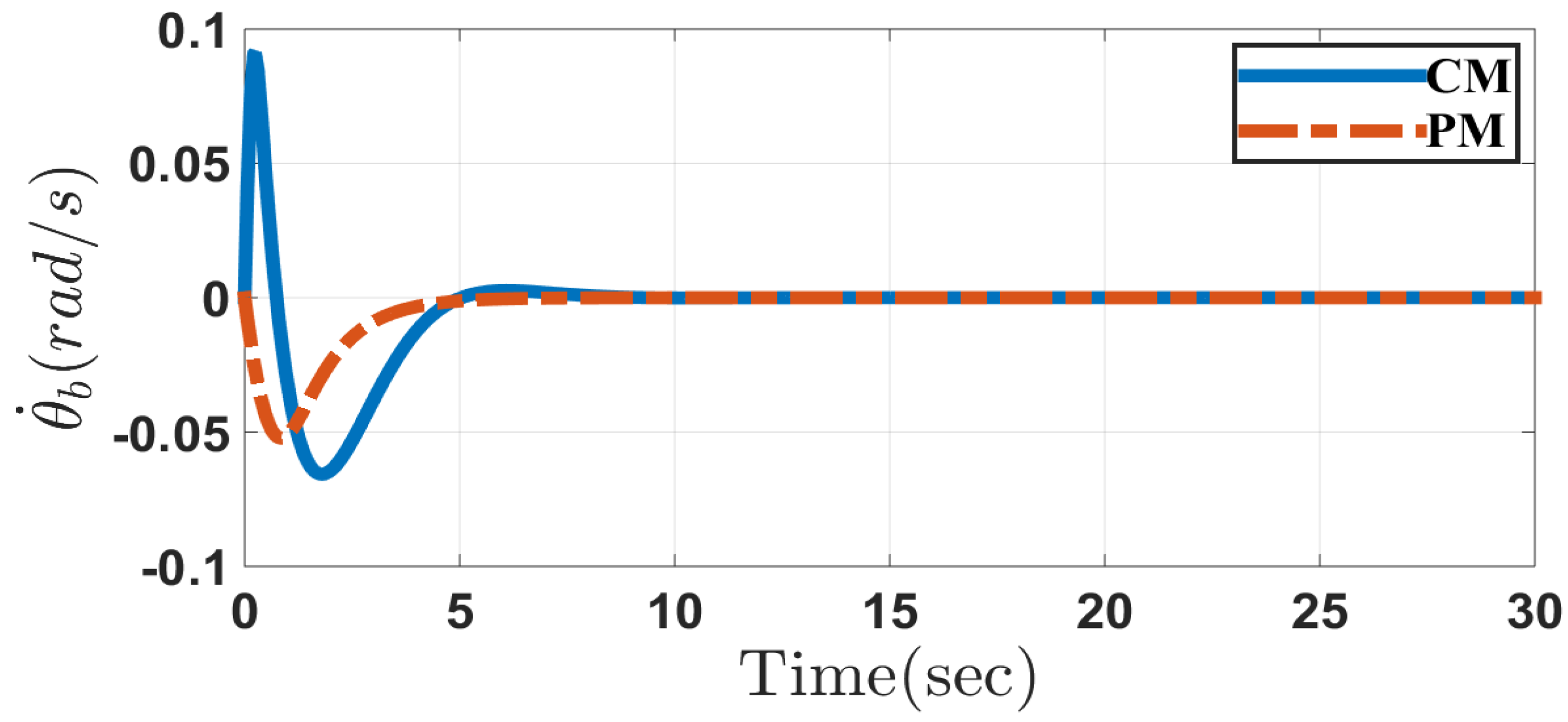
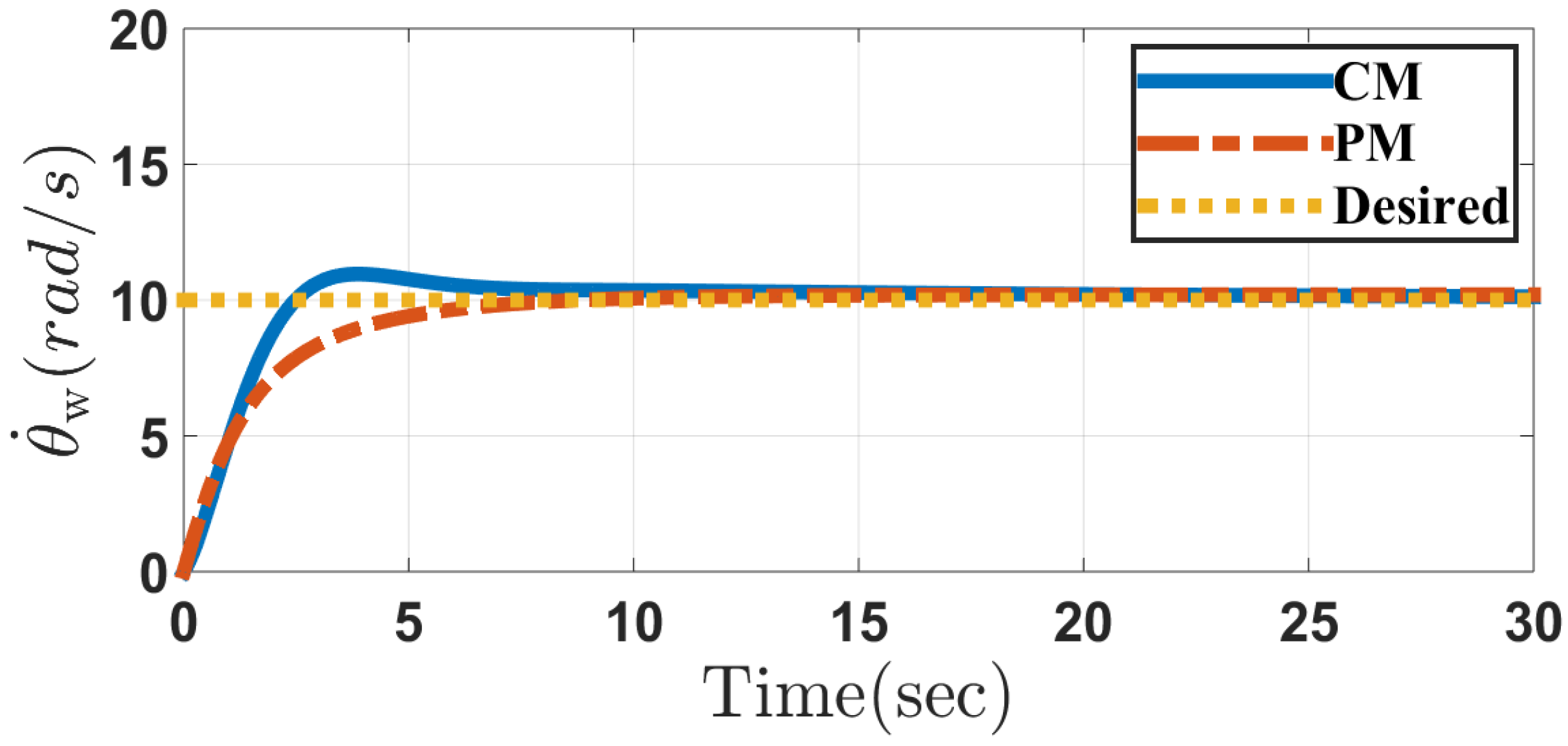
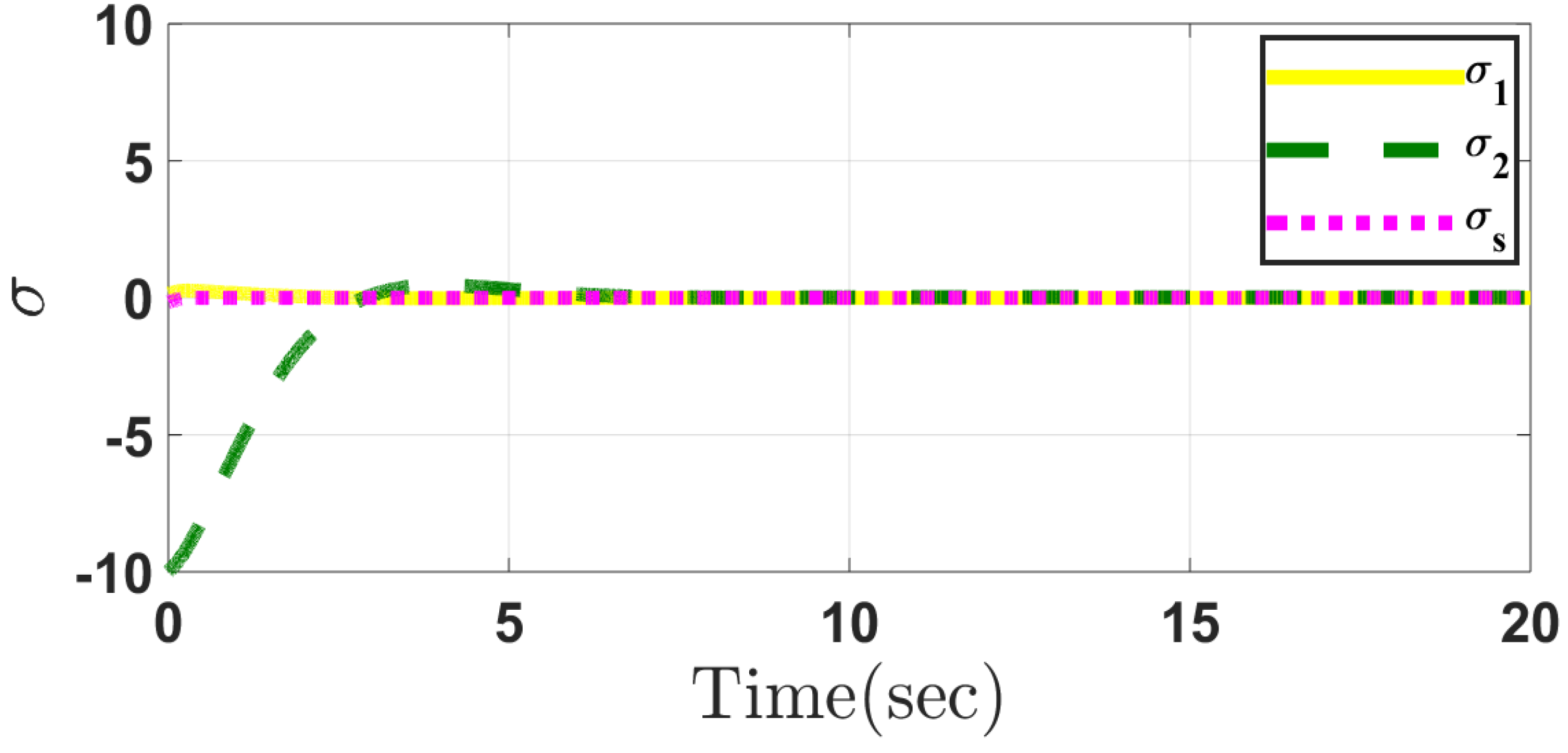
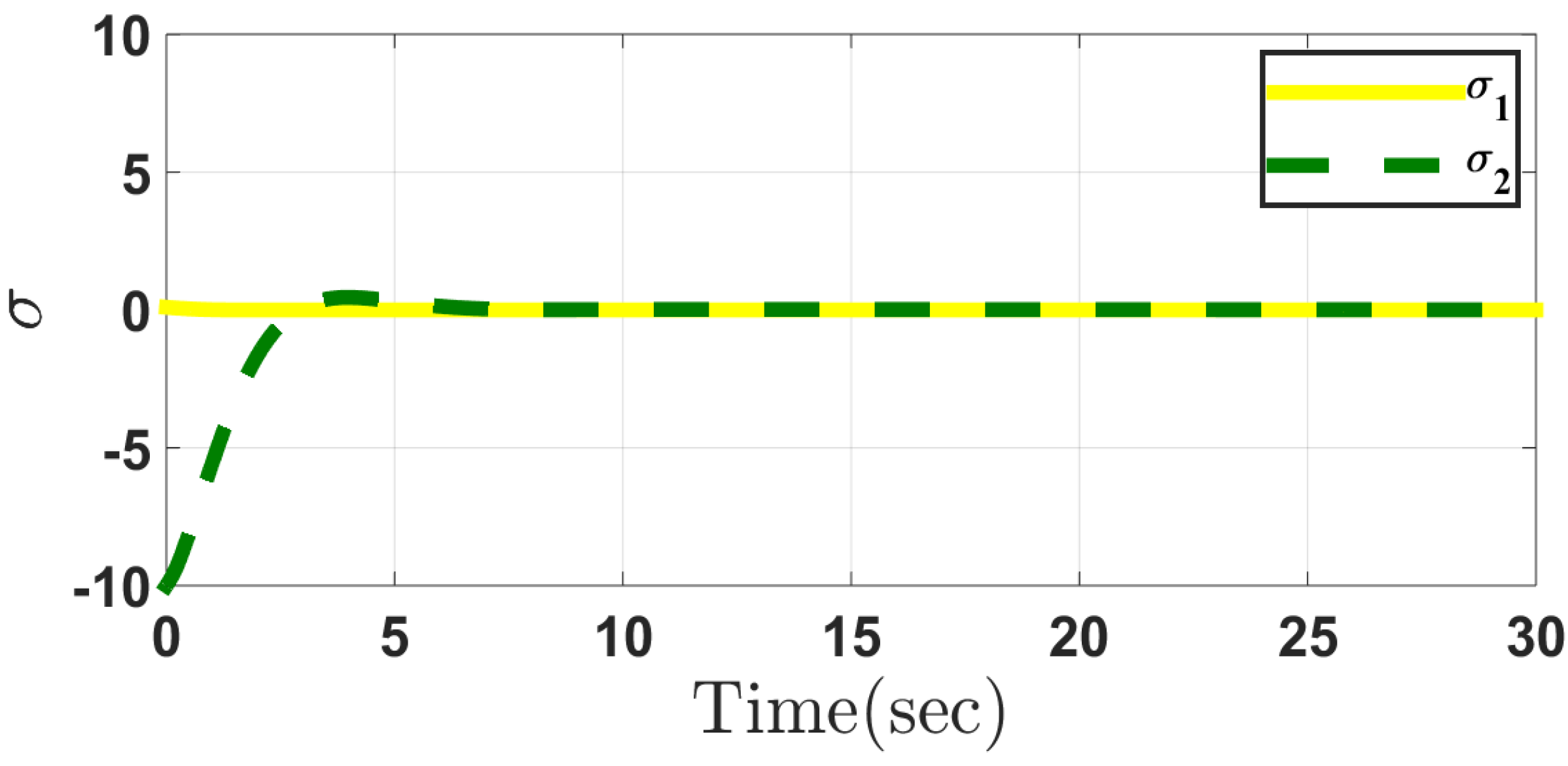
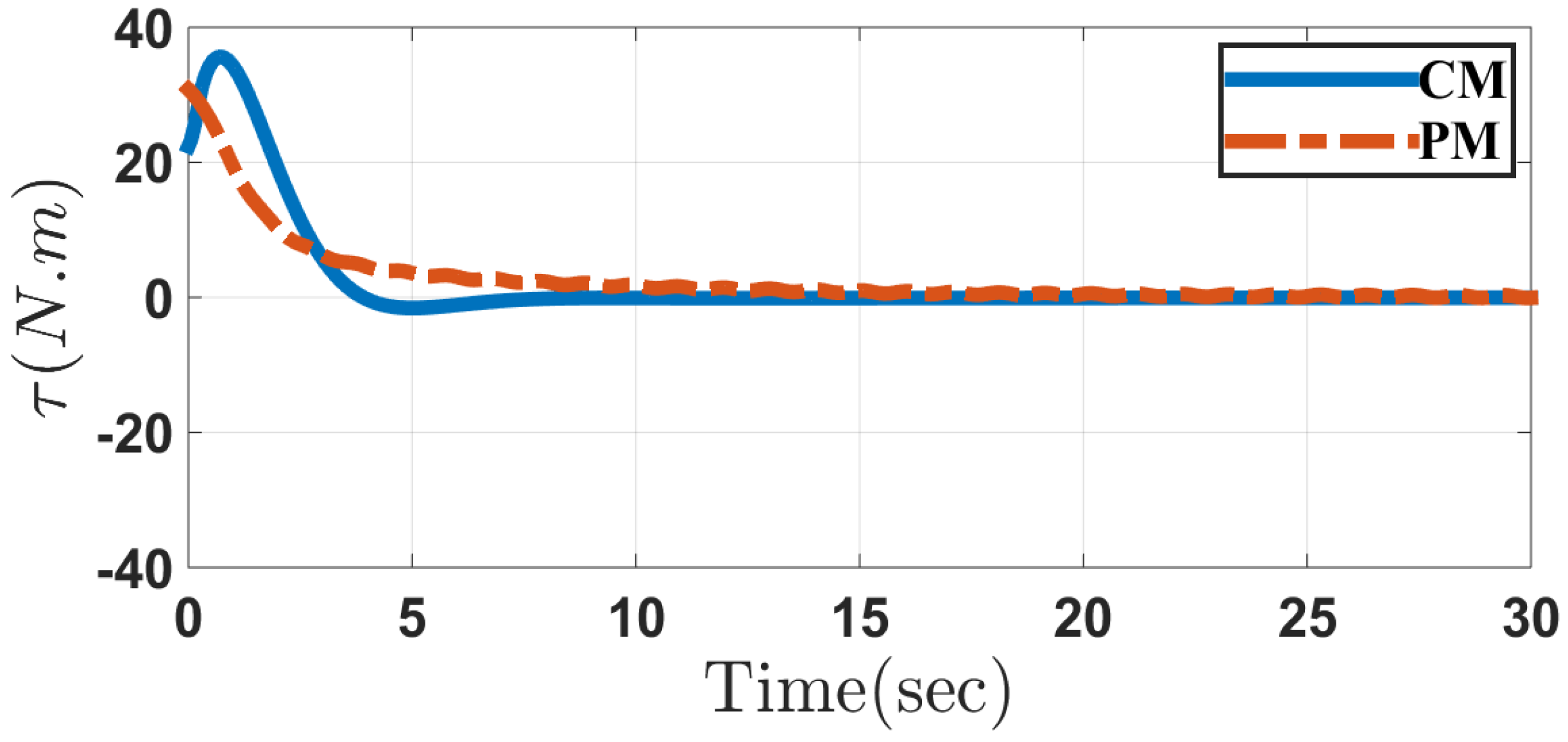
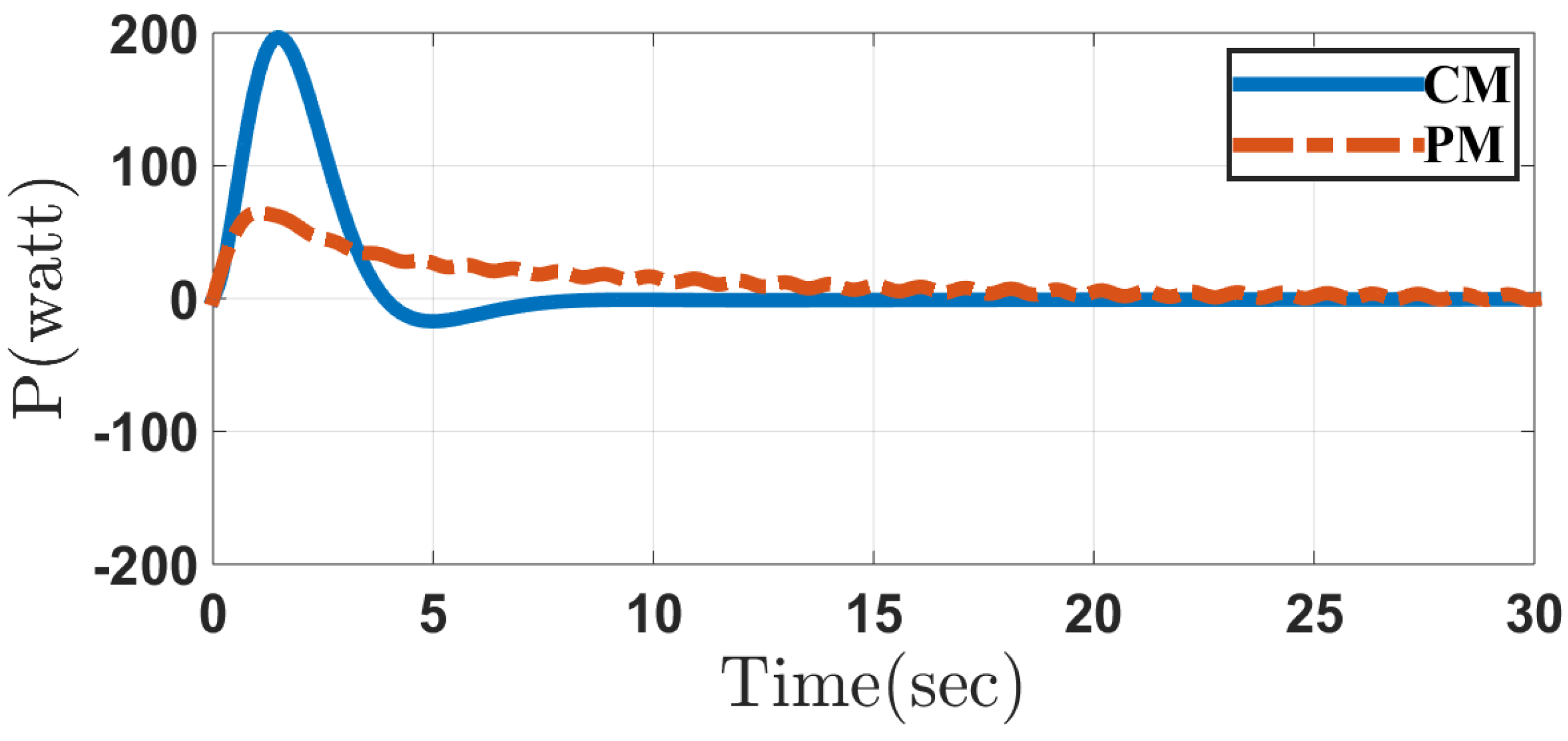
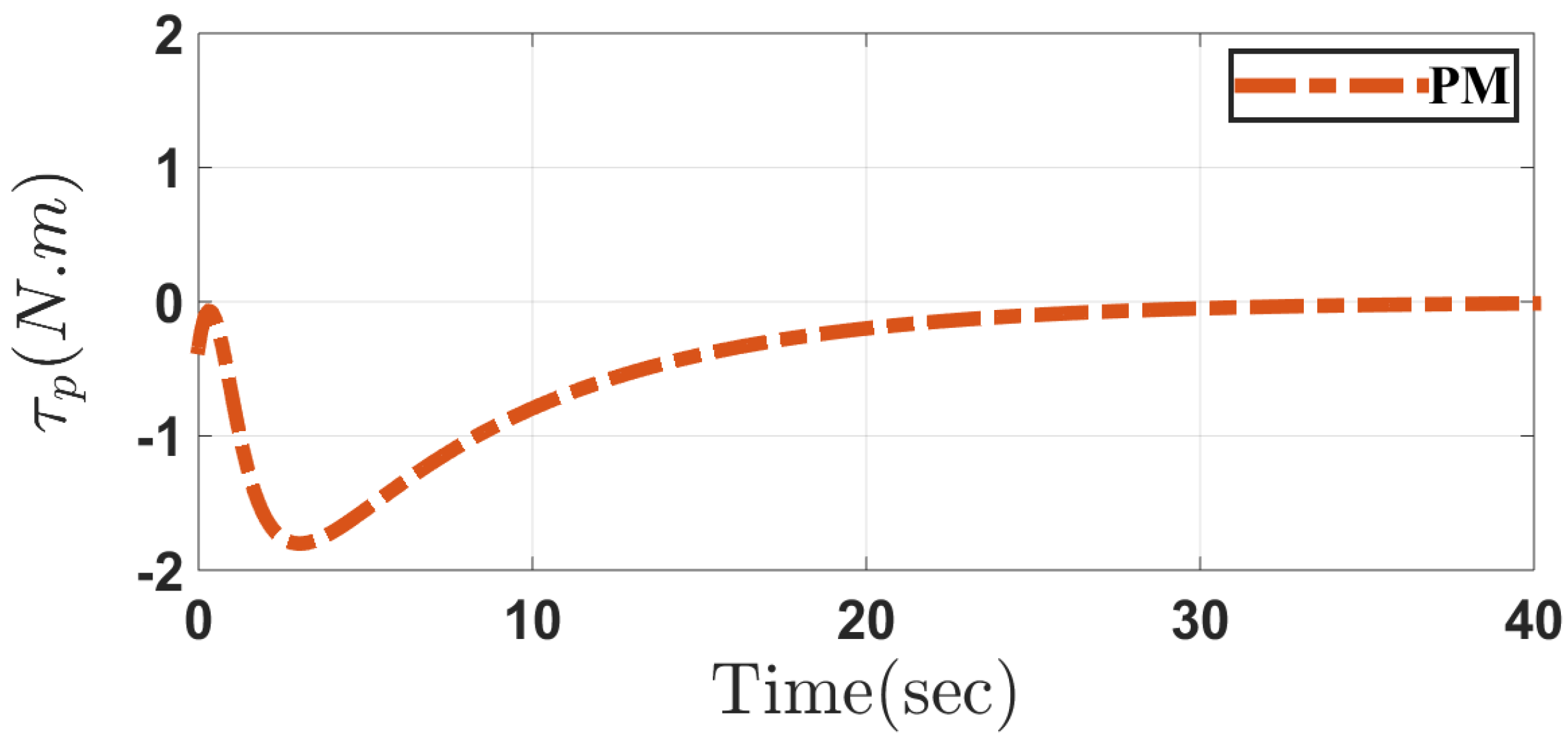
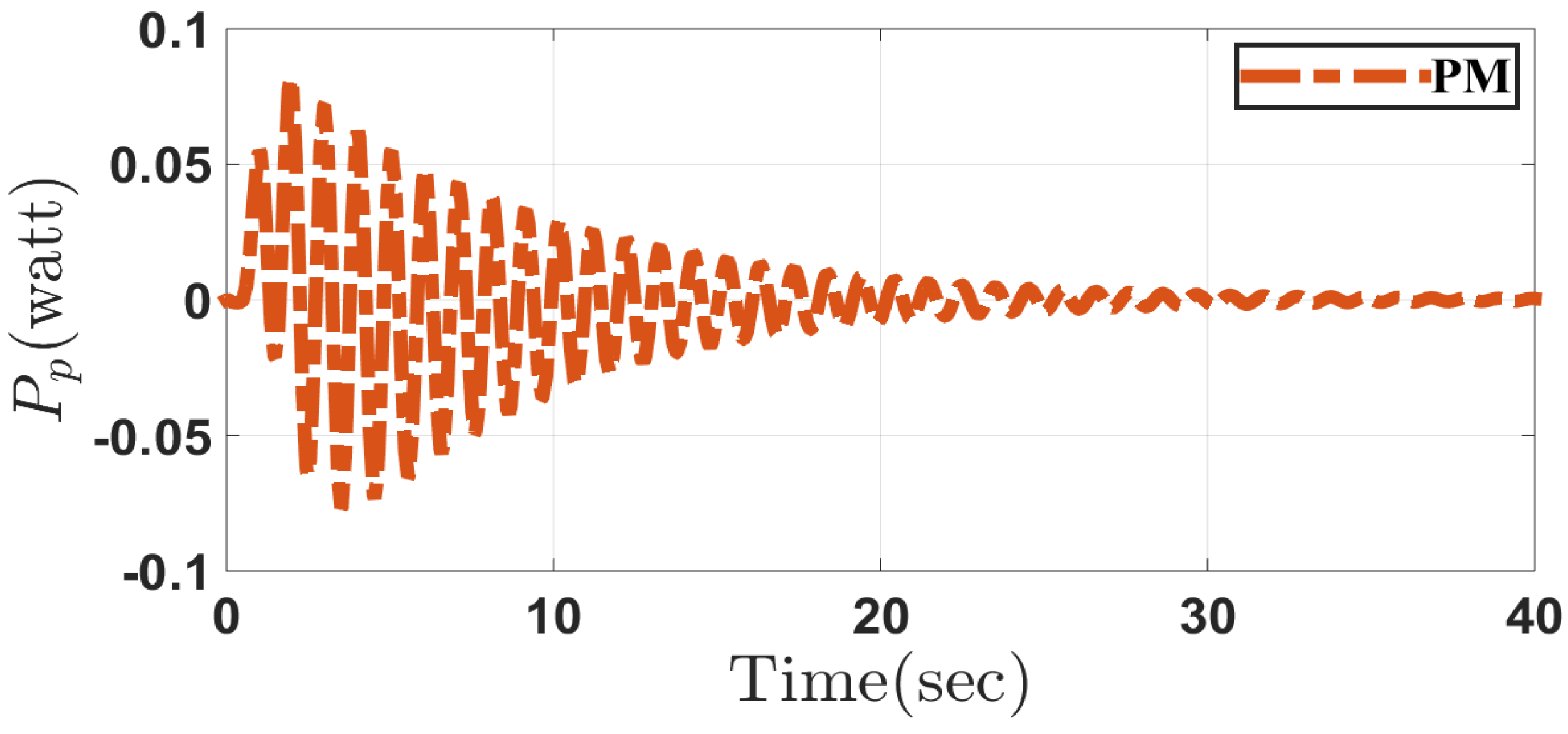
5. Simulation Results
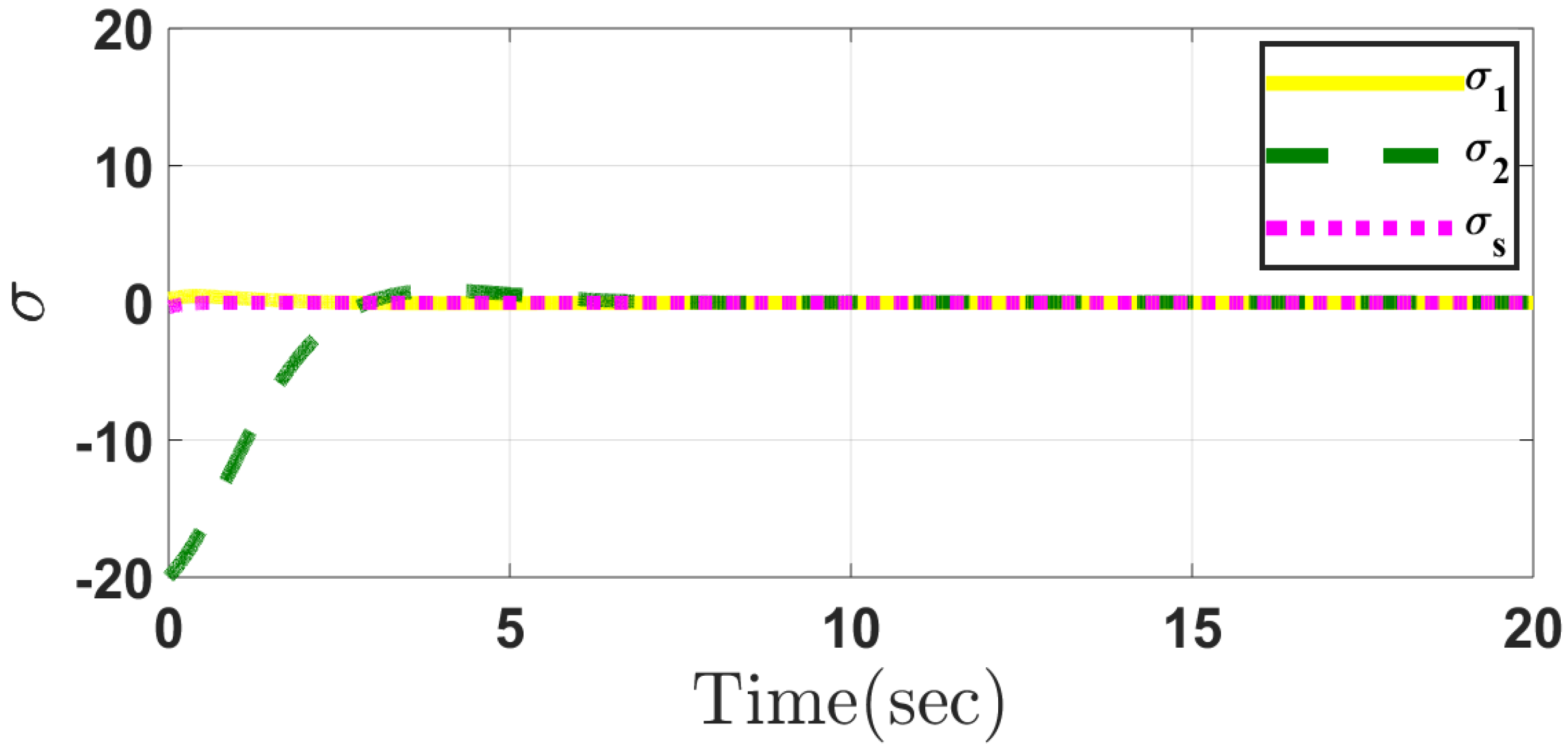
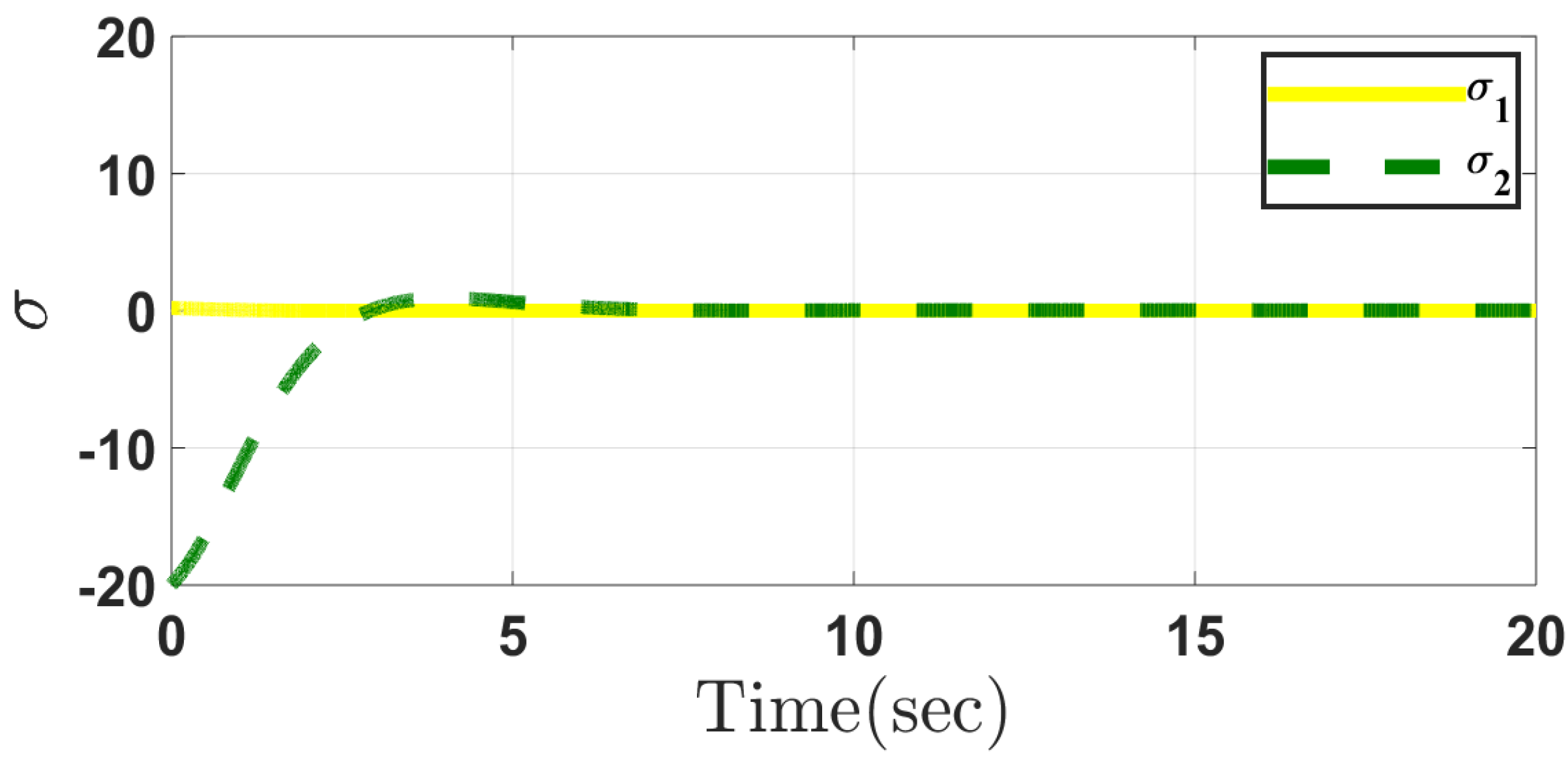
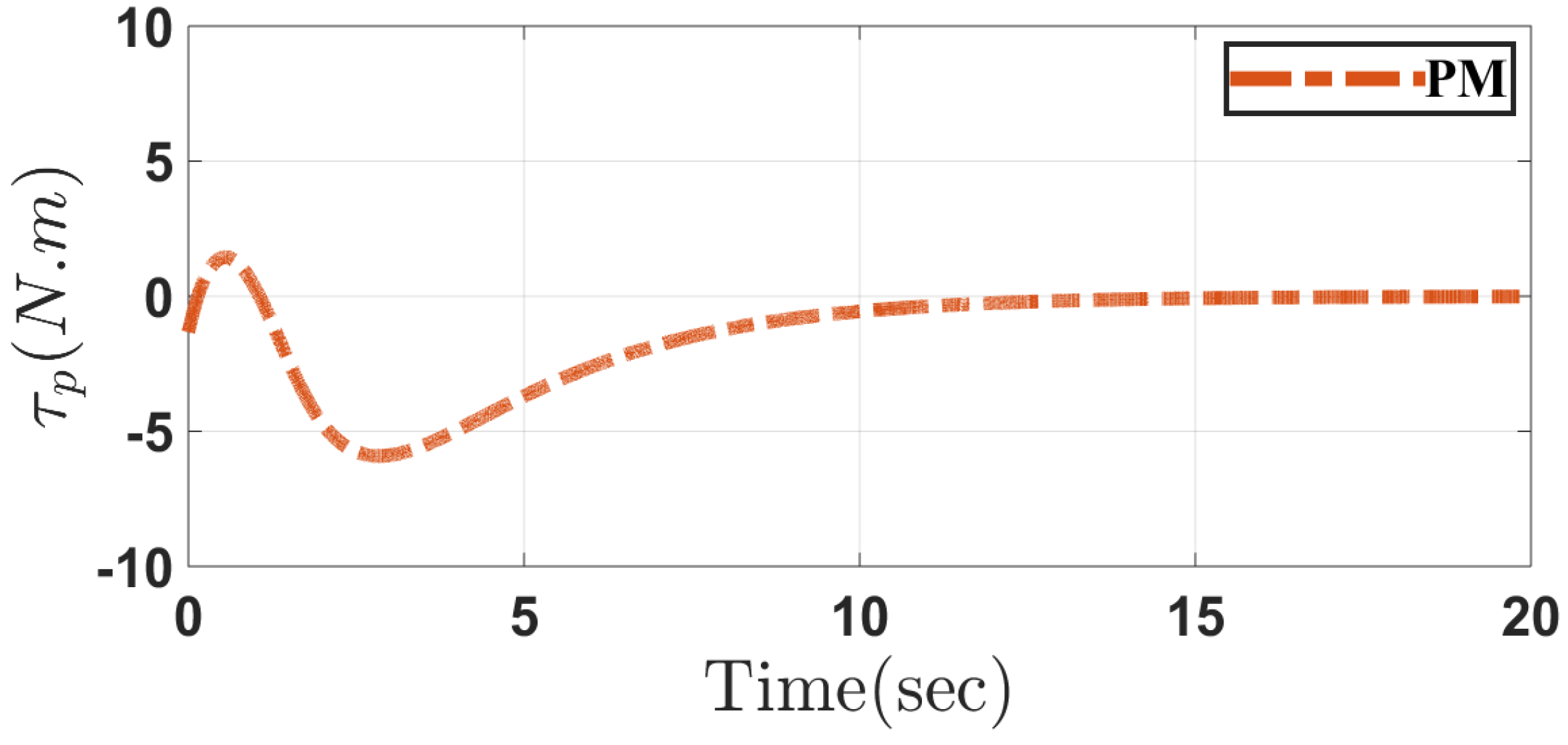
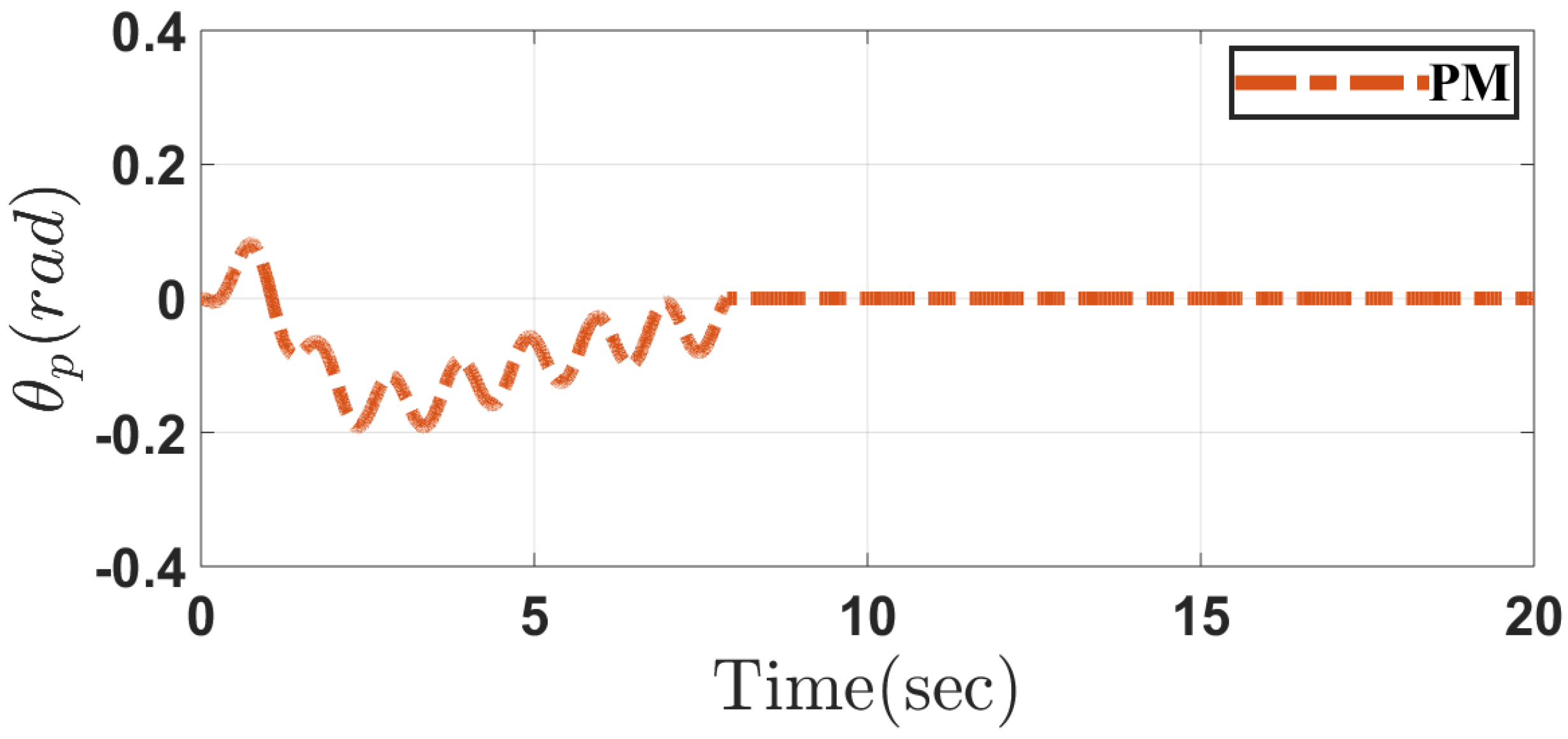
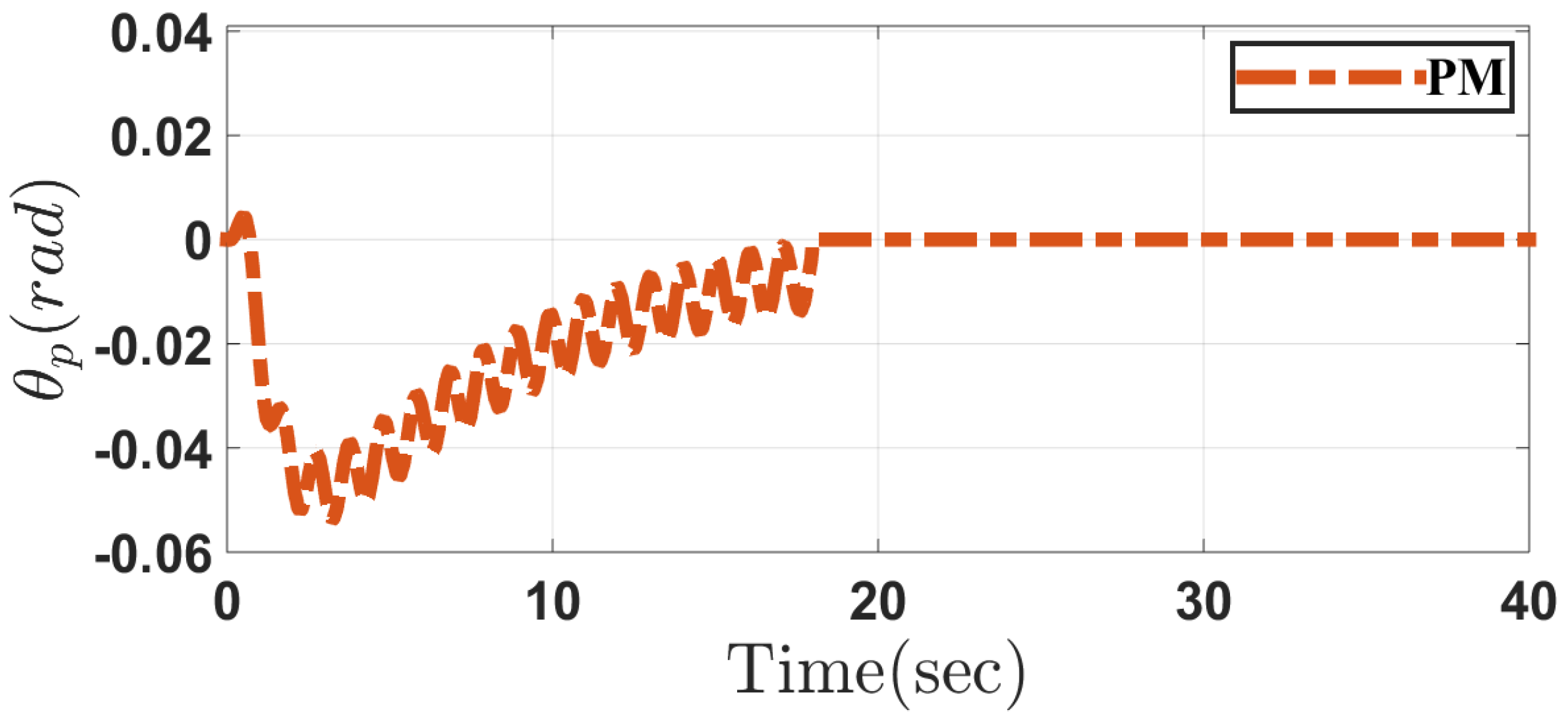
5.1. Case 1
5.2. Case 2
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Dynamic Model Components of Proposed Method
References
- Stout, G. Some aspects of high performance indoor/outdoor wheelchairs. Bull. Prosthet Res. 1979, 16, 135–175. [Google Scholar] [PubMed]
- Abdulghani, M.M.; Al-Aubidy, K.M.; Ali, M.M.; Hamarsheh, Q.J. Wheelchair Neuro Fuzzy Control and Tracking System Based on Voice Recognition. Sensors 2020, 20, 2872. [Google Scholar] [CrossRef] [PubMed]
- Ren, T.J.; Chen, T.C. Modelling and control of a power-assisted mobile vehicle based on torque observer. IET Control Theory Appl. 2007, 1, 1405–1412. [Google Scholar] [CrossRef]
- Seki, H.; Sugimoto, T.; Tadakuma, S. Novel straight road driving control of power assisted wheelchair based on disturbance estimation and minimum jerk control. In Proceedings of the 2005 Conference Record of the Industry Applications, Fourtieth IAS Annual Meeting, Hong Kong, China, 2–6 October 2005; pp. 1711–1717. [Google Scholar]
- Almeshal, A.M.; Goher, K.M.; Nasir, A.N.K.; Tokhi, M.O. Steering and dynamic performance of a new configuration of a wheelchair on two wheels in various indoor and outdoor environments. In Proceedings of the 2013 18th International Conference on Methods & Models in Automation & Robotics, MMAR, Miedzyzdroje, Poland, 26–29 August 2013; pp. 223–228. [Google Scholar]
- Zhou, Y.; Wang, Z.; Chung, K.W. Turning Motion Control Design of a Two-Wheeled Inverted Pendulum Using Curvature Tracking and Optimal Control Theory. J. Optim. Theory Appl. 2019, 181, 634–652. [Google Scholar] [CrossRef] [Green Version]
- Wieczorek, B.; Warguła, Ł.; Rybarczyk, D. Impact of a hybrid assisted wheelchair propulsion system on motion kinematics during climbing up a slope. Appl. Sci. 2020, 10, 1025. [Google Scholar] [CrossRef] [Green Version]
- Hirata, K.; Murakami, T. Stability analysis of disturbance observer based controllers for two-wheel wheelchair systems. Adv. Robot. 2014, 28, 467–477. [Google Scholar] [CrossRef]
- Vermeiren, L.; Dequidt, A.; Guerra, T.M.; Rago-Tirmant, H.; Parent, M. Modeling, control and experimental verification on a two-wheeled vehicle with free inclination: An urban transportation system. Control Eng. Pract. 2011, 19, 744–756. [Google Scholar] [CrossRef]
- Han, J.; Li, X.; Qin, Q. Design of two-wheeled self-balancing robot based on sensor fusion algorithm. Int. J. Autom. Technol. 2014, 8, 216–221. [Google Scholar] [CrossRef]
- Cooper, R.A.; Boninger, M.L.; Cooper, R.; Kelleher, A. Use of the INDEPENDENCE 3000 IBOT™ transporter at home and in the community: A case report. Disabil. Rehabil. Assist. Technol. 2006, 1, 111–117. [Google Scholar] [CrossRef]
- Arthanat, S.; Desmarais, J.M.; Eikelberg, P. Consumer perspectives on the usability and value of the iBOT® wheelchair: Findings from a case series. Disabil. Rehabil. Assist. Technol. 2012, 7, 153–167. [Google Scholar] [CrossRef] [PubMed]
- Uustal, H.; Minkel, J.L. Study of the Independence IBOT 3000 Mobility System: An innovative power mobility device, during use in community environments. Arch. Phys. Med. Rehabil. 2004, 85, 2002–2010. [Google Scholar] [CrossRef]
- Baloh, M.; Parent, M. Modeling and model verification of an intelligent self-balancing two-wheeled vehicle for an autonomous urban transportation system. In Proceedings of the Conference on Computational Intelligence, Robotics, and Autonomous Systems, Singapore, 15 December 2003; pp. 1–7. [Google Scholar]
- Karkoub, M.A.; Parent, M. Modelling and non-linear feedback stabilization of a two-wheel vehicle. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2004, 218, 675–686. [Google Scholar] [CrossRef]
- Ghaffari, A.; Shariati, A.; Shamekhi, A.H. A modified dynamical formulation for two-wheeled self-balancing robots. Nonlinear Dyn. 2016, 83, 217–230. [Google Scholar] [CrossRef]
- Nikpour, M.; Huang, L.; Al-Jumaily, A.M.; Lotfi, B. Stability control of mobile inverted pendulum through an added movable mechanism. In Proceedings of the 25th International Conference on Mechatronics and Machine Vision in Practice, M2VIP, Stuttgart, Germany, 20–22 November 2018; pp. 1–6. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Madero, V.; Rubio, F.R. Two-wheeled self-balanced pendulum workspace improvement via underactuated robust nonlinear control. Control Eng. Pract. 2015, 44, 231–242. [Google Scholar] [CrossRef]
- Ahmad, N.S. Robust H∞-Fuzzy Logic Control for Enhanced Tracking Performance of a Wheeled Mobile Robot in the Presence of Uncertain Nonlinear Perturbations. Sensors 2020, 20, 3673. [Google Scholar] [CrossRef]
- Raffo, G.V.; Madero, V.; Ortega, M.G. An application of the underactuated nonlinear H∞ controller to two-wheeled self-balanced vehicles. In Proceedings of the IEEE 15th Conference on Emerging Technologies & Factory Automation, ETFA, Bilbao, Spain, 13–16 September 2010; pp. 1–6. [Google Scholar]
- Shen, H.; Iorio, J.; Li, N. Sliding Mode Control in Backstepping Framework for a Class of Nonlinear Systems. J. Mar. Sci. Eng. 2019, 7, 452. [Google Scholar] [CrossRef] [Green Version]
- Hong, G.S.; Yu, D.; Wong, Y.S. Integral sliding mode control for fast tool servo diamond turning of micro-structured surfaces. Int. J. Autom. Technol. 2011, 5, 4–10. [Google Scholar]
- Nikpour, M.; Huang, L.; Al-Jumaily, A.M. Stability and Direction Control of a Two-Wheeled Robotic Wheelchair Through a Movable Mechanism. IEEE Access 2020, 8, 45221–45230. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Control for Dynamic Positioning and Way-point Tracking of Underactuated Autonomous Underwater Vehicles Using Sliding Mode Control. J. Intell. Robot. Syst. 2019, 95, 1113–1132. [Google Scholar] [CrossRef]
- Yue, M.; Wei, X. Dynamic balance and motion control for wheeled inverted pendulum vehicle via hierarchical sliding mode approach. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2014, 228, 351–358. [Google Scholar] [CrossRef]
- Huang, J.; Guan, Z.H.; Matsuno, T.; Fukuda, T.; Sekiyama, K. Sliding-mode velocity control of mobile-wheeled inverted-pendulum systems. IEEE Trans. Robot. 2010, 26, 750–758. [Google Scholar] [CrossRef]
- Huang, J.; Ding, F.; Fukuda, T.; Matsuno, T. Modeling and velocity control for a novel narrow vehicle based on mobile wheeled inverted pendulum. IEEE Trans. Control Syst. Technol. 2013, 21, 1607–1617. [Google Scholar] [CrossRef]
- Sago, Y.; Noda, Y.; Kakihara, K.; Terashima, K. Parallel two-wheel vehicle with underslung vehicle body. Mech. Eng. J. 2014, 1, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Sago, Y.; Terashima, K.; Noda, Y.; Kakihara, K. Attitude control using active-mass-system in parallel two-wheel vehicle with underslung vehicle body. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics, SMC, San Diego, CA, USA, 5–8 October 2014; pp. 1532–1537. [Google Scholar]
- Rao, S.S.; Yap, F.F. Mechanical Vibrations; Prentice Hall: Upper Saddle River, NJ, USA, 2011; Volume 4. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Education: Bengaluru, India, 2009; Volume 3/E. [Google Scholar]
- Bolton, W. Mechatronics: Electronic Control Systems in Mechanical and Electrical Engineering; Pearson Education: London, UK, 2003. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Qian, D.; Yi, J. Hierarchical Sliding Mode Control for Under-Actuated Cranes; Springer: Heidelberg/Berlin, Germany, 2016. [Google Scholar]
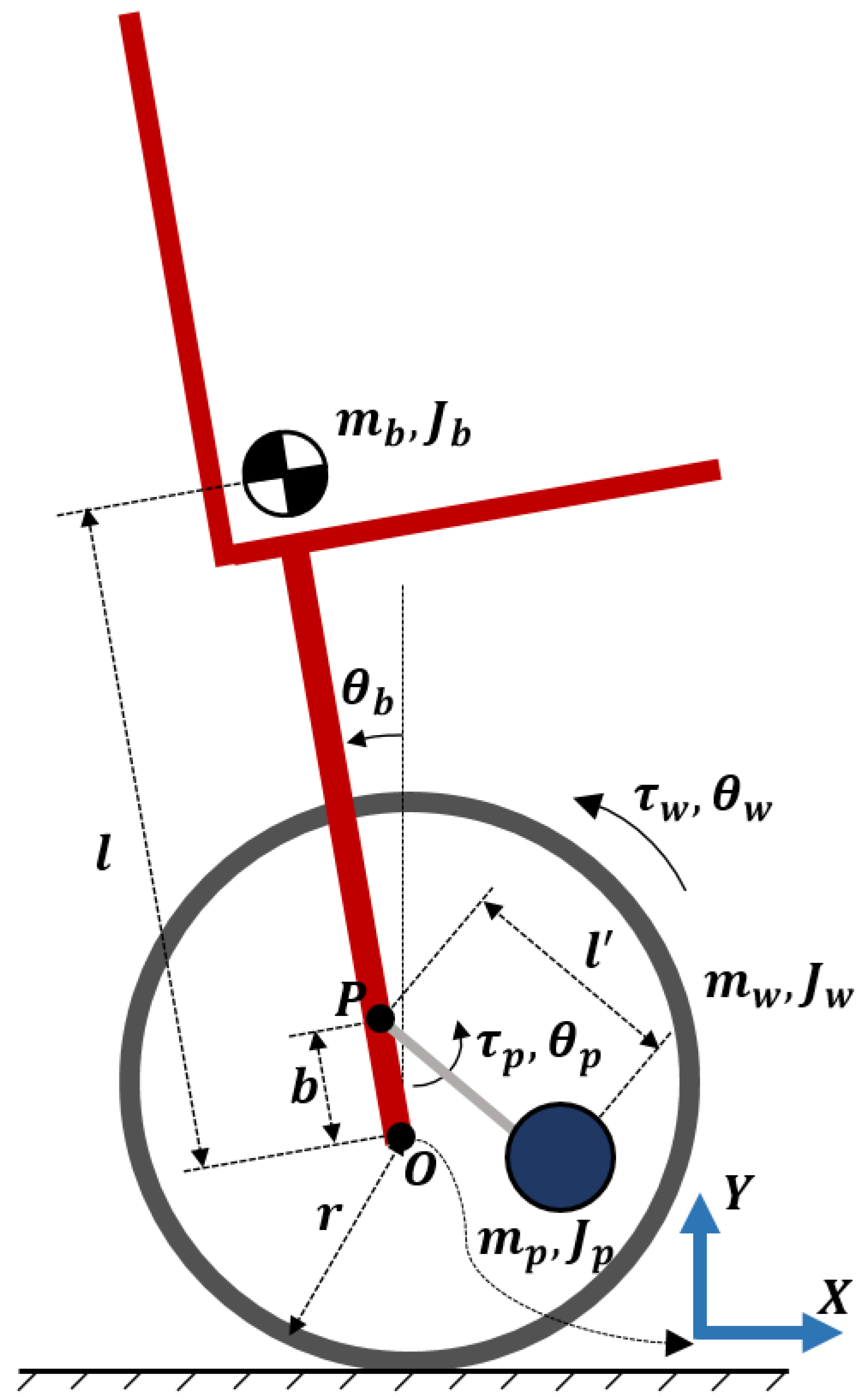




| Symbol | Description |
|---|---|
| Mass of each wheel | |
| Mass of body | |
| Mass of movable mechanism | |
| Moment of inertia of each wheel | |
| Moment of inertia of body | |
| Moment of inertia of movable mechanism | |
| O | Centre of the wheels’ axle |
| P | Contact point of the movable mechanism and wheelchair |
| r | Radius of each wheel |
| l | Distance from the body’s CoG to point P |
| Length of the rod of the pendulum (movable mechanism) | |
| b | Distance from point O to point P |
| Rotation angle of the wheel | |
| Rotation angle of the body (pitch angle) | |
| Rotation angle of the pendulum | |
| Input torque of the right wheel | |
| Input torque of the left wheel | |
| Total input torque of the wheels | |
| Input torque of the pendulum | |
| Input power of the wheels | |
| Input power of the pendulum |
| Property | r | l | b | |||||||
| Value | 16 | 48 | 15.45 | 0.64 | 0 | 0.19 | 0.26 | 0.3 | 0.2 | 0 |
| Unit | kg | kg | kg | kg·m2 | kg·m2 | kg·m2 | m | m | m | m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikpour, M.; Huang, L.; Al-Jumaily, A.M. An Approach on Velocity and Stability Control of a Two-Wheeled Robotic Wheelchair. Appl. Sci. 2020, 10, 6446. https://doi.org/10.3390/app10186446
Nikpour M, Huang L, Al-Jumaily AM. An Approach on Velocity and Stability Control of a Two-Wheeled Robotic Wheelchair. Applied Sciences. 2020; 10(18):6446. https://doi.org/10.3390/app10186446
Chicago/Turabian StyleNikpour, Mostafa, Loulin Huang, and Ahmed M. Al-Jumaily. 2020. "An Approach on Velocity and Stability Control of a Two-Wheeled Robotic Wheelchair" Applied Sciences 10, no. 18: 6446. https://doi.org/10.3390/app10186446





