XOR Binary Gravitational Search Algorithm with Repository: Industry 4.0 Applications
Abstract
1. Introduction
2. Gravitational Search Algorithm
2.1. Basic Gravitational Search Algorithm
2.2. Binary Gravitational Search Algorithm
2.3. Analysis of Binary Gravitational Search Algorithm
- (1)
- In the case when or . One has which results in no acceleration for the dimension k which is reasonable. In this case, the value of bits in the kth dimension for the corresponding object and the best solutions are exactly the same and no change is required in that dimension.
- (2)
- If , resulting in a positive acceleration term. In this case, if the velocity in kth dimension is positive, this acceleration term works fine and adds up to the speed. However, if the velocity in kth dimension is negative, the acceleration term decreases the absolute value of velocity and makes the probability of change smaller which is completely undesirable.
- (3)
- If , results in a negative acceleration term. In this case, if the velocity in kth dimension is positive, this acceleration term decreases the velocity and consequently the probability of change. Since is different from , this behaviour is not desirable. On the other hand, if the velocity in the kth dimension is negative, the acceleration term increases the absolute value of velocity and makes the probability of change larger, which is desirable.
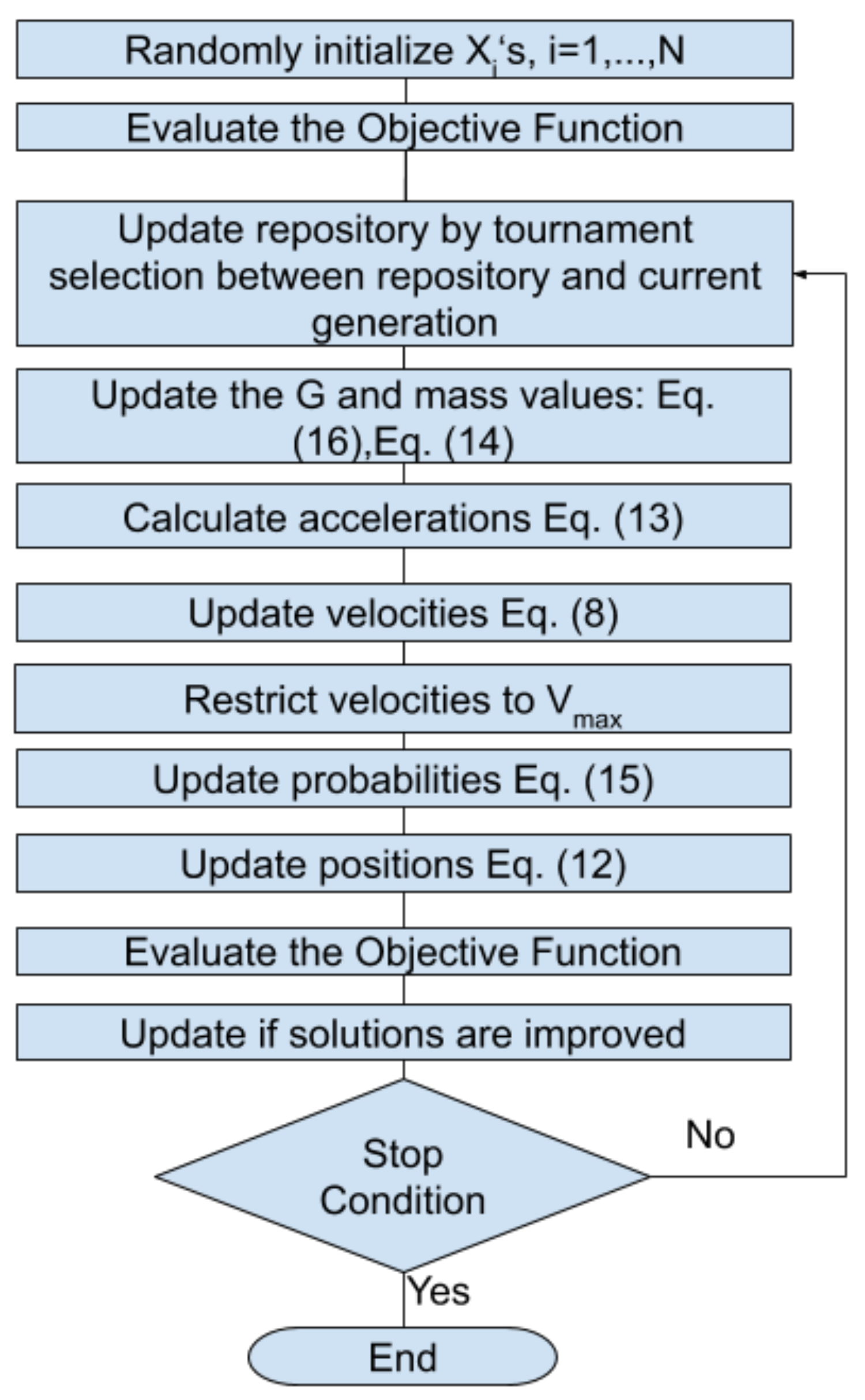
3. Proposed XOR Binary Gravitational Search Algorithm
4. Theoretical Analysis of the Proposed XOR Binary Gravitational Algorithm with Repository
4.1. General Analysis of the Proposed XOR BGSA
- (1)
- If or , in these cases . It is expected from the acceleration term that since the corresponding bit in the best particle is the same as the bit in the current particle, the probability of change reduces. This expectation is fulfilled using (13).
- (2)
- In the case , , the acceleration term introduces a positive value which contributes positively to the probability of change and increases its value.
- (3)
- In the case when , . Similar to the previous case, since the corresponding bit in the better particle is different than that of the current particle, a positive acceleration term is obtained which results in higher probability of change. This is an expected behaviour from the system.
4.2. Full Statistical Analysis of the Proposed Method
- In the case when , the acceleration term is non-positive and the velocity term is a non-increasing function of time and the probability of change converges to zero.
- In the case when , the acceleration term is non-negative and the velocity vector is a non-decreasing function of time and the probability of change converges to zero.
- If , , the probability of change becomes smaller than 0.5:
- If , , the probability of change becomes larger than 0.5:
5. Simulation Results
5.1. Benchmark Optimization Problem
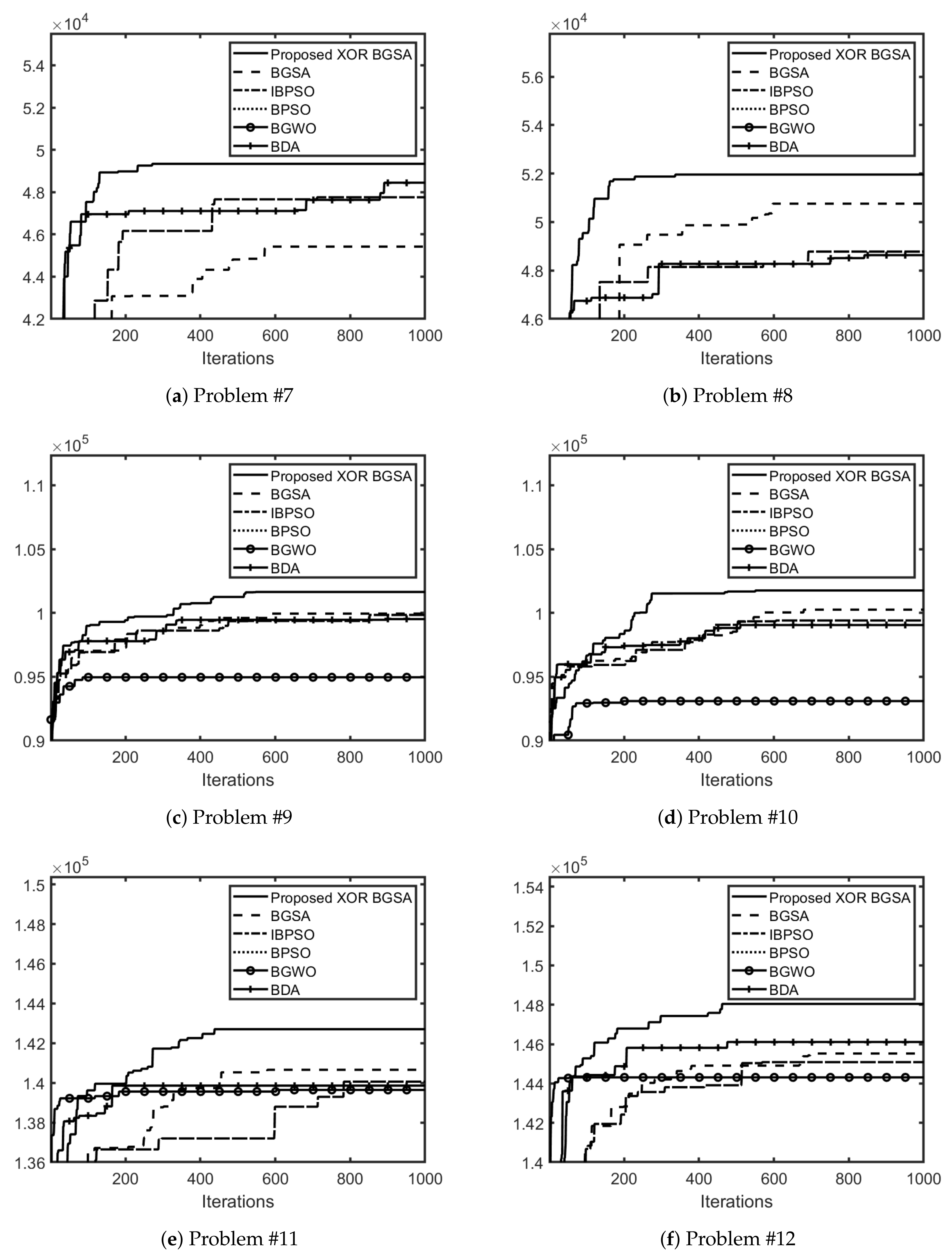
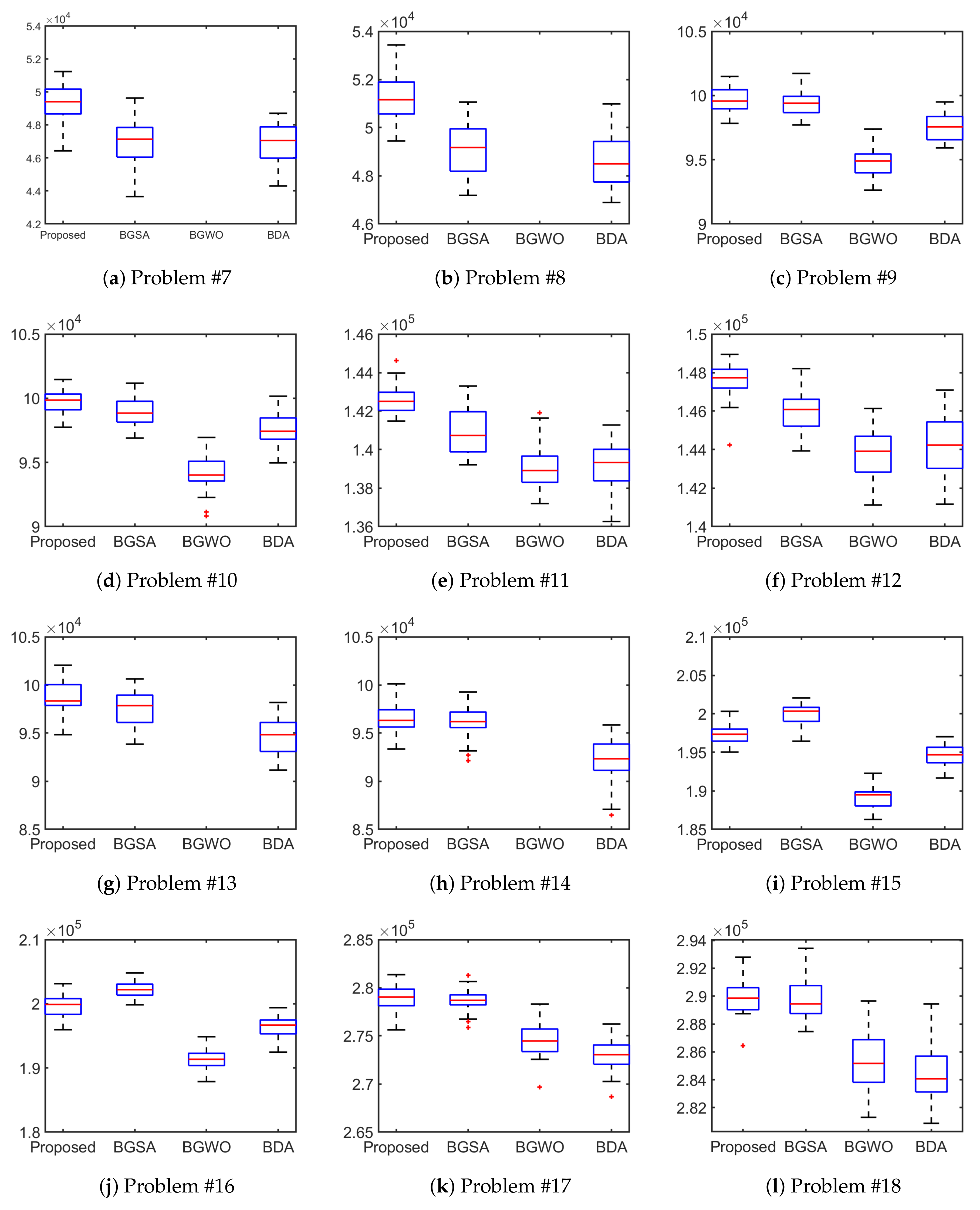
5.2. Application to Knapsack
6. Industry 4.0 Applications
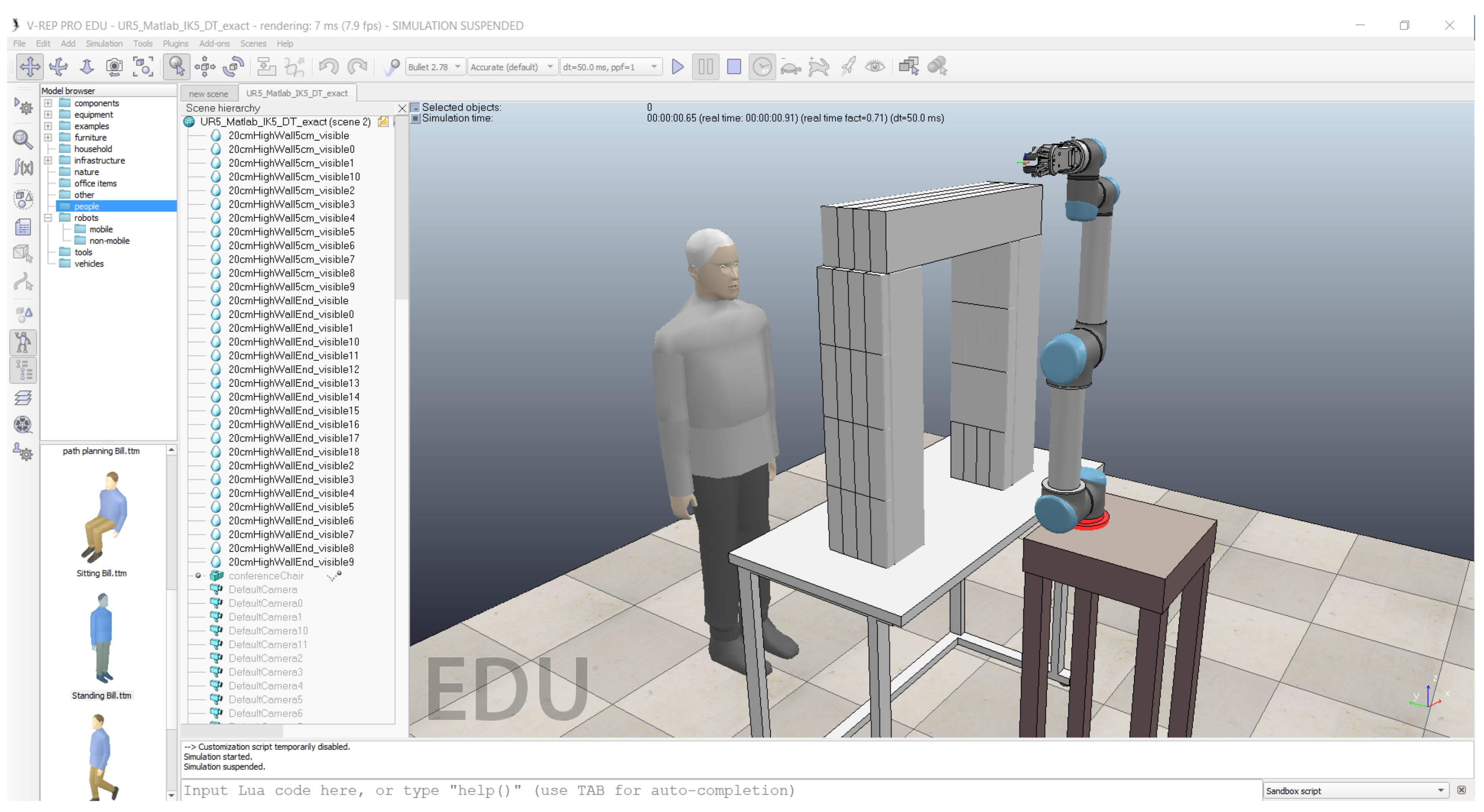
6.1. Motion Planning of Industrial Robots Inside a Digital Twin Created by V-REP Software
6.1.1. Encoding Movements
6.1.2. Kinematic and Inverse Kinematic of UR5
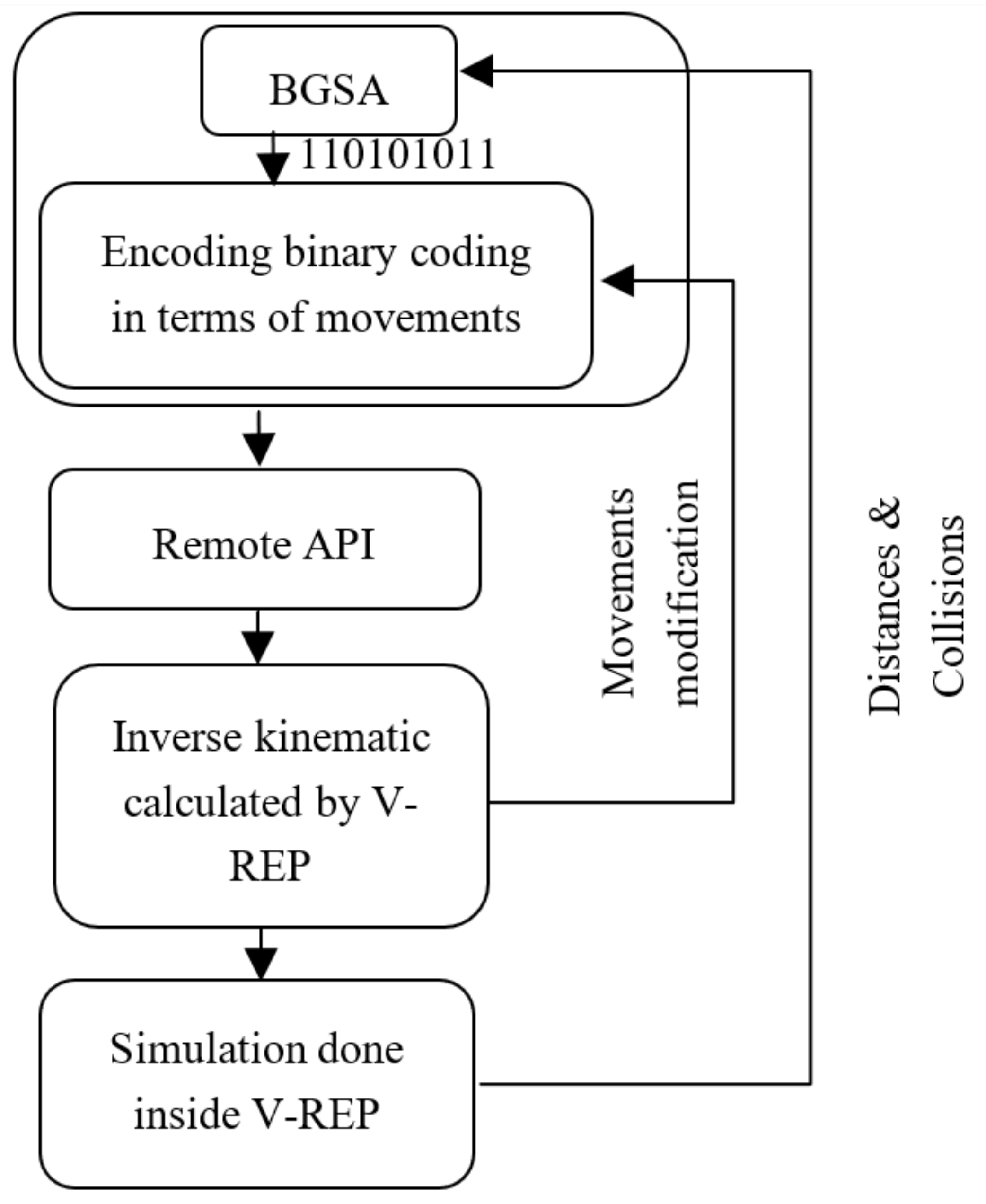
6.1.3. Communication between Matlab and V-REP
6.1.4. Cost Function to Be Optimized
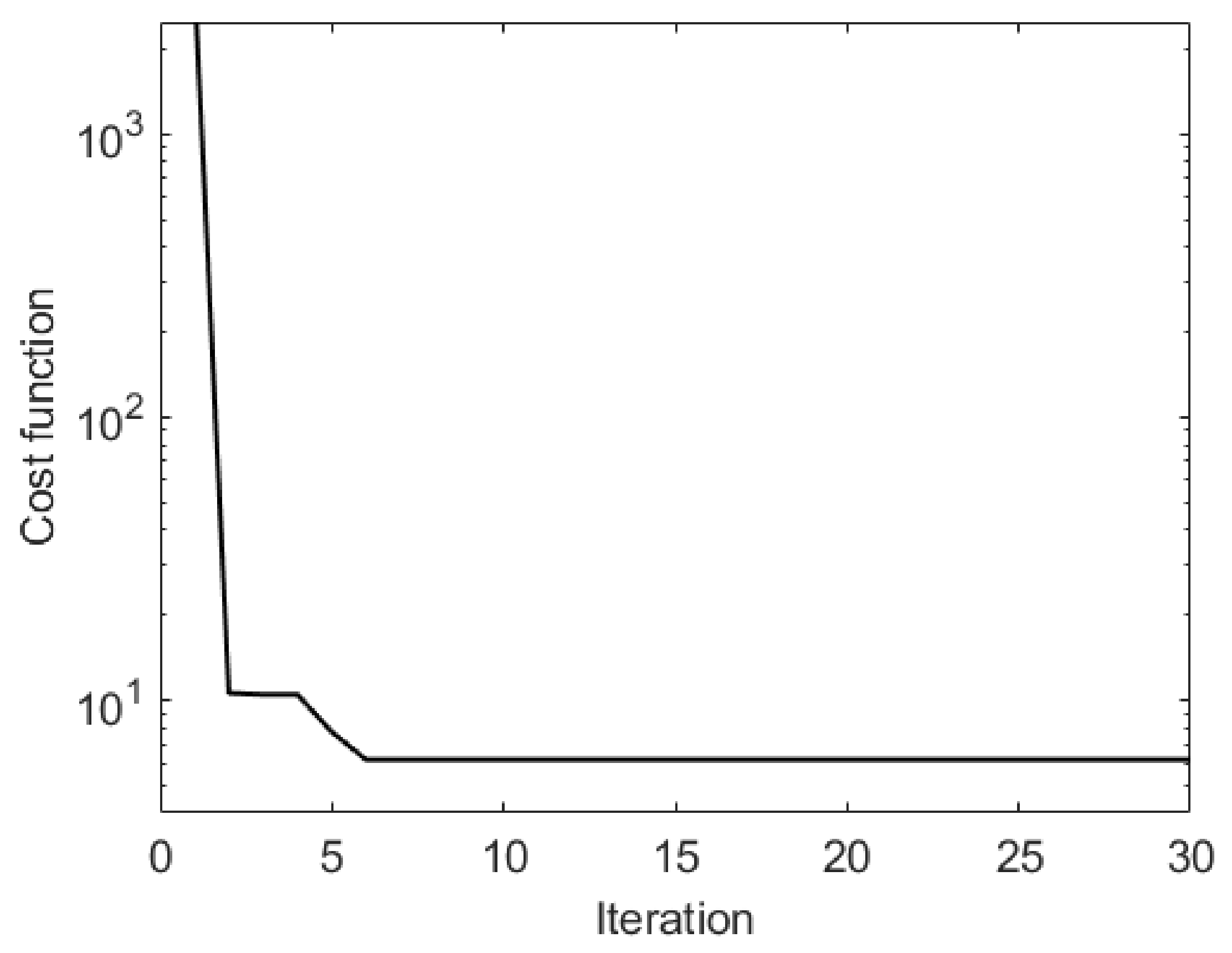
6.1.5. Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Burnap, P.; Branson, D.; Murray-Rust, D.; Preston, J.; Richards, D.; Burnett, D.; Edwards, N.; Firth, R.; Gorkovenko, K.; Khanesar, M. Chatty factories: A vision for the future of product design and manufacture with IoT. In Living in the Internet of Things (IoT 2019); IET: London, UK, 2019. [Google Scholar]
- Zhang, H.; Liu, Q.; Chen, X.; Zhang, D.; Leng, J. A digital twin-based approach for designing and multi-objective optimization of hollow glass production line. IEEE Access 2017, 5, 26901–26911. [Google Scholar] [CrossRef]
- Kongchuenjai, J.; Prombanpong, S. Binary Integer Programming to Solve the Process Planning Problem for Prismatic Mixed Parts. Int. J. Mech. Prod. Eng. IJMPE 2018, 6, 107–110. [Google Scholar]
- Liang, J.; Wang, P.; Guo, L.; Qu, B.; Yue, C.; Yu, K.; Wang, Y. Multi-objective flow shop scheduling with limited buffers using hybrid self-adaptive differential evolution. Memetic Comp. 2019, 11, 407–422. [Google Scholar]
- Özmen, Ö.; Batbat, T.; Özen, T.; Sinanoğlu, C.; Güven, A. Optimum assembly sequence planning system using discrete artificial bee colony algorithm. Math. Probl. Eng. 2018, 2018, 3407646. [Google Scholar] [CrossRef]
- Oesterle, J.; Amodeo, L. Efficient multi-objective optimization method for the mixed-model-line assembly line design problem. Procedia CIRP 2014, 17, 82–87. [Google Scholar] [CrossRef]
- Rekiek, B.; Dolgui, A.; Delchambre, A.; Bratcu, A. State of art of optimization methods for assembly line design. Annu. Rev. Control. 2002, 26, 163–174. [Google Scholar]
- Jin, Y.; Branke, J. Evolutionary optimization in uncertain environments-a survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- Engelbretch, A. Fundamentals of Computational Swarm Intelligence; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2005; pp. 5–129. [Google Scholar]
- Biswas, A.; Mishra, K.; Tiwari, S.; Misra, A. Physics-inspired optimization algorithms: A survey. J. Optim. 2013, 2013, 438152. [Google Scholar] [CrossRef]
- Genc, H.M.; Eksin, I.; Erol, O.K. Big bang-big crunch optimization algorithm with local directional moves. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 1359–1375. [Google Scholar]
- Formato, R.A. Central force optimization. Prog. Electromagn. Res. 2007, 77, 425–491. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Rashedi, E.; Rashedi, E.; Nezamabadi-pour, H. A comprehensive survey on gravitational search algorithm. Swarm Evol. Comput. 2018, 41, 141–158. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; IEEE: Piscataway, NJ, USA, 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. BGSA: Binary gravitational search algorithm. Nat. Comput. 2010, 9, 727–745. [Google Scholar] [CrossRef]
- Yuan, X.; Nie, H.; Su, A.; Wang, L.; Yuan, Y. An improved binary particle swarm optimization for unit commitment problem. Expert Syst. Appl. 2009, 36, 8049–8055. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Schumer, M.; Steiglitz, K. Adaptive step size random search. IEEE Trans. Autom. Control. 1968, 13, 270–276. [Google Scholar] [CrossRef]
- Surjanovic, S.; Bingham, D. Virtual Library of Simulation Experiments: Test Functions and Datasets; Simon Fraser University: Burnaby, BC, Canada, 2013; Volume 13, p. 2015. [Google Scholar]
- Surjanovic, D.B.S. Evolution and Optimum Seeking. 1995. Available online: https://www.sfu.ca/~ssurjano/optimization.html (accessed on 6 July 2020).
- Silagadze, Z. Finding two-dimensional peaks. Phys. Part. Nucl. Lett. 2007, 4, 73–80. [Google Scholar] [CrossRef]
- Bäck, T.; Schwefel, H.P. An overview of evolutionary algorithms for parameter optimization. Evol. Comput. 1993, 1, 1–23. [Google Scholar] [CrossRef]
- Liu, J.; Mei, Y.; Li, X. An analysis of the inertia weight parameter for binary particle swarm optimization. IEEE Trans. Evol. Comput. 2015, 20, 666–681. [Google Scholar]
- Alcácer, V.; Cruz-Machado, V. Scanning the industry 4.0: A literature review on technologies for manufacturing systems. Eng. Sci. Technol. Int. J. 2019, 22, 899–919. [Google Scholar]
- Bansal, R.; Khanesar, M.A.; Branson, D. Ant Colony Optimization Algorithm for Industrial Robot Programming in a Digital Twin. In Proceedings of the 2019 25th International Conference on Automation and Computing (ICAC), Lancaster, UK, 5–7 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Nogueira, L. Comparative analysis between gazebo and v-rep robotic simulators. Semin. Interno Cognicao Artif. SICA 2014. [Google Scholar] [CrossRef]
- Hawkins, K.P. Analytic Inverse Kinematics for the Universal Robots; Georgia Institute of Technology: Atlanta, GA, USA, 2013. [Google Scholar]
- Andersen, R.S. Kinematics of a UR5; Aalborg University: Aalborg, Denmark, 2018. [Google Scholar]





| A | B | |
|---|---|---|
| 0 | 0 | −1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | −1 |
| Function Number | n | d | Proposed | BGSA [16] | IBPSO [17] | BPSO [15] | BGWO [18] | BDA [19] |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3.64E-10 | 6.55E-10 | 0.003499 | 2.98E-07 | 0.079185 | 9.09E-11 | |
| 1 | 2 | 7.28E-10 | 0.000421 | 0.110086 | 0.004851 | 3.173297 | 8.66E-08 | |
| 1 | 5 | 1.82E-09 | 0.01808 | 3.837217 | 3.492558 | 54.25284 | 0.025257 | |
| 1 | 10 | 1.24E-07 | 1.640722 | 23.62139 | 43.34931 | 212.2319 | 0.892732 | |
| 2 | 1 | 3.64E-10 | 3.64E-10 | 8.62E-05 | 2.73E-07 | 0.153546 | 9.09E-11 | |
| 2 | 2 | 2.65E-19 | 2.81E-18 | 0.000454 | 2.5E-07 | 0.358629 | 2.25E-16 | |
| 2 | 5 | 7.65E-46 | 7.08E-34 | 7.45E-05 | 7.57E-05 | 2.79E-05 | 1E-22 | |
| 2 | 10 | 8.3E-82 | 2.57E-56 | 12.26801 | 1274.831 | 2.09E-11 | 5.44E-22 | |
| 3 | 1 | −1 | −0.9999 | −0.99705 | −1 | −0.98737 | −1 | |
| 3 | 2 | −0.99488 | −0.99375 | −0.98506 | −0.99787 | −0.94229 | −0.99901 | |
| 3 | 5 | −0.95717 | −0.96513 | −0.90313 | −0.91313 | −0.74288 | −0.96923 | |
| 3 | 10 | −0.90475 | −0.89211 | −0.64083 | −0.5024 | −0.51453 | −0.88339 | |
| 4 | 1 | −19.4256 | −19.4253 | −3.94361 | −3.9453 | −18.4693 | −3.9453 | |
| 4 | 2 | −38.8511 | −38.8511 | −7.8514 | −7.8897 | −31.8297 | −7.89018 | |
| 4 | 5 | −97.1278 | −97.1165 | −19.0216 | −19.1181 | −55.8132 | −19.6948 | |
| 4 | 10 | −194.255 | −193.588 | −35.5675 | −31.5541 | −79.5703 | −39.2195 | |
| 5 | 1 | 3.64E-10 | 3.64E-10 | 7.76E-05 | 3.32E-07 | 0.372345 | 9.09E-11 | |
| 5 | 2 | 3.64E-10 | 0.006168 | 0.140178 | 0.002341 | 1.452548 | 1.08E-09 | |
| 5 | 5 | 3.64E-10 | 0.13037 | 9.419671 | 4.551582 | 2659.276 | 0.002952 | |
| 5 | 10 | 3.64E-10 | 17.81345 | 4293.123 | 2334.993 | 1.06E+08 | 4.71886 | |
| 6 | 1 | −78.3323 | −78.1186 | −77.5076 | −78.3323 | −67.8744 | −78.3323 | |
| 6 | 2 | −156.094 | −147.94 | −151.238 | −156.496 | −116.85 | −156.659 | |
| 6 | 5 | −338.666 | −327.884 | −314.902 | −322.303 | 984.8181 | −369.827 | |
| 6 | 10 | −641.095 | −630.392 | −431.271 | −400.089 | 21937.59 | −645.258 | |
| 7 | 1 | −0.99419 | −0.97691 | −0.88143 | −0.98787 | −0.88543 | −0.98792 | |
| 7 | 2 | −1.95034 | −1.95069 | −1.68317 | −1.89381 | −1.66732 | −1.95806 | |
| 7 | 5 | −4.66631 | −4.67197 | −3.45559 | −2.81238 | −3.45303 | −4.40256 | |
| 1 | 1 | 3.64E-10 | 6.55E-10 | 0.003499 | 2.98E-07 | 0.079185 | 9.09E-11 | |
| 7 | 10 | −8.83999 | −9.00763 | −5.11393 | −3.84276 | −5.97745 | −7.38148 | |
| 8 | 1 | 7.63E-05 | 7.63E-05 | 0.17688 | 0.001563 | 1.270744 | 3.82E-05 | |
| 8 | 2 | 7.63E-05 | 0.002378 | 0.873989 | 0.346521 | 3.054737 | 0.00026 | |
| 8 | 5 | 7.63E-05 | 0.497182 | 4.210083 | 4.515039 | 9.078786 | 0.311861 | |
| 8 | 10 | 0.07325 | 1.479706 | 6.721189 | 8.003571 | 11.92714 | 2.243791 | |
| 9 | 1 | 3.64E-10 | 3.64E-10 | 0.000344 | 2.89E-07 | 0.052176 | 9.09E-11 | |
| 9 | 2 | 1.09E-09 | 1.09E-09 | 0.285221 | 0.005263 | 3.989166 | 2.82E-08 | |
| 9 | 5 | 5.46E-09 | 0.267058 | 10.71721 | 7.755365 | 108.3779 | 0.011655 | |
| 9 | 10 | 3.09E-07 | 7.555599 | 125.9897 | 176.937 | 1128.728 | 5.058231 | |
| 10 | 1 | 4.63E-06 | 2.32E-06 | 0.000547 | 2.03E-05 | 0.008308 | 2.88E-06 | |
| 10 | 2 | 0.000948 | 0.000326 | 0.015704 | 0.003854 | 0.111948 | 0.000223 | |
| 10 | 5 | 0.045093 | 0.021953 | 0.898418 | 1.041691 | 1.199264 | 0.080774 | |
| 10 | 10 | 0.189655 | 0.304581 | 3.68566 | 6.668867 | 5.377988 | 0.748952 | |
| 11 | 1 | −400.1 | −400.1 | −99.9787 | −100.093 | −398.391 | −100.1 | |
| 11 | 2 | −800.2 | −799.77 | −196.958 | −198.57 | −786.66 | −200.195 | |
| 11 | 5 | −2000.5 | −1996.02 | −461.362 | −442.035 | −1900.74 | −498.794 | |
| 11 | 10 | −4000.99 | −3983.41 | −839.887 | −740.219 | −3875.63 | −974.665 |
| Problem Number | Dimension | Tightness Ratio | m | N | Filename | Proposed | BGSA [16] | IBPSO [17] | BPSO [15] | BGWO [18] | BDA [19] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 100 | 0.25 | 5 | 10 | OR5x100-0.25_1.dat | 21675.33 | 20,742.73 | −7E+13 | −1.4E+14 | −3.6E+14 | 20,278.77 |
| 2 | 100 | 0.25 | 5 | 10 | OR5x100-0.25_2.dat | 21,223.93 | 20,663 | −9.2E+13 | −1.4E+14 | −3.4E+14 | 19,938.63 |
| 3 | 100 | 0.5 | 5 | 10 | OR5x100-0.50_1.dat | 39,835.93 | 39,302.37 | 37,097.47 | 37,573.93 | 37,093.93 | 38,813.2 |
| 4 | 100 | 0.5 | 5 | 10 | OR5x100-0.50_2.dat | 39,812.4 | 39,372.73 | 36,388.13 | 37,300.47 | 36,902.1 | 38,704.93 |
| 5 | 100 | 0.75 | 5 | 10 | OR5x100-0.75_1.dat | 57,626 | 56,945.5 | 52,385.83 | 50,954.87 | 55,652.37 | 56,107.47 |
| 6 | 100 | 0.75 | 5 | 10 | OR5x100-0.75_2.dat | 59,946.2 | 59,272.1 | 55,457.23 | 53,529.87 | 57,861.93 | 58,294.9 |
| 7 | 250 | 0.25 | 5 | 10 | OR5x250-0.25_1.dat | 49,323.17 | 46,860.27 | −5.9E+14 | −7.6E+14 | −1.1E+15 | 46,805.43 |
| 8 | 250 | 0.25 | 5 | 10 | OR5x250-0.25_2.dat | 51,256.37 | 49,071.9 | −6.1E+14 | −7.7E+14 | −1.2E+15 | 48,596.37 |
| 9 | 250 | 0.5 | 5 | 10 | OR5x250-0.50_1.dat | 99,682.27 | 99,393.17 | 94,943.5 | 94,993.6 | 94,801.07 | 97,535.43 |
| 10 | 250 | 0.5 | 5 | 10 | OR5x250-0.50_2.dat | 99,759 | 99,000.57 | 94,482.33 | 94,256.9 | 94,158.23 | 97621.53 |
| 11 | 250 | 0.75 | 5 | 10 | OR5x250-0.75_1.dat | 142,598.2 | 140,975.2 | 120,843.3 | 115,794.4 | 139,086.3 | 139,172.7 |
| 12 | 250 | 0.75 | 5 | 10 | OR5x250-0.75_2.dat | 147,544.4 | 145,975.8 | 124,749.9 | 119,751.7 | 143,700.6 | 144207.3 |
| 13 | 500 | 0.25 | 5 | 15 | OR5x500-0.25_1.dat | 98,610.83 | 97,553.3 | −1.5E+15 | −1.9E+15 | −2.4E+15 | −3.2E+11 |
| 14 | 500 | 0.25 | 5 | 15 | OR5x500-0.25_2.dat | 96,512.53 | 96,034.53 | −1.4E+15 | −2E+15 | −2.5E+15 | 92,190.13 |
| 15 | 500 | 0.5 | 5 | 15 | OR5x500-0.50_1.dat | 197448.2 | 200,036.1 | 189,901.2 | 188,863.1 | 189,116.2 | 194,592.8 |
| 16 | 500 | 0.5 | 5 | 15 | OR5x500-0.50_2.dat | 199,792.7 | 202,340 | 192,444.5 | 190,561.9 | 191,162.6 | 196,350 |
| 17 | 500 | 0.75 | 5 | 15 | OR5x500-0.75_1.dat | 278,893.6 | 278,751.9 | 228,713.8 | 215,389.8 | 274,491.7 | 272,973.2 |
| 18 | 500 | 0.75 | 5 | 15 | OR5x500-0.75_2.dat | 289,925.9 | 289,654.3 | 238,158.3 | 223,533.2 | 285,228 | 284,254.3 |
| 19 | 100 | 0.25 | 10 | 10 | OR10x100-0.25_1.dat | 20,393.63 | 18,793.87 | −1.8E+14 | −2.9E+14 | −7.4E+14 | 18,583.23 |
| 20 | 100 | 0.25 | 10 | 10 | OR10x100-0.25_2.dat | 19,867.93 | 18,857.43 | −1.8E+14 | −2.6E+14 | −7.1E+14 | 18,583.03 |
| 21 | 100 | 0.5 | 10 | 10 | OR10x100-0.50_1.dat | 39051.77 | 38,258.77 | 35,430.33 | 36,021.43 | 35,607.37 | 37669.33 |
| 22 | 100 | 0.5 | 10 | 10 | OR10x100-0.50_2.dat | 40,356.13 | 39,734.97 | 37007.3 | 37,450.4 | 36,969.97 | 38,926.1 |
| 23 | 100 | 0.75 | 10 | 10 | OR10x100-0.75_1.dat | 55,408.4 | 54,477.57 | 50,067.83 | 49,302.2 | 53,058.4 | 53,580.87 |
| 24 | 100 | 0.75 | 10 | 10 | OR10x100-0.75_2.dat | 56,950.7 | 56,234.7 | 51,602.53 | 50,940.77 | 54,119.3 | 55,144.23 |
| 25 | 250 | 0.25 | 10 | 10 | OR10x250-0.25_1.dat | 49,901.6 | 49,401.6 | 46,393.33 | 46,438.4 | 46,738.6 | 48,197.13 |
| 26 | 250 | 0.25 | 10 | 10 | OR10x250-0.25_2.dat | 49,978.63 | 49,191.07 | 46,514.7 | 46,100.77 | 46,874.6 | 48,557.03 |
| 27 | 250 | 0.5 | 10 | 10 | OR10x250-0.50_1.dat | 101,134.7 | 100,792.5 | 96,179.27 | 95,810.07 | −4.8E+11 | 99,126.03 |
| 28 | 250 | 0.5 | 10 | 10 | OR10x250-0.50_2.dat | 98,053 | 97,841.1 | 92,281.53 | 92,293.1 | −8.8E+11 | 95,604.23 |
| 29 | 250 | 0.75 | 10 | 10 | OR10x250-0.75_1.dat | 144,205 | 141,717.6 | 121,695.7 | 117142 | 139,645.4 | 139,894.6 |
| 30 | 250 | 0.75 | 10 | 10 | OR10x250-0.75_2.dat | 141,698.4 | 139,494.2 | 120,037.3 | 115,081.9 | 137,321.4 | 138,109.7 |
| 31 | 500 | 0.25 | 10 | 15 | OR10x500-0.25_1.dat | 97,327.1 | 96,654.03 | −2.9E+15 | −3.9E+15 | −4.9E+15 | 93,571.07 |
| 32 | 500 | 0.25 | 10 | 15 | OR10x500-0.25_2.dat | 96,865.7 | 96,662.67 | −3.1E+15 | −4.1E+15 | −5.1E+15 | 93,284.37 |
| 33 | 500 | 0.5 | 10 | 15 | OR10x500-0.50_1.dat | 195,540.6 | 199,151.9 | 188,580.9 | 187,265 | −8.1E+11 | 192,963.6 |
| 34 | 500 | 0.5 | 10 | 15 | OR10x500-0.50_2.dat | 196,987.5 | 199,922.2 | 189,706.1 | 187,867.3 | 188,244 | 194,179 |
| 35 | 500 | 0.75 | 10 | 15 | OR10x500-0.75_1.dat | 286,164.6 | 285,945.3 | 237,022 | 220,772.4 | 281,163.6 | 279,953.5 |
| 36 | 500 | 0.75 | 10 | 15 | OR10x500-0.75_2.dat | 284,177.3 | 283,569.9 | 235,502.1 | 219,917.2 | 278,756.1 | 277,475.7 |
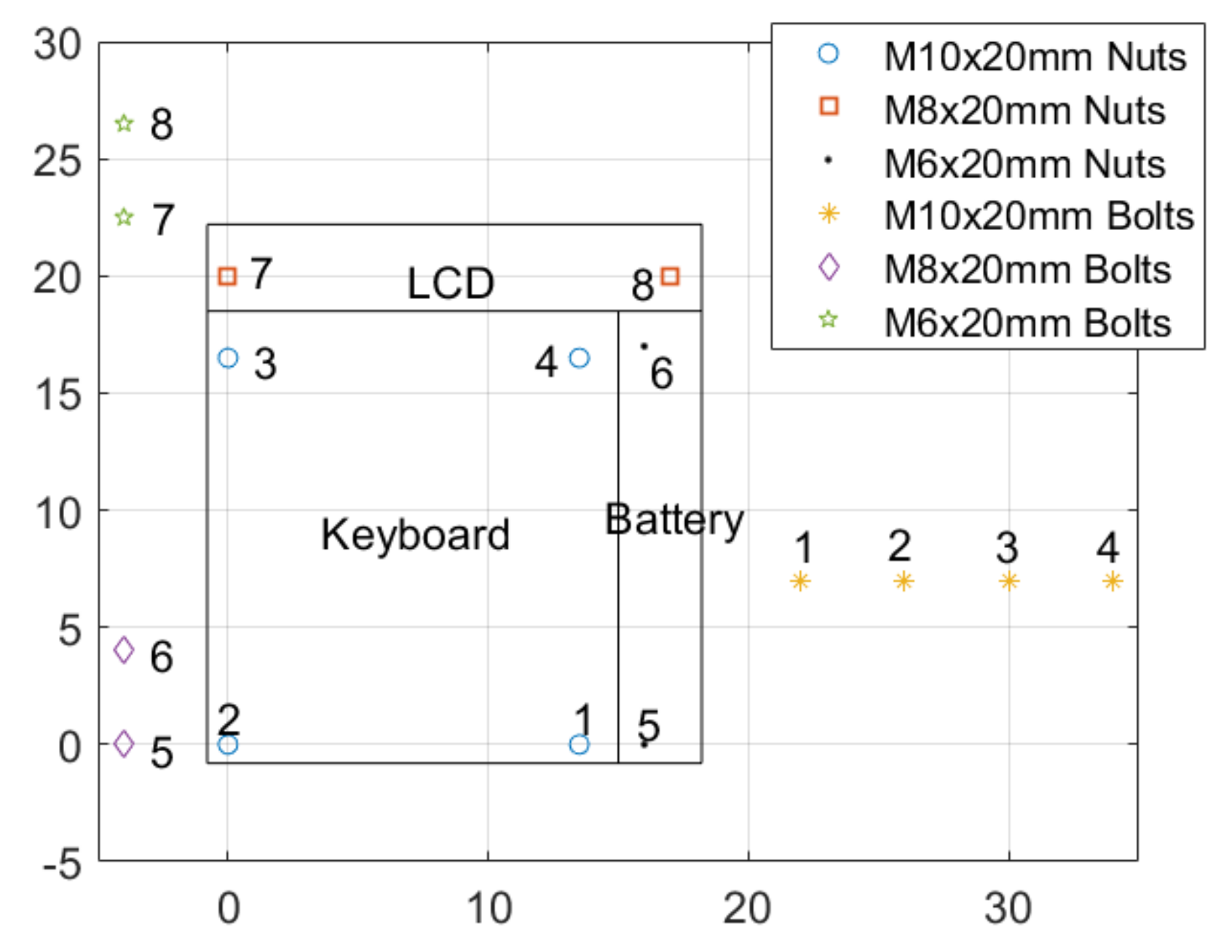
| Action | Bolt | Nut |
|---|---|---|
| Step 1 | #8 | #8 |
| Step 2 | #7 | #7 |
| Step 3 | #4 | #1 |
| Step 4 | #5 | #5 |
| Step 5 | #3 | #4 |
| Step 6 | #6 | #6 |
| Step 7 | #2 | #3 |
| Step 8 | #1 | #2 |
| Movements | Rotations | ||
|---|---|---|---|
| Value | Interpretation | Value | Interpretation |
| 0 | 4 | ||
| 1 | 5 | ||
| 2 | 6 | ||
| 3 | 7 | ||
| i | ||||
|---|---|---|---|---|
| 0 | – | – | 0 | 0 |
| 1 | 89.16 | 0 | ||
| 2 | 0 | −425 | 0 | |
| 3 | 0 | −392.25 | 0 | |
| 4 | 109.15 | 0 | ||
| 5 | 94.65 | 0 | ||
| 6 | 82.3 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadieh Khanesar, M.; Bansal, R.; Martínez-Arellano, G.; Branson, D.T. XOR Binary Gravitational Search Algorithm with Repository: Industry 4.0 Applications. Appl. Sci. 2020, 10, 6451. https://doi.org/10.3390/app10186451
Ahmadieh Khanesar M, Bansal R, Martínez-Arellano G, Branson DT. XOR Binary Gravitational Search Algorithm with Repository: Industry 4.0 Applications. Applied Sciences. 2020; 10(18):6451. https://doi.org/10.3390/app10186451
Chicago/Turabian StyleAhmadieh Khanesar, Mojtaba, Ridhi Bansal, Giovanna Martínez-Arellano, and David T. Branson. 2020. "XOR Binary Gravitational Search Algorithm with Repository: Industry 4.0 Applications" Applied Sciences 10, no. 18: 6451. https://doi.org/10.3390/app10186451
APA StyleAhmadieh Khanesar, M., Bansal, R., Martínez-Arellano, G., & Branson, D. T. (2020). XOR Binary Gravitational Search Algorithm with Repository: Industry 4.0 Applications. Applied Sciences, 10(18), 6451. https://doi.org/10.3390/app10186451






