Lightweight Stacked Hourglass Network for Human Pose Estimation
Abstract
Featured Application
Abstract
1. Introduction
- A proposed stacked hourglass network structure improves performance in human pose estimation with fewer parameters (Section 3.1, Section 3.2.1 and Section 3.2.2).
- A new structured residual block, known as a multidilated light residual block, which expands the receptive field of convolution operation, effectively represents the relationship of the full human body, and supports multiscale performance through multiple dilations (Section 3.2).
- An additional skip connection in an encoder of the hourglass module that reflects the low-level features of previous stacks on a subsequent stack. This additional skip connection improves performance in pose estimation without increasing the number of parameters. (Section 3.1).
2. Related Work
2.1. Network Architecture
2.2. Residual Block
2.3. Human Pose Estimation
3. Proposed Method
3.1. Network Architecture
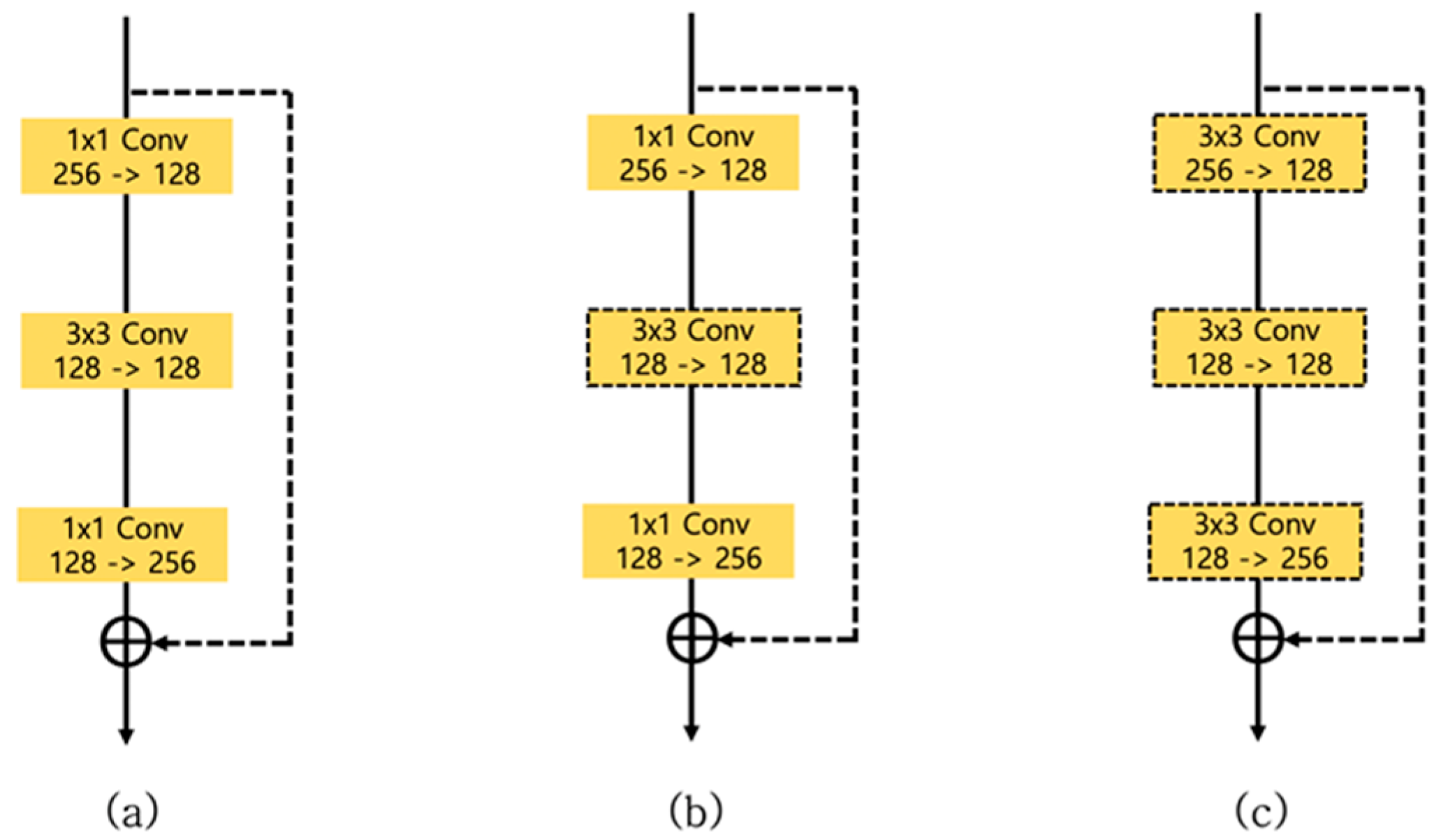
3.2. Residual Block Design
3.2.1. Dilated Convolution
3.2.2. Depthwise Separable Convolution
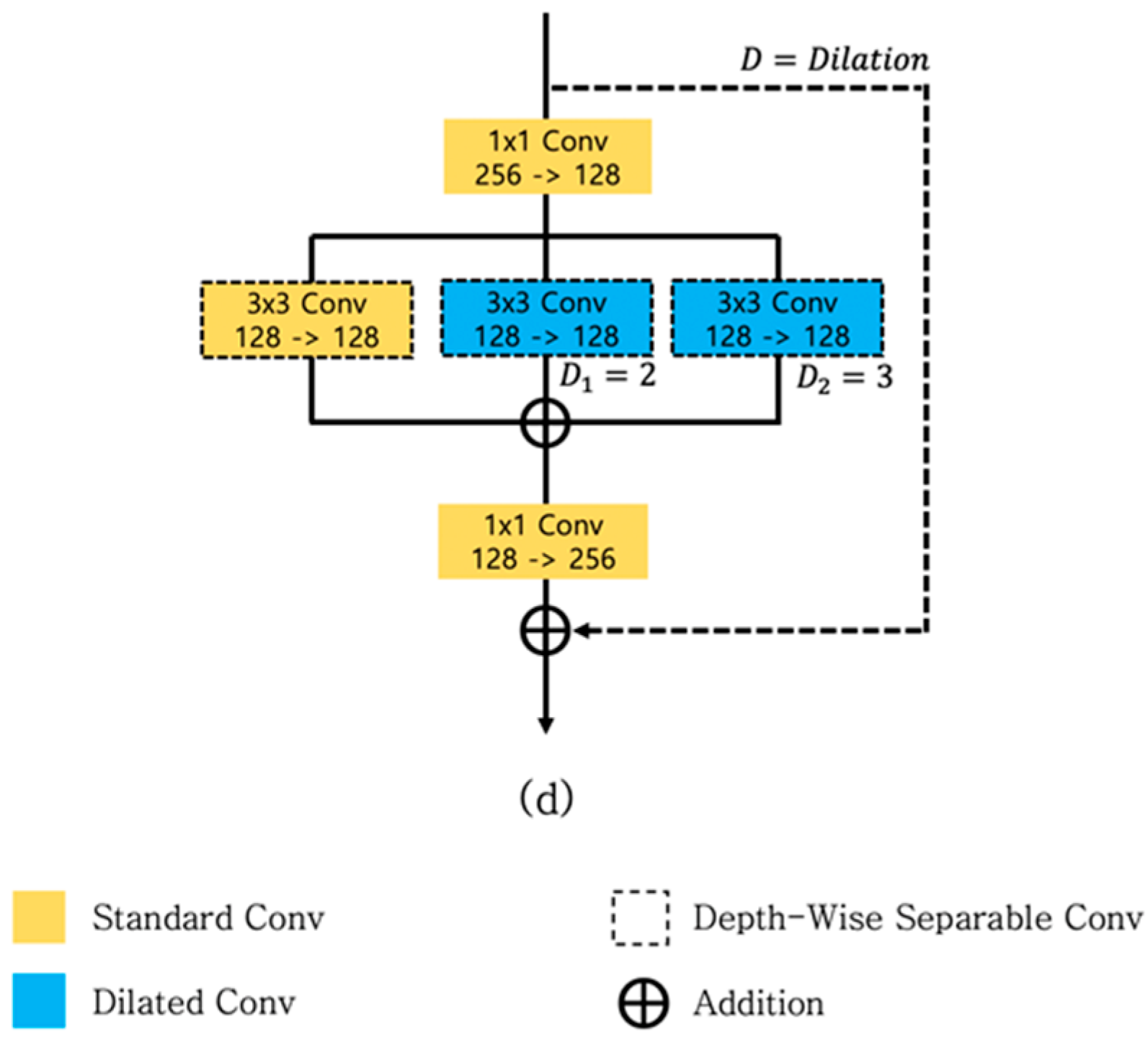
3.2.3. Proposed Multidilated Light Residual Block
4. Experiments and Results
4.1. Dataset and Evaluation Matrix
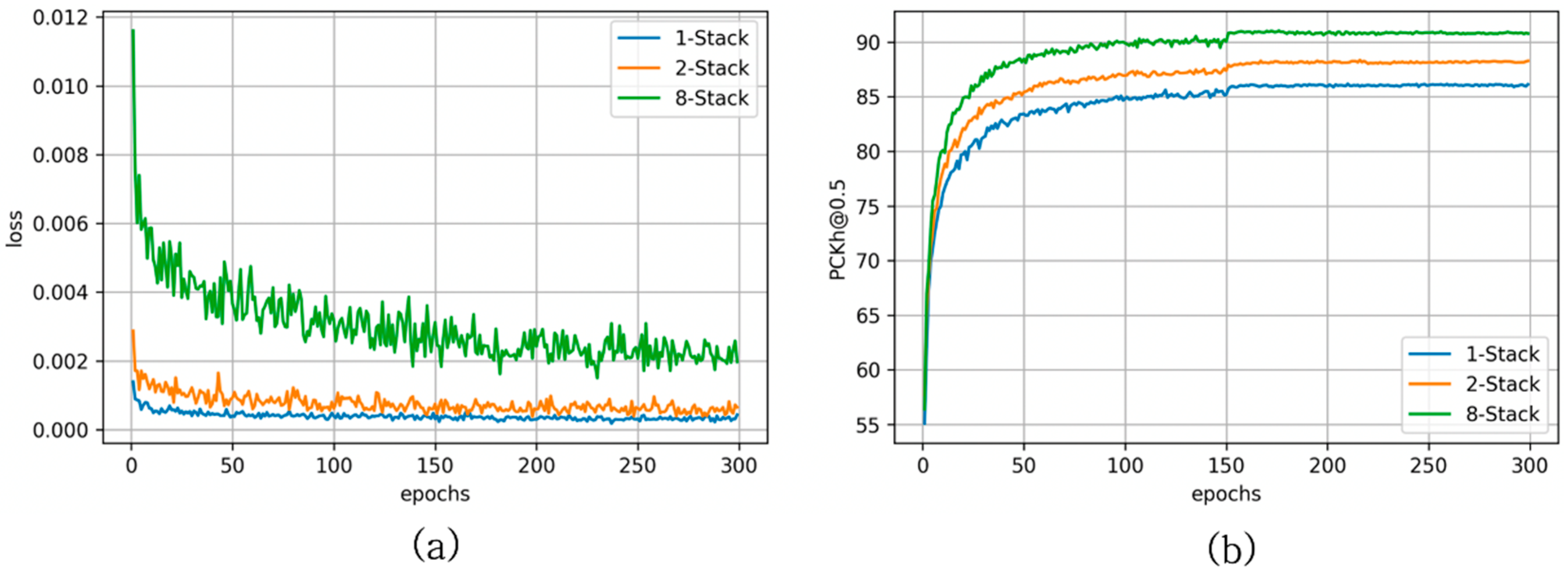
4.2. Training Details
4.3. Lightweight and Bottleneck Structure
4.4. Additional Skip Connection
4.5. Effect of the Dilation Scale
4.6. Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bulat, A.; Tzimiropoulos, G. Human pose estimation via convolutional part heatmap regression. In Proceedings of the Haptics: Science, Technology, Applications, London, UK, 4–7 July 2016; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2016; Volume 9911, pp. 717–732. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked hourglass networks for human pose estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Tompson, J.J.; Jain, A.; LeCun, Y.; Bregler, C. Joint training of a convolutional network and a graphical model for human pose estimation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Wang, R.; Cao, Z.; Wang, X.; Liu, Z.; Zhu, X.; Wanga, X. Human pose estimation with deeply learned Multi-scale compositional models. IEEE Access 2019, 7, 71158–71166. [Google Scholar] [CrossRef]
- Chu, X.; Yang, W.; Ouyang, W.; Ma, C.; Yuille, A.L.; Wang, X. Multi-context Attention for Human Pose Estimation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 5669–5678. [Google Scholar]
- Peng, X.; Tang, Z.; Yang, F.; Feris, R.S.; Metaxas, D. Jointly optimize data augmentation and network training: Adversarial data augmentation in human pose estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 2226–2234. [Google Scholar]
- Bulat, A.; Tzimiropoulos, G. Hierarchical binary CNNs for landmark localization with limited resources. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 343–356. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Li, S.; Ouyang, W.; Li, H.; Wang, X. Learning feature pyramids for human pose estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 1290–1299. [Google Scholar]
- Tang, W.; Wu, Y. Does learning specific features for related parts help human pose estimation? In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2019; pp. 1107–1116. [Google Scholar]
- Ning, G.; Zhang, Z.; He, Z. Knowledge-guided deep fractal neural networks for human pose estimation. IEEE Trans. Multimed. 2018, 20, 1246–1259. [Google Scholar] [CrossRef]
- Ke, L.; Chang, M.-C.; Qi, H.; Lyu, S. Multi-scale structure-aware network for human pose estimation. In Proceedings of the Haptics: Science, Technology, Applications, Pisa, Italy, 13–16 June 2018; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 731–746. [Google Scholar]
- Zhang, Y.; Liu, J.; Huang, K. Dilated hourglass networks for human pose estimation. Chin. Autom. Congr. 2018, 2597–2602. [Google Scholar] [CrossRef]
- Artacho, B.; Savakis, A. UniPose: Unified human pose estimation in single images and videos. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020; pp. 7033–7042. [Google Scholar]
- Wei, S.-E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional pose machines. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 4724–4732. [Google Scholar]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2D human pose estimation: New benchmark and state of the art analysis. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 3686–3693. [Google Scholar]
- Johnson, S.; Everingham, M. Clustered pose and nonlinear appearance models for human pose estimation. In Proceedings of the British Machine Vision Conference 2010, Aberystwyth, UK, 31 August–3 September 2010; British Machine Vision Association and Society for Pattern Recognition: Durham, UK, 2010. [Google Scholar]
- Bulat, A.; Tzimiropoulos, G. Binarized convolutional landmark localizers for human pose estimation and face alignment with limited resources. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 3726–3734. [Google Scholar]
- Toshev, A.; Szegedy, D. DeepPose: Human pose estimation via deep neural networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 1653–1660. [Google Scholar]
- Yang, Y.; Ramanan, D. Articulated pose estimation with flexible mixtures-of-parts. In Proceedings of the CVPR 2011, Providence, RI, USA, 20–25 June 2011; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2011; pp. 1385–1392. [Google Scholar]
- Ferrari, V.; Marín-Jiménez, M.J.; Zisserman, A. Progressive search space reduction for human pose estimation. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, Alaska, USA, 24–26 June 2008; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2008; pp. 1–8. [Google Scholar]
- Li, S.; Liu, Z.; Chan, A.B. Heterogeneous multi-task learning for human pose estimation with deep convolutional neural network. Int. J. Comput. Vis. 2014, 113, 19–36. [Google Scholar] [CrossRef]
- Jain, A.; Tompson, J.; Andriluka, M.; Taylor, G.W.; Bregler, C. Learning human pose estimation features with convolutional networks. arXiv 2013, arXiv:1312.7302. [Google Scholar]
- Belagiannis, V.; Zisserman, A. Recurrent human pose estimation. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 468–475. [Google Scholar]
- Chu, X.; Ouyang, W.; Li, H.; Wang, X. Structured feature learning for pose estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 4715–4723. [Google Scholar]
- Yang, W.; Ouyang, W.; Li, H.; Wang, X. End-to-end learning of deformable mixture of parts and deep convolutional neural networks for human pose estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 3073–3082. [Google Scholar]
- Cao, Z.; Šimon, T.; Wei, S.-E.; Sheikh, Y. Realtime multi-person 2d pose estimation using part affinity fields. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 1302–1310. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar]
- Badrinarayanan, V.; Badrinarayanan, V.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: New York, NY, USA, 2015; pp. 234–241. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 5686–5696. [Google Scholar]
- Xiao, B.; Wu, H.; Wei, Y. Simple Baselines for Human Pose Estimation and Tracking. In Proceedings of the Haptics: Science, Technology, Applications, Munich, Germany, 8–14 September 2018; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 472–487. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Proceedings of the Haptics: Science, Technology, Applications, London, UK, 4–7 July 2016; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2016; Volume 9908, pp. 630–645. [Google Scholar]
- Johnson, S.; Everingham, M. Learning effective human pose estimation from inaccurate annotation. In Proceedings of the CVPR 2011, Providence, RI, USA, 20–25 June 2011; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2011; pp. 1465–1472. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the NeurIPS Workshop, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Pishchulin, L.; Andriluka, M.; Gehler, P.; Schiele, B. Strong appearance and expressive spatial models for human pose estimation. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3487–3494. [Google Scholar]
- Carreira, J.; Agrawal, P.; Fragkiadaki, K.; Malik, J. Human pose estimation with iterative error feedback. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4733–4742. [Google Scholar]
- Tompson, J.; Goroshin, R.; Jain, A.; LeCun, Y.; Bregler, C. Efficient object localization using convolutional NETWORKS. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 648–656. [Google Scholar]
- Hu, P.; Ramanan, D. Bottom-Up and Top-Down Reasoning with Hierarchical Rectified Gaussians. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5600–5609. [Google Scholar]
- Pishchulin, L.; Insafutdinov, E.; Tang, S.; Andres, B.; Andriluka, M.; Gehler, P.; Schiele, B. Deepcut: Joint subset partition and labeling for multi person pose estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4929–4937. [Google Scholar]
- Lifshitz, I.; Fetaya, E.; Ullman, S. Human pose estimation using deep consensus voting. In European Conference on Computer Vision; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2016; Volume 9906, pp. 246–260. [Google Scholar]
- Gkioxari, G.; Toshev, A.; Jaitly, N. Chained Predictions Using Convolutional Neural Networks. In Proceedings of the Haptics: Science, Technology, Applications, London, UK, 4–7 July 2016; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2016; Volume 9908, pp. 728–743. [Google Scholar]
- Rafi, U.; Leibe, B.; Gall, J.; Kostrikov, I.; Wilson, R.C.; Hancock, E.R.; Smith, W.A.P.; Pears, N.E.; Bors, A.G. An efficient convolutional network for human pose estimation. In Proceedings of the British Machine Vision Conference 2016, York, UK, 19–22 September 2016; British Machine Vision Association and Society for Pattern Recognition: Durham, UK, 2016. [Google Scholar]
- Insafutdinov, E.; Pishchulin, L.; Andres, B.; Andriluka, M.; Schiele, B. Deepercut: A deeper, stronger, and faster multi-person pose estimation model. In Proceedings of the Haptics: Science, Technology, Applications, London, UK, 4–7 July 2016; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2016; Volume 9910, pp. 34–50. [Google Scholar]



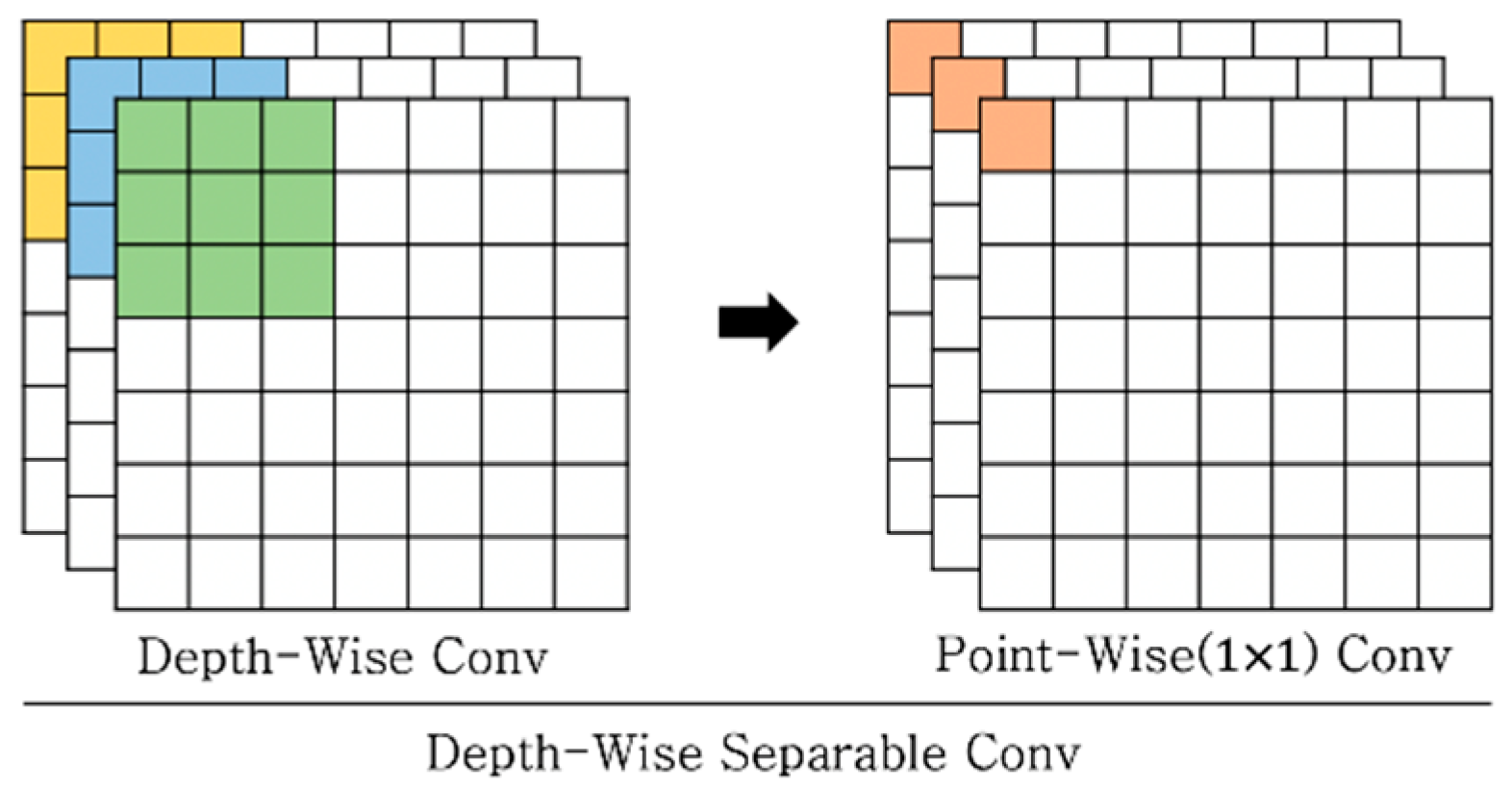

| Type | Input Size (C, H, W) | Output Size (C, H, W) | Kernel Size | Dilation Scale (D) | |
|---|---|---|---|---|---|
| INPUT | (256, H, W) | - | - | - | |
| Layer 1 | |||||
| ReLU | (256, H, W) | (256, H, W) | - | - | |
| Batch Norm | (256, H, W) | (256, H, W) | - | - | |
| Conv | (256, H, W) | (128, H, W) | 1 | ||
| Layer 2 | |||||
| ReLU | (128, H, W) | (128, H, W) | - | - | |
| Batch Norm | (128, H, W) | (128, H, W) | - | - | |
| Conv | (128, H, W) | (128, H, W) | 1 | ||
| ReLU | (128, H, W) | (128, H, W) | - | - | |
| Batch Norm | (128, H, W) | (128, H, W) | - | - | |
| Depthwise Conv | (128, H, W) | (128, H, W) | 2 | ||
| Conv | (128, H, W) | (128, H, W) | 1 | ||
| ReLU | (128, H, W) | (128, H, W) | - | - | |
| Batch Norm | (128, H, W) | (128, H, W) | - | - | |
| Depthwise Conv | (128, H, W) | (128, H, W) | 3 | ||
| Conv | (128, H, W) | (128, H, W) | 1 | ||
| ADD () | (128, H, W) | (128, H, W) | - | - | |
| Layer 3 | |||||
| ReLU | (128, H, W) | (128, H, W) | - | - | |
| Batch Norm | (128, H, W) | (128, H, W) | - | - | |
| Conv | (128, H, W) | (256, H, W) | 1 | ||
| ADD () | (256, H, W) | (256, H, W) | - | - | |
| OUTPUT | - | (256, H, W) | - | - | |
| Residual Block | # Params | PCKh@0.5 (Mean) |
|---|---|---|
| Bottleneck (Original) (Figure 5a) | 3.6M | 86.21 |
| Bottleneck (Original) + Depthwise Separable (Figure 5b) | 1.4M | 85.41 |
| Bottleneck () + Depthwise Separable (Figure 5c) | 1.6M | 85.67 |
| Multidilated Light Residual Block (Ours) (Figure 5d) | 2.0M | 86.12 |
| Network Architecture | Residual Block | # Params | PCKh@0.5 (Mean) |
|---|---|---|---|
| Hourglass (Original) | Bottleneck (Original) (Figure 5a) | 6.7M | 87.72 |
| Ours | Bottleneck (Original) (Figure 5a) | 6.7M | 88.68 |
| Ours | Ours (Figure 5d) | 3.9M | 87.60 |
| Method | PCKh@0.5 (Mean) |
|---|---|
| Ours () [×1] | 86.12 |
| Ours () [×1] | 85.67 |
| Ours () [×2] | 87.89 |
| Ours () [×2] | 87.19 |
| Method | [8]-Real | [8]-Real | Ours | Ours |
|---|---|---|---|---|
| Head | 96.8 | 97.4 | 96.3 | 98.1 |
| Shoulder | 93.8 | 96.0 | 94.1 | 96.2 |
| Elbow | 86.4 | 90.7 | 85.7 | 90.9 |
| Wrist | 80.3 | 86.2 | 80.4 | 87.2 |
| Hip | 87.0 | 89.6 | 85.6 | 89.8 |
| Knee | 80.4 | 86.1 | 80.3 | 87.3 |
| Ankle | 75.7 | 83.2 | 76.0 | 83.5 |
| # Params | 6M | 25M | 2M | 14.8M |
| PCKh@0.5 (Mean) | 85.5 | 89.8 | 86.1 | 90.8 |
| Method | Head | Sho. | Elb. | Wri. | Hip | Knee | Ank. | Mean |
|---|---|---|---|---|---|---|---|---|
| Pishchulin et al. [39] | 74.3 | 49.0 | 40.8 | 34.1 | 36.5 | 34.4 | 35.2 | 44.1 |
| Tompson et al. [3] | 95.8 | 90.3 | 80.5 | 74.3 | 77.6 | 69.7 | 62.8 | 79.6 |
| Carreira et al. [40] | 95.7 | 91.7 | 81.7 | 72.4 | 82.8 | 73.2 | 66.4 | 81.3 |
| Tompson et al. [41] | 96.1 | 91.9 | 83.9 | 77.8 | 80.9 | 72.3 | 64.8 | 82.0 |
| Hu et al. [42] | 95.0 | 91.6 | 83.0 | 76.6 | 81.9 | 74.5 | 69.5 | 82.4 |
| Pishchulin et al. [43] | 94.1 | 90.2 | 83.4 | 77.3 | 82.6 | 75.7 | 68.6 | 82.4 |
| Lifshitz et al. [44] | 97.8 | 93.3 | 85.7 | 80.4 | 85.3 | 76.6 | 70.2 | 85.0 |
| Gkioxary et al. [45] | 96.2 | 93.1 | 86.7 | 82.1 | 85.2 | 81.4 | 74.1 | 86.1 |
| Rafi et al. [46] | 97.2 | 93.9 | 86.4 | 81.3 | 86.8 | 80.6 | 73.4 | 86.3 |
| Belagiannis et al. [24] | 97.7 | 95.0 | 88.2 | 83.0 | 87.9 | 82.6 | 78.4 | 88.1 |
| Insafutdinov et al. [47] | 96.8 | 95.2 | 89.3 | 84.4 | 88.4 | 83.4 | 78.0 | 88.5 |
| Wei et al. [15] | 97.8 | 95.0 | 88.7 | 84.0 | 88.4 | 82.8 | 79.4 | 88.5 |
| Bulat et al. [8] | 97.9 | 95.1 | 89.9 | 85.3 | 89.4 | 85.7 | 81.7 | 89.7 |
| Ours | 98.1 | 96.2 | 90.9 | 87.2 | 89.8 | 87.3 | 83.5 | 90.8 |
| Method | Head | Shoulder | Elbow | Wrist | Hip | Knee | Ankle | Mean |
|---|---|---|---|---|---|---|---|---|
| Lifshitz et al. [44] | 96.8 | 89.0 | 82.7 | 79.1 | 90.9 | 86.0 | 82.5 | 86.7 |
| Pishchulin et al. [43] | 97.0 | 91.0 | 83.8 | 78.1 | 91.0 | 86.7 | 82.0 | 87.1 |
| Insafutdinov et al. [47] | 97.4 | 92.7 | 87.5 | 84.4 | 91.5 | 89.9 | 87.2 | 90.1 |
| Wei et al. [15] | 97.8 | 92.5 | 87.0 | 93.9 | 91.5 | 90.8 | 89.9 | 90.5 |
| Bulat et al. [8] | 97.2 | 82.1 | 88.1 | 85.2 | 92.2 | 91.4 | 88.7 | 90.7 |
| Ours | 98.1 | 93.1 | 89.2 | 86.1 | 92.7 | 92.8 | 90.4 | 91.7 |
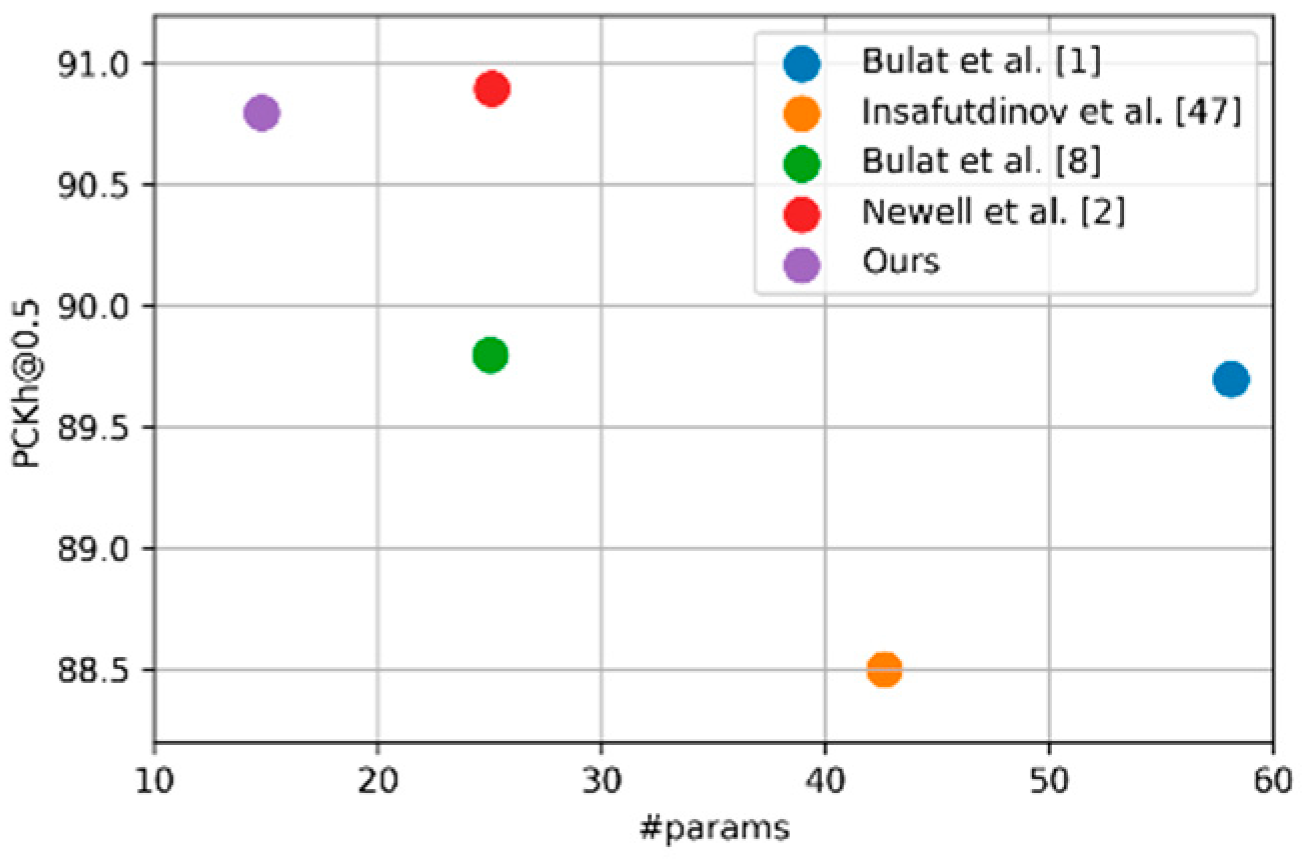
| Method | # Params | PCKh@0.5 (Mean) |
|---|---|---|
| Bulat et al. [1] | 58.1M | 89.7 |
| Insafutdinov et al. [47] | 42.6M | 88.5 |
| Bulat et al. [8] | 25.0M | 89.8 |
| Newell et al. [2] | 25.1M | 90.9 |
| Ours | 14.8M | 90.8 |
| Method | # Params | PCKh@0.5 (Mean) |
|---|---|---|
| 2.0M | 86.12 | |
| 3.9M | 87.89 | |
| 14.8M | 90.78 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-T.; Lee, H.J. Lightweight Stacked Hourglass Network for Human Pose Estimation. Appl. Sci. 2020, 10, 6497. https://doi.org/10.3390/app10186497
Kim S-T, Lee HJ. Lightweight Stacked Hourglass Network for Human Pose Estimation. Applied Sciences. 2020; 10(18):6497. https://doi.org/10.3390/app10186497
Chicago/Turabian StyleKim, Seung-Taek, and Hyo Jong Lee. 2020. "Lightweight Stacked Hourglass Network for Human Pose Estimation" Applied Sciences 10, no. 18: 6497. https://doi.org/10.3390/app10186497
APA StyleKim, S.-T., & Lee, H. J. (2020). Lightweight Stacked Hourglass Network for Human Pose Estimation. Applied Sciences, 10(18), 6497. https://doi.org/10.3390/app10186497




