Transverse Vibration of Functionally Graded Tapered Double Nanobeams Resting on Elastic Foundation
Abstract
:1. Introduction
2. Theory
2.1. Chebyshev Spectral Collocation Method
2.2. Nonlocal Theory
3. Problem Formulation
3.1. Mathematical Model
3.2. Solution Procedure
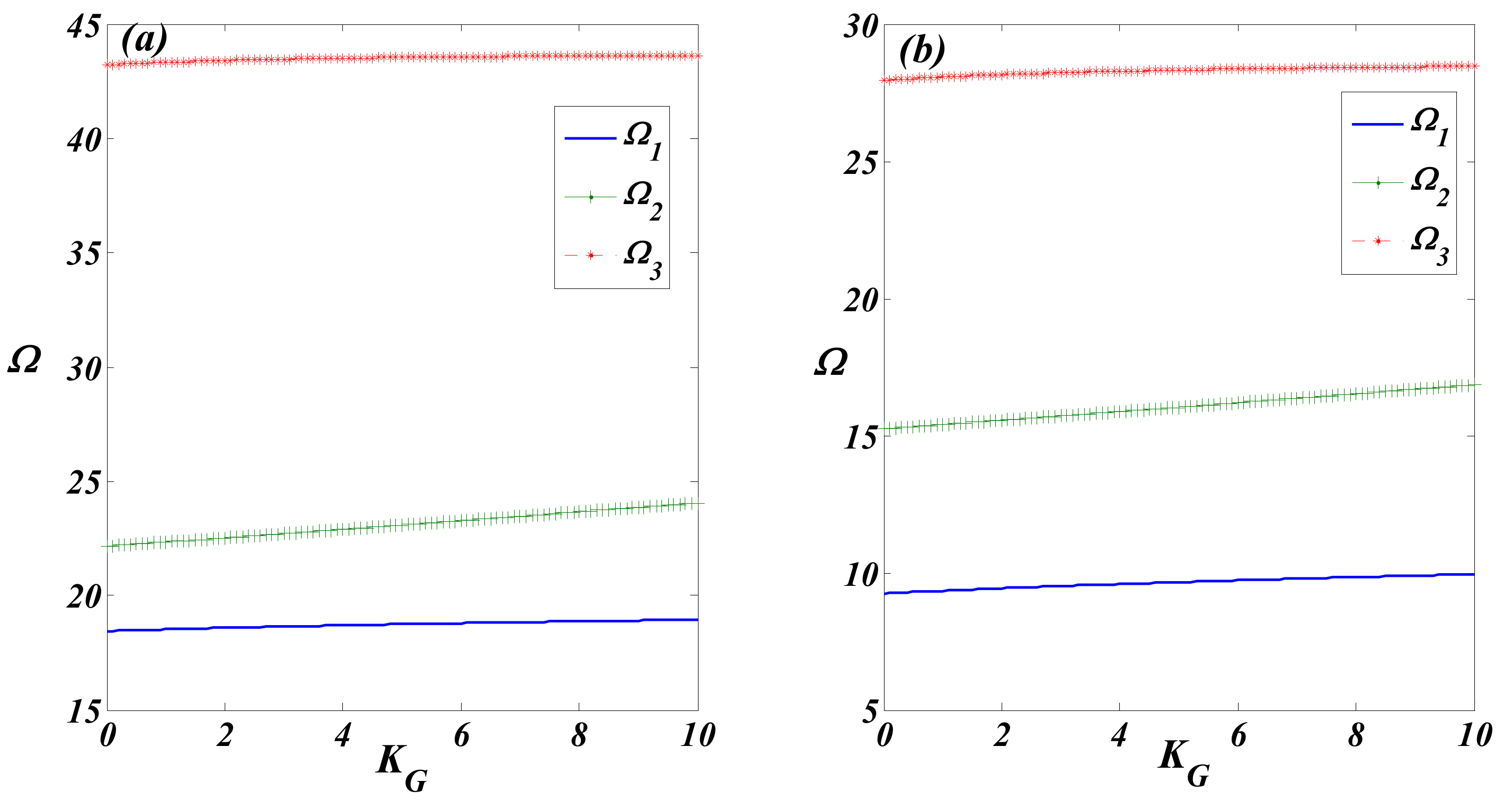
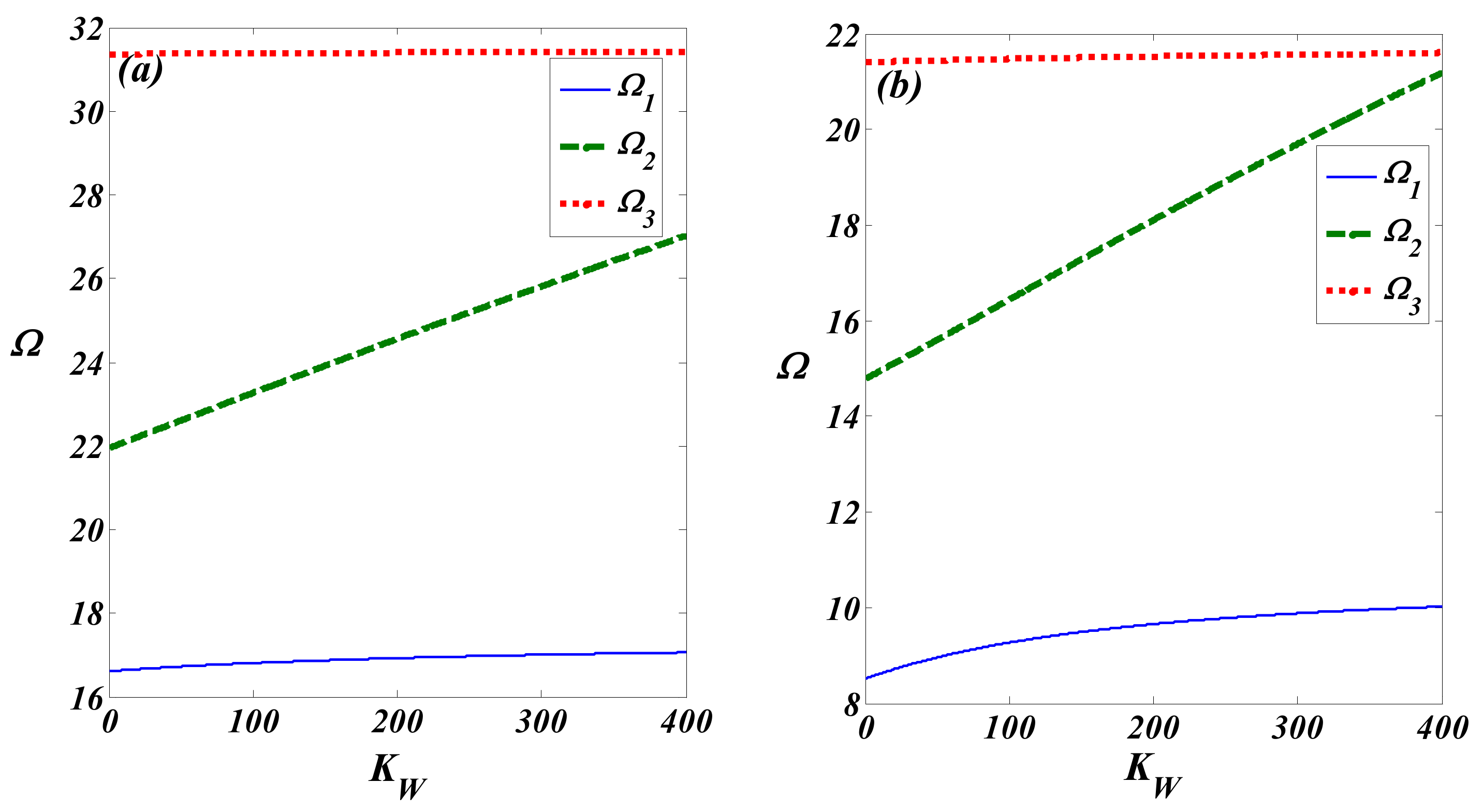
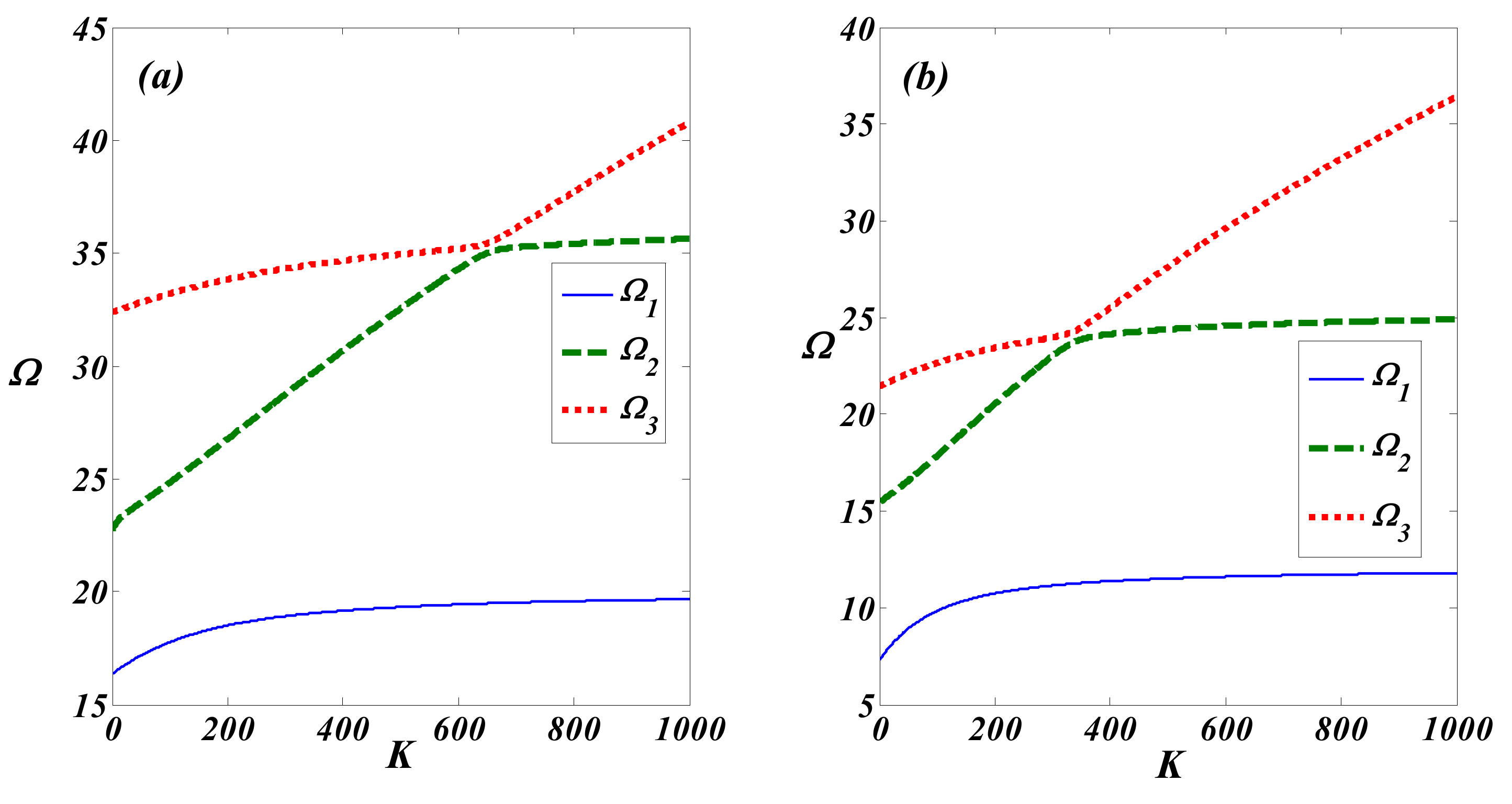
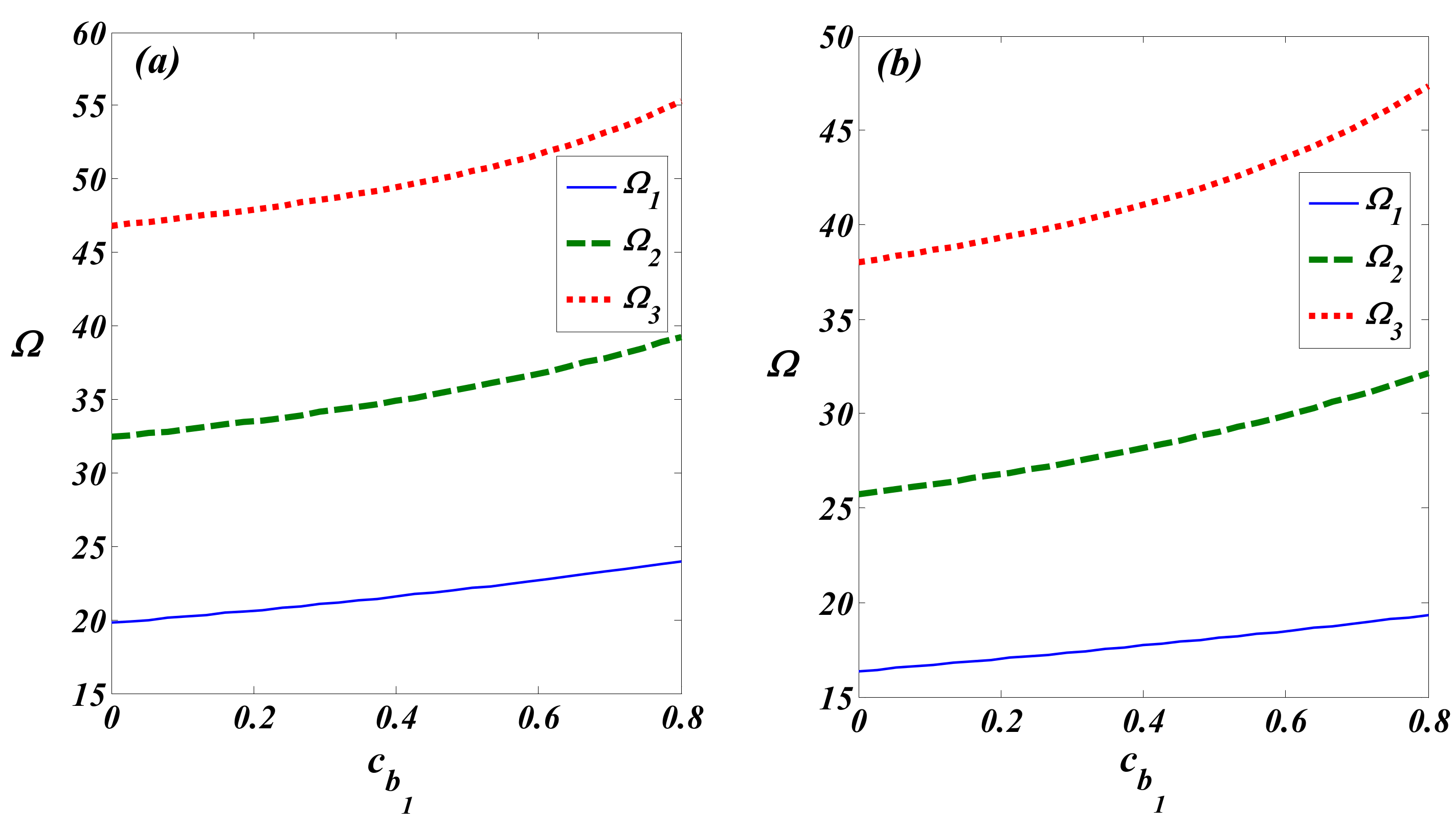
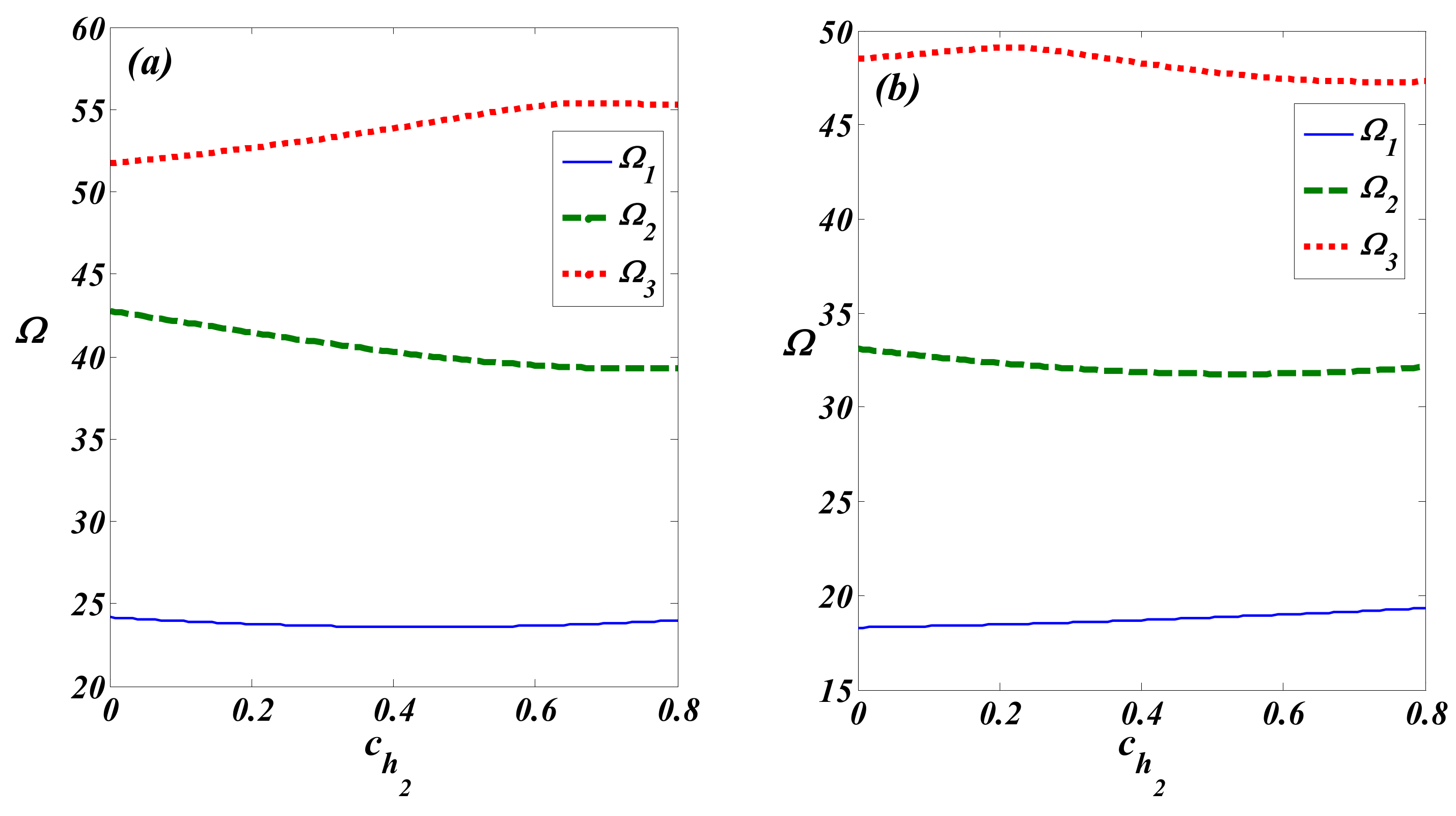
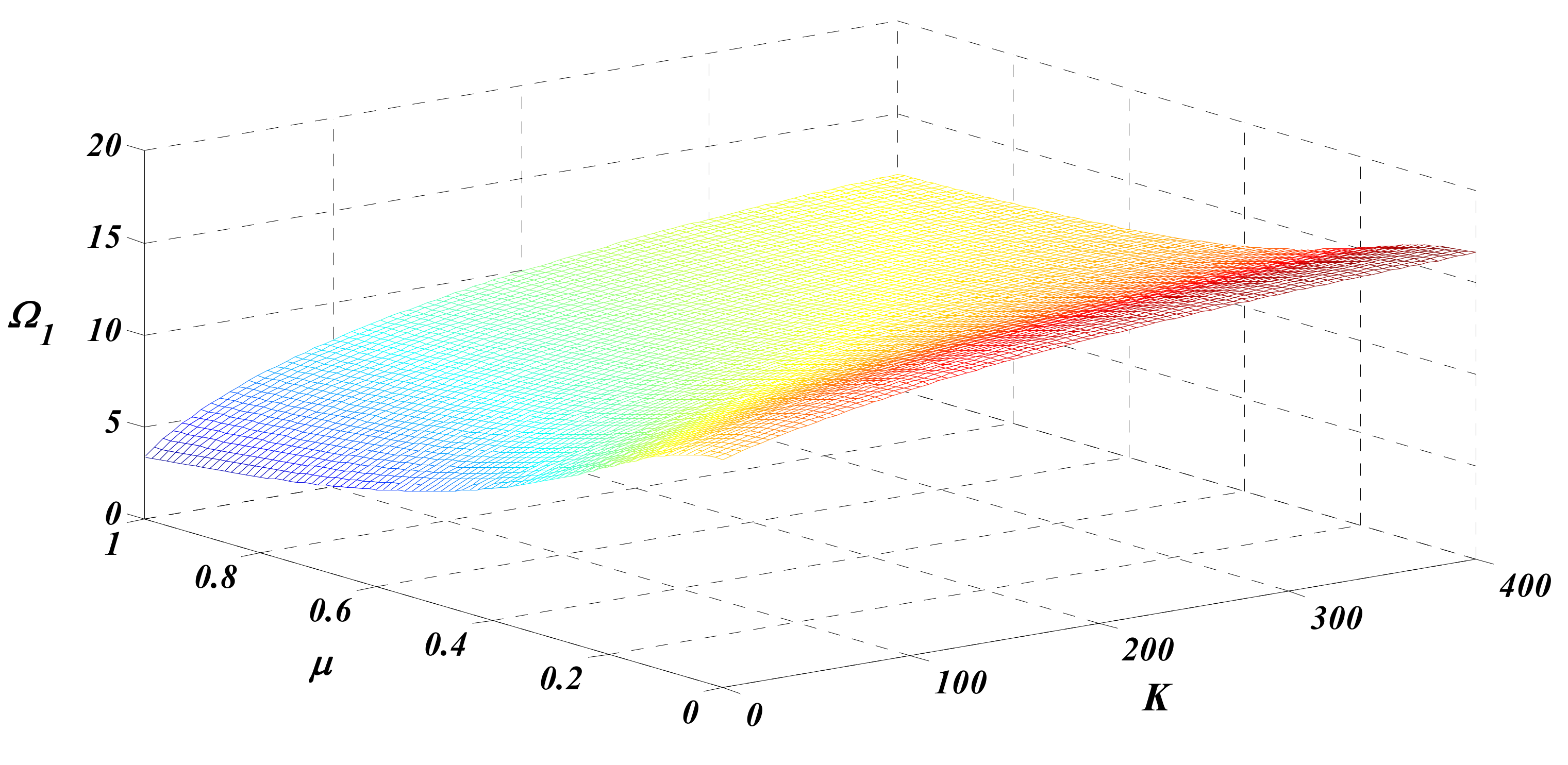
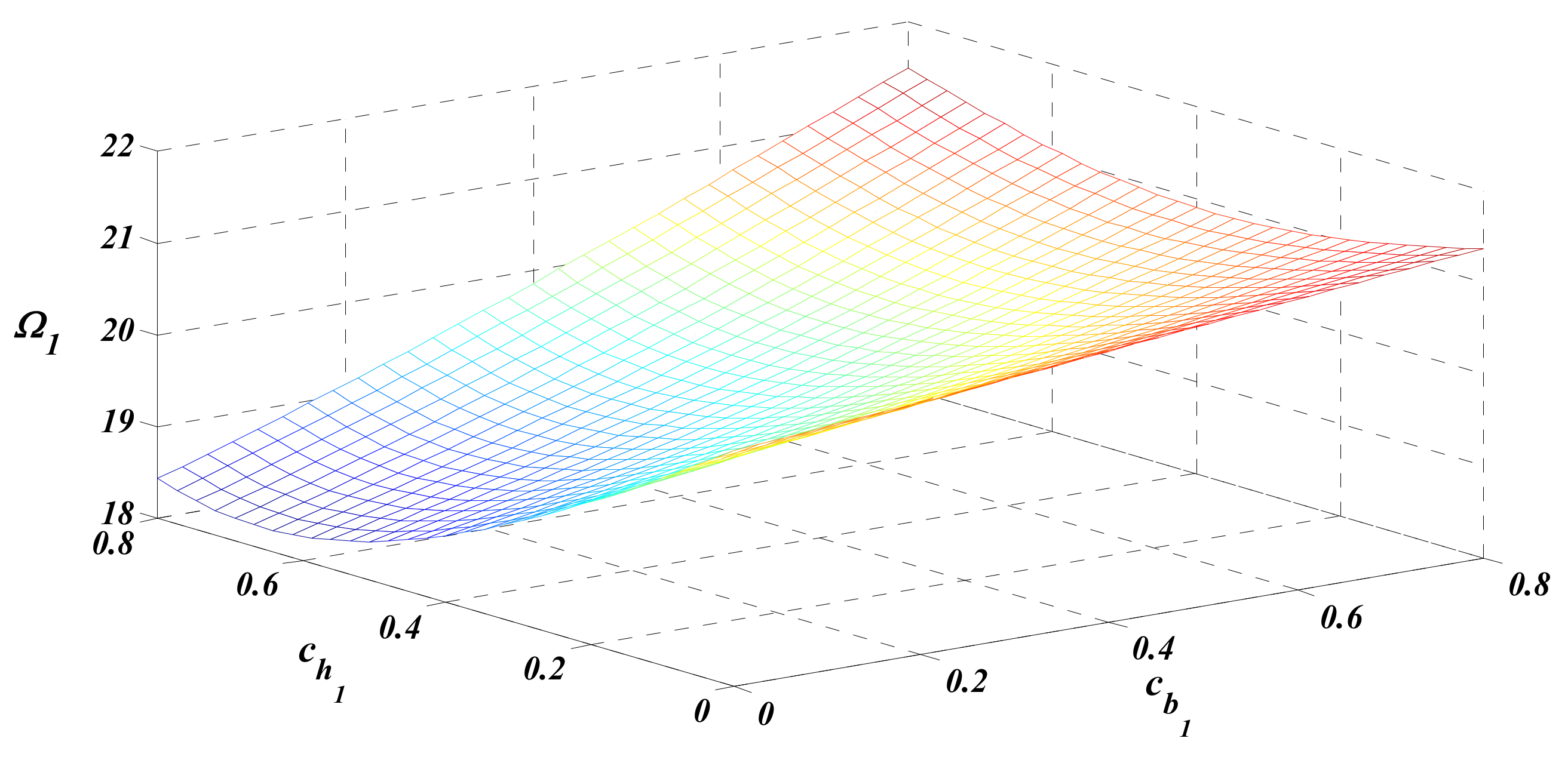
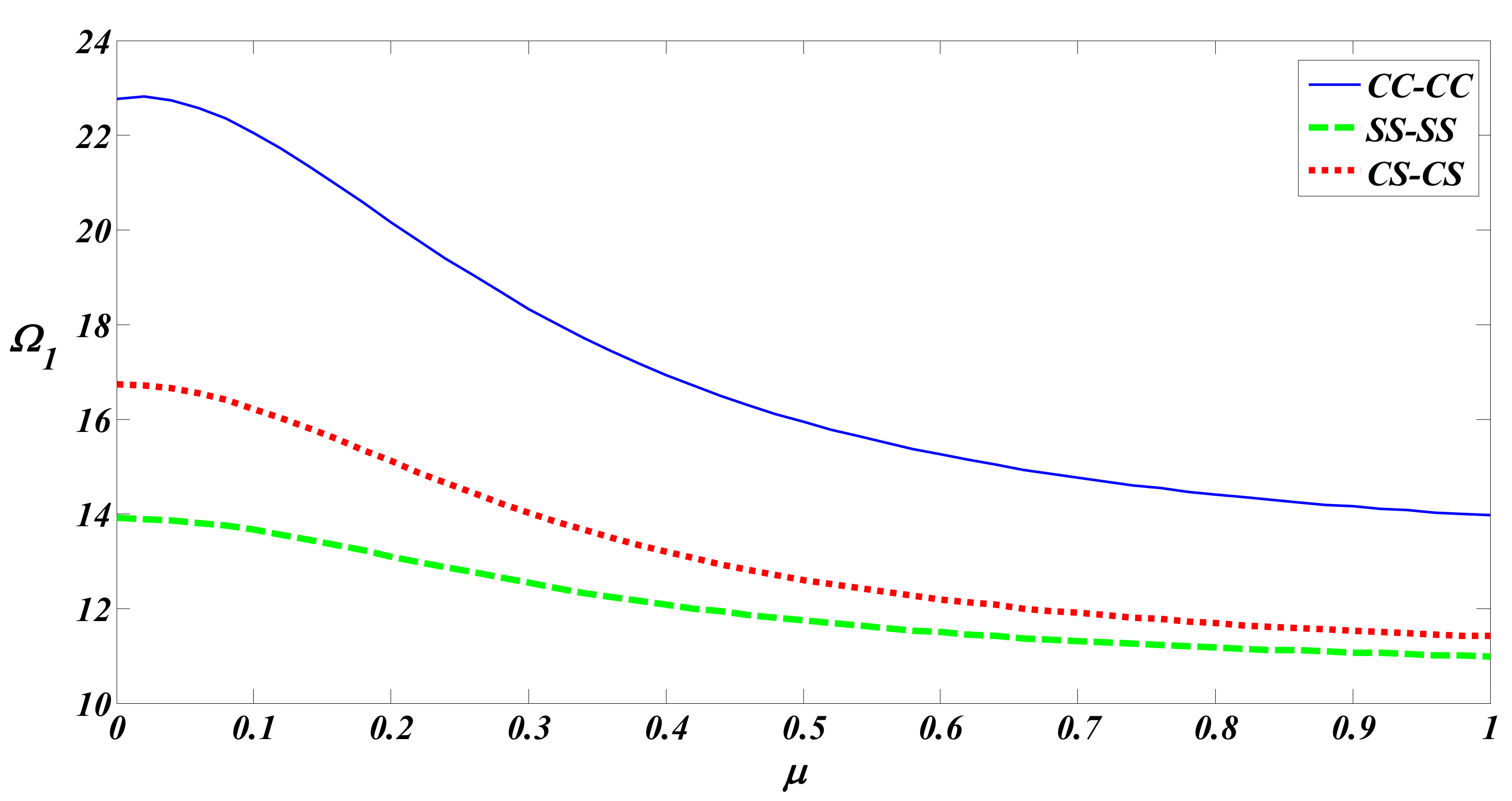
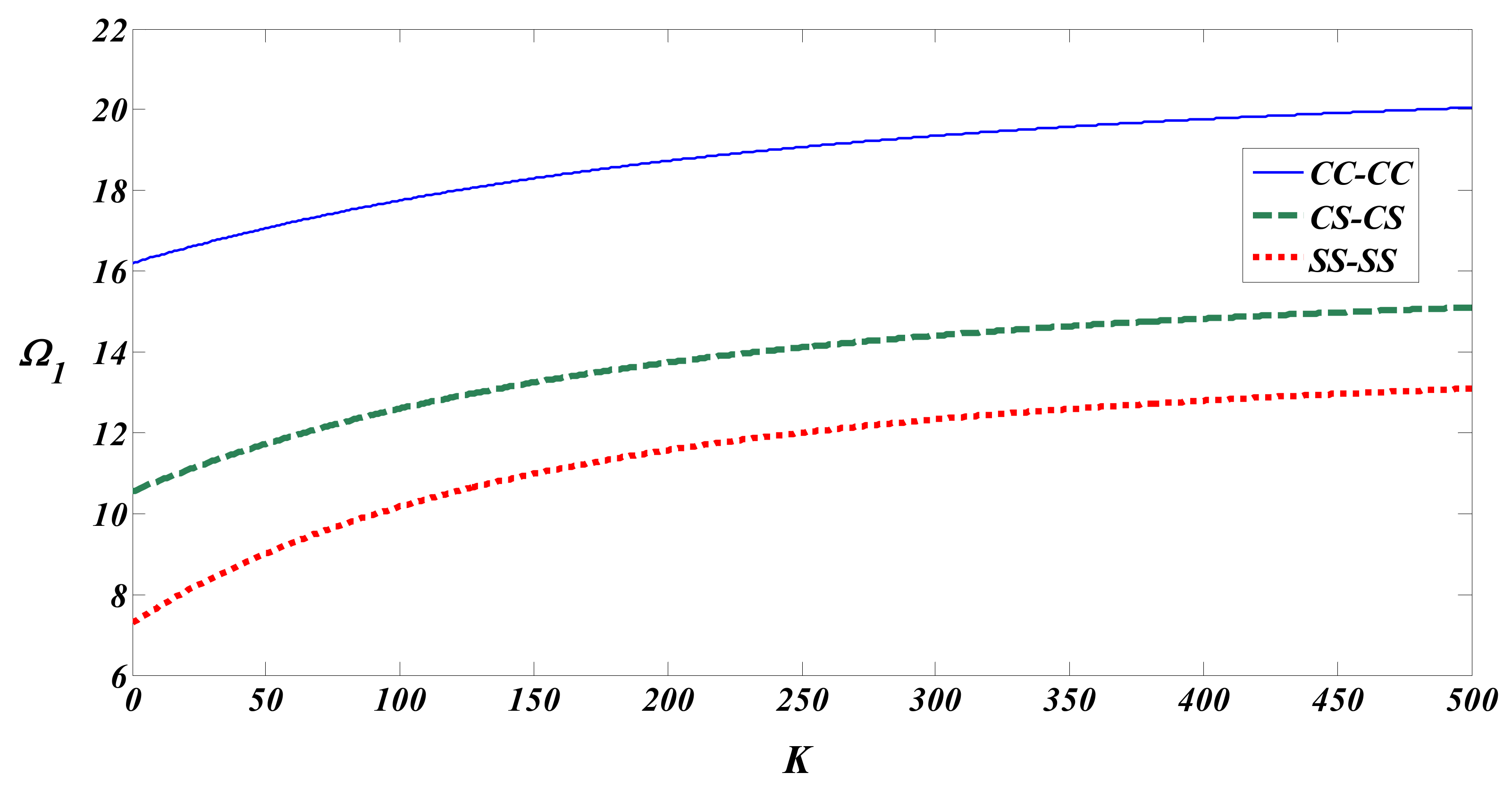
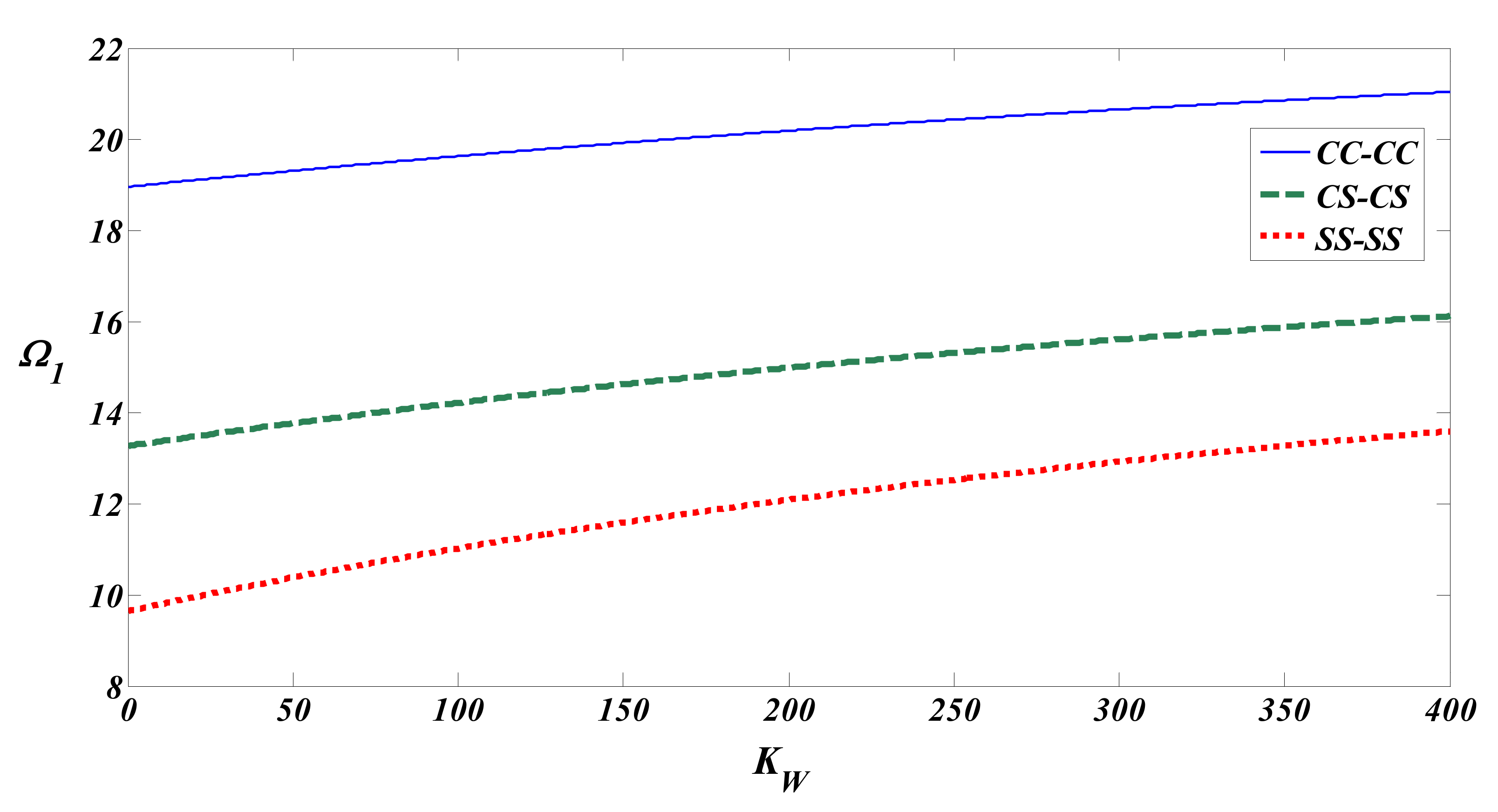
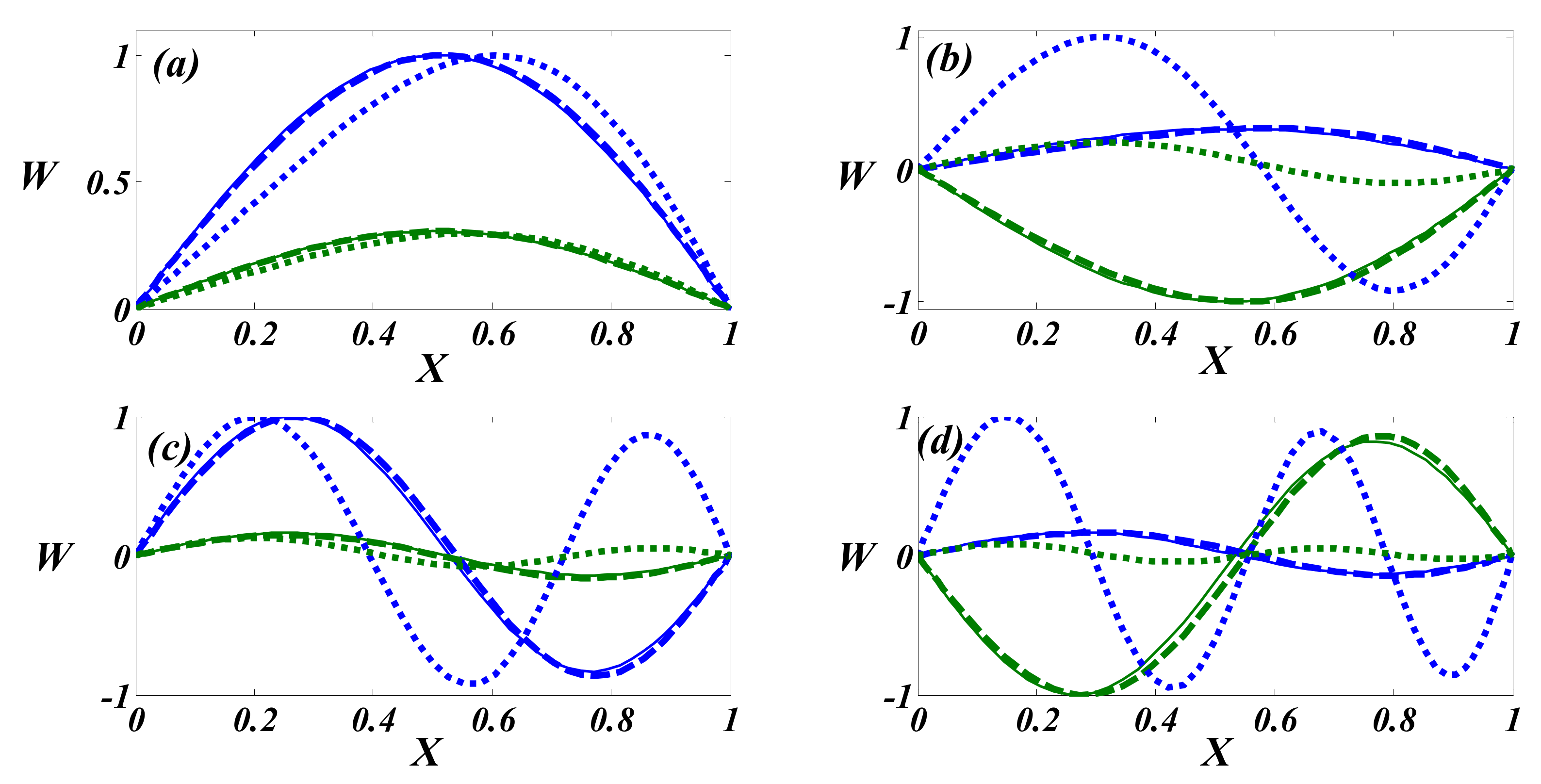
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Natarajan, S.; Ferreira, A.J.M.; Bordas, S.; Carrera, E.; Cinefra, M.; Zenkour, A.M. Analysis of Functionally Graded Material Plates Using Triangular Elements with Cell-Based Smoothed Discrete Shear Gap Method. Math. Probl. Eng. 2014, 2014, 247932. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.M.; Zhang, Y.Y.; He, X.Q. Vibration of nonlocal Timoshenko beams. Nanotechnology 2007, 18, 105401. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Challamel, N.; Hache, F.; Elishakoff, I.; Wang, C.M. Buckling and vibrations of microstructured rectangular plates considering phenomenological and lattice-based nonlocal continuum models. Compos. Struct. 2016, 149, 145–156. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Fan, L. Nonlocal vibration and biaxial buckling of double-viscoelastic-FGM-nanoplate system with viscoelastic Pasternak medium in between. Phys. Lett. A 2017, 381, 1228–1235. [Google Scholar] [CrossRef]
- Shahidi, A.R.; Anjomshoa, A.; Shahidi, S.H.; Kamrani, M. Fundamental size dependent natural frequencies of non-uniform orthotropic nano scaled plates using nonlocal variational principle and finite element method. Appl. Math. Model. 2013, 37, 7047–7061. [Google Scholar] [CrossRef]
- Namin, S.F.A.; Pilafkan, R. Vibration analysis of defective graphene sheets using nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2017. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Torsional vibration of bi-directional functionally graded nanotubes based on nonlocal elasticity theory. Compos. Struct. 2017, 172, 242–250. [Google Scholar] [CrossRef]
- Demir, Ç.; Civalek, Ö. A new nonlocal FEM via Hermitian cubic shape functions for thermal vibration of nano beams surrounded by an elastic matrix. Compos. Struct. 2017, 168, 872–884. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S. Nonlocal vibration of bonded double-nanoplate-systems. Compos. Part B Eng. 2011, 42, 1901–1911. [Google Scholar] [CrossRef]
- Mechab, I.; El Meiche, N.; Bernard, F. Free vibration analysis of higher-order shear elasticity nanocomposite beams with consideration of nonlocal elasticity and Poisson effect. J. Eng. Mech. 2016, 6, 04016006. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.M.; Challamel, N. Eringen’s length-scale coefficients for vibration and buckling of nonlocal rectangular plates with simply supported edges. J. Eng. Mech. 2015, 141, 04014117. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C.M.; Zhang, H.; Kitipornchai, S. Exact and Nonlocal Solutions for Vibration of Axial Lattice with Direct and Indirect Neighboring Interactions. J. Eng. Mech. 2018, 144, 04018025. [Google Scholar] [CrossRef]
- Zorica, D.; Atanackovi, T.M.; Vrcelj, Z.; Novakovic, B. Dynamic stability of axially loaded nonlocal rod on generalized Pasternak foundation. J. Eng. Mech. 2017, 143, D4016003. [Google Scholar] [CrossRef]
- Mehar, K.; Mahapatra, T.R.; Panda, S.K.; Katariya, P.V.; Tompe, U.K. Finite-Element Solution to Nonlocal Elasticity and Scale Effect on Frequency Behavior of Shear Deformable Nanoplate Structure. J. Eng. Mech. 2018, 144, 04018094. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; de Sciarra, F.M. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R. Vibrations of Bernoulli-Euler beams using the two-phase nonlocal elasticity theory. Int. J. Eng. Sci. 2017, 119, 232–248. [Google Scholar] [CrossRef]
- Rezaee, M.; Lotfan, S. Non-linear nonlocal vibration and stability analysis of axially moving nanoscale beams with time-dependent velocity. Int. J. Mech. Sci. 2015, 96, 3–46. [Google Scholar] [CrossRef]
- Wu, C.P.; Lai, W.W. Free vibration of an embedded single-walled carbon nanotube with various boundary conditions using the RMVT-based nonlocal Timoshenko beam theory and DQ method. Phys. E Low Dimens. Syst. Nanostruct. 2015, 68, 8–21. [Google Scholar] [CrossRef]
- Nazemnezhad, R. Nonlocal Timoshenko beam model for considering shear effect of van der Waals interactions on free vibration of multilayer graphene nanoribbons. Compos. Struct. 2015, 133, 522–528. [Google Scholar] [CrossRef]
- Glabisz, W.; Jarczewska, K.; Hołubowski, R. Stability of Timoshenko beams with frequency and initial stress dependent nonlocal parameters. Arch. Civ. Mech. Eng. 2019, 19, 1116–1126. [Google Scholar] [CrossRef]
- Niknam, H.; Aghdam, M.M. A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation. Compos. Struct. 2015, 119, 452–462. [Google Scholar] [CrossRef]
- Lal, R.; Dangi, C. Thermomechanical vibration of bi-directional functionally graded non-uniform timoshenko nanobeam using nonlocal elasticity theory. Compos. Part B Eng. 2019, 172, 724–742. [Google Scholar] [CrossRef]
- Fuschi, P.; Pisano, A.A.; Polizzotto, C. Size effects of small-scale beams in bending addressed with a strain-difference based nonlocal elasticity theory. Int. J. Mech. Sci. 2019, 151, 661–671. [Google Scholar] [CrossRef]
- Loghmani, M.; Yazdi, M.R.H. An analytical method for free vibration of multi cracked and stepped nonlocal nanobeams based on wave approach. Results Phys. 2018, 11, 166–181. [Google Scholar] [CrossRef]
- Emam, S.A.; Eltaher, M.A.; Khater, M.E.; Abdalla, W.S. Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load. Appl. Sci. 2018, 8, 2238. [Google Scholar] [CrossRef] [Green Version]
- Naghinejad, M.; Ovesy, H.R. Viscoelastic free vibration behavior of nano-scaled beams via finite element nonlocal integral elasticity approach. J. Vib. Control 2018, 25, 445–459. [Google Scholar] [CrossRef]
- Karličić, D.Z.; Ayed, S.; Flaieh, E. Nonlocal axial vibration of the multiple Bishop nanorod system. Math. Mech. Solids 2018, 24, 1668–1691. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, S.; Dai, L.; Hu, H. Analysis of a micro piezoelectric vibration energy harvester by nonlocal elasticity theory. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Waksmanski, N.; Pan, E. An analytical three-dimensional solution for free vibration of a magneto-electro-elastic plate considering the nonlocal effect. J. Intell. Mater. Syst. Struct. 2016, 28, 1501–1513. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB, Software, Enviroments, and Tools; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Sari, M.S. Free Vibration Analysis of Annular Sector Mindlin Plates Using the Nonlocal Continuum Theory. Int. J. Mech. Sci. 2015, 96, 25–35. [Google Scholar] [CrossRef]
- Sari, M.S.; Al-Kouz, W.G. Vibration analysis of non-uniform orthotropic Kirchhoff plates resting on elastic foundation based on nonlocal elasticity theory. Int. J. Mech. Sci. 2016, 114, 1–11. [Google Scholar] [CrossRef]
- Sari, M.; Shaat, M.; Abdelkefi, A. Frequency and mode veering phenomena of axially functionally graded non-uniform beams with nonlocal residuals. Compos. Struct. 2017, 163, 280–292. [Google Scholar] [CrossRef]
- Shahba, A.; Rajasekaran, S. Free vibration and stability of tapered Euler–Bernoulli beams made of axially functionally graded materials. Appl. Math. Model. 2012, 36, 3094–3111. [Google Scholar] [CrossRef] [Green Version]
- Murmu, T.; Adhikari, S. Nonlocal transverse vibration of double-nanobeam-systems. J. Appl. Phys. 2010, 108, 083514. [Google Scholar] [CrossRef] [Green Version]



| Present Study | Ref. [36] | Present Study | Ref. [36] | ||
|---|---|---|---|---|---|
| 0 | 0 | 20.4721 | 20.4721 | 56.5482 | 56.5482 |
| 0.4 | 20.2883 | 20.2883 | 56.2971 | 56.2971 | |
| 0.8 | 19.3844 | 19.3844 | 54.9699 | 54.9699 | |
| 0.4 | 0 | 15.8281 | 15.8281 | 44.0236 | 44.0236 |
| 0.4 | 15.8349 | 15.8349 | 44.0359 | 44.0359 | |
| 0.8 | 15.4021 | 15.4021 | 43.4043 | 43.4042 | |
| 0.8 | 0 | 10.2217 | 10.2217 | 28.7406 | 28.7406 |
| 0.4 | 10.4234 | 10.4234 | 29.0311 | 29.0310 | |
| 0.8 | 10.5301 | 10.5301 | 29.2240 | 29.2239 | |
| K | µ | |||||
|---|---|---|---|---|---|---|
| 100 | 0.2 | Present Study | 8.3569 | 16.4267 | 24.5823 | 28.3600 |
| Ref. [37] | 8.3569 | 16.4267 | 24.5823 | 28.3600 | ||
| 0.4 | Present Study | 6.1456 | 14.5951 | 15.4197 | 20.3228 | |
| Ref. [37] | 6.1456 | 14.5951 | 15.4197 | 20.3228 | ||
| 0.8 | Present Study | 3.6488 | 7.7030 | 11.6787 | 14.6053 | |
| Ref. [37] | 3.6488 | 7.7030 | 11.6787 | 14.6053 | ||
| 500 | 0.2 | Present Study | 8.3569 | 24.5823 | 32.7084 | 40.0536 |
| Ref. [37] | 8.3569 | 24.5823 | 32.7084 | 40.0536 | ||
| 0.4 | Present Study | 6.1456 | 14.5951 | 22.7743 | 30.8121 | |
| Ref. [37] | 6.1456 | 14.5951 | 22.7743 | 30.8121 | ||
| 0.8 | Present Study | 3.6488 | 7.7030 | 11.6787 | 15.6308 | |
| Ref. [37] | 3.6488 | 7.7030 | 11.6787 | 15.6308 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
S. Sari, M.; G. Al-Kouz, W.; M. Atieh, A. Transverse Vibration of Functionally Graded Tapered Double Nanobeams Resting on Elastic Foundation. Appl. Sci. 2020, 10, 493. https://doi.org/10.3390/app10020493
S. Sari M, G. Al-Kouz W, M. Atieh A. Transverse Vibration of Functionally Graded Tapered Double Nanobeams Resting on Elastic Foundation. Applied Sciences. 2020; 10(2):493. https://doi.org/10.3390/app10020493
Chicago/Turabian StyleS. Sari, Ma’en, Wael G. Al-Kouz, and Anas M. Atieh. 2020. "Transverse Vibration of Functionally Graded Tapered Double Nanobeams Resting on Elastic Foundation" Applied Sciences 10, no. 2: 493. https://doi.org/10.3390/app10020493





