MAP-Vis: A Distributed Spatio-Temporal Big Data Visualization Framework Based on a Multi-Dimensional Aggregation Pyramid Model
Abstract
:1. Introduction
- (1)
- We introduce a generic hierarchical aggregation model, named MAP, designed to organize, explore, and visualize massive multi-dimensional spatio-temporal data.
- (2)
- We leverage distributed computing to develop a prototype system, MAP-Vis, which implements the proposed MAP model; this system supports parallel model generation, scalable storage and efficient interactive visualization, especially for spatio-temporal point-type data.
- (3)
- We use several real spatio-temporal datasets to validate the performance and efficiency of both the proposed MAP model and the MAP-Vis system.
2. Related Work
2.1. Data Reduction Techniques for Big Data Visualization
2.2. Parallel Implementations for Big Data Visualization
3. The Hierarchical Multi-Dimensional Aggregate Pyramid (MAP) Model
3.1. Space-Time-Attribute Cube
3.2. Definition of the 2D Tile Pyramid Model
3.3. Multi-Dimensional Aggregated Pyramid Model
4. Spatio-Temporal Big Data Visualization Framework
4.1. The MAP-Vis Framework
4.2. The Generation of the MAP Pyramid
| Algorithm 1 The pseudocode of the MAP preprocessing algorithm |
| Input: Original record, Rm(lng, lat, time, attributes), m = 1, 2, …, N; Input: The maximum map level, ln; Input: The time granularity; Output: ln (i = 0, 1, 2, …, n), hierarchical aggregation result; |
| 1: for each record Ri in original records do 2: faa_tree = flatten(attributes) 3: tj = tBin(time) 4: ST-Pixelij = Extract(lng, lat, ln, faa_tree, tj) 5: end for 6: for each Pixelij in the same Tile with Tilekj do 7: Group Pixelij to Tilekj 8: end for 9: for each Tilekj with Faa_tree = Aall, A1, …, As do 10: Key-Value Tilekj to Tilekjs 11: end for 12: Tileln ←All(Tilekjs) 13: for i = ln−1, ln−2, …, 1 do 14: Tileli = Aggregate(Tileli+1) 15: end for 16: return Tileli, i = 0, 1, 2, …, n; |
4.3. Distributed Storage of the MAP Pyramid in Hbase
4.4. Multidimensional Query for Interactive Visualization
- (1)
- The interactive visualization operations will produce a collection of requests, which will later be sent to the server separately in an asynchronous mode. When the server receives the query request, the middleware parses the request parameters into the space/ time/attribute filters.
- (2)
- For the spatial filters, the query geometry will be recursively divided into multi-level SFC cells, while the translated spatial ranges are calculated using our recursive approximation algorithm, published in [35];
- (3)
- The temporal and attribute filters will be discretized and appended to the translated spatial ranges and derive the final scan ranges according to the rowkey schema;
- (4)
- The scan ranges are sent to HBase for scan operations, filtering out of false positive data from the initial scan results and aggregating final query results for client rendering.
| Algorithm 2 The pseudocode of the multidimensional query in MAP-Vis |
| Input: Qtime(Tstart,Tend) Qbbox (minLat,minLon,maxLat,maxLon) AttributeList Output: ResultSet |
| 1: SpatialRanges = getSpatialRangeswithSFC(Qbbox); 2: QtimeBins = getTimeBins(Qtime,timeCoarseBin); 3: AttributeFilter = getQualifierFilter(AttributeList); 4: for each timeBin in QtimeBins do: 5: for each range in SpatialRanges do: 6: strartRowkey = Tstart + range.rangeStart; 7: endRowkey = Tend + range.rangeEnd; 8: rowkeyRange = (startrowkey, endrowkey); 9: Scan = scan(rowkeyRange, AttributeFilter); 10: ResultScanner = table.getScanner(Scan); 11: for each Result in ResultScanner do: 12: if Result in Qrange and Result in Qtime: 13: Resultset.add(Result); 14: end if 15: end for 16: end for 17: end for 18: return ResultSet |
5. Experiments and Discussions
5.1. Experimental Environment and Datasets
5.2. Validation of the MAP Model’s Efficiency
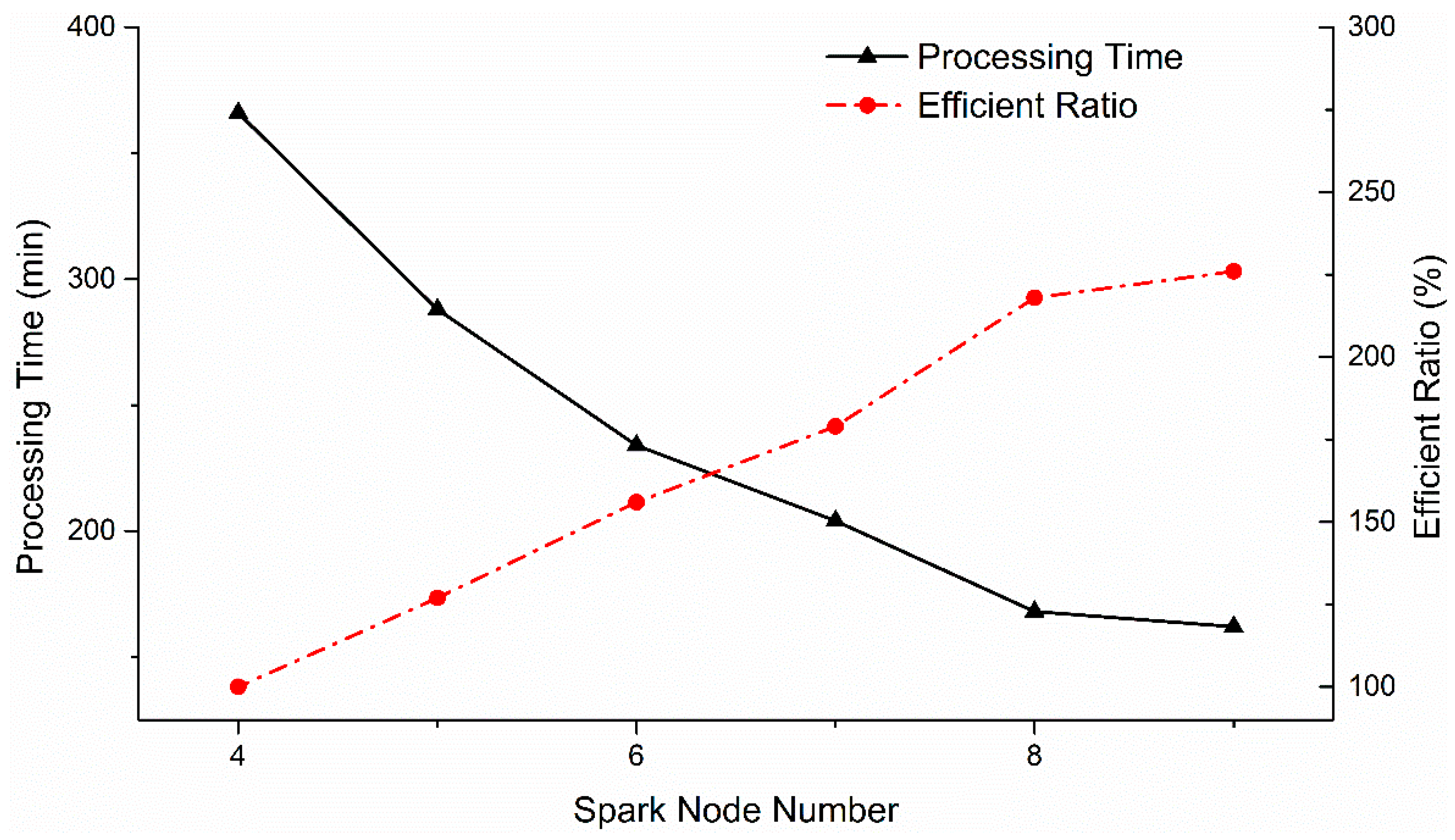
5.3. Experiments on Data Preprocessing Capability
6. Conclusions and Future Work
- (1)
- Our research work currently concentrates on massive point data; however, polyline or polygon types of spatio-temporal big data (e.g., vehicle trajectory) are not well-addressed. Thus, we will extend our proposed framework to accommodate these more complex data types.
- (2)
- Other acceleration mechanisms, e.g., GPU, will be considered for quicker pre-processing. In addition, parallel generation of query ranges will be also implemented to improve the query efficiency.
- (3)
- Direct GPU-based rendering methods such as WebGL will be further used to increase the data visualization speed.
- (4)
- Current functions provided by the MAP-Vis framework are still limited. More analysis functions (including point distribution pattern, time-series prediction, etc.) will be added in the near future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, Q.; Zeng, W.; Ye, Y.; Arisona, S.M.; Schubiger, S.; Burkhard, R.; Qu, H. StreetVizor: Visual Exploration of Human-Scale Urban Forms Based on Street Views. IEEE Trans. Vis. Comput. Graph. 2018, 24, 1004–1013. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Chen, W.; Andrienko, G.; Andrienko, N. Semantics-Space-Time Cube. A Conceptual Framework for Systematic Analysis of Texts in Space and Time. IEEE Trans. Vis. Comput. Graph. 2018. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Xu, P.; Ren, L. TPFlow: Progressive Partition and Multidimensional Pattern Extraction for Large-Scale Spatio-Temporal Data Analysis. IEEE Trans. Vis. Comput. Graph. 2018, 25, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Oppermann, M.; Moeller, T.; Sedlmair, M. Bike Sharing Atlas: Visual Analysis of Bike-Sharing Networks. Int. J. Transp. 2018, 6, 1–14. [Google Scholar] [CrossRef]
- Agrawal, R.; Kadadi, A.; Dai, X.; Andres, F. Challenges and opportunities with big data visualization. In Proceedings of the 7th International Conference on Management of Computational and Collective Intelligence in Digital EcoSystems, Caraguatatuba, Brazil, 25–29 October 2015. [Google Scholar]
- Li, S.; Dragicevic, S.; Castro, F.A.; Sester, M.; Winter, S.; Coltekin, A.; Pettit, C.; Jiang, B.; Haworth, J.; Stein, A. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, G.; Alexander, C.A. Big data and visualization: Methods, challenges and technology progress. Digit. Technol. 2015, 1, 33–38. [Google Scholar] [CrossRef]
- De Oliveira, M.C.F.; Levkowitz, H. From visual data exploration to visual data mining: A survey. IEEE Trans. Vis. Comput. Graph. 2003, 9, 378–394. [Google Scholar] [CrossRef] [Green Version]
- Bach, B.; Dragicevic, P.; Archambault, D.; Hurter, C.; Carpendale, S. A Descriptive Framework for Temporal Data Visualizations Based on Generalized Space-Time Cubes. Comput. Graph. Forum 2017, 36, 36–61. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Nie, Y. Tile-based map service GeoWebCache middleware. In Proceedings of the 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems (ICIS), Xiamen, China, 29–31 October 2010. [Google Scholar]
- Lindstrom, P.; Pascucci, V. Terrain simplification simplified: A general framework for view-dependent out-of-core visualization. IEEE Trans. Vis. Comput. Graph. 2002, 8, 239–254. [Google Scholar] [CrossRef]
- Battle, L.; Chang, R.; Stonebraker, M. Dynamic prefetching of data tiles for interactive visualization. In Proceedings of the 2016 International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016. [Google Scholar]
- Jeong, D.H.; Ziemkiewicz, C.; Fisher, B.; Ribarsky, W.; Chang, R. iPCA: An Interactive System for PCA-based Visual Analytics. Comput. Graph. Forum 2009, 28, 767–774. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Godfrey, P.; Gryz, J.; Lasek, P. Interactive visualization of large data sets. IEEE Trans. Knowl. Data Eng. 2016, 28, 2142–2157. [Google Scholar] [CrossRef]
- Bojko, A. Informative or Misleading? Heatmaps Deconstructed. In Proceedings of the HCI International 2009 13th International Conference on Human–Computer Interaction, San Diego, CA, USA, 19–24 July 2009. [Google Scholar]
- Gray, J.; Chaudhuri, S.; Bosworth, A.; Layman, A.; Reichart, D.; Venkatrao, M.; Pellow, F.; Pirahesh, H. Data Cube: A Relational Aggregation Operator Generalizing Group-By, Cross-Tab, and Sub-Totals. Data Min. Knowl. Discov. 1997, 1, 29–53. [Google Scholar] [CrossRef]
- Lins, L.; Klosowski, J.T.; Scheidegger, C. Nanocubes for real-time exploration of spatiotemporal datasets. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2456–2465. [Google Scholar] [CrossRef]
- Miranda, F.; Lins, L.; Klosowski, J.T.; Silva, C.T. TOPKUBE: A rank-aware data cube for real-time exploration of spatiotemporal data. IEEE Trans. Vis. Comput. Graph. 2018, 24, 1394–1407. [Google Scholar] [CrossRef]
- Pahins, C.A.; Stephens, S.A.; Scheidegger, C.; Comba, J.L. Hashedcubes: Simple, low memory, real-time visual exploration of big data. IEEE Trans. Vis. Comput. Graph. 2017, 23, 671–680. [Google Scholar] [CrossRef]
- Wang, Z.; Ferreira, N.; Wei, Y.; Bhaskar, A.S.; Scheidegger, C. Gaussian cubes: Real-time modeling for visual exploration of large multidimensional datasets. IEEE Trans. Vis. Comput. Graph. 2017, 23, 681–690. [Google Scholar] [CrossRef]
- Li, M.; Choudhury, F.; Bao, Z.; Samet, H.; Sellis, T. ConcaveCubes: Supporting Cluster-based Geographical Visualization in Large Data Scale. Comput. Graph. Forum 2018, 37, 217–228. [Google Scholar] [CrossRef]
- Sismanis, Y.; Deligiannakis, A.; Roussopoulos, N.; Kotidis, Y. Dwarf: Shrinking the petacube. In Proceedings of the 2002 ACM SIGMOD International Conference on Management of Data, Madison, WI, USA, 3–6 June 2002; pp. 464–475. [Google Scholar]
- Liu, Z.; Jiang, B.; Heer, J. imMens: Real-time Visual Querying of Big Data. Comput. Graph. Forum 2013, 32, 421–430. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Cashman, D.; Li, M.; Li, J.; Berger, M.; Levine, J.A.; Chang, R.; Scheidegger, C. NeuralCubes: Deep Representations for Visual Data Exploration. arXiv 2018, arXiv:1808.08983v08983. [Google Scholar]
- Doraiswamy, H.; Vo, H.T.; Silva, C.T.; Freire, J. A GPU-based index to support interactive spatio-temporal queries over historical data. In Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering (ICDE), Helsinki, Finland, 16–20 May 2016; pp. 1086–1097. [Google Scholar]
- Perrot, A.; Bourqui, R.; Hanusse, N.; Lalanne, F.; Auber, D. Large interactive visualization of density functions on big data infrastructure. In Proceedings of the 2015 IEEE 5th Symposium on Large Data Analysis and Visualization (LDAV), Chicago, IL, USA, 25–26 October 2015; pp. 99–106. [Google Scholar]
- Root, C.; Mostak, T. MapD: A GPU-powered big data analytics and visualization platform. In Proceedings of the ACM SIGGRAPH 2016 Talks, Anaheim, CA, USA, 24–28 July 2016; pp. 1–2. [Google Scholar]
- Im, J.-F.; Villegas, F.G.; McGuffin, M.J. VisReduce: Fast and responsive incremental information visualization of large datasets. In Proceedings of the 2013 IEEE International Conference on Big Data, Santa Clara, CA, USA, 6–9 October 2013; pp. 25–32. [Google Scholar]
- Cheng, D.; Schretlen, P.; Kronenfeld, N.; Bozowsky, N.; Wright, W. Tile based visual analytics for Twitter big data exploratory analysis. In Proceedings of the 2013 IEEE International Conference on Big Data, Santa Clara, CA, USA, 6–9 October 2013. [Google Scholar]
- Hughes, J.N.; Annex, A.; Eichelberger, C.N.; Fox, A.; Hulbert, A.; Ronquest, M. Geomesa: A distributed architecture for spatio-temporal fusion. In Proceedings of the Geospatial Informatics, Fusion, and Motion Video Analytics V, Baltimore, MD, USA, 20–24 April 2015; p. 94730F. [Google Scholar]
- Whitby, M.A.; Fecher, R.; Bennight, C. GeoWave: Utilizing Distributed Key-Value Stores for Multidimensional Data. In Proceedings of the Advances in Spatial and Temporal Databases, Arlington, VA, USA, 21–23 August 2017; pp. 105–122. [Google Scholar]
- Wu, H.; Guan, X.; Liu, T.; You, L.; Li, Z. A High-Concurrency Web Map Tile Service Built with Open-Source Software. In Modern Accelerator Technologies for Geographic Information Science; Springer: New York, NY, USA, 2013; pp. 183–195. [Google Scholar]
- Cheng, B.; Guan, X. Design and Evaluation of a High-concurrency Web Map Tile Service Framework on a High Performance Cluster. Int. J. Grid Distrib. Comput. 2016, 9, 127–142. [Google Scholar] [CrossRef]
- Guan, X.; Van Oosterom, P.; Cheng, B. A Parallel N-Dimensional Space-Filling Curve Library and Its Application in Massive Point Cloud Management. ISPRS Int. J. Geo-Inf. 2018, 7, 327. [Google Scholar] [CrossRef] [Green Version]











| Rowkey | CF:Heatmap | CF:Sum | ||||||
|---|---|---|---|---|---|---|---|---|
| F1 | F2 | … | Fn | F1 | F2 | … | Fn | |
| L_T _Z2 | Aall | A1 | … | An | Sall | S1 | … | Sn |
| Name | Records | Raw Data Size | Time Span | Table Size |
|---|---|---|---|---|
| NYC Taxi | 1.17 billion | 170 GB | 2008.01–2015.12 | 90 GB |
| BrightKite | 11.19 million | 740 MB | 2008.04–2010.10 | 50 GB |
| China Enterprise Data | 20 million | 2.3 GB | 1945.01–2010.12 | 7 GB |
| Global Earthquakes | 3.38 million | 580 MB | 1970.01–2018.12 | 41 GB |
| Group No. | Spatial Extent | GeoHash Search Depth | Temporal Span | Attribute Filter | Tile Number | Time Size (MB) | Query Time (ms) |
|---|---|---|---|---|---|---|---|
| 1 | 0.58 × 0.22 | 12 | 1 year | All | 32 | 0.874 | 6 |
| 1 month | All | 32 | 0.391 | 6 | |||
| Single | 32 | 0.255 | 6 | ||||
| 1 day | All | 32 | 0.155 | 6 | |||
| 2 | 0.08 × 0.03 (urban) | 15 | 1 year | All | 32 | 3.808 | 10 |
| 1 month | All | 32 | 2.204 | 10 | |||
| Single | 32 | 1.311 | 9 | ||||
| 1 day | All | 32 | 0.370 | 6 | |||
| 3 | 0.08 × 0.03 (suburb) | 15 | 1 year | All | 36 | 0.889 | 7 |
| 1 month | All | 36 | 0.238 | 7 | |||
| Single | 36 | 0.097 | 7 | ||||
| 1 day | All | 36 | 0.041 | 6 | |||
| 4 | 0.018 × 0.008 | 17 | 1 year | All | 40 | 5.538 | 12 |
| 1 month | All | 40 | 1.853 | 12 | |||
| Single | 40 | 0.609 | 9 | ||||
| 1 day | All | 40 | 0.110 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Xie, C.; Han, L.; Zeng, Y.; Shen, D.; Xing, W. MAP-Vis: A Distributed Spatio-Temporal Big Data Visualization Framework Based on a Multi-Dimensional Aggregation Pyramid Model. Appl. Sci. 2020, 10, 598. https://doi.org/10.3390/app10020598
Guan X, Xie C, Han L, Zeng Y, Shen D, Xing W. MAP-Vis: A Distributed Spatio-Temporal Big Data Visualization Framework Based on a Multi-Dimensional Aggregation Pyramid Model. Applied Sciences. 2020; 10(2):598. https://doi.org/10.3390/app10020598
Chicago/Turabian StyleGuan, Xuefeng, Chong Xie, Linxu Han, Yumei Zeng, Dannan Shen, and Weiran Xing. 2020. "MAP-Vis: A Distributed Spatio-Temporal Big Data Visualization Framework Based on a Multi-Dimensional Aggregation Pyramid Model" Applied Sciences 10, no. 2: 598. https://doi.org/10.3390/app10020598
APA StyleGuan, X., Xie, C., Han, L., Zeng, Y., Shen, D., & Xing, W. (2020). MAP-Vis: A Distributed Spatio-Temporal Big Data Visualization Framework Based on a Multi-Dimensional Aggregation Pyramid Model. Applied Sciences, 10(2), 598. https://doi.org/10.3390/app10020598





