Shape Optimization Design for a Centrifuge Structure with Multi Topological Configurations Based on the B-Spline FCM and GCMMA

Abstract

The geotechnical centrifuge applied in various geotechnical engineering fields provides physical data for investigating mechanisms of deformation and failure and for validating analytical and numerical methods by simulating and studying the geotechnical problems. The basket, as one of the important components used to place the inspection model of centrifugal test, is designed to withstand complex loads. This paper presents an optimization design method for the basket based on the weighted B-Spline Finite Cell Method (FCM) and the globally-convergent method of moving asymptotes (GCMMA). In order to obtain a superior design solution, four topological configurations, i.e., original single web, porous dual web, open deep groove dual web, and connected closed dual web, are investigated and optimized. The mass is selected as the optimization objective, while key shape parameters and stress are regarded as design variables and the constraint, respectively. By optimization, the final masses of the four configurations are reduced greatly compared with the initial configurations, where the greatest weight loss, in case 4, is 10.6%. This indicates that the weighted B-Spline FCM and GCMMA can be well applied for shape optimization of structure in engineering design. In contrast to the final single web adopted in the traditional basket design in case 1, the final configuration in case 4, i.e., connected closed dual web, has the least mass. The final mass is reduced by 133.38 kg when the centrifuge strength requirement is met. Therefore, the final configuration in case 4, where the maximum von-Mises stress is 398.72MPa and mass is 781.82 kg, is superior to the three other configurations.

1. Introduction

The centrifuge simulating composite environment loads with acceleration is designed to meet the requirements of geotechnical, medical, and bio-industrial research, etc. [1]. In recent decades, along with the development of military and social demands, the centrifuge has attracted continuous research interest. An advanced centrifuge which is capable of high rotational speed and with a more precise structure is seriously needed. Due to the high rotational speed, both the stress level significantly affecting the reliability, and the weight involving the performance of the centrifuge, are sensitive parameters. Several cases involving centrifuge failure have been reported. A centrifuge was destroyed due to excessive mechanical stress in a Beckman L2-65B ultracentrifuge at Cornell University [2]. A failure analysis of the cause of the burst of the centrifuge rotor was reported in Ref. [3]. A failed centrifuge caused by the basket employed for starch production is investigated in Ref. [4]. The geotechnical centrifuge, a large-scale centrifuge, provides physical data for investigating mechanisms of deformation and failure and for validating analytical and numerical methods [5] by simulating and studying geotechnical problems. It is currently applied in various geotechnical engineering fields, such as foundation systems, earth structures, offshore systems, earthquake-related problems, geo-environment studies, etc. [6]. With the continually increasing demand for the geotechnical centrifuge experiments in industrial engineering, the need for a centrifuge facility with advanced capabilities is urgent. One of the most important components of a geotechnical centrifuge is the basket. It is connected to the rotating arm via the pin shaft, which is used to place the inspection model. As a variety of topological configurations of this component are possible, the specific installation and basic shape will be described in detail later (as shown in Figure 1). The basket is designed to withstand complex loads, such as the tensile stress from the arm caused by the rotation, vibration torque, gravity, centrifugal force, and so on. With the high rotational speed, loads make the basket stretch and change in size, which may cause it to fail. In addition, the weight of the basket has a significant influence on the stress of the mounting hole of the arm connected with it. Several failure cases of the centrifuge have been caused by the basket [4,7]; therefore, one of the major tasks of the geotechnical centrifuge design is make the basket as light as possible while satisfying the requirement of its strength.

Shape optimization is important in seeking to improve mechanical properties and reduce weight [8,9,10,11,12,13]. In engineering practice, the shape optimization design of the basket is mostly based on the traditional finite element method (FEM), which makes the optimization design process time-consuming and complicated. There are two reasons for this; one is that the traditional FEM uses conforming mesh discretization and the perturbation method of structural optimization and shape sensitivity analysis [14,15,16]. During the optimization process, the mesh should be updated based on shape changes. Unfortunately, conforming the mesh is a huge challenge, especially for complex structures. Statistics show that [17] the conversion of geometric models to finite element models represents 80% of structural analysis work, so the meshing and repartitioning process is very time consuming, especially for the shape optimization of complex structures. Even with some advanced mesh generation methods, such as mesh mapping, Laplacian deformation, adaptive mesh generation, and so on [18], in some cases, mesh deformation caused by the finite element approximation error [19] is still inevitable. The other reason is the difficulty of solving sensitivity in a gradient-based optimization process. Therefore, achieving an optimal basket shape in a geotechnical centrifuge is a significant engineering challenge.

In this work, motivated by the easier remeshing and sensitivity analysis of the Finite Cell Method (FCM) [20,21] compared to traditional FEM, the shape optimization of the basket is investigated and achieved by weighted B-Spline FCM [22,23,24], where the critical component, i.e., the lifting lug, is put into the computational domain divided with the fixed grid, the geometric model is represented by the level set function [25] and R-functions [26], the boundary cells are refined by the Quadtree or Octree method, and a homogeneous Dirichlet boundary condition is applied by the weighted function. Based on the weighted B-Spline FCM, an effective optimization model is built. The structure mass is selected as the optimization objective, and key shape parameters and stress are regarded as design variables and s constraint, respectively. Additionally, the highly-efficient optimization design flow for the lifting lug based on the gradient is developed, and a gradient-based optimization algorithm named the “globally convergent method of moving asymptotes” (GCMMA) [27] is implemented. With four cases containing different topological configurations, the superior design solution of the lifting lug is chosen. The main contributions are as follows.

(1)

Extend the B-Spline FCM for structure shape optimization design into engineering applications;

(2)

Develop a complete shape optimization process of the basket of a geotechnical centrifuge based on the competitive weighted B-Spline FCM and the GCMMA, which settles the light-weighting design of the basket with multi topological configurations whilst also meeting the requirement of the geotechnical centrifuge strength.

The rest of the paper is organized as follows. In Section 2, based on the overall structure of the geotechnical centrifuge, the key component of the basket, i.e., the lifting lug, is investigated. Firstly, the parameterized geometric representation of the lifting lug is established by the level set and Rfunctions. Then, the geometric structure is divided by the fixed grid, the homogeneous Dirichlet boundary is applied exactly by the weighted function, and the force of the lifting lug is analyzed. Finally, for the four topological configurations, the stress analysis is carried out by weighted B-Spline FCM. The stress distribution and mass of each configuration are obtained. Section 3 carries out the shape optimization of the four configurations by the GCMMA. The optimization results are analyzed in Section 4. Some conclusions are given in Section 5.

2. Review on the Weighted B-Spline FCM

2.1. The Implicit Level Set Function

Different from the classical finite element method, the element meshing is transferred to the grid identifying in the fixed grid. The implicit level set function [25] of a physical domain is usually employed to determine which grids are inside, outside, or cut by the boundary. Suppose a physical domain with a level set function $\Phi (x)$, the position of an arbitrary point $x$ with respect to the physical domain can be determined by Equation (1).

$$\{\begin{array}{l}\Phi (x)>0\hspace{1em}\forall \mathit{x}\in \Omega \\ \Phi (x)=0\hspace{1em}\forall x\in \partial \Omega \\ \Phi (x)<0\hspace{1em}\forall x\in D\backslash (\Omega \cup \partial \Omega )\end{array}$$

(1)

where $\Omega$, $\partial \Omega$, and $D$, denote the physical domain, the boundary of the physical domain, and the computational domain, respectively. Taking an arbitrary structure for example, the level set function of the structure is depicted in Figure 2. According to Equation (1), the property of the point $\mathit{x}$ can be identified.

For any complicated physical domain consisting of basic geometric elements, the level set function and R-functions [26] can be formulated by:

$$\Phi =\{\begin{array}{l}{\Phi }_1\cup {\Phi }_2\\ {\Phi }_1\cap {\Phi }_2\end{array}$$

(2)

in which

$$\begin{array}{l}{\Phi }_1\cup {\Phi }_2={\Phi }_1+{\Phi }_2+\sqrt{{\Phi }_1^2+{\Phi }_2^2}\\ {\Phi }_1\cap {\Phi }_2={\Phi }_1+{\Phi }_2-\sqrt{{\Phi }_1^2+{\Phi }_2^2}\end{array}$$

(3)

where ${\Phi }_1$ and ${\Phi }_2$ denote the level set functions of the basic geometric elements.

2.2. The B-Spline Finite Cell Method

The finite cell method [20,21] is an extension to the core principle and concept using high-order basis functions to approximate the unknown physical domain. Without losing generality, this paper focuses on 3D linear elasticity problems. The original physical domain ${\Omega }_p$ with boundary $\partial {\Omega }_p$ is embedded into a cubic domain $\Omega$, as shown in Figure 3.

The strong form of the boundary value problem for embedded domain $\Omega$ can be expressed as

$$\{\begin{array}{ll}-\mathrm{div}\sigma (\mathit{u})=\beta \mathit{f}& \mathrm{in}\Omega \\ \mathit{u}=\mathit{g}& \mathrm{on}{\Gamma }_D\\ \sigma (\mathit{u})\cdot \mathit{n}=\mathit{t}& \mathrm{on}{\Gamma }_N\end{array}$$

(4)

where $\sigma$ denotes the stress tensor, $\mathit{u}$ is the displacement field, $\mathit{t}$ expresses the traction vector defining on ${\Gamma }_N$, $\mathit{g}$ is the prescribed displacement vector defining Dirichelt boundary condition (DBC) on ${\Gamma }_D$, $\mathit{f}$ denotes the body force on ${\Omega }_p$, and $\mathit{n}$ is the unit outward normal vector on ${\Gamma }_N$. The scalar factor $\beta$ can be defined as

$$\beta =\{\begin{array}{l}1\hspace{1em}\mathrm{in}{\Omega }_p\\ 0\hspace{1em}\mathrm{in}\Omega \backslash {\Omega }_p\end{array}$$

(5)

The weak form of Equation (4) can be stated as

$$a(\mathit{u},\mathit{v})=l(\mathit{v})\hspace{1em}\mathit{u},\mathit{v}\in H^1(\Omega )$$

(6)

with the bilinear form being

$$a(\mathit{u},\mathit{v})={\int }_{\Omega }\epsilon (\mathit{v}):\beta \mathit{D}:\epsilon (\mathit{u})\mathrm{d}\Omega$$

(7)

and the load function being

$$l(\mathit{v})={\int }_{\Omega }\mathit{v}\cdot \beta \mathit{f}\mathrm{d}\Omega +{\int }_{{\Gamma }_N}\mathit{v}\cdot \mathit{t}\mathrm{d}\Gamma$$

(8)

in which $H^1(\Omega )$ expresses the Sobolev space of order 1. $\mathit{v}$ denotes the admissible test displacement in kinematics. $\epsilon$ and $\mathit{D}$ are the strain tensor and the constitutive elasticity tensor of ${\Omega }_p$, respectively.

Similar to the finite element method, the embedded domain $\Omega$ is discretized by a general Cartesian grid. As illustrated in Figure 4a, cells are simply hexahedrons, and can be classified into physical cells, fictitious cells, and boundary cells, according to the implicit level set function of ${\Omega }_p$.

In the B-spline FCM [22,23,24], the B-spline basis functions are used as the interpolation functions over the hexahedral cells. The standard parametric domain (see Figure 4b) is mapped to the discretization of the embedded domain. For 3D problem mapping, it can be easily constructed by taking the tensor product of corresponding univariate B-spline basis functions.

$$M_s(\xi ,\eta ,\gamma )=N_{i,p}(\xi )\cdot N_{j,q}(\eta )\cdot N_{h,r}(\gamma )\hspace{1em}s=i+n\cdot (j-1)+m\cdot n\cdot (h-1)$$

(9)

in which $N_{i,p}(\xi )$, $N_{j,q}(\eta )$ and $N_{h,r}(\gamma )$ are three univariate B-spline basis functions defined over $\Xi =\left\{{\xi }_1,{\xi }_2,\dots ,{\xi }_{n+p+1}\right\}$, $\mathit{H}=\left\{{\eta }_1,{\eta }_2,\dots ,{\eta }_{m+q+1}\right\}$ and $\mathit{\Psi }=\left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_{k+r+1}\right\}$, respectively. $n$, $m$, and $k$ are numbers of $N_{i,p}(\xi )$, $N_{j,q}(\eta )$, and $N_{h,r}(\gamma )$, respectively. $p$, $q$, and $r$ denote the polynomial degree, in this paper $p=q=r=2$. The following recurrence relation (10) is included by the above expression.

$$\{\begin{array}{l}{N}_{i,0}(\xi )=\{\begin{array}{l}1\hspace{1em}\mathrm{if} {\xi }_i\le \xi \le {\xi }_{i+1}\\ 0\hspace{1em}\mathrm{otherwise}\end{array}\\ N_{i,p}(\xi )=\frac{\xi -{\xi }_i}{{\xi }_{i+p}-{\xi }_i}{N}_{i,p-1}(\xi )+\frac{{\xi }_{i+p+1}-\xi }{{\xi }_{i+p+1}-{\xi }_{i+1}}{N}_{i+1,p-1}(\xi )\\ \mathrm{provide}:\frac{0}{0}=0\end{array}$$

(10)

In this paper,$\Xi$, $\mathit{H}$, and $\mathit{\Psi }$ are uniform and open knot vectors. At the same time, these original knot vectors are all defined as $\left\{0,0,1,1\right\}$ in parametric space. The quadratic univariate B-spline basis functions defined by this uniform and open knot vector are depicted in Figure 5.

Let us assume an arbitrary point $\mathit{P}={\left\{x,y,z\right\}}^{\mathrm{T}}$ inside $\Omega$; this can be interpolated by the following mapping relation:

$$\mathit{P}=\sum _{s=1}^{m\times n\times k}{M}_s(\xi ,\eta ,\gamma ){\mathit{P}}_s$$

(11)

where ${\mathit{P}}_s={\left\{x_s,y_s,z_s\right\}}^{\mathrm{T}}$ refers to the $s\mathrm{th}$ control point, as illustrated in Figure 4c.

The trial functions ${\mathit{u}}^h$ and the test functions ${\mathit{v}}^h$ are defined over $R^h$, which is a finite-dimensional subspace. The discrete form of the weak form Equation (6) can be stated as

$$a({\mathit{u}}^h,{\mathit{v}}^h)=l({\mathit{v}}^h)\hspace{1em}\forall {\mathit{v}}^h\in R^h$$

(12)

where $\mathit{v}$ is spanned by the B-spline basis function $\mathit{M}$. A linear combination of shape functions is considered concerning the numerical approximation ${\mathit{u}}^h$.

$${\mathit{u}}^h={\displaystyle \sum _{s=1}^{m\times \mathit{n}\times k}{M}_s}{u}_s=\mathit{MU}$$

(13)

with

$$\mathit{M}=\left[\begin{array}{cccccccccc}{M}_1& 0& 0& M_2& 0& 0& \cdots & M_{m\times \mathit{n}\times k}& 0& 0\\ 0& M_1& 0& 0& M_2& 0& \cdots & 0& M_{m\times \mathit{n}\times k}& 0\\ 0& 0& M_1& 0& 0& M_2& \cdots & 0& 0& M_{m\times \mathit{n}\times k}\end{array}\right]$$

(14)

in which $\mathit{U}$ denotes the unknown displacement vector of control points.

Based on Ritz-Galerkin approach, inserting Equation (13) into Equation (12), the finite cell formulation, which is identical to the FEM in form, is obtained as

$$\mathit{KU}=\mathit{F}$$

(15)

where $\mathit{K}$ and $\mathit{F}$ are the global stiffness matrix and the global load vector that can be assembled in the traditional fashion from all cell stiffness matrices ${\mathit{K}}_c$ and load vectors ${\mathit{F}}_c$, respectively. ${\mathit{K}}_c$ and ${\mathit{F}}_c$ are acquired by

$${\mathit{K}}_c={\displaystyle \underset{{\Omega }_c}{\int }{\mathit{B}}^{\mathrm{T}}\beta \mathit{DB}\mathrm{d}\Omega }$$

(16)

$${\mathit{K}}_c={\displaystyle \underset{{\Omega }_c}{\int }{\mathit{B}}^{\mathrm{T}}\beta \mathit{DB}\mathrm{d}\Omega }(1){\mathit{F}}_c={\displaystyle \underset{{\Omega }_c}{\int }{\mathit{M}}^{\mathrm{T}}\beta \mathit{f}\mathrm{d}\Omega +{\displaystyle \underset{{\Gamma }_{Nc}}{\int }{\mathit{M}}^{\mathrm{T}}\mathit{t}\mathrm{d}\Gamma }}$$

(17)

in which ${\Omega }_c$ illustrates one cell domain. ${\Gamma }_{Nc}$ is the Neumann boundary related to one cell. $\mathit{B}$ is the strain-displacement matrix, written as

$$\mathit{B}=\left[\begin{array}{ccc}\frac{\partial }{\partial x}& 0& 0\\ 0& \frac{\partial }{\partial y}& 0\\ 0& 0& \frac{\partial }{\partial z}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}& 0\\ 0& \frac{\partial }{\partial z}& \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}& 0& \frac{\partial }{\partial x}\end{array}\right]\mathit{M}$$

(18)

2.3. The Weighted Dirichlet Boundary Conditions

Comparing the FCM with the classical FEM, the difficulty of generating meshes for complex structures shifts to the problem of implementing boundary conditions. In particular, when the boundary $\partial {\Omega }_p$ does not conform to the cells, this problem arises. At present, the weighted method is usually employed to implement the Dirichlet boundary condition.

In this paper, the weighted B-spline is used to penalize locally the interpolation displacement field defined by Equation (13). For homogeneous Dirichlet boundary conditions, the prescribed displacement $\mathit{g}$ applied on ${\Gamma }_D$ is equal to zero. With the weighted function $w(\mathit{x})$, an alternative Equation (13) can be stated as

$$\mathit{u}(\mathit{x})=w(\mathit{x})\mathit{MU}=\overline{\mathit{M}}\mathit{U}$$

(19)

in which

$$w(\mathit{x})=w(x,y,z)=0\hspace{1em}\forall (x,y,z)\in {\Gamma }_D$$

(20)

Therefore, the geometry equation can be addressed as

$$\epsilon =\overline{\mathit{B}}\mathit{U}$$

(21)

where

$$\overline{\mathit{B}}=\left[\begin{array}{ccc}\frac{\partial }{\partial \mathit{x}}& 0& 0\\ 0& \frac{\partial }{\partial y}& 0\\ 0& 0& \frac{\partial }{\partial z}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial \mathit{x}}& 0\\ 0& \frac{\partial }{\partial z}& \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}& 0& \frac{\partial }{\partial \mathit{x}}\end{array}\right]\overline{\mathit{M}}$$

(22)

with

$$\overline{\mathit{M}}=\left[\begin{array}{cccccccccc}w{M}_1& 0& 0& w{M}_2& 0& 0& \cdots & w{M}_{m\times \mathit{n}\times k}& 0& 0\\ 0& w{M}_1& 0& 0& w{M}_2& 0& \cdots & 0& w{M}_{m\times \mathit{n}\times k}& 0\\ 0& 0& w{M}_1& 0& 0& w{M}_2& \cdots & 0& 0& w{M}_{m\times \mathit{n}\times k}\end{array}\right]$$

(23)

and

$$\frac{\partial (w{M}_i)}{\partial y}=\frac{\partial w}{\partial y}{M}_i+w\frac{\partial M_i}{\partial y}$$

(24)

$$\frac{\partial (w{M}_i)}{\partial y}=\frac{\partial w}{\partial y}{M}_i+w\frac{\partial M_i}{\partial y}$$

(25)

$$\frac{\partial (w{M}_i)}{\partial z}=\frac{\partial w}{\partial z}{M}_i+w\frac{\partial M_i}{\partial z}$$

(26)

Thus, Equations (16) and (17) are modified as

$${\mathit{K}}_c={\displaystyle \underset{{\Omega }_c}{\int }{\overline{\mathit{B}}}^{\mathrm{T}}\beta \mathit{D}\overline{\mathit{B}}\mathrm{d}\Omega }$$

(27)

$${\mathit{F}}_c={\displaystyle \underset{{\Omega }_c}{\int }{\overline{\mathit{M}}}^{\mathrm{T}}\beta \mathit{f}\mathrm{d}\Omega +{\displaystyle \underset{{\Gamma }_{Nc}}{\int }{\overline{\mathit{M}}}^{\mathrm{T}}\mathit{t}\mathrm{d}\Gamma }}$$

(28)

3. Geometric Representation and Mechanical Analysis

3.1. Geometric Representation Based on Level-Set Function

The basket, as one of the most important components in a geotechnical centrifuge, is used to contain the inspection model. Figure 1a demonstrates the structure of a typical geotechnical centrifuge, where the basket consists of the lifting lug, mounting base plate, and a pin shaft, and is at the farthest end of the rotation radius of the geotechnical centrifuge. As shown in Figure 1b, the shape of lifting lug may be trapezoidal, but its contour line is not necessarily a simple straight line. Based on the different strength requirements, it can be designed as circular arcs, quadratic curves, and so on. The material of the lifting lug is usually 34CrNi1Mo; thus, the upper bound of the von-Mises stress with safety factor 2 is 400 MPa, and Young’s modulus and Poisson’s ratio are 207.5 GPa and 0.3, respectively.

In order to carry out the shape optimization of the lifting lug based on the weighted B-Spline FCM, the level set function [25], as a competitive parametric modeling method, is adopted in this paper. Based on the statement described in Section 2.1, the level set function $\Phi$ of the lifting lug established by Boolean operations is derived as follows.

$$\Phi =({\Phi }_1\cup {\Phi }_2\cap (-{\Phi }_3)\cap (-{\Phi }_4)\cap (-{\Phi }_5)\cap (-{\Phi }_6))\cup ((-{\Phi }_7)\cap {\Phi }_8\cup {\Phi }_9\cap (-{\Phi }_{10})\cap (-{\Phi }_{11})\cap (-{\Phi }_{12}))$$

(29)

in which ${\Phi }_i(i=1,2,\dots ,12)$ denotes the level set function of ${\Omega }_i$ in Figure 6, and the design variables are included by some of the level set function ${\Phi }_i(i=1,2,\dots ,12)$. With the changing of design variables, the value of $\Phi$ changes, which leads to a change in the cells properties in the fixed grid. Therefore, shape optimization can be carried out.

3.2. Grid Identification

Based on the zero level set function of the lifting lug, the grids are classified into physical cells, boundary cells, and fictitious cells, as described in Figure 7. In order to improve the accuracy of the analysis, the boundary cells are refined by the Octree technique.

3.3. Topological Configurations and Related Design Variables

In order to obtain a superior shape solution, four topological configurations forthe lifting lug are taken into account in this paper, as illustrated in Figure 8.

Case 1. Original single web. The single web is widely used in the lifting lug structure, supposing that the outer contour has eight design variables.

Case 2. Porous dual web. In order to reduce the weight of the lifting lug, a topological opening is carried out inside the web, where the shape of the holes is an ellipse, so each hole contains two design variables. Therefore, the structure contains a total of 17 design variables.

Case 3. Open deep groove dual web. On the basis of the initial single web, the lifting lug is grooved to achieve the purpose of weight reduction. The number of design variables is 12.

Case 4. Connected closed dual web. Based on the open deep groove dual web, the connected closed dual wed with the bottom of the connection to the mount base plate is designed. The total number of design variables is 13.

3.4. Mechanical Analysis

The lifting lug used to connect the rotating arm and the mounting base plate is taken as the research object, and the loads are analyzed in combination with the working environment. Generally, the load type mainly includes two parts, i.e., the centrifugal force caused by its self-mass, and the tensile stress generated by the centrifugal force of other connected parts. The centrifugal force $F_C$ is represented by Equation (30).

$$F_C=mr{\omega }^2$$

(30)

where $m$ is the mass of the lifting lug, $r$ is the radius of rotation of the lifting lug, and $\omega$ represents the rotary angular velocity.

With the high-speed rotation of the centrifuge, the stress ${\sigma }_a$ generated by the centrifugal load of the mounting base plate and the inspection model of centrifugal test at the joint and the centrifugal force $F_C$ act simultaneously, and the combination of the two causes significant strength problems for the lifting lug. Assuming that the load caused by the centrifugal loads of the mounting base plate and the inspection model of centrifugal test are evenly distributed over the edge of the lifting lug connection, the radial stress of the load is defined by

$${\sigma }_a=\frac{F}{2\pi RL}$$

(31)

where $F$ represents the centrifugal load of the mounting base plate and the inspection model of centrifugal test, $R$ is the rotary radius of the lifting lug edge, i.e., the distance from the position where the mounting base plate is attached to the lifting lug to the center axis of the centrifuge, $L$ represents the width of the edge of the lifting lug.

Based on the loads and boundary conditions stated above, the weighted B-spline FCM is employed to compute the von-Mises stress distribution of the lifting lug in fixed grid. Figure 9 shows the initial von-Mises stress distribution of the four cases. A comparison of the maximum von-Mises stress and mass among the four cases is demonstrated, as described in Figure 10. From these figures, it can be noted that the maximum von-Mises stresses of the four cases appear at the junction of the lifting lug and the mounting base plate, wherein both of the maximum von-Mises stress and mass in the case 1 are the largest. The four cases with these topological configurations all satisfy the stress condition with a safety factor greater than or equal to 2. Thus, in order to obtain a superior solution of the lifting lug based on the four topological configurations, shape optimization is carried out for the four cases.

4. Shape Optimization

4.1. Shape Optimization Model

In order to solve the problem of designing a light-weight basket which meets the requirement of the geotechnical centrifuge in terms of strength, shape optimization is implemented. The optimization model is constructed by

$$\{\begin{array}{ll}\mathrm{find}& \mathit{\theta }=[y_1,y_2,\dots ,y_{l_y},d_1,d_2,\dots ,d_{l_d}]\\ \min & m={\int }_{\Omega }\rho d\Omega \\ s.t.& \mathit{KU}=\mathit{F}\\ & \max \left\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_q\right\}\le \overline{\sigma }\\ & \underset{\_}{y_i}\le y_i\le \overline{y_i}\hspace{1em}i=1,2,\dots ,l_y\\ & \underset{\_}{d_j}\le d_j\le \overline{d_j}\hspace{1em}j=1,2,\dots ,l_d\end{array}$$

(32)

where $\mathit{\theta }$ stands for the vector of design variables characterizing geometric shapes of the lifting lug. The objective function is to minimize the mass of the physical domain $\Omega$. In the equilibrium equation $\mathit{KU}=\mathit{F}$, $\mathit{K}$ is the stiffness matrix, $\mathit{U}$ denotes the displacement vector, and $\mathit{F}$ represents the load vector. The constraints concern the maximum von-Mises stress in the lifting lug being limited by the allowable value $\overline{\sigma }$. $q$ is the number of nodes of the finite cells. $l_d$ and $l_y$ are numbers of design variables $d_i$ and $y_j$, respectively. $\underset{\_}{y_i}$ and $\overline{y_i}$ denote the lower and upper bounds of the ith design variable $y_i$, respectively. ${\underset{\_}{d}}_j$ and ${\overline{d}}_j$ denote the lower and upper bounds of the jth design variable $d_j$, respectively.

4.2. The Flowchart of Shape Optimization

The whole optimization solution is based on the weighted B-Spline FCM [23,24] and the GCMMA [27,28]. The weighted B-Spline FCM analysis process is as follows: including geometric modeling based on level set function and R-functions, determining the properties of all the cells in fixed grid, refining the boundary cells with the Quadtree or Octree technique, imposing the homogeneous Dirichlet boundary condition exactly with the weighted function, and calculating the shape sensitivity. The optimization solution is implemented by the GCMMA algorithm integrated into Boss-Quattro optimization platform [29]. A flowchart of the shape optimization based on the weighted B-Spline FCM and GCMMA is presented in Figure 11.

4.3. Sensitivity Analysis

In shape optimization based on Equation (32), sensitivity analysis, i.e., stress sensitivity and mass sensitivity with respect to design variables, is essential for gradient-based optimization algorithms.

For the level set function $\Phi (\mathit{x},\mathit{d})$ of a physical domain $\Omega$, the Dirac delta function $\widehat{\delta }(\mathit{x},\mathit{d})$ denotes the directional derivative of the Heaviside function $H$ in the normal direction, i.e.,

$$\widehat{\delta }=\nabla H\left(\Phi \right)\cdot \frac{\nabla \Phi }{\Vert \nabla \Phi \Vert }=\frac{\mathrm{d}H\left(\Phi \right)}{\mathrm{d}\Phi }\cdot \nabla \Phi \cdot \frac{\nabla \Phi }{\Vert \nabla \Phi \Vert }=\frac{\mathrm{d}H\left(\Phi \right)}{\mathrm{d}\Phi }\Vert \nabla \Phi \Vert$$

(33)

Then, the mass sensitivity is calculated by

$$\begin{array}{ll}\frac{\partial m}{\partial {\theta }_i}& ={\int }_{\Omega }\rho \frac{\partial H\left(\Phi \right)}{\partial {\theta }_i}\mathrm{d}\Omega \\ & ={\int }_{\Omega }\rho \frac{\partial \Phi }{\partial {\theta }_i}\frac{1}{\Vert \nabla \Phi \Vert }\frac{\mathrm{d}H\left(\Phi \right)}{\mathrm{d}\Phi }\Vert \nabla \Phi \Vert \mathrm{d}\Omega \hfill \\ & ={\int }_{\Omega }\rho \frac{\partial \Phi }{\partial {\theta }_i}\frac{1}{\Vert \nabla \Phi \Vert }\widehat{\delta }\mathrm{d}\Omega \hfill \\ & ={\int }_{\Gamma }\rho \frac{\partial \Phi }{\partial {\theta }_i}\frac{1}{\Vert \nabla \Phi \Vert }\mathrm{d}\Gamma \hfill \end{array}$$

(34)

in which $\Gamma$ represents the boundary of the physical domain, i.e., $\Gamma =\partial \Omega$.

Based on the stress-strain relationship $\mathit{\sigma }=\mathit{D}\mathit{\epsilon }=\mathit{D}\overline{\mathit{B}}\mathit{U}$, the stress sensitivity is estimated by

$$\frac{\partial \mathit{\sigma }}{\partial {\theta }_i}=\mathit{D}\overline{\mathit{B}}\frac{\partial \mathit{U}}{\partial {\theta }_i}+\mathit{D}\frac{\partial \overline{\mathit{B}}}{\partial {\theta }_i}\mathit{U}$$

(35)

where $\mathit{D}$ represents the elastic modulus, $\mathit{U}$ denotes the displacement field, and $\overline{\mathit{B}}$ is the strain-displacement matrix corrected by the weighted function.

For the four topological configurations of the lifting lug are considered in Section 2.3. Since the design variables are all on the free boundary, $\overline{\mathit{B}}$ is independent of the design variables. Thus, the stress sensitivity is derived as

$$\frac{\partial \mathit{\sigma }}{\partial {\theta }_i}=\mathit{D}\overline{\mathit{B}}\frac{\partial \mathit{U}}{\partial {\theta }_i}$$

(36)

According to the equilibrium equation $\mathit{K}\mathit{U}=\mathit{F}$, the stress sensitivity is deduced as

$$\frac{\partial \sigma }{\partial {\theta }_i}=\mathit{D}\overline{\mathit{B}}{\mathit{K}}^{-1}\left(\frac{\partial \mathit{F}}{\partial {\theta }_i}-\frac{\partial \mathit{K}}{\partial {\theta }_i}\mathit{U}\right)$$

(37)

where

$$\frac{\partial \mathit{K}}{\partial {\theta }_i}={{\displaystyle \int }}_{\Gamma }{\overline{\mathit{B}}}^{\mathrm{T}}\mathit{D}\overline{\mathit{B}}\frac{\partial (\Phi )}{\partial {\theta }_i}\frac{1}{\Vert \nabla \Phi \Vert }\mathrm{d}\Gamma$$

(38)

and

$$\frac{\partial \mathit{F}}{\partial {\theta }_i}={{\displaystyle \int }}_{\Gamma }\omega {\mathit{M}}^{\mathrm{T}}\mathit{f}\frac{\partial \Phi }{\partial {\theta }_i}\frac{1}{\Vert \nabla \Phi \Vert }\mathrm{d}\Gamma$$

(39)

5. Optimization Results

Based on the weighted B-Spline FCM performed in Matlab script and GCMMA implemented in the Boss-Quattro optimization platform, the shape optimization results for the four cases are obtained. The final design solutions of the four cases provide us with the minimum mass that removes material to the maximum extent. Meanwhile, the allowable von-Mises stresses are all still satisfied. The final design solutions of the four cases of the lifting lug and the von-Mises stress distributions are depicted in Figure 12.

The corresponding iteration histories of the von-Mises stress and the mass of the four cases are shown in Figure 13.

Figure 14a,b compare the maximum von-Mises stress and the mass between the initial and the final design solutions of the four cases, respectively. The results are listed in

Table 1. Results of the initial and the final maximum von-Mises stress and mass of the four cases.

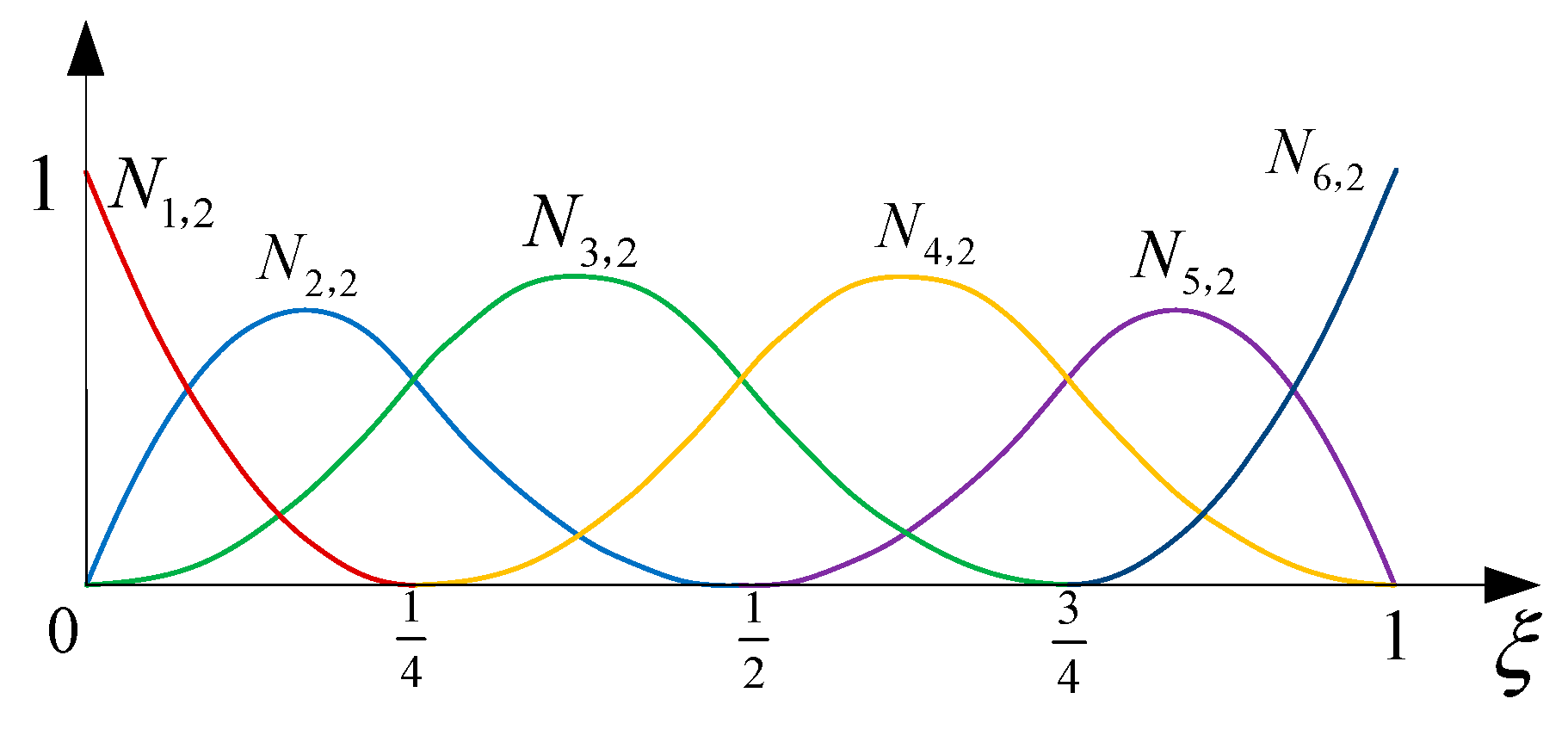
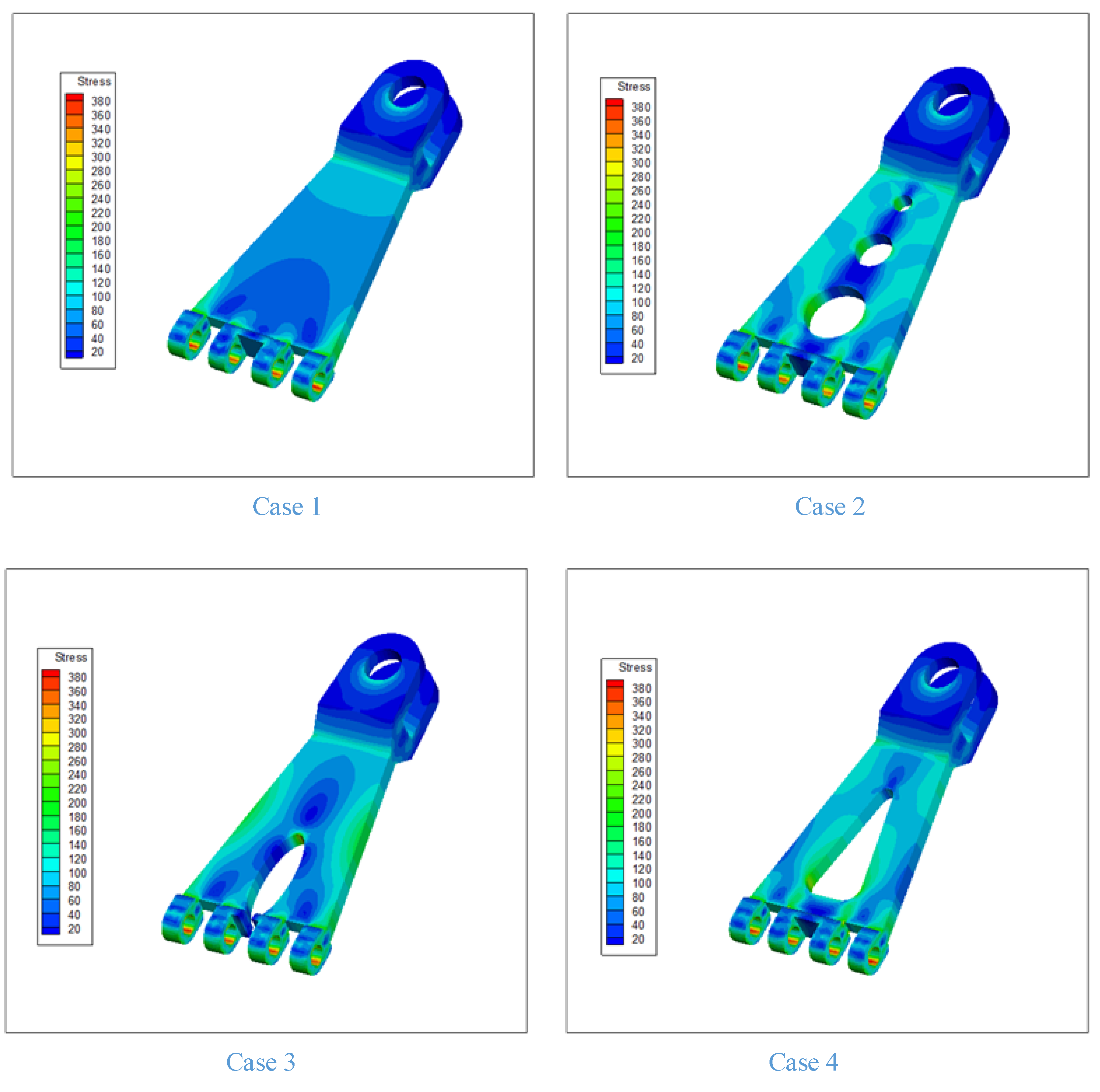
	Maximum Von-Mises Stress/MPa		Mass/kg
	Initial	Final	Initial	Final
Case 1	396.95	398.25	987.51	915.20
Case 2	390.03	399.32	909.86	819.76
Case 3	394.68	399.68	921.60	827.51
Case 4	390.34	398.72	874.57	781.82

.

In Table 1 and Figure 12, Figure 13 and Figure 14, it can be seen that in contrast to the initial configurations, although the maximum von-Mises stresses of the four cases all increased, they still meet the strength requirements of the lifting lug, i.e., ${\sigma }_{\max }\le 400\mathrm{MPa}$. The mass reduction by shape optimization in the four cases is very obvious. Below, the four cases are discussed in detail.

Case 1: Compared with the initial configuration, the maximum stress change is very small; however, by the optimization design for the outer contour of the lifting lug, the final mass was reduced by 72.31 kg, i.e., 7.3%, which is still the largest among the four cases. This indicates that although the original single web configuration can achieve the goal of weight reduction by shape optimization on the premise of meeting the strength requirements, the effect of weight reduction is limited.

Case 2: With the maximum stress increasing by 9 MPa based on the shape optimization, the mass decreases by 90.1 kg from 909.86 kg to 819.76 kg, i.e., by 10%. Compared with the optimized single web, the weight loss of the porous dual web is about 96 kg, which shows the configuration of case 2 is better than that of case 1.

Case 3: The maximum stress in the optimized configuration does not change much, but as seen in Figure 12, the stress distribution changes greatly. The maximum stress in the initial configuration occurs at the connection hole with the mounting base plate, while that in the final configuration occurs in multiple places. Additionally, the final mass declines by 94.09 kg based on shape optimization, i.e., by 10%. In contrast to the optimized single web in case 1, the final open deep groove dual web in case 3 reduces 87.69 kg, which is less than that of case 2.

Case 4: Compared with the initial configuration, the maximum stress and stress distribution in the optimized configuration do not change substantially, but the final mass drops by 92.75 kg, i.e., by 10.6%. Compared with the optimized single web, the weight loss of the connected closed dual web is 133.38 kg, which indicates that the final configuration of case 4 is the best among the four cases.

The above results indicate that while satisfying the stress requirement, the final mass of case 4 is the least. Therefore, considering the matching, cost, and other factors, the optimized shape configuration of the case 4 is superior to those of the other three cases.

6. Conclusions

The lifting lug, as one key structure of the geotechnical centrifuge, is the focus of this research. This paper presents an effective and systematic structure design and shape optimization for the lifting lug with multi topological configurations based on the weighted B-Spline FCM and GCMMA. It provides a complete shape optimization process for the lifting lug of the geotechnical centrifuge, which addresses the problem of the light-weight design of the lifting lug while satisfying the requirement of the geotechnical centrifuge strength. Four topological configurations, i.e., original single web, porous dual web, open deep groove dual web, and connected closed dual web, are investigated and optimized. Two main conclusions can be drawn.

First, through shape optimization design based on the weighted B-Spline FCM and GCMMA, the final mass of the four configurations is greatly reduced compared with the initial configurations, where the greatest weight loss was observed in case 4 is 10.6%. This indicates that the weighted B-Spline FCM and GCMMA can be applied for shape optimization of the complex structure in the engineering design.

Second, in contrast to the final single web adopted in the traditional basket design in case 1, the final configuration in case 4, i.e., connected closed dual web, has the least mass. The final mass was reduced by 133.38 kg with the centrifuge strength requirement being satisfied. Therefore, the final configuration in case 4 is superior to other three configurations.

In this work, the design procedure extending the weighted B-Spline FCM and GCMMA into shape optimization is developed for the rotational structure concerning the important role it plays in engineering applications. However, our mechanical analysis was restricted to the static loads; vibrating loads, also as a common load condition during the operation of centrifuges, were not tested. Further investigation on this problem will make the design of the centrifuge within the FCM and GCMMA framework more comprehensive.