Control Points Selection Based on Maximum External Reliability for Designing Geodetic Networks
Abstract
:1. Introduction
2. Conventional Reliability Theory
- is the critical value. The critical value is the the tabular value from the cumulative distribution function (cdf) of the standard normal based on the chosen of a significance level . Because we perform a two-sided test of the form we have . For example, for , we obtain . In this case, if for some one may reject .
- denotes the inverse of the normal cumulative distribution function.
- is the least-squares residuals vector under and the covariance matrix of the best linear unbiased estimator of under .
3. Automatic Procedure to Design the Location of Control Points in the Geodetic Network
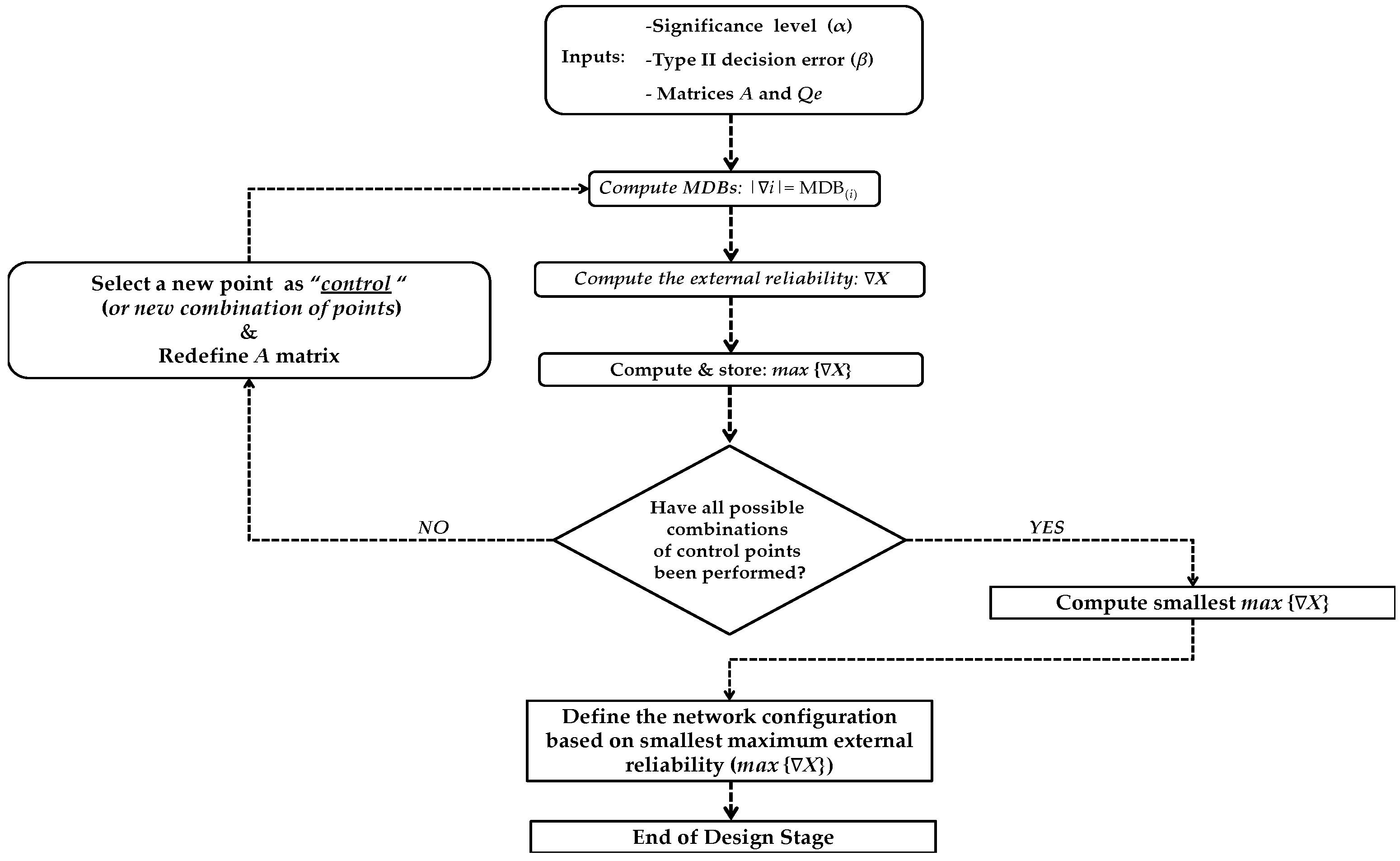
- Defining a significance level and the type II error in order to compute the non-centrality parameter. Here, we use the recursive algorithm based on the work by Aydin and Demirel [33], namely bisection algorithm, in order to obtain the non-centrality parameter for one degree of freedom, i.e., . Typically a value of the level and is adopted (see, e.g., [4]).
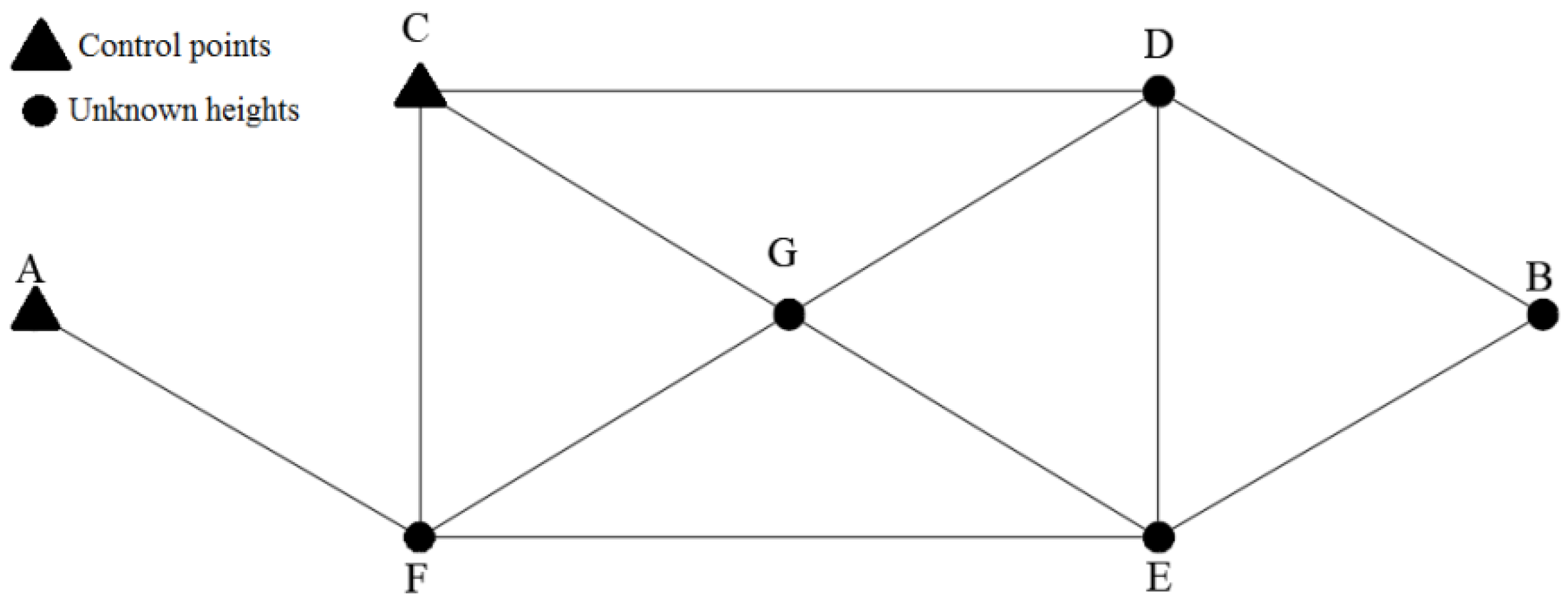
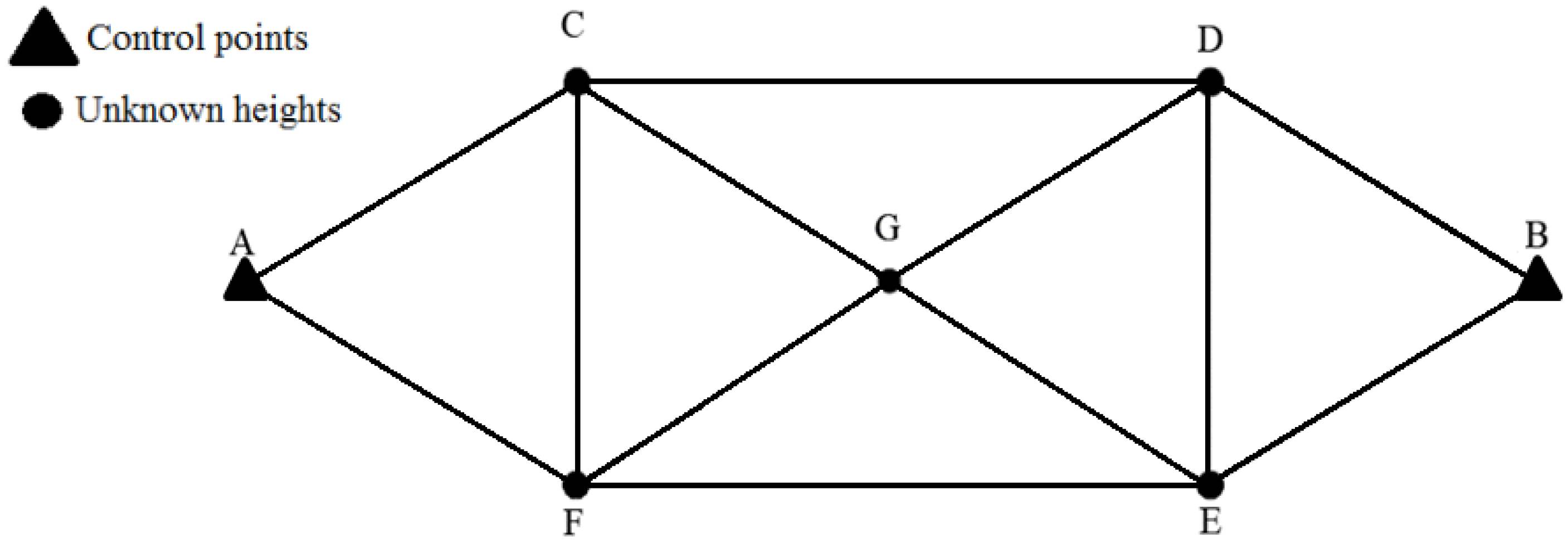
- Defining a geodetic network configuration as well as the uncertainties of the observations, i.e., the design matrix and the covariance matrix of the observations , respectively. The covariance matrix of the observations may consist of random effects and the uncertainties associated with the correction of systematic effects. The latter follows from the instrument precision, measurement techniques and field condition. In this step, the design matrix and covariance matrix are conditioned to the position of the control point (or by the combination of control points) in the network. It is important to mention that the design matrix defined must have a minimum configuration to avoid rank deficiency [47].
- Computing the external reliability according to Equation (10).
- Computing and store the maximum external reliability according to Equation (11).
- Checking whether all the points (or all combination of points) of the network were configured as control point. If not, select a new control point (or new combination of control points) and return to Step 3. Otherwise, the algorithm selects the configuration of the network that has the lowest value of the maximum external reliability. Important to mention that matrix is modified when a new point (or a new combination of points) is selected as the control.
4. Results and Discussion
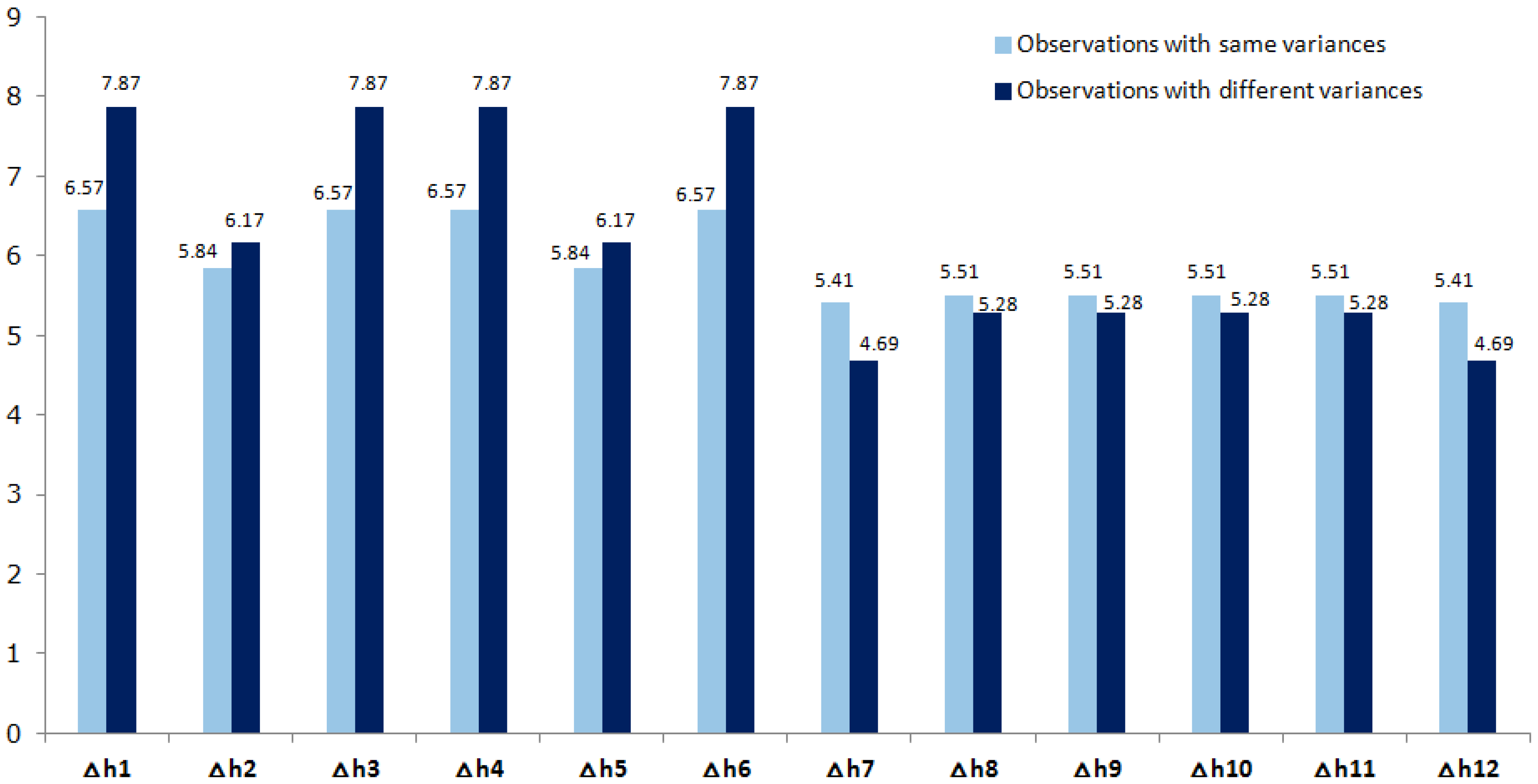
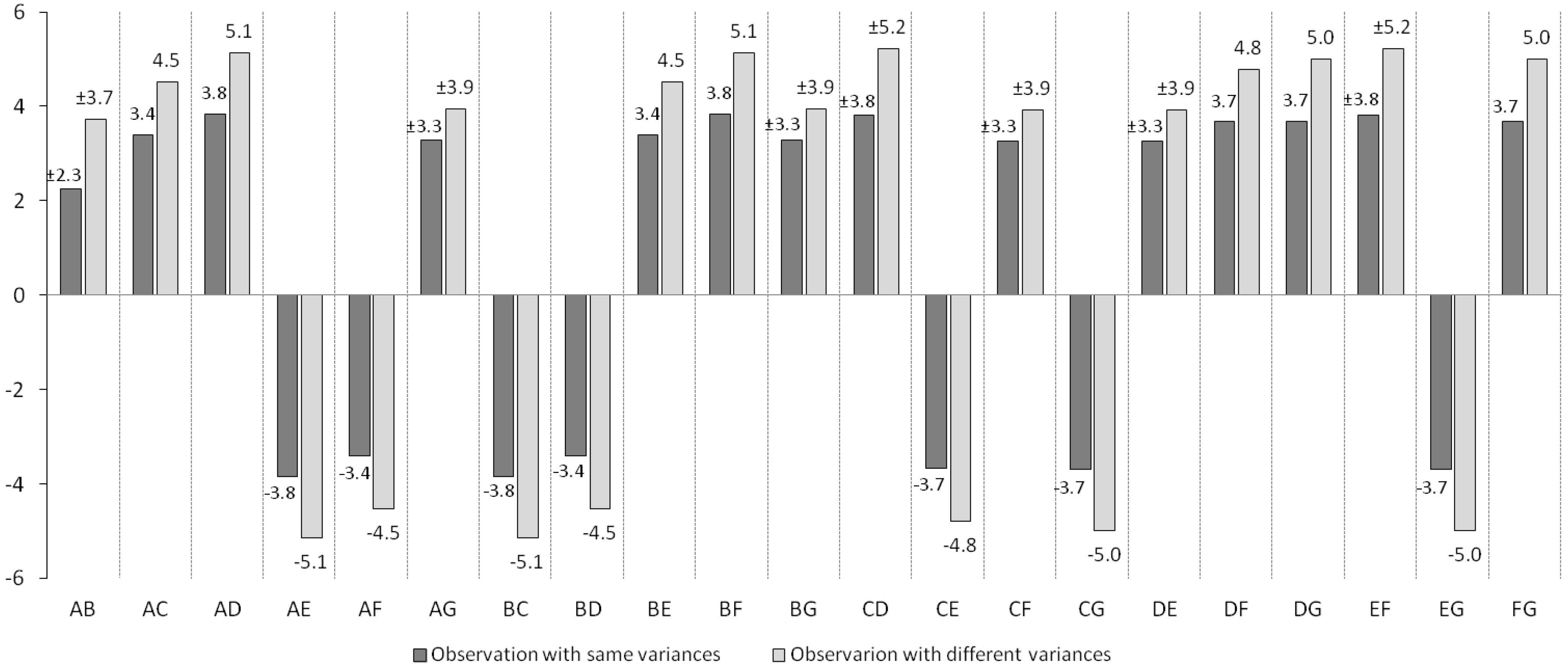
- all lengths of the differential levelling with 1 km, and therefore the variances equal to 1 mm; and
- lines with diversified lengths, and therefore levelling lines with different variances, whose values are given in Table 1.
5. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klein, I.; Matsuoka, M.T.; Guzatto, M.P.; Nievinski, F.G.; Veronez, M.R.; Rofatto, V.F. A new relationship between the quality criteria for geodetic networks. J. Geod. 2019, 93, 529–544. [Google Scholar] [CrossRef]
- Lehmann, R.; Neitzel, F. Testing the compatibility of constraints for parameters of a geodetic adjustment model. J. Geod. 2013, 87, 555–566. [Google Scholar] [CrossRef] [Green Version]
- Baarda, W. Statistical concepts in geodesy. Publ. Geod. New Ser. 1967, 2, 74. [Google Scholar]
- Baarda, W. A testing procedure for use in geodetic networks. Publ. Geod. New Ser. 1968, 2, 5. [Google Scholar]
- Teunissen, P. Testing Theory: An Introduction, 2nd ed.; Delft University Press: Delft, The Netherlands, 2006. [Google Scholar]
- Seemkooei, A.A. Comparison of reliability and geometrical strength criteria in geodetic networks. J. Geod. 2001, 75, 227–233. [Google Scholar] [CrossRef]
- Seemkooei, A.A. Strategy for Designing Geodetic Network with High Reliability and Geometrical Strength. J. Surv. Eng. 2001, 127, 104–117. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, R. On the formulation of the alternative hypothesis for geodetic outlier detection. J. Geod. 2013, 87, 373–386. [Google Scholar] [CrossRef] [Green Version]
- Baarda, W. S-transformations and criterion matrices. Publ. Geod. New Ser. 1973, 5, 168. [Google Scholar]
- Grafarend, E.W. Optimization of Geodetic Networks. Can. Surv. 1974, 28, 716–723. [Google Scholar] [CrossRef]
- Grafarend, E.W.; Sansò, F. (Eds.). Optimization and Design of Geodetic Networks; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Quality Control in Geodetic Networks. In Optimization and Design of Geodetic Networks; Grafarend, E.W., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 526–547. [Google Scholar]
- Vaníček, P.; Craymer, M.R.; Krakiwsky, E.J. Robustness analysis of geodetic horizontal networks. J. Geod. 2001, 75, 199–209. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A. A new method for second order design of geodetic networks: Aiming at high reliability. Surv. Rev. 2004, 37, 552–560. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Sharifi, M.A. Approach for Equivalent Accuracy Design of Different Types of Observations. J. Surv. Eng. 2004, 130, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Hekimoglu, S.; Erenoglu, R.C.; Sanli, D.U.; Erdogan, B. Detecting Configuration Weaknesses in Geodetic Networks. Surv. Rev. 2011, 43, 713–730. [Google Scholar] [CrossRef]
- Hekimoglu, S.; Erdogan, B. New Median Approach to Define Configuration Weakness of Deformation Networks. J. Surv. Eng. 2012, 138, 101–108. [Google Scholar] [CrossRef]
- Klein, I.; Matsuoka, M.T.; Souza, S.F.d.; Collischonn, C. Planejamento de redes georesistentes a moutliers. Boletim CiGeod. 2012, 18, 480–507. [Google Scholar]
- Rofatto, V.; Matsuoka, M.; Klein, I. Design of geodetic networks based on outlier identification criteria: An example applied to the leveling network. Bull. Geod. Sci. 2018, 24, 152–170. [Google Scholar] [CrossRef]
- Knight, N.L.; Wang, J.; Rizos, C. Generalised measures of reliability for multiple outliers. J. Geod. 2010, 84, 625–635. [Google Scholar] [CrossRef]
- Imparato, D.; Teunissen, P.; Tiberius, C. Minimal Detectable and Identifiable Biases for quality control. Surv. Rev. 2019, 51, 289–299. [Google Scholar] [CrossRef]
- Rofatto, V.F.; Matsuoka, M.T.; Klein, I.; Veronez, M.R.; Bonimani, M.L.; Lehmann, R. A half-century of Baarda’s concept of reliability: A review, new perspectives, and applications. Surv. Rev. 2018, 0, 1–17. [Google Scholar] [CrossRef]
- Rofatto, V.F.; Matsuoka, M.T.; Klein, I.; Veronez, M.R. Monte-Carlo-based uncertainty propagation in the context of Gauss–Markov model: A case study in coordinate transformation. Sci. Plena 2019, 15, 1–17. [Google Scholar] [CrossRef]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models, 2nd ed.; Springer: Berlin, Germany, 1999. [Google Scholar]
- Ghilani, C.D. Adjustment Computations: Spatial Data Analysis, 6th ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Lehmann, R. Improved critical values for extreme normalized and studentized residuals in Gauss–Markov models. J. Geod. 2012, 86, 1137–1146. [Google Scholar] [CrossRef]
- Kargoll, B. On the Theory and Application of Model Misspecification Tests in Geodesy. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2007. [Google Scholar]
- Yang, L.; Wang, J.; Knight, N.L.; Shen, Y. Outlier separability analysis with a multiple alternative hypotheses test. J. Geod. 2013, 87, 591–604. [Google Scholar] [CrossRef]
- Teunissen, P. Distributional theory for the DIa method. J. Geod. 2018, 92, 59–80. [Google Scholar] [CrossRef]
- Teunissen, P. An Integrity and Quality Control Procedure for use in Multi Sensor Integration. In ION GPS Redbook Volume VII Integrated Systems; Institute of Navigation (ION): Manassas, VA, USA, 1990. [Google Scholar]
- Vaníček, P.; Krakiwsky, E.J. Geodesy: The Concepts, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Lehmann, R. Observation error model selection by information criteria vs. normality testing. Stud. Geophys. Geod. 2015, 59, 489–504. [Google Scholar] [CrossRef] [Green Version]
- Aydin, C.; Demirel, H. Computation of Baarda’s lower bound of the non-centrality parameter. J. Geod. 2004, 78, 437–441. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y. On the reliability measure of observations. Acta Geod. Cartogr. Sin. 1994, 4, 42–51. [Google Scholar]
- Pelzer, H. Detection of errors in the functional adjustment model. In Mathematical Models of Geodetic/Photogrammetric Point Determination with Regard to Outliers and Systematic Errors; Ackermann, F., Ed.; German Geodetic Commission: Munich, Germany, 1983. [Google Scholar]
- Prószyński, W. Criteria for internal reliability of linear least squares models. Bull. GÉOdÉSique 1994, 68, 162–167. [Google Scholar] [CrossRef]
- Schaffrin, B. Reliability Measures for Correlated Observations. J. Surv. Eng. 1997, 123, 126–137. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Minimal detectable biases of GPS data. J. Geod. 1998, 72, 236–244. [Google Scholar] [CrossRef] [Green Version]
- Prószyński, W. Another approach to reliability measures for systems with correlated observations. J. Geod. 2010, 84, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Coleman, R. Multiple outlier detection by evaluating redundancy contributions of observations. J. Geod. 1996, 70, 489–498. [Google Scholar] [CrossRef]
- Gui, Q.; Li, X.; Gong, Y.; Li, B.; Li, G. a Bayesian unmasking method for locating multiple gross errors based on posterior probabilities of classification variables. J. Geod. 2011, 85, 191–203. [Google Scholar] [CrossRef]
- Gökalp, E.; Güngör, O.; Boz, Y. Evaluation of Different Outlier Detection Methods for GPS Networks. Sensors 2008, 8, 7344–7358. [Google Scholar] [CrossRef] [PubMed]
- Baselga, S. Nonexistence of Rigorous Tests for Multiple Outlier Detection in Least-Squares Adjustment. J. Surv. Eng. 2011, 137, 109–112. [Google Scholar] [CrossRef]
- Klein, I.; Matsuoka, M.T.; Guzatto, M.P.; Nievinski, F.G. An approach to identify multiple outliers based on sequential likelihood ratio tests. Surv. Rev. 2017, 49, 449–457. [Google Scholar] [CrossRef]
- Lehmann, R.; Lösler, M. Multiple Outlier Detection: Hypothesis Tests versus Model Selection by Information Criteria. J. Surv. Eng. 2016, 142, 04016017. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Zhang, J.; Li, R.; Cao, X.; Wang, J. Vision-Aided RAIM: A New Method for GPS Integrity Monitoring in Approach and Landing Phase. Sensors 2015, 15, 22854–22873. [Google Scholar] [CrossRef] [Green Version]
- Xu, P. Sign-constrained robust least squares, subjective breakdown point and the effect of weights of observations on robustness. J. Geod. 2005, 79, 146–159. [Google Scholar] [CrossRef] [Green Version]


| Observation | Length of Line (km) | () |
|---|---|---|
| 1.000 | 1.00 | |
| 1.000 | 1.00 | |
| 1.000 | 1.00 | |
| 1.000 | 1.00 | |
| 1.414 | 2.00 | |
| 1.414 | 2.00 | |
| 1.732 | 3.00 | |
| 1.732 | 3.00 | |
| 1.732 | 3.00 | |
| 1.732 | 3.00 | |
| 2.000 | 4.00 | |
| 2.000 | 4.00 |
| Maximum External Reliability (mm) | Maximum External Reliability (mm) | |
|---|---|---|
| Control Point | Observations with Same Variance | Observations with Different Variances |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
| G |
| MDB (in ) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Observations with Same Variances | Observations with Different Variances | |||||||
| Control Point | Average | Max. | Min. | Sth. Dev. | Average | Max. | Min. | Std. Dev. |
| AB | 5.41 | 5.41 | 5.41 | 0.00 | 5.52 | 6.39 | 4.69 | 0.67 |
| AC, AF, DB or BE | 5.64 | 6.56 | 5.1 | 0.50 | 5.86 | 7.83 | 4.49 | 1.16 |
| CD or EF | 5.69 | 6.45 | 4.98 | 0.63 | 5.93 | 7.5 | 4.6 | 1.28 |
| CG, DG, EG or FG | 5.69 | 6.56 | 5.00 | 0.65 | 5.97 | 7.85 | 4.57 | 1.35 |
| AD, AE, CB or BF | 5.46 | 6.47 | 4.99 | 0.50 | 5.61 | 7.43 | 4.59 | 1.00 |
| AG or BG | 5.48 | 6.57 | 4.95 | 0.57 | 5.69 | 7.87 | 4.57 | 1.19 |
| DE or CF | 5.65 | 6.53 | 5.06 | 0.50 | 5.8 | 7.73 | 4.66 | 1.03 |
| CE or DF | 5.51 | 6.36 | 4.90 | 0.66 | 5.68 | 7.16 | 4.53 | 1.12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsuoka, M.T.; Rofatto, V.F.; Klein, I.; Roberto Veronez, M.; da Silveira, L.G., Jr.; Neto, J.B.S.; Alves, A.C.R. Control Points Selection Based on Maximum External Reliability for Designing Geodetic Networks. Appl. Sci. 2020, 10, 687. https://doi.org/10.3390/app10020687
Matsuoka MT, Rofatto VF, Klein I, Roberto Veronez M, da Silveira LG Jr., Neto JBS, Alves ACR. Control Points Selection Based on Maximum External Reliability for Designing Geodetic Networks. Applied Sciences. 2020; 10(2):687. https://doi.org/10.3390/app10020687
Chicago/Turabian StyleMatsuoka, Marcelo Tomio, Vinicius Francisco Rofatto, Ivandro Klein, Maurício Roberto Veronez, Luiz Gonzaga da Silveira, Jr., João Batista Silva Neto, and Ana Cristina Ramos Alves. 2020. "Control Points Selection Based on Maximum External Reliability for Designing Geodetic Networks" Applied Sciences 10, no. 2: 687. https://doi.org/10.3390/app10020687
APA StyleMatsuoka, M. T., Rofatto, V. F., Klein, I., Roberto Veronez, M., da Silveira, L. G., Jr., Neto, J. B. S., & Alves, A. C. R. (2020). Control Points Selection Based on Maximum External Reliability for Designing Geodetic Networks. Applied Sciences, 10(2), 687. https://doi.org/10.3390/app10020687





