Failure Trends of High-Voltage Porcelain Insulators Depending on the Constituents of the Porcelain
Abstract
:1. Introduction
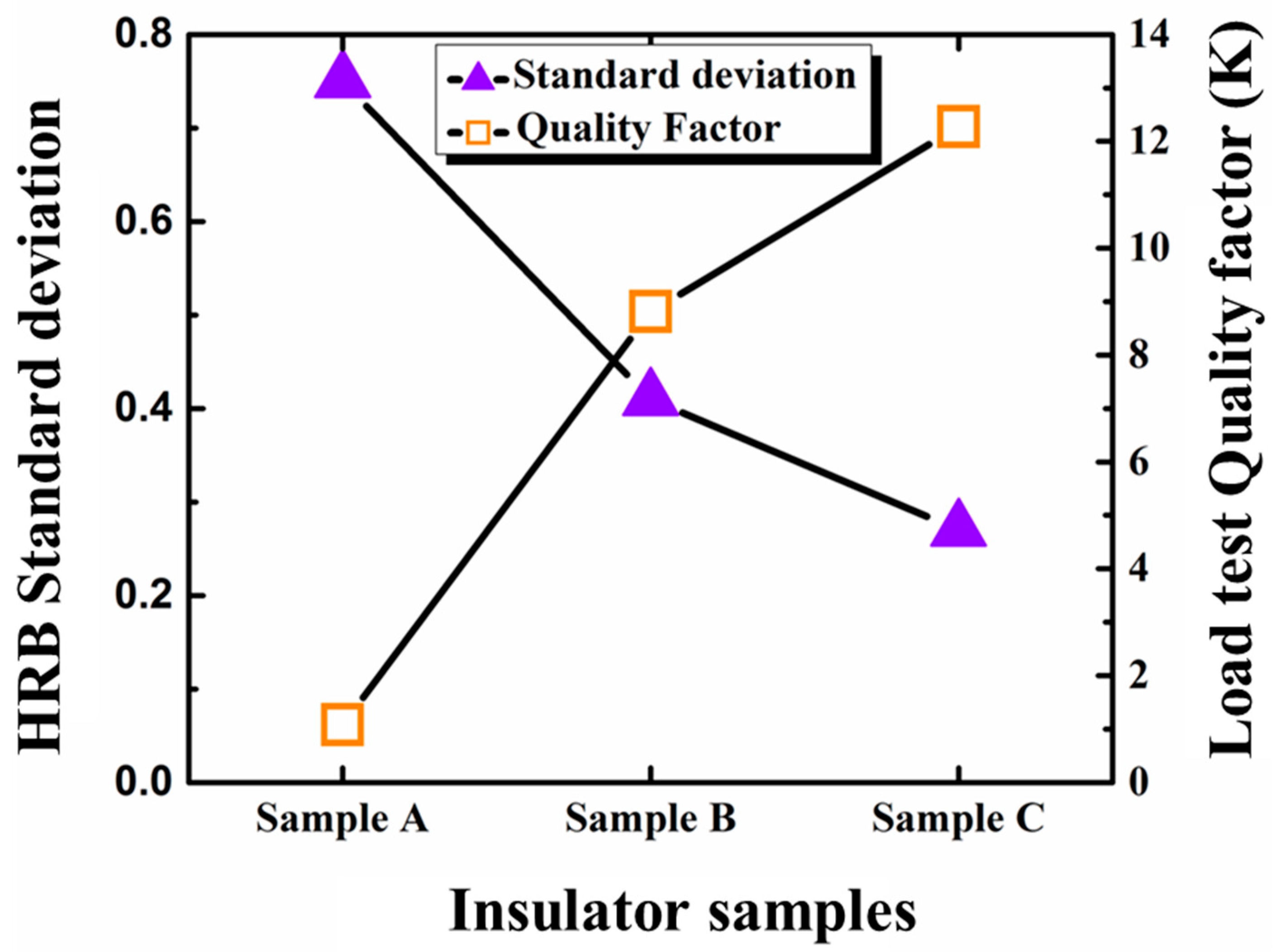
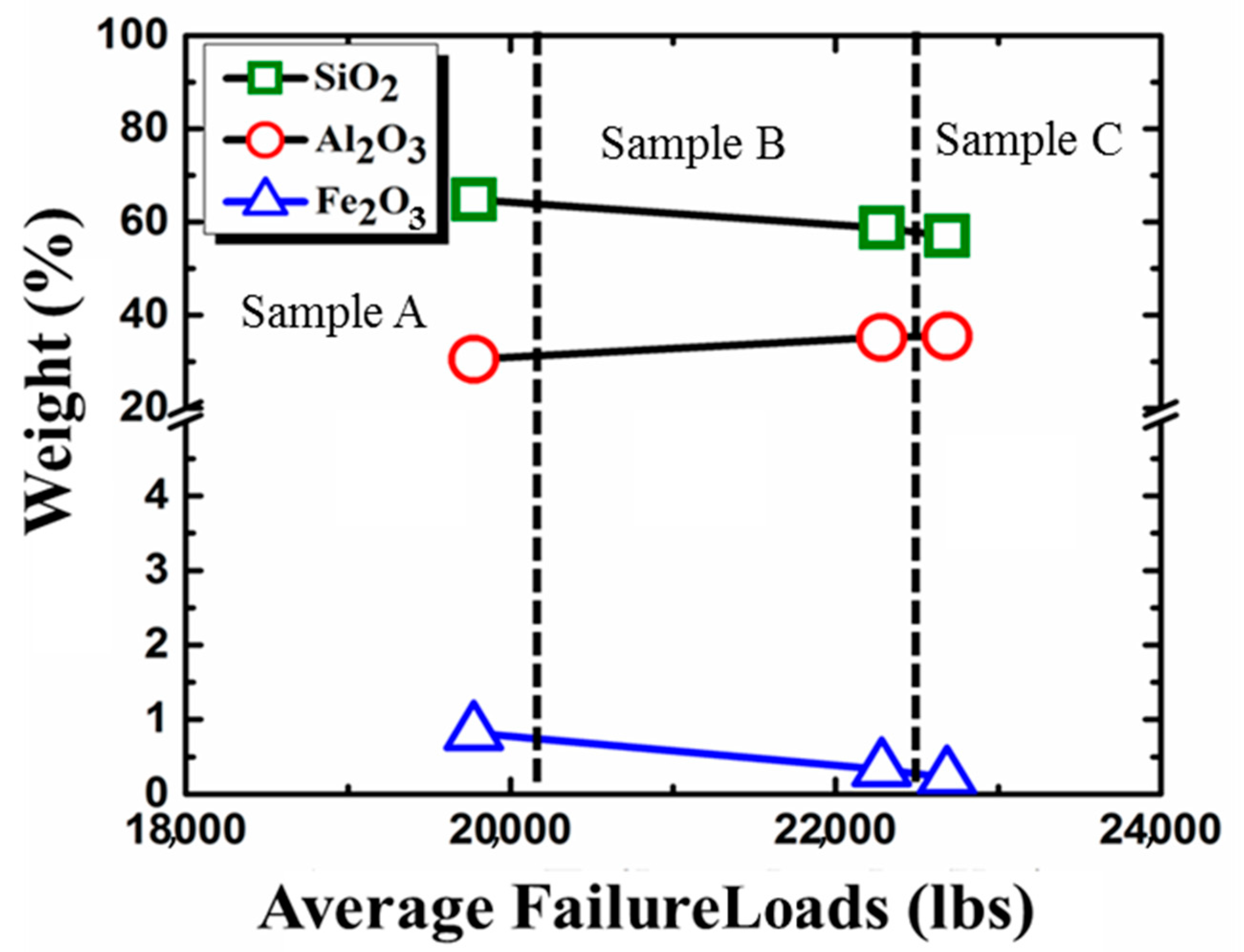
2. Influence of the Material Contents of Porcelain Body on the Electrical and Mechanical Properties of Porcelain Insulators
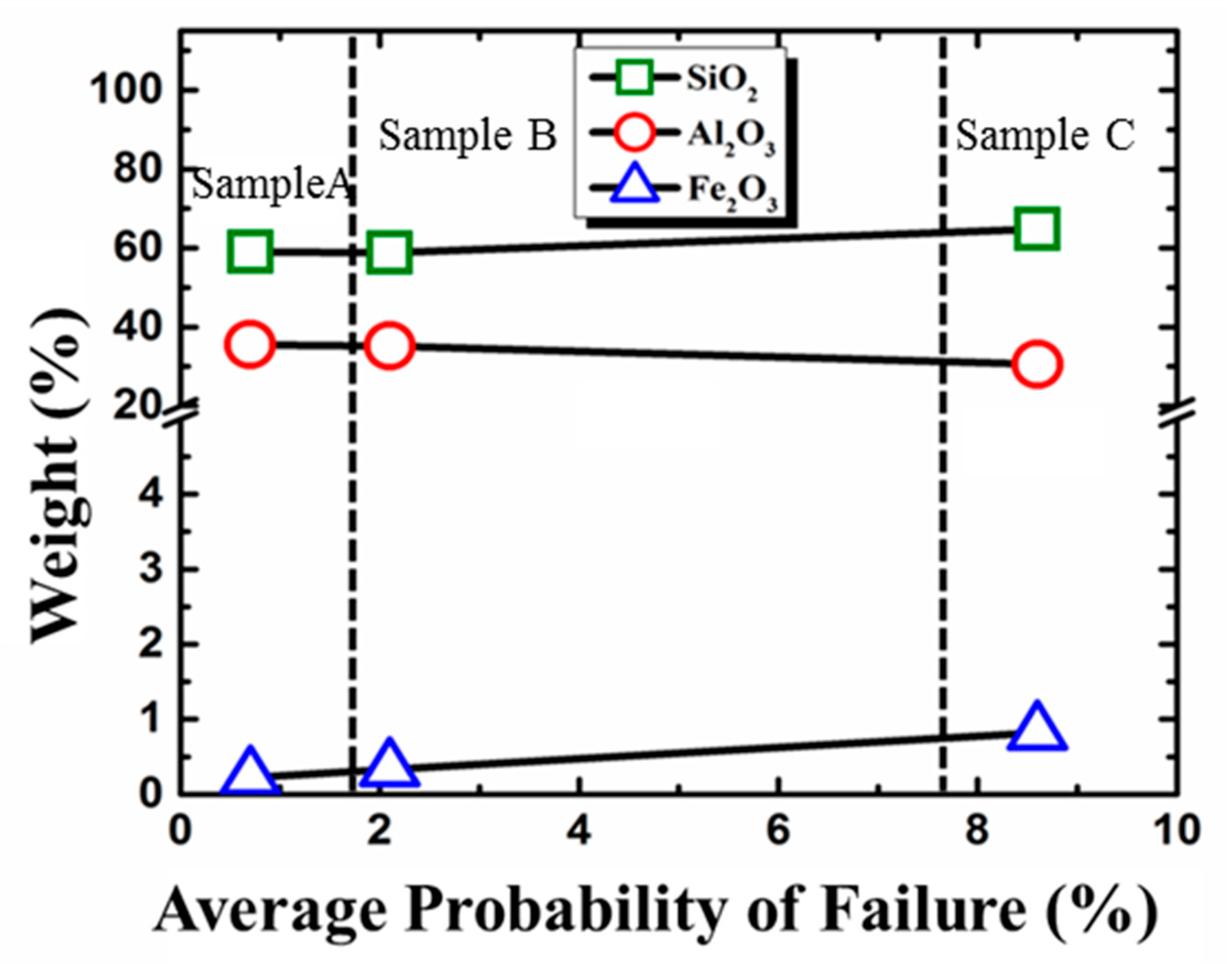
3. Statistical Analysis of the Constituents of Porcelain and the Probability of Failure of Porcelain Insulators
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mishra, A.P.; Gorur, R.S.; Venkataraman, S. Evaluation of Porcelain and Toughened Glass Suspension Insulators Removed from Service. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 467–475. [Google Scholar] [CrossRef]
- Gorur Ravi, S. Failure Modes of Porcelain and Toughened Glass Suspension Insulators. In Proceedings of the IEEE Electrical Insulation Conference, Annapolis, MD, USA, 5–8 June 2011; pp. 221–225. [Google Scholar]
- Han, S.W. Thermal mechanical performance test on suspended insulators for transmission line. In Proceedings of the Conference Record of the 2004 IEEE International Symposium on Electrical Insulation, Indianapolis, IN, USA, 19–22 September 2004; pp. 300–303. [Google Scholar]
- Chaudhuri, S.P.; Sarkar, P. Dielectric behavior of porcelain in relation to constitution. Ceram. Int. 2000, 26, 865–875. [Google Scholar] [CrossRef]
- Mishra, A.P.; Gorur, R.S.; Venkataraman, S.; Kingsbury, D. Condition assessment of porcelain and toughened glass insulators from residual strength tests. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Kansas City, MO, USA, 15–18 October 2006; pp. 413–416. [Google Scholar]
- Gorur, R.S.; Shaffner, D.; Clark, W.; Vinson, R.; Ruff, D. Utilities Share Their Insulator Field Experience. Transm. Distrib. World 2005, 57, 17–27. [Google Scholar]
- Meng, Y.; Gong, G.; Wu, Z.; Yin, Z.; Xie, Y.; Liu, S. Fabrication and microstructure investigation of ultra-high-strength porcelain insulator. J. Eur. Ceram. Soc. 2012, 32, 3043–3049. [Google Scholar] [CrossRef]
- Hettich, P.; Schell, K.G.; Oberacker, R.; Bucharsky, E.C.; Schulte Fischedick, J.; Hoffmann, M.J. Failure behavior of high performance porcelain insulators. Mater. Sci. Eng. Technol. 2017, 48, 792–799. [Google Scholar] [CrossRef]
- Riahi Noori, N.; Sarraf Mamoory, R.; Mehraeen, S. Effect of Materials Design on Properties of Porcelain Insulators. Am. Ceram. Soc. Bull. 2007, 86, 9201–9205. [Google Scholar]
- Cho, H.G.; Han, S.W.; Park, K.H.; Han, D.H. Ageing Characteristics of Porcelain Suspension Insulators for Transmission Line by Cool and Heat Accelerate Method. In Proceedings of the 7th International Conference on Properties and Applications of Dielectric Materials, Nagoya, Japan, 1–5 June 2003; pp. 161–167. [Google Scholar]
- Han, S.W.; Cho, H.G. A study on electrical and mechanical simulation for designing porcelain insulators with high strength. In Proceedings of the ICEE 2002 Proceeding, Jeju, Korea, 14–17 June 2002; Volume 13, pp. 1191–1194. [Google Scholar]
- Pivaa, R.H.; Vilarinhob, P.; Morellic, M.R.; Fiorid, M.A.; Montedod, O.R.K. Influence of Fe2O3 content on the dielectric behavior of aluminous porcelain insulators. Ceram. Int. 2013, 39, 7323–7330. [Google Scholar] [CrossRef]
- Schulte-Fischedick, J.; Singh, P.; Lehretz, F.; Hettich, P.; Bucharsky, C.; Schell, G.; Hoffmann, M.J.; Marthen, W.; Wekenborg, H.; Pohlmann, H. Materials Based Lifetime Assessment of Porcelain Insulators. In The International Symposium on High Voltage Engineering ISH, Proceedings of the 21st International Symposium on High Voltage Engineering; Springer: Berlin/Heidelberg, Germany, 2019; Volume 599, pp. 528–539. [Google Scholar]
- Choi, I.; Kim, T.; Yoon, Y.; Yi, J.; Kim, S. Lifetime Assessments on 154 kV Transmission Porcelain Insulators with a Bayesian Approach. Korean Inst. Electr. Electron. Mater. Eng. 2017, 30, 551–557. [Google Scholar]
- Rawat, A.; Gorur, R.S. Microstructure based evaluation of field aged and new porcelain suspension insulators. IEEE Trans. Electr. Insul. 2009, 16, 107–115. [Google Scholar] [CrossRef]
- Baker, A.C.; Bernstorf, R.A.; Cherney, E.A.; Gorur, R.S.; Hill, R.J.; Lodi, Z.; Marra, S.; Powell, D.G.; Schwalm, A.E.; Shaffner, D.H.; et al. High voltage insulators mechanical load limits—Part I: Overhead line load and strength requirements. IEEE Trans. Power Del. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Abernethy, R. An Overview of Weibull Analysis, 5th ed.; Robert Abernethy: West Palm Beach, FL, USA, 1983; pp. 1–11. [Google Scholar]
- Se-Won, H.; In-Hyuk, C.; Dong-ll, L. Accelerating Aging of Transmission Line Porcelain Suspension Insulators by Autoclaving. In Proceedings of the Electrical Insulation Conference and Electrical Manufacturing Expo, Nashville, TN, USA, 22–24 October 2007; pp. 114–117. [Google Scholar]
- Cherney, E.A.; Baker, A.C.; Kuffel, J.; Lodi, Z.; Phillips. A.; Powell, D.G.; Stewart, G.A. Evaluation of and Replacement Strategies for Aged High Voltage Porcelain Suspension-Type Insulators. IEEE Trans. Power Del. 2014, 29, 275–282. [Google Scholar] [CrossRef]
- Baker, A.C.; Bernstorf, R.A.; Cherney, E.A.; Gorur, R.S.; Hill, R.J.; Lodi, Z.; Marra, S.; Powell, D.G.; Schwalm, A.E.; Shaffner, D.H.; et al. High voltage insulators mechanical load limits—Part II: Standards and recommendations. IEEE Trans. Power Del. 2012, 27, 2342–2349. [Google Scholar] [CrossRef]
- Han, S.-W.; Cho, H.-G.; Choi, I.-H.; Lee, D.-I. Failure Characteristics of Suspension-Type Porcelain Insulators on a 154kV Transmission Line. In Proceedings of the IEEE International Symposium on Electrical Insulation, Toronto, ON, Canada, 11–14 June 2006; pp. 118–121. [Google Scholar]
- ANSI/IEEE Std930. IEEE Guide for the Statistical Analysis of Electrical Insulation Voltage Endurance Data; IEEE: Piscataway, NJ, USA, 1987. [Google Scholar]



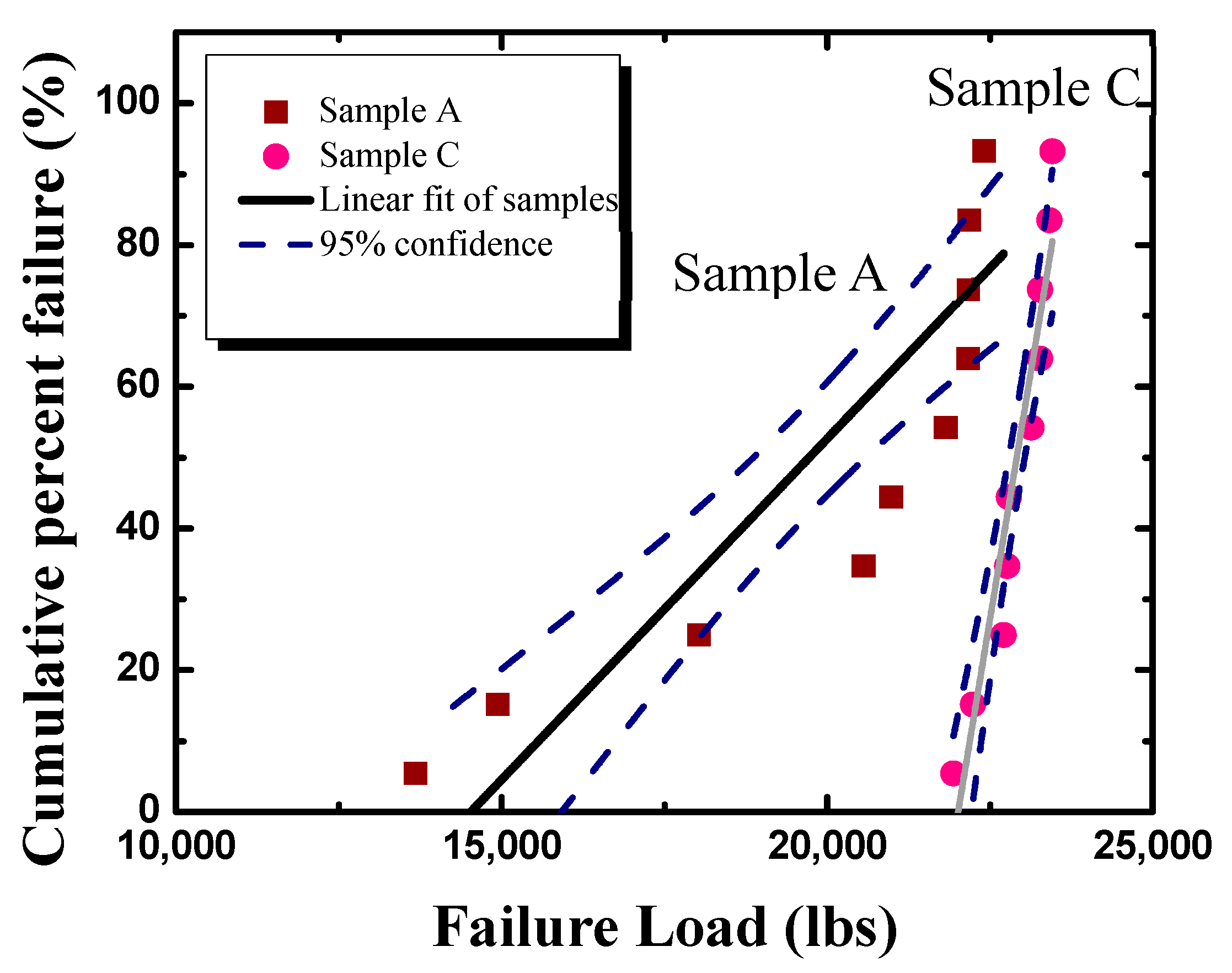
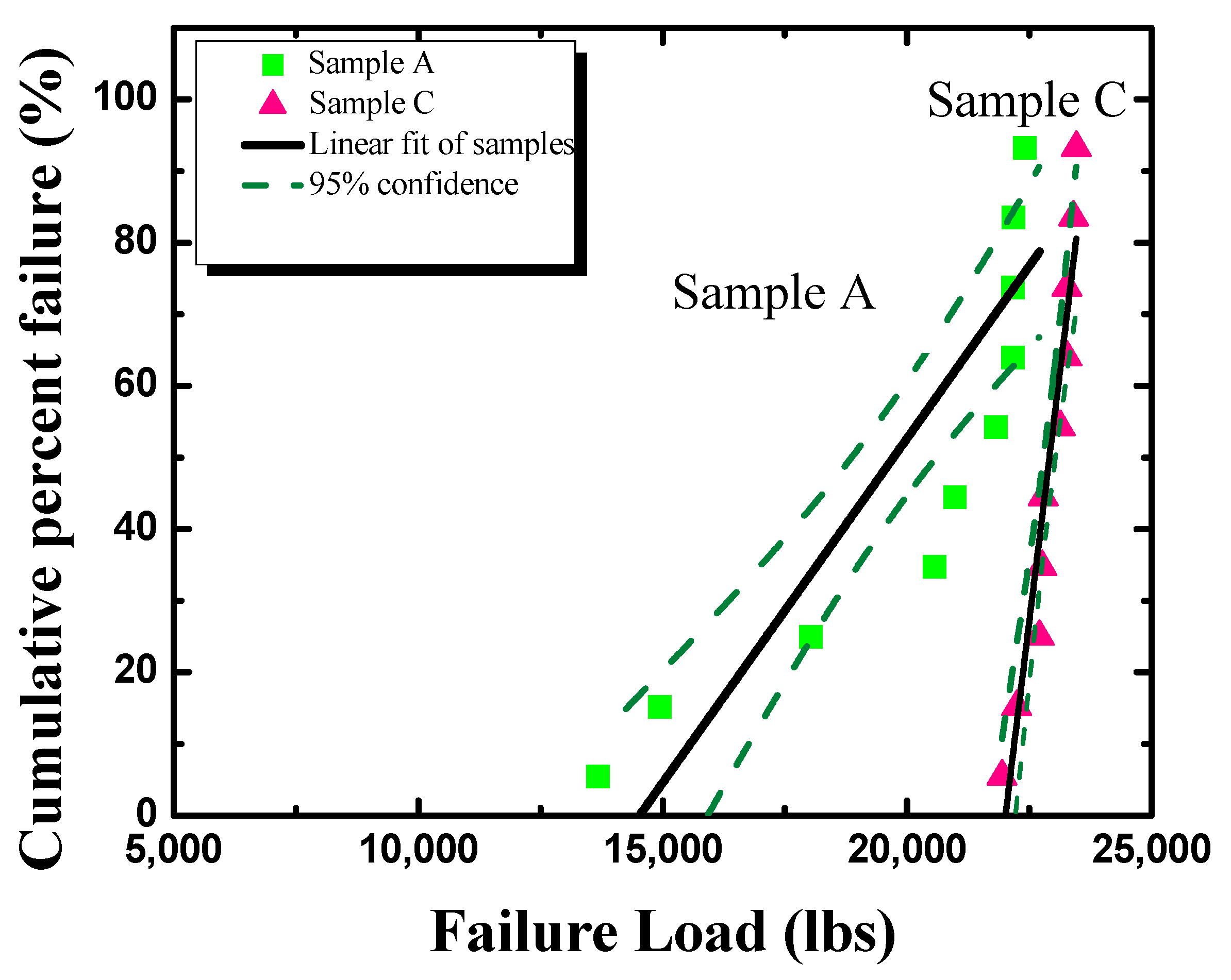
| Insulator I | Failure Load (lbs) | |||||
|---|---|---|---|---|---|---|
| Sample A (1975) | Remarks | Sample B (1995) | Remarks | Sample C (2005) | Remarks | |
| 1 | 20,980 | Neck | 22,960 | Pin | 22,760 | Pin |
| 2 | 20,560 | Neck | 22,400 | Pin | 22,240 | Pin |
| 3 | 22,160 | Pin | 23,100 | Pin | 23,460 | Pin |
| 4 | 21,820 | Pin | 22,710 | Pin | 22,710 | Pin |
| 5 | 22,180 | Pin | 21,450 | Neck | 23,140 | Pin |
| 6 | 13,680 | Neck | 22,690 | Pin | 23,270 | Pin |
| 7 | 14,940 | Neck | 22,750 | Pin | 22,790 | Pin |
| 8 | 22,160 | Pin | 22,480 | Pin | 21,940 | Pin |
| 9 | 18,030 | Neck | 21,960 | Pin | 23,270 | Pin |
| 10 | 22,410 | Pin | 23,300 | Pin | 23,410 | Pin |
| Insulator ID | Failure Load (lbs) | |||||
|---|---|---|---|---|---|---|
| Sample A (1975) | Remarks | Sample B (1995) | Remarks | Sample C (2005) | Remarks | |
| 1 | 21,020 | Neck | 22,450 | Pin | 22,740 | Pin |
| 2 | 19,080 | Neck | 22,180 | Pin | 22,490 | Pin |
| 3 | 22,250 | Pin | 22,530 | Pin | 22,380 | Neck |
| 4 | 19,910 | Neck | 21,780 | Pin | 22,580 | Pin |
| 5 | 20,750 | Neck | 22,140 | Pin | 22,940 | Pin |
| 6 | 22,220 | Pin | 22,710 | Pin | 21,200 | Pin |
| 7 | 14,250 | Neck | 19,780 | Pin | 22,880 | Pin |
| 8 | 15,300 | Neck | 21,640 | Pin | 23,120 | Pin |
| 9 | 19,070 | Neck | 22,240 | Pin | 21,790 | Pin |
| 10 | 22,710 | Neck | 22,420 | Pin | 22,580 | Pin |
| Constituents (wt.%) | 1975 | 1995 | 2005 |
|---|---|---|---|
| SiO2 | 64.82 | 58.77 | 59.03 |
| Al2O3 | 30.56 | 35.22 | 35.52 |
| CaO | 0.76 | 0.25 | 0.54 |
| MgO | 0.25 | 1.01 | 0.98 |
| Fe2O3 | 0.82 | 0.33 | 0.22 |
| TiO2 | 0.45 | 0.17 | 0.41 |
| Na2O | 1.56 | 1.87 | 1.76 |
| K2O | 1.83 | 1.96 | 1.54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanyal, S.; Kim, T.; Yi, J.; Koo, J.-B.; Son, J.-A.; Choi, I.-H. Failure Trends of High-Voltage Porcelain Insulators Depending on the Constituents of the Porcelain. Appl. Sci. 2020, 10, 694. https://doi.org/10.3390/app10020694
Sanyal S, Kim T, Yi J, Koo J-B, Son J-A, Choi I-H. Failure Trends of High-Voltage Porcelain Insulators Depending on the Constituents of the Porcelain. Applied Sciences. 2020; 10(2):694. https://doi.org/10.3390/app10020694
Chicago/Turabian StyleSanyal, Simpy, Taeyong Kim, Junsin Yi, Ja-Bin Koo, Ju-Am Son, and In-Hyuk Choi. 2020. "Failure Trends of High-Voltage Porcelain Insulators Depending on the Constituents of the Porcelain" Applied Sciences 10, no. 2: 694. https://doi.org/10.3390/app10020694
APA StyleSanyal, S., Kim, T., Yi, J., Koo, J.-B., Son, J.-A., & Choi, I.-H. (2020). Failure Trends of High-Voltage Porcelain Insulators Depending on the Constituents of the Porcelain. Applied Sciences, 10(2), 694. https://doi.org/10.3390/app10020694





