1. Introduction
Reciprocating compressors are key equipment most commonly used in oil extraction, gas production, oil refining, chemical industries, refrigeration, and gas transmission. The rated capacity of the reciprocating compressor is fixed, which was determined at the time of design. However, the actual demand is lower than the rated capacity of the compressor due to a change in the production process or an insufficient air source; therefore, the capacity of compressor needs to be adjusted. However, the capacity of the compressor is usually regulated by means of bypass backflow which results in a large amount of wasted energy. In order to solve the problem of the reciprocating compressor’s high energy waste, many capacity regulation methods for reciprocating compressors have been developed, including intermittent operation of the compressor, a suction-gas throttling scheme, a compressed-gas by-pass scheme, and a cylinder unloading scheme [
1]. These technologies have their own disadvantages and suitable application conditions. With the advantages of a wide, adjustable range and high energy savings, the method of controlling the suction valve has become the most popular method to solve the reciprocating compressor’s high energy consumption.
In his invention which relates to a system for the infinitely variable capacity control of compressors, Richard first proposed the compressor capacity control method based on controlling the suction valve in 1966 [
2]. In the literature [
3,
4], a mathematical model was established to theoretically deduce the principle and the method of capacity regulation for reciprocating compressors. In addition, a stepless capacity regulation system (SCRS) for reciprocating compressors was designed based on the regulation method of suction valve unloading. The movement rule of the inlet valve plate, the cylinder’s thermodynamic characteristics, and the system dynamic characteristics were essentially analyzed under variable load conditions based on the system [
5,
6,
7,
8]. Li et al. took the influence of variable load conditions on the compressor’s mechanical characteristics into account. The variation rules of some important parameters of compressor were analyzed and compared under different load conditions, such as piston rod stress and reversal angle [
9].
Other researchers also focused on the joint modeling of a reciprocating compressor equipped with the SCRS and on the optimization of operating parameters. Wang et al. presented a modified reciprocating compressor model to analyze the suction valve plate movement rule under variable load. Some important parameters of SCRS, such as unloader speed, unloader displacement, and oil pressure, were optimized [
10]. The influence of key design parameters of the SCRS, such as oil pressure, stiffness of the unloader reset spring, hydraulic cylinder diameter, and flow diameter of the solenoid valve, on the motion characteristics of the inlet valve were analyzed with the help of the proposed model coupling a hydraulic actuator and a compressor [
11]. The optimized operating parameters made the system have higher security, economy, and reliability at the beginning of the system’s operation. However, the influence of the parameter changes due to the degradation of system components in long-term operation on the system regulation performance had not been considered.
Nevertheless, investigating the field application of SCRS, the regulation failure and (or) performance degradation often occurred in long-term operation. The failure of capacity regulation extremely affected the safe and stable operation of the reciprocating compressor. According to statistics, there are many factors that affect the regulation performance of the system. The main factors and their effects are listed in
Table 1. Among these factors, the most commonly encountered factors include valve leakage, deviation of the solenoid valve’s characteristics, and degradation of the unloader reset spring. An electro-hydraulic actuator is a high frequency action part, and its action frequency is directly related to the compressor speed. The high frequency action inevitably leads to the fatigue degradation of the reset spring of the unloader in long-term operation. The solenoid valve dynamic characteristics also offset due to continuous charging and discharging. Unfortunately, since the SCRS is a complex system with mechanical, electrical, and hydraulic coupling, the characteristic parameters of the reset spring and solenoid valve cannot be directly measured during system operation. Therefore, if there is a decrease in system regulation performance, it is extremely challenging, even impossible, to locate the fault through the technical method of single factor analysis.
To address this issue, it is necessary to study the influence law between the system regulation performance and each coupling component and explore the degradation law of system performance caused by valve leakage, characteristic parameter deviation of the solenoid valve, and reset spring stiffness degradation. Therefore, this paper develops a multi-subsystem coupling model to analyze the relationship between the system regulation performance and the parameters of each component.
Some research has been done on system modeling. Liu et al. proposed a mathematical model that is coupled with a control system, hydraulic system, actuator, buffer tank, and other components [
12]. However, the coupling model did not take the influence of the gas pipeline between compressor and buffer tank and the valve leakage into account. The opening and closing processes of the solenoid valve were also ignored. Based on the coupling multi-system model established in [
12], an improved multi-subsystem integrated mathematical model, including compressor, gas pipeline, buffer tank, and actuator, was established, which took the solenoid valve dynamics and valve leakage into consideration.
Here, the framework of degradation-based optimization (DBO) was developed. The flow diagram of the developed DBO framework for SCRS is shown in
Figure 1. In the operation of the SCRS, the load prediction model predicts the actual load of the compressor, and the degradation model calculates the degradation rate of the system based on the prediction results. At the initial time, the degradation rate of the system was very low and close to zero. With the degradation of the system’s regulating performance, the degradation rate gradually increased. The adaptive optimization compensation model generates control parameter compensation to compensate for the degraded part, which minimizes the degradation rate of the whole system and ensures the acceptable regulation accuracy and performance of the system.
The load prediction model is the most important part of the whole compensation-based optimization framework. Generally speaking, the load prediction model can be realized through mechanism modeling, but the mechanism model requires a large number of system structure parameters and process parameters which are not even measurable. Therefore, these models are unsuitable for engineering applications, especially in real-time control systems. Encouragingly, artificial neural networks (ANNs) have been widely used in reciprocating compressor modeling and system optimization due to their advantages of being adaptive, self-learning, and fault-tolerant and working with nonlinear mapping. Belman et al. set up a physical mechanism model and an artificial neural network model of a reciprocating compressor, respectively, with an experimental refrigeration device as the research object and analyzed and compared these models through parameters such as exhaust volume, exhaust temperature, and energy consumption [
13]. Barroso-Maldonado et al. developed two models: one using an artificial neural network and another one using a probabilistic neural network to predict and simulate the behavior of a reciprocating compressor [
14]. The artificial neural network models for the non-injection, vapor injection, and two-phase injection heat pumps were developed to predict the performance indexes during cooling and heating seasons [
15]. An ANN was trained and validated with the experimental data and the same was proposed for the predicting performance of a work recovery scroll expander in closed-loop operation with a CO
2 refrigeration system in the sub-critical zone [
16]. In addition, artificial neural networks are also widely used in parameter and system optimization. Mohammadi et al. assigned an ANN to investigate a logical interaction among dependent and independent variables and to define a cost function based on the empirical data; then the function was optimized by Genetic Algorithm to determine the best amount for each parameter [
17]. A hybrid ANN model was trained as well as tested with experimental data sampled from statistical methods, and the model was used to predict the optimal process parameters of injection molding process of a bi-aspheric lens [
18].
Hence, this study proposes an ANN-based model to predict the load of a compressor for evaluating the degradation rate of the SCRS. Although various methods have been developed to improve the prediction accuracy of ANN models, a back propagation (BP) neural network is still one of the most popular techniques in this field [
19]. A gradient descent algorithm is usually used in a typical BP neural network. However, the typical BP neural network has the limitation of slow convergence speed and is easy to fall into a local extremum. As is well known, the particle swarm optimization (PSO) has the advantages of good global search capability and fast convergence speed. Therefore, PSO is used to optimize the initial connection weight and threshold of BP neural networks. Comparing an ANN model with and without PSO, the prediction error of an ANN model with PSO is lower than without using PSO. Since the optimization is a steady-state optimization, an adaptive optimization method based on the degradation rate is proposed to avoid the over-optimization caused by the load prediction error.
In this work, a multi-subsystem coupling mathematical model including compressor, gas pipeline, buffer tank, actuators, and other components is developed to study the performance degradation law of the SCRS caused by changes in the actuator’s dynamic characteristic parameters and valve leakage. Then the degraded performance of the SCRS is optimized based on the developed DBO framework. The objective of performance optimization is to minimize the degradation rate of the SCRS. The key outcomes resulting from the proposed DBO framework are the control parameter compensation which leads the SCRS to operate at minimum degradation rate and to guarantee acceptable regulation accuracy. The effectiveness of the proposed DBO framework was verified by the implementation results.
This paper is organized as follows:
Section 2 introduces the composition and working principle of the SCRS.
Section 3 describes the multi-subsystem coupling model. The law of performance degradation is analyzed in
Section 4.
Section 5 provides the load prediction model based on improved PSO-BP and proposes an optimization method. The model prediction accuracy and implementation results of the proposed optimization method are also discussed in
Section 5. Finally,
Section 6 concludes the paper.
2. System Description
The basic principle of capacity regulation of a reciprocating compressor is that the movement of the suction valve is controlled by external forces which delay its closure [
6]. A part or all of the gas in the cylinder flows back to the inlet line before it is compressed, and only the required gas is compressed. The power consumption and actual volume gas are directly proportional [
1]. Therefore, the power consumption of the compressor is reduced when it is not under full load.
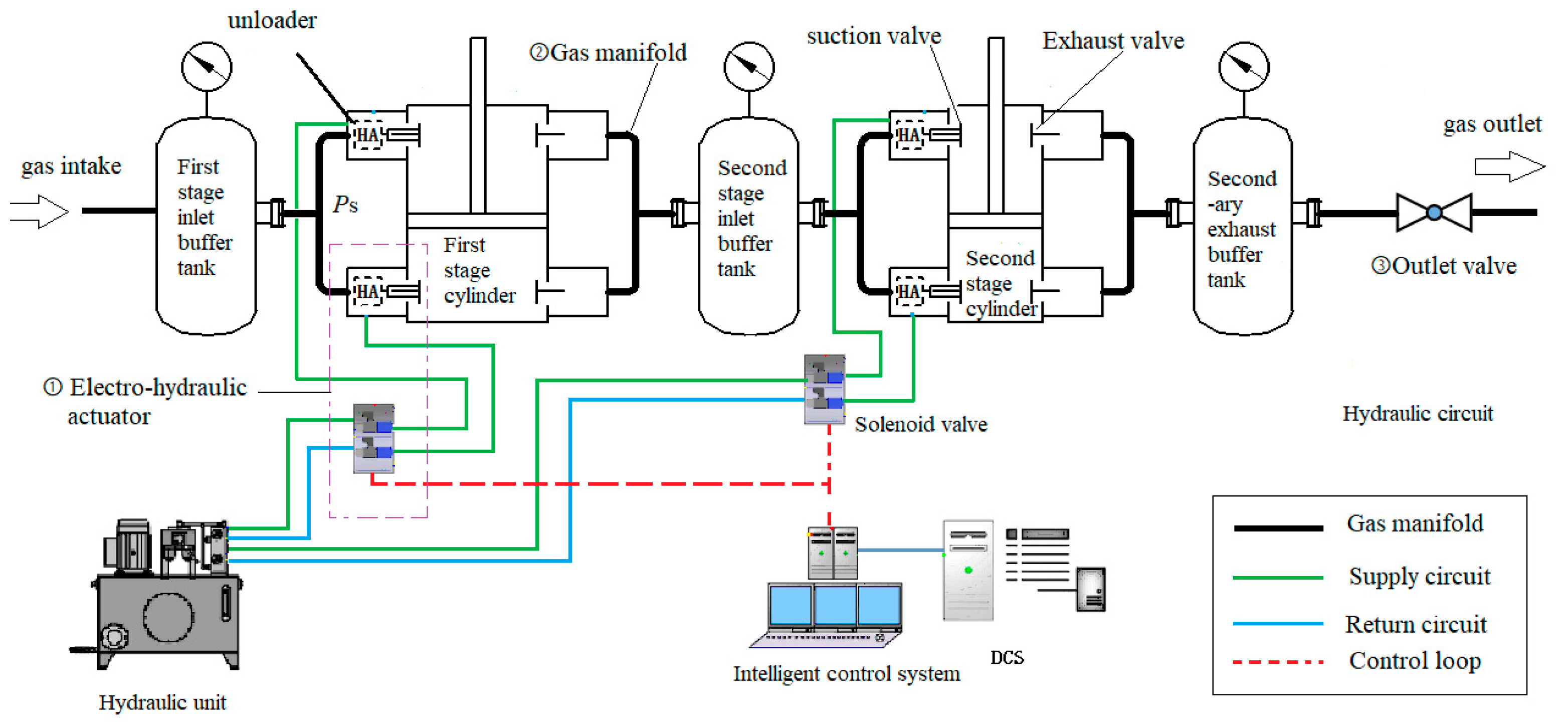
The reciprocating compressor pressure system with SCRS can be called the variable capacity reciprocating compressor pressure system (VCRCPS). The VCRCPS consists of a reciprocating compressor, buffer tanks, an outlet valve, and a SCRS which is integrated with a hydraulic system, an intelligent control system, and an electro-hydraulic actuator, as shown in
Figure 2. The gas is compressed by a reciprocating compressor to realize a pressure boost. The hydraulic system provides the hydraulic driving force. The intelligent control system records the exhaust pressure, temperature, and the signal of the top dead center (TDC) of the compressor to calculate the load and output-corresponding control signal. The electro-hydraulic actuator responds according to the control signal to make part of the gas return into the inlet line without compressing, so as to realize capacity regulation.
The object studied in this paper is a two-stage reciprocating compressor with SCRS, as shown in
Figure 3, including a control system, hydraulic system, gas pipeline, buffer tank, electro-hydraulic actuator, etc. The main operating parameters are listed in
Table 2.
The load regulation experiments were carried out on the test bench to verify the modified multi-subsystem mathematical model. The performance optimization method proposed in this paper was also verified on this test bench.
5. Prediction Modeling and System Optimization
Fortunately, by studying the dynamic characteristics and the degradation law of the system and combining the actual operation experience, it is found that there are corresponding relations among exhaust flow, inlet and outlet pressure, inlet temperature, and compressor load. The load prediction model can be constructed by using the inlet and outlet pressure , the inlet and outlet temperature , and the exhaust flow Q. Under capacity regulation condition, the performance of the SCRS can be predicted, and the estimated value of the actual operating load of the cylinder can be obtained. Through the estimated value of the load , the control parameters of the SCRS can be optimized online.
5.1. Load Predicting Model
A BP neural network is an artificial neural network based on a back-propagation learning algorithm, which is the main component of an artificial neural network [
24]. Most of the existing BP neural network models are variations or improvements of the standard BP neural network model. In this study, the improved PSO-BP neural network is used to build the load prediction model. The structure of the prediction model is illustrated in
Figure 16. The initial thresholds and weights of the BP neural network are obtained through PSO optimization. Then the improved BP neural network is trained. The flow chart is plotted in
Figure 17.
The particle swarm optimization (PSO) algorithm presents an efficient technique for solving optimization problems, especially the problem of a non-differentiable function where it is hard to find the optimum. PSO is a swarm intelligence algorithm inspired by the foraging behavior of birds. The position and the velocity of the population members are calculated by using a mathematical operator so they can be expected to head toward the best solution. The updating operation is defined as follows:
where
presents the inertia weight,
is the initial weight,
is the inertia weight when the iteration reaches the maximum number,
is the maximum number of iterations,
and
c2 are positive constant parameters usually in the range of [0 2] called acceleration coefficients and known also as the cognitive and collective parameters,
is the adaptive descending factor of the optimal solution of individual history, and its value is in the range of [0 1],
r1 and
r2 are random variables generated for each velocity update between [0 1],
is the velocity of the
ith particle at each iteration
k, and
xi(
k) is the position of the
ith the particle at each iteration
k. In order to prevent the particle from searching blindly, the position and speed of the particle are limited as follows:
where
is maximum rate of velocity of particle,
is minimum rate of velocity of particle, and
and
are minimum and maximum position values, respectively. Last,
denotes the local best position of the
ith particle at each iteration
k, and
defines the global best position at each iteration
k.
In the traditional BP neural network method, the selection of the learning rate depends on experience. If the selection is too small, the convergence rate will be slow. If the selection is too large, it will lead to oscillation or even divergence. For this problem, this paper applies the adaptive learning rate, which is expressed as follows.
where
is a symbolic function,
is the negative gradient of weight
of the index function at the time k, and
is the negative gradient at time
k − 1. As can be seen from Equation (18), when the gradient direction of two consecutive iterations is the same, the descent speed is too slow, and the learning rate can be doubled. When the gradient direction of two successive iterations is the opposite, the decreasing speed is too fast, and the learning rate can be halved to achieve an adaptive adjustment of the learning rate.
5.2. Testing the Performance of the ANN Models
Simulation experiments of different loads were carried out through the established multi-subsystem coupling model (15) and collected dynamic data of inlet temperature, pressure, and exhaust flow. Then the data on temperature, pressure, and flow were preprocessed under a stable state of each load segment. A total of 47 groups of experimental data were obtained and are listed in
Table 5. A total of 24 experimental data sets were selected as the training dataset, and the other 23 experimental data sets were used to test the ANN model. The conventional ANN model and the modified ANN model using PSO were both trained by the training data.
After a lot of trial and error, the initial fixed learning rate was selected as 0.2 and the number of hidden layers was eight. The particle cycle number was 60. The number of iterations was 40. During the training process, it was found that the BP neural network with PSO-optimized initial parameters converges faster. After the training process was completed, both ANN models were tested with the 23 experimental data sets. A prediction performance comparison of the ANN models with and without PSO is presented in this subsection.
Figure 18 displays the comparison of the test results of the conventional ANN model and the experimental data. It can be seen that the overall prediction trend is acceptable. To further evaluate the conventional ANN model, prediction errors are shown in
Figure 19. It can be concluded that the ANN model had high prediction errors at some points. As can be seen in
Figure 19a, the maximum prediction absolute error of the first-stage load ratio reached up to −0.12, and the maximum prediction absolute error of the second-stage load ratio was −0.1. Most of their absolute prediction errors were between −0.05 and 0.05.
Figure 19b indicates the relative prediction errors. It can be observed that their relative prediction errors were in the range of −12% to 8%.
To improve the prediction precision, particle swarm optimization is used to optimize the initial weight and threshold of the ANN model.
Figure 20 shows a comparison of ANN test results with PSO and experimental data. Compared with
Figure 18, ANN predictions with PSO matched better with the experimental data. Therefore, it can be concluded from
Figure 18 and
Figure 20 that the ANN model established in this work shows great robustness no matter whether PSO is adopted or not.
Figure 21 displays the prediction errors of the ANN model with PSO. It can be seen that the prediction errors of the ANN model with PSO were lower than without PSO, as shown in
Figure 21. Most of the absolute prediction errors of the ANN model with PSO were between −0.02 and 0.02, while the relative prediction errors ranged from −2% to 2%. Compared with the experimental data, the maximum relative error was less than 4%. Therefore, the proposed ANN model with PSO shows strong learning ability and good generalization performance and can be used to predict the power output of the capacity regulation system.
To verify the consistency of the optimization results, the conventional ANN model and the modified ANN model with PSO were trained repeatedly (five times). After each training, the test data were tested, and it was found that in different tests, the prediction deviation of the traditional ANN model was larger at some points, while the improved ANN model was close to the real value every time. Therefore, the optimization results show a good consistency.
5.3. Parametric Optimization Based on ANN Model
It is explained in
Section 3 that the capacity regulation system realizes the capacity regulation of the compressor by controlling the energizing time of the high-speed solenoid valve. The calculation formulas of the energizing time of solenoid valve are Equations (10) and (11). In order to facilitate the compensation optimization of control parameters, Equations (10) and (11) are converted into the following forms.
where
represents the output control signal, that is, the solenoid valve total energizing time,
T0, representing the shortest energized time of the solenoid valve, is determined by the initial response characteristic of the solenoid valve and the designed stiffness of the actuator spring and the phase of the actuator to complete the ejection action.
f (
η) is the relationship between the load and the increase in energized time and can be expressed as:
In order to realize system regulation optimization, the optimization compensation item is introduced into Equation (19) to overcome system regulation degradation caused by spring stiffness degradation or (and) changes in the dynamic characteristics of the electro-hydraulic actuator.
To obtain the system optimization compensation parameter
and to evaluate the degradation efficiency of the capacity regulation system, the deviation of the load was taken into account. To simplify the optimization objective, we computed the degradation rate of the SCRS as follows:
where
is the load feedback value which can be calculated by the ANN prediction model,
is the given load output to the actuator, and
m is the number of compressor stages. The optimization objective is the minimized degradation rate
E in (22). Since the optimization is a steady-state optimization, an adaptive optimization method based on the degradation rate of SCRS is proposed to reduce the over-optimization caused by the load prediction error. If the degradation rate is low, the compensation amount of the control signal is small, ensuring no over-optimization. On the contrary, when the degradation rate is high, a large amount of compensation is generated to accelerate the system performance recovery. Therefore, the following adaptive adjustment formula can be used to optimize control signal compensation.
where
is a constant that influences the speed of parameter optimization, and
E is the degradation rate. The parameter
can be adjusted according to the performance of the system optimization.
5.4. The Implementation Effect of the Optimization Method
In order to verify the proposed system parameter optimization method, two experimental tests were carried out on a two-stage reciprocating compressor test bench equipped with SCRS as shown in
Figure 3.
In order to accurately know the delayed closing phase of the valve plate, a displacement sensor was installed inside the actuator to test the real-time displacement of the valve plate which is extremely dangerous in practical applications and is not allowed.
Figure 22 shows the simulation of valve leakage by making leak holes into the suction valve plate. The comparison of the actuator response tested by the displacement sensor at different hydraulic oil temperatures is shown in
Figure 23. It was found that under the same control signal, the actuator’s response became faster as the temperature of the hydraulic oil increased. Therefore, it is possible to change the temperature of the hydraulic oil to replace the change in solenoid valve performance and spring stiffness to affect the system regulation performance.
Under the normal condition of the SCRS, the given load of the first and the second stage are both 80%. After the capacity regulation was stable, the operating condition of the SCRS was changed. The normal operation condition of the SCRS is that all valves have no leakage and the temperature of the hydraulic oil is 35 °C. The effectiveness of the optimization method was proved by the following two test experiments.
Experiment 1. Valve leaks in the first stage caused the hydraulic temperature driving the high-pressure stage actuator to rapidly drop from 35 to 25 °C. The optimization result was adjusted by adjusting the adaptive optimization parameter. In this study, the parameter was set as α = [0.6, 0.6].
Figure 24 shows that the system was in normal operation until point A, and the pressure of the first and the second exhaust buffer tank were stable at 251 kPa and 541 kPa, respectively. Leakage holes were made in the first-stage suction valve between point A and point B, and at the same time the second-stage hydraulic oil was rapidly cooled from 35 to 25 °C. When the steady-state point B was reached, the system optimization function started to work, and the adaptive control parameter compensations were generated. Similarly, the optimized compensations were generated at the stable point C and point D, respectively. The compensation amount and predicted load at different points are shown in
Table 6. Since the compensation amount was generated adaptively according to the degradation rate of the system, the compensation amount decreased with the decrease of the degradation rate. At point B, the system degradation rate was 12.28. With the help of optimization, the system degradation rate eventually decreased to 1.41, which is very close to 2.03 under normal conditions. The deviation between the final pressure at the optimized completion point E and the pressure under normal working conditions was 1 kPa. The adaptive optimization strategy ensured that there was no over-optimization in the case of errors in the load prediction, and the duration of the whole optimization was 50 s.
Experiment 2. The temperature of the hydraulic oil driving the low-pressure stage actuator increased rapidly from 35 to 45 °C, while the temperature of the hydraulic oil driving the high-pressure stage actuator decreased rapidly from 35 to 25 °C.
The temperature of the hydraulic oil was 35 °C under normal working conditions. The given load of the first and the second stage were both 80%, and the pressure in the steady state was 253 kPa and 543 kPa, respectively. The temperature of the hydraulic oil driving the first actuator was raised from 35 to 45 °C, and the temperature of the hydraulic oil driving the second actuator was lowered from 35 to 25 °C.
Figure 25 shows that the pressure of the first exhaust buffer tank rose rapidly, and the pressure of the second exhaust buffer tank rose slightly. When it reached the stable point B, the system started to optimize to overcome the load deviation caused by the change of hydraulic temperature. After repeated optimization, the pressure of the first-stage exhaust buffer tank decreased from 331 to 252 kPa and returned to the normal range. The results of multiple optimizations are shown in
Table 7. After optimizing twice, the degradation rate of the system decreased from the maximum 13.78 to 1.8, and the duration of the whole optimization was 60 s.
6. Conclusions
Aiming to overcome the performance degradation and the regulation accuracy decrease of SCRS for reciprocating compressors in long-term running processes, in this paper, the mathematical model of multi-subsystem coupling was established to analyze the key components and parameters that affect the regulating performance of the system, such as dynamic characteristics of the solenoid valve, reset spring stiffness, and valve leakage. The law of system performance degradation was obtained.
In order to restore the regulation performance and precision of the system when the system degenerates, firstly, the PSO-BP load prediction model was established, and the model was trained and tested with experimental data. The results show that the load prediction error of the improved PSO-BP model was less than 2%. The actual load of the compressor was predicted online by using steady state pressure, temperature, and flow rate, and the system degradation rate was calculated. A system control parameters compensation optimization method based on predictive load and system degradation rate was proposed. Secondly, in order to prevent overcompensation of the control parameters, an adaptive optimization compensation method was developed, and the compensation amount of the control parameters was adjusted adaptively according to the degradation rate. Finally, two system optimization experiments were set up, and the experimental results verified the feasibility and effectiveness of the compensation optimization method in this paper.
Therefore, the system compensation optimization framework proposed in this paper provides an effective solution to the field performance degradation of the stepless capacity regulating system for reciprocating compressors. However, this framework can be expanded to any other complex mechatronics system.