Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis
Abstract
1. Introduction
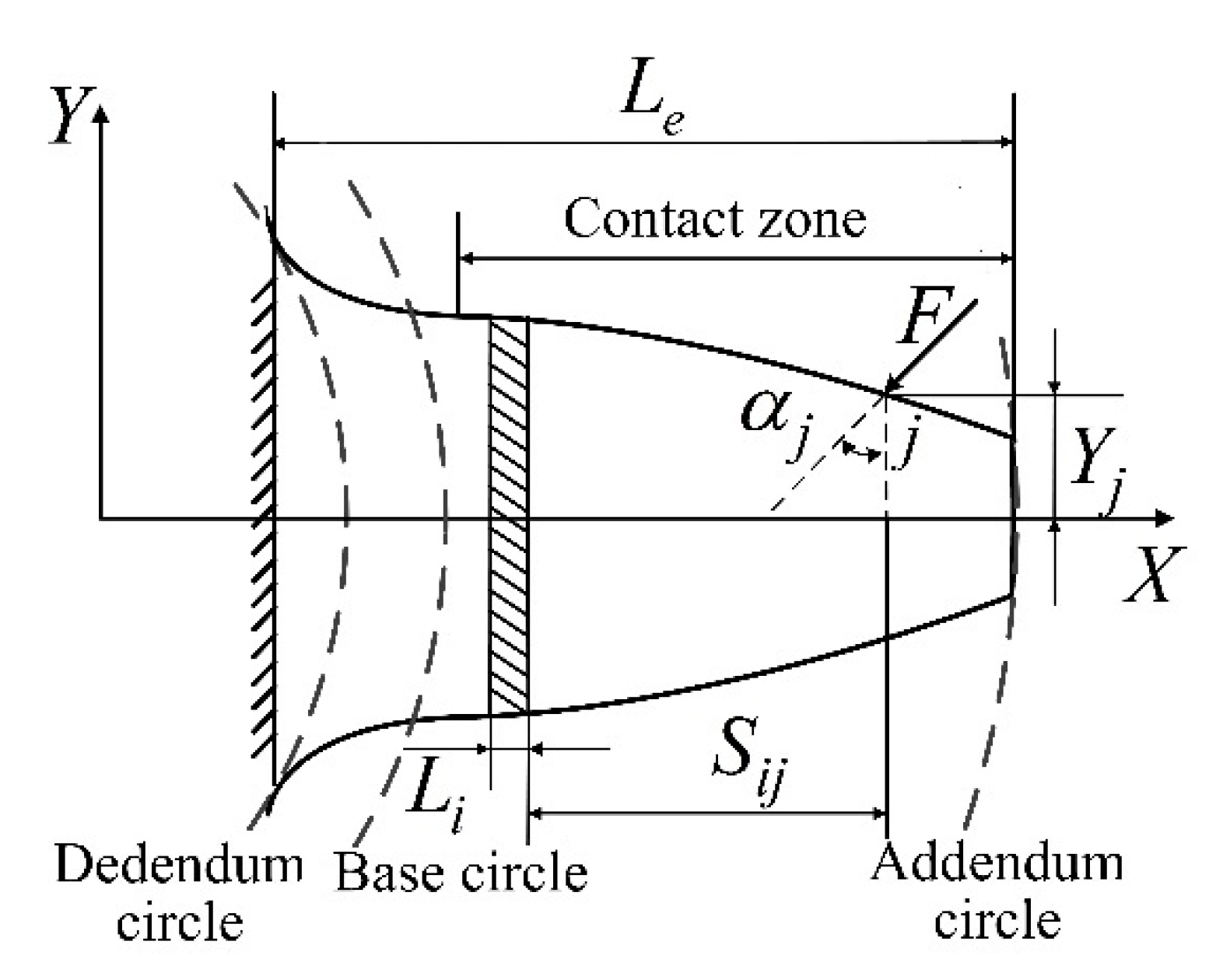
2. Mesh Stiffness Calculation of Gears
2.1. Mesh Stiffness Calculation of Gears with Healthy Teeth
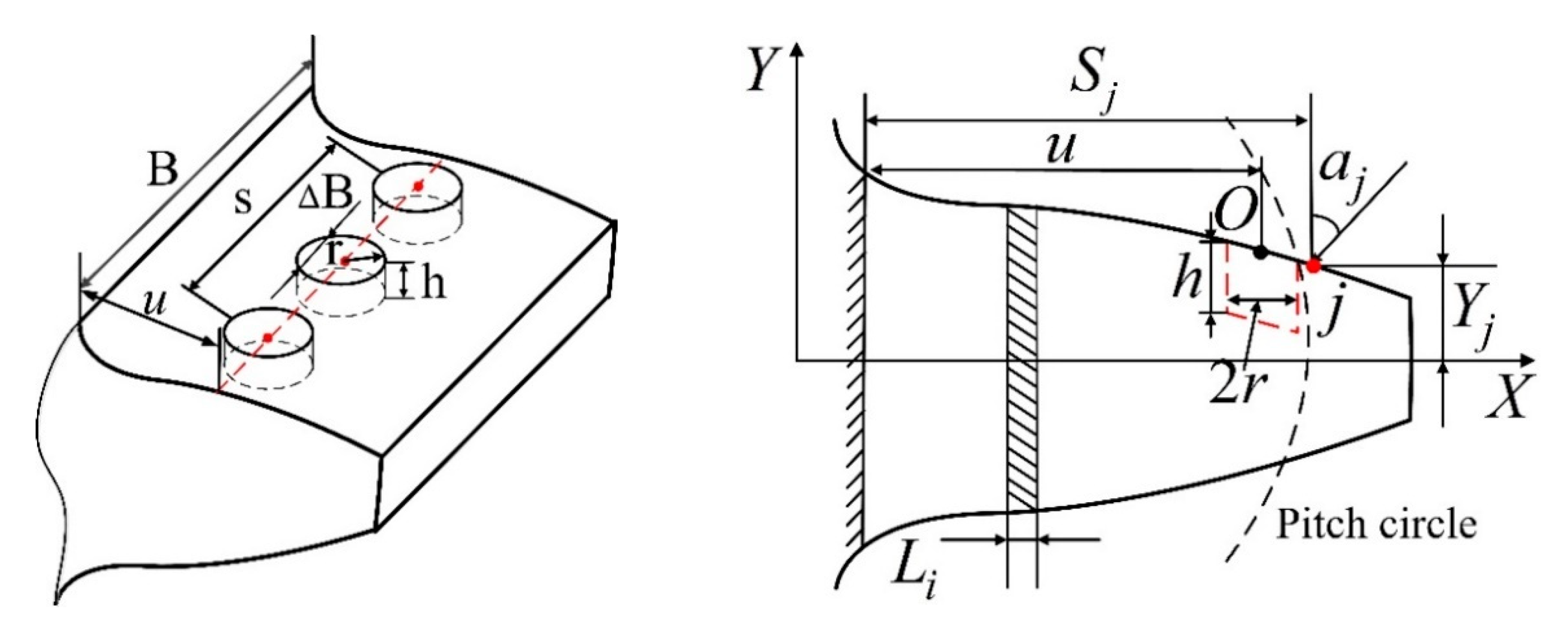
2.2. Mesh Stiffness Calculation of Gears with Tooth Spalling
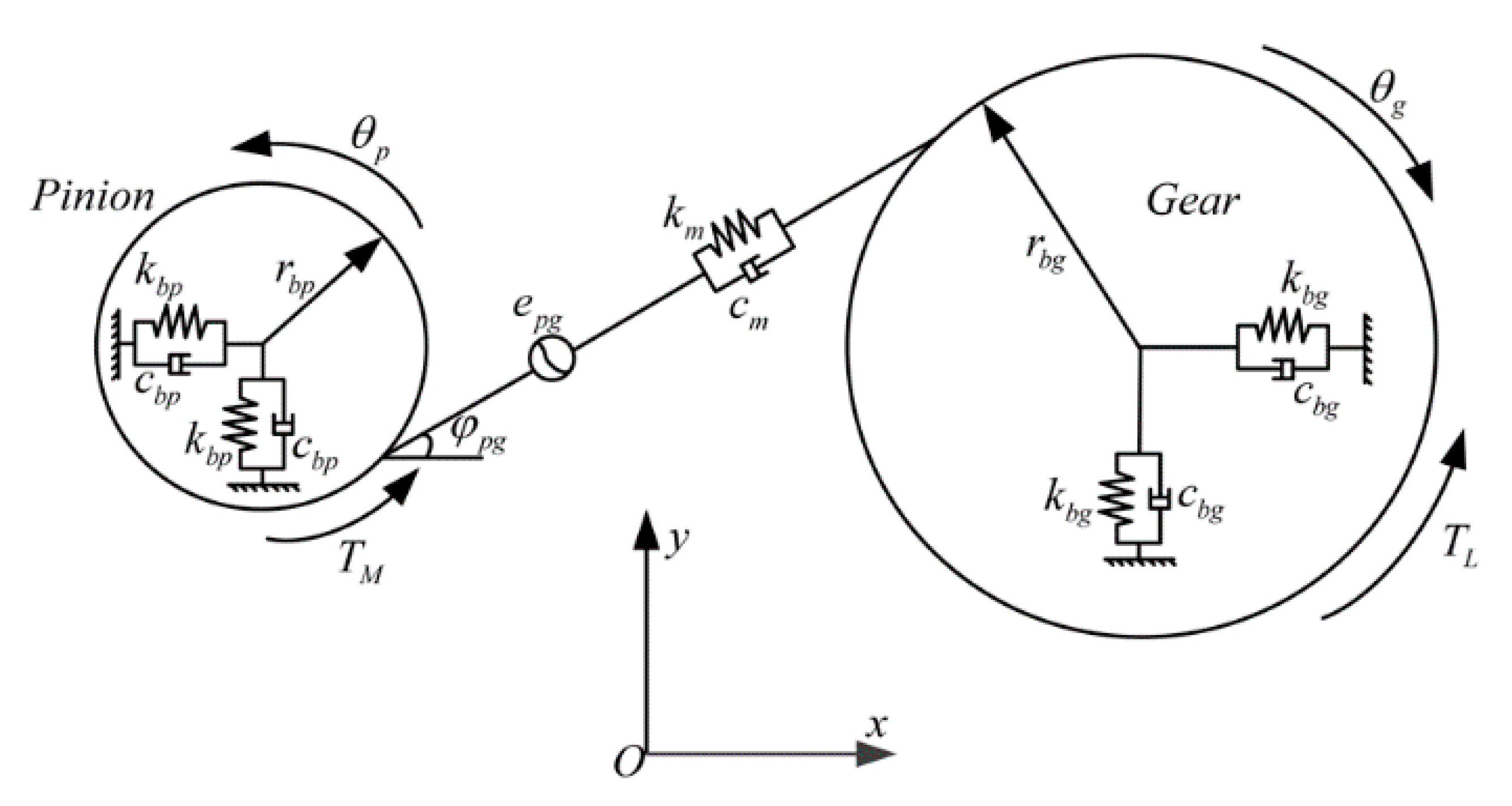
3. Dynamic Model of a Gear System
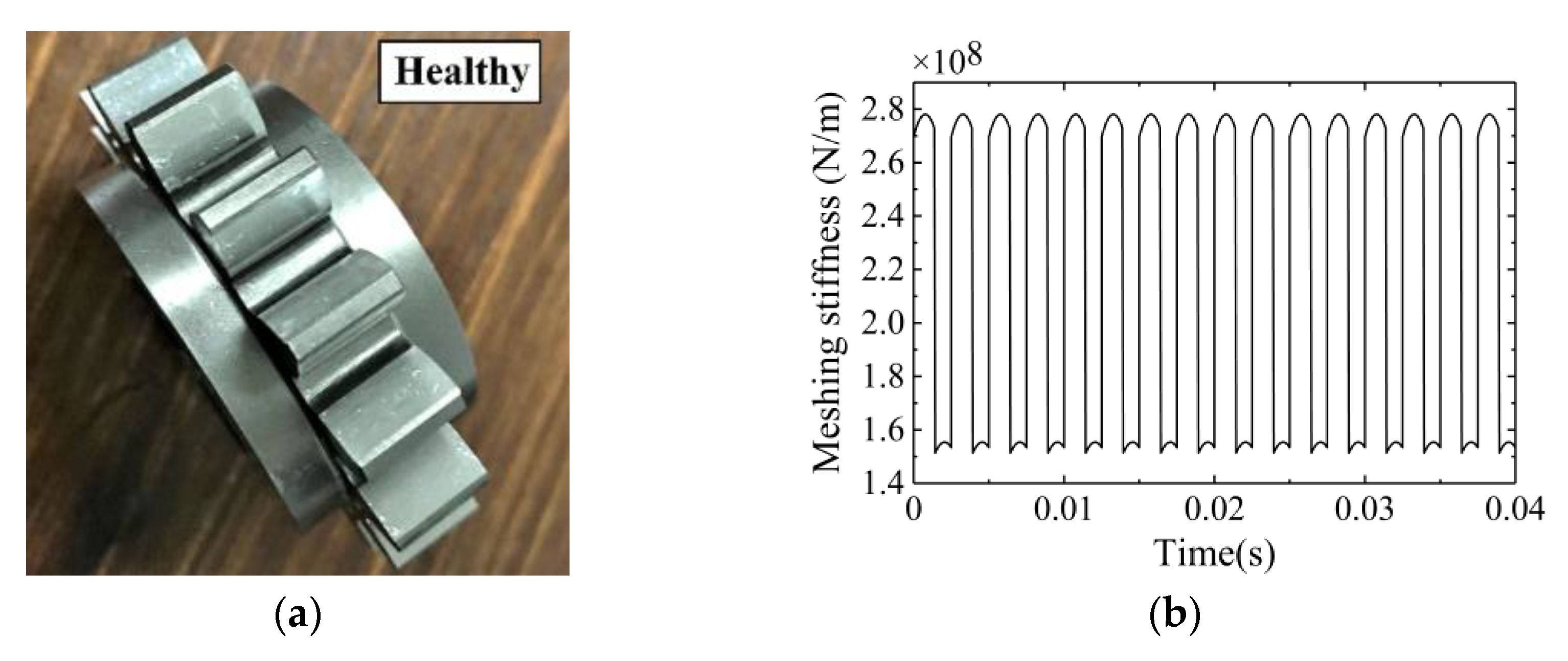
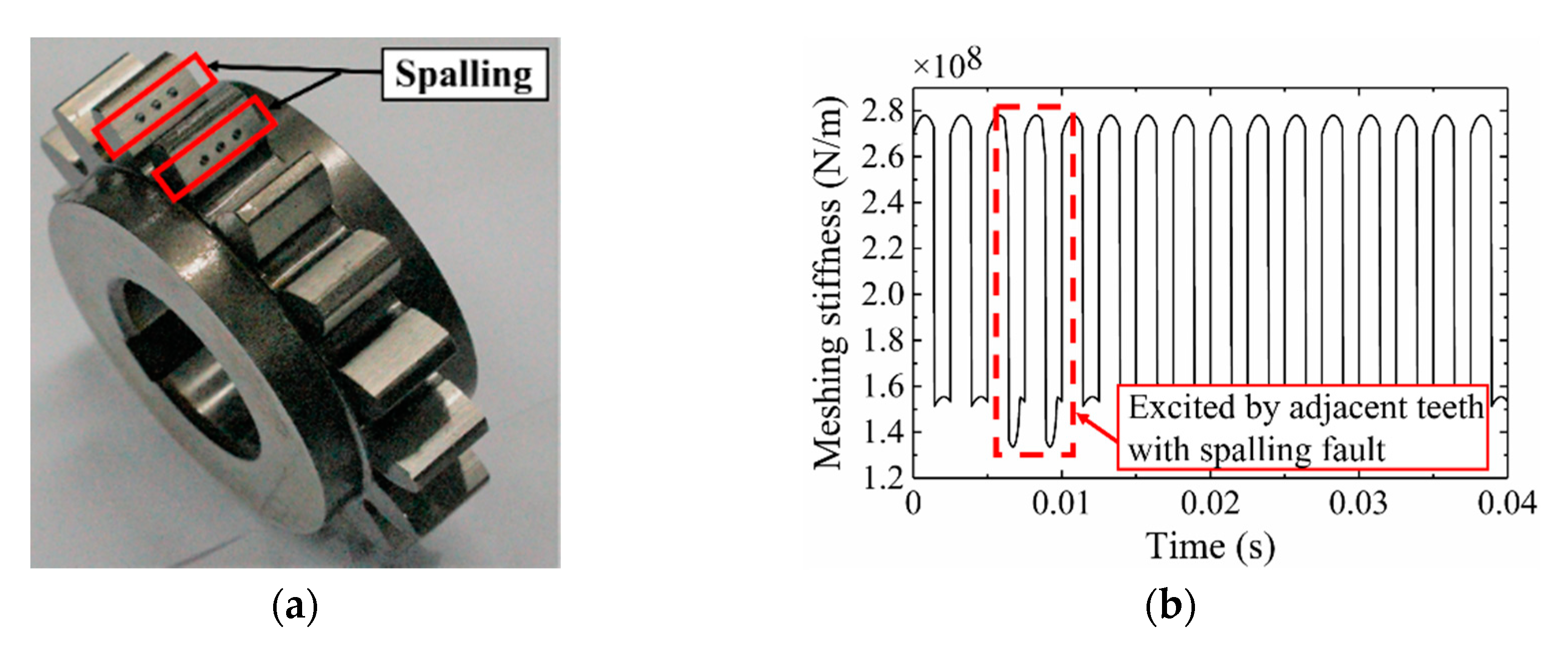
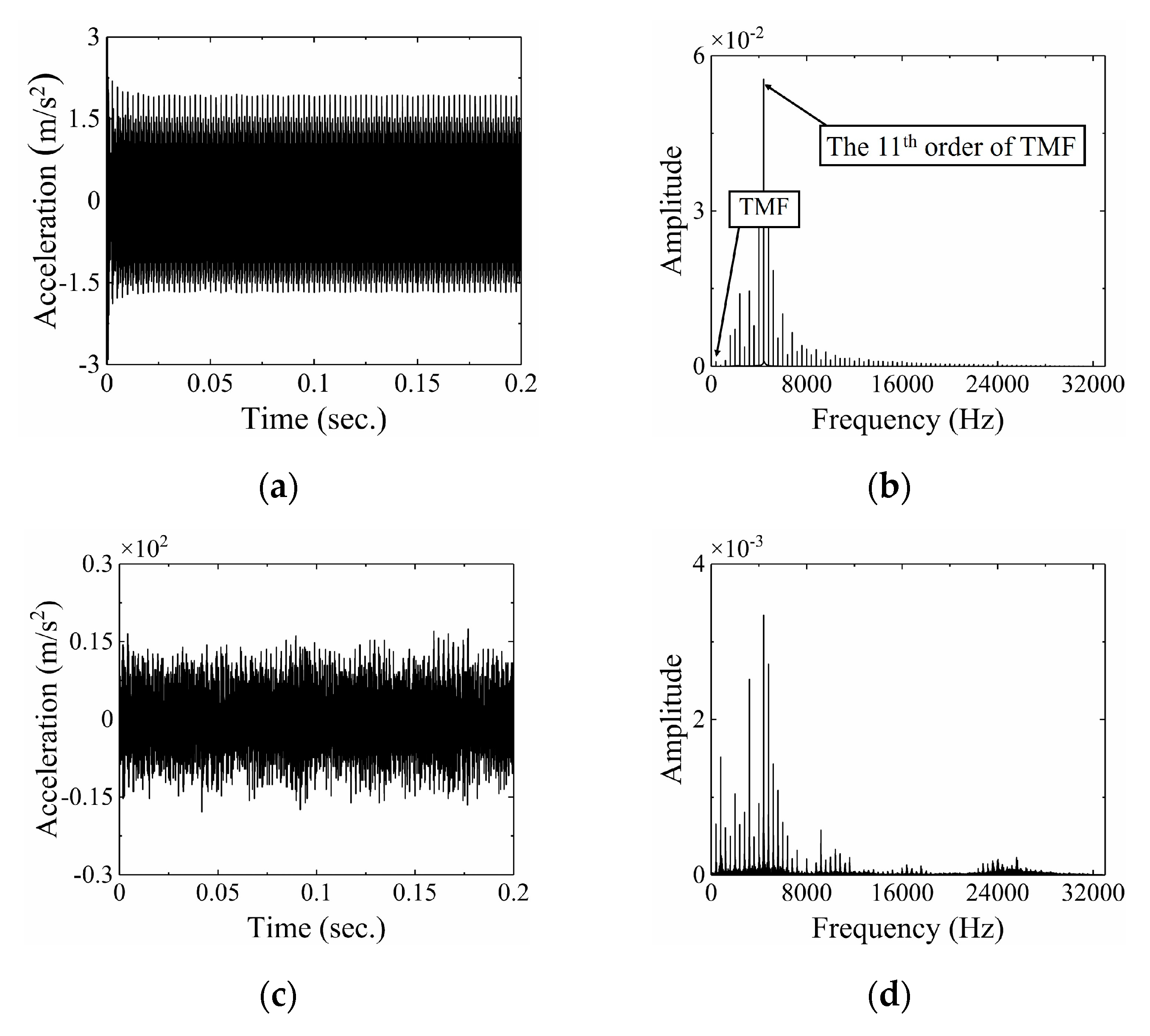
4. Dynamic Simulation and Experimental Verification
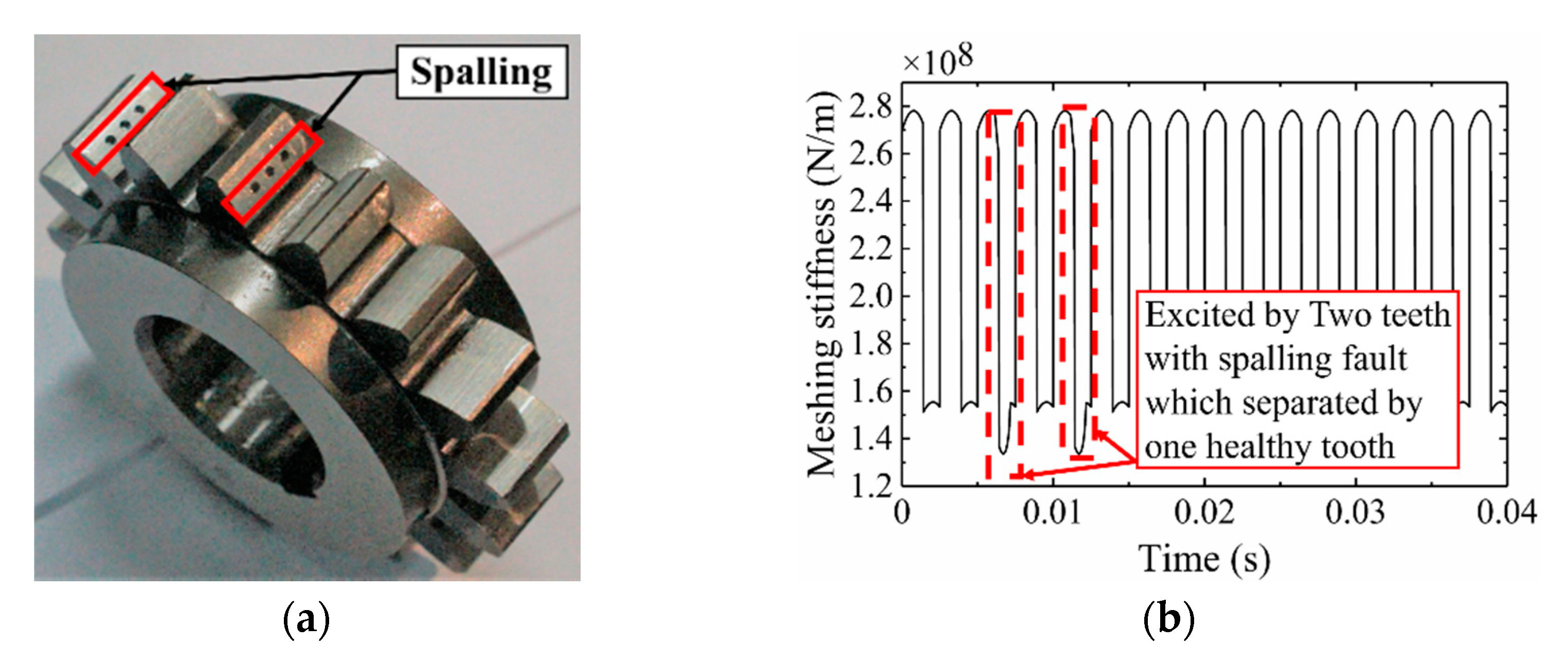
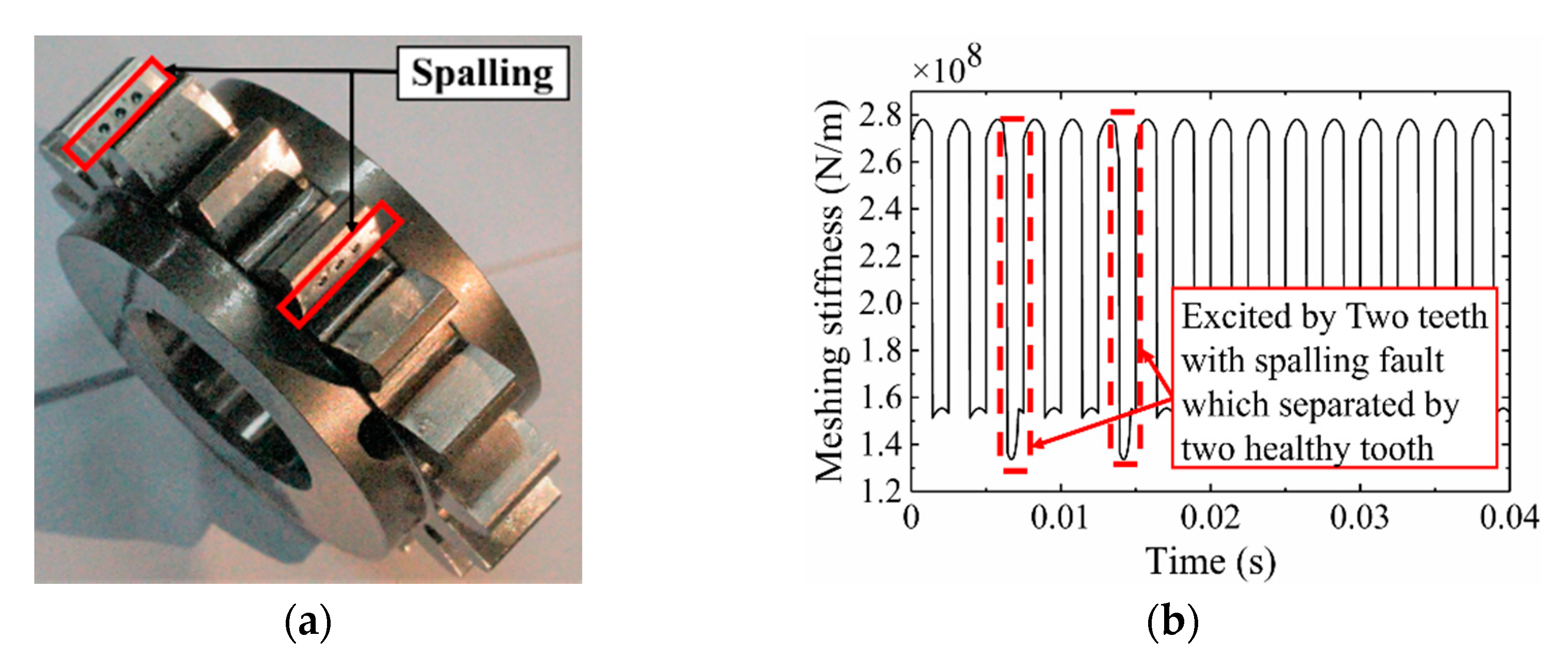
4.1. Effect of the Number of Spalling Faulty Teeth on Dynamic Characteristics of Gears
4.2. Effect of the Relative Position of the Faulty Teeth on Dynamic Characteristics of Gears
5. Background Noise Elimination Method
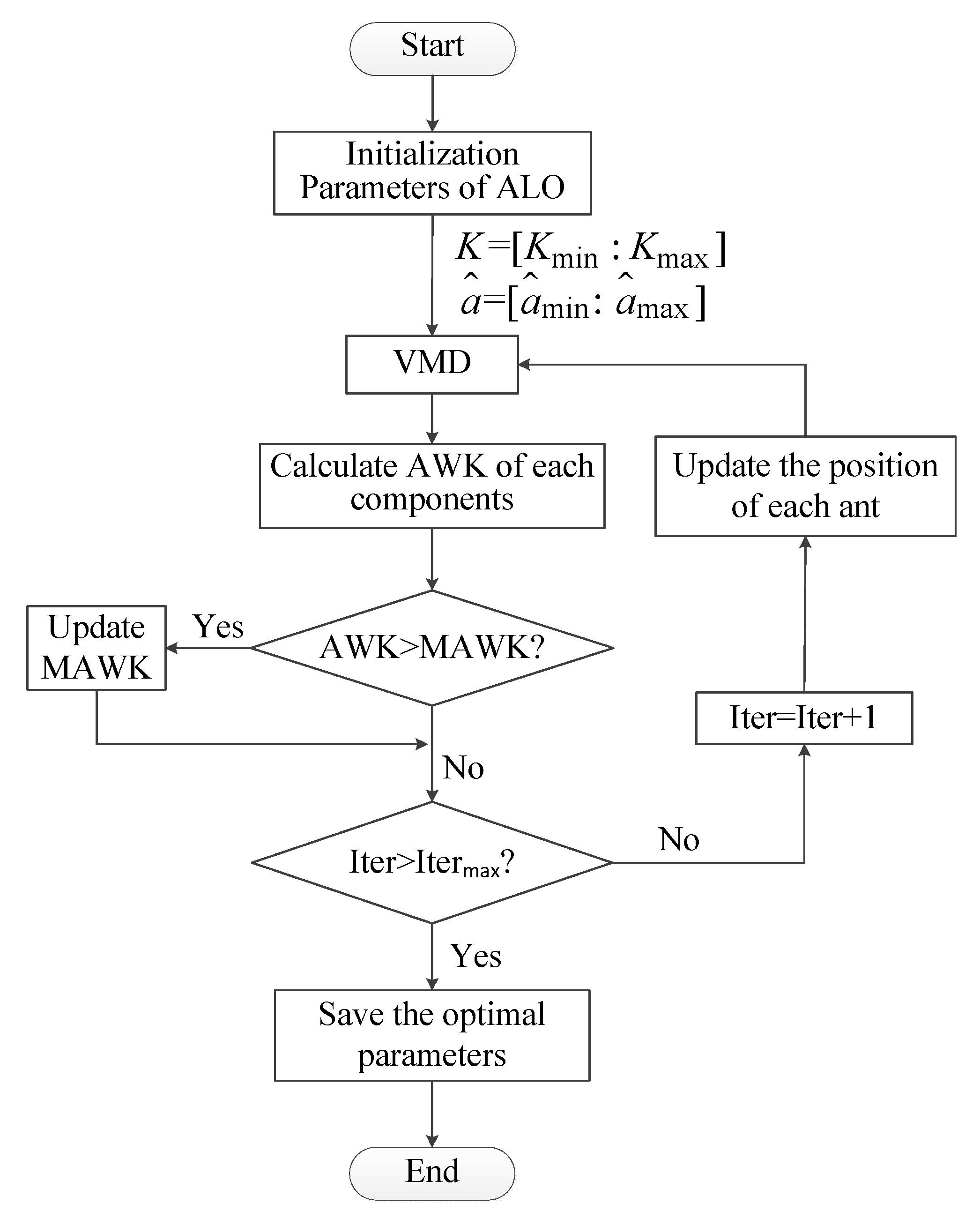
5.1. The Principle of ALO-VMD Method
5.1.1. VMD Method
5.1.2. Ant Lion Optimization Method
5.1.3. The Proposed ALO-VMD Method
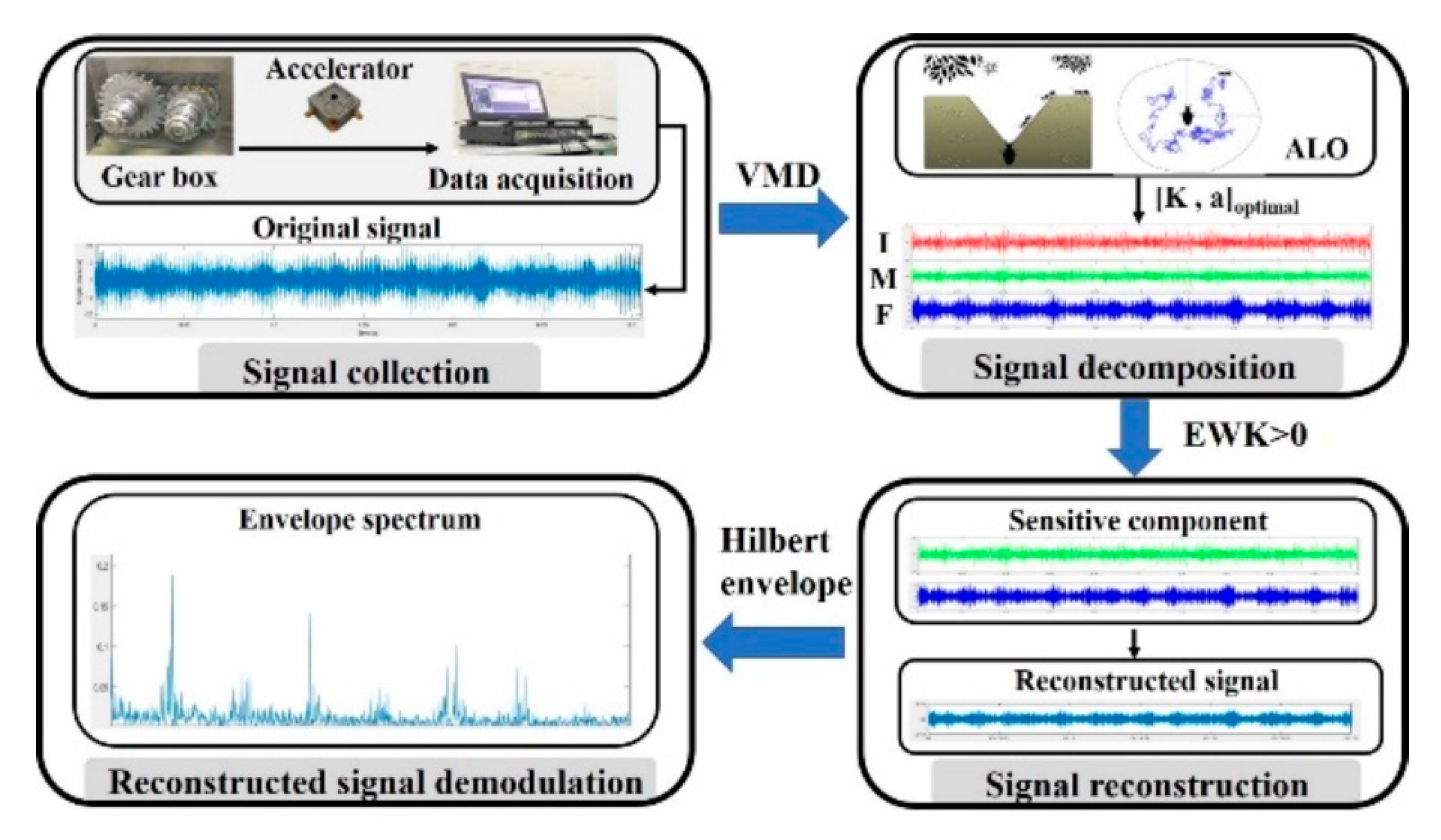
5.2. The Framework of the Background Noise Elimination Method
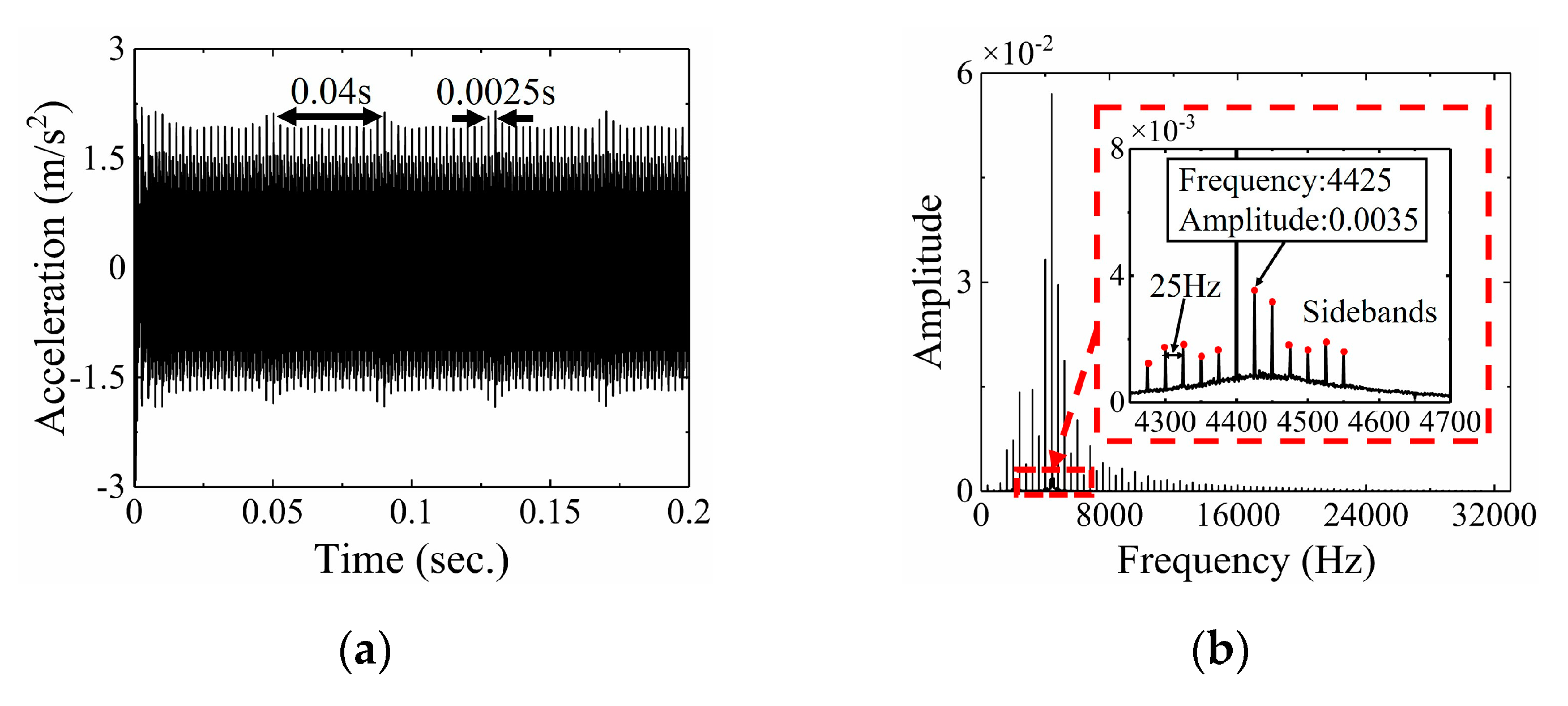
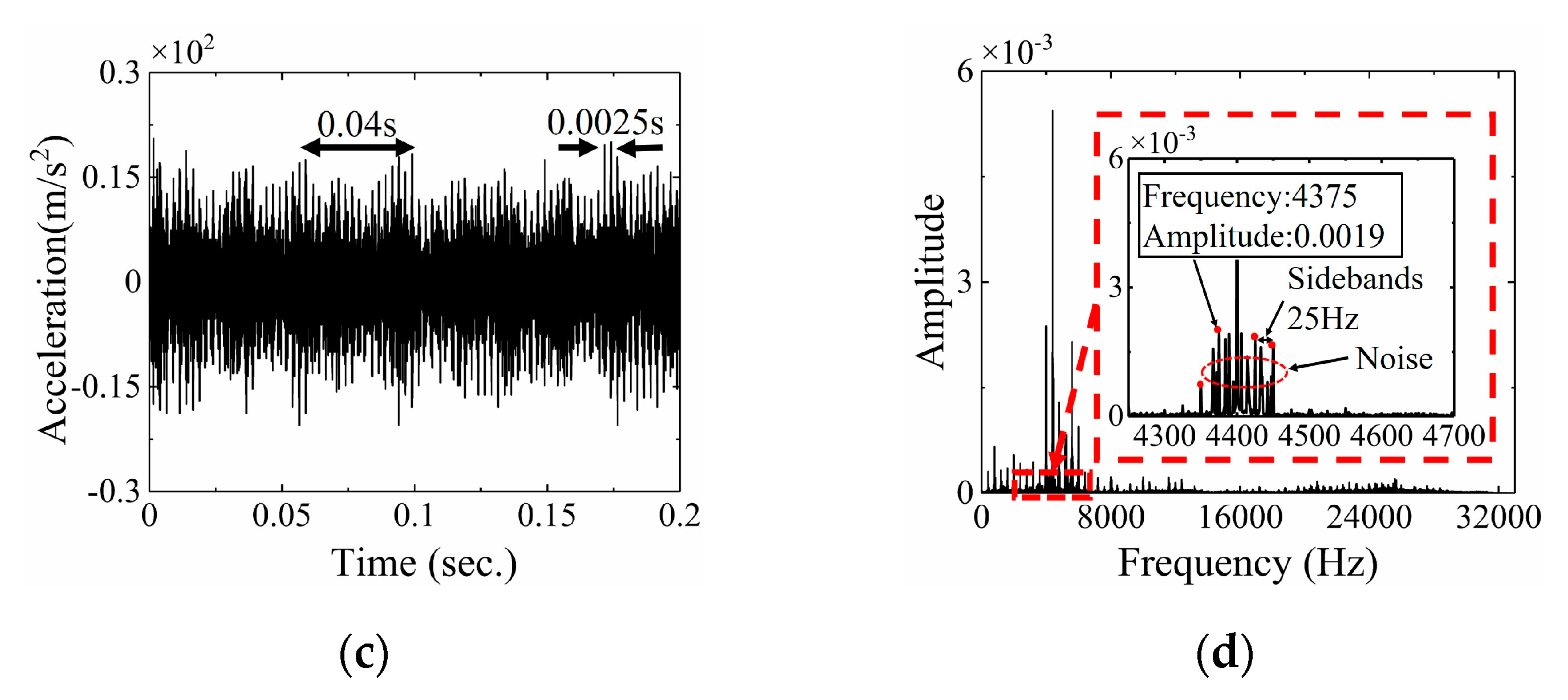
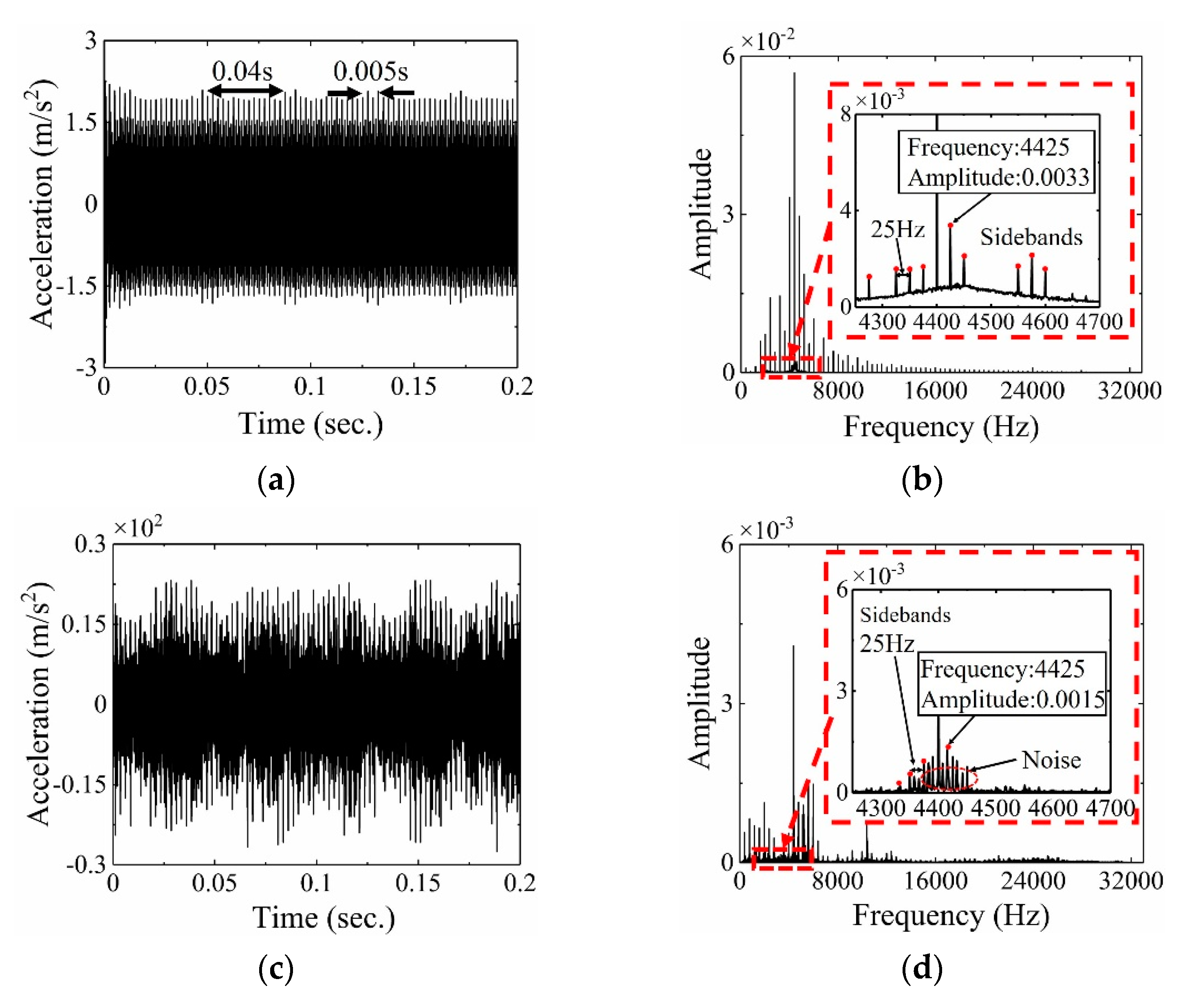
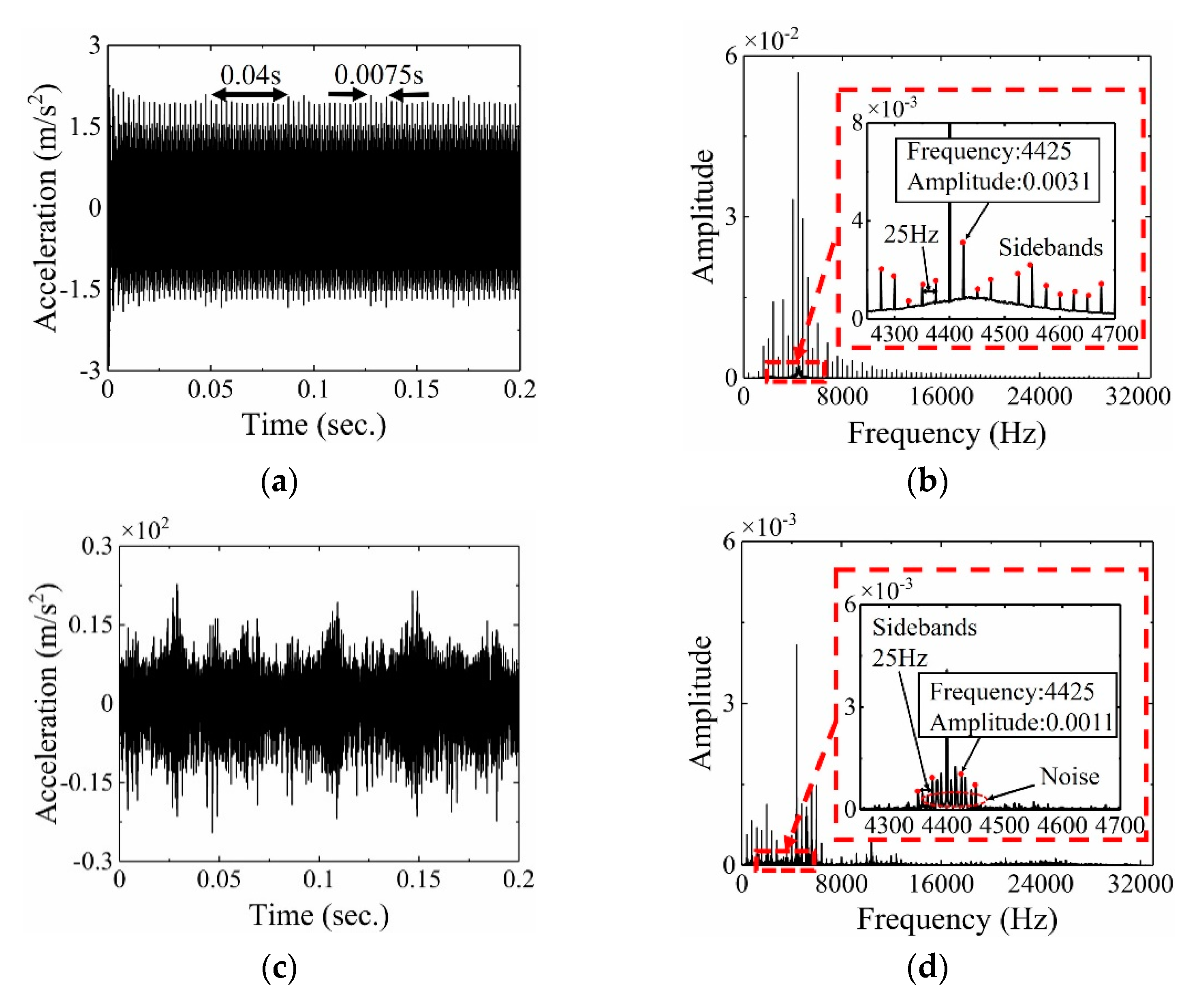
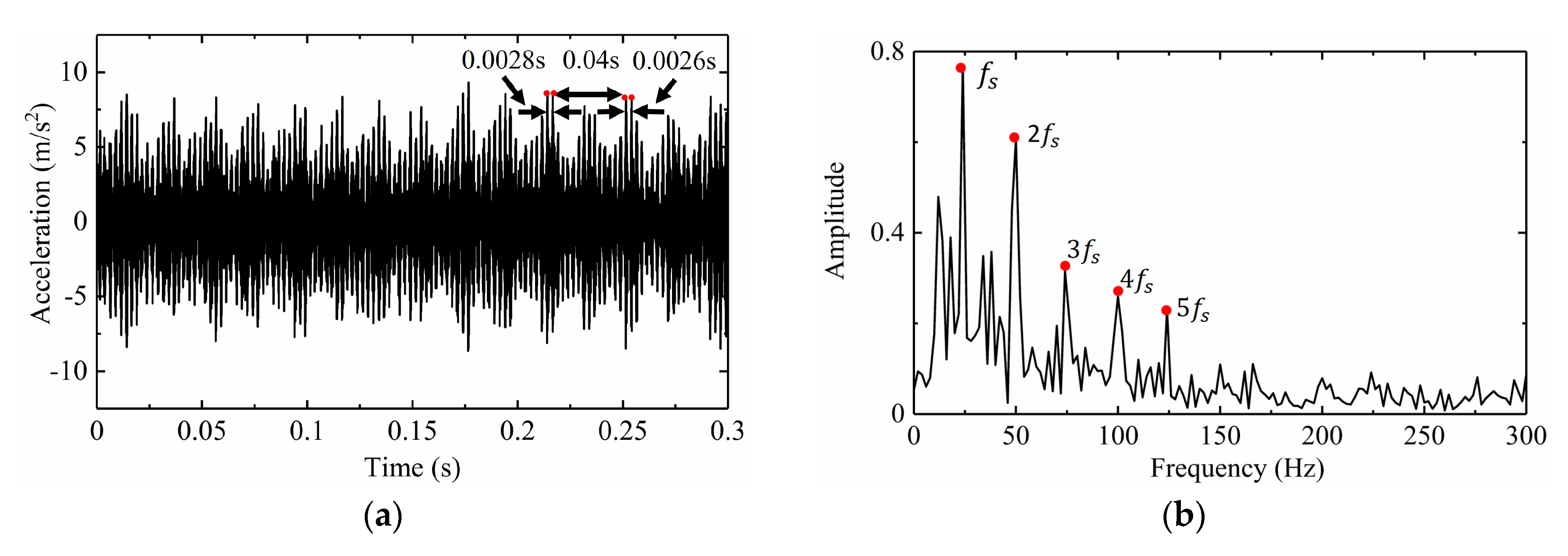
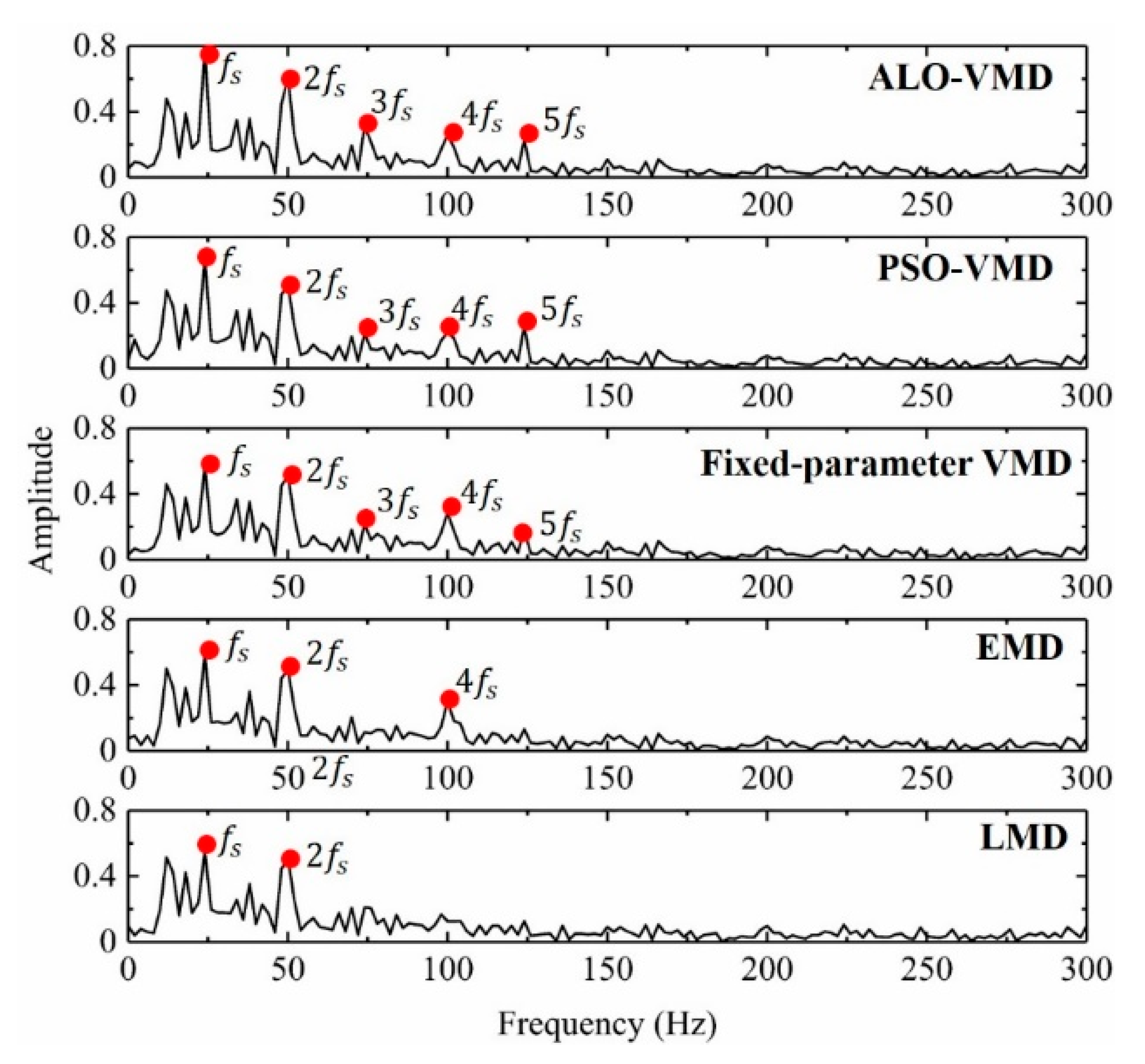
5.3. Background Elimination and Comparative Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kumar, A.; Gandhi, C.P.; Zhou, Y.; Kumar, R.; Xiang, J. Latest developments in gear defect diagnosis and prognosis: A review. Measurement 2020, 158, 107735. [Google Scholar] [CrossRef]
- Davidson, T.; Ku, P. The effect of lubricants on gear tooth surface fatigue. ASLE Trans. 1958, 1, 40–50. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Wang, K. Locomotive dynamic performance under traction/braking conditions considering effect of gear transmissions. Veh. Syst. Dyn. 2018, 56, 1097–1117. [Google Scholar] [CrossRef]
- Feng, K.; Borghesani, P.; Smith, W.A.; Randall, R.B.; Chin, Z.Y.; Ren, J.; Peng, Z. Vibration-based updating of wear prediction for spur gears. Wear 2019, 426, 1410–1415. [Google Scholar] [CrossRef]
- Weibring, M.; Gondecki, L.; Tenberge, P. Simulation of fatigue failure on tooth flanks in consideration of pitting initiation and growth. Tribol. Int. 2019, 131, 299–307. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Wang, J.; Xin, Y.; Jiang, X. Enhanced sparse filtering with strong noise adaptability and its application on rotating machinery fault diagnosis. Neurocomputing 2020, 398, 31–44. [Google Scholar] [CrossRef]
- Zeman, J. Dynamische Zusatzkrafter in Zahnbradgetrieben. Z. Ver. Dtsch. Ingiere 1957, 9, 244. [Google Scholar]
- Harris, S.L. Dynamic loads on the teeth of spur gears. Proc. Inst. Mech. Eng. 1958, 172, 87–112. [Google Scholar] [CrossRef]
- Tobe, T. Dynamic loads on spur gear teeth. Bull. JSME 1961, 4, 417–422. [Google Scholar] [CrossRef]
- Johnson, D. Modes and frequencies of shafts coupled by straight spur gears. J. Mech. Eng. Sci. 1962, 4, 241–250. [Google Scholar] [CrossRef]
- Kohler, H.; Pratt, A.; Thompson, A. Paper 14: Dynamics and Noise of Parallel-Axis Gearing. In Proceedings of the Institution of Mechanical Engineers, Conference Proceedings; SAGE Publications Sage UK: London, UK, 1969; pp. 111–121. [Google Scholar]
- Wu, S.; Zuo, M.J.; Parey, A. Simulation of spur gear dynamics and estimation of fault growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- Kahraman, A.; Blankenship, G.W. Experiments on nonlinear dynamic behavior of an oscillator with clearance and periodically time-varying parameters. J. Appl. Mech. 1997, 64, 217–226. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M.; Aidanpää, J.-O. Dynamic modelling of a one-stage spur gear system and vibration-based tooth crack detection analysis. Mech. Syst. Signal Process. 2015, 54, 293–305. [Google Scholar] [CrossRef]
- Ren, F.; Luo, G.; Shi, G.; Wu, X.; Wang, N. Influence of manufacturing errors on dynamic floating characteristics for herringbone planetary gears. Nonlinear Dyn. 2018, 93, 361–372. [Google Scholar] [CrossRef]
- Ding, Y.; Rieger, N.F. Spalling formation mechanism for gears. Wear 2003, 254, 1307–1317. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Ma, H.; Li, Z.; Feng, M.; Feng, R.; Wen, B. Time-varying mesh stiffness calculation of spur gears with spalling defect. Eng. Fail. Anal. 2016, 66, 166–176. [Google Scholar] [CrossRef]
- Saxena, A.; Parey, A.; Chouksey, M. Time varying mesh stiffness calculation of spur gear pair considering sliding friction and spalling defects. Eng. Fail. Anal. 2016, 70, 200–211. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Liu, L.; Zuo, M.J. The influence of tooth pitting on the mesh stiffness of a pair of external spur gears. Mech. Mach. Theory 2016, 106, 1–15. [Google Scholar] [CrossRef]
- Luo, Y.; Baddour, N.; Han, G.; Jiang, F.; Liang, M. Evaluation of the time-varying mesh stiffness for gears with tooth spalls with curved-bottom features. Eng. Fail. Anal. 2018, 92, 430–442. [Google Scholar] [CrossRef]
- Chen, T.; Wang, Y.; Chen, Z. A novel distribution model of multiple teeth pits for evaluating time-varying mesh stiffness of external spur gears. Mech. Syst. Signal Process. 2019, 129, 479–501. [Google Scholar] [CrossRef]
- Luo, Y.; Baddour, N.; Liang, M. Dynamical modeling and experimental validation for tooth pitting and spalling in spur gears. Mech. Syst. Signal Process. 2019, 119, 155–181. [Google Scholar] [CrossRef]
- Abouel-seoud, S.A.; Dyab, E.S.; Elmorsy, M.S. Influence of tooth pitting and cracking on gear meshing stiffness and dynamic response of wind turbine gearbox. Int. J. Sci. Adv. Technol. 2012, 2, 151–165. [Google Scholar]
- Jiang, H.; Shao, Y.; Mechefske, C.K. Dynamic characteristics of helical gears under sliding friction with spalling defect. Eng. Fail. Anal. 2014, 39, 92–107. [Google Scholar] [CrossRef]
- Totten, G.E. ASM Handbook, Volume 18: Friction, Lubrication, and Wear Technology; ASM International: Cleveland, OH, USA, 1992. [Google Scholar]
- Tan, C.K.; Irving, P.; Mba, D. A comparative experimental study on the diagnostic and prognostic capabilities of acoustics emission, vibration and spectrometric oil analysis for spur gears. Mech. Syst. Signal Process. 2007, 21, 208–233. [Google Scholar] [CrossRef]
- Liang, X.H.; Liu, Z.L.; Pan, J.; Zuo, M.J. Spur Gear Tooth Pitting Propagation Assessment Using Model-based Analysis. Chin. J. Mech. Eng. 2017, 30, 1369–1382. [Google Scholar] [CrossRef]
- Prabhakar, S.; Sekhar, A.S.; Mohanty, A.R. Detection and Monitoring of Cracks in a Rotor-Bearing System Using Wavelet Transforms. Mech. Syst. Signal Process. 2001, 15, 447–450. [Google Scholar] [CrossRef]
- Liang, P.; Deng, C.; Wu, J.; Yang, Z.; Zhu, J.; Zhang, Z. Compound fault diagnosis of gearboxes via multi-label convolutional neural network and wavelet transform. Comput. Ind. 2019, 113, 103132. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. Bearing performance degradation assessment based on a combination of empirical mode decomposition and k-medoids clustering. Mech. Syst. Signal Process. 2017, 93, 16–29. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; He, Z.; Guo, W.; Tang, Z. A hybrid fault diagnosis method based on second generation wavelet de-noising and local mean decomposition for rotating machinery. ISA Trans. 2016, 61, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Jiang, Z.; He, S.; Mo, Q. Complex variational mode decomposition for signal processing applications. Mech. Syst. Signal Process. 2017, 86, 75–85. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- An, X.; Zhang, F. Pedestal looseness fault diagnosis in a rotating machine based on variational mode decomposition. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2493–2502. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Wei, Y.; Liu, B.; Liang, X. Health condition identification of planetary gearboxes based on variational mode decomposition and generalized composite multi-scale symbolic dynamic entropy. ISA Trans. 2018, 81, 329–341. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, G.; Liu, C.; Chen, X. Study on planetary gear fault diagnosis based on variational mode decomposition and deep neural networks. Measurement 2018, 130, 94–104. [Google Scholar] [CrossRef]
- Li, F.; Li, R.; Tian, L.; Chen, L.; Liu, J. Data-driven time-frequency analysis method based on variational mode decomposition and its application to gear fault diagnosis in variable working conditions. Mech. Syst. Signal Process. 2019, 116, 462–479. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Zhang, J.; Yao, X.; Zhang, Y. Impact fault detection of gearbox based on variational mode decomposition and coupled underdamped stochastic resonance. ISA Trans. 2019, 95, 320–329. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Ali, E.; Abd Elazim, S.; Abdelaziz, A. Ant lion optimization algorithm for renewable distributed generations. Energy 2016, 116, 445–458. [Google Scholar] [CrossRef]
- Kanimozhi, G.; Kumar, H. Modeling of solar cell under different conditions by Ant Lion Optimizer with LambertW function. Appl. Soft Comput. 2018, 71, 141–151. [Google Scholar]
- Chaari, F.; Fakhfakh, T.; Haddar, M. Analytical modelling of spur gear tooth crack and influence on gearmesh stiffness. Eur. J. Mech. A/Solids 2009, 28, 461–468. [Google Scholar] [CrossRef]
- Li, R.; Wang, J. Gear System Dynamics; Science Press: Beijing, China, 1997. [Google Scholar]
- Bartelmus, W. Mathematical modelling and computer simulations as an aid to gearbox diagnostics. Mech. Syst. Signal Process. 2001, 15, 855–871. [Google Scholar] [CrossRef]
- Chen, H.T.; Wu, X.L.; Qin, D.T.; Yang, J.; Zhou, Z.G. Effects of gear manufacturing error on the dynamic characteristics of planetary gear transmission system of wind turbine. Appl. Mech. Mater. 2011, 86, 518–522. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Gu, R.; Chen, J.; Hong, R.; Wang, H.; Wu, W. Incipient fault diagnosis of rolling bearings based on adaptive variational mode decomposition and Teager energy operator. Measurement 2020, 149, 106941. [Google Scholar] [CrossRef]
- Wang, X.-B.; Yang, Z.-X.; Yan, X.-A. Novel particle swarm optimization-based variational mode decomposition method for the fault diagnosis of complex rotating machinery. IEEE/ASME Trans. Mechatron. 2017, 23, 68–79. [Google Scholar] [CrossRef]
- Sainsot and, P.; Velex, P.; Duverger, O. Contribution of gear body to tooth deflections—A new bidimensional analytical formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]






| Parameters | Pinion | Gear |
|---|---|---|
| Number of teeth | 16 | 24 |
| Pressure angle (deg) | 20 | |
| Teeth module (mm) | 4.5 | |
| Teeth width (mm) | 14 | |
| Mass (kg) | 0.676 | 1.084 |
| Mass moment inertia (kg·m2) | 0.000407 | 0.001168 |
| Young’s modulus (N/mm2) | 2.06 × 105 | |
| Poisson’s ratio | 0.3 | |
| Bearing damping (N·s/m) | 4.86 × 103 | 6.16 × 103 |
| Bearing stiffness (N/m) | 3.5 × 109 | 3.5 × 109 |
| Torque (N·m) | 23.5 | 35.3 |
| Fault Gear | Speed (r/min) | Sampling Frequency (Hz) | Fault Feature Frequency (Hz) |
|---|---|---|---|
| Pinion | 1.500 | 65.536 | 25 |
| Parameters | Methods | |
|---|---|---|
| ALO | PSO | |
| (K,a) | (3,1626) | (3,3580) |
| Iterations | 4 | 7 |
| Optimal fitness | 1.606 | 1.576 |
| Component | u1 | u2 | u3 |
|---|---|---|---|
| EWK | 0.286 | 0.605 | −0.891 |
| Selection | √ | √ |
| Method | ALO-VMD | PSO-VMD | Fixed-Parameter VMD | EMD | LMD |
|---|---|---|---|---|---|
| SNR | 10.464 | 9.916 | 9.854 | 9.217 | 9.101 |
| RMSE | 1.577 | 1.669 | 1.772 | 1.964 | 2.004 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Wen, J.; Pan, B.; Xiang, Y.; Zhang, Q.; Lin, C. Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis. Appl. Sci. 2020, 10, 7058. https://doi.org/10.3390/app10207058
Shi L, Wen J, Pan B, Xiang Y, Zhang Q, Lin C. Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis. Applied Sciences. 2020; 10(20):7058. https://doi.org/10.3390/app10207058
Chicago/Turabian StyleShi, Luojie, Juan Wen, Baisong Pan, Yongyong Xiang, Qi Zhang, and Congkai Lin. 2020. "Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis" Applied Sciences 10, no. 20: 7058. https://doi.org/10.3390/app10207058
APA StyleShi, L., Wen, J., Pan, B., Xiang, Y., Zhang, Q., & Lin, C. (2020). Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis. Applied Sciences, 10(20), 7058. https://doi.org/10.3390/app10207058





