FTn Finite Volume Analysis of Ultrafast Laser Radiation Transport through Human Skin Cancer
Abstract
:Featured Application
Abstract
1. Introduction
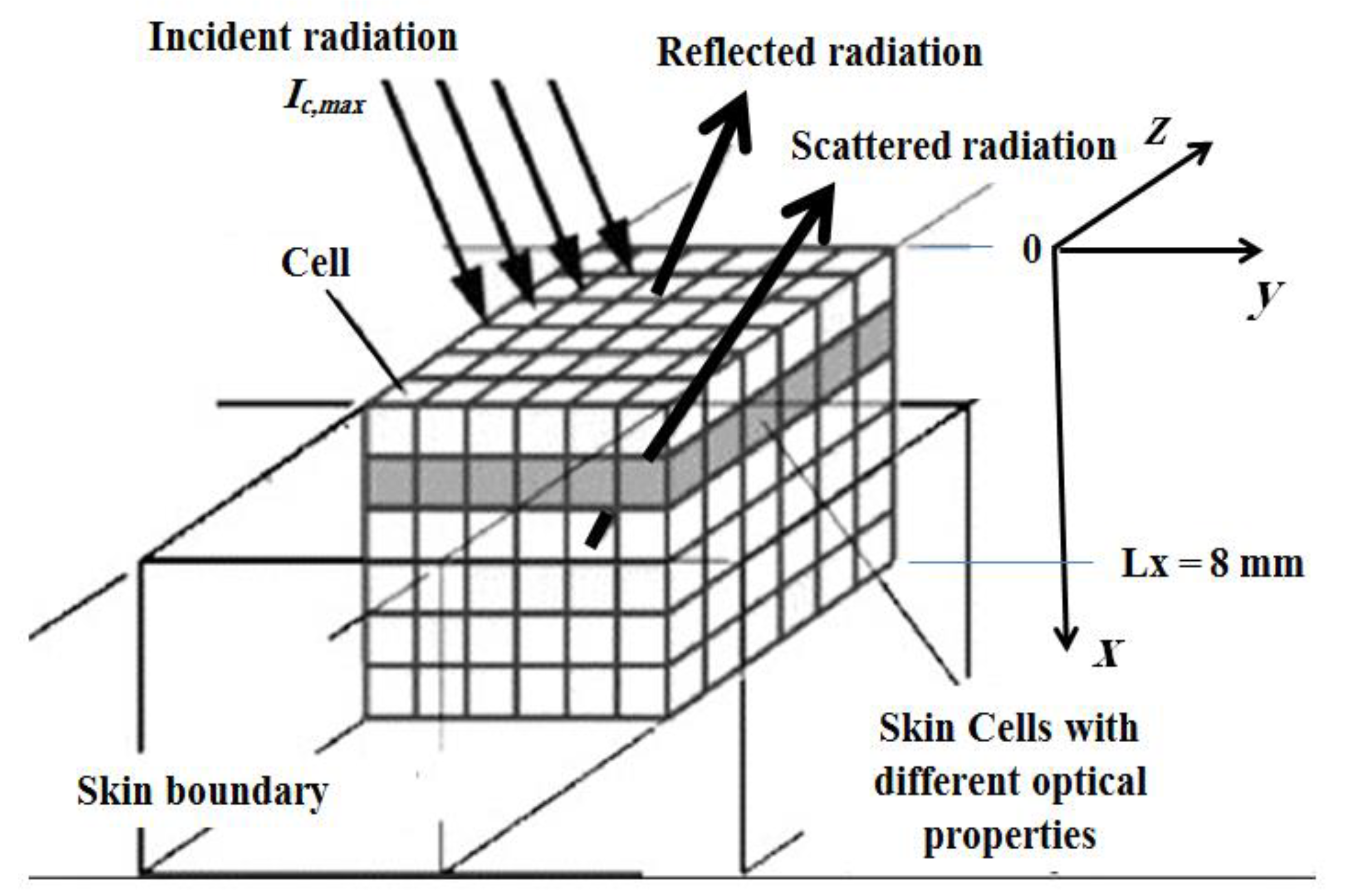
2. Mathematical Formulation
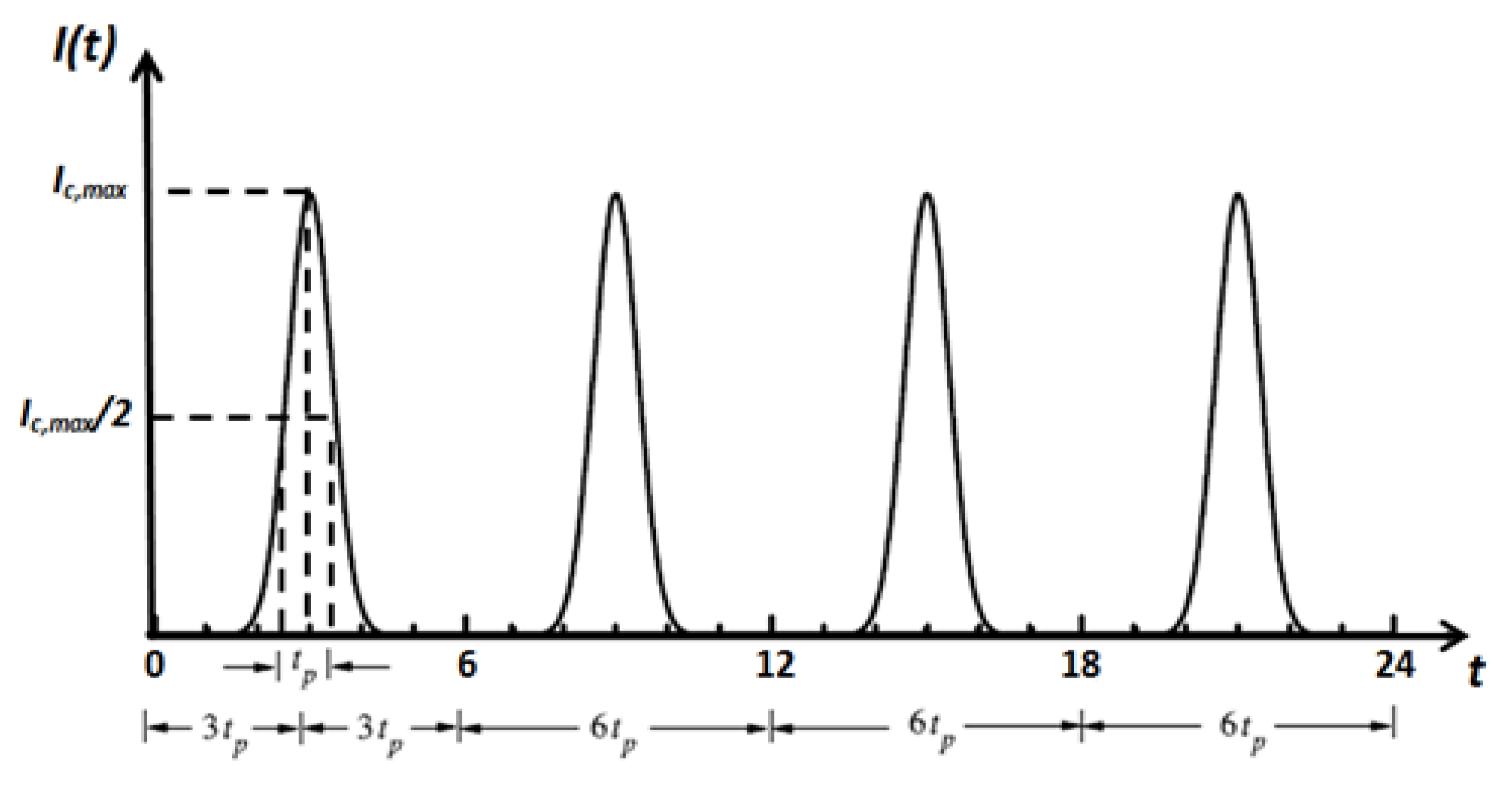
2.1. Transient Radiative Transfer Equation (TRTE)
2.2. Discretization of Transient Radiative Transfer Equation (TRTE)
3. Results and Discussions
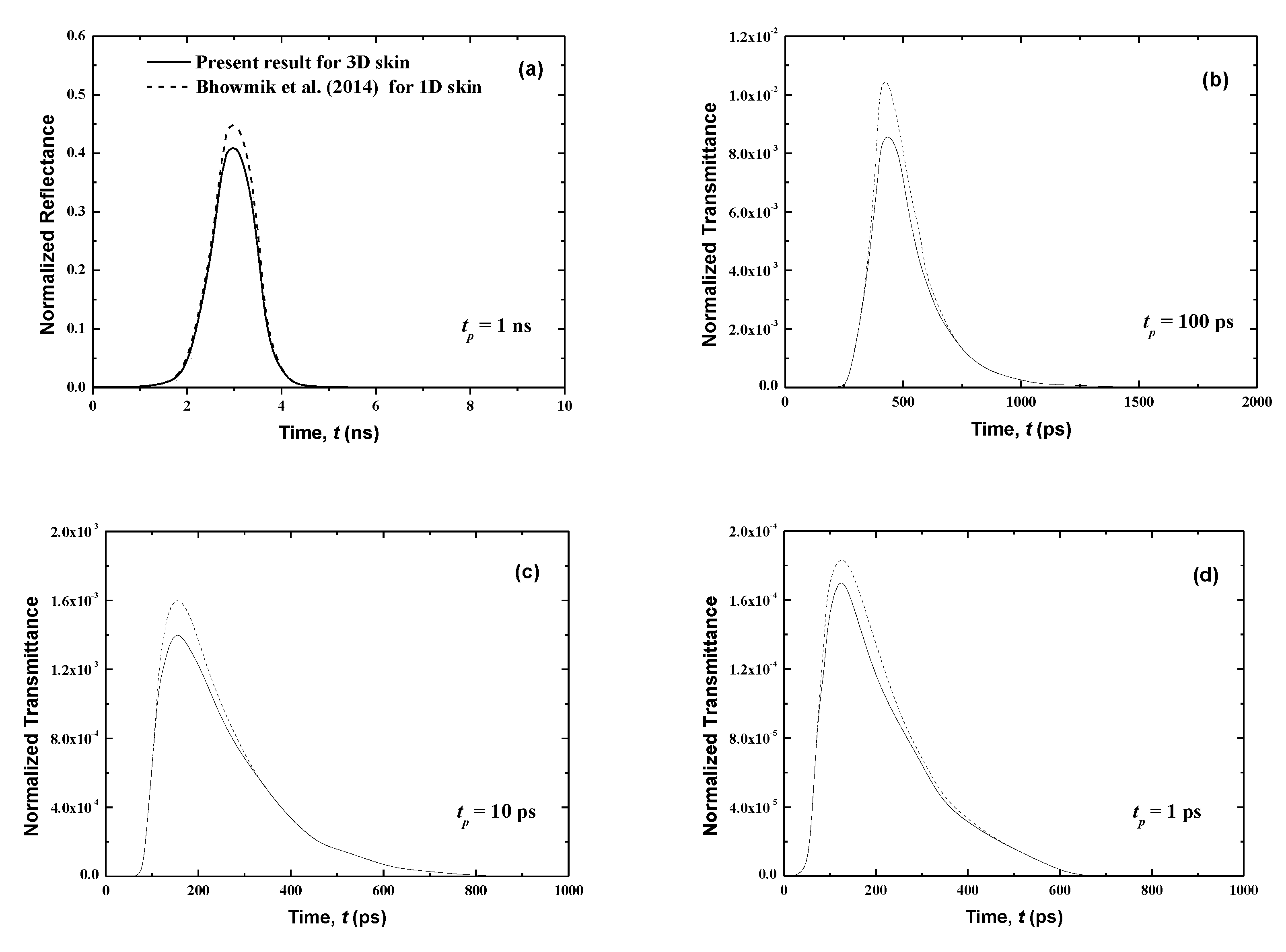
3.1. Human Skin without Malignancies
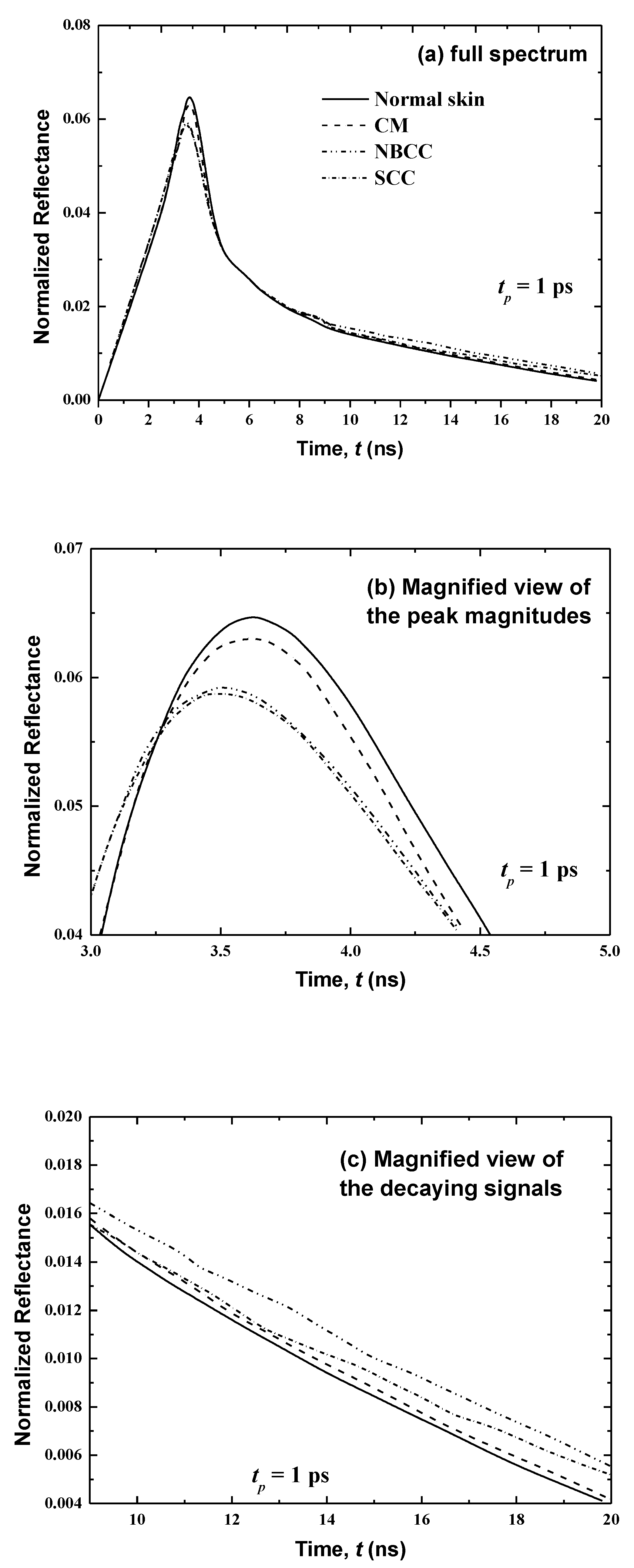
3.2. Human Skin with Malignancies
3.3. Parametric Analysis
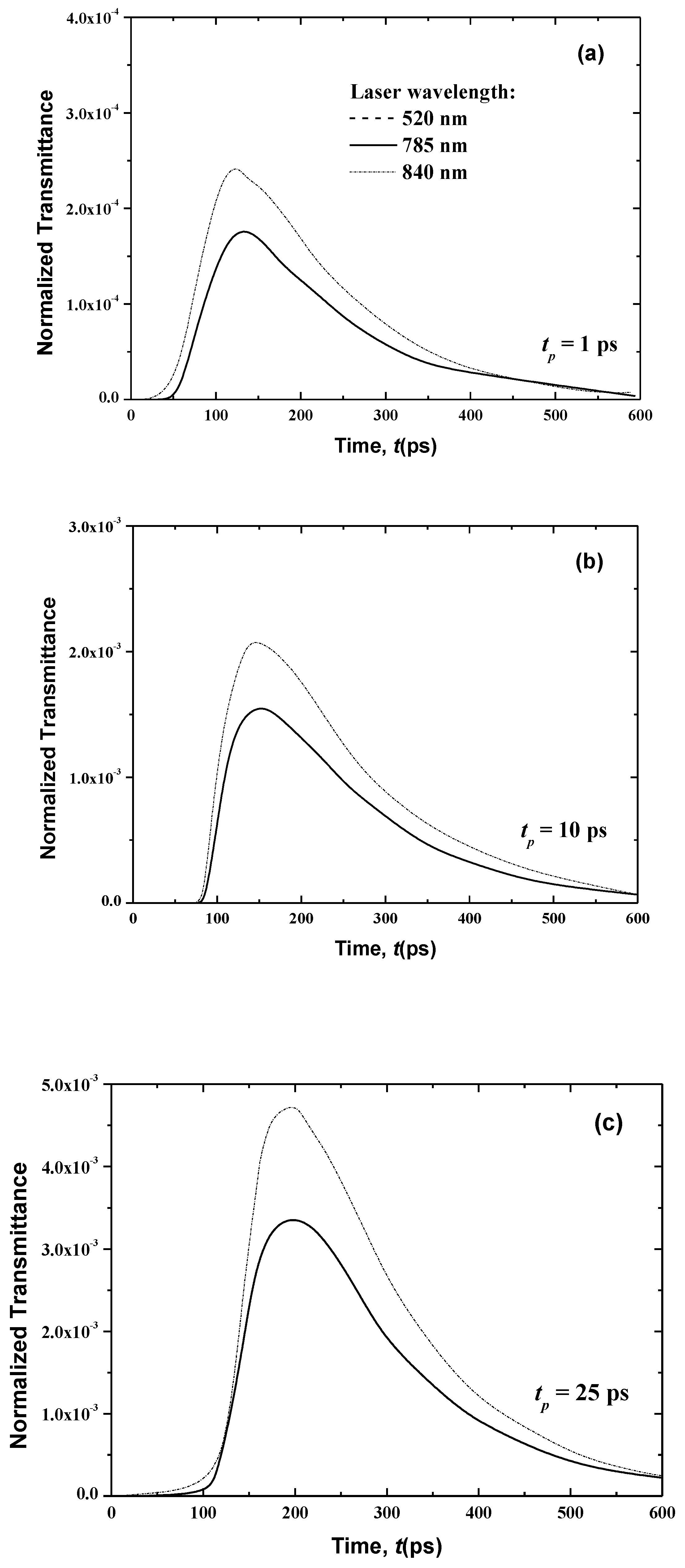
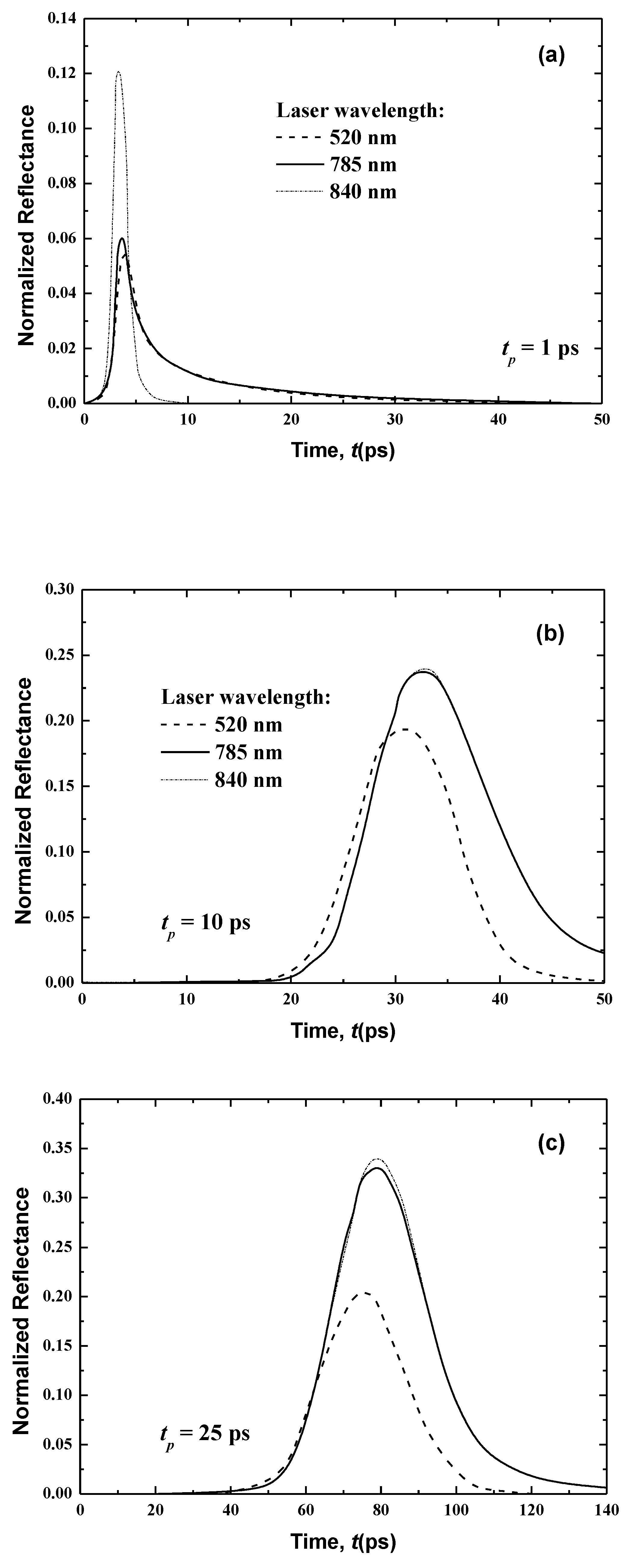
3.3.1. Effects of Laser Light Wavelength
3.3.2. Effect of Different Growth Phases of Cutaneous Melanoma
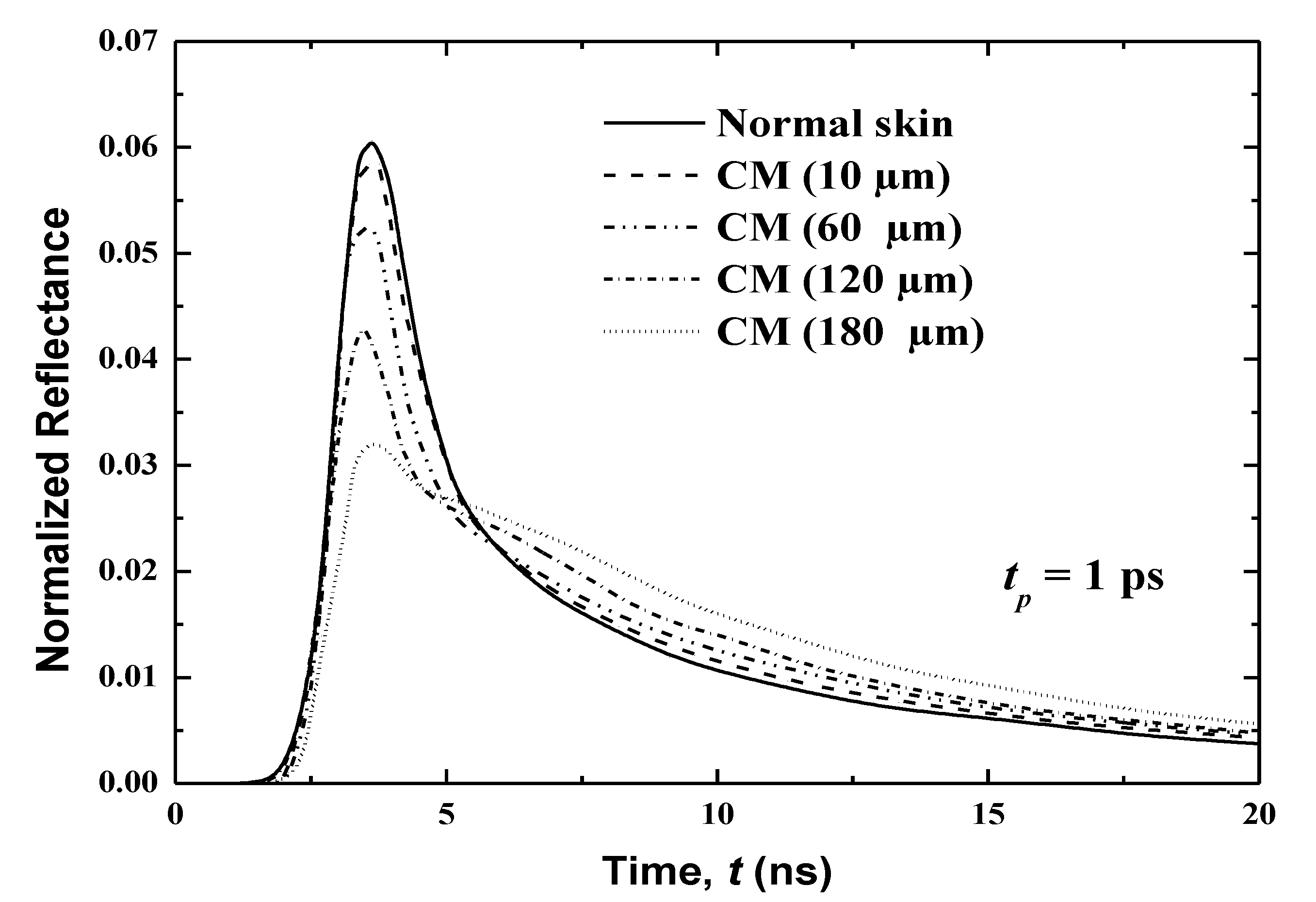
3.3.3. Effect of the Volume of the Cancerous Region
3.3.4. Effect of the Scattering Coefficient of the Cancerous Region
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| c | speed of light |
| CM | cutaneous melanoma |
| I | intensity |
| Ib | black body intensity |
| Ic | collimated intensity |
| Id | diffuse component of the intensity |
| g | anisotropic factor |
| L | total number of discrete solid angles |
| NBCC | Nodular Basal Cell Carcinoma |
| SCC | Squamous Cell Carcinoma |
| Sc | source term due to collimated radiation |
| Sd | source term due to diffuse radiation |
| t | time |
| T | temperature |
| Greek symbols | |
| β | extinction coefficient |
| ∆Ω | control solid angle |
| εw | emissivity |
| Φ | scattering phase function |
| absorption coefficient | |
| scattering coefficient | |
| nondimensional optical thickness | |
| scattering albedo | |
| unit vector in direction of intensity | |
| Superscripts | |
| l, l’ | discrete angular directions |
References
- Akamatsu, M.; Guo, Z. Ultrafast Laser Pulse Train Radiation Transfer in a Scattering-Absorbing 3D Medium with an Inhomogeneity. Heat Transf. Res. 2015, 46, 861–879. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Kumar, S.; San, K.-C. Multidimensional Monte Carlo Simulation of Short-Pulse Laser Transport in Scattering Media. J. Thermophys. Heat Transf. 2000, 14, 504–511. [Google Scholar] [CrossRef]
- Jang, C.; Jung, H.; Lee, J.; Song, T.-H. Radiative heat transfer analysis in pure scattering layers to be used in vacuum insulation panels. Appl. Energy 2013, 112, 703–709. [Google Scholar] [CrossRef]
- Wang, C.-H.; Zhang, Y.; Yi, H.-L.; Tan, H.-P. Transient radiative transfer in two-dimensional graded index medium by Monte Carlo method combined with the time shift and superposition principle. Num. Heat Transfer Part A 2016, 69, 574–588. [Google Scholar] [CrossRef]
- Tan, Z.-M.; Hsu, P.-F. An Integral Formulation of Transient Radiative Transfer. J. Heat Transf. 2000, 123, 466–475. [Google Scholar] [CrossRef]
- Hunter, B.; Guo, Z. Improved Treatment of Anisotropic Scattering for Ultrafast Radiative Transfer Analysis. J. Heat Transf. 2015, 137, 091004. [Google Scholar] [CrossRef]
- Hunter, B.; Guo, Z. Numerical smearing, ray effect, and angular false scattering in radiation transfer computation. Int. J. Heat Mass Transf. 2015, 81, 63–74. [Google Scholar] [CrossRef]
- Coelho, P.J. Bounded Skew High-Order Resolution Schemes for the Discrete Ordinates Method. J. Comput. Phys. 2002, 175, 412–437. [Google Scholar] [CrossRef]
- Guedri, K.; Bouzid, A.; Nasr, A.; Al-Ghamdi, A.S. Three-dimensional FTn Finite Volume Analysis of Short Pulse Laser Propagation through Biomedical Tissue Phantoms. Int. J. Applied Eng. Res. 2018, 13, 4764–4775. [Google Scholar]
- Ettaleb, A.; Ammar, A.M.; Farhat, H.; Guedri, K.; Omri, A.; Borjini, M.N.; Goodarzi, M.; Sarafraz, M. Radiation Heat Transfer in a Complex Geometry Containing Anisotropically-Scattering Mie Particles. Energies 2019, 12, 3986. [Google Scholar] [CrossRef] [Green Version]
- Guedri, K.; Al-Ghamdi, A.S. Radiative Heat Transfer in Complex Enclosures Using NVD Differencing Schemes of the FTn Finite Volume Method. Heat Transf. Res. 2017, 48, 1379–1398. [Google Scholar] [CrossRef]
- Guedri, K.; Al-Ghamdi, A.S. Improved Finite Volume Method for Three-Dimensional Radiative Heat Transfer in Complex Enclosures Containing Homogenous and Inhomogeneous Participating Media. Heat Transf. Eng. 2017, 39, 1364–1376. [Google Scholar] [CrossRef]
- Guedri, K.; Al-Ghamdi, A.S.; Oreijah, M. Application of high-resolution NVD differencing schemes to the FTn finite volume method for radiative heat transfer. Heat Transfer-Asian Res. 2017, 47, 366–388. [Google Scholar] [CrossRef]
- Guedri, K.; Bouzid, A.; Nasr, A.; Al-Ghamdi, A.S. Three-dimensional FTn finite volume solution of short-pulse laser propagation through heterogeneous medium. Therm. Sci. 2018, 24, 186. [Google Scholar] [CrossRef]
- Park, H.; Chacón, L.; Matsekh, A.; Chen, G. A multigroup moment-accelerated deterministic particle solver for 1-D time-dependent thermal radiative transfer problems. J. Comput. Phys. 2019, 388, 416–438. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.W.; Byun, D.Y.; Kang, S.J. The combined Monte-Carlo and finite-volume method for radiation in a two-dimensional irregular geometry. Int. J. Heat Mass Transf. 2000, 43, 2337–2344. [Google Scholar] [CrossRef]
- Chai, J.C.; Moder, J.P. Radiation Heat Transfer Calculation Using an Angular-Multiblock Procedure. Numer. Heat Transf. Part B Fundam. 2000, 38, 1–13. [Google Scholar] [CrossRef]
- Kim, S.H.; Huh, K.Y. A new angular discretization scheme of the finite volume method for 3-D radiative heat transfer in absorbing, emitting and anisotropically scattering media. Int. J. Heat Mass Transf. 2000, 43, 1233–1242. [Google Scholar] [CrossRef]
- Guo, Z.; Kumar, S. Discrete-ordinates solution of short-pulsed laser transport in two-dimensional turbid media. Appl. Opt. 2001, 40, 3156–3163. [Google Scholar] [CrossRef]
- Hiroyuki, F.; Moegi, U.; Kazumichi, K.; Masao, M. Characteristic Length and Time Scales of the Highly Forward Scattering of Photons in Random Media. Appl. Sci. 2020, 10, 93. [Google Scholar]
- Bhowmik, A.; Repaka, R.; Mishra, S.C.; Mitra, K. Analysis of radiative signals from normal and malignant human skins subjected to a short-pulse laser. Int. J. Heat Mass Transf. 2014, 68, 278–294. [Google Scholar] [CrossRef]
- Guo, Z.; Kim, K. Ultrafast-laser-radiation transfer in heterogeneous tissues with the discrete-ordinates method. Appl. Opt. 2003, 42, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Guedri, K.; Al-Ghamdi, A.S.; Bouzid, A.; Abbassi, M.A.; Ghulman, H.A. Evaluation of the FT n Finite Volume Method for Transient Radiative Transfer in Anisotropically Scattering Medium. Numer. Heat Transf. Part A Appl. 2015, 68, 1137–1154. [Google Scholar] [CrossRef]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Garcia-Uribe, A.; Smith, E.B.; Zou, J.; Duvic, M.; Prieto, V.; Wang, L.V. In-vivo characterization of optical properties of pigmented skin lesions including melanoma using oblique incidence diffuse reflectance spectrometry. J. Biomed. Opt. 2011, 16, 020501. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.R.; Parrish, J.A. The Optics of Human Skin. J. Investig. Dermatol. 1981, 77, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000 nm. J. Phys. D Appl. Phys. 2005, 38, 2543–2555. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical Properties of Skin, Subcutaneous, and Muscle Tissues: A Review. J. Innov. Opt. Health Sci. 2011, 4, 9–38. [Google Scholar] [CrossRef]
- Simpson, R.C.; Kohl, M.; Essenpris, E.; Cope, M. Near-infrared optical properties on ex vivo human skin and subcutaneous tissues measured using Monte Carlo inversion technique. Phys. Med. Biol. 1998, 43, 2465–2478. [Google Scholar] [CrossRef]
- Wang, S.; Zhong, S.-L.; Lui, H.; He, Q.; Zeng, H. Monte Carlo simulation of near infrared autofluorescence measurements of in vivo skin. J. Photochem. Photobiol. B Biol. 2011, 105, 183–189. [Google Scholar] [CrossRef]
- Cheong, W.F.; Prahl, S.A.; Welch, A.J. A review on optical properties of biological tissues. IEEE J. Quantum Electron. 1990, 26, 2166–2184. [Google Scholar] [CrossRef] [Green Version]




| Layers | d (mm) | n | ||||||
|---|---|---|---|---|---|---|---|---|
| g | g | |||||||
| Stratum corneum | 0.01 | 1.45 | 4.0 | 57.0 | 0.77 | 0.00091 | 17.6125 | 0.8 |
| Living epidermis | 0.08 | 1.4 | 4.0 | 57.0 | 0.77 | 0.13 | 17.6125 | 0.8 |
| Papillary dermis | 0.1 | 1.4 | 0.5 | 50.0 | 0.77 | 0.105 | 10.625 | 0.8 |
| Upper blood plexus | 0.08 | 1.39 | 2.45 | 50.0 | 0.79 | 0.15875 | 15.485 | 0.818 |
| Reticular dermis | 1.50 | 1.4 | 0.5 | 50.0 | 0.77 | 0.105 | 10.625 | 0.8 |
| Deep blood plexus | 0.07 | 1.34 | 18.1 | 50.0 | 0.96 | 0.444. | 46.0625 | 0.962 |
| Dermis | 0.16 | 1.4 | 0.5 | 50.0 | 0.77 | 0.105 | 10.625 | 0.8 |
| Hypodermis | 3.0 | 1.44 | 0.4778 | 33.72 | 0.9 | 0.009 | 11.13 | 0.9 |
| Muscle tissues | 3.0 | 1.37 | 0.1366 | 8.88 | 0.9054 | 0.029 | 6.71 | 0.9 |
| Layers | d (mm) | n | g | ||
|---|---|---|---|---|---|
| Stratum corneum | 0.01 | 1.4 | 0.00089 | 18.95 | 0.8 |
| Living epidermis | 0.08 | 1.4 | 0.19 | 18.95 | 0.8 |
| Papillary dermis | 0.1 | 1.4 | 0.13 | 11.65 | 0.8 |
| Upper blood plexus | 0.08 | 1.39 | 0.15875 | 15.485 | 0.818 |
| Reticular dermis | 1.50 | 1.4 | 0.13 | 11.65 | 0.8 |
| Deep blood plexus | 0.07 | 1.34 | 0.38875 | 46.165 | 0.962 |
| Dermis | 0.16 | 1.4 | 0.13 | 11.65 | 0.8 |
| Hypodermis | 3.0 | 1.44 | 0.008 | 11.44 | 0.9 |
| Muscle tissues | 3.0 | 1.37 | 0.031 | 7.130 | 0.9 |
| Total thickness (mm) | 8.0 |
| Skin Carcinoma | n | g | |||
|---|---|---|---|---|---|
| Non-melanoma | Nodular basal cell carcinoma (NBCC) | 1.4 | 0.035 | 8.140 | 0.8 |
| Squamous cell carcinoma (SCC) | 1.4 | 0.062 | 6.680 | 0.8 | |
| Melanoma | Cutaneous melanoma (CM) | 1.4 | 0.0075 | 9.185 | 0.8 |
| Angular Discretization Scheme | Average Relative Error (%) |
|---|---|
| FT4 | 7.28 |
| FT6 | 4.2 |
| FT8 | 1.8 |
| FT10 | 1.5 |
| Spatial Discretization Scheme | Average Relative Error (%) |
|---|---|
| (200 × 11 × 11) | 6.4 |
| (200 × 21 × 21) | 5.2 |
| (400 × 21 × 21) | 1.8 |
| (400 × 41 × 41) | 1.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guedri, K.; Abosuliman, S.S.; Oreijah, M. FTn Finite Volume Analysis of Ultrafast Laser Radiation Transport through Human Skin Cancer. Appl. Sci. 2020, 10, 7090. https://doi.org/10.3390/app10207090
Guedri K, Abosuliman SS, Oreijah M. FTn Finite Volume Analysis of Ultrafast Laser Radiation Transport through Human Skin Cancer. Applied Sciences. 2020; 10(20):7090. https://doi.org/10.3390/app10207090
Chicago/Turabian StyleGuedri, Kamel, Shougi Suliman Abosuliman, and Mowffaq Oreijah. 2020. "FTn Finite Volume Analysis of Ultrafast Laser Radiation Transport through Human Skin Cancer" Applied Sciences 10, no. 20: 7090. https://doi.org/10.3390/app10207090
APA StyleGuedri, K., Abosuliman, S. S., & Oreijah, M. (2020). FTn Finite Volume Analysis of Ultrafast Laser Radiation Transport through Human Skin Cancer. Applied Sciences, 10(20), 7090. https://doi.org/10.3390/app10207090





