Analysis of Dynamic Characteristics of Deformed Concrete Slab Track on Transition Zone in High-Speed Train Line According to Train Speeds
Abstract
:Featured Application
Abstract
1. Introduction
2. Theoretical Background
Impact Load Due to Discordance between Wheel and Rail
3. Field Measurement
3.1. Site Summary
3.2. Designation of the Predicted Impact Point
3.3. Wheel Load Measuring Process
3.4. Wheel Load Measurement Results
4. Numerical Analysis
4.1. Numerical Analysis Summary
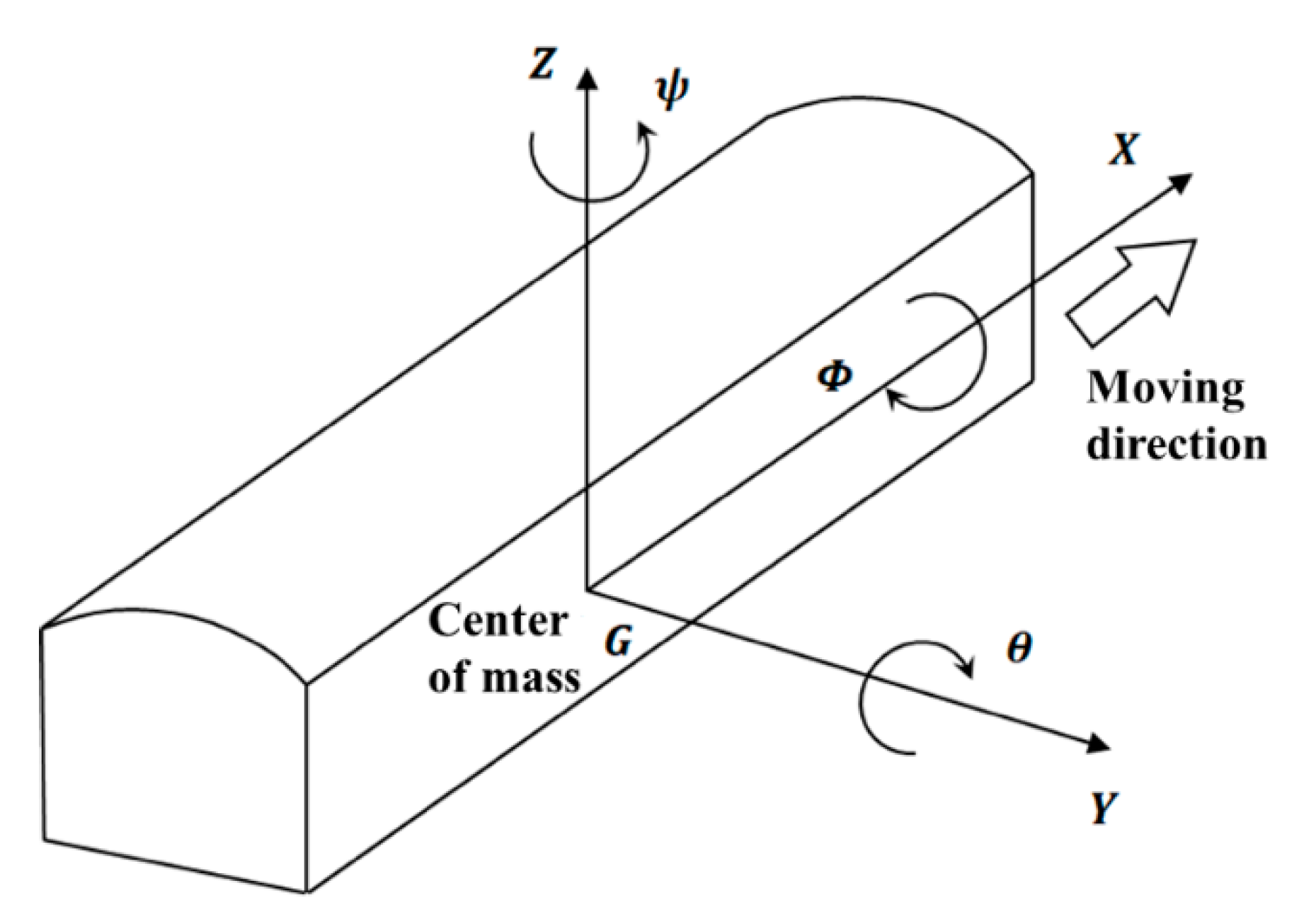
4.1.1. Vehicle Model Including Suspension System
4.1.2. Track and Trackbed Modeling
4.1.3. Numerical Analysis Model Considering Site Conditions
4.2. Validation of Numerical Modeling
4.3. Analysis of Dynamic Response of Concrete Slab Track
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, J.Y. Trackbed Stress Analysis under Concrete Slab Track According to Speed Variation of High Speed Train. Ph.D. Thesis, Seoul National University of Science and Technology, Seoul, Korea, 2018. [Google Scholar]
- Baek, C.J. A Numerical Study on the Behavior Characteristics with Different Loading Cases. Master’s Thesis, Seoul National University of Science and Technology, Seoul, Korea, 2014. [Google Scholar]
- Dimitrovová, Z.; Varandas, J.N. Critical velocity of a load moving on a beam with a sudden change of foundation stiffness: Applications to high-speed trains. Comput. Struct. 2009, 87, 1224–1232. [Google Scholar] [CrossRef]
- Ang, K.K.; Dai, J. Response analysis of high-speed rail system accounting for abrupt change of foundation stiffness. J. Sound Vibrat. 2013, 332, 2954–2970. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, C.; Chen, S.J.; Wang, Y.; Wang, W.; Duan, W.H. Dynamic responses of bridge–embankment transitions in high speed railway: Field tests and data analyses. Eng. Struct. 2018, 175, 565–576. [Google Scholar] [CrossRef]
- Gao, Y. A 3D dynamic train-track interaction model to study track performance under trains running at critical speed. Master’s Thesis, The Pennsylvania State University, State College, PA, USA, 2013. [Google Scholar]
- Lei, X.; Zhang, B. Influence of Track Stiffness Distribution on Vehicle and Track Interactions in Track Transition. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2010, 224, 592–604. [Google Scholar] [CrossRef]
- Dahlberg, T. Railway Track Stiffness Variations–Consequences and Countermeasures. Int. J. Civil Eng. 2010, 8, 1. [Google Scholar]
- Varandas, J.N.; Hölscher, P.; Silva, M.A.G. Dynamic behaviour of railway tracks on transitions zones. Comput. Struct. 2011, 89, 1468–1479. [Google Scholar] [CrossRef]
- Shahraki, M.; Warnakulasooriya, C.; Witt, K.J. Numerical study of transition zone between ballasted and ballastless railway track. Trans. Geotech. 2015, 3, 58–67. [Google Scholar] [CrossRef]
- Shan, Y.; Albers, B.; Savidis, S.A. Influence of different transition zones on the dynamic response of track–subgrade systems. Comput. Geotech. 2013, 48, 21–28. [Google Scholar] [CrossRef]
- Doyle, N.F. Railway Track Design: A Review of Current Practice; Australian Government Publisher Service: Canberra, Australia, 1980. [Google Scholar]
- Esveld, C. Modern Railway Track; MRT-Productions: Zaltbommel, The Netherlands, 2001; Volume 385. [Google Scholar]
- Lichtberger, B. Track Compendium: Track System, Substructure, Maintenance, Economics; Eurailpress: Hamburg, Germany, 2011. [Google Scholar]
- Shan, Y.; Shu, Y.; Zhou, S. Finite-infinite element coupled analysis on the influence of material parameters on the dynamic properties of transition zones. Construct. Build. Mater. 2017, 148, 548–558. [Google Scholar] [CrossRef]
- Eum, K.Y. Analysis on the Behavior of Trackbed under the Tilting Train Operation at the Curved Track and the Turnout System. Ph.D. Thesis, Seoul National University of Science and Technology, Seoul, Korea, 2008. [Google Scholar]
- Ordinance of Ministry of Land, Infrastructure and Transport. Enforcement Rule of Railway Vehicle Safety Criteria; Ministry of Land, Infrastructure and Transport: Sejong, Korea, 2013; Article 30 (2). [Google Scholar]
- Lee, J. Dynamic Characteristics of High Speed Railway Track with Hanging Sleepers. Ph.D. Thesis, Konkuk University, Seoul, Korea, 2005. [Google Scholar]
- UIC Code 713R. Design of Monoblock Concrete Sleepers; International Union of Railways: Paris, France, 2004. [Google Scholar]
- Sun, Y.Q.; Dhanasekar, M. A dynamic model for the vertical interaction of the rail track and wagon system. Int. J. Solids Struct. 2002, 39, 1337–1359. [Google Scholar] [CrossRef]
- Lei, X.; Noda, N.-A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile. J. Sound Vibrat. 2002, 258, 147–165. [Google Scholar] [CrossRef]
- Zhai, W.; Cai, Z. Dynamic interaction between a lumped mass vehicle and a discretely supported continuous rail track. Comput. Struct. 1997, 63, 987–997. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, Q.; Tan, S.J.; Zhong, W.X. A precise integration method for solving coupled vehicle–track dynamics with nonlinear wheel–rail contact. J. Sound Vibrat. 2012, 331, 4763–4773. [Google Scholar] [CrossRef]
- Psarropoulos, P.N.; Klonaris, G.; Gazetas, G. Seismic earth pressures on rigid and flexible retaining walls. Soil Dynam. Earth Eng. 2005, 25, 795–809. [Google Scholar] [CrossRef]
- Kim, D.R. A Study on the Deformation Behavior Characteristics of the Underground Pipe under the Influence of External Load. Master’s Thesis, Hanyang University, Seoul, Korea, 2007. [Google Scholar]
- Authority, Korea Rail Network. KR C-14040: Concrete Track Structure; Korea Rail Network Authority: Daejeon, Korea, 2019. [Google Scholar]




















| Classification | Material Properties | Classification | Material Properties |
|---|---|---|---|
| Speed (km/h) | 300 | Wheel diameter (mm) | 460 |
| Car body weight (kN) | 269.58 | Wheel elastic modulus (kN/m2) | 2.1 × 108 |
| Bogie weight (kN) | 11.87 | Bogie distance (m) | 14.0 |
| Wheel weight (kN) | 10.05 | wheelbase (m) | 3.0 |
| Primary suspension spring coefficient (kN/m) | 1.252 × 103 | Secondary suspension spring coefficient (kN/m) | 1.26 × 103 |
| Primary suspension damping factor (kN∙s/m) | 16.0 | Secondary suspension damping factor (kN∙s/m) | 28.5 |
| Number of bogies | 4 |
| Model Type | (kN/m3) | (Pa) | (kPa) | (°) | ||
|---|---|---|---|---|---|---|
| Rail | Elastic | 78.50 | 2.1 × 1011 | 0.3 | - | 0 |
| TCL | Elastic | 20.58 | 30.0 × 109 | 0.21 | - | 0 |
| HSB | Elastic | 20.58 | 13.0 × 109 | 0.25 | - | - |
| Abutment | Elastic | 24.50 | 20.0 × 109 | 0.21 | - | - |
| Cement treated gravel | Mohr–Coulomb | 20.50 | 2.5 × 108 | 0.21 | 20 | 35 |
| Gravel | Mohr–Coulomb | 19.60 | 1.6 × 108 | 0.21 | 35 | |
| Reinforced trackbed | Mohr–Coulomb | 19.60 | 1.6 × 108 | 0.21 | - | 35 |
| Upper trackbed | Mohr–Coulomb | 17.64 | 8.0 × 107 | 0.2 | 3.0 | 32 |
| Lower trackbed | Mohr–Coulomb | 17.64 | 6.0 × 107 | 0.2 | 5.0 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Kim, J.Y.; Kim, J.; Lee, S.; Cho, K.-H. Analysis of Dynamic Characteristics of Deformed Concrete Slab Track on Transition Zone in High-Speed Train Line According to Train Speeds. Appl. Sci. 2020, 10, 7174. https://doi.org/10.3390/app10207174
Park S, Kim JY, Kim J, Lee S, Cho K-H. Analysis of Dynamic Characteristics of Deformed Concrete Slab Track on Transition Zone in High-Speed Train Line According to Train Speeds. Applied Sciences. 2020; 10(20):7174. https://doi.org/10.3390/app10207174
Chicago/Turabian StylePark, Sungbum, Ja Yeon Kim, Jongwon Kim, Sehee Lee, and Kook-Hwan Cho. 2020. "Analysis of Dynamic Characteristics of Deformed Concrete Slab Track on Transition Zone in High-Speed Train Line According to Train Speeds" Applied Sciences 10, no. 20: 7174. https://doi.org/10.3390/app10207174
APA StylePark, S., Kim, J. Y., Kim, J., Lee, S., & Cho, K.-H. (2020). Analysis of Dynamic Characteristics of Deformed Concrete Slab Track on Transition Zone in High-Speed Train Line According to Train Speeds. Applied Sciences, 10(20), 7174. https://doi.org/10.3390/app10207174





