An Improved Investigation into the Effects of the Temperature-Dependent Parasitic Elements on the Losses of SiC MOSFETs
Abstract
:Featured Application
Abstract
1. Introduction
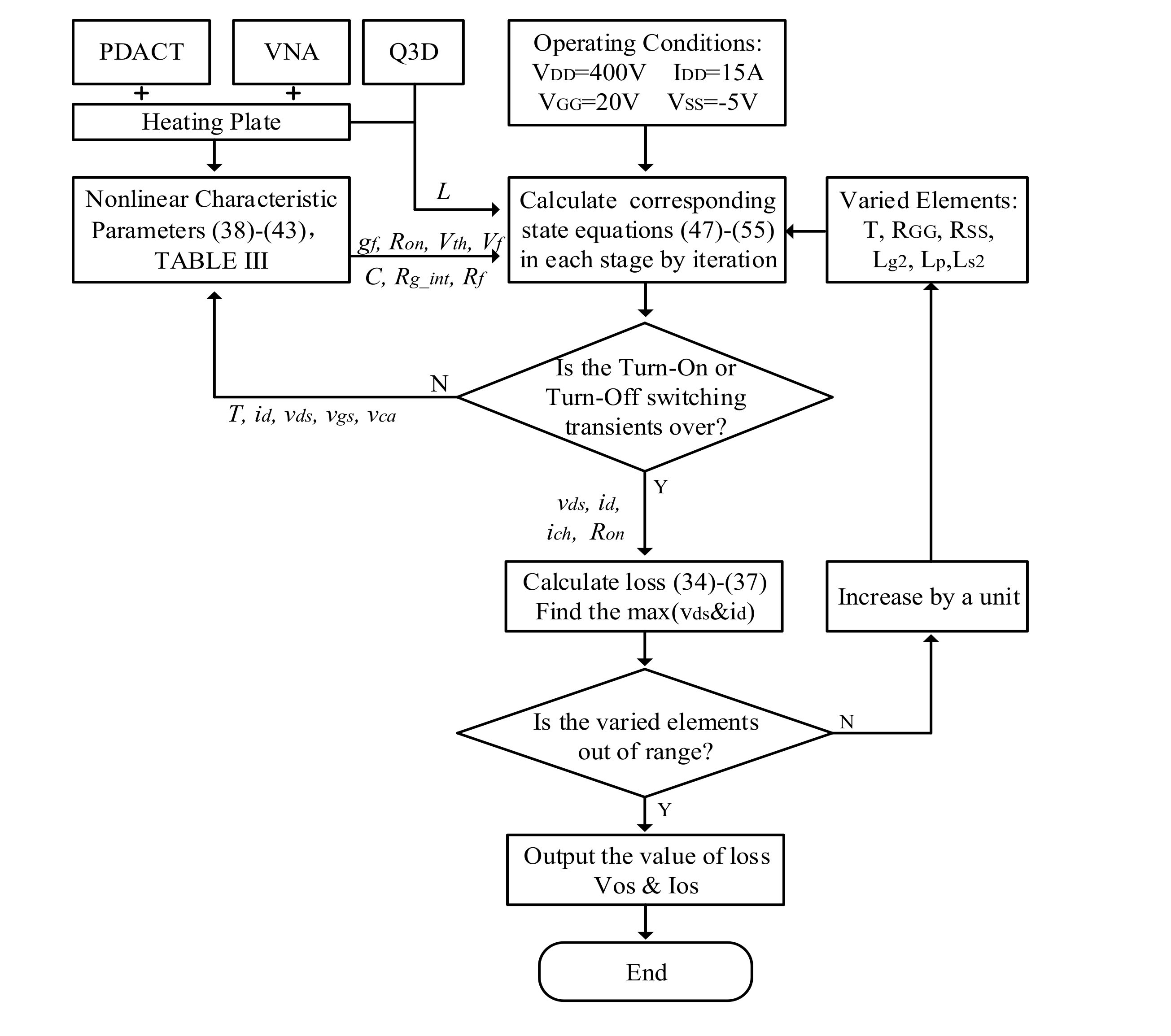
2. The Basis of the Analytical Model
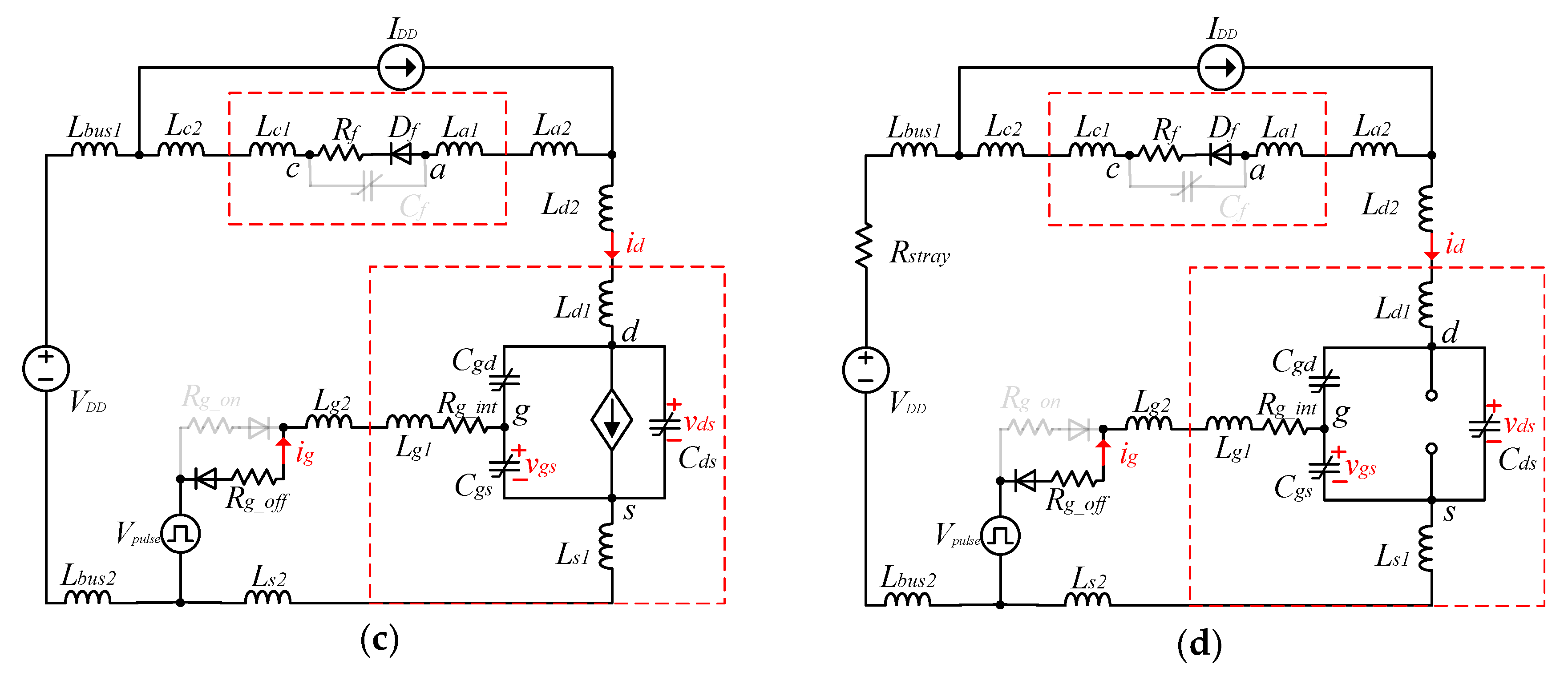
3. Analysis of the Switching Transients
3.1. Turn-On Switching Transients
3.2. Turn-Off Switching Transients
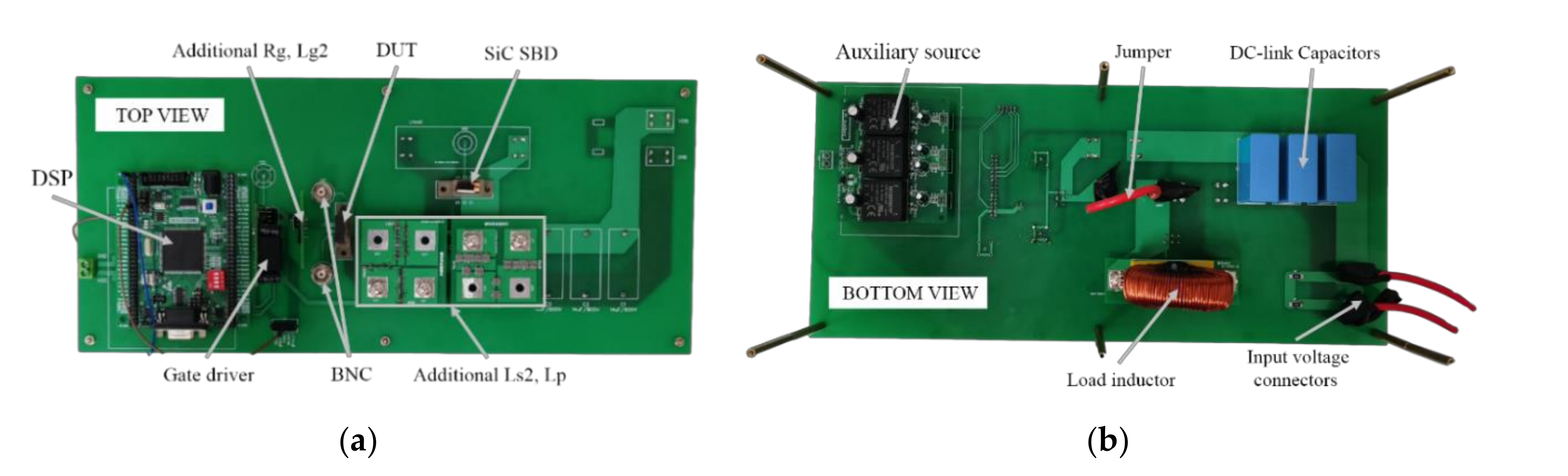
4. Experimental Setup
4.1. Static Characteristic Test Platform
4.2. ANSYS Q3D Extractor
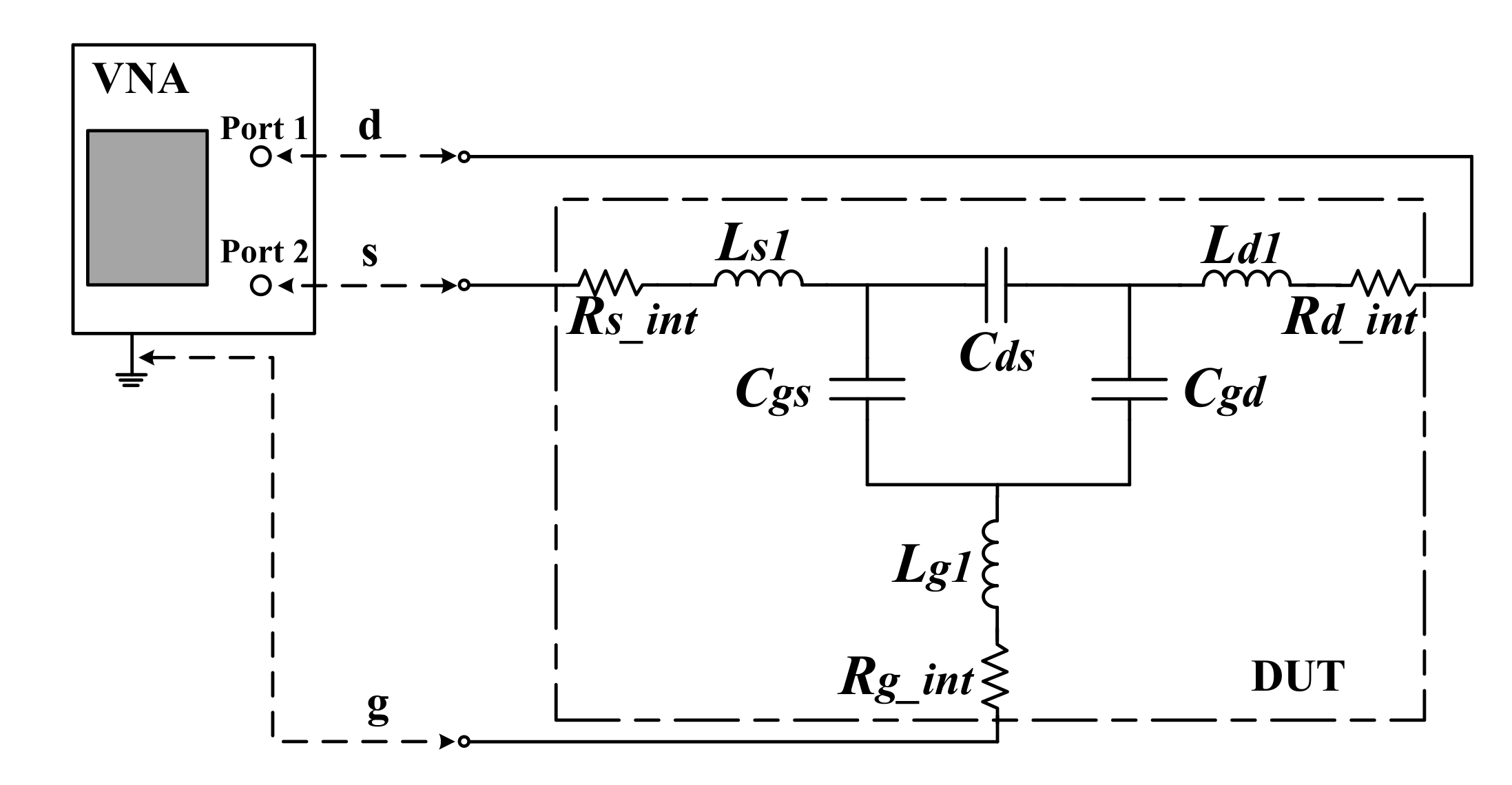
4.3. Vector Network Analyzer
5. Results
5.1. Experimental Results
5.2. Fitting to the Key Parameters
5.3. Loss Assessment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Baliga, B.J. Fundamentals of Power Semiconductor Devices; Springer: New York, NY, USA, 2008. [Google Scholar]
- Ning, P.; Wang, F.; Ngo, K.D. High-temperature SiC power module electrical evaluation procedure. IEEE Trans. Power Electron. 2011, 26, 3079–3083. [Google Scholar] [CrossRef]
- Han, D.; Noppakunkajorn, J.; Sarlioglu, B. Efficiency comparison of SiC and Si-Based bidirectional DC-DC converters. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Piscataway, NJ, USA, 16–19 June 2013; pp. 1–7. [Google Scholar]
- Josifovic, I.; Popovic-Gerber, J.; Ferreira, J.A. Improving SiC JFET switching behavior under influence of circuit parasitic. IEEE Trans. Power Electron. 2012, 27, 3843–3854. [Google Scholar] [CrossRef]
- Yan, Q.; Yuan, X.; Geng, Y.; Charalambous, A.; Wu, X. Performance evaluation of split output converters with SiC MOSFETs and SiC schottky diodes. IEEE Trans Power Electron. 2017, 32, 406–422. [Google Scholar] [CrossRef] [Green Version]
- Kadavelugu, A.; Baek, S.; Dutta, S.; Bhattacharya, S.; Das, M.; Agarwal, A.; Scofield, J. High-frequency design considerations of dual active bridge 1200 V SiC MOSFET dc-dc converter. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 314–320. [Google Scholar]
- Wang, Y.; de Haan, S.W.H.; Ferreira, J.A. Potential of improving PWM converter power density with advanced components. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Ren, Y.; Xu, M.; Zhou, J.; Lee, F.C. Analytical loss model of power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- Rainer, K.; Alberto, C. A physics-based compact model of SiC power MOSFETs. IEEE Trans. Power Electron. 2016, 31, 5863–5870. [Google Scholar]
- Kumar, P.; Bhowmick, B. A physics-based threshold voltage model for hetero-dielectric dual material gate Schottky barrier MOSFET. Int. J. Numer. Model. 2018, 31, 1–11. [Google Scholar] [CrossRef]
- Boram, Y.; Yeong-Hun, P.; Ji-Woon, Y. Physics-based compact model of transient leakage current caused by parasitic bipolar junction transistor in gate-all-around MOSFETs. Solid State Electron. 2020, 164, 1–12. [Google Scholar]
- Potbhare, S.; Goldsman, N.; Lelis, A.; McGarrity, J.M.; McLean, F.B.; Habersat, D. A physical model of high temperature 4H-SiC MOSFETs. IEEE Trans. Electron. Devices 2008, 55, 2029–2039. [Google Scholar] [CrossRef]
- Fu, R.; Grekov, A.; Peng, K.; Santi, E. Parasitic modeling for accurate inductive switching simulation of converters using SiC devices. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1259–1265. [Google Scholar]
- Wang, J.; Zhao, T.; Li, J.; Huang, A.Q.; Callanan, R.; Husna, F. Characterization, modeling, and application of 10-kV SiC MOSFET. IEEE Trans. Electron Devices 2008, 55, 1798–1806. [Google Scholar] [CrossRef]
- Sun, K.; Wu, H.; Lu, J.; Xing, Y.; Huang, L. Improved modeling of medium voltage SiC MOSFET within wide temperature range. IEEE Trans. Power Electron. 2014, 29, 2229–2236. [Google Scholar] [CrossRef]
- Jin, M.; Gao, Q.; Wang, Y.; Xu, D. A temperature-dependent sic MOSFET modeling method based on MATLAB/Simulink. IEEE Access 2018, 6, 4497–4505. [Google Scholar] [CrossRef]
- Zhang, Z.; Eberle, W.; Yang, Z.; Liu, Y.; Sen, P. Optimal design of resonant gate driver for buck converter based on a new analytical loss model. IEEE Trans. Power Electron. 2008, 23, 653–666. [Google Scholar] [CrossRef]
- Eberle, W.; Zhang, Z.; Liu, Y.; Sen, P. A practical switching loss model for buck voltage regulator. IEEE Trans. Power Electron. 2009, 24, 700–713. [Google Scholar] [CrossRef]
- Rodríguez, M.; Rodriguez, A.; Miaja, P.F.; Lamar, D.G.; Zúniga, J.S. An insight into the switching process of power MOSFETs: an improved analytical losses model. IEEE Trans. Power Electron. 2010, 25, 1626–1640. [Google Scholar] [CrossRef]
- Wang, J.; Chung, H.S. Impact of parasitic elements on the spurious triggering pulse in synchronous buck converter. IEEE Trans. Power Electron. 2014, 29, 6672–6685. [Google Scholar] [CrossRef]
- Wang, J.; Li, R.T.; Chung, H.S. An investigation into the effects of the gate drive resistance on the losses of the MOSFET–Snubber–Diode configuration. IEEE Trans. Power Electron. 2012, 27, 2657–2672. [Google Scholar] [CrossRef]
- Wang, J.; Chung, H.S.; Li, R.T. Characterization and experimental assessment of the effects of parasitic elements on the MOSFET switching performance. IEEE Trans. Power Electron. 2013, 28, 573–590. [Google Scholar] [CrossRef]
- Liang, M.; Zheng, T.Q.; Li, Y. An improved analytical model for predicting the switching performance of SiC MOSFETs. J. Power Electron. 2016, 16, 374–387. [Google Scholar] [CrossRef] [Green Version]
- Christen, D.; Biela, J. Analytical switching loss modeling based on datasheet parameters for MOSFETs in a half-bridge. IEEE Trans. Power Electron. 2019, 34, 3700–3710. [Google Scholar] [CrossRef]
- Williams, R.K.; Darwish, M.N.; Blanchard, R.A.; Siemieniec, R.; Rutter, P.; Kawaguchi, Y. The trench power MOSFET—Part II: application specific VDMOS, IDMOS, packaging, and reliability. IEEE Trans. Electron Devices 2017, 64, 692–712. [Google Scholar] [CrossRef]
- Mihir, M.; Shanmin, A.; Nance, E.; Frank, S.S. Datasheet driven silicon carbide power MOSFET model. IEEE Trans. Power Electron. 2014, 29, 2220–2228. [Google Scholar]
- IEC 60747-8:2010.Semiconductor Devices—Discrete Devices—Part 8: Field-Effect Transistors. Available online: https://webstore.iec.ch/ publication /3289 (accessed on 18 July 2019).
- CREE SiC MOSFET C2M0025120D Datasheet. Available online: https://www.wolfspeed.com/media/downloads/161 C2M0025120D.pdf (accessed on 24 July 2019).
- CREE SiC Diode C4D20120D Datasheet. Available online: https://www.wolfspeed.com/media/downloads/106/C4D20120D.pdf (accessed on 8 August 2019).
- Lee, H.; Smet, V.; Tummala, R. A review of sic power module packaging technologies: Challenges, advances, and emerging issues. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 239–255. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Lee, F.C.; Li, Q. Package parasitic inductance extraction and simulation model development for the high voltage cascade GaN HEMT. IEEE Trans. Power Electron. 2014, 29, 1977–1985. [Google Scholar] [CrossRef]
- Liu, T.; Wong, T.T.Y.; Shen, Z.J. A new characterization technique for extracting parasitic inductances of sic power MOSFETs in discrete and module packages based on two-port s-parameters measurement. IEEE Trans. Power Electron. 2018, 33, 9819–98331985. [Google Scholar] [CrossRef]
- Keysight Technologies, Application Note 1287-9, In-Fixture Measurements Using Vector Network Analyzers. 2017. Available online: https://www.keysight.com/cn/zh/assets/7018-06814/application-notes/5968-5329.pdf (accessed on 6 May 2020).
- Liu, T.; Feng, Y.; Ning, R.; Wong, T.T.; Shen, Z.J. Extracting parasitic inductances of IGBT power modules with two-port S-parameter measurement. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 281–287. [Google Scholar]
- Chen, K.; Zhao, Z.; Yuan, L.; Lu, T.; He, F. The impact of nonlinear junction capacitance on switching transient and its modeling for SiC MOSFET. IEEE Trans. Electron. Devices 2015, 62, 333–338. [Google Scholar] [CrossRef]
- Costinett, D.; Maksimovic, D.; Zane, R. Circuit-oriented treatment of nonlinear capacitances in switched-mode power supplies. IEEE Trans. Power Electron. 2015, 30, 985–995. [Google Scholar] [CrossRef]
- Ahmed, M.R.; Todd, R.; Forsyth, A.J. Predicting SiC MOSFET behavior ender hard-switching, soft-switching, and false turn-on conditions. IEEE Trans. Ind. Electron. 2017, 64, 9001–9011. [Google Scholar] [CrossRef]
- Wang, J.; Chung, S.H. A novel RCD level shifter for elimination of spurious turn-on in the bridge-leg configuration. IEEE Trans. Power Electron. 2015, 30, 976–984. [Google Scholar] [CrossRef]

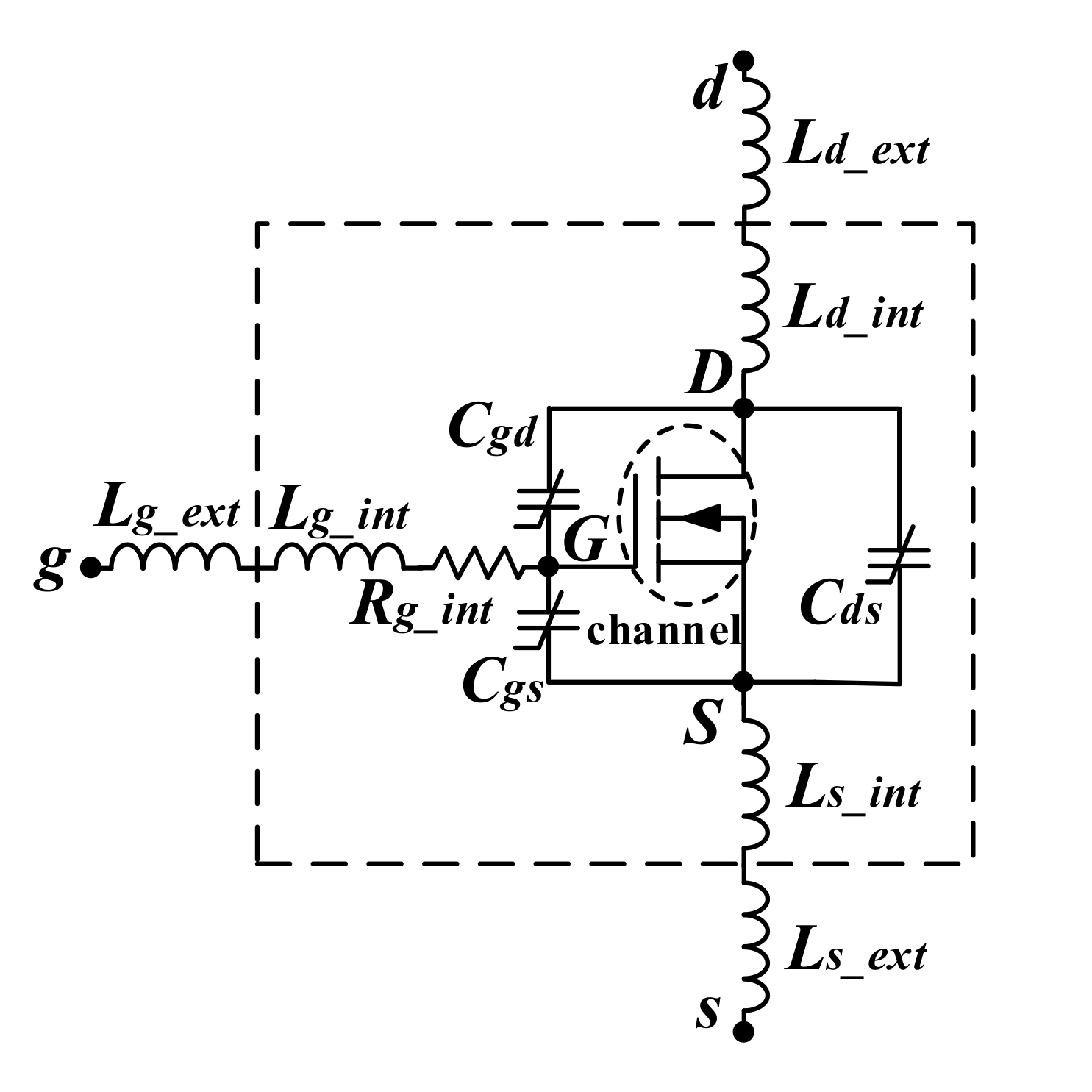
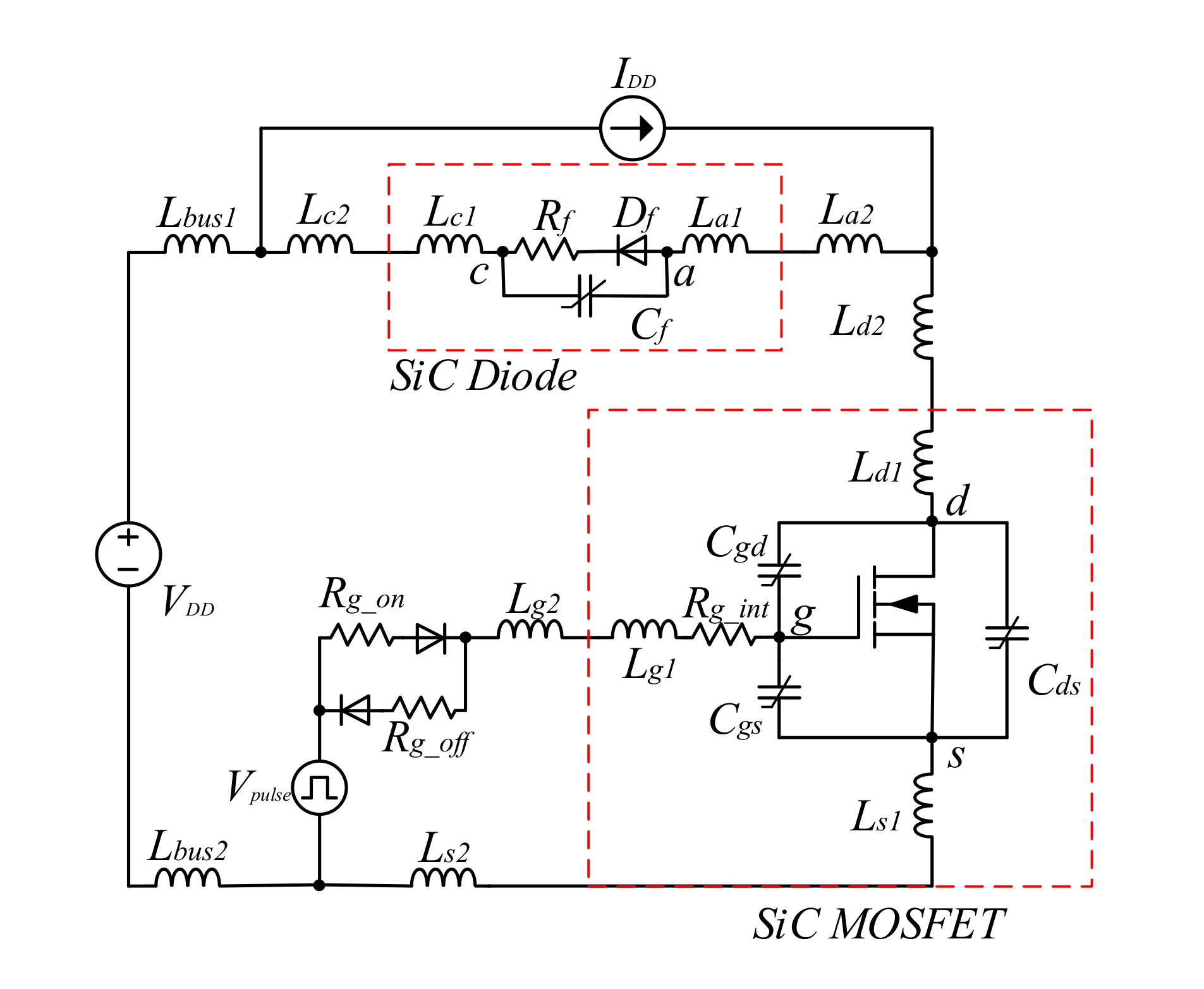
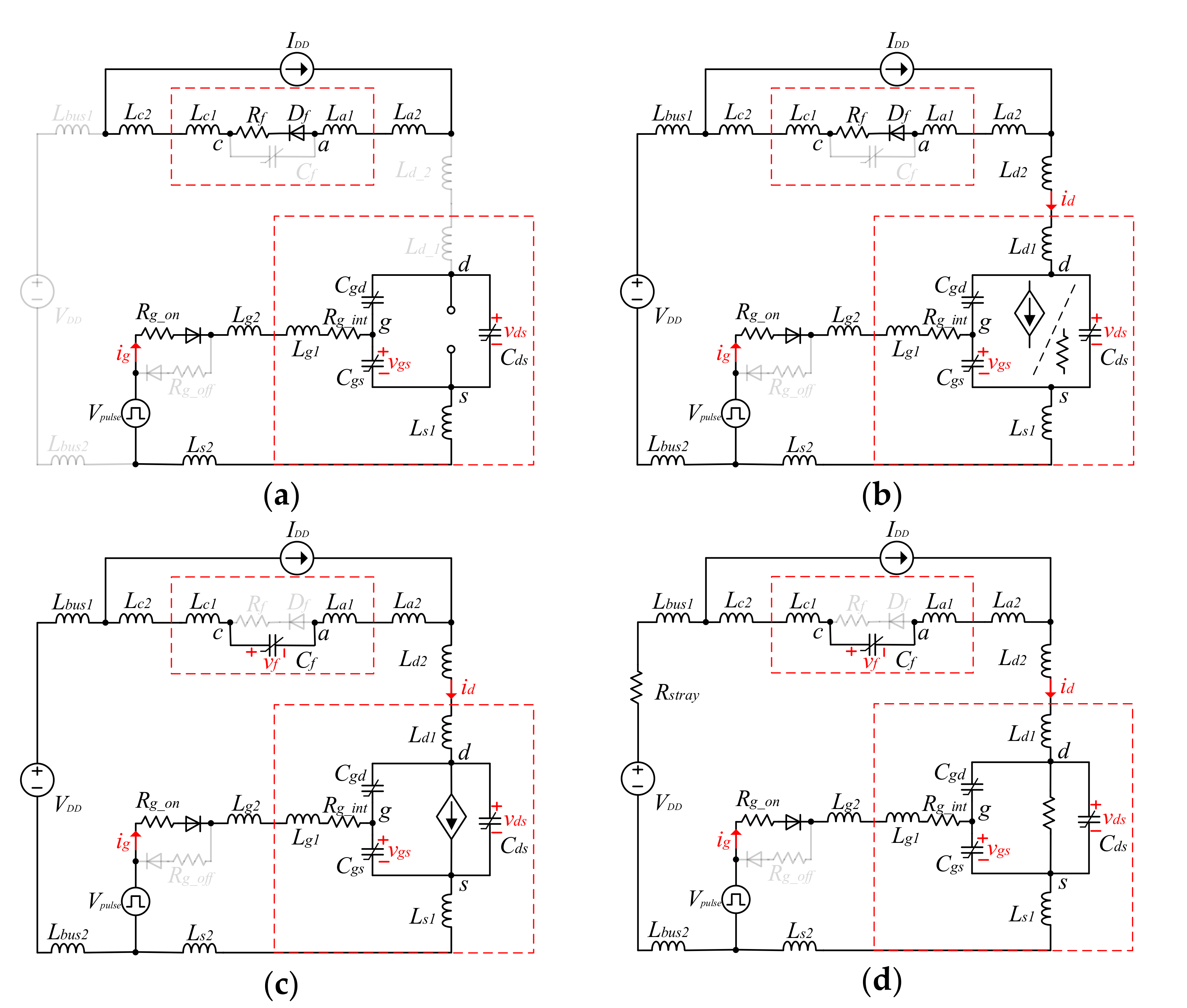
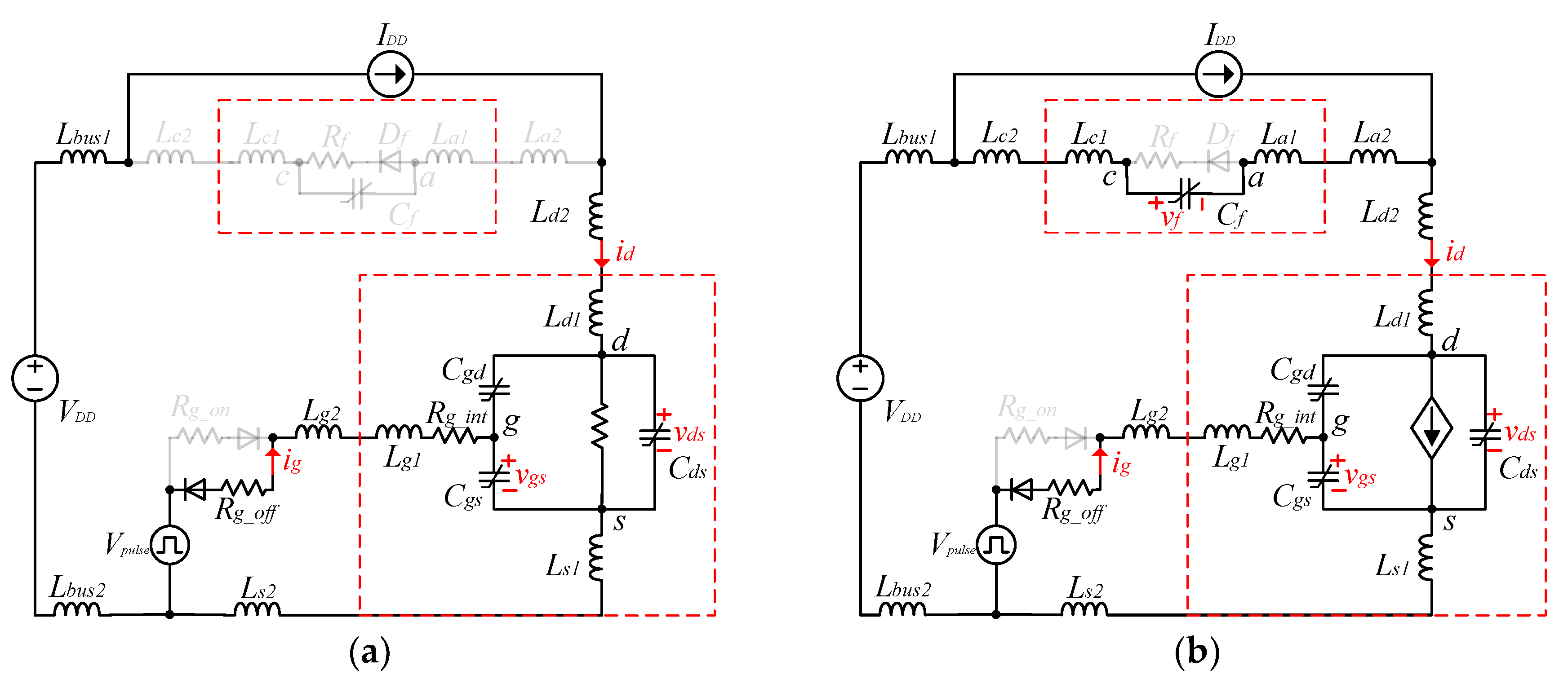


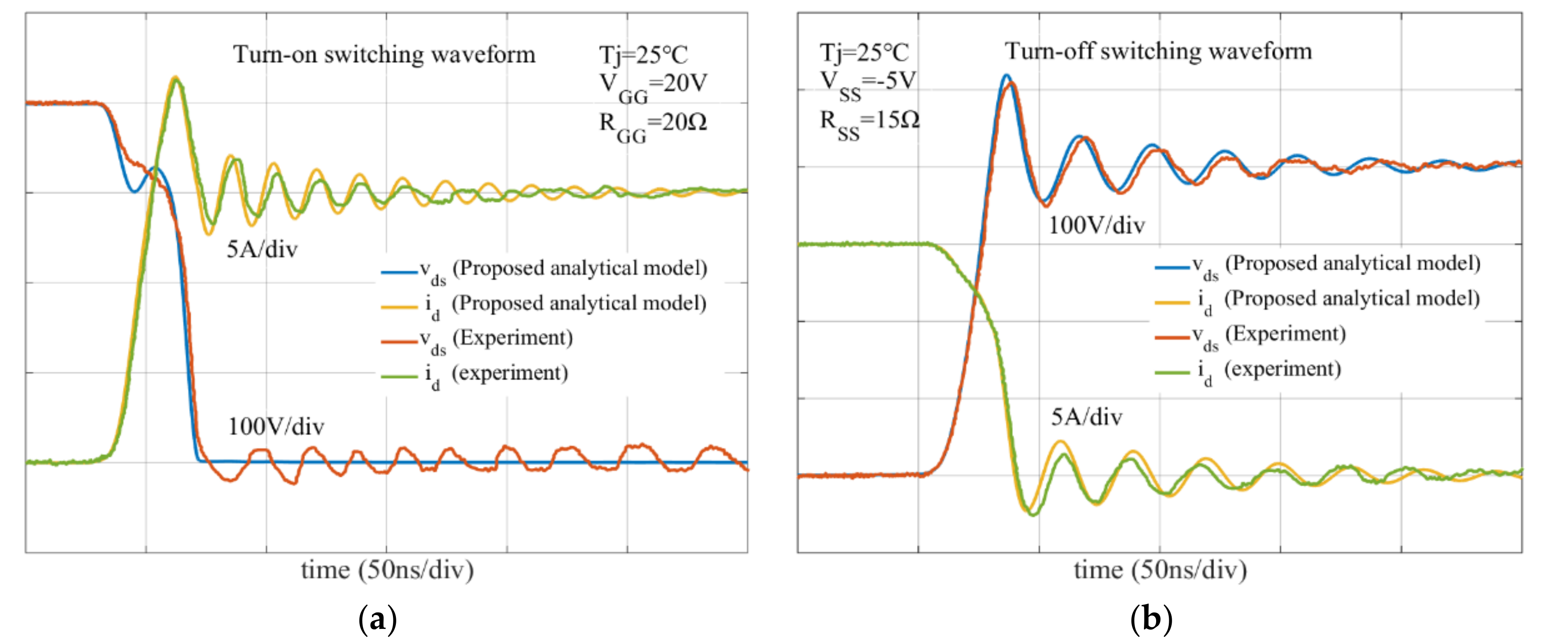
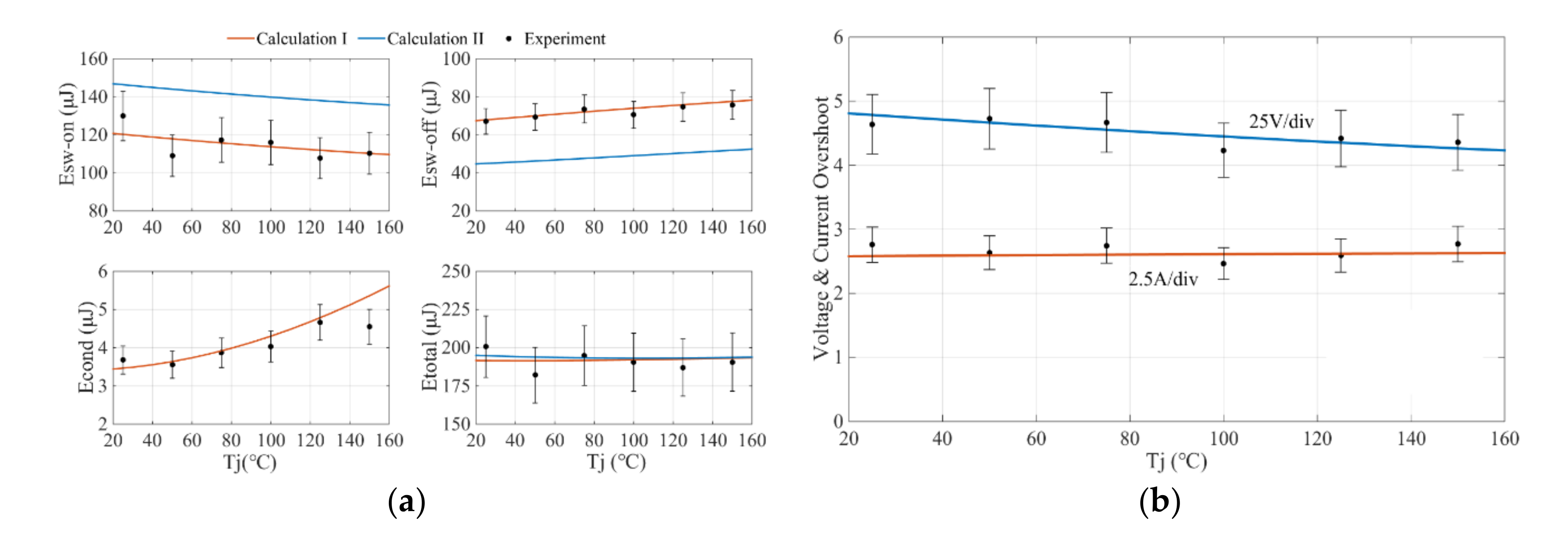
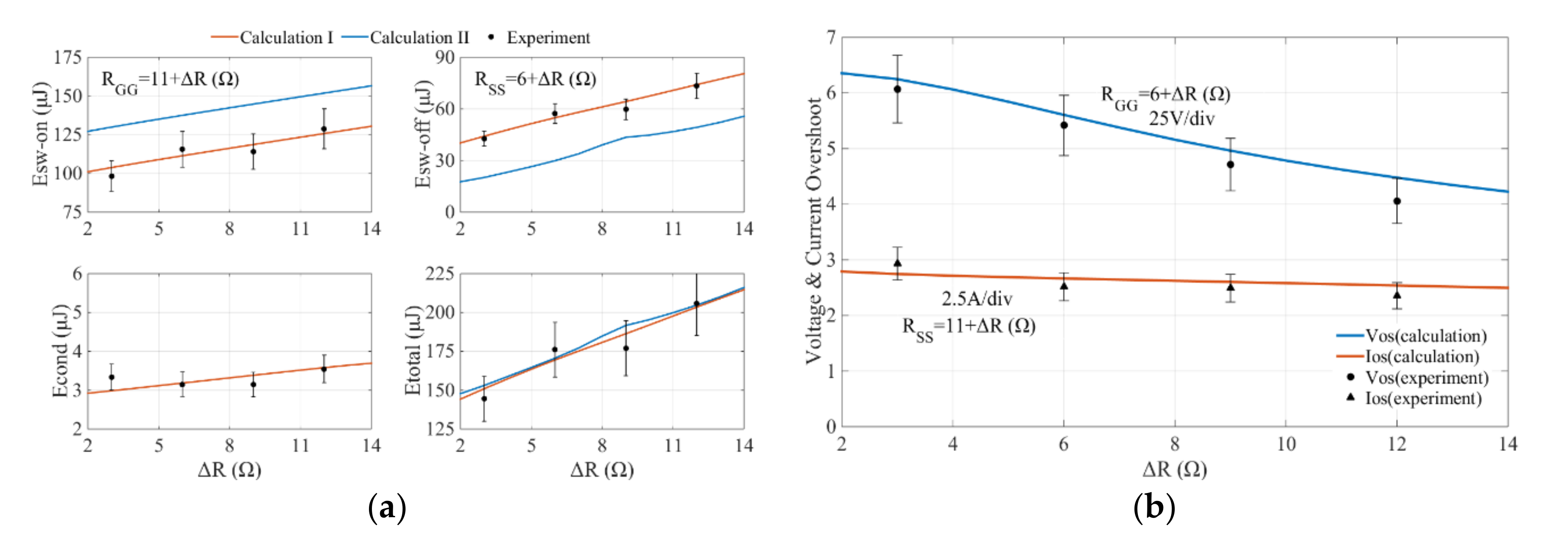
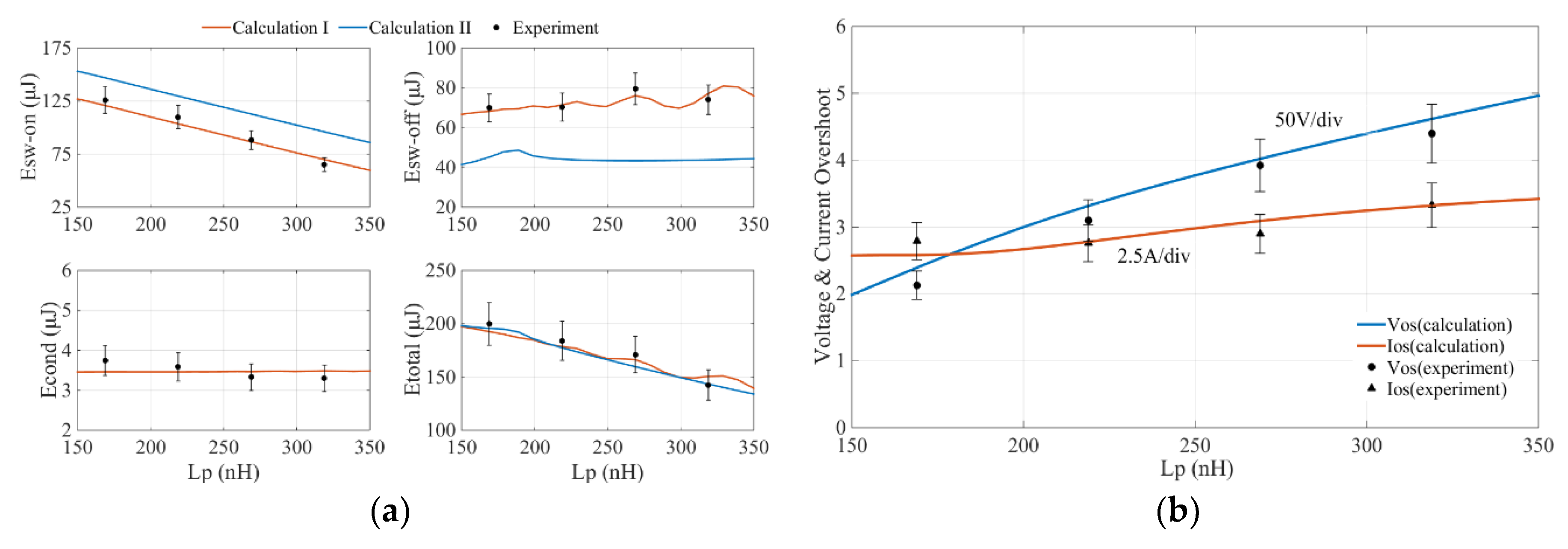
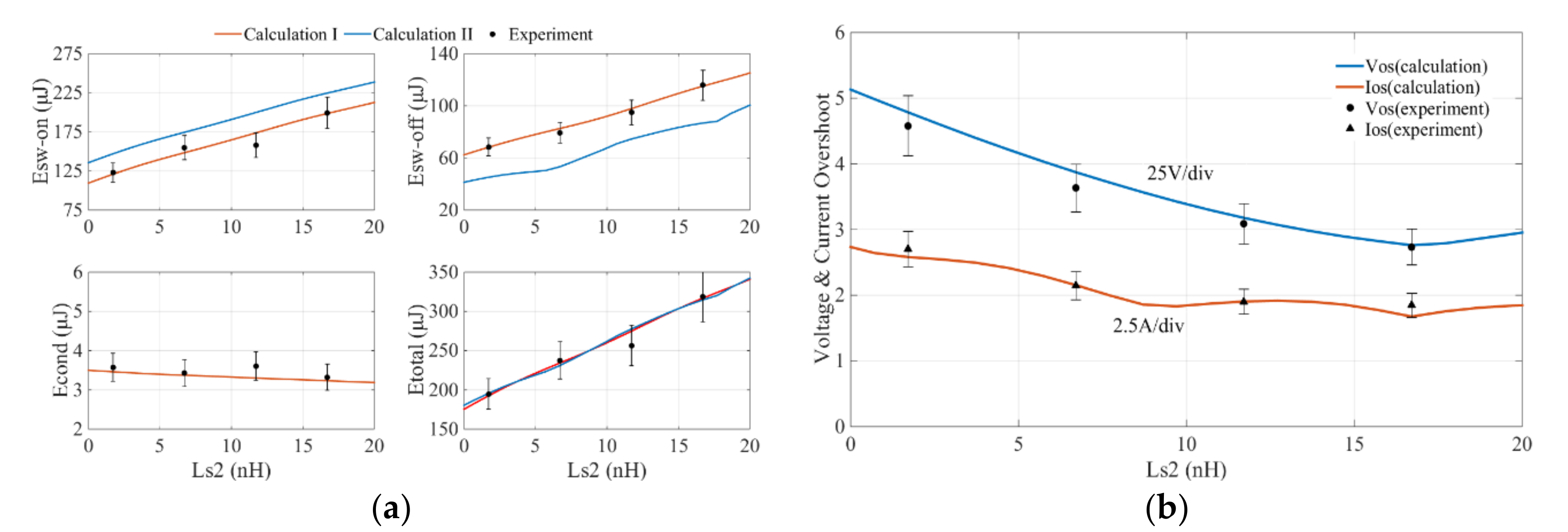
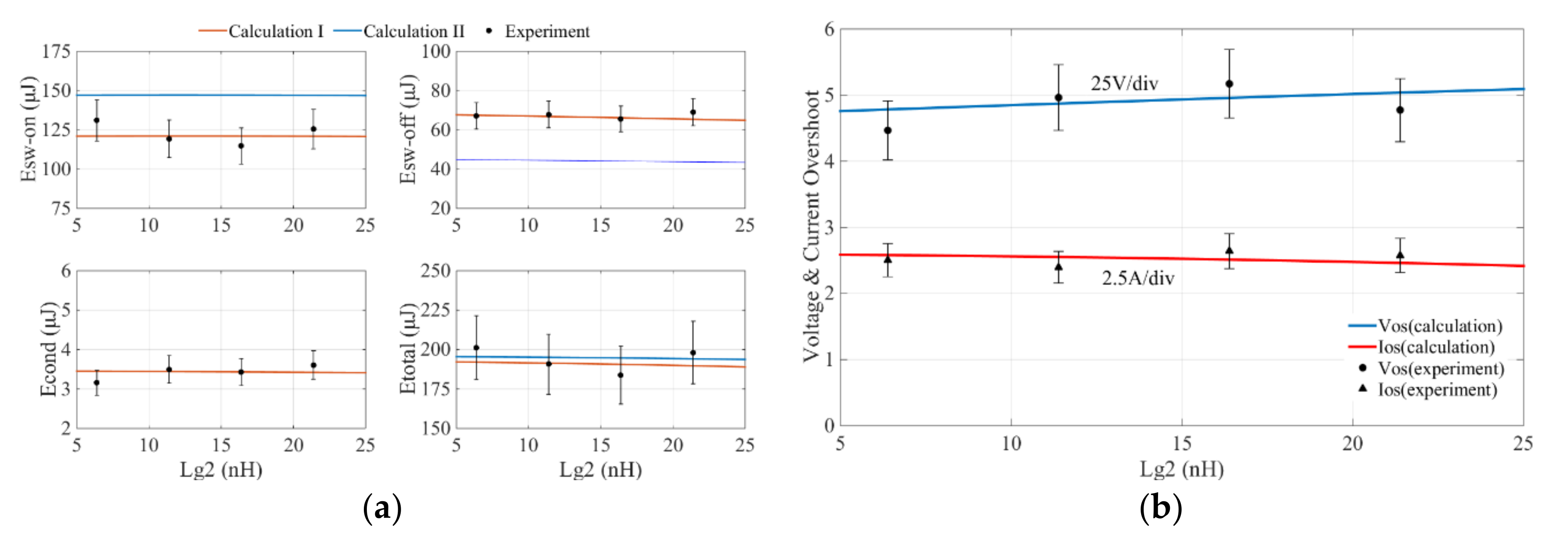
| Static Characteristic | Part Number | Parameter | Gate-Source Voltage/Step | Applied Voltage/Step | Temperature/Step |
|---|---|---|---|---|---|
| Transfer characteristic | B1510A and B1512A | gf | 0 to 12 V/0.25 V | 20 V (fixed) | 25 to 150 °C/25 °C |
| Output characteristic | Ron | 10 to 20 V/2 V | 0 to 10 V/2 V | ||
| Threshold voltage | Vth, Vf | 0 to 5 V/0.1 V | 10 V, Id = 15 mA (fixed) | 25 to 145 °C/10 °C | |
| Junction capacitance | B1520A | Ciss, Coss, Ciss, Cf | Sweep signal | Applied voltage | Temperature/step |
| VAC = 25 mV, f = 1 MHz | 0 to 1000 V | 25 to 150 °C/25 °C |
| Q3D | Parameter | Lbus1 | Lbus2 | Lc2 | La2 | Lg2 | Ld2 | Ls2 | Rstray | ||
| Value(nH) | 51.24 | 72.85 | 4.25 | 4.12 | 6.39 | 12.08 | 1.71 | 1.85 Ω | |||
| VNA | Package | TO-247-3 | TO-220-2 | ||||||||
| Parameter | Lg1 (nH) | Ld1 (nH) | Ls1 (nH) | La1 + Lc1 (nH) | |||||||
| Maximum | 9.57 (@ 50 °C) | 4.71 (@ 25 °C) | 8.39 (@ 50 °C) | 10.12 (@ 25 °C) | |||||||
| Minimum | 9.13 (@ 75 °C) | 4.54 (@ 125 °C) | 8.06 (@ 150 °C) | 9.79 (@ 100 °C) | |||||||
| Difference | 4.77% | 3.79% | 4.21% | 3.34% | |||||||
| Average | 9.218 | 4.623 | 8.176 | 9.889 | |||||||
| Cf (pF) | ||
| Ciss (pF) | 4000 | 3300 |
| Coss (pF) | ||
| Crss (pF) |
| Part No. | Description | Bandwidth | Measured Signal |
|---|---|---|---|
| RTH1004 | Oscilloscope | 500 MHz | |
| RT-ZI10 | Passive probe | 500 MHz | vds |
| TPP0201 | Passive probe | 200 MHz | vgs |
| TCP0030A | Current probe | 120 MHz | id |
| Experiment | Calculation I | Error | |
|---|---|---|---|
| Esw-on(μJ) | 119.06 | 121.05 | 1.67% |
| Esw-off(μJ) | 66.27 | 67.51 | 1.87% |
| Econd(μJ) | 3.71 | 3.45 | 7.01% |
| Vos(V) | 111.65 | 119.61 | 7.13% |
| Ios(A) | 6.22 | 6.45 | 3.70% |
| Elements | T | Rg | Lp | Ls2 | Lg2 |
|---|---|---|---|---|---|
| Esw-on | ↓ | ↑ | ↓ | ↑ | → |
| Esw-off | ↑ | ↑ | → | ↑ | → |
| Etotal | → | ↑ | ↓ | ↑ | → |
| Vos | ↓ | ↓ | ↑ | ↓ | → |
| Ios | → | ↓ | ↑ | ↓ | → |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Yi, Y.; Liu, P. An Improved Investigation into the Effects of the Temperature-Dependent Parasitic Elements on the Losses of SiC MOSFETs. Appl. Sci. 2020, 10, 7192. https://doi.org/10.3390/app10207192
Zeng Y, Yi Y, Liu P. An Improved Investigation into the Effects of the Temperature-Dependent Parasitic Elements on the Losses of SiC MOSFETs. Applied Sciences. 2020; 10(20):7192. https://doi.org/10.3390/app10207192
Chicago/Turabian StyleZeng, Yinong, Yingping Yi, and Pu Liu. 2020. "An Improved Investigation into the Effects of the Temperature-Dependent Parasitic Elements on the Losses of SiC MOSFETs" Applied Sciences 10, no. 20: 7192. https://doi.org/10.3390/app10207192
APA StyleZeng, Y., Yi, Y., & Liu, P. (2020). An Improved Investigation into the Effects of the Temperature-Dependent Parasitic Elements on the Losses of SiC MOSFETs. Applied Sciences, 10(20), 7192. https://doi.org/10.3390/app10207192




