Particle Swarm Optimization of a Passivity-Based Controller for Dynamic Positioning of Ships
Abstract
:1. Introduction
2. The Port-Hamiltonian Modeling of the Surface Ship
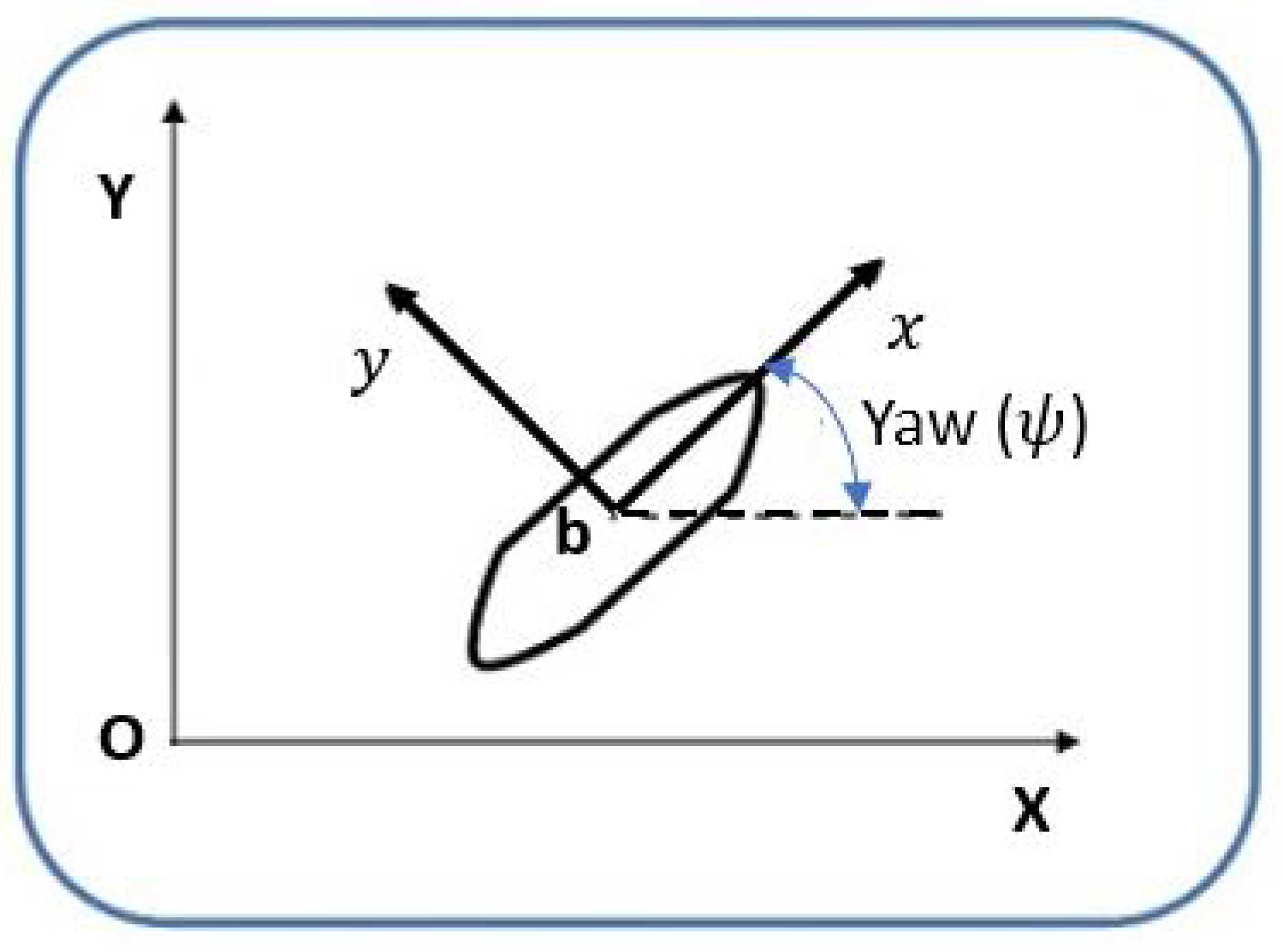
2.1. The DP System Overview
- Power System. It compromises all components and units responsible to supply the DP system with its power requirements including: Prime movers, Generators, Switchboards, Electrical distribution system (cabling and piping), transformers. It may also include more advanced subsystems for energy storage and power management purposes.
- Thruster system. The vessel’s horizontal motion is influenced and controlled by means of thrusters and propellers which are also the sole source of position/heading keeping. They supply the DP system with thrust force and direction and it includes thrusters with electronic drive units, propellers and rudders, cabling and piping and other associated auxiliary subsystems.
- Control System. it compromises all hardware and software components including processors and computers, joystick control unit, Sensors and instrumentation and signal processing units, Position and heading reference systems (navigation, acoustic, microwaves and laser systems), operator and display panels.
2.2. The Mathematical Model
3. The IDA-PBC Controller Design
4. The PSO Method for DP of Ship
4.1. An Overview of PSO Method
4.2. Application of PSO Algorithm for DP of Ship
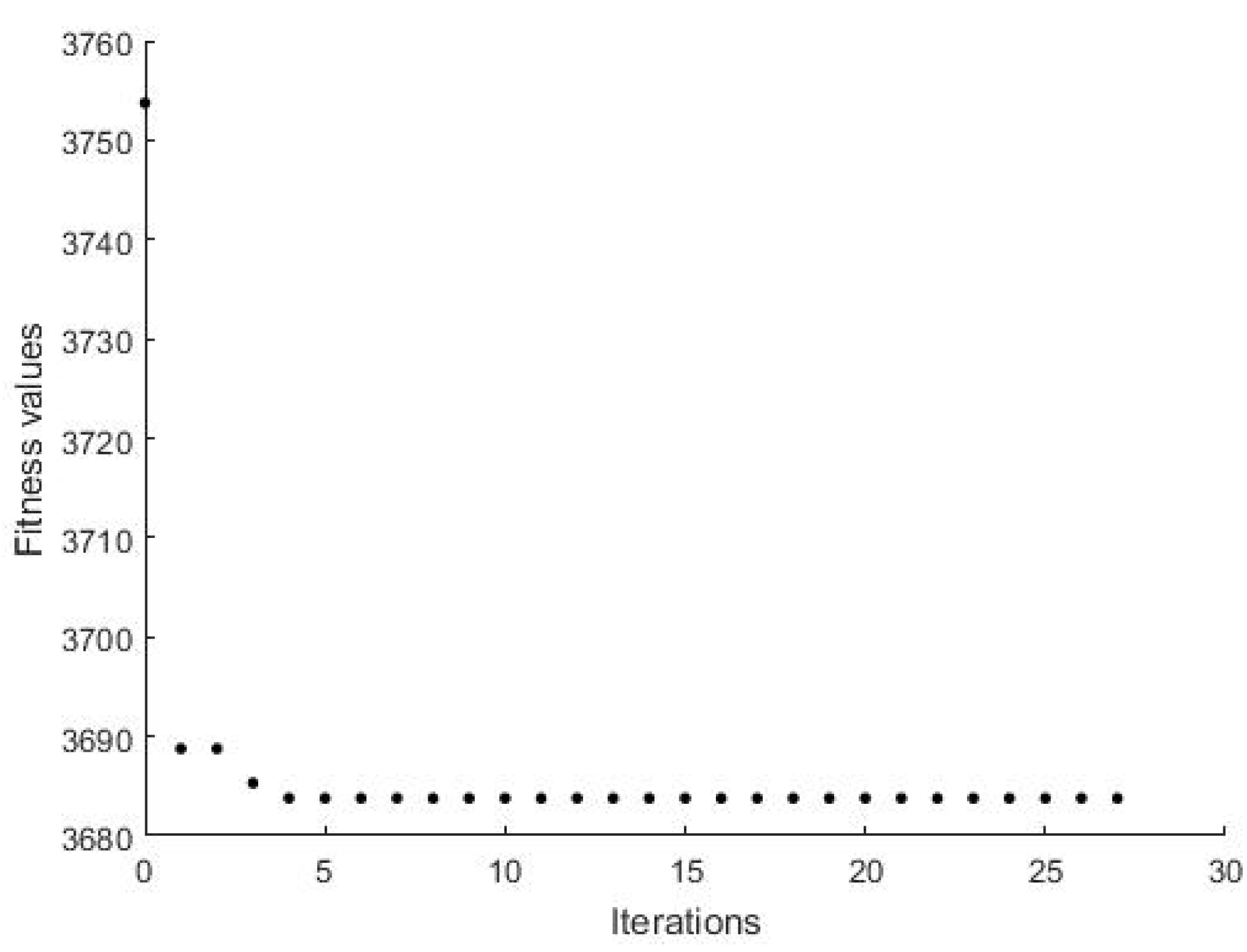
4.3. Convergence to the Optimal Solution Using PSO Method
5. Numerical Simulations
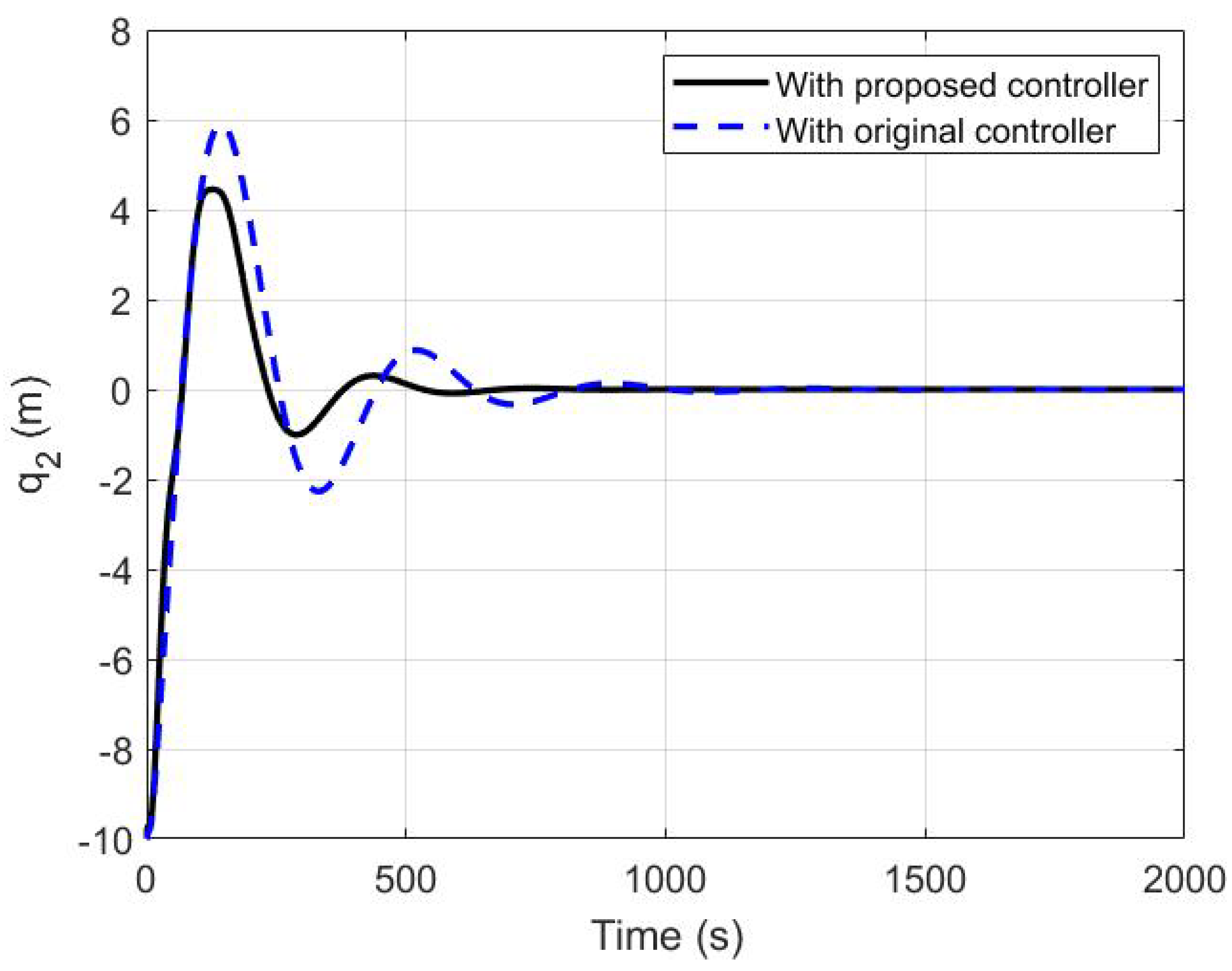
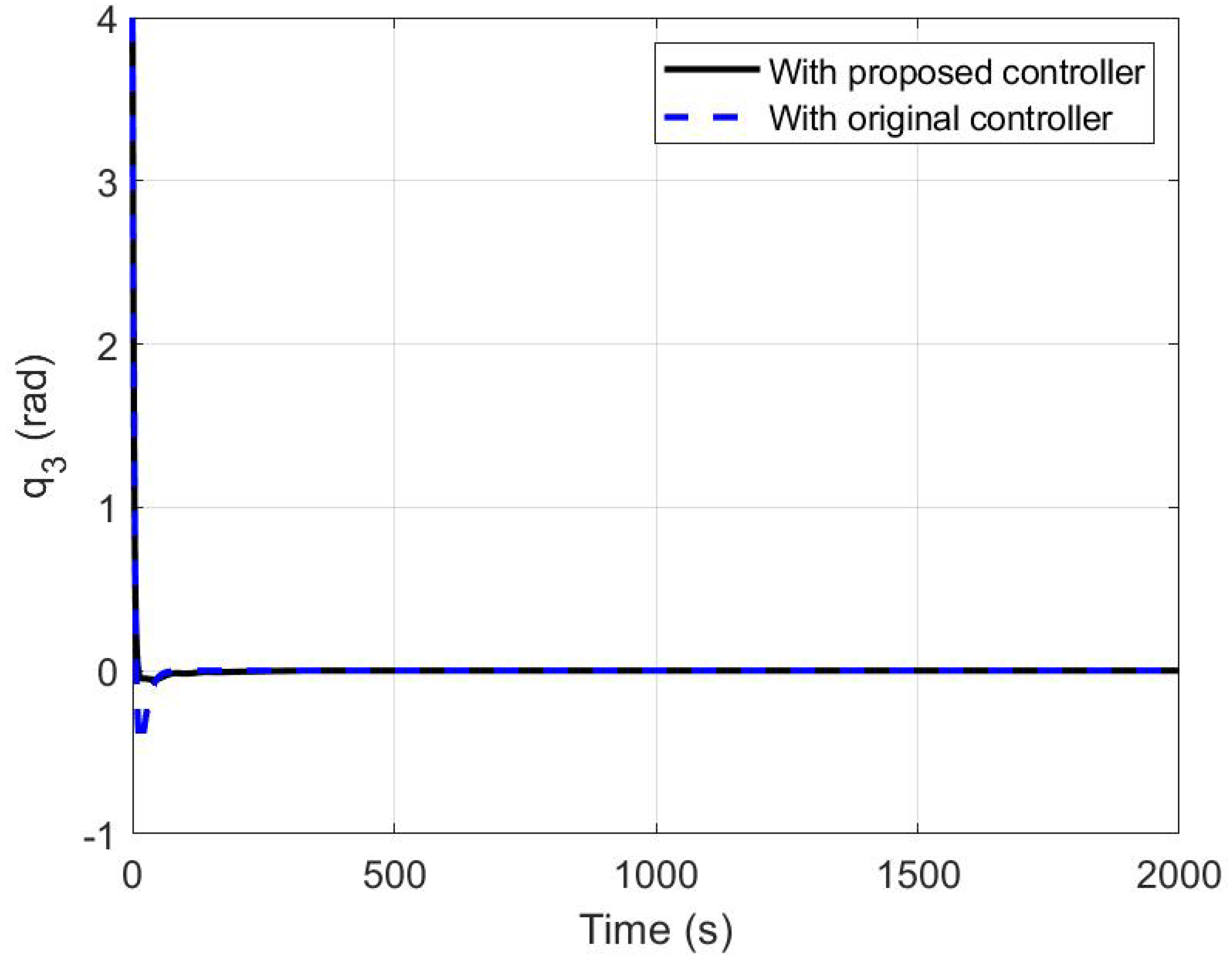
5.1. A Comparison between the Modified and the Original Controllers
5.2. The PSO Tuning of the Proposed Controller
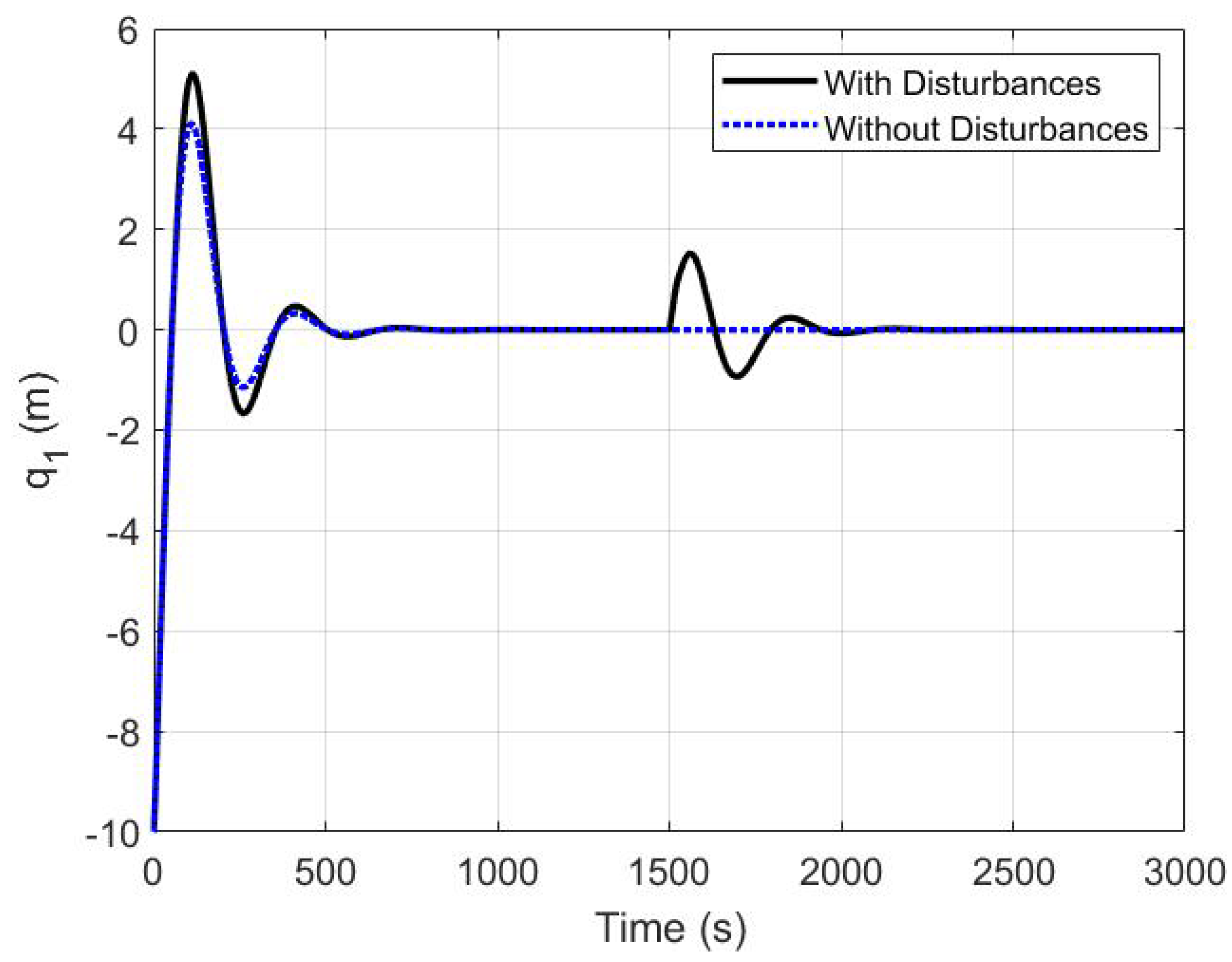
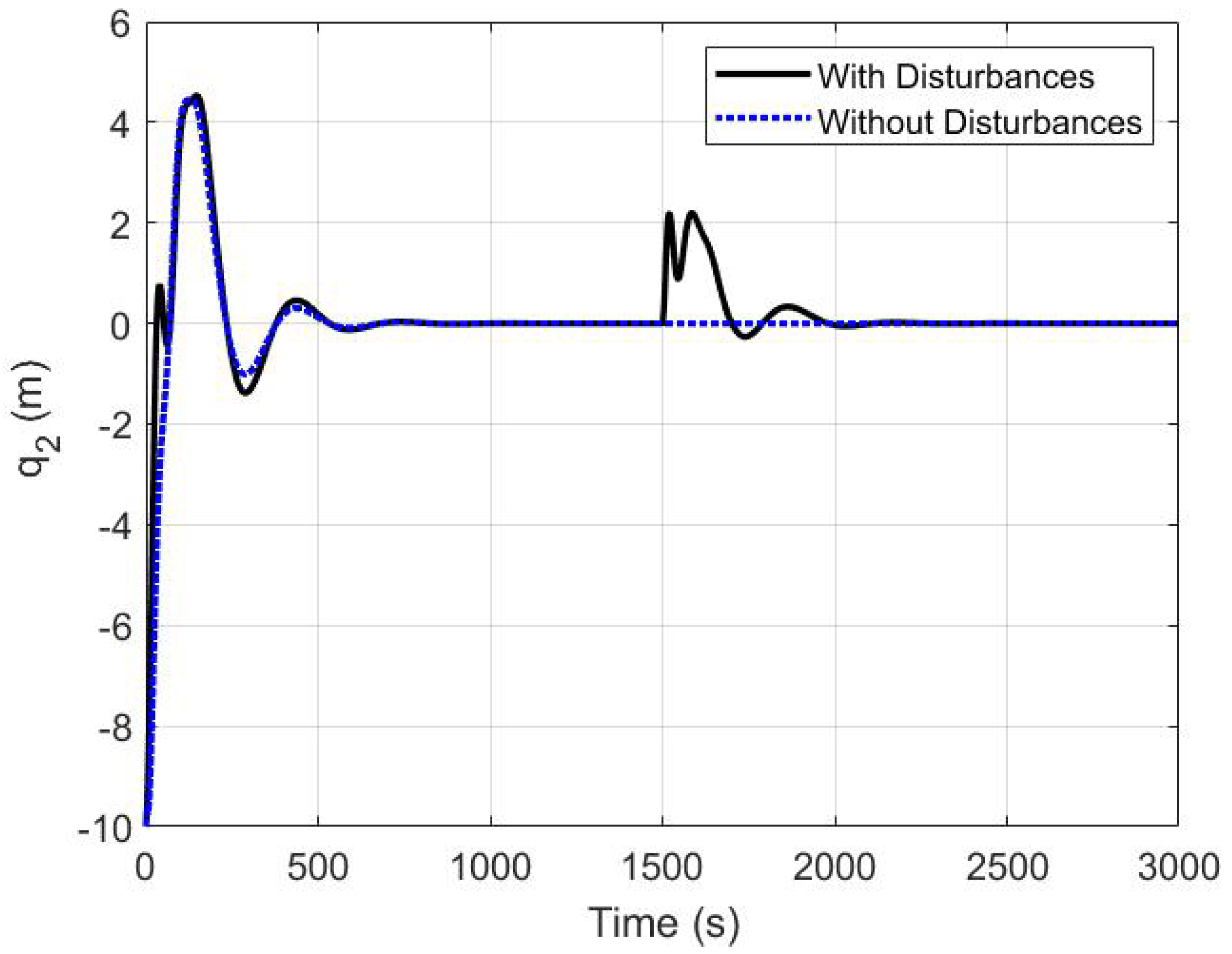
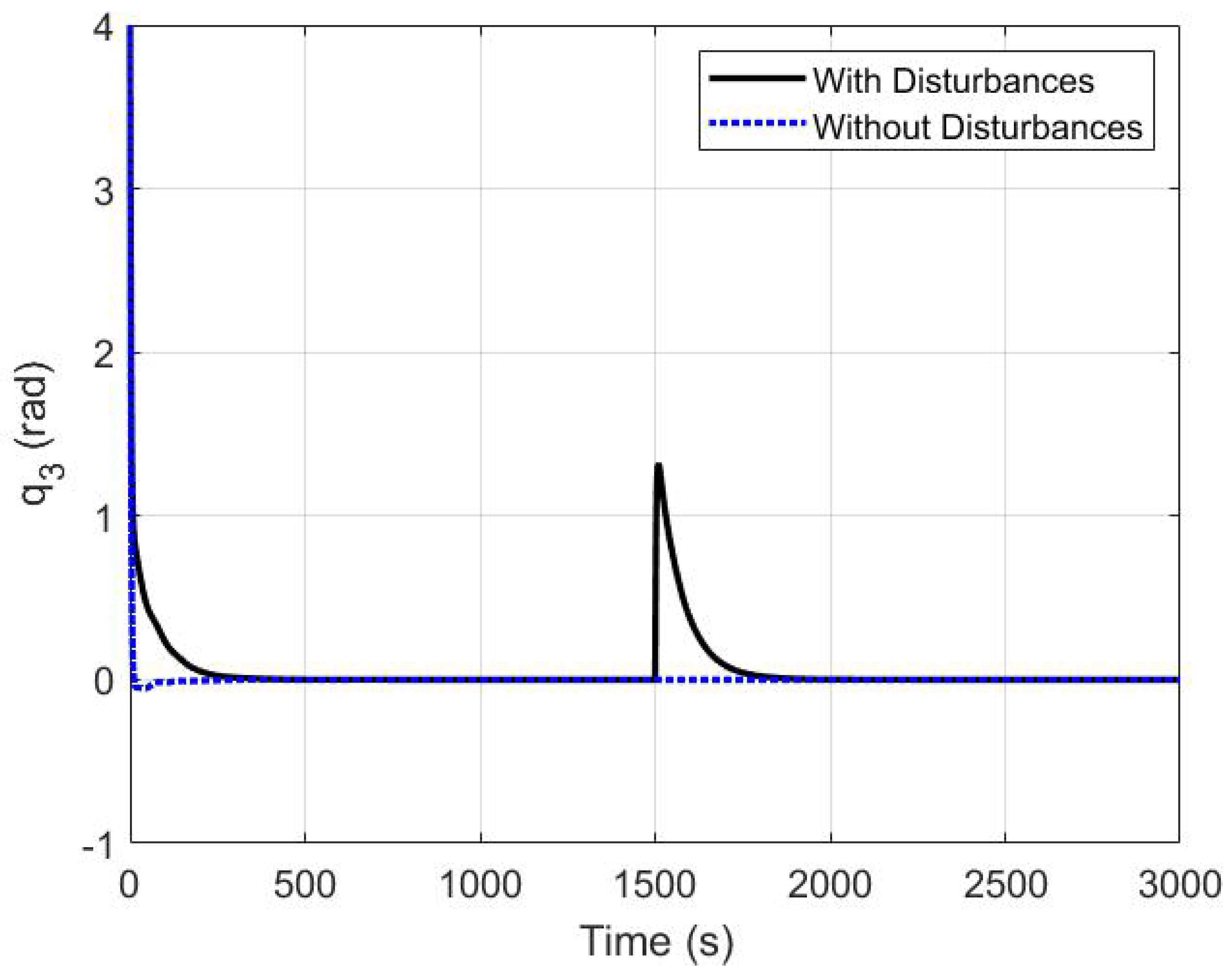
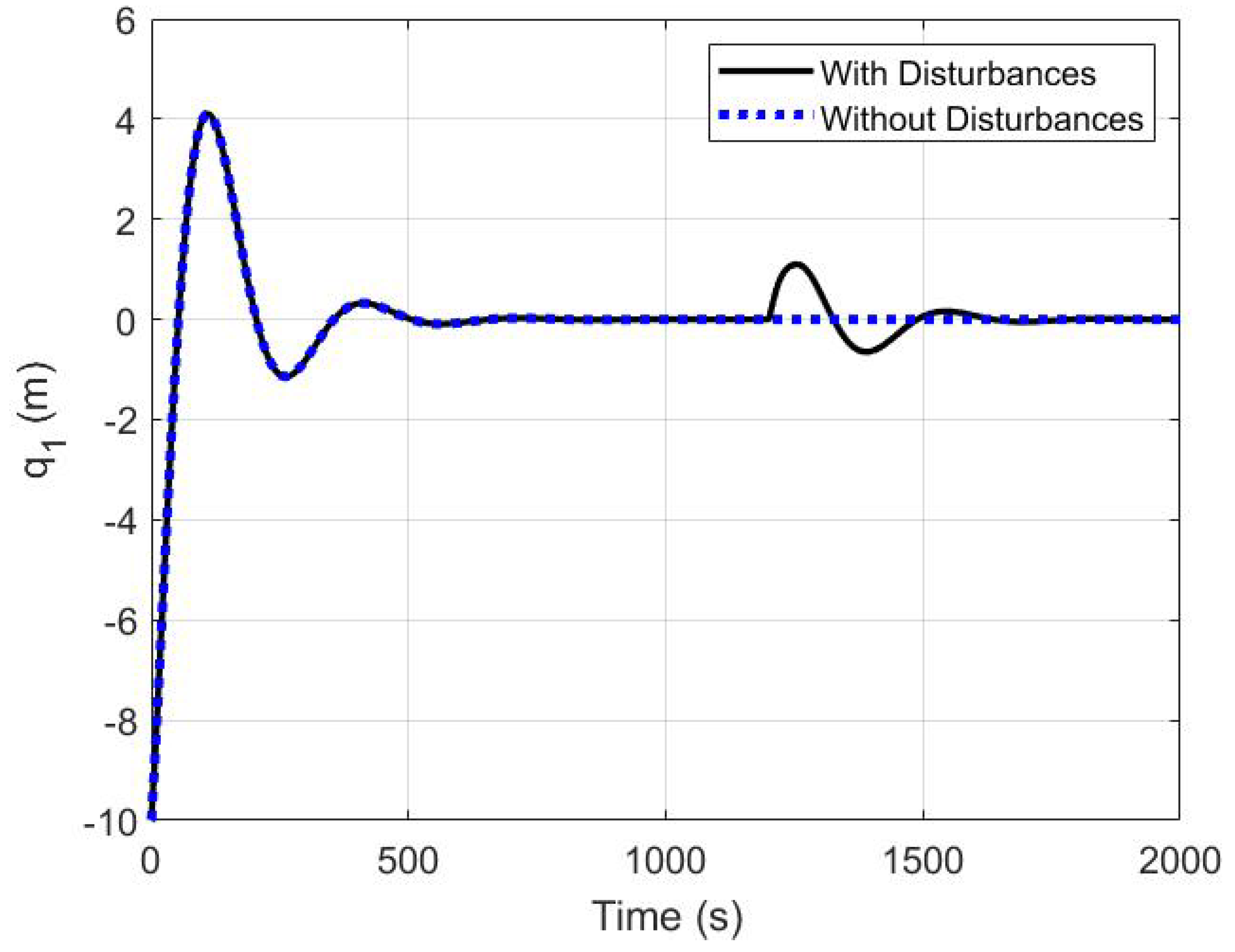
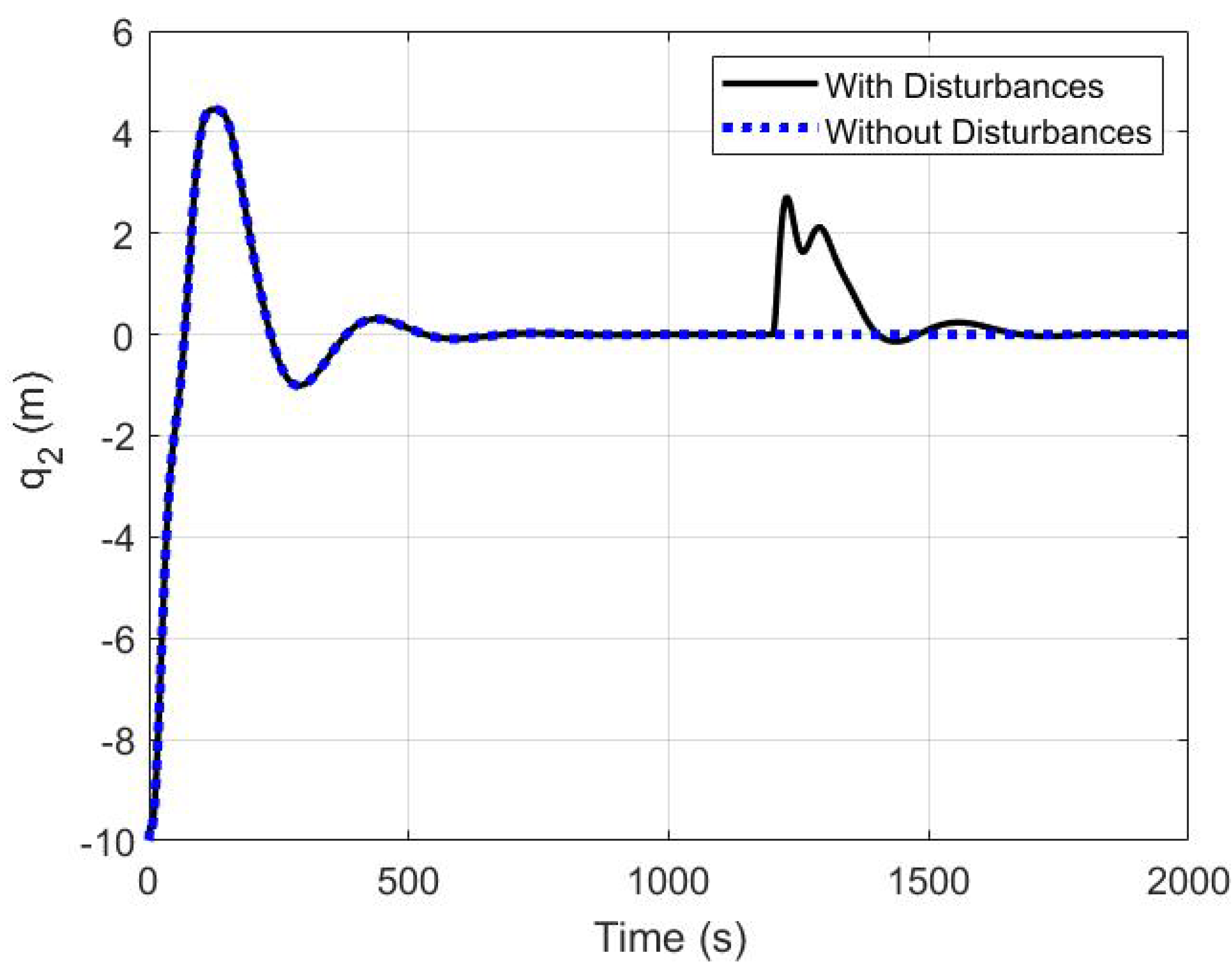
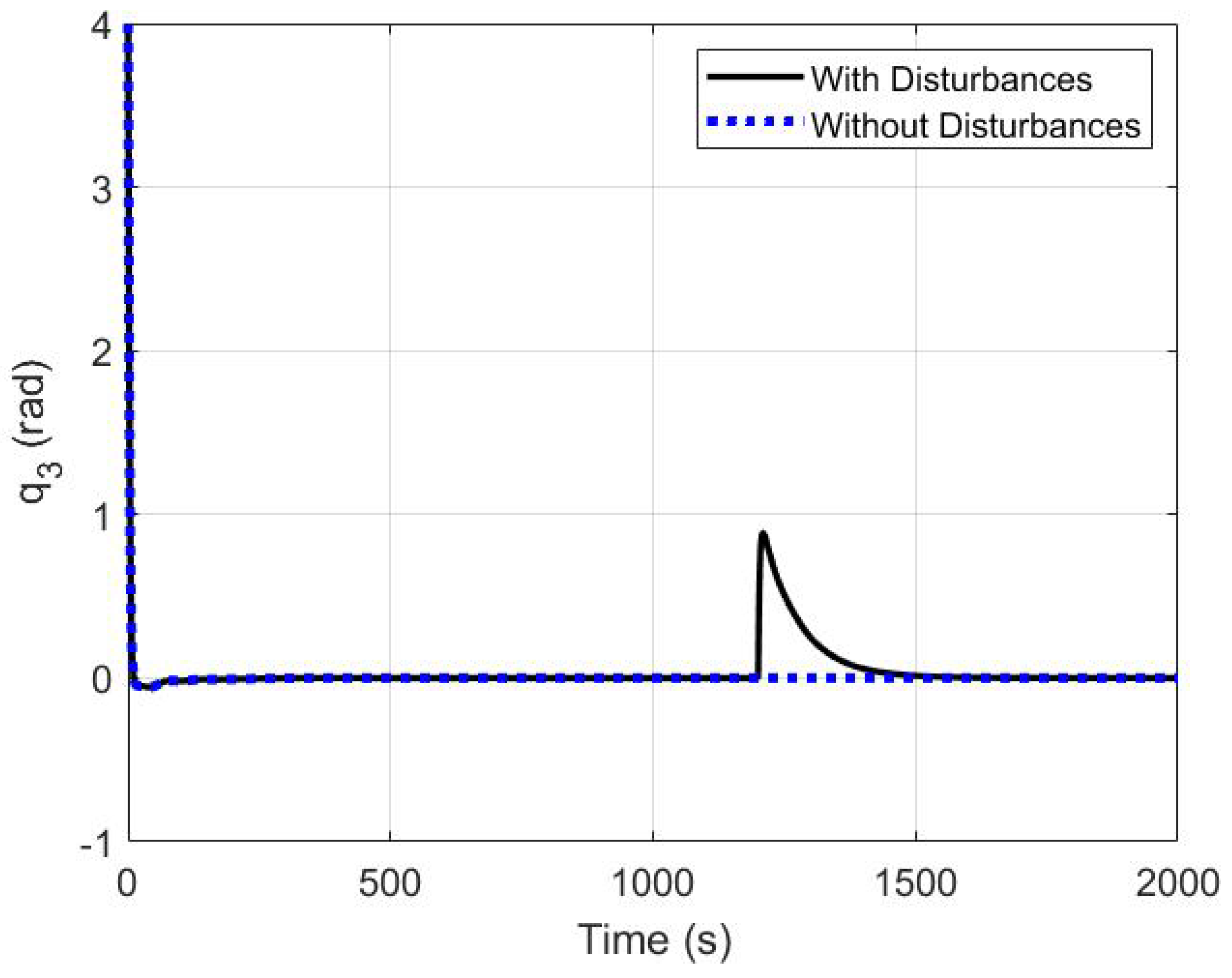
5.3. The Robustness of the Proposed Controller
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Mehrzadi, M.; Terriche, Y.; Su, C.-L.; Othman, M.B.; Vasquez, J.C.; Guerrero, J.M. Review of Dynamic Positioning Control in Maritime Microgrid Systems. Energies 2020, 13, 3188. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, L.; Li, S. Dynamic analysis of vessel/riser/equipment system for deep-sea mining with RBF neural network approximations. Mar. Georesources Geotechnol. 2020, 38, 174–192. [Google Scholar] [CrossRef]
- Sørensen, A.J. A survey of dynamic positioning control systems. Annu. Rev. Control 2011, 35, 123–136. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, J.; Wu, W.; Zhang, Y. Robust dynamic positioning of autonomous surface vessels with tube-based model predictive control. Ocean Eng. 2020, 199, 106820. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Yang, J.; Wang, L. A fuzzy rule-based PID controller for dynamic positioning of vessels in variable environmental disturbances. J. Mar. Sci. Technol. 2020, 25, 914–924. [Google Scholar] [CrossRef]
- Fossen, T.I. A survey on Nonlinear Ship Control: From Theory to Practice. IFAC Proc. Vol. 2000, 33, 1–16. [Google Scholar] [CrossRef]
- Martin, P.; Katebi, R. Multivariable PID tuning of dynamic ship positioning control systems. J. Mar. Eng. Technol. 2005, 1, 11–24. [Google Scholar] [CrossRef]
- Balchen, J.G.; Jenssen, N.A.; Sælid, S. Dynamic positioning using Kalman filtering and optimal control theory. In Proceedings of the IFAC/IFIP Symposium on Automation in Offshore oil Field Operation, Amsterdam, The Netherlands, 14–17 June 1976; pp. 183–186. [Google Scholar]
- Balchen, J.G.; Jenssen, N.A.; Mathisen, E.; Sælid, S. A dynamic positioning system based on Kalman filtering and optimal control. Model. Identif. Control 1980, 1, 135–163. [Google Scholar] [CrossRef]
- Mandzuka, S.; Vukic, Z. Use of optimal constrained covariance control (OC3) in dynamic positioning. In Proceedings of the IFAC Conference on Control Applications in Marine Systems, Trondheim, Norway, 10–12 May 1995. [Google Scholar]
- Kijima, K.; Murata, K.; Furukawa, Y. Design of a dynamic positioning system for self-propulsive barge under external disturbances. In Proceedings of the IFAC Conference on Control Applications in Marine Systems, Fukuoka, Japan, 27–30 October 1998. [Google Scholar]
- Volovodov, S.K.; Chernjaev, M.G.; Kaverinsky, A.J.; Volovodov, S.S.; Lampe, B.P. Control principle for dynamic positioning of offshore drilling platforms and ships. In Proceedings of the 11th Symposium on Maritime Elektrotechnik, Elektronik und Informationstechnik; Rostock University: Rostock, Germany, 2004. [Google Scholar]
- Fossen, T.I.; Paulsen, M.J. Adaptive feedback linearization applied to steering of ships. In Proceedings of the IEEE Conference on Control Applications, Dayton, OH, USA, 13–16 September 1992; pp. 1088–1093. [Google Scholar]
- Bertin, D.; Bittanti, S.; Meron, S.; Savaresi, S.M. Dynamic positioning of a single-thruster vessel by feedback linearization. In Proceedings of the IFAC Conference on Manoeuvring and Control of Marine Craft, Aalborg, Denmark, 23–25 August 2000; pp. 275–280. [Google Scholar]
- Fossen, T.I.; Strand, J.P. Passive nonlinear observer design for ships using Lyapunov methods: Full-scale experiments with a supply vessel. Automatica 1999, 35, 3–16. [Google Scholar] [CrossRef]
- He, W.; Yin, Z.; Sun, C. Adaptive neural network control of a marine vessel with constraints using the asymmetric barrier Lyapunov function. IEEE Trans. Cybern. 2017, 47, 1641–1651. [Google Scholar] [CrossRef] [PubMed]
- Xia, G.; Xue, J.; Sun, C.H.; Zhao, B. Backstepping Control Using Barrier Lyapunov Function for Dynamic Positioning Control System with Passive Observer. Math. Probl. Eng. 2019, 2019, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Tannuri, E.A.; Agostinho, A.C.; Morishita, H.M.; Moratelli, L., Jr. Dynamic positioning systems: An experimental analysis of sliding mode control. Control Eng. Pract. 2010, 18, 1121–1132. [Google Scholar] [CrossRef]
- Liang, K.; Lin, X.; Chen, Y.; Li, J.; Ding, F. Adaptive sliding mode output feedback control for dynamic positioning ships with input saturation. Ocean Eng. 2020, 206, 107245. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J. Model Predictive Control for Tracking of Underactuated Vessels Based on Recurrent Neural Networks. IEEE J. Ocean. Eng. 2012, 37, 717–726. [Google Scholar] [CrossRef]
- Do, V.-D.; Dang, X.-K. The fuzzy particle swarm optimization algorithm design for dynamic positioning system under unexpected impacts. J. Mech. Eng. Sci. 2019, 13, 5407–5423. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- Fang, M.C.; Lee, Z.Y. Application of neuro-fuzzy algorithm to portable dynamic positioning control system for ships. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 38–52. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Negenborn, R.R.; Lodewijks, G. Trajectory tracking of autonomous vessels using model predictive control. IFAC Proc. Vol. 2014, 47, 8812–8818. [Google Scholar] [CrossRef] [Green Version]
- van der Schaft, A. L2 Gain and Passivity Techniques in Nonlinear Control; Springer: New York, NY, USA, 1996. [Google Scholar]
- Ortega, R.; van der Schaft, A.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, S.; Dória-Cerezo, A. Passivity-based control applied to the dynamic positioning of ships. IET Control Theory Appl. 2012, 6, 680–688. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Zhao, J.; Fei, C.; Li, D.; Zhu, Y.; Li, Z.; Guo, R.; Lou, L.; Feng, W.; Yang, Y. Particle Swarm Optimization Algorithm-Based Design Method for Ultrasonic Transducers. Micromachines 2020, 11, 715. [Google Scholar] [CrossRef]
- Abachizadeh, M.; Yazdi, M.; Yousefi-Koma, A. Optimal tuning of pid controllers using artificial bee colony algorithm. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Montreal, QC, Canada, 6–9 July 2010; pp. 379–384. [Google Scholar]
- Chiha, I.; Liouane, N.; Borne, P. Tuning PID controller using multiobjective ant colony optimization. Appl. Comput. Intell. Soft Comput. 2012, 2012, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Bayoumi, E.H.E.; Salem, F. PID controller for series parallel resonant converters using bacterial foraging optimization. Electromotion Sci. J. 2012, 19, 64–78. [Google Scholar]
- Kumar, A.; Suhag, S. Multiverse optimized fuzzy-PID controller with a derivative filter for load frequency control of multisource hydrothermal power system. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 4187–4199. [Google Scholar] [CrossRef]
- Saiful, M.; Aziz, I.; Wahyudi, S.; Sudin, S.; Abdul, N.; Faramarzi, M. Gravitational Search Algorithm Optimization for PID Controller Tuning in Waste-water Treatment Process. J. Teknol 2015, 73, 103–109. [Google Scholar]
- Solihin, M.I.; Tack, L.F.; Kean, M.L. Tuning of PID controller using particle swarm optimization (PSO). Int. J. Adv. Sci. Eng. Inf. Technol. 2011, 1, 458–461. [Google Scholar] [CrossRef] [Green Version]
- Yacef, F.; Bouhali, O.; Hamerlain, M.; Rezoug, A. PSO optimization of Integral backstepping controller for quadrotor attitude stabilization. In Proceedings of the 3rd International Conference on Systems and Control, Algiers, Algeria, 29–31 October 2013; pp. 462–466. [Google Scholar]
- Naderi, E.; Narimani, H.; Fathi, M.; Narimani, M.R. A novel fuzzy adaptive configuration of particle swarm optimization to solve large-scale optimal reactive power dispatch. Appl. Soft Comput. 2017, 35, 441–456. [Google Scholar] [CrossRef]
- Tristan, P.; Fossen, T.I. Kinematic Models for Manoeuvring and Seakeeping of Marine Vessels. Model. Identif. Control 2007, 28, 19–30. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley and Sons Ltd.: West Sussex, UK, 2011. [Google Scholar]
- Donaire, A.; Romero, J.; Ortega, R.; Siciliano, B.; Crespo, M. Robust IDA-PBC for underactuated mechanical systems subject to matched disturbances. Int. J. Robust Nonlinear Control 2017, 27, 1000–1016. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neuron Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Dai, H.-P.; Chen, D.-D.; Zheng, Z.-S. Effects of Random Values for Particle Swarm Optimization Algorithm. Algorithms 2018, 11, 23. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Kvasov, D.; Mukhametzhanov, M. Metaheuristic vs. deterministic global optimization algorithms: The univariate case. Appl. Math. Comput. 2018, 318, 245–259. [Google Scholar] [CrossRef]
- Bandarua, S.; Debb, K. Metaheuristic Techniques; Published in Decision Sciences: Theory and Practice; Sengupta, R.N., Gupta, A., Dutta, J., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2020. [Google Scholar]
- Sergeyev, Y.D.; Kvasov, D.E.; Mukhametzhanov, M.S. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, H.; Pei, W.; Dong, Z.; Kong, L.; Wang, D. Application and Comparison of Metaheuristic and New Metamodel Based Global Optimization Methods to the Optimal Operation of Active Distribution Networks. Energies 2018, 11, 85. [Google Scholar] [CrossRef] [Green Version]
- What Is Global Optimization? Available online: https://www.mathworks.com/help/gads/what-is-global-optimization.html#bsbalkx-1 (accessed on 12 October 2020).
- The MathWorks, Inc. Global Optimization Toolbox User’s Guide. Available online: https://www.mathworks.com/help/pdf-doc/gads/gads.pdf (accessed on 12 October 2020).
- Du, J.; Hu, X.; Krstić, M.; Sun, Y. Robust dynamic positioning of ships with disturbances under input saturation. Automatica 2016, 73, 207–214. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Krstić, M.; Sun, Y. Dynamic positioning of ships with unknown parameters and disturbances. Control Eng. Pract. 2018, 76, 22–30. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Li, J.; Sun, Y. Asymptotic Regulation of Dynamically Positioned Vessels with Unknown Dynamics and External Disturbances. J. Navig. 2020, 73, 253–266. [Google Scholar] [CrossRef]




| Time Characteristics | Modified Controller | Original Controller |
|---|---|---|
| Rise time(s) | 40.7935 | 59.0104 |
| Settling time(s) | 457.7632 | 1062.9 |
| Overshoot percentage | 41.0047 | 49.7733 |
| Rise time(s) | 47.6423 | 46.8955 |
| Settling time(s) | 480.8057 | 765.8472 |
| Overshoot percentage | 44.4818 | 59.0281 |
| Rise time(s) | 5.4699 | 5.3337 |
| Settling time(s) | 9.1445 | 41.6431 |
| Overshoot percentage | 1.3724 (under) | 11.4531 (under) |
| Parameter Name | Value |
|---|---|
| Maximum iteration | 500 |
| Swarm Size | 30 |
| Self-Weight acceleration coefficient () | 1.494 |
| Social-Weight acceleration coefficient () | 1.494 |
| Inertia weight (w) | 0.729 |
| kq1 range | 0.001–10 |
| kq2 range | 0.001–10 |
| kq3 range | 0.001–10 |
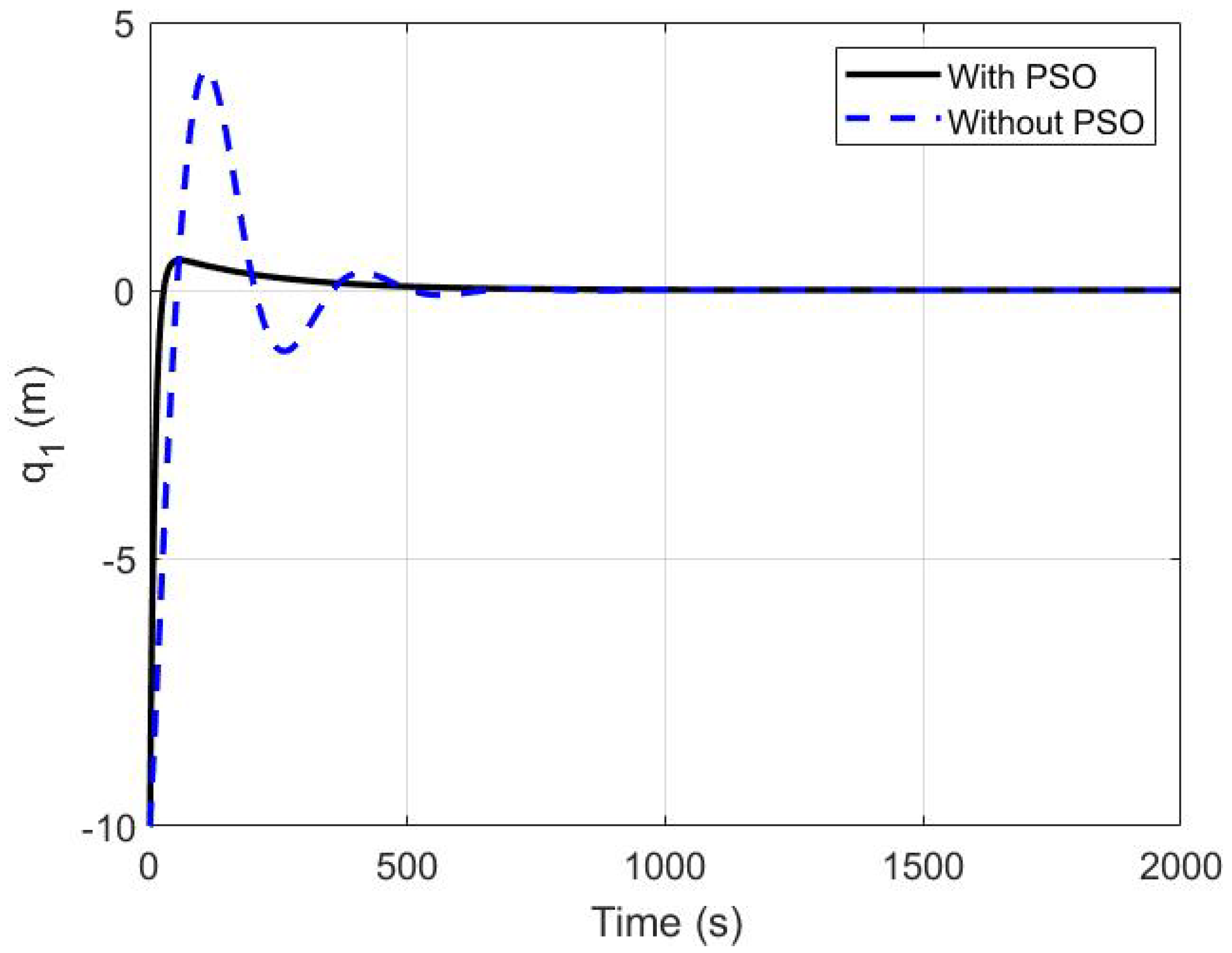
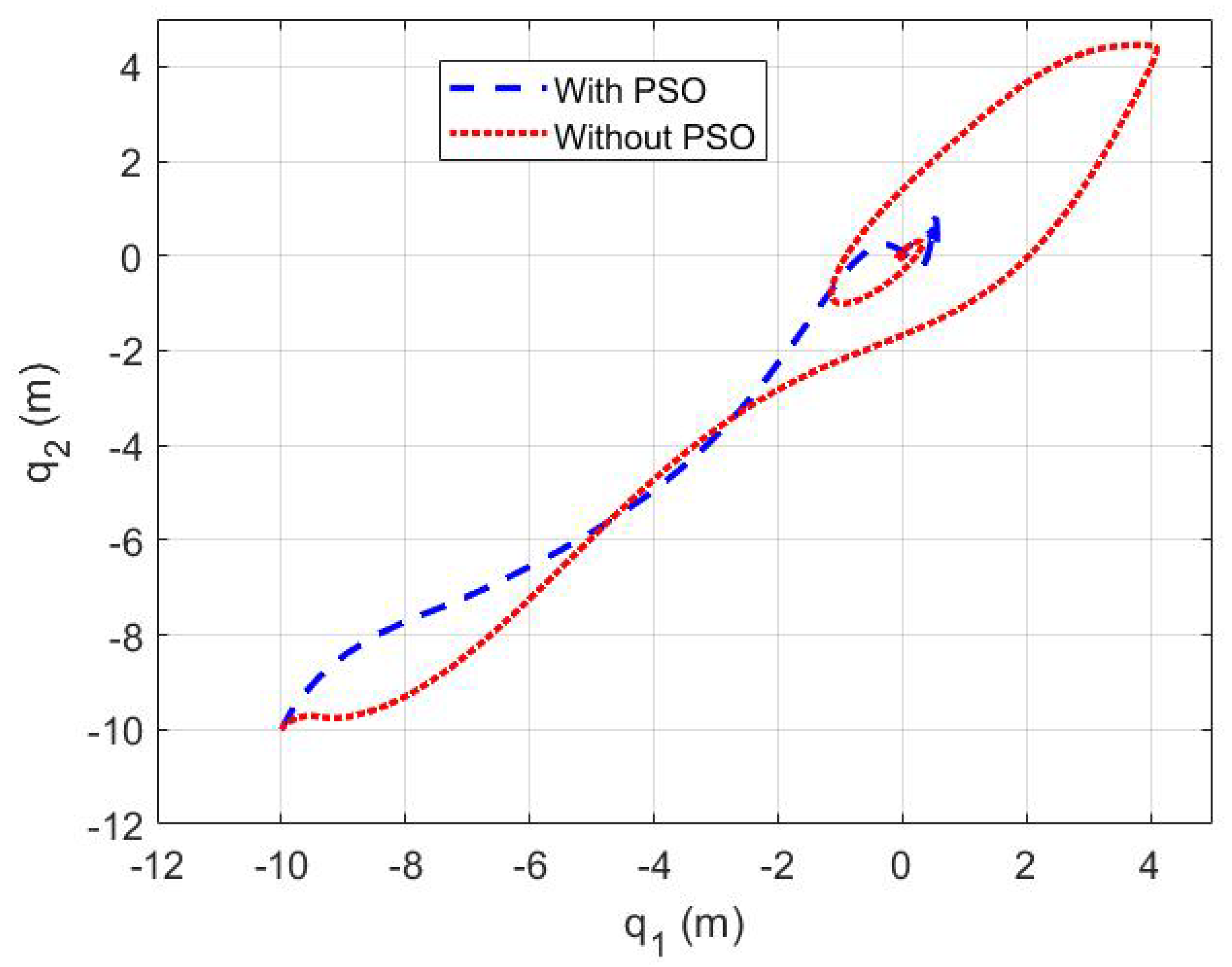
| Time Characteristics | Without PSO | with PSO |
|---|---|---|
| Rise time(s) | 40.7935 | 17.0299 |
| Settling time(s) | 457.7632 | 277.9465 |
| Overshoot percentage | 41.0047 | 5.6116 |
| Rise time(s) | 47.6423 | 15.9123 |
| Settling time(s) | 480.8057 | 398.5471 |
| Overshoot percentage | 44.4818 | 7.9774 |
| Rise time(s) | 5.4699 | 3.4137 |
| Settling time(s) | 9.1445 | 6.2746 |
| Overshoot percentage | 1.3724 (under) | 0.6043 (under) |
| Sea State Code | Description of Sea | Wave Height Observed (m) | World Wide Probability (%) |
|---|---|---|---|
| 0 | Calm (glassy) | 0 | - |
| 1 | Calm (ripples) | 0–0.1 | 11.2486 |
| 2 | Smooth | 0.1–0.5 | - |
| 3 | Slight | 0.5–1.25 | 31.6851 |
| 4 | Moderate | 1.25–2.5 | 40.1944 |
| 5 | Rough | 2.5–4.0 | 12.8005 |
| 6 | Very rough | 4.0–6.0 | 3.0253 |
| 7 | High | 6.0–9.0 | 0.9263 |
| 8 | Very high | 9.0–14.0 | 0.1190 |
| 9 | Extreme | Over 14.0 | 0.0009 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryalat, M.; Salim Damiri, H.; ElMoaqet, H. Particle Swarm Optimization of a Passivity-Based Controller for Dynamic Positioning of Ships. Appl. Sci. 2020, 10, 7314. https://doi.org/10.3390/app10207314
Ryalat M, Salim Damiri H, ElMoaqet H. Particle Swarm Optimization of a Passivity-Based Controller for Dynamic Positioning of Ships. Applied Sciences. 2020; 10(20):7314. https://doi.org/10.3390/app10207314
Chicago/Turabian StyleRyalat, Mutaz, Hazem Salim Damiri, and Hisham ElMoaqet. 2020. "Particle Swarm Optimization of a Passivity-Based Controller for Dynamic Positioning of Ships" Applied Sciences 10, no. 20: 7314. https://doi.org/10.3390/app10207314
APA StyleRyalat, M., Salim Damiri, H., & ElMoaqet, H. (2020). Particle Swarm Optimization of a Passivity-Based Controller for Dynamic Positioning of Ships. Applied Sciences, 10(20), 7314. https://doi.org/10.3390/app10207314







