2.2. Theory Models
A ray-tracing method was used to build an inner heat-sources model of the laser rod. A linear LD array has an effective emitting area of about 1.0 μm by 4 mm. In the direction of the LD bar’s fast axis, the pump beam has an approximately Gaussian shape and a larger beam divergence angle of 40°. The laser diodes are considered as point light sources because of the small emitting width of 1.0 μm. In our simulation, the pump beam parallel to a profile of the laser rod was discretized to be rays carrying energy along the beam divergence angle. In contrast, the pump beam in the direction of the LD bar’s slow axis had an approximate flat-top shape and a smaller beam divergence angle of 10°. The pump power distribution along the direction of the laser rod axis (the LD’s slow axis) was deemed to be uniform within a pump segment because of the longer-width (10 mm) LD bars. Therefore, the inner heat-sources distribution was determined by tracing all pump rays in the laser rod cross-section.
Figure 3 illustrates the ray-tracing in a laser rod cross-section from any ray in the LD beam divergence angle. The
x,y-coordinate system is established with the origin at the center of the laser rod, and the angles between rays and
x-axis are defined as positive angles in the condition of counterclockwise rotation from
x-direction to the direction of ray propagation. The point
O1 indicates a laser diode emitter. Any ray of
O1I is refracted into the laser rod at the incidence point
I, and the coordinates (
xI, yI) are obtained by:
where
is the angle of the ray from a laser diode and the
x-direction,
r is the radius of the laser rod, and
d is the distance between
O1 and the surface of the laser rod.
With some geometry and the law of refraction, the angle of
between the ray
IR1 and the
x-direction is solved by:
where
and
are the incidence and refraction angles at the incident point
I, respectively.
With the coordinates (
xI, yI) and the angle
, the refraction ray of
IR1 is expressed as:
The refraction ray
is reflected first at point
R1, second at
R2, and
nth at
RN. With the same method, the coordinates of
R1(
x1,
y1),
R2(
x2,
y2),
RN(xN, yN), and the angles between the corresponding reflection ray and the
x-direction are determined. Using the method of induction, the general expression of the reflected rays is written as:
where
n is the number of rays reflected in the inner surface of the laser rod.
According to the Fresnel formulae, the reflectivity
of a laser rod’s inner surface is solved by:
where
and
are the incidence and refraction angles in the plane of incidence, respectively;
and
are the reflectivity of
s and
p waves, respectively; and
is the angle of the
E vector of the incident wave with the plane of incidence.
Then, the power carried by the
nth reflective wave at the reflective point of
RN is expressed as:
where
indicates the power of the incident wave at the reflective point
RN.
Line
O1I in
Figure 3 indicates any incident ray from a laser diode whose light power
is:
where
is the angle of the ray and the
x-axis,
is half of the beam divergence angle in the direction of the fast axis, and
A is a normalized coefficient:
where
is the power produced by a laser diode.
Based on gridding the profiles of the laser rod, the absorbed power of the grids was calculated by tracing all rays emitted from around laser diodes within the beam divergence angle of −
to
.
Figure 4a shows a gridding profile of the laser rod and
Figure 4b depicts the absorbed power of a grid from any ray of
.
In
Figure 4a, the laser rod cross-section is discretized as the grids of 2N × 2N, and the length
of a grid is:
In
Figure 4b, the length
of the ray
through any grid
Gmn is calculated using the geometry method. The absorbed power of grid
Gmn from the ray of
is written in the form:
where
is the power carried by the ray of
before inputting the grid
Gmn, and
is the absorption coefficient of the laser rod.
Then, the absorbed power of grid
Gmn from a laser diode is obtained using the integral in the beam divergence angle:
where
i is the mark number of a laser diode around the profile of the laser rod.
The
x,y-coordinate system rotation around origin
O is used to trace the rays from laser diodes not on the
x-axis, and the rotation equations are written as:
where
is the rotation angle of the
x,y-coordinate system.
There are
laser diodes around the profile of the laser rod. Thus, the inner heat source density profile
Z0 along the length (
z-direction) of the laser rod is expressed as:
where
is the quantum efficiency and
is the pump time.
The temperature distributions of
in an isotropic Nd:YAG rod is solved using the finite element analysis (FEA) method [
13] from the heat equation:
where
is the density,
is the specific heat,
is the thermal conductivity,
is the inner-sources density, and
denotes the gradient operator.
In steady-state conditions, Equation (14) can be rewritten as:
For Nd:YAG crystal,
is normally assumed to be constant with moderate temperature increases. Under higher heat load conditions,
is given in the first approximation [
14] by:
where
is the reference temperature of the cooling heat sinks,
is the heat conductivity at
, and
is the difference in
.
With the help of Equations (13) and (14), we used ANSYS software (ANSYS, Canonsburg, PA, USA) to calculate the radial temperature distribution of the laser rod with liquid cooling as previously described [
1] ch.7, and the result is illustrated in
Figure 5a,b.
Figure 5a shows the radial temperature profile of the laser rod corresponding to the radial temperature curve shown in
Figure 5b. Comparing
Figure 5b with the Figure 7.1 in [
1], the results agree well, which validates the accuracy and validity of the numerical models.
The temperature-dependent variation of the refractive index provides the main contribution to the thermal lens. The variation in the refractive index caused by that of temperature is:
where
is the ambient temperature and
is the change in the refractive index with temperature.
From Equation (17), the refractive index distribution in the laser rod is written in the form:
where
is the refractive index of the laser rod in ambient temperature, and
is the variation in the refractive index in the laser rod.
The average refractive index profile of the laser rod is obtained by the integral along the length
of the laser rod:
Then, the complex amplitude equivalent transfer function of the laser rod is expressed as:
Where is the wave vector and is the length of the laser rod.
The laser rod is considered as a phase plate with refractive index distribution
and Fresnel diffraction propagation distance
. For the thermal-lensing of the laser rod, the phase plate was illuminated using a coherent planar wave at 1064 nm in the simulation, and the wave-front distortion
after a planar wave passing through the laser rod of length
was evaluated by:
where
is the amplitude of the planar wave, the
x–y plane is the incident plane
z of
in the laser rod, the
x’–y’ plane is the output plane
z of
in the laser rod.
Finally, the optical distortions influenced by thermo-optic effects were evaluated using Equation (21).
2.3. Simulation Methods and Boundary Conditions
The details of the simulation methods and processes are described in the following. Firstly, we used MATLAB software (MathWorks, Natick, MA, USA) to calculate the inner heat source density of the laser rods in three different side-pumping schemes according to the same boundary conditions with the help of the derived Equation (13). Secondly, the temperature distributions of in the laser rods were analyzed and discussed by deriving Equation (14) considering heat conduction using FEA in ANSYS software (ANSYS, Canonsburg, PA, USA), because the major contribution to the thermal lens was from the temperature-dependent variation of the refractive index. Thirdly, MATLAB software (MathWorks, Natick, MA, USA) was used again to obtain the change in the refractive index in the laser rod using Equation (17) and the complex amplitude equivalent transfer function of laser rod by deriving Equation (20). Next, a planar wave was employed to measure the thermal lensing in the laser rod. The wave-front distortion after a planar wave passing through the laser rods was determined using Equation (21) in MATLAB (MathWorks, Natick, MA, USA). Finally, the thermo-optic effects in the laser rods were further evaluated in three different side-pumping schemes.
In our simulations, the variations in the refractive index caused by thermal stress were not considered due to the minimal influence in low- and medium-power applications. In addition, the end effects were ignored because their influence is rather limited in the side-pumping configuration.
To facilitate comparison, it was necessary to set the same boundary conditions in the three different side-pumping configurations.
In the side-pumping configurations models, the same Nd:YAG rods with a diameter of 5 mm and length of 65 mm were employed. The properties of the Nd:YAG used in the simulation are listed in
Table 1.
The same semicircular LD array modules were used in the three different side-pumping schemes. A three-dimensional (3D) geometrical model of semicircular LD arrays is shown in
Figure 6.
Ten bars 10 mm in length and 1.4 mm in width were fixed on the surface with a 5 mm radius of curvature. A bar of peak power of 100 W contained 10–20 independent laser emitters and the laser output produced by an emitter was emitted from a 200 × 1.0 μm area with a 40° fast axis × 10° slow axis beam divergence. The peak power output of a semicircular LD array is about 1000 W and six semicircular LD arrays were employed in the three different side-pumping schemes, corresponding to a total peak power of 6000 W. The LD arrays with a center wavelength of 808 nm worked at a pumping rate of 10 Hz with a pump pulse duration of 230 μs, and the wavelength changed with the temperature at 0.3 nm/°C. The copper base on which the semicircular LD arrays were mounted was a cuboid with a length of 20 mm, a width of 10 mm, and a height of 15 mm, with screws on the heat sink. The properties and parameters of the semicircular LD array modules used in the simulation are listed in
Table 2.
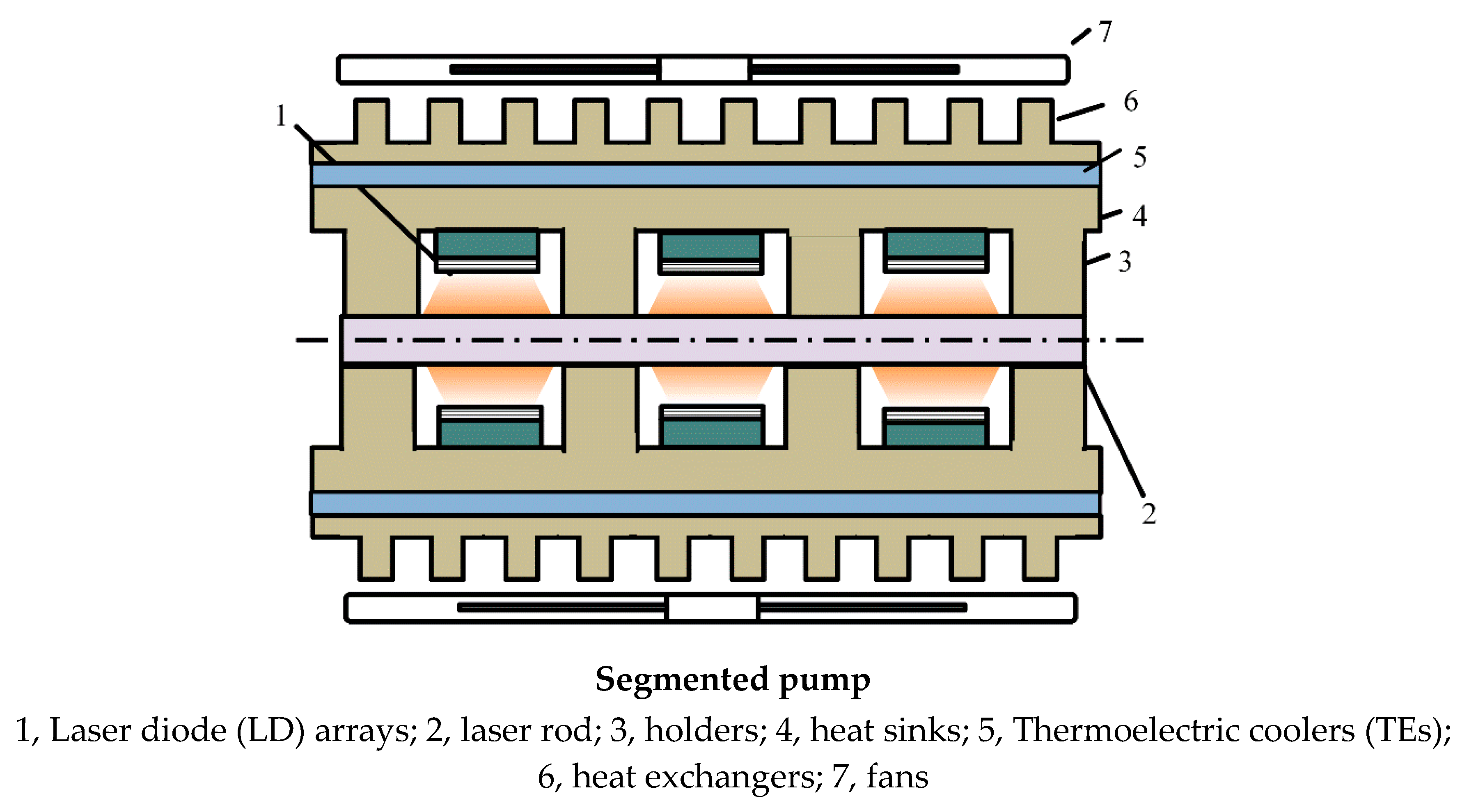
In the model of the segmented scheme shown in
Figure 1, the length of the circular holder was about 8 mm and that of the circular pump was 10 mm. The cooled cylindrical surfaces of the laser rod, on which the boundary conditions of heat conduction were a constant reference temperature of 25 °C under Dirichlet conditions, were controlled at 25 °C by the temperature controllers. In contrast, the boundary conditions of the thermal simulation were assumed to be a convective heat transfer of zero to the surrounding air (Neumann condition) on the pumped cylindrical surfaces of the laser rod.
In the model of the liquid-cooling scheme shown in
Figure 2a, the boundary conditions for the heat equation were assumed to be a constant reference temperature of 25 °C under Dirichlet conditions on the cooled cylindrical surface of the laser rod.
In the model of the compensated scheme shown in
Figure 2b, the length of the pump region containing three semicircular LD modules was about 30 mm and that of the cooling region was 32 mm. The boundary conditions of heat were also assumed to be a constant reference temperature of 25 °C under Dirichlet conditions on the cooled cylindrical half-surfaces of the laser rod, and the boundary conditions of the thermal simulation included a convective heat transfer of zero to the surrounding air (Neumann condition) on the pumped cylindrical half-surfaces of the laser rod.
In the three different side-pumping schemes, the initial temperature conditions were set to an ambient temperature of 25 °C. A thermal conductivity of 14 Wm−1K−1 at 300 K (27 °C) in the laser rod was used in our simulation because of moderate temperature increases in a lower heat load application.
Any traced ray of was multi-reflected at the inner surface of the laser rod, which has the same reflectivity due to having the same incident angles. To minimize calculation, the number n of reflections needed to be determined in the simulation. At the maximum laser diode beam divergence angle of 40° corresponding to 20° of , the reflectivity of 5.6% was obtained according to the Fresnel formulae in Equation (5). The power carried by the second reflective wave can be ignored according to Equation (6). So, the number of reflections was set to be 1 in our simulation.
The boundary conditions and parameters in the thermal simulation are summarized in
Table 3.