Teleoperation Control Design with Virtual Force Feedback for the Cable-Driven Hyper-Redundant Continuum Manipulator
Abstract
:1. Introduction
2. Configuration and Kinematics Modeling
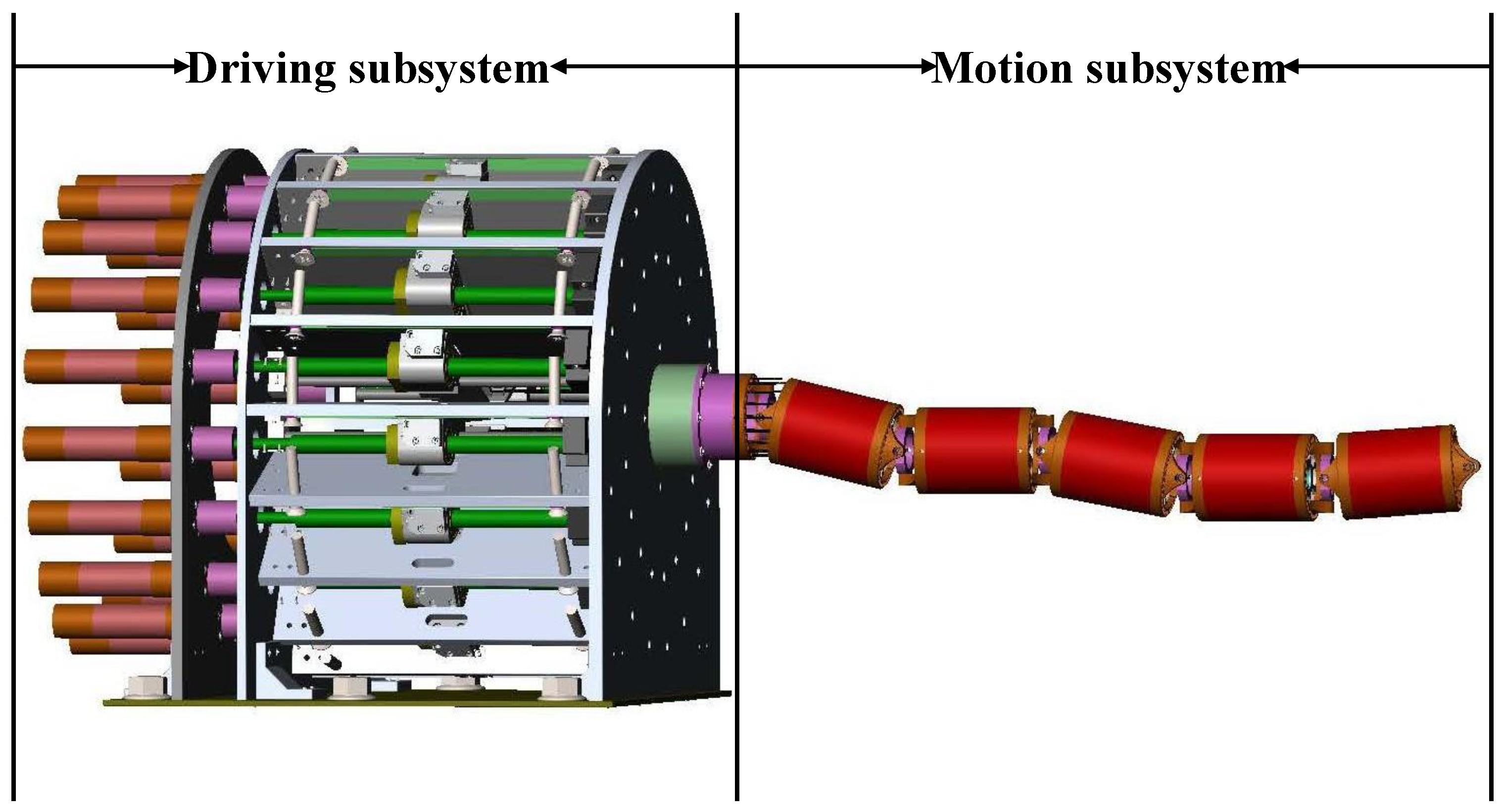
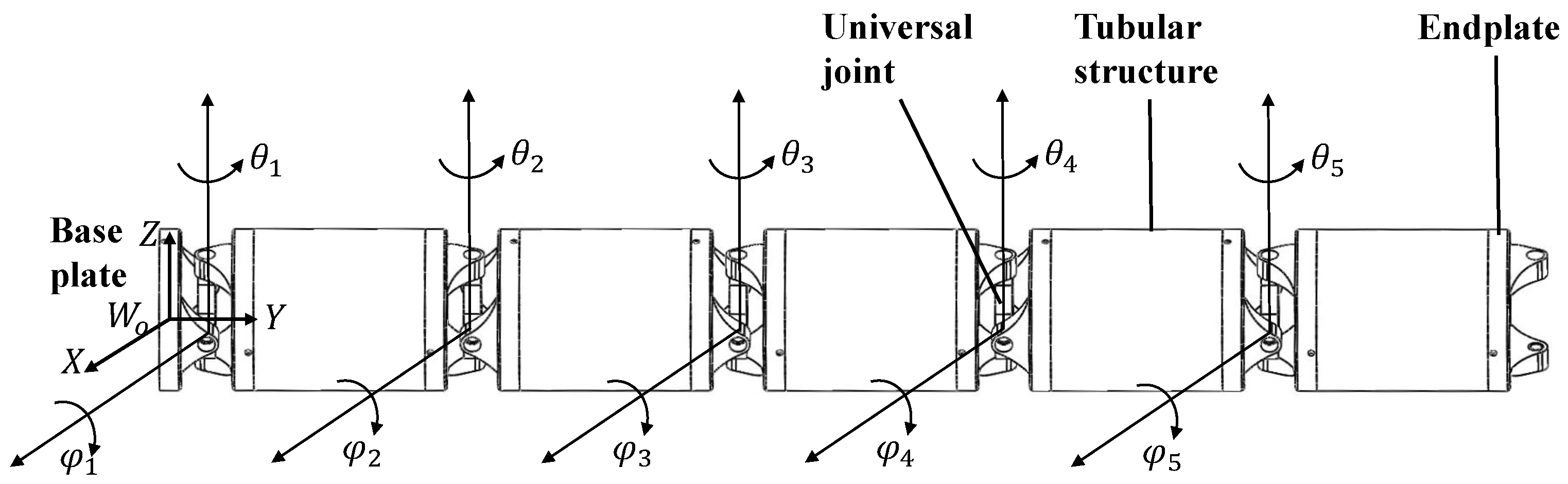
2.1. General Structure of CHCM
2.2. Forward and Inverse Kinematics Based on Geometrical Relationships
2.2.1. Kinematics between Cable Lengths and Joint Angles
2.2.2. Kinematics between Joint Angles and End-Effector Position
- The position of the end-effector is mainly in an optional plane perpendicular to the Y-axis.
- The last tubular structure is parallel to the Y-axis.
- The movement of the end-effector in the Y-axis direction is achieved by selecting different optional planes.
3. Teleoperation Control Design with Wave Variable and Virtual Force Feedback
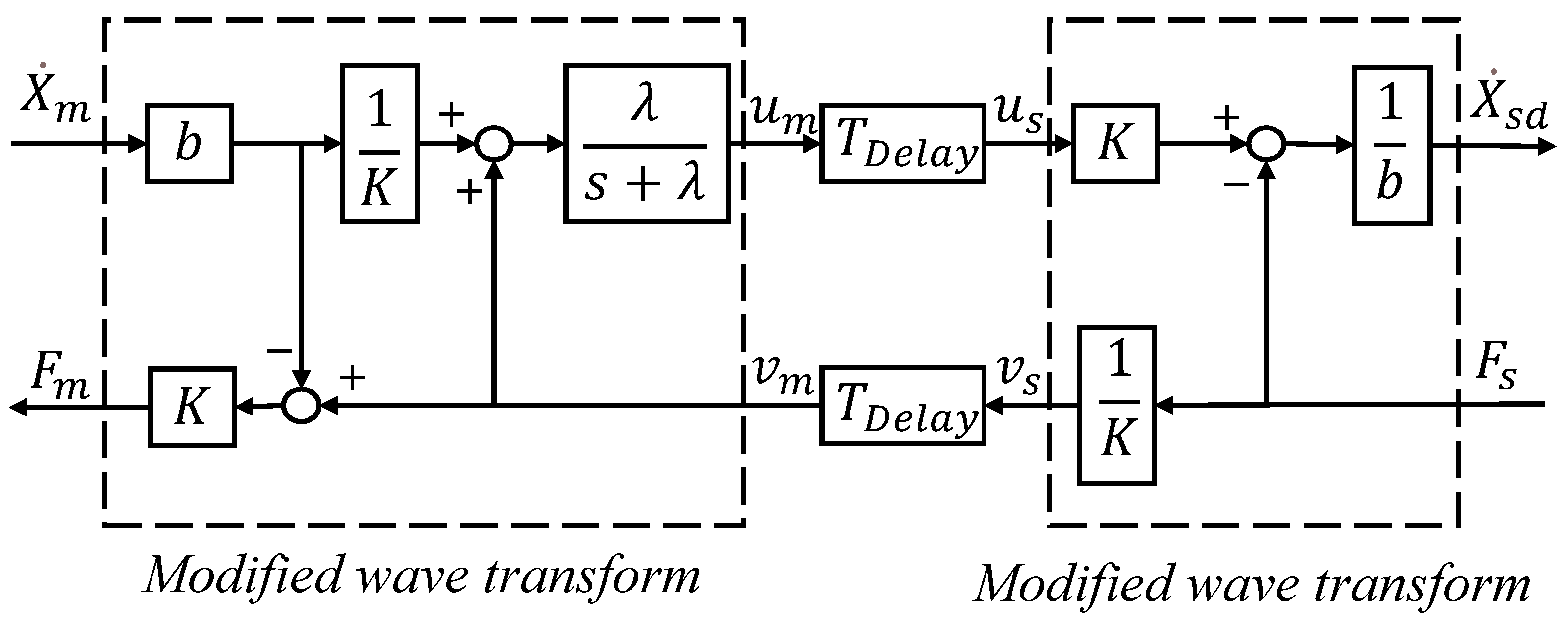
3.1. Modified Wave Variable Architecture
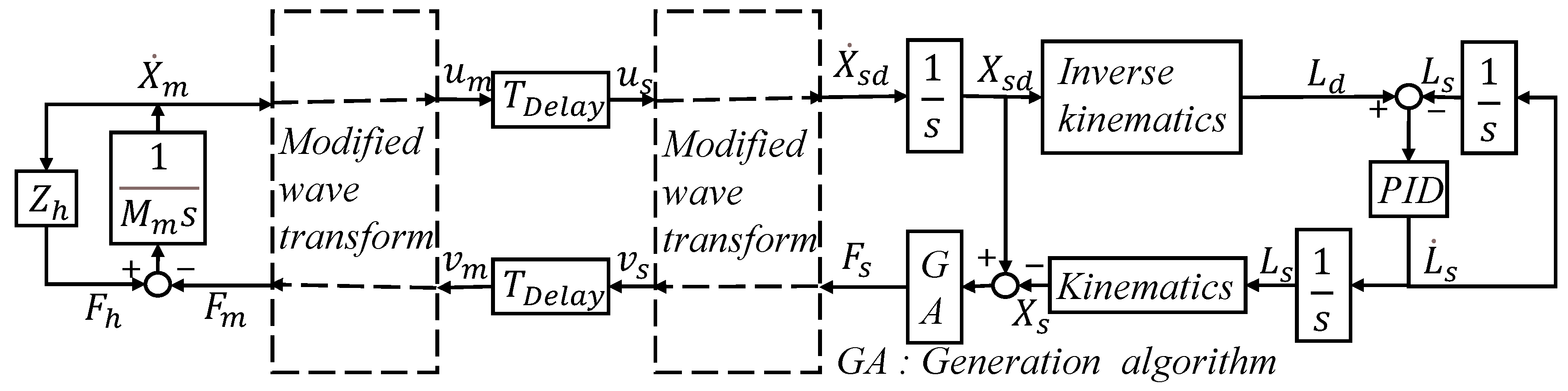
3.2. Virtual Force Feedback Generation and Controller Design
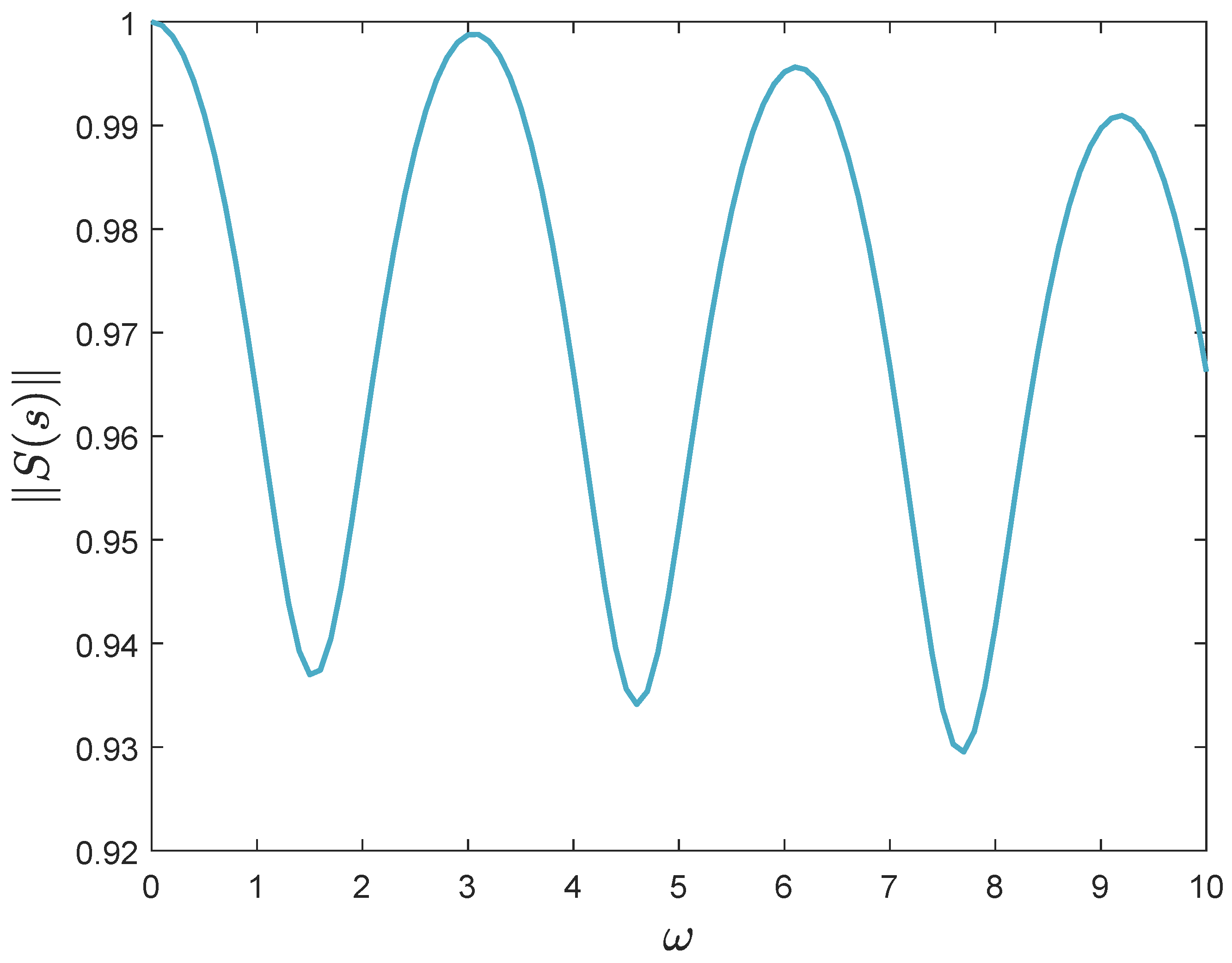
3.3. Stability and Transparency Analysis
4. Experiment
- To demonstrate that the derived forward and inverse kinematics of CHCM based on geometrical relationships are validated and applicable for CHCM due to its real-time performance.
- To illustrate that the teleoperation system of CHCM remains stable with time delays and shows better transparency adopting the proposed teleoperation control scheme including wave variable architecture and virtual force feedback generation method.
4.1. Experiment Platform
4.2. Experiment Setup
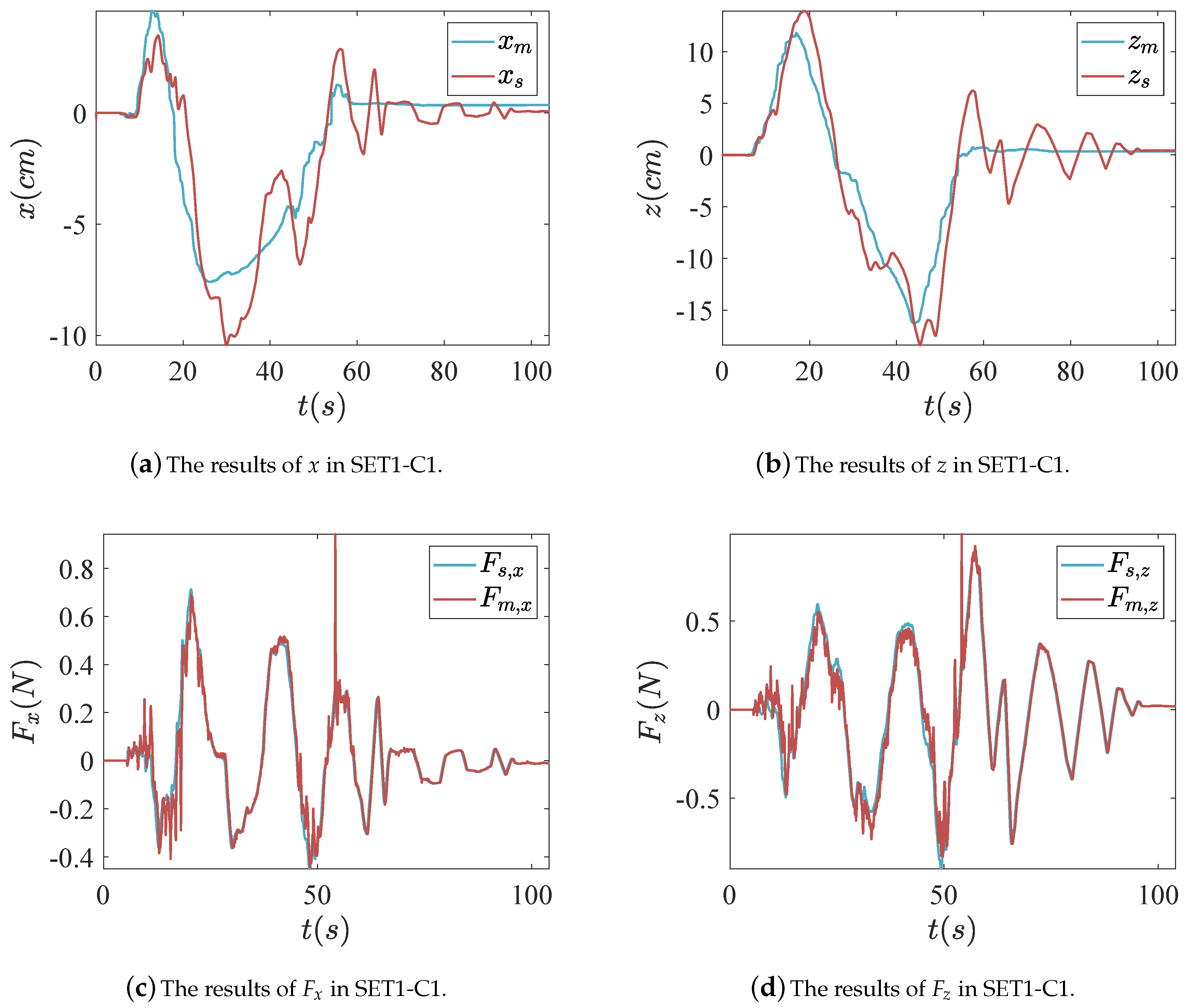
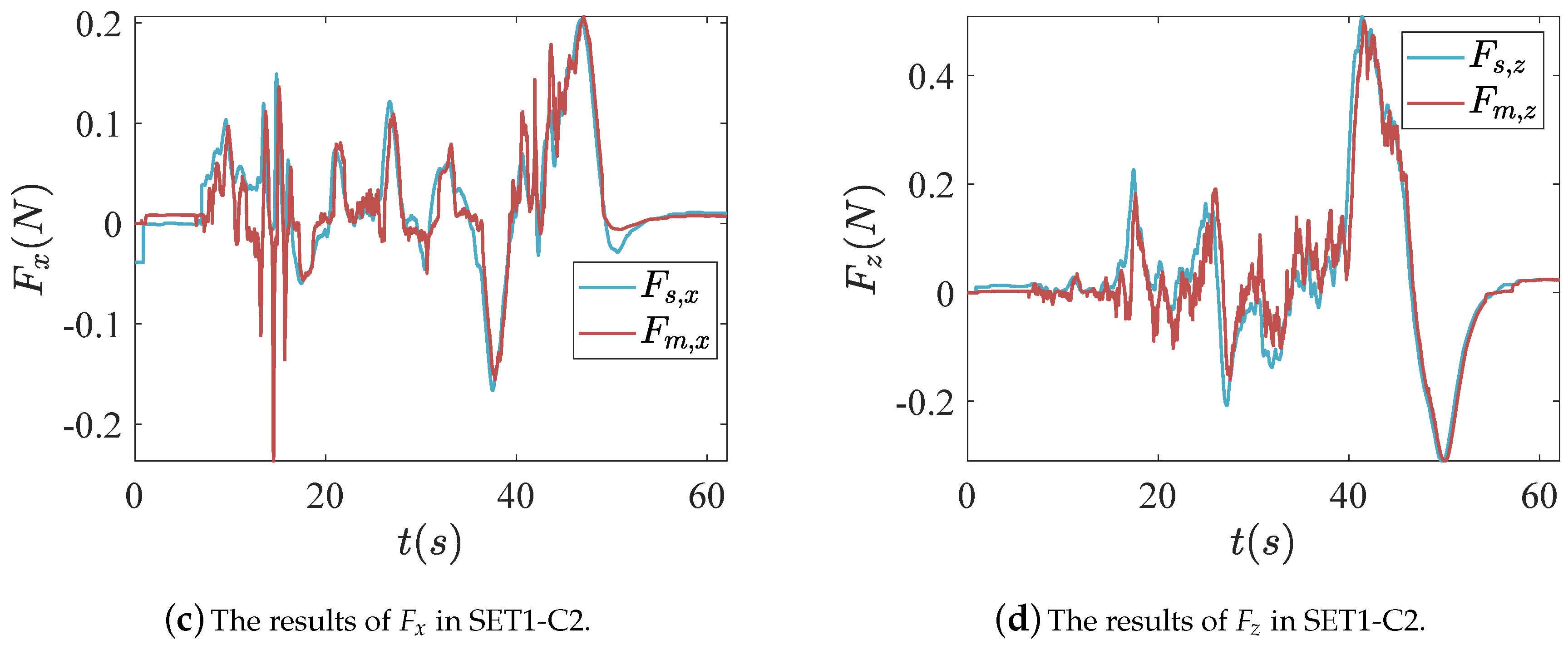
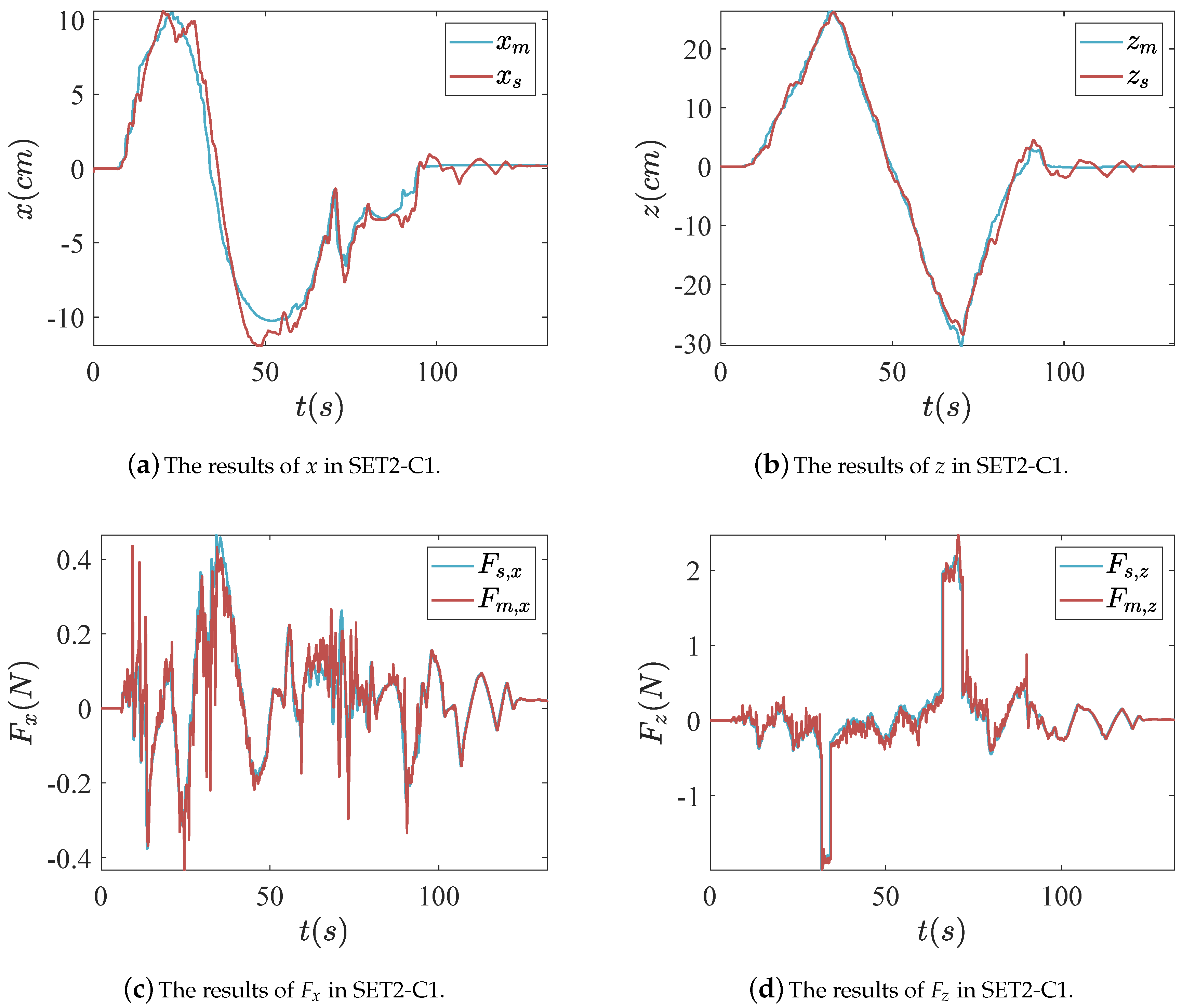
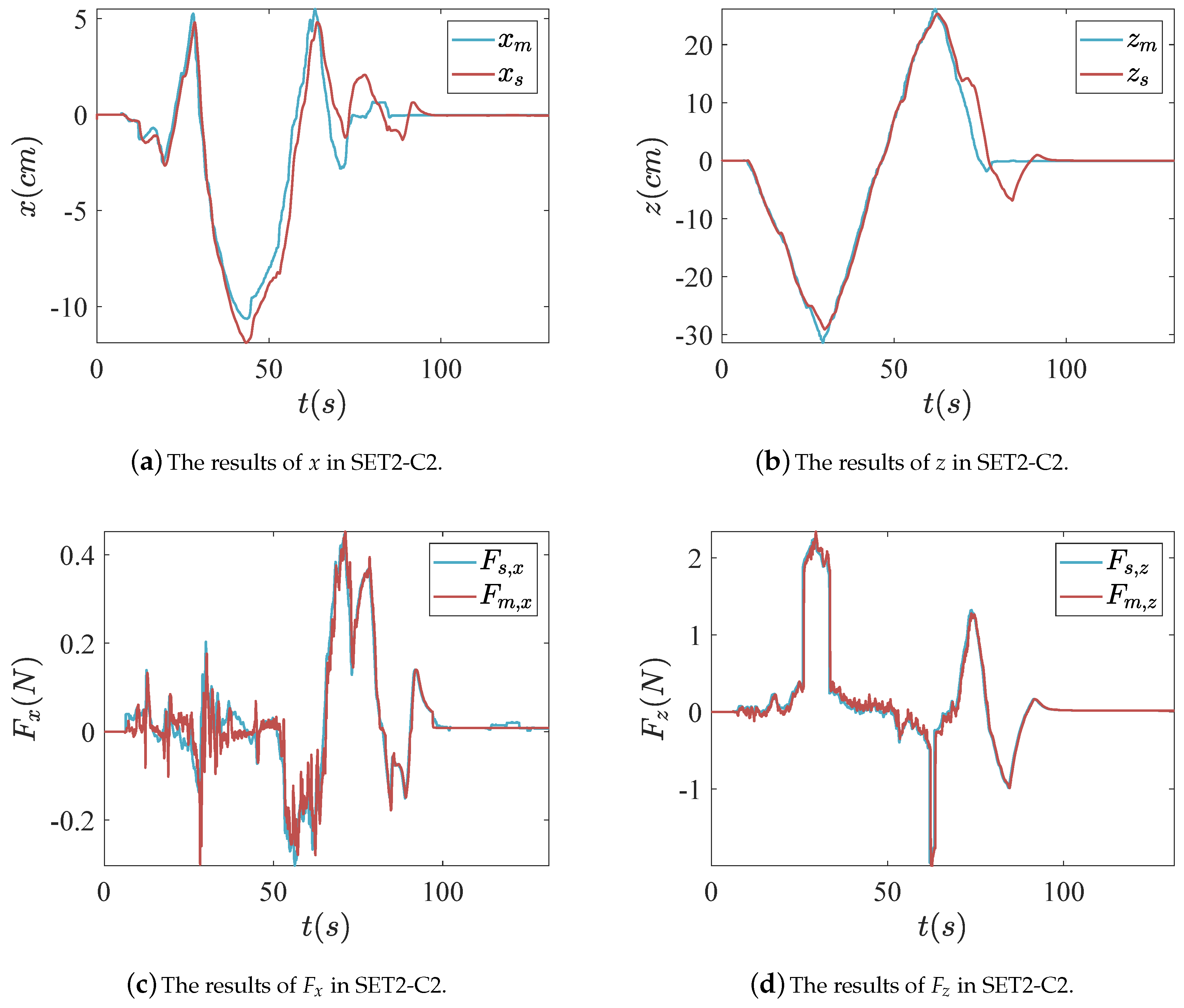
4.3. Experiment Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moran, M.E. Evolution of robotic arms. J. Robot. Surg. 2007, 1, 103–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbalata, C.; Dunnigan, M.W.; Petillot, Y. Coupled and decoupled force/motion controllers for an underwater vehicle-manipulator system. J. Mar. Sci. Eng. 2018, 6, 96. [Google Scholar] [CrossRef] [Green Version]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- McMahan, W.; Chitrakaran, V.; Csencsits, M.; Dawson, D.; Walker, I.D.; Jones, B.A.; Pritts, M.; Dienno, D.; Grissom, M.; Rahn, C.D. Field trials and testing of the OctArm continuum manipulator. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Anscombe, R.; Bryant, A.; Buckingham, R.; Ferguson, G.; Graham, A.; Lichon, M.; Green, B. Snake-Arm Robots: A New Approach to Aircraft Assembly; SAE Aerotech Congress: Warrendale, PA, USA, 2007. [Google Scholar]
- Tang, J.; Zhang, Y.; Huang, F.; Li, J.; Chen, Z.; Song, W.; Zhu, S.; Gu, J. Design and kinematic control of the cable-driven hyper-redundant manipulator for potential underwater applications. Appl. Sci. 2019, 9, 1142. [Google Scholar] [CrossRef] [Green Version]
- Webster, R.J.; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Rob. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Xu, W.; Liu, T.; Li, Y. Kinematics, dynamics, and control of a cable-driven hyper-redundant manipulator. IEEE/ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Zaraki, A.; Hayashi, Y.; Thorpe, H.; Strong, V.; Larsen, G.A.; Holderbaum, W. A leader-follower kinematic-based control system for a cable-driven hyper-redundant manipulator. In Proceedings of the International Conference on Advances in Robot Kinematics, London, UK, 18–19 November 2019. [Google Scholar]
- Liljebäck, P.; Pettersen, K.Y.; Stavdahl, ∅.; Gravdahl, J.T. A review on modelling implementation and control of snake robots. Robot. Auton. Syst. 2012, 1, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Lipkin, K.; Brown, I.; Peck, A.; Choset, H.; Rembisz, J.; Gianfortoni, P.; Naaktgeboren, A. Differentiable and piecewise differentiable gaits for snake robots. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1864–1869. [Google Scholar]
- Rollinson, D.; Choset, H. Pipe network locomotion with a snake robot. J. Field Robot. 2016, 33, 322–336. [Google Scholar] [CrossRef]
- Wright, C.; Buchan, A.; Brown, B.; Geist, J.; Schwerin, M.; Rollinson, D.; Tesch, M.; Choset, H. Design and architecture of the unified modular snake robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 4347–4354. [Google Scholar]
- Tesch, M.; Schneider, J.; Choset, H. Using response surfaces and expected improvement to optimize snake robot gait parameters. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1069–1074. [Google Scholar]
- Liljebäck, P.; Stavdahl, ∅.; Pettersen, K.Y.; Gravdahl, J.T. A modular and waterproof snake robot joint mechanism with a novel force/torque sensor. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 4898–4905. [Google Scholar]
- Zhang, Z.; Yang, G.; Yeo, S.H. Inverse kinematics of modular cable-driven snake-like robots with flexible backbones. In Proceedings of the 2011 IEEE 5th International Conference on Robotics, Automation and Mechatronics (RAM), Qingdao, China, 17–19 September 2011; pp. 41–46. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef]
- McMahan, W.; Jones, B.A.; Walker, I.D. Design and implementation of a multi-section continuum robot: Air-Octor. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 2578–2585. [Google Scholar]
- Wooten, M.; Frazelle, C.; Walker, I.D.; Kapadia, A.; Lee, J.H. Exploration and inspection with vine-inspired continuum robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–5. [Google Scholar]
- Ananthanarayanan, H.; Ordóëez, R. Real-time inverse kinematics of (2n+1) DOF hyper-redundant manipulator arm via a combined numerical and analytical approach. Mech. Mach. Theory 2015, 91, 209–226. [Google Scholar] [CrossRef]
- Martín, A.; Barrientos, A.; Del, C.J. The Natural-CCD algorithm, a novel method to solve the inverse kinematics of hyper-redundant and soft robots. Soft Robot. 2018, 5, 242–257. [Google Scholar] [CrossRef] [PubMed]
- Espinoza, M.S.; Gonçalves, J.; Leitão, P.; Sánchez, J.L.G.; Herreros, A. Inverse kinematics of a 10 DOF modular hyper-redundant robot resorting to exhaustive and error-optimization methods: A comparative study. In Proceedings of the 2012 Brazilian Robotics Symposium and Latin American Robotics Symposium, Fortaleza, Brazil, 16–19 October 2012; pp. 125–130. [Google Scholar]
- Braganza, D.; Dawson, D.M.; Walker, I.D.; Nath, N. A neural network controller for continuum robots. IEEE Trans. Robot. 2007, 23, 1270–1277. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, Y.J.; Gu, J. Integrated adaptive robust control for multilateral teleoperation systems under arbitrary time delays. Int. J. Robust Nonlinear Control 2016, 26, 2708–2728. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Sun, W.; Gu, J.; Yao, B. RBF-Neural-Network-Based Adaptive Robust Control for Nonlinear Bilateral Teleoperation Manipulators With Uncertainty and Time Delay. IEEE/ASME Trans. Mechatron. 2020, 25, 906–918. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Yang, C.; Yao, B. Adaptive Fuzzy Backstepping Control for Stable Nonlinear Bilateral Teleoperation Manipulators With Enhanced Transparency Performance. IEEE Trans. Ind. Electron. 2020, 67, 746–756. [Google Scholar] [CrossRef]
- Andrés, M.B.; Juan, R.G.; Iván, R.; Jaime, C.; Antonio, B. Design of a Hyper-Redundant Robot and Teleoperation Using Mixed Reality for Inspection Tasks. Sensors 2020, 20, 2181. [Google Scholar]
- Ren, L.; Omisore, O.M.; Han, S.; Wang, L. A master-slave control system with workspaces isomerism for teleoperation of a snake robot. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 4343–4346. [Google Scholar]
- Rayne, P.B.; Leibrandt, K.; Gras, G.; Fraisse, P.; Crosnier, A.; Yang, G. Inverse kinematics control methods for redundant snakelike robot teleoperation during minimally invasive surgery. IEEE Robot. Autom. Lett. 2018, 3, 2501–2508. [Google Scholar] [CrossRef]
- Lawrence, D.A. Stability and transparency in bilateral teleoperation. IEEE Trans. Robot. Autom. 1992, 9, 625–637. [Google Scholar]
- Yang, X.; Hua, C.; Yan, J.; Guan, X. An exact stability condition for bilateral teleoperation with delayed communication channel. IEEE Trans. Syst. Man, Cybern. Syst. 2016, 46, 434–439. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Chen, W.; Zhang, J.; Sun, W.; Chen, J.; Gu, J.; Zhu, S. RBFNN-based adaptive sliding mode control design for delayed nonlinear multilateral tele-robotic system with cooperative manipulation. IEEE Trans. Ind. Inform. 2020, 16, 1236–1247. [Google Scholar] [CrossRef]
- Tanner, N.A.; Niemeyer, G. Improving perception in time-delayed telerobotics. Int. J. Robot. Res. 2005, 24, 631–644. [Google Scholar] [CrossRef]
- Niemeyer, G.; Slotine, J.E. Stable adaptive teleoperation. IEEE J. Ocean. Eng. 1991, 16, 152–162. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Sun, W.; Song, W. An improved wave-variable based four-channel control design in bilateral teleoperation system for time-delay compensation. IEEE Access 2018, 6, 12848–12857. [Google Scholar] [CrossRef]
- Bate, L.; Cook, C.D.; Li, Z. Reducing wave-based teleoperator reflections for unknown environments. IEEE Trans. Ind. Electron. 2011, 58, 392–397. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, P.X. Improving trajectory tracking in wave-variable-based teleoperation. IEEE/ASME Trans. Mechatron. 2010, 15, 321–326. [Google Scholar]
- Ye, Y.; Liu, P.X. Improving haptic feedback fidelity in wave-variable-based teleoperation orientated to telemedical applications. IEEE Trans. Instrum. Meas. 2009, 58, 2847–2855. [Google Scholar]
- Hokayem, P.F.; Spong, M.W. Bilateral teleoperation: An historical survey. Automatica 2006, 42, 2035–2057. [Google Scholar] [CrossRef]





| Symbol | Property | Value |
|---|---|---|
| N | Number of all joints | 5 |
| M | Number of through holes at endplates | 18 |
| R | Radius of tubular structure | 33.8 mm |
| D | Distance from tubular structure to the center of universal joint | 12 mm |
| H | Length of tubular structure | 106 mm |
| Device or Software | Model or Version |
|---|---|
| Actuators | Maxon EC-max 30 |
| Linear magnetic encoder | LM10 |
| Data acquisition device | Quanser QPID-e |
| Real-time control software | MATLAB 2018a, Quanser QUARC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Huang, F.; Chen, Z.; Song, W.; Zhu, S. Teleoperation Control Design with Virtual Force Feedback for the Cable-Driven Hyper-Redundant Continuum Manipulator. Appl. Sci. 2020, 10, 8031. https://doi.org/10.3390/app10228031
Qin L, Huang F, Chen Z, Song W, Zhu S. Teleoperation Control Design with Virtual Force Feedback for the Cable-Driven Hyper-Redundant Continuum Manipulator. Applied Sciences. 2020; 10(22):8031. https://doi.org/10.3390/app10228031
Chicago/Turabian StyleQin, Long, Fanghao Huang, Zheng Chen, Wei Song, and Shiqiang Zhu. 2020. "Teleoperation Control Design with Virtual Force Feedback for the Cable-Driven Hyper-Redundant Continuum Manipulator" Applied Sciences 10, no. 22: 8031. https://doi.org/10.3390/app10228031
APA StyleQin, L., Huang, F., Chen, Z., Song, W., & Zhu, S. (2020). Teleoperation Control Design with Virtual Force Feedback for the Cable-Driven Hyper-Redundant Continuum Manipulator. Applied Sciences, 10(22), 8031. https://doi.org/10.3390/app10228031







