Steering Pull Model and Its Sensitivity Analysis

Abstract

When a vehicle goes on the straight road with a bank angle, a steering pull makes the driver exert a constant steering torque to the steering wheel, which causes an annoying steering feel to the driver. This paper proposes a steering pull model and sensitivity analysis on the steering pull. In order to develop the steering pull model, pulling forces on the tires, such as plysteer and conicity forces, lateral force due to slip angle, lifting forces due to cast and kingpin, and camber force are modeled. A steering system is also modeled because the generated pulling forces are attenuated as it is transmitted through the steering system. Each component of the steering system, such as lower body linkages, rack and pinion gear, universal joint, and steering column with electric power steering (EPS) system is modeled, and then they are integrated into a complete steering system. Finally, the steering pull model is developed by integrating the pulling force model with the steering system model. For verification, the steering pull of a vehicle is estimated based on the model, and the results are compared with the experimental results. For the verification experiments, a steering pull measurement system using a global positioning system (GPS) and its accessories are used. The result comparison showed that the developed steering pull model provides very accurate estimation results. Based on the steering pull model, the sensitivity of steering pull factors, such as caster angle, kingpin angle, camber angle, rack friction force, and anti-rattle spring (ARS) stiffness is analyzed.

1. Introduction

The straight-ahead stability of vehicles at high speeds is a great concern to automotive manufacturers because a high straight-ahead stability makes the driver comfortable, which leads to driver’s high dependability and loyalty to the brand. When the driver releases the steering wheel of a vehicle on the straight road with a bank angle, the vehicle starts to deviate from the intended path. This deviation is called ‘steering pull’, also known as ‘vehicle pull’ or ‘steering drift’, and it increases as the vehicle moves forward [1]. Therefore, the driver applies a corrective steering torque to maintain the driving course, which gives the driver an annoying steering feel, and sometimes, the steering pull can lead to a serious accident when the driver is distracted at the wheel. For these reasons, the steering pull is a key factor that determines the straight-ahead stability and accordingly, should be managed by automotive manufacturers. It is also one of important evaluation factors in the initial quality survey (IQS) of J.D. Power [2].

The steering pull during braking has been studied by researchers. Mirza et al. presented the dynamic characteristics of suspension parameters on a vehicle experiencing steering pull under straight line braking [3]. For multi-body dynamics analysis, the paper modeled the front and rear suspension parameters as rigid links joined with flexible bushes so as to access their effect on the vehicle during braking. Klaps and Day studied the sensitivity of suspension compliances and steering offset on braking-related steering pull and presented the experimental results from kinematic and compliance (K&C) tests [4]. Rosa et al. analyzed the effects on handling due to suspension component and assembly tolerances focusing on steering pull [5]. The paper focused on the causes and reduction of steering pull in the specific case of vehicles with front double wishbone suspension and rear five arms suspension.

The improvement of steering pull in electric power steering (EPS) systems has been also studied by researchers. They developed the control strategies of EPS systems to reduce steering pull. Kubota et al. developed a new algorithm to reduce steering pull in an EPS system [6]. A compensation method applying corrective steering torque using an EPS motor was developed and then, it was validated through field tests. Koyama and Matsunaga proposed a control method using an EPS system to improve steering maneuverability and reduce steering pull on rutted roads [7]. The proposed method detects the amount of disturbance torque caused by the ruts in the road, and only when disturbance torque is detected, the EPS system applies compensation torque to the steering system.

For parameter studies on steering pull, many researchers focused on the steering pull generated by tire characteristics. Mundl et al. studied the simulation procedure of a ply steer residual aligning torque (PRAT) using a stationary global rolling finite-element method (FEM) tire model combined with a detailed local FEM tread pattern model [8]. The simulated results of the PRAT for eight pattern variants are compared with measured values of experimental tires to show a high correlation. Lee studied the behaviors of tires and vehicle system in the straight-line motion and identified the effect of tires using two degrees of freedom vehicle model [9]. Then, the results were verified through field tests and simulations with a full-car model.

This paper proposes a complete steering pull model and the sensitivity of steering pull factors based on the model. To develop the steering pull model, a tire pulling force and a steering system are also modeled, and the integration of these models is achieved. In the tire pulling force model, the factors of a tire pulling force, such as road bank angle, plysteer and conicity, kingpin and caster angles, and camber angle, are investigated and mathematically modeled. Then, a steering system that consists of lower body linkages, rack and pinion gear, universal joint, and steering column is also modeled. Finally, a complete steering pull model is developed by integrating the tire pulling force model and the steering system model.

2. Tire Pulling Force

In order to predict steering pull of a vehicle, tire pulling forces needs to be modeled according to the driving conditions and the geometrical characteristics of the vehicle. In this study, external and internal factors that affect a tire pulling force are considered and theoretical approaches are made to model these factors. For a complete steering pull model, this tire pulling force model is integrated with the steering system model in Chapter 3.

A tire pulling force consists of three parts—pulling force by road bank angle, tire characteristics, and wheel alignment. When a vehicle drives on a banked road, a pulling force is applied to the tire. This pulling force is affected by the tire characteristics, such as PRAT, conicity residual aliging torque (CRAT), and lateral forces. Along with the tire characteristics, the pulling force is also affected by the wheel alignment characteristics of the vehicle such as camber, caster, and kingpin angles.

2.1. Road Bank Angle

Road generally has a bank angle between 0.6 and 2.0 degrees to drain water and prevent puddles in raining [4]. This bank angle causes a pulling force to the vehicle, which appears in the form of centripetal force. Figure 1 shows a centripetal force due to a road bank angle.

This centripetal force can be represented by Equation (1).

$$M{a}_n\mathit{cos}{\theta }_{BA}=M\frac{V^2}{r}\mathit{cos}{\theta }_{BA}=Mg\mathit{sin}{\theta }_{BA}$$

(1)

$$r=\frac{V^2\mathit{cos}{\theta }_{BA}}{g\mathit{sin}{\theta }_{BA}}=\frac{V^2}{g\mathit{tan}{\theta }_{BA}}$$

(2)

where $M=$ vehicle mass, $a_n=$ centripetal acceleration, $V=$ vehicle speed, $r=$ turning radius, ${\theta }_{BA}=$ bank angle.

As shown in Equation (2), a turning radius is determined by the vehicle’s driving speed, and the higher the vehicle speed, the larger the turning radius.

Figure 2 shows a pulling distance of the vehicle. The pulling distance is determined by the turning radius and the vehicle moving distance, as shown in the following Equation (3).

$$d=\sqrt{L^2+r^2}-r=\sqrt{L^2+{\left(\frac{V^2}{g\mathit{tan}{\theta }_{BA}}\right)}^2}-\frac{V^2}{g\mathit{tan}{\theta }_{BA}}$$

(3)

where $L=$ vehicle moving distance, $d=$ pulling distance.

2.2. Plysteer and Conicity Forces

When a vehicle turns, it has one center of rotation, and thus each tire has its direction of travel. Each tire also has its direction of heading, on the other hand, and the angle difference between the direction of travel and heading is called ‘slip angle’ [10]. Due to this slip angle, the tread sideways with respect to the tire and this yields the lateral force in the contact patch [11]. Accordingly, in vehicle dynamics, the lateral force of a tire is zero when its slip angle is zero. However, in many pneumatic tires, the lateral force is also caused by the structure of the tire such as the asymmetry of carcass and tread. This lateral force by the tire structures is called ‘residual cornering force’ [12].

The residual cornering force of a tire results from the tire’s plysteer and conicity. A typical radial tire structure is made with multiple layers of plies bonded together. If the tire rolls, the shape of the tire becomes flat at the contact patch, which causes the generation of lateral and longitudinal shear stresses in the contact area. These shear stresses cause coupled reaction forces which is called ‘plysteer force’. This plysteer force is generated in typical radial tires under straight rolling conditions, and it is an inherent property which means the nonzero lateral force at zero slip angles [13]. The acting direction of a plysteer force depends on the rolling direction of the tire as shown in Figure 3a. Generally, a plysteer force is constant for a given tire design and has very few variations between samples but it rather varies with tire design.

The conicity force of a tire is caused by manufacturing errors and can be explained by a rolling cone [11]. The acting direction of conicity force does not depends on the rolling direction of the tire as shown in Figure 3b. For the tires recently produced by modern tire manufacturing systems, the conicity force is known to be very small due to high precision manufacturing processes, and when two tires from the same manufacturing system are installed in a vehicle, they usually have the same direction and magnitude of conicity force. In addition, when installed in the opposite direction, they offset each other, which results in a counterbalance. For these reasons, the conicity force is neglected in this study.

On the other hand, the plysteer forces of left and right tires have the same direction and therefore, they need to be considered in the tire pulling force model. There have been several theoretical approaches to predict the plysteer force of a tire, as mentioned in Chapter 1, but this study employed experimental values of a tire in order to build an accurate steering pull model. The plysteer force of a tire can be obtained by averaging the plysteer values which are measured in two opposite rolling directions. The plysteer force of a tire is (Equation (4))

$$F_{y,ply}=\frac{F_{y,ply\_cw}-F_{y,ply\_ccw}}{2}$$

(4)

where, $F_{y,ply}$ = plysteer force, $F_{y,ply\_cw}$ = measured plysteer force in clockwise direction, $F_{y,ply}$ = measured plysteer force in counter clockwise direction.

2.3. Wheel Alignment

2.3.1. Kingpin and Caster

When a tire is turned by external forces, such as driver steering force or tire pulling force, the tire turns with respect to a kingpin axis. This kingpin axis, as viewed from the front of the vehicle, is set at an angle relative to the vertical line. This angle is called ‘steering angle inclination (SAI)’ or ‘king pin inclination (KPI)’ [10,14]. In the same manner, the kingpin axis is set at an angle relative to the vertical line as viewed from the side of the vehicle. This angle is called ‘caster angle’. These KPI and caster angle are described in Figure 4. Because of the KPI, the tire basically turns towards the ground as it turns. As the reaction from the ground, the tire lifts up the vehicle. Assuming the camber angle is neglected as it is small, the lifting moment by the KPI of left and right tires can be represented by Equation (5) [15].

$$M_{lift}=\left(F_{zl}-F_{zr}\right)d_{kp}\mathit{sin}\nu \mathit{cos}\delta -\left(F_{zl}+F_{zr}\right)d\mathit{sin}\lambda \mathit{sin}\delta$$

(5)

where $M_{lift}$ = lifting moment, $F_{zl}$ = normal force at left tire, $F_{zr}$ = normal force at right tire, $d_{kp}$ = kingpin offset, $\nu$ = caster angle, $\lambda$ = kingpin angle, $\delta$ = tire turning angle. By dividing the lifting moment by pneumatic trail of the tire, as described in Equation (6), the lifting force is obtained.

$$F_{lift}=\frac{\left(F_{zl}-F_{zr}\right)d_{kp}\mathit{sin}\nu \mathit{cos}\delta -\left(F_{zl}+F_{zr}\right)d\mathit{sin}\lambda \mathit{sin}\delta }{2t_p}$$

(6)

where $F_{lift}$ = lifting force due to caster and kingpin, $t_p$ = pneumatic trail.

In order to analyze the relation between tire contact area and lateral force, the tire model proposed by Rajamani is employed [16]. Due to the friction force generated between the tires and ground, the treads of the tire are deformed to the opposite direction of the tire turning direction. Assuming a parabolic force distribution at the contact patch, the lateral force of the tire can be obtained by Equation (7) [16].

$$F_y=\frac{8kb{a}^2}{6\theta }\left[1-{\left(\frac{x_S}{2a}\right)}^3\right]$$

(7)

where $k$ = lateral stiffness of tire per unit area, $a$ = half length of contact patch, $b$ = half width of contact patch, $\theta$ = constant (a function of tire parameters and normal force), $x_S$ = initiation point in contact patch for sliding.

2.3.2. Camber

Camber angle is the inclination angle of a tire with respect to the vertical line. This camber angle produces distortion of the contact surface of the tire and it causes a lateral force called ‘camber force’ or ‘camber thrust’. A camber force can be obtained by Equation (8) [12].

$$F_{y,c}=C_{\gamma }\gamma =C_C\left(F_{zl}+F_{zr}\right)\gamma$$

(8)

where $F_{y,c}$ = lateral force due to camber angle, $C_{\gamma }$ = camber stiffness, $C_C$ = camber stiffness coefficient, $\gamma$ = camber angle.

Typically, a camber angle is set under 2 degrees and thus, the camber force caused by the camber angle is smaller than the lateral force by a slip angle. However, it can have a significant effect on the steering pull since the lateral force by a small slip angle is also very small. For a small tire angle, the camber and lateral forces can be treated as the independent as shown in Equation (9) [12].

$$F_{y,t}=F_{y,\alpha }+F_{y,c}=F_{y,\alpha }+C_C\left(F_{zl}+F_{zr}\right)\gamma$$

(9)

where $F_{y,t}$ = total lateral force, $F_{y,\alpha }$ = lateral force due to slip angle.

3. Steering System Model

A steering system generally consists of a steering column, a universal joint, and a rack and pinion gear. When a wheel is turned by external forces, such as driver steering force and tire pulling force, it turns with respect to the kingpin axis which is produced by the upper and lower body linkages, and thus these linkages are also considered in this study. In many studies, each component of a steering system is represented by a mass-spring-damper system. However, the friction forces generated within the components are also important for a steering pull model because they substantially affect steering pull by attenuating the tire pulling force.

3.1. Lower Body Linkage Model

A tire pulling force is transmitted through the lower body linkages of the vehicle. In the case of modern vehicles, a tire is mechanically connected to a knuckle arm, and then to a rack and pinion gear through a tie rod. Figure 5 shows the relation between the tire pulling force and the rack force. The relation can be calculated by Equations (10)–(12).

$${\overrightarrow{F}}_1=\frac{M_z}{\left|\overrightarrow{r_{KP}}\right|}{C}_{KP}\times \frac{\left(\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right)}{\left|\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right|}, \left|\overrightarrow{r_{KP}}\right|=\frac{\left|\left(\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right)\times \overrightarrow{C_{KP}}\right|}{\left|\overrightarrow{C_{KP}}\right|}$$

(10)

$${\overrightarrow{F}}_2=\left|{\overrightarrow{F}}_1\right|\frac{\left(\overrightarrow{P_4}-\overrightarrow{P_3}\right)}{\left|\overrightarrow{P_4}-\overrightarrow{P_3}\right|}\mathit{cos}{\theta }_1, \mathit{cos}{\theta }_1=\frac{\left(C_{KP}\times \frac{\left(\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right)}{\left|\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right|}\right)\left(\frac{\left(\overrightarrow{P_4}-\overrightarrow{P_3}\right)}{\left|\overrightarrow{P_4}-\overrightarrow{P_3}\right|}\right)}{\left|C_{KP}\times \frac{\left(\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right)}{\left|\overrightarrow{P_3}-\overrightarrow{P_{KP}}\right|}\right|\left|\frac{\left(\overrightarrow{P_4}-\overrightarrow{P_3}\right)}{\left|\overrightarrow{P_4}-\overrightarrow{P_3}\right|}\right|}$$

(11)

$${\overrightarrow{F}}_R=\left|{\overrightarrow{F}}_2\right|\frac{\left(-\overrightarrow{P_4}\right)}{\left|\overrightarrow{P_4}\right|}\mathit{cos}{\theta }_2, \mathit{cos}{\theta }_2=\frac{\left(\frac{\left(\overrightarrow{P_4}-\overrightarrow{P_3}\right)}{\left|\overrightarrow{P_4}-\overrightarrow{P_3}\right|}\right)\left(\frac{\left(-\overrightarrow{P_4}\right)}{\left|\overrightarrow{P_4}\right|}\right)}{\left|\frac{\left(\overrightarrow{P_4}-\overrightarrow{P_3}\right)}{\left|\overrightarrow{P_4}-\overrightarrow{P_3}\right|}\right|\left|\frac{\left(-\overrightarrow{P_4}\right)}{\left|\overrightarrow{P_4}\right|}\right|}$$

(12)

where ${\overrightarrow{F}}_1$ = force vector acting on knuckle arm, $M_Z$ = tire turning moment, $\overrightarrow{r_{KP}}$ = effective turning radius vector of knuckle arm, $P_3$ = position of knuckle arm after tire turning, $P_{KP}$ = position of kingpin axis, $C_{KP}$ = unit vector of kingpin axis, ${\overrightarrow{F}}_2$ = force vector acting on tie rod, ${\theta }_1$ = acting angle between knuckle arm and tie rod, ${\overrightarrow{F}}_R$ = force vector of rack, $P_4$ = position of one end of rack, ${\theta }_2$ = acting angle between tie rod and rack.

3.2. Rack and Pinion Gear Model

A rack and pinion gear is connected to the knuckle arm through the tie rod. It transmits tire pulling forces to the universal joint. Since steering motions usually include repetitive direction changes, backlashes within the steering system should be avoided. Furthermore, due to these direction changes, uneven wear can easily occur in the rack teeth. In order to prevent these undesirable phenomena, a yoke spring is introduced in the rack and pinion gear. A plunger is placed on the yoke spring and against the rack gear while a yokenut is placed under the yoke spring [17]. The compressive force of the yoke spring is controlled by tightening the yokenut, and by this compressive force, the backlash of the rack and pinion gear can be prevented. On the other hand, the compressive force can also cause a friction force between the rack and the plunger, which may have an influence on the steering pull. In this study, Coulomb friction generated between the rack and the plunger is also considered. A rack and pinion gear can be modeled by the following Equation (13).

$$M_R{\ddot{x}}_R+B_R\left({\dot{x}}_R-{\dot{x}}_U\right)+K_R\left(x_R-x_U\right)=\frac{T_U}{R_{pn}}-F_F\cdot \mathit{sgn}({\dot{x}}_U),$$

$$x_U=R_{pn}{\theta }_U, F_R=K_R\left(x_U-x_R\right)$$

(13)

where $M_R$ = rack mass, $x_R$ = rack displacement, $x_U$ = displacement by rotation of universal joint, $B_R$ = damping coefficient of rack, $K_R$ = stiffness of rack, $T_U$ = universal joint torque, $R_{pn}$ = radius of pinion, $F_F$ = Coulomb friction force of rack, ${\theta }_U$ = universal joint angle, $F_R$ = rack force.

3.3. Universal Joint Model

A universal joint is connected to a rack and pinion gear. It links the pinion gear to the steering column while allowing the transmission of steering torque. Its friction is relatively very small, compared to other steering system components, and therefore, the friction force generated in the joint is neglected. A universal joint can be modeled by the following Equation (14) [18].

$$T_U=\frac{{\mathit{sin}}^2{\theta }_B+{\mathit{cos}}^2{\varphi }_{BU}{\mathit{cos}}^2{\theta }_B}{\mathit{cos}{\varphi }_{BU}}\cdot \frac{{\mathit{sin}}^2{\theta }_C+{\mathit{cos}}^2{\varphi }_{CA}{\mathit{cos}}^2{\theta }_C}{\mathit{cos}{\varphi }_{CA}}{T}_C,$$

$${\theta }_B={\mathit{tan}}^{-1}\left(\frac{\mathit{tan}{\theta }_C}{\mathit{cos}{\varphi }_{CA}}\right)+{\varphi }_{AB}, {\theta }_U={\mathit{tan}}^{-1}\left(\frac{\mathit{tan}{\theta }_B}{\mathit{cos}{\varphi }_{BU}}\right)$$

(14)

where $T_C$ = steering column torque, ${\theta }_B$ = angle of intermediate bar of universal joint, ${\theta }_C$ = steering column angle, ${\varphi }_{BU}$ = tilt angle between universal joint and rack & pinion gear, ${\varphi }_{CA}$ = tilt angle between steering column and universal joint, ${\varphi }_{AB}$ = phase difference angle of intermediate bar of universal joint.

3.4. Steering Column Model

A steering column is located between the universal joint and the steering wheel. In the case of a column type electric power steering (C-EPS) system, the steering assist components, such as a torque sensor, a worm gear, and an electric motor, are connected to the steering column. The worm gear that consists of a worm shaft and a worm wheel is basically designed to work under the condition in which their pitch circles are mating each other [19]. However, as the vehicle goes on a bumpy road, the worm gear is subjected to vibration which causes the mismatch of the pitch circles so that undesirable rattling of the worm gear occurs. For this reason, an anti-rattle spring (ARS) is usually employed in the C-EPS system [19].

An ARS applies preload to the worm shaft, and this preload causes misalignment and friction to the worm shaft [20]. The friction appears in two types—Coulomb friction and viscous friction. Coulomb friction is represented by a linear function of the ARS constant while viscous friction is represented by an exponential equation of the steering rate [21]. The entire steering column including steering assist components can be modeled by the following Equation (15).

$$J_C{\ddot{\theta }}_C+B_C({\dot{\theta }}_C-{\dot{\theta }}_S)+K_C\left({\theta }_C-{\theta }_S\right)=T_{wh}-T_{TF}\cdot \mathit{sgn}({\dot{\theta }}_S)$$

$$T_{CF}=C{K}_{ARS}, T_{VF}=a{\dot{\theta }}_S^b, T_C=K_C\left({\theta }_S-{\theta }_C\right), T_{TF}=T_{CF}+T_{VF}$$

(15)

where $J_C$ = inertia coefficient of steering column, ${\theta }_C$ = steering column angle, $B_C$ = damping coefficient of steering column, $K_C$ = stiffness of steering column, ${\theta }_S$ = steering wheel angle, $T_{wh}$ = steering wheel torque, $T_{TF}$ = total friction torque of steering column, $T_{CF}$ = Coulomb friction of steering column, $C$ = coefficient of Coulomb friction, $K_{ARS}$ = ARS stiffness, $T_{VF}$ = viscous friction of steering column, $a$,$b$ = coefficient of viscous friction.

3.5. Friction Model in Steering System

Friction forces are generated within each component of the steering system and these friction forces were modeled [22]. In the case of steering pull, dynamic characteristics of the steering system can be neglected because the steering pull occurs very slowly. Therefore, the friction forces generated within the steering system is assumed to be a static process rather than a dynamic process in this study. A friction force acting on the tires is obtained by Equation (16).

$$\begin{gathered} F_{fric}=\left(T_{TF}\times \frac{{\mathit{sin}}^2{\theta }_B+{\mathit{cos}}^2{\varphi }_{BU}{\mathit{cos}}^2{\theta }_B}{\mathit{cos}{\varphi }_{BU}}\cdot \frac{{\mathit{sin}}^2{\theta }_C+{\mathit{cos}}^2{\varphi }_{CA}{\mathit{cos}}^2{\theta }_C}{\mathit{cos}{\varphi }_{CA}}\times \frac{1}{R_{pn}}+F_F\right) \\ \times \mathit{cos}{\theta }_1·\mathit{cos}{\theta }_2 \end{gathered}$$

(16)

3.6. Integration of Steering System Models

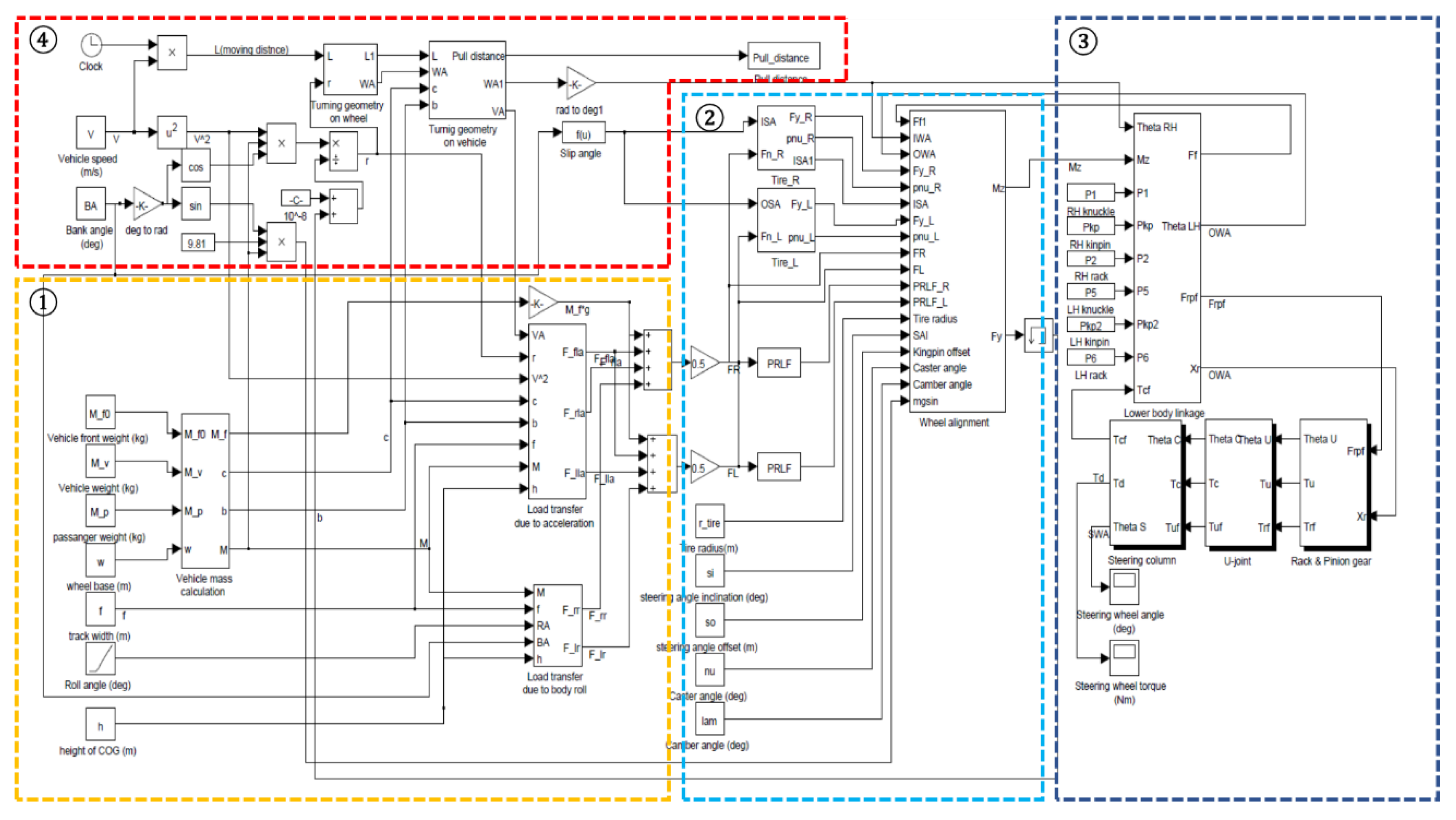
For a complete steering system model, each model of the steering system needs to be integrated in one steering system model. In Simulink environment, each model has input and output ports, and they can be interconnected with each other. The complete steering system model is shown in Figure 6. As shown in the left side of Figure 6, the design parameters of the vehicle and the tire pulling force are input into the steering system model. The complete steering system model consists of four Simulink subsystems—lower body linkage, rack and pinion gear, universal joint, and steering column—and each subsystem contains the mathematical models described earlier in this chapter. Finally, the steering torque and angle, which are generated by the tire pulling force and delivered through the steering system to the driver, can be obtained as shown in the right side of Figure 6.

4. Steering Pull Model

4.1. Integration of Acting Forces on Tires

The steering pull distance of a vehicle is determined by the force acting on the tires. When a vehicle goes on the road with a bank angle, the force acting on the tires is shown Figure 7. However, as mentioned in Chapter 2 and 3, there are several forces that hinder the tires from turning and therefore, Equation (1) is modified and the tire turning force can be represented as Equation (17).

$$M{a}_n\mathit{cos}{\theta }_{BA}=M\frac{V^2}{r}\mathit{cos}{\theta }_{BA}=Mg\mathit{sin}{\theta }_{BA}-F_{tire}$$

(17)

where $F_{tire}$ = force that hinders tire turning.

For the calculation of $F_{tire}$, the bicycle model is employed. As shown in Figure 7, when a vehicle moves, the longitudinal and lateral forces acting on the tires are represented as the following Equation (18).

$$M\frac{V^2}{r}\mathit{cos}{\theta }_{BA}=Mg\mathit{sin}{\theta }_{BA}-\left(F_{xf}\mathit{sin}{\theta }_{WA}+F_{yf}\mathit{cos}{\theta }_{WA}\right)$$

(18)

where ${\theta }_{WA}$ = heading angle of wheel, $F_{xf}$ = longitudinal force acting on front tire, $F_{yf}$ = lateral force acting on front tire.

In the case of steering pull in which the vehicle has a small wheel angle and a constant vehicle speed, the longitudinal force can be neglected because it hardly has an influence on the steering pull. On the other hand, plysteer force, lateral force due to slip angle, lifting force of cast & kingpin, camber force, and friction force transferred from the steering system should be considered. When all factors are considered, Equation (18) can be rewritten as Equation (19).

$$M\frac{V^2}{r}\mathit{cos}{\theta }_{BA}=Mg\mathit{sin}{\theta }_{BA}+F_{y,ply}-F_y-F_{y,c}-F_{lift}-F_{fric}$$

(19)

where $F_{y,ply}$ = plysteer force, $F_y$ = lateral force due to slip angle, $F_{y,c}$ = lateral force due to camber, $F_{lift}$ = lifting force due to caster and kingpin, $F_{fric}$ = transferred friction force of steering system.

4.2. Estimation of Steering Pull Distance

A steering pull distance is determined by the turning radius. The turning radius of a wheel is (Equation (20))

$$r=\frac{M{V}^2\mathit{cos}{\theta }_{BA}}{Mg\mathit{sin}{\theta }_{BA}-F_{yf}}$$

(20)

and the steering pull distance is (Equation (21))

$$d_W=\sqrt{L^2+r^2}-r=\sqrt{L^2+{\left(\frac{M{V}^2\mathit{cos}{\theta }_{BA}}{Mg\mathit{sin}{\theta }_{BA}-F_{yf}}\right)}^2}-\frac{M{V}^2\mathit{cos}{\theta }_{BA}}{Mg\mathit{sin}{\theta }_{BA}-F_{yf}}$$

(21)

where $d_W$ = steering pull distance of a wheel, $L$ = moving distance.

Equation (21) represents the steering pull distance of the wheel, and therefore, the steering pull distance of the vehicle can be derived by employing the turning geometry of the bicycle model. The steering pull distance of the vehicle is (Equation (22))

$$d_V=\frac{c}{b+c}\left(\sqrt{L^2+{\left(\frac{M{V}^2\mathit{cos}{\theta }_{BA}}{Mg\mathit{sin}{\theta }_{BA}-F_{yf}}\right)}^2}-\frac{M{V}^2\mathit{cos}{\theta }_{BA}}{Mg\mathit{sin}{\theta }_{BA}-F_{yf}}\right)$$

(22)

where $d_V$ = steering pull distance of vehicle.

By integrating all models, a complete steering pull model can be derived. The block diagram of the developed steering pull model on SIMULINK environment is described in Figure 8. The steering pull model consists of four parts—1. load transfer with vehicle dimension parameters, 2. wheel alignment with tire characteristics and suspension design parameters, 3. steering system, and 4. steering pull estimation based on experimental conditions.

5. Results and Verification

In this study, the steering pull of a vehicle is estimated by the developed steering pull model, and then the results are verified by experimental results.

5.1. Estimation Results

For a steering pull estimation, a vehicle is designated and its design parameters such as tire properties, wheel alignment settings, mechanical characteristics of the steering system, and lower body linkages are adopted in the model. In addition to the vehicle, driving conditions are also prepared for the estimation. 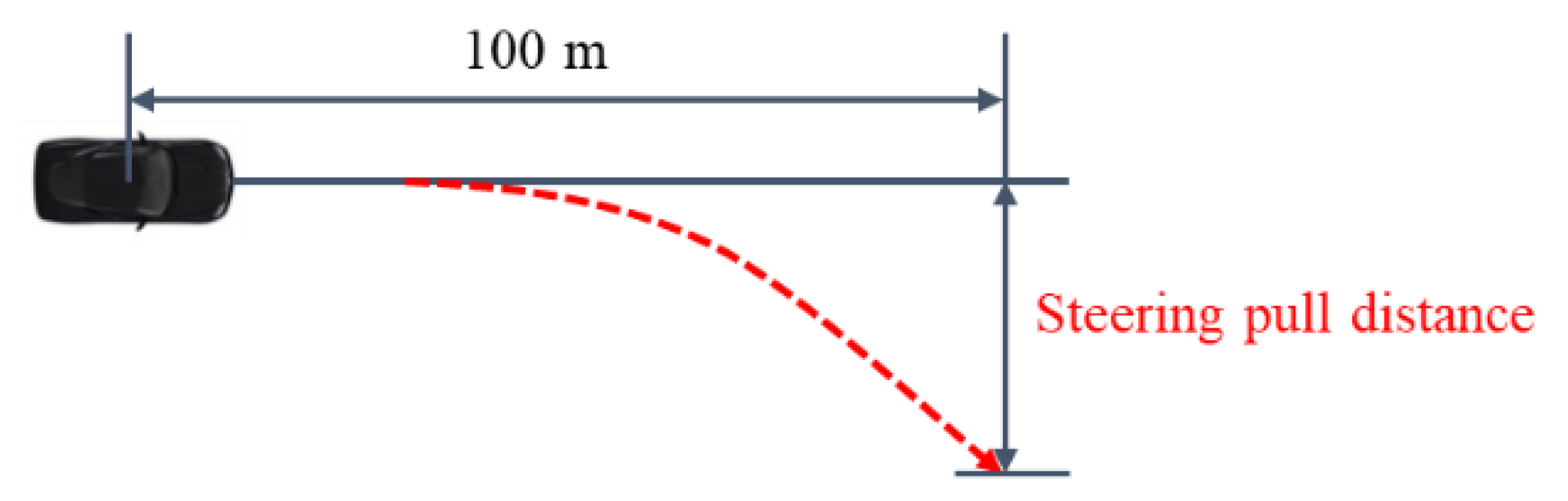Typically, there are two types of test modes for steering pull evaluation—free control test and fixed control test [23]. In the case of the free control test, the driver drives straight at the constant speed of 80 km/h with one passenger onboard. When the vehicle reaches the target speed, the driver releases the steering wheel to have the vehicle in a free state. The vehicle starts to drift and when the driving distance reaches 100 m, the steering pull distance of the vehicle is measured as shown in Figure 9. In the case of the fixed control test, the steering wheel is not released but fixed by the driver. Instead, a torque sensor mounted in the steering column measures the torque generated by the steering pull.

In this study, the free control test is employed for steering pull evaluation. The driving conditions and design parameters of the designated vehicle are described in

Table 1. The estimation conditions of steering pull.

Driving Conditions
Vehicle speed (km/h)	80
Passengers	2 (150 kg)
Driving distance (m)	100
Bank angle (deg)	0.7, 1.6
Design parameters
Caster angle (deg)	4.5
Kingpin angle (deg)	12.7
Camber angle (deg)	−0.5
Tire size	215/55 R17

.

Figure 10 shows the steering pull estimation results. As expected, the steering pull distance increases as the vehicle moving distance increases and its increasing tendency is exponential rather than linearly proportional. When the vehicle reaches 100 m, the steering pull distances at 0.7 and 1.6 degrees of bank angle are 0.58 and 0.96 m, respectively.

5.2. Verification

For verification, the steering pull distance of the vehicle is measured through field tests. In order to measure the steering pull, a global positioning system (GPS) is adopted. The verification experiments are performed through the following procedures. First, a GPS system is mounted on the roof of the vehicle and the driver drives the vehicle straight on the test road. The GPS system measures the driving path of the vehicle. By repeating the measurement and averaging the measured driving paths, the reference line of the steering pull is obtained. Second, the driver drives the vehicle along the reference line, and when the vehicle reaches 80 km/h, the driver releases the steering wheel. The vehicle starts to deviate from the reference line, and by repeating the measurement and averaging the deviation, the pulling line is obtained. Finally, the steering pull distance of the vehicle can be obtained by comparing the pulling line and the reference line.

The GPS measurement system consists of a GPS, a GPS data acquisition device, and a laptop. The program for the data acquisition and creating the reference and pulling lines is coded in LabVIEW. The experimental setup for the steering pull measurement is shown in Figure 11 and the specifications of the measurement system are described in

Table 2. Specifications of measurement system.

Update rate (Hz)	100 Hz
Velocity accuracy (km/h)	0.1
Velocity resolution (km/h)	0.01
Moving distance accuracy (%)	0.05
Moving distance resolution (m)	0.01
Heading accuracy (deg)	0.1
Heading resolution (deg)	0.01

.

Figure 12 shows the theoretical estimation and the experimental verification results. As the simulated results, the measured steering pull distance increases with the increase of the vehicle moving distance. There are slight differences between the model and the verification results, but the differences can be neglected considering the uneven road condition of the verification experiments. Throughout the entire steering pull distance, the model provides very accurate estimation results.

6. Sensitivity Analysis and Discussion

In this study, a sensitivity analysis on various design parameters is performed based on the steering pull model. The sensitivity values of each factor were obtained by Equation (23).

$$Sensitivity=\frac{\left(\frac{d_M}{d_R}\right)}{\left(\frac{P_M}{P_R}\right)}$$

(23)

where $d_M$ = steering pull distance with modified parameter, $d_R$ = steering pull distance with reference parameter, $P_M$ = modified parameter, $P_R$ = reference parameter. To observe individual parameter sensitivity on steering pull, a single parameter is changed, and its sensitivity is obtained while the other parameters are fixed to be their reference parameters. For the design parameters, caster angle, kingpin angle, camber angle, rack friction force, and ARS stiffness are considered. The variation of each factor is described in

Table 3. Variation of steering pull parameters.

Bank angle (deg)	0.5 ~ 2.5
Caster angle (deg)	2 ~ 7
Kingpin angle (deg)	5.5 ~ 20.5
Camber angle (deg)	−3.5 ~ 1.5
Rack friction force (N)	60 ~ 260
Anti-rattle spring stiffness (N/mm)	0 ~ 30

.

First of all, it is certainly expected that the steering pull distance will increases with the increase of bank angle. The sensitivity analysis results showed that the steering pull distance proportionally increases as the bank angle increases from 0.5 to 2.5 degrees, as shown in Figure 13a.

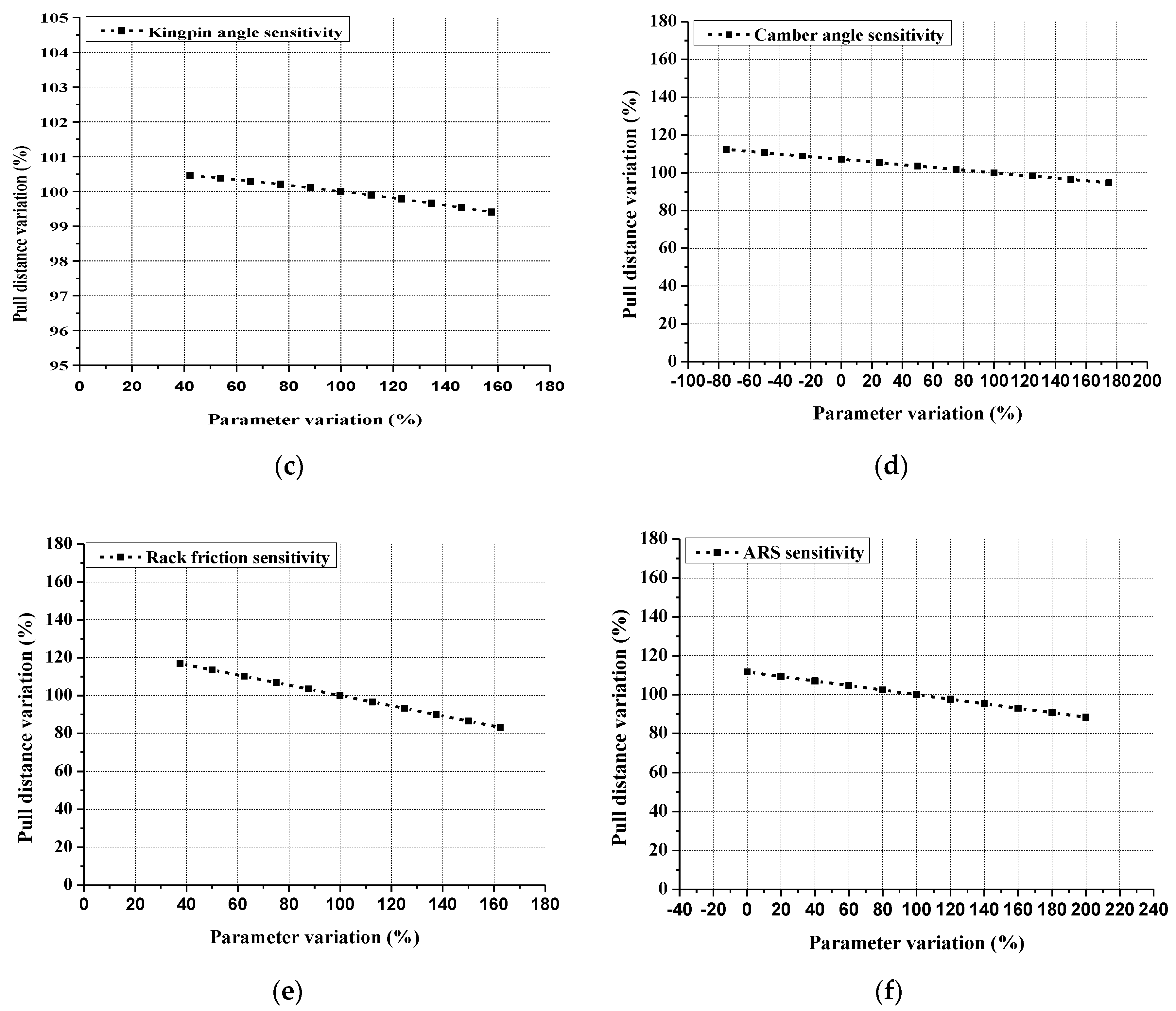
The reference value of caster angle is 4.5 degrees. The caster angle is changed from 2 to 7 degrees with 0.5 degrees increments. As shown in Figure 13b, the caster angle hardly has any influence on the steering pull. Figure 13c shows the sensitivity of the kingpin angle. The kingpin angle is changed from 5.5 to 20.5 degrees and its reference value is 12.7 degrees. As shown in Figure 13c, the steering pull distance rapidly decreases as the kingpin angle increases. The sensitivity of the kingpin is not completely linear, but its mean value is −0.01.

The camber angle, on the other hand, also has a substantial influence on the steering pull as shown in Figure 13d. Its reference value is −2.0 degrees and it is changed from −3.5 to 1.5 degrees with 0.5 degrees increments. As the tendency of kingpin angle, the steering pull distance rapidly decreases as the camber angle increases. The sensitivity of the camber angle is −0.071, which means that it also has a substantial influence on the steering pull, but it is slightly less than the kingpin angle. From the sensitivity results of the camber angle, a positive camber angle is thought to be desirable for steering pull. However, considering that modern passenger vehicles generally adopt a negative camber angle for the improvement of cornering performance [24], the camber angle setting needs to be compromised.

Among five design parameters except the bank angle, the rack friction force has the most influence on the steering pull as shown in Figure 13e. Its reference value is 160 N and it is changed from 60 to 260 N with 20 increments. The sensitivity of the rack friction force is −0.271. It has the highest sensitivity on steering pull among the design parameters and can be easily adjusted by tightening the yokenut. However, considering that a high friction force can lead to a sticky and bad steering feel, this also needs to be compromised [22].

The ARS stiffness also has a considerable influence on the steering pull. The sensitivity result is shown in Figure 13f. The reference value is 30 N/mm and it is changed from 0 to 30 N/mm with 3 N/mm increments. The sensitivity of the ARS stiffness is −0.177, which also means that the higher the ARS stiffness is, the shorter the steering pull is. In the same manner of the rack friction force, it also needs to be compromised because a high ARS stiffness causes a misalignment of the worm shaft and it leads to a sticky steering feel [20].

7. Conclusions

A complete steering pull model is developed, and the sensitivity of steering pull factors is analyzed based on the model in this study. To develop the steering pull model, an approach organized into three steps—tire pulling force model, steering system model, and the model integration—is achieved in this study. First, the factors of tire pulling forces, such as road bank angle, plysteer and conicity, kingpin and caster angles, and camber angle, are investigated and mathematically modeled. Second, a steering system that consists of lower body linkages, rack and pinion gear, universal joint, and steering column is modeled. For the steering column modeling, a C-EPS system and the friction generated in the system, which includes Coulomb and viscous friction, are also considered. Then, each model is integrated into a complete steering system model. Finally, a steering pull model is developed by integrating the tire pulling force model and the steering system model. All models are built on SIMULINK environment.

Prior to a sensitivity analysis on the steering pull, the developed steering pull model is experimentally verified. A vehicle is designated, and its driving conditions and design parameters are adopted into the model. Two profiles of the steering pull distance at 0.7 and 1.6 degrees of bank angle are estimated by the model. For an experimental verification, a steering pull measurement system using a GPS device is set up in the designated vehicle. The experimental steering pull distances by the measurement system are compared with the estimated. The estimated and the experimented show the same tendency, i.e., the steering pull distance increases with the increase of vehicle moving distance. There are slight differences between the estimated and the experimented but throughout the entire steering pull distance, the steering pull model developed in this study provided very accurate estimation results.

As the final procedure, sensitivity analysis on the steering pull is performed. First, the sensitivity of bank angle is analyzed, and then, the sensitivity of design parameters, such as caster angle, kingpin angle, camber angle, rack friction force, and ARS stiffness, are analyzed. Among the design parameters, the rack friction force has the highest sensitivity on the steering pull, and the ARS stiffness has the second highest sensitivity. On the other hand, the caster angle has the lowest sensitivity, which means that it hardly has any influence on the steering pull.

The steering pull causes an annoying steering feel to the driver in that it forces the driver to exert a constant steering torque to the steering wheel. Therefore, many automotive engineers have been trying to improve the steering pull. The steering pull model proposed in this study can be used as a basic model in designing automotive components and help the improvement of steering pull.